Miura-Ori Inspired Smooth Sheet Attachments for Zipper-Coupled Tubes

Abstract

Zipper-coupled tubes are a broadly applicable, deployable mechanism with an angular surface that can be smoothed by attaching an additional smooth sheet pattern. The existing design for the smooth sheet attachment, however, leaves small gaps that can only be covered by adding flaps that unfold separately, limiting applicability in situations requiring a seamless surface and simultaneous deployment. We provide a novel construction of the smooth sheet attachment that unfolds simultaneously with zipper-coupled tubes to cover the entire surface without requiring additional actuation and without inhibiting the tubes’ motion up to an ideal, unfolded state of stability. Furthermore, we highlight the mathematics underlying the design and motion of the new smooth sheet pattern, thereby demonstrating its rigid-foldability and compatibility with asymmetric zipper-coupled tubes.

1. Introduction

Origami is the basis for many deployable mechanisms, including self-scaling, modular robots [1], satellite reflectarray antennas that pack efficiently [2], and multimodal biomedical devices that actuate electromagnetically [3]. Zipper-coupled tubes are multistable origami structures that fold up compactly and unfold bidirectionally to fill space and resist compression [4]. An asymmetric generalization of zipper-coupled tubes with smooth sheet attachments was introduced previously [5]. Together, these origami-based mechanisms form a deployable device with a smooth surface that is advantageous in applications, such as prefab architecture, when drivability and walkability are important, and in smooth medical devices, when sharp edges could harm the body. The smooth sheet attachment we presented previously, however, does not fully cover the surface of zipper-coupled tubes without additional flaps that actuate separately [5]. We rectify this problem by offering an alternative, Miura-ori inspired [6,7,8], construction of a smooth sheet attachment that fully covers the surface of, and deploys simultaneously with, asymmetric zipper-coupled tubes.

In this paper we briefly review the design of asymmetric zipper-coupled tubes and then demonstrate how to (1) construct a Miura-ori inspired smooth sheet attachment without gaps that attaches to the mountain folds of asymmetric zipper-coupled tubes and (2) handle design variations in the symmetric case. We present a mathematically robust design method, decomposing the attachment into pairs of compatible, tessellating cells inspired by the Miura-ori pattern and then defining the cells’ vertices throughout the folding motion, thereby confirming rigid-foldability of the smooth sheet attachment and highlighting the mathematical processes involved in mechanism design. Our Miura-ori-based smooth sheet attachment expands the utility of asymmetric zipper-coupled tubes; combined, these origami-inspired mechanisms are ideal for applications requiring a rigidly deployable structure with a smooth surface.

2. Zipper-Coupled Tubes Review

Zipper-coupled tubes are an origami pattern consisting of two or more deployable tubes coupled together in a zipper fashion that makes their motion compatible. Designed by Filipov et al., this structure is remarkable for its ability to deploy from a flat, stowable form into a stable, space-filling structure with only one degree of freedom [4]. In this section we review briefly the construction of asymmetric zipper-coupled tubes from two tube segments that are each, in turn, composed of two degree-four vertex cells; the interested reader may refer to our previous work for a thorough treatment of the construction [5].

Throughout this paper we use the notational convention that an arbitrary vector $\mathbf{x}$ has unit length direction vector $\widehat{\mathbf{x}}$ with length x, and hence

$$\mathbf{x}=x\widehat{\mathbf{x}}$$

Thus, the notation $\widehat{\mathbf{x}}$ always represents a unit length vector associated with a vector denoted $\mathbf{x}$, where $\mathbf{x}=x\widehat{\mathbf{x}}$.

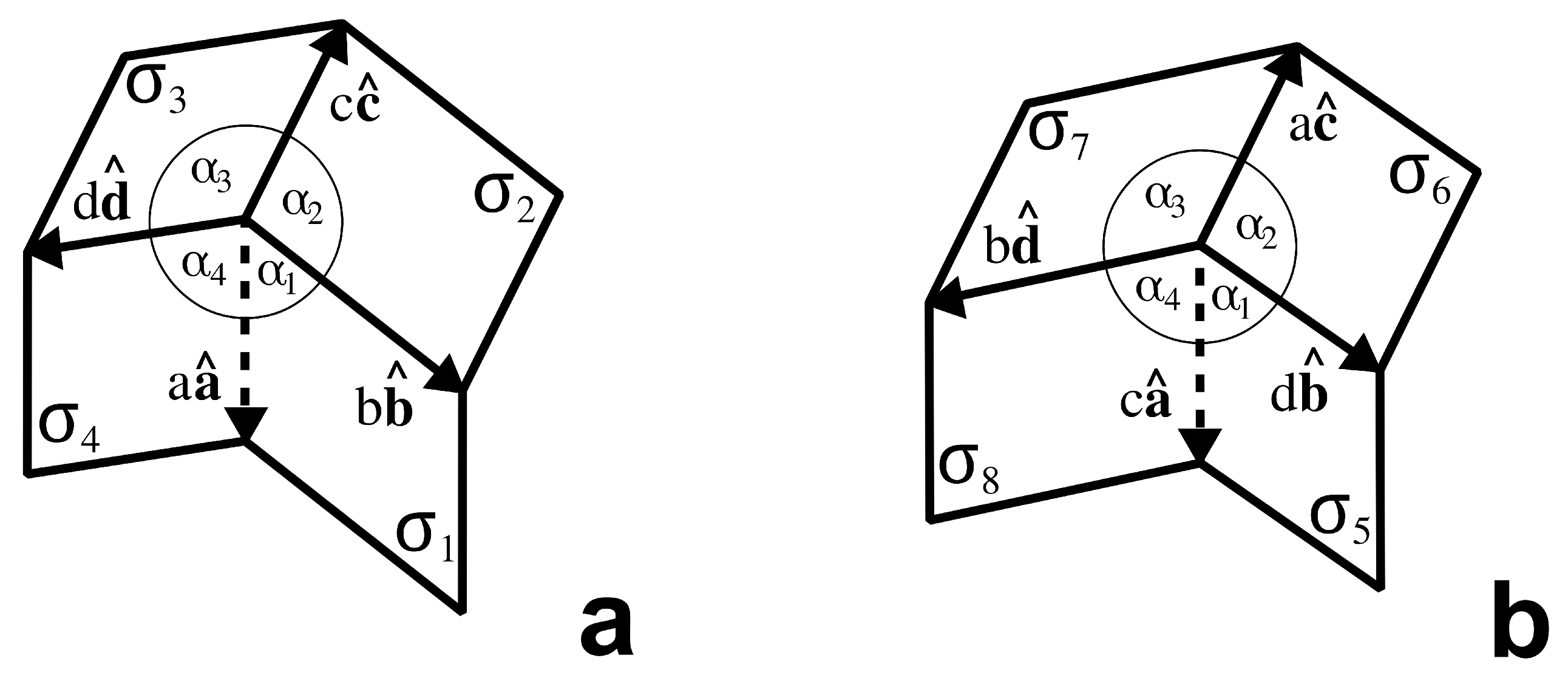
The building blocks for zipper-coupled tubes are the compatible degree-four vertex cells ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$ illustrated in Figure 1 and Figure 2. When combined, they form a single tube segment [5]. To couple correctly and satisfy rigid and flat-foldability [9], the design constraints of these degree-four vertex cells include:

$$\begin{array}{ccccc}\hfill {\alpha }_3=\pi -{\alpha }_1& \hfill & \hfill {\alpha }_1+{\alpha }_3={\alpha }_2+{\alpha }_4& \hfill & \hfill {\alpha }_1<{\alpha }_2\\ \hfill {\alpha }_4=\pi -{\alpha }_2& \hfill & \hfill dsin{a}_4=bsin{a}_1& \hfill & \hfill {\alpha }_1+{\alpha }_2\le \pi \end{array}$$

If ${\alpha }_1+{\alpha }_2<\pi$, the zipper-coupled tubes are called asymmetric, having a characteristic tilt and a customizable unfolding motion. In the special case that ${\alpha }_1+{\alpha }_2=\pi$ and $c=a$, the two cells in Figure 1 are congruent, symmetric Miura-ori cells and the resulting zipper-coupled tubes are those constructed by Filipov et al. [4].

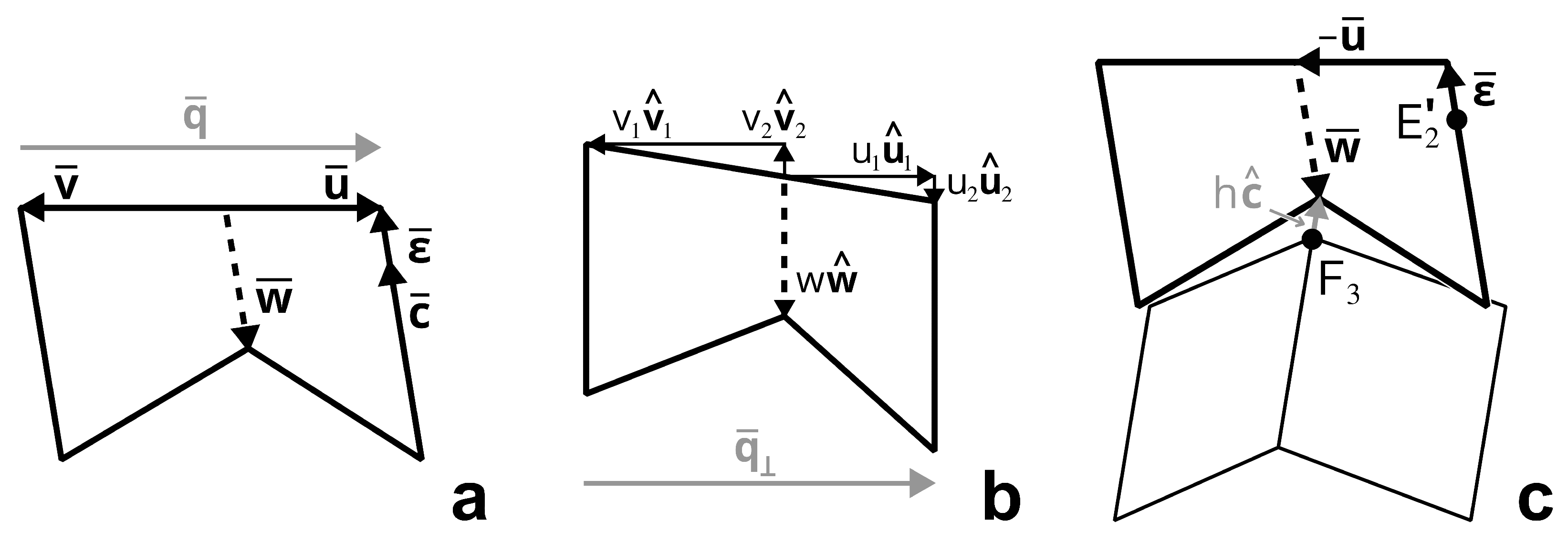
Like a Miura-ori cell, the basic degree-four vertex cell has one degree of freedom in its motion. Let the basic and complementary cells lie flat in the $xz$-plane when unfolded, as depicted in Figure 1 and Figure 2, and let the angles between the $xz$-plane and panels ${\sigma }_1$ and ${\sigma }_4$, respectively, be equal as ${\sigma }_1$ and ${\sigma }_4$ fold toward each other (see Figure 1a). Call this motion parameter $\gamma$. Then, placing $F_0$ at the origin and fixing $F_1$ on the negative z-axis in ${\mathbb{R}}^3$ (see Figure 2a), the motion of the basic cell is determined by the following vector paths:

$$\begin{array}{cc}\hfill & \widehat{\mathbf{a}}\left(\gamma \right)={\left[0,0,-1\right]}^T\hfill \\ & \widehat{\mathbf{b}}\left(\gamma \right)={\left[-sin{\alpha }_{1}cos\gamma ,sin{\alpha }_{1}sin\gamma ,-cos{\alpha }_1\right]}^T\hfill \\ & \widehat{\mathbf{c}}\left(\gamma \right)={\left[\frac{a_x{c}_3+b_x}{kcos\gamma },\frac{a_y{c}_3+b_y}{ksin\gamma },-\frac{a_x{b}_x{sin}^2\gamma +a_y{b}_y{cos}^2\gamma +k^2{sin}^2\gamma {cos}^2\gamma }{a_x^2{sin}^2\gamma +a_y^2{cos}^2\gamma +k^2{sin}^2\gamma {cos}^2\gamma }\right]}^T\hfill \\ & \widehat{\mathbf{d}}\left(\gamma \right)={\left[sin{\alpha }_{4}cos\gamma ,sin{\alpha }_{4}sin\gamma ,-cos{\alpha }_4\right]}^T\hfill \end{array}$$

where

$$\begin{array}{cccc}\hfill & a_x=sin{\alpha }_{1}cos{\alpha }_4-sin{\alpha }_{4}cos{\alpha }_1\hfill & \hfill & b_x=sin{\alpha }_{1}cos{\alpha }_3-sin{\alpha }_{4}cos{\alpha }_2\hfill \\ & a_y=sin{\alpha }_{1}cos{\alpha }_4+sin{\alpha }_{4}cos{\alpha }_1\hfill & \hfill & b_y=sin{\alpha }_{1}cos{\alpha }_3+sin{\alpha }_{4}cos{\alpha }_2\hfill \\ \hfill & k=2sin{\alpha }_{1}sin{\alpha }_4\hfill & \hfill & \widehat{\mathbf{c}}=\langle c_1,c_2,c_3\rangle \hfill \end{array}$$

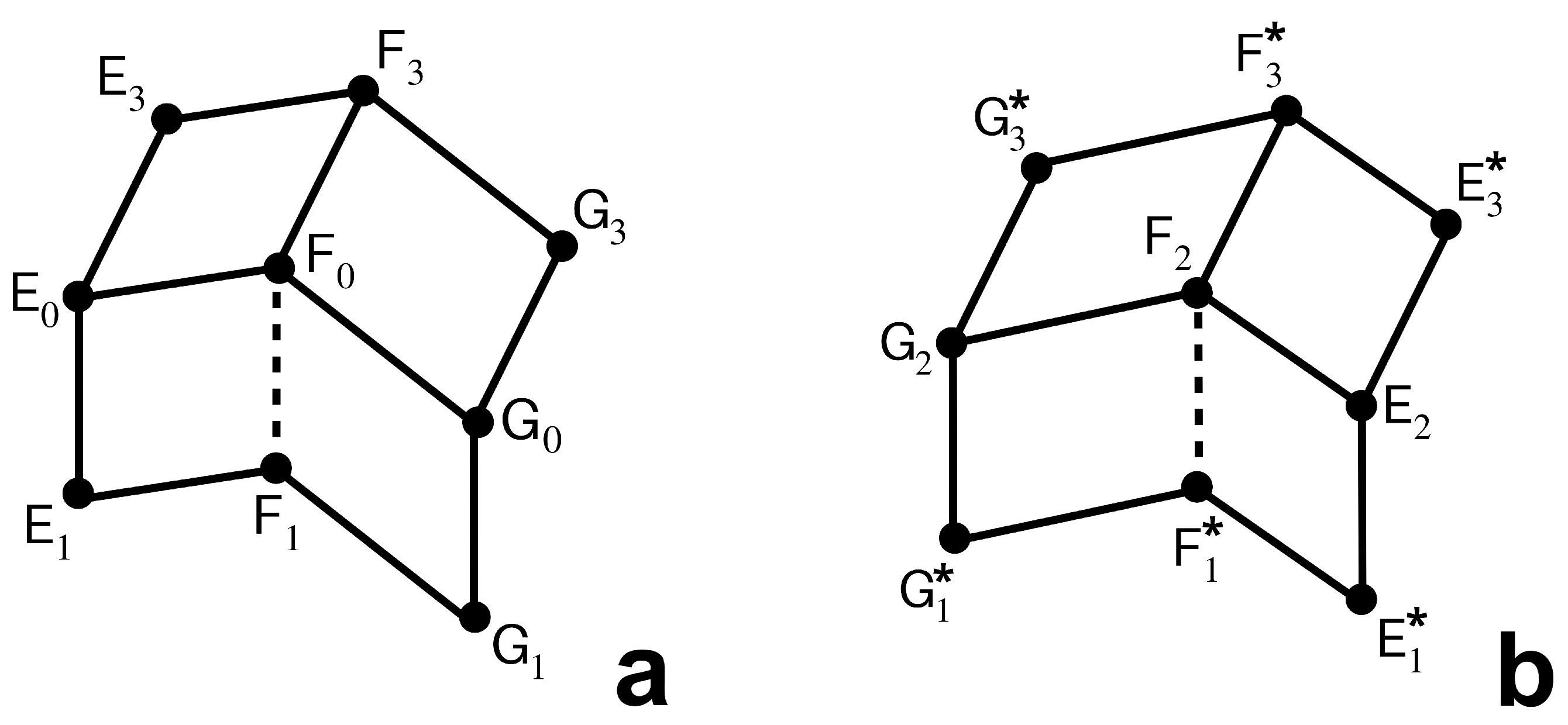
The same vectors define the motion of both basic and complementary cells. By combining one basic cell (${\mathcal{C}}_1$) and one complementary cell (${\mathcal{C}}_2$), we obtain the first tube segment in a zipper-coupled pair, illustrated in Figure 3a. Its vertices, identified with their corresponding position vectors, are given by:

$$\begin{array}{cccccc}\hfill & E_0\left(\gamma \right)=\mathbf{d}\left(\gamma \right)\hfill & \hfill & F_0\left(\gamma \right)=\mathbf{0}\hfill & \hfill & G_0\left(\gamma \right)=\mathbf{b}\left(\gamma \right)\hfill \\ \hfill & E_1\left(\gamma \right)=\mathbf{a}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)\hfill & \hfill & F_1\left(\gamma \right)=\mathbf{a}\left(\gamma \right)\hfill & \hfill & G_1\left(\gamma \right)=\mathbf{a}\left(\gamma \right)+\mathbf{b}\left(\gamma \right)\hfill \\ \hfill & E_2\left(\gamma \right)=\mathbf{a}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)\hfill & \hfill & F_2\left(\gamma \right)=\mathbf{a}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)\hfill & \hfill & G_2\left(\gamma \right)=\mathbf{a}\left(\gamma \right)+\mathbf{b}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)\hfill \\ \hfill & E_3\left(\gamma \right)=\mathbf{c}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)\hfill & \hfill & F_3\left(\gamma \right)=\mathbf{c}\left(\gamma \right)\hfill & \hfill & G_3\left(\gamma \right)=\mathbf{b}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)\hfill \end{array}$$

The second tube segment is a copy of the first, but rotated ${180}^{\circ }$ about the y-axis and then shifted by an offset vector so that it attaches to the first tube segment along the vertical creases (illustrated in Figure 3b). Let ${\mathcal{C}}_3$ and ${\mathcal{C}}_4$ denote the copies of ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$, respectively, comprising the second tube segment. To define the motion of the second tube segment, let $\overline{\mathbf{x}}$ denote the ${180}^{\circ }$ rotation of a vector $\mathbf{x}$ about the y-axis and define the offset vector:

$$\mathbf{s}\left(\gamma \right)=\left(1+\frac{bcos{\alpha }_1+dcos{\alpha }_4}{2a}\right)\mathbf{a}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)$$

Then the vertices of the second tube segment are defined by:

$$\begin{array}{cccccc}\hfill & E_0^{\prime }\left(\gamma \right)=\overline{\mathbf{d}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)\hfill & \hfill & F_0^{\prime }\left(\gamma \right)=\mathbf{s}\left(\gamma \right)\hfill & \hfill & G_0^{\prime }\left(\gamma \right)=\overline{\mathbf{b}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)\hfill \\ \hfill & E_1^{\prime }\left(\gamma \right)=\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)\hfill & \hfill & F_1^{\prime }\left(\gamma \right)=\overline{\mathbf{a}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)\hfill & \hfill & G_1^{\prime }\left(\gamma \right)=\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{b}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)\hfill \\ \hfill & E_2^{\prime }\left(\gamma \right)=\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)\hfill & \hfill & F_2^{\prime }\left(\gamma \right)=\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)\hfill & \hfill & G_2^{\prime }\left(\gamma \right)=\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{b}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)\hfill \\ \hfill & E_3^{\prime }\left(\gamma \right)=\overline{\mathbf{c}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)\hfill & \hfill & F_3^{\prime }\left(\gamma \right)=\overline{\mathbf{c}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)\hfill & \hfill & G_3^{\prime }\left(\gamma \right)=\overline{\mathbf{b}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)\hfill \end{array}$$

The pair of tube segments, with vertices positioned as indicated above, form a single component in a pair of zipper-coupled tubes (Figure 3b), which will be denoted as ${\mathcal{Z}}_0$. The zipper-coupled tubes can be extended by taking multiple copies of ${\mathcal{Z}}_0$ and attaching them end-to-end. In particular, for $i=1\dots n$, let

$${\mathcal{Z}}_i={\mathcal{Z}}_0+i(\mathbf{d}-\mathbf{b})$$

Then

$$\mathcal{Z}=\bigcup _{i=0}^n{\mathcal{Z}}_i$$

denotes zipper-coupled tubes with $n+1$ components.

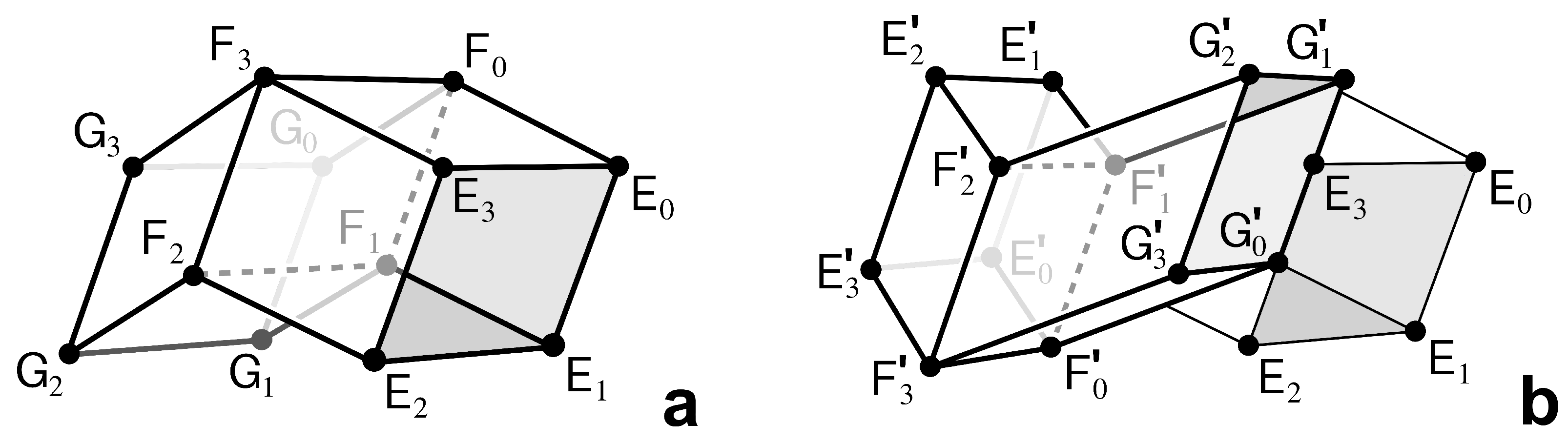
Of critical importance, at a certain point in the motion of $\mathcal{Z}$, the upper (or lower) creases simultaneously become coplanar, as bolded in Figure 4b. This state is the ideal state, and it occurs at a parameter value:

$$\begin{array}{c}\hfill {\gamma }_0={cos}^{-1}\left(\sqrt{\frac{a_y{b}_y-a_x^2+k^2+\sqrt{{\left(a_y{b}_y+a_x^2+k^2\right)}^2-4a_y^2{a}_x{b}_x}}{2k^2}}\right)\end{array}$$

The value ${\gamma }_0$ will be the terminal value for the deployment of $\mathcal{Z}$ with a smooth sheet attachment. Thus, by construction, the smooth sheet attachment lies flat on the surface of the zipper-coupled tubes when $\gamma ={\gamma }_0$ and folds up with the zipper-coupled tubes until $\gamma =\pi /2$, at which point the entire structure lies in a plane and has no volume.

3. Asymmetric Smooth Sheet Attachment

In this section we design a Miura-ori inspired smooth sheet attachment that actuates simultaneously with the asymmetric zipper-coupled tubes pattern, folding up flat and unfolding into a rigid sheet without gaps in the ideal state. This additional pattern broadens the potential applications of the zipper-coupled tubes structure and expands on the design of the attachment described previously [5]. As with the zipper-coupled tubes, we decomposed the overall structure into its basic units: four distinct smooth sheet cells that tesselate. We define the vectors used to construct each cell to describe the motion of the cell’s vertices and confirm its compatibility with the zipper-coupled tubes structure.

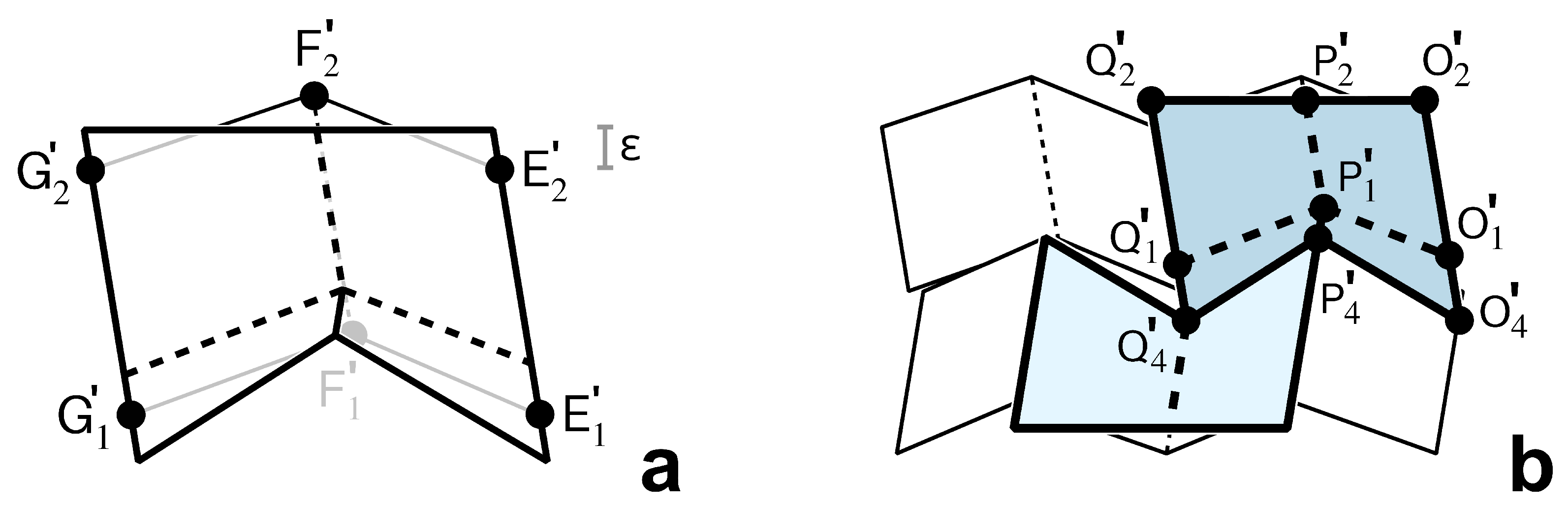
The seamless smooth sheet attachment consists of four distinct cells denoted ${\mathcal{S}}_i$, for $i=1,2,3,4$. In Figure 4a, the lightly shaded cell is ${\mathcal{S}}_1$ and the darkly shaded cell is ${\mathcal{S}}_4$, while in Figure 4c, the lightly shaded cell is half of ${\mathcal{S}}_3$ and the darkly shaded cell is ${\mathcal{S}}_2$. Cells ${\mathcal{S}}_1$ and ${\mathcal{S}}_3$ share the same configuration, but like the zipper-coupled tube segments, one is rotated ${180}^{\circ }$ about the y-axis; the same is true of ${\mathcal{S}}_2$ and ${\mathcal{S}}_4$. The manner in which the smooth sheet cells attach to $\mathcal{Z}$ in the ideal state ($\gamma ={\gamma }_0$) is highlighted in Figure 4b. When the mechanism is fully deployed, cells on the top sheet meet along their jagged edges, as seen in Figure 4a. The cells on the bottom sheet, however, meet along their straight edges, as seen in Figure 4c—this is a key feature in defining a design that will cover zipper-coupled tubes without gaps and deploy without restricting the tubes’ motion up to the ideal state.

Regarding the single component ${\mathcal{Z}}_0$, the cell ${\mathcal{S}}_i$ attaches to ${\mathcal{C}}_i$. However, whereas the cells ${\mathcal{S}}_2$ and ${\mathcal{S}}_4$ form a bridge between a pair of creases in ${\mathcal{Z}}_0$, the cells ${\mathcal{S}}_1$ and ${\mathcal{S}}_3$ form a bridge between a crease of ${\mathcal{Z}}_0$ and a crease of ${\mathcal{Z}}_1$ (bolded in Figure 4b). Upon careful examination of the zipper-coupled tubes, we observed that ${\mathcal{S}}_1$ can be designed as though it bridged two creases of ${\mathcal{C}}_4$ and then moved to bridge creases of the copies of ${\mathcal{C}}_1$ in ${\mathcal{Z}}_0$ and ${\mathcal{Z}}_1$; this strategy eliminates some complexity in defining ${\mathcal{S}}_1$. In contrast, ${\mathcal{S}}_4$ is designed directly, transversing the two creases of ${\mathcal{C}}_4$ where it attaches. Designing both cells atop ${\mathcal{C}}_4$ allows us to re-use the same vectors and enables the interested reader to easily compare the Miura-ori inspired cells and the original smooth sheet cells with gaps [5].

3.1. Design of ${\mathcal{S}}_1$

The first smooth sheet cell, ${\mathcal{S}}_1$, has two panels that fold toward each other as the zipper-coupled tubes fold up. We first discuss the design of ${\mathcal{S}}_1$ when built atop ${\mathcal{C}}_4$—the desired relation between ${\mathcal{S}}_1$ and ${\mathcal{C}}_4$ is shown in Figure 5a. The vectors that define ${\mathcal{S}}_1$ in this temporary configuration will be re-used to define ${\mathcal{S}}_4$, allowing the edges of these two cells to mesh when placed opposite each other. After construction, the smooth sheet cell ${\mathcal{S}}_1$ will be moved to attach to ${\mathcal{C}}_1$, as seen in Figure 5b.

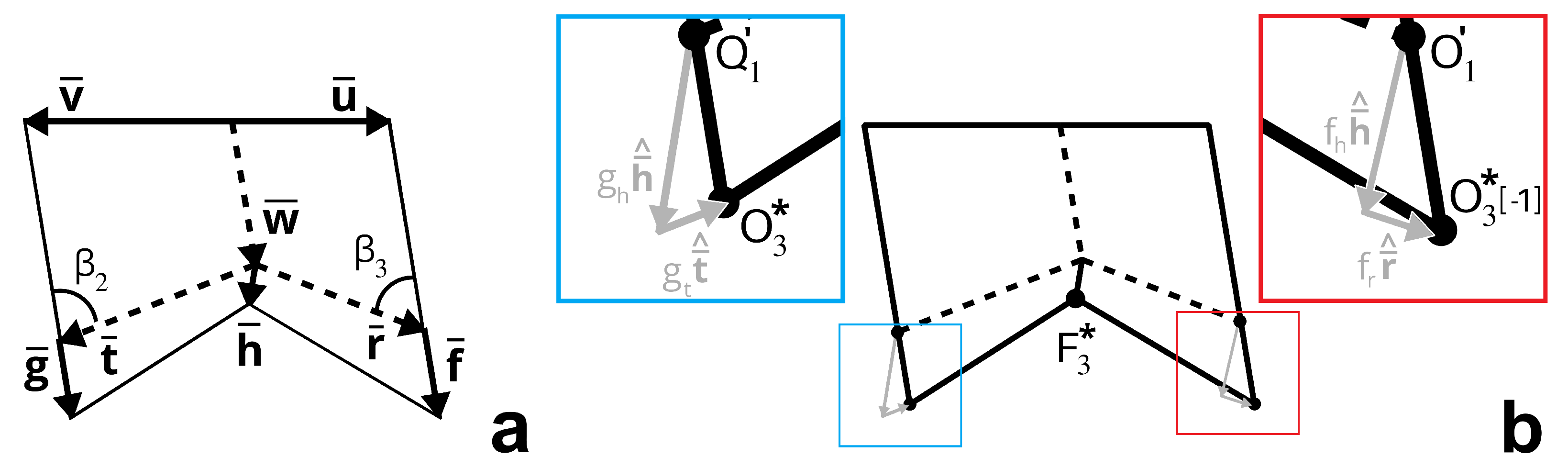
In preparation of the design of ${\mathcal{S}}_1$, let the displacement between $G_2^{\prime }\left(\gamma \right)$ and $E_2^{\prime }\left(\gamma \right)$ be described by

$$\overline{\mathbf{q}}\left(\gamma \right)=\overline{\mathbf{d}}\left(\gamma \right)-\overline{\mathbf{b}}\left(\gamma \right)$$

and

$${\overline{\mathbf{q}}}_{\perp }\left(\gamma \right)=\overline{\mathbf{q}}\left(\gamma \right)-\left(\overline{\mathbf{q}}\left(\gamma \right)·\widehat{\overline{\mathbf{c}}}\left(\gamma \right)\right)\widehat{\overline{\mathbf{c}}}\left(\gamma \right)$$

As depicted in Figure 6a,b, ${\overline{\mathbf{q}}}_{\perp }\left(\gamma \right)$ is the component vector of $\overline{\mathbf{q}}\left(\gamma \right)$ orthogonal to $\overline{\mathbf{c}}\left(\gamma \right)$, the displacement between $E_1^{\prime }\left(\gamma \right)$ and $E_2^{\prime }\left(\gamma \right)$ (or equivalently, the displacement between $G_1^{\prime }\left(\gamma \right)$ and $G_2^{\prime }\left(\gamma \right)$). In the ideal state of the zipper-coupled tubes, the distance between the ridges of $\mathcal{Z}$ on which the smooth sheet will be attached is

$$\Delta =\parallel {\overline{\mathbf{q}}}_{\perp }\left({\gamma }_0\right)\parallel$$

Note that, of necessity and by design, the top edges of both ${\mathcal{S}}_1$ and ${\mathcal{S}}_4$ are parallel with $\overline{\mathbf{q}}\left({\gamma }_0\right)$. To remove gaps between zipper-coupled tubes stacked laterally to ${\mathcal{Z}}_0$ and in anticipation of the behavior depicted in Figure 4c, we extended the side edges of ${\mathcal{S}}_1$ in the direction of $\overline{\mathbf{c}}$ by the length $\epsilon$, as shown in Figure 5a and Figure 6a, where

$$\epsilon =\frac{bsin{\alpha }_{1}sin{\gamma }_0}{2|c_2\left({\gamma }_0\right)|}$$

Toward this end, let

$$\overline{\mathbf{\epsilon }}\left(\gamma \right)=\epsilon \widehat{\overline{\mathbf{c}}}$$

The smooth sheet cell is determined by the vectors $\overline{\mathbf{u}}$, $\overline{\mathbf{v}}$, and $\overline{\mathbf{w}}$ illustrated in Figure 6a. As highlighted in Figure 6b, let

$$\begin{array}{cc}\hfill u_1& =\frac{dsin{\alpha }_1-bsin{\alpha }_4+\Delta }{2}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill v_1& =\frac{bsin{\alpha }_4-dsin{\alpha }_1+\Delta }{2}\hfill \end{array}$$

(2)

Note that $\Delta =u_1+v_1$. Examining the components of $\overline{\mathbf{u}}$ and $\overline{\mathbf{v}}$ in the ideal state, as shown in Figure 6a,b, we see that $u_2+v_2=\left|\right|\overline{\mathbf{q}}\left({\gamma }_0\right)-{\overline{\mathbf{q}}}_{\perp }\left({\gamma }_0\right)\left|\right|$. Since

$$\frac{u_2}{u_2+v_2}=\frac{u_1}{u_1+v_1}=\frac{u_1}{\Delta }\mathrm{and}\frac{v_2}{v_1}=\frac{u_2}{u_1}$$

it follows that

$$\begin{array}{cc}\hfill u_2& =\frac{u_1}{\Delta }\left|\right|\overline{\mathbf{q}}\left({\gamma }_0\right)-{\overline{\mathbf{q}}}_{\perp }\left({\gamma }_0\right)\left|\right|\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill v_2& =v_1\frac{u_2}{u_1}\hfill \end{array}$$

(4)

Rodrigues’ rotation formula [10] rotates a vector $\mathbf{x}$ by angle $\theta$ in a counter-clockwise direction about a unit vector $\mathbf{k}$, and is given by:

$$R[\mathbf{k},\theta ]\left(\mathbf{x}\right)=\mathbf{x}cos\theta +(\mathbf{k}\times \mathbf{x})sin\theta +\mathbf{k}\langle \mathbf{k},\mathbf{x}\rangle (1-cos\theta )$$

Let

$$\begin{array}{cc}\hfill {\widehat{\mathbf{u}}}_1\left(\gamma \right)& =R\left[-\widehat{\overline{\mathbf{c}}}\left(\gamma \right),\lambda \left(\gamma \right)\right]\left({\widehat{\overline{\mathbf{q}}}}_{\perp }\left(\gamma \right)\right)\hfill \\ \hfill {\widehat{\mathbf{u}}}_2\left(\gamma \right)& =-\widehat{\overline{\mathbf{c}}}\left(\gamma \right)\hfill \end{array}$$

where

$$\begin{array}{c}\hfill \lambda \left(\gamma \right)={cos}^{-1}\left(\frac{\parallel {\overline{\mathbf{q}}}_{\perp }{\left(\gamma \right)\parallel }^2+u_1^2-v_1^2}{2\parallel {\overline{\mathbf{q}}}_{\perp }\left(\gamma \right)\parallel u_1}\right)\end{array}$$

Then we define $\overline{\mathbf{u}}\left(\gamma \right)$ and $\overline{\mathbf{v}}\left(\gamma \right)$ as

$$\begin{array}{cc}\hfill \overline{\mathbf{u}}\left(\gamma \right)& =u_1{\widehat{\mathbf{u}}}_1\left(\gamma \right)+u_2{\widehat{\mathbf{u}}}_2\left(\gamma \right)\hfill \\ \hfill \overline{\mathbf{v}}\left(\gamma \right)& =\overline{\mathbf{u}}\left(\gamma \right)-\overline{\mathbf{q}}\left(\gamma \right)\hfill \end{array}$$

In order to satisfy flat-foldability, the direction of the vector $\overline{\mathbf{w}}$ must be the same as the direction of $-\overline{\mathbf{c}}$. Thus, for some positive constant w:

$$\overline{\mathbf{w}}\left(\gamma \right)=-w\widehat{\overline{\mathbf{c}}}\left(\gamma \right)$$

The primary concern in choosing the length w was to avoid intersections with the zipper-coupled tubes during deployment. So that the smooth sheet cells ${\mathcal{S}}_1$ and ${\mathcal{S}}_4$ lined up correctly, we defined w and h to be the lengths necessary so that in the ideal state, the tips of the vectors $\overline{\mathbf{w}}$ ($-w\widehat{\overline{\mathbf{c}}}$) and $h\widehat{\mathbf{c}}$ meet, as shown in Figure 6c. In particular, we set

$$\begin{array}{c}\hfill h\widehat{\mathbf{c}}\left({\gamma }_0\right)+F_3\left({\gamma }_0\right)=-w\widehat{\overline{\mathbf{c}}}\left({\gamma }_0\right)+\left(E_2^{\prime }\left({\gamma }_0\right)+\overline{\mathbf{\epsilon }}\left({\gamma }_0\right)-\overline{\mathbf{u}}\left({\gamma }_0\right)\right)\end{array}$$

Then, w (and h) can be obtained as follows:

$$\begin{array}{c}\hfill {\left[h,w\right]}^T={\left[\mathrm{proj}\left(\widehat{\mathbf{c}}\left({\gamma }_0\right)\right),\mathrm{proj}\left(\widehat{\overline{\mathbf{c}}}\left({\gamma }_0\right)\right)\right]}^{-1}\mathrm{proj}\left(\overline{\mathbf{a}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}+\mathbf{s}+\overline{\mathbf{\epsilon }}-\overline{\mathbf{u}}-\mathbf{c}\right)\left({\gamma }_0\right)\end{array}$$

(5)

where the function $\mathrm{proj}:{\mathbb{R}}^3\to {\mathbb{R}}^2$ is defined such that

$$\mathrm{proj}{[x,y,z]}^T={[x,y]}^T$$

Remark 1.

Note that the matrix that is inverted in Equation (5) will be singular only in the symmetric case when $\overline{\mathbf{c}}$ has the same direction as $-\mathbf{c}$.

We have now stipulated all three vectors—$\overline{\mathbf{u}}$, $\overline{\mathbf{v}}$, and $\overline{\mathbf{w}}$—which define ${\mathcal{S}}_1$ when it is attached to ${\mathcal{C}}_4$. What remains is to move ${\mathcal{S}}_1$ so that it attaches to ${\mathcal{C}}_1$. The desired placement is depicted in Figure 5b, where ${\mathcal{S}}_1$ is positioned on top of ${\mathcal{C}}_1$ and bridges ${\mathcal{Z}}_0$ and ${\mathcal{Z}}_1$; note that the zipper-coupled tubes have been rotated about the y-axis in this figure so that ${\mathcal{S}}_1$ lies parallel with the $xy$-plane (see [5] for further details). Let $X\left[i\right]$ denote the point in ${\mathcal{Z}}_i$ that is a copy of X in ${\mathcal{Z}}_0$, for $i\ge 1$. Then, the vertex ${F_3}^{*}$ in ${\mathcal{S}}_1$ attaches to $F_3$ in ${\mathcal{Z}}_0$ and the vertex ${F_3}^{*}\left[1\right]$ in ${\mathcal{S}}_1$ attaches to $F_3\left[1\right]$ in ${\mathcal{Z}}_1$. More particularly, the edge $\overline{P_0{F}_3^{*}}$ attaches to $\overline{F_0{F}_3}$ and $\overline{P_0\left[1\right]F_3^{*}\left[1\right]}$ attaches to $\overline{F_0\left[1\right]F_3\left[1\right]}$.

Recall that the ${180}^{\circ }$ rotation of a vector $\overline{\mathbf{x}}$ about the y-axis is denoted $\mathbf{x}$. Thus, the vertices in ${\mathcal{S}}_1$ when attached to ${\mathcal{C}}_1$ as desired are:

$$\begin{array}{cccccc}\hfill & F_3\left(\gamma \right)=\mathbf{c}\left(\gamma \right)\hfill & \hfill & O_0\left(\gamma \right)=-\mathbf{\epsilon }\left(\gamma \right)+\mathbf{u}\left(\gamma \right)\hfill & \hfill & F_3\left[1\right]\left(\gamma \right)=\mathbf{c}\left(\gamma \right)-\mathbf{b}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)\hfill \\ \hfill & P_0\left(\gamma \right)=-\mathbf{\epsilon }\left(\gamma \right)\hfill & \hfill & O_3\left(\gamma \right)=-\mathbf{\epsilon }\left(\gamma \right)+\mathbf{u}\left(\gamma \right)-\mathbf{w}\left(\gamma \right)\hfill & \hfill & P_0\left[1\right]\left(\gamma \right)=-\mathbf{\epsilon }\left(\gamma \right)-\mathbf{b}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)\hfill \end{array}$$

3.2. Design of ${\mathcal{S}}_3$

The cell ${\mathcal{S}}_3$ is a rotated copy of ${\mathcal{S}}_1$ attached to ${\mathcal{C}}_3$, so the vectors that define ${\mathcal{S}}_3$ are rotated copies of the vectors that define ${\mathcal{S}}_1$, shifted by $\mathbf{s}$. Let the vertices on smooth sheet cells attached to the rotated tube segment in ${\mathcal{Z}}_0$—i.e., the vertices in ${\mathcal{S}}_2$ and ${\mathcal{S}}_3$—be denoted with primes. Note that the smooth sheet cell ${\mathcal{S}}_3$ bridges ${\mathcal{Z}}_0$ and ${\mathcal{Z}}_{-1}$, so the smooth sheet cell contains the vertices $F_3^{\prime }$ and $F_3^{\prime }[-1]$. Thus, the vertices of ${\mathcal{S}}_3$ when attached to ${\mathcal{C}}_3$ are:

$$\begin{array}{cccccc}\hfill & F_3^{\prime }\left(\gamma \right)=\overline{\mathbf{c}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)\hfill & \hfill & O_0^{\prime }\left(\gamma \right)=\mathbf{s}\left(\gamma \right)-\overline{\mathbf{\epsilon }}\left(\gamma \right)+\overline{\mathbf{u}}\left(\gamma \right)\hfill & \hfill & F_3^{\prime }[-1]\left(\gamma \right)=\overline{\mathbf{c}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)-\overline{\mathbf{b}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)\hfill \\ \hfill & P_0^{\prime }\left(\gamma \right)=\mathbf{s}\left(\gamma \right)-\overline{\mathbf{\epsilon }}\left(\gamma \right)\hfill & \hfill & O_3^{\prime }\left(\gamma \right)=\mathbf{s}\left(\gamma \right)-\overline{\mathbf{\epsilon }}\left(\gamma \right)+\overline{\mathbf{u}}\left(\gamma \right)-\overline{\mathbf{w}}\left(\gamma \right)\hfill & \hfill & P_0^{\prime }[-1]\left(\gamma \right)=\mathbf{s}\left(\gamma \right)-\overline{\mathbf{\epsilon }}\left(\gamma \right)-\overline{\mathbf{b}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)\hfill \end{array}$$

3.3. Design of ${\mathcal{S}}_4$

The smooth sheet cell ${\mathcal{S}}_4$ attaches on top of ${\mathcal{C}}_4$ and fits together with ${\mathcal{S}}_1$ in the ideal state, as illustrated in Figure 7. We make the edge of ${\mathcal{S}}_4$ opposite of ${\mathcal{S}}_1$ straight in the ideal state so that zipper-coupled tubes with smooth sheet attachments can be stacked laterally without gaps. From another point of view, the edge is made straight in preparation of the design of ${\mathcal{S}}_2$, a copy of ${\mathcal{S}}_4$ attached to the bottom of ${\mathcal{Z}}_0$—the straight edges of ${\mathcal{S}}_2$ and ${\mathcal{S}}_3$ meet in the ideal state, as illustrated in Figure 4c.

The smooth sheet cell ${\mathcal{S}}_4$ has a degree-four vertex folding pattern inspired by the Miura-ori cell, as shown in Figure 8a. This allows the cell to close the gap on the top of ${\mathcal{Z}}_0$ in the ideal state and fold up without intersecting the adjacent tube segment. For flat-foldability of the cell, we require the sum of opposite angles at the interior vertex to be ${180}^{\circ }$ (see Kawasaki-Justin theorem [11,12]). The pattern in Figure 8a is described by the previously defined vectors $\overline{\mathbf{u}}$, $\overline{\mathbf{v}}$, and $\overline{\mathbf{w}}$ and the yet-to-be-defined vectors $\overline{\mathbf{r}}$, $\overline{\mathbf{t}}$, $\overline{\mathbf{h}}$, $\overline{\mathbf{f}}$, and $\overline{\mathbf{g}}$.

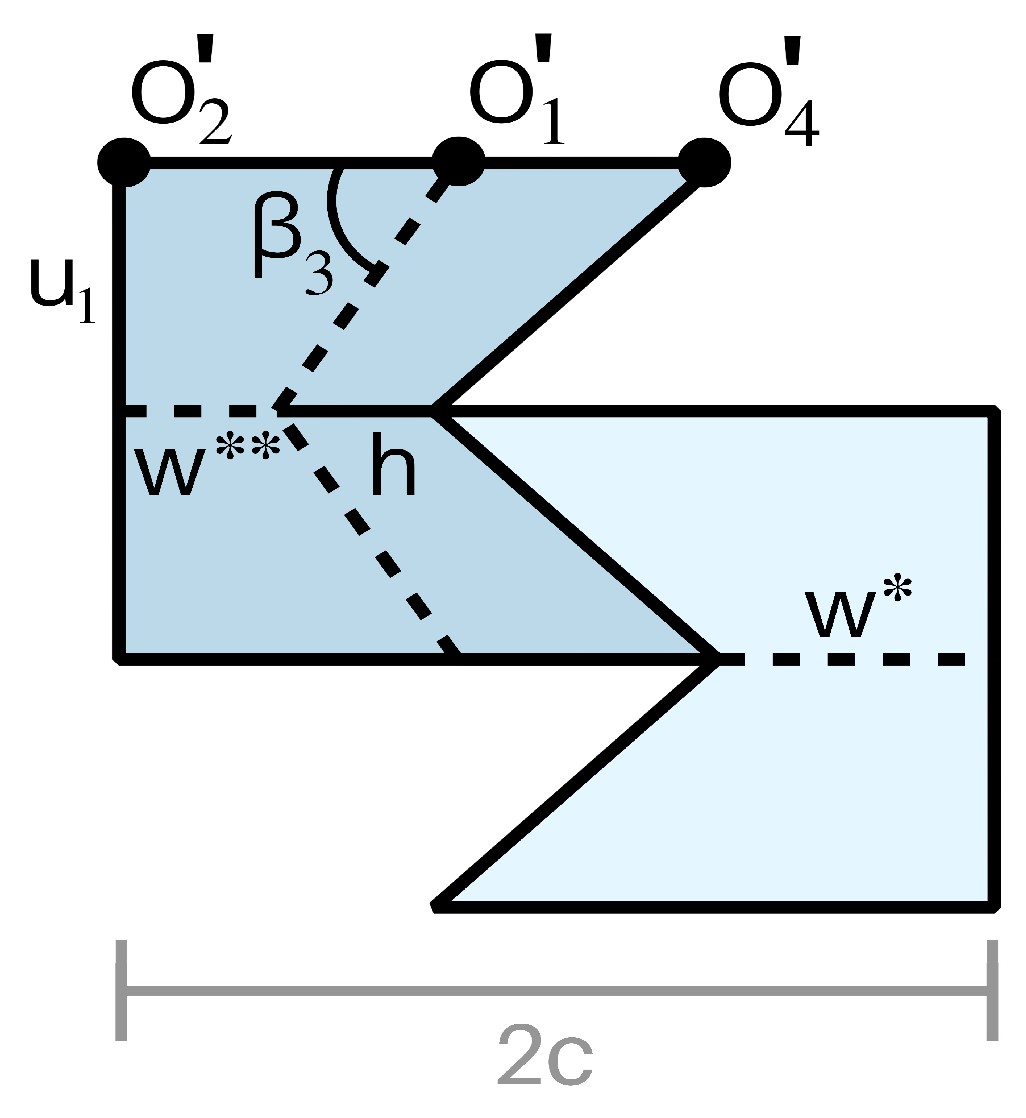
In the ideal state, $\overline{\mathbf{r}}$ and $\overline{\mathbf{t}}$ are the projections of $\mathbf{b}$ and $\mathbf{d}$, respectively, into the xy-plane; this is necessary to ensure flat foldability. Thus (see Figure 3 and Figure 8a),

$${\beta }_2=\angle P_1^{\prime }{Q}_1^{\prime }{Q}_2^{\prime }=\angle F_3{G}_1^{\prime }{G}_2^{\prime }\mathrm{and}{\beta }_3=\angle P_1^{\prime }{O}_1^{\prime }{O}_2^{\prime }=\angle F_3{E}_1^{\prime }{E}_2^{\prime }$$

In particular,

$$\begin{array}{cc}\hfill {\beta }_2& ={cos}^{-1}\left(-\widehat{\overline{\mathbf{c}}}\left({\gamma }_0\right)·\frac{\mathbf{d}\left({\gamma }_0\right)-s_0\mathbf{a}\left({\gamma }_0\right)}{\parallel \mathbf{d}\left({\gamma }_0\right)-s_0\mathbf{a}\left({\gamma }_0\right)\parallel }\right)\hfill \\ \hfill {\beta }_3& ={cos}^{-1}\left(-\widehat{\overline{\mathbf{c}}}\left({\gamma }_0\right)·\frac{\mathbf{b}\left({\gamma }_0\right)-s_0\mathbf{a}\left({\gamma }_0\right)}{\parallel \mathbf{b}\left({\gamma }_0\right)-s_0\mathbf{a}\left({\gamma }_0\right)\parallel }\right)\hfill \end{array}$$

Having derived these angles, we are now ready to define $\overline{\mathbf{r}}$ and $\overline{\mathbf{t}}$ as follows (see Equations (1)–(4)):

$$\begin{array}{cc}\hfill \overline{\mathbf{r}}\left(\gamma \right)& =-\left(\frac{u_1}{tan{\beta }_3}-u_2\right)\widehat{\overline{\mathbf{c}}}\left(\gamma \right)+\overline{\mathbf{u}}\left(\gamma \right)\hfill \\ \hfill \overline{\mathbf{t}}\left(\gamma \right)& =-\left(\frac{v_1}{tan{\beta }_2}+v_2\right)\widehat{\overline{\mathbf{c}}}\left(\gamma \right)+\overline{\mathbf{v}}\left(\gamma \right)\hfill \end{array}$$

Observing Figure 8a, note that r and t can be expressed simply as:

$$r=\frac{u_1}{sin{\beta }_3}t=\frac{v_1}{sin{\beta }_2}$$

In the ideal state, the crease defined by $\overline{\mathbf{h}}$ must have the same direction as $-\mathbf{c}$ to satisfy flat-foldability. Moreover, so that there are no gaps when ${\mathcal{S}}_1$ and ${\mathcal{S}}_4$ come together in the ideal state, the length of $\overline{\mathbf{h}}$ should be the value h given by Equation (5), according to the premise upon which Equation (5) was derived (see also Figure 6c). Thus,

$$\overline{\mathbf{h}}\left({\gamma }_0\right)=-h\widehat{\mathbf{c}}\left({\gamma }_0\right)$$

For an arbitrary parameter value $\gamma$, the unit vectors adjacent to $\widehat{\overline{\mathbf{h}}}\left(\gamma \right)$ that emanate from the degree-four vertex in the interior of ${\mathcal{S}}_4$ are $\widehat{\overline{\mathbf{r}}}\left(\gamma \right)$ and $\widehat{\overline{\mathbf{t}}}\left(\gamma \right)$. Because opposite angles in a degree-four vertex sum to ${180}^{\circ }$ [11,12] and we require a rigid folding, $\overline{\mathbf{h}}\left(\gamma \right)$ is determined by the following system of equations:

$$\begin{array}{cc}\hfill \widehat{\overline{\mathbf{h}}}\left(\gamma \right)·\widehat{\overline{\mathbf{r}}}\left(\gamma \right)& =cos\left(\pi -{cos}^{-1}\left(\widehat{\overline{\mathbf{c}}}\left(\gamma \right)·\widehat{\overline{\mathbf{t}}}\left(\gamma \right)\right)\right)\hfill \\ \hfill \widehat{\overline{\mathbf{h}}}\left(\gamma \right)·\widehat{\overline{\mathbf{t}}}\left(\gamma \right)& =cos\left(\pi -{cos}^{-1}\left(\widehat{\overline{\mathbf{c}}}\left(\gamma \right)·\widehat{\overline{\mathbf{r}}}\left(\gamma \right)\right)\right)\hfill \\ \hfill \widehat{\overline{\mathbf{h}}}\left(\gamma \right)·\widehat{\overline{\mathbf{h}}}\left(\gamma \right)& =1\hfill \end{array}$$

The first two equations are linear and the third is quadratic. Hence, there are precisely two solutions: one corresponding to a valley fold assignment and one corresponding to a mountain fold assignment. The solution corresponding to a mountain fold is the correct solution.

Because $\overline{\mathbf{g}}$ corresponds to an edge of the panel defined by $\overline{\mathbf{h}}$ and $\overline{\mathbf{t}}$, we can define it in terms of these vectors. We want the position of vertex $Q_4^{\prime }$ in ${\mathcal{S}}_4$ to equal that of $O_3$ in ${\mathcal{S}}_1$ when in the ideal state. This is equivalent to saying that $g_h\widehat{\overline{\mathbf{h}}}$ and $-g_t\widehat{\overline{\mathbf{t}}}$ define the same point when the former is extended from $Q_1^{\prime }$ and the latter is extended from $O_3$ in the ideal state, as shown in Figure 8b. The reader will recognize that this problem is formulated similarly to that in the end of Section 3.1, where the lengths h and w were computed using a system of equations based on two intersecting vectors. We employ the same technique, with the following system of equations:

$$\begin{array}{c}\hfill g_h\widehat{\overline{\mathbf{h}}}\left({\gamma }_0\right)+Q_1^{\prime }\left({\gamma }_0\right)=-g_t\widehat{\overline{\mathbf{t}}}\left({\gamma }_0\right)+O_3\left({\gamma }_0\right)\end{array}$$

giving us

$$\begin{array}{c}\hfill {\left[g_h,g_t\right]}^T={\left[\mathrm{proj}\left(\widehat{\overline{\mathbf{h}}}\left({\gamma }_0\right)\right),\mathrm{proj}\left(\widehat{\overline{\mathbf{t}}}\left({\gamma }_0\right)\right)\right]}^{-1}\mathrm{proj}\left(-\mathbf{\epsilon }+\mathbf{u}-\mathbf{w}-\overline{\mathbf{a}}-\overline{\mathbf{c}}-\overline{\mathbf{d}}-\mathbf{s}-\overline{\mathbf{\epsilon }}+\overline{\mathbf{u}}-\overline{\mathbf{w}}-\overline{\mathbf{t}}\right)\left({\gamma }_0\right)\end{array}$$

We solve for $g_h$ and $g_t$ and use these components of projection to define $\overline{\mathbf{g}}$, using $\widehat{\overline{\mathbf{h}}}$ and $\widehat{\overline{\mathbf{t}}}$ as a basis:

$$\overline{\mathbf{g}}\left(\gamma \right)=g_h\widehat{\overline{\mathbf{h}}}\left(\gamma \right)+g_t\widehat{\overline{\mathbf{t}}}\left(\gamma \right)$$

We define $\overline{\mathbf{f}}$ similarly, solving for $f_h$ and $f_r$ via the same method and another system of equations:

$$\begin{array}{c}\hfill f_h\widehat{\overline{\mathbf{h}}}\left({\gamma }_0\right)+O_1^{\prime }\left({\gamma }_0\right)=-f_r\widehat{\overline{\mathbf{r}}}\left({\gamma }_0\right)+O_3[-1]\left({\gamma }_0\right)\end{array}$$

This gives us

$$\begin{array}{c}\hfill {\left[f_h,f_r\right]}^T={\left[\mathrm{proj}\left(\widehat{\overline{\mathbf{h}}}\left({\gamma }_0\right)\right),\mathrm{proj}\left(\widehat{\overline{\mathbf{r}}}\left({\gamma }_0\right)\right)\right]}^{-1}\mathrm{proj}\left(-\mathbf{\epsilon }+\mathbf{u}-\mathbf{w}-\overline{\mathbf{a}}-\overline{\mathbf{b}}-\overline{\mathbf{c}}-\mathbf{s}-\overline{\mathbf{\epsilon }}+\overline{\mathbf{u}}-\overline{\mathbf{w}}-\overline{\mathbf{r}}\right)\left({\gamma }_0\right)\end{array}$$

Thus, we have

$$\overline{\mathbf{f}}\left(\gamma \right)=f_h\widehat{\overline{\mathbf{h}}}\left(\gamma \right)+f_r\widehat{\overline{\mathbf{r}}}\left(\gamma \right)$$

Now that we have defined all the essential vectors in ${\mathcal{S}}_4$, we are ready to attach the degree-four vertex to ${\mathcal{C}}_4$ in the zipper-coupled tubes structure. In the ideal state, this smooth sheet cell matches exactly with the edges of ${\mathcal{S}}_1$, providing a smooth surface devoid of gaps on the top of asymmetric zipper-coupled tubes (Figure 4a). In particular, the edge $\overline{O_1^{\prime }{O}_2^{\prime }}$ attaches to $\overline{E_1^{\prime }{E}_2^{\prime }}$ and $\overline{Q_1^{\prime }{Q}_2^{\prime }}$ attaches to $\overline{G_1^{\prime }{G}_2^{\prime }}$. Likewise, the edges $\overline{O_1^{\prime }{O}_4^{\prime }}$ and $\overline{Q_1^{\prime }{Q}_4^{\prime }}$ align perfectly with adjacent cells in the ideal state and fold up at different rates to avoid intersections. The vertices in ${\mathcal{S}}_4$ identified with their corresponding position vectors are:

$$\begin{array}{cc}\hfill O_1^{\prime }\left(\gamma \right)& =\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)+\overline{\mathbf{\epsilon }}\left(\gamma \right)-\overline{\mathbf{u}}\left(\gamma \right)+\overline{\mathbf{w}}\left(\gamma \right)+\overline{\mathbf{r}}\left(\gamma \right)\hfill \\ \hfill O_2^{\prime }\left(\gamma \right)& =\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)+\overline{\mathbf{\epsilon }}\left(\gamma \right)\hfill \\ \hfill O_4^{\prime }\left(\gamma \right)& =\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)+\overline{\mathbf{\epsilon }}\left(\gamma \right)-\overline{\mathbf{u}}\left(\gamma \right)+\overline{\mathbf{w}}\left(\gamma \right)+\overline{\mathbf{r}}\left(\gamma \right)+\overline{\mathbf{f}}\left(\gamma \right)\hfill \\ \\ \hfill P_1^{\prime }\left(\gamma \right)& =\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)+\overline{\mathbf{\epsilon }}\left(\gamma \right)-\overline{\mathbf{u}}\left(\gamma \right)+\overline{\mathbf{w}}\left(\gamma \right)\hfill \\ \hfill P_2^{\prime }\left(\gamma \right)& =\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)+\overline{\mathbf{\epsilon }}\left(\gamma \right)-\overline{\mathbf{u}}\left(\gamma \right)\hfill \\ \hfill P_4^{\prime }\left(\gamma \right)& =\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)+\overline{\mathbf{\epsilon }}\left(\gamma \right)-\overline{\mathbf{u}}\left(\gamma \right)+\overline{\mathbf{w}}\left(\gamma \right)+\overline{\mathbf{h}}\left(\gamma \right)\hfill \\ \\ \hfill Q_1^{\prime }\left(\gamma \right)& =\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)+\overline{\mathbf{\epsilon }}\left(\gamma \right)-\overline{\mathbf{u}}\left(\gamma \right)+\overline{\mathbf{w}}\left(\gamma \right)+\overline{\mathbf{t}}\left(\gamma \right)\hfill \\ \hfill Q_2^{\prime }\left(\gamma \right)& =\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{b}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)+\overline{\mathbf{\epsilon }}\left(\gamma \right)\hfill \\ \hfill Q_4^{\prime }\left(\gamma \right)& =\overline{\mathbf{a}}\left(\gamma \right)+\overline{\mathbf{c}}\left(\gamma \right)+\overline{\mathbf{d}}\left(\gamma \right)+\mathbf{s}\left(\gamma \right)+\overline{\mathbf{\epsilon }}\left(\gamma \right)-\overline{\mathbf{u}}\left(\gamma \right)+\overline{\mathbf{w}}\left(\gamma \right)+\overline{\mathbf{t}}\left(\gamma \right)+\overline{\mathbf{g}}\left(\gamma \right)\hfill \end{array}$$

3.4. Design of ${\mathcal{S}}_2$

The smooth sheet cell ${\mathcal{S}}_2$ is a rotated copy of ${\mathcal{S}}_4$ that attaches to ${\mathcal{C}}_2$. The vertices in this smooth sheet cell are

$$\begin{array}{cc}\hfill O_1\left(\gamma \right)& =\mathbf{a}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)+\mathbf{\epsilon }\left(\gamma \right)-\mathbf{u}\left(\gamma \right)+\mathbf{w}\left(\gamma \right)+\mathbf{r}\left(\gamma \right)\hfill \\ \hfill O_2\left(\gamma \right)& =\mathbf{a}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)+\mathbf{\epsilon }\left(\gamma \right)\hfill \\ \hfill O_4\left(\gamma \right)& =\mathbf{a}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)+\mathbf{\epsilon }\left(\gamma \right)-\mathbf{u}\left(\gamma \right)+\mathbf{w}\left(\gamma \right)+\mathbf{r}\left(\gamma \right)+\mathbf{f}\left(\gamma \right)\hfill \\ \\ \hfill P_1\left(\gamma \right)& =\mathbf{a}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)+\mathbf{\epsilon }\left(\gamma \right)-\mathbf{u}\left(\gamma \right)+\mathbf{w}\left(\gamma \right)\hfill \\ \hfill P_2\left(\gamma \right)& =\mathbf{a}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)+\mathbf{\epsilon }\left(\gamma \right)-\mathbf{u}\left(\gamma \right)\hfill \\ \hfill P_4\left(\gamma \right)& =\mathbf{a}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)+\mathbf{\epsilon }\left(\gamma \right)-\mathbf{u}\left(\gamma \right)+\mathbf{w}\left(\gamma \right)+\mathbf{h}\left(\gamma \right)\hfill \\ \\ \hfill Q_1\left(\gamma \right)& =\mathbf{a}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)+\mathbf{\epsilon }\left(\gamma \right)-\mathbf{u}\left(\gamma \right)+\mathbf{w}\left(\gamma \right)+\mathbf{t}\left(\gamma \right)\hfill \\ \hfill Q_2\left(\gamma \right)& =\mathbf{a}\left(\gamma \right)+\mathbf{b}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)+\mathbf{\epsilon }\left(\gamma \right)\hfill \\ \hfill Q_4\left(\gamma \right)& =\mathbf{a}\left(\gamma \right)+\mathbf{c}\left(\gamma \right)+\mathbf{d}\left(\gamma \right)+\mathbf{\epsilon }\left(\gamma \right)-\mathbf{u}\left(\gamma \right)+\mathbf{w}\left(\gamma \right)+\mathbf{t}\left(\gamma \right)+\mathbf{g}\left(\gamma \right)\hfill \end{array}$$

We have now completed the details for the smooth sheet attachment in the asymmetric case; a summary of the edges and vertices in the attachment is given in

Table A1. Defining the edges in Miura-ori based, smooth sheet attachments for a pair of asymmetric zipper-coupled tubes.

${\mathcal{S}}_1$		${\mathcal{S}}_2$			${\mathcal{S}}_3$		${\mathcal{S}}_4$
$\overline{O_0{P}_0}$	$\overline{O_0{P}_0\left[1\right]}$	$\overline{O_1{P}_1}$	$\overline{O_2{P}_2}$	$\overline{O_4{P}_4}$	$\overline{O_0^{\prime }{P}_0^{\prime }}$	$\overline{O_0^{\prime }{P}_0^{\prime }[-1]}$	$\overline{O_1^{\prime }{P}_1^{\prime }}$	$\overline{O_2^{\prime }{P}_2^{\prime }}$	$\overline{O_4^{\prime }{P}_4^{\prime }}$
$\overline{O_3{F}_3}$	$\overline{O_3{F}_3\left[1\right]}$	$\overline{P_1{Q}_1}$	$\overline{P_2{Q}_2}$	$\overline{P_4{Q}_4}$	$\overline{O_3^{\prime }{F}_3^{\prime }}$	$\overline{O_3^{\prime }{F}_3^{\prime }[-1]}$	$\overline{P_1^{\prime }{Q}_1^{\prime }}$	$\overline{P_2^{\prime }{Q}_2^{\prime }}$	$\overline{P_4^{\prime }{Q}_4^{\prime }}$
$\overline{O_0{O}_3}$	$\overline{P_0{F}_3}$	$\overline{O_1{O}_2}$	$\overline{O_1{O}_4}$	$\overline{P_1{P}_2}$	$\overline{O_0^{\prime }{O}_3^{\prime }}$	$\overline{P_0^{\prime }{F}_3^{\prime }}$	$\overline{O_1^{\prime }{O}_2^{\prime }}$	$\overline{O_1^{\prime }{O}_4^{\prime }}$	$\overline{P_1^{\prime }{P}_2^{\prime }}$
$\overline{P_0\left[1\right]F_3\left[1\right]}$		$\overline{P_1{P}_4}$	$\overline{Q_1{Q}_2}$	$\overline{Q_1{Q}_4}$	$\overline{P_0^{\prime }[-1]F_3^{\prime }[-1]}$		$\overline{P_1^{\prime }{P}_4^{\prime }}$	$\overline{Q_1^{\prime }{Q}_2^{\prime }}$	$\overline{Q_1^{\prime }{Q}_4^{\prime }}$

and

Table A2. Defining the vertices in Miura-ori inspired smooth sheet attachments for a pair of asymmetric zipper-coupled tubes.

Vertex	Position	Vertex	Position
$O_0$	$-\mathbf{\epsilon }+\mathbf{u}$	$O_0^{\prime }$	$\mathbf{s}-\overline{\mathbf{\epsilon }}+\overline{\mathbf{u}}$
$O_1$	$\mathbf{a}+\mathbf{c}+\mathbf{d}+\mathbf{\epsilon }-\mathbf{u}+\mathbf{w}+\mathbf{r}$	$O_1^{\prime }$	$\overline{\mathbf{a}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}+\mathbf{s}+\overline{\mathbf{\epsilon }}-\overline{\mathbf{u}}+\overline{\mathbf{w}}+\overline{\mathbf{r}}$
$O_2$	$\mathbf{a}+\mathbf{c}+\mathbf{d}+\mathbf{\epsilon }$	$O_2^{\prime }$	$\overline{\mathbf{a}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}+\mathbf{s}+\overline{\mathbf{\epsilon }}$
$O_3$	$-\mathbf{\epsilon }+\mathbf{u}-\mathbf{w}$	$O_3^{\prime }$	$\mathbf{s}-\overline{\mathbf{\epsilon }}+\overline{\mathbf{u}}-\overline{\mathbf{w}}$
$O_4$	$\mathbf{a}+\mathbf{c}+\mathbf{d}+\mathbf{\epsilon }-\mathbf{u}+\mathbf{w}+\mathbf{r}+\mathbf{f}$	$O_4^{\prime }$	$\overline{\mathbf{a}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}+\mathbf{s}+\overline{\mathbf{\epsilon }}-\overline{\mathbf{u}}+\overline{\mathbf{w}}+\overline{\mathbf{r}}+\overline{\mathbf{f}}$
$P_0$	$-\mathbf{\epsilon }$	$P_0^{\prime }$	$\mathbf{s}-\overline{\mathbf{\epsilon }}$
$P_1$	$\mathbf{a}+\mathbf{c}+\mathbf{d}+\mathbf{\epsilon }-\mathbf{u}+\mathbf{w}$	$P_1^{\prime }$	$\overline{\mathbf{a}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}+\mathbf{s}+\overline{\mathbf{\epsilon }}-\overline{\mathbf{u}}+\overline{\mathbf{w}}$
$P_2$	$\mathbf{a}+\mathbf{c}+\mathbf{d}+\mathbf{\epsilon }-\mathbf{u}$	$P_2^{\prime }$	$\overline{\mathbf{a}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}+\mathbf{s}+\overline{\mathbf{\epsilon }}-\overline{\mathbf{u}}$
$P_4$	$\mathbf{a}+\mathbf{c}+\mathbf{d}+\mathbf{\epsilon }-\mathbf{u}+\mathbf{w}+\mathbf{h}$	$P_4^{\prime }$	$\overline{\mathbf{a}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}+\mathbf{s}+\overline{\mathbf{\epsilon }}-\overline{\mathbf{u}}+\overline{\mathbf{w}}+\overline{\mathbf{h}}$
$Q_1$	$\mathbf{a}+\mathbf{c}+\mathbf{d}+\mathbf{\epsilon }-\mathbf{u}+\mathbf{w}+\mathbf{t}$	$Q_1^{\prime }$	$\overline{\mathbf{a}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}+\mathbf{s}+\overline{\mathbf{\epsilon }}-\overline{\mathbf{u}}+\overline{\mathbf{w}}+\overline{\mathbf{t}}$
$Q_2$	$\mathbf{a}+\mathbf{b}+\mathbf{c}+\mathbf{\epsilon }$	$Q_2^{\prime }$	$\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}+\mathbf{s}+\overline{\mathbf{\epsilon }}$
$Q_4$	$\mathbf{a}+\mathbf{c}+\mathbf{d}+\mathbf{\epsilon }-\mathbf{u}+\mathbf{w}+\mathbf{t}+\mathbf{g}$	$Q_4^{\prime }$	$\overline{\mathbf{a}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}+\mathbf{s}+\overline{\mathbf{\epsilon }}-\overline{\mathbf{u}}+\overline{\mathbf{w}}+\overline{\mathbf{t}}+\overline{\mathbf{g}}$
$F_3$	$\mathbf{c}$	$F_3^{\prime }$	$\overline{\mathbf{c}}+\mathbf{s}$
$F_3\left[1\right]$	$\mathbf{c}-\mathbf{b}+\mathbf{d}$	$F_3^{\prime }[-1]$	$\overline{\mathbf{c}}+\mathbf{s}-\overline{\mathbf{b}}+\overline{\mathbf{d}}$
$P_0\left[1\right]$	$-\mathbf{\epsilon }-\mathbf{b}+\mathbf{d}$	$P_0^{\prime }[-1]$	$\mathbf{s}-\overline{\mathbf{\epsilon }}-\overline{\mathbf{b}}+\overline{\mathbf{d}}$

, suppressing $\gamma$ for concision. This attachment folds up flat and actuates with the zipper-coupled tubes structure to form a smooth surface, leaving no gaps between the various asymmetric cells we have described. The symmetric case merits more discussion, however, because there are fewer constraints on the vectors in the ${\mathcal{S}}_i$, allowing for multiple rigidly foldable patterns given specific design parameters.

4. Symmetric Smooth Sheet Attachment

Unlike their asymmetric counterparts, symmetric zipper-coupled tubes have no tilt and fold parallel with the x-axis [5]. Furthermore, the center creases in ${\mathcal{S}}_1$ and ${\mathcal{S}}_4$ lie parallel with the y-axis in the ideal state, as illustrated in Figure 9. There are multiple valid lengths for these creases, therefore, in a design that covers all the gaps in the surface while maintaining rigid foldability without prohibitive intersections. In this section we comment on the diversity in symmetric, Miura-ori inspired smooth sheet cell construction and recommend values for certain lengths.

The design parameters for the smooth sheet cells ${\mathcal{S}}_i$ are uniquely determined for all cases where ${\alpha }_1+{\alpha }_2<\pi$. When ${\alpha }_1+{\alpha }_2=\pi$, however, there is no longer a unique solution to Equation (5). In particular, $\overline{\mathbf{c}}\left({\gamma }_0\right)$ has the same direction as $-\mathbf{c}\left({\gamma }_0\right)$ in the symmetric case, so the matrix inverted in Equation (5) is singular and the values h and w are not uniquely defined. Similarly, ${\beta }_2$ and ${\beta }_3$ are no longer constrained, and we may define these features of the design problem advantageously by choosing a solution that minimizes the amount by which the smooth sheet attachment protrudes from the structure when folded.

In the design of ${\mathcal{S}}_1$ and ${\mathcal{S}}_3$, let $w^{*}$ replace the value of w. Likewise, in the design of ${\mathcal{S}}_4$ and ${\mathcal{S}}_2$, let $w^{**}$ replace the value of w. As highlighted in Figure 9, for the symmetric case we no longer require that $w^{*}=w^{**}$. In selecting a value for $w^{*}$, we set it as large as possible to maximize the surface area of ${\mathcal{S}}_1$, thus minimizing the amount by which the edges of ${\mathcal{S}}_4$ can protrude from the zipper-coupled tubes structure. Applying the analysis given in [5] (see Section 7.1.3), the largest value for $w^{*}$ can be shown to be

$$w^{*}=c-\frac{dsin{\alpha }_1+bsin{\alpha }_4-\Delta }{2tan\left({\alpha }_2-{\alpha }_1\right)}-\epsilon$$

The only requirements for h, $w^{**}$, ${\beta }_2$, and ${\beta }_3$ in the symmetric case are

$$h+w^{**}=c-\epsilon \mathrm{and}{\beta }_2={\beta }_3$$

Adjustments to the values h, $w^{**}$, ${\beta }_2$, and ${\beta }_3$ can also assist in minimizing the protrusion of ${\mathcal{S}}_4$ from the zipper-coupled tubes. Optimal values can be determined by numerical methods according to the specific design application. However, care should be taken in making these adjustments to avoid intersections with the structure underneath.

On a final note, although $\overline{\mathbf{f}}$ and $\overline{\mathbf{g}}$ are determined after defining the previous quantities, a convenient simplification in their definition: because ${\mathcal{S}}_4$ is symmetric, the vectors $\overline{\mathbf{f}}$ and $\overline{\mathbf{g}}$ are parallel to $\overline{\mathbf{h}}$ and have equal lengths. Moreover, in the ideal state,

$$O_1^{\prime }{O}_4^{\prime }=O_2^{\prime }{O}_4^{\prime }-O_1^{\prime }{O}_2^{\prime }$$

Therefore,

$$g_t=f_r=0\mathrm{and}{g}_h=f_h=\left(2c-w^{*}\right)-\left(w^{**}+\frac{u_1}{tan{\beta }_3}\right)$$

5. Conclusions

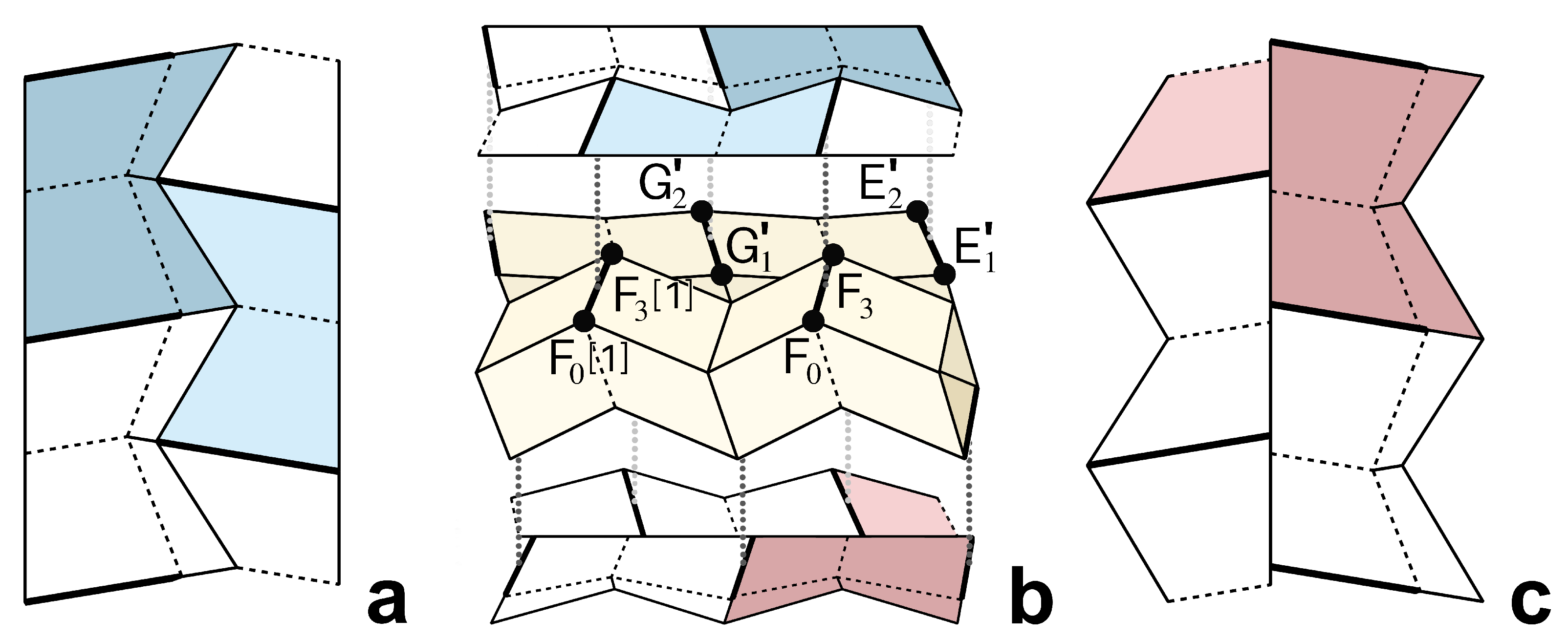
We have successfully defined a smooth sheet attachment that folds up with the zipper-coupled tubes and unfolds to the ideal state without inhibiting their motion to form a flat surface without any gaps (Figure 10). This pattern is defined for both the asymmetric and symmetric cases, and we provide access to code which the reader may use to visualize the origami structures described and print out the corresponding fold patterns: https://github.com/dylanwebbc/azct (accessed on 23 July 2022).

Note that the smooth sheet cells protrude from the zipper-coupled tubes structure when folded. When gaps are tolerable and the folded state must be minimized for transportation, constraining the cells to fold up within the zipper-coupled tubes while maximizing surface area in the ideal state results in the smooth sheet attachment described previously [5]. Thus, the smooth sheet design can be tailored to the situation, much like zipper-coupled tubes themselves. To inform future applications of these structures, we suggest dynamic and quasi-static analyses. Constructing a device for architectural applications will likely require the use of thick origami and compliant hinges, and remote self-actuation via magnetism or heat could be useful in space or medical applications [13,14,15].

Miura-ori-inspired smooth sheet attachments enhance the utility of zipper-coupled tubes in various situations. The tubes are useful in architecture because they pack tight and deploy to a rigid state [4]; our gapless smooth sheet attachments improve existing designs by increasing drivability and walkability. If a local bridge collapses, for example, a prefabricated bridge based on zipper-coupled tubes with smooth sheet attachments can easily be transported on a single vehicle and swiftly deployed on-site to provide smooth, emergency transit. Space structures are another popular application of origami-inspired mechanisms—the Miura-ori pattern that the smooth sheet is based on is common in deployable space array design. Accommodating for material thickness, however, makes Miura-ori sheets challenging to deploy [16]. In contrast, a thin solar array constructed from Miura-ori inspired smooth sheet cells can deploy rigidly because it is supported by zipper-coupled tubes.

The design of smooth sheet attachments without gaps is key to the development of more versatile zipper-coupled tubes. We have communicated a clear design method for the origami-based structure, examining the mathematics of its motion in detail. By elucidating the possibility for further enhancements on the zipper-coupled tubes structure, we hope to spur many novel and exciting applications beyond those mentioned.