A Mathematical Perspective on Post-Quantum Cryptography

Abstract

In 2016, the National Institute of Standards and Technology (NIST) announced an open competition with the goal of finding and standardizing suitable algorithms for quantum-resistant cryptography. This study presents a detailed, mathematically oriented overview of the round-three finalists of NIST’s post-quantum cryptography standardization consisting of the lattice-based key encapsulation mechanisms (KEMs) CRYSTALS-Kyber, NTRU and SABER; the code-based KEM Classic McEliece; the lattice-based signature schemes CRYSTALS-Dilithium and FALCON; and the multivariate-based signature scheme Rainbow. The above-cited algorithm descriptions are precise technical specifications intended for cryptographic experts. Nevertheless, the documents are not well-suited for a general interested mathematical audience. Therefore, the main focus is put on the algorithms’ corresponding algebraic foundations, in particular LWE problems, NTRU lattices, linear codes and multivariate equation systems with the aim of fostering a broader understanding of the mathematical concepts behind post-quantum cryptography.

1. Introduction

In recent years, significant progress in researching and building quantum computers has been made. The existence of such computers threatens the security of many modern cryptographic systems. This affects, in particular, asymmetric cryptography, i.e., KEMs and digital signatures. By leveraging Shor’s quantum algorithm to find the period of a function in a large group, a quantum computer can solve a distinct set of mathematical problems. In particular, this includes integer factorization and the discrete logarithm, which are the basis for a wide range of cryptographic schemes. Therefore, a fully fledged quantum computer would be able to efficiently break the security of many modern cryptosystems. To defend against this threat, the need for novel mathematical problems which are resistant to Shor’s algorithm arises. Such problems are thereby promising candidates to withstand the superior computing possibilities of quantum computers.

In 2016, NIST announced an open competition with the goal of finding and standardizing suitable algorithms for quantum-resistant cryptography. The standardization effort by NIST is aimed at KEMs and digital signatures [1]. This process is currently in its third round of candidate selection (April 2022).

At this point, the submitted algorithms are complex technical specifications without a presentation of the underlying mathematical fundamentals and therefore do not allow an easy access to these novel post-quantum algorithm approaches. As some of these algorithms will probably become widely used in industrial areas very soon, it is vital to foster a broad understanding of these mathematical concepts. In this document, we therefore address the described lack of educational presentation. As we do not intend to give a detailed comparison of the presented methods and their performance in practice, we would like to refer to the post-quantum database PQDB [2]. This website is an internal project within Fraunhofer AISEC and aims to provide an up-to-date overview of implementation details and performance measurements of post-quantum secure cryptographic schemes according to available research.

In the following sections, the round-three finalists of NIST’s competition are presented, and their mathematical details and properties are outlined. For a quick access to any of these algorithms, we have structured the document in separate parts containing distinct mathematical concepts, which thereby offer independent readability. These concepts correspond to the algorithms’ respective algebraic foundations, which are LWE problems as well as NTRU lattices in Section 2, linear codes in Section 3 and multivariate equation systems in Section 4.

2. Lattice-Based Cryptography

2.1. Lattice Fundamentals

The cryptographic interest in lattices mainly arises from the fact that a given lattice L can have widely different bases. While a good basis can simplify some computational tasks significantly, a bad basis can make them almost impossible. In this section, we will give a short introduction to the fundamental mathematics and the two most important computational problems of lattices.

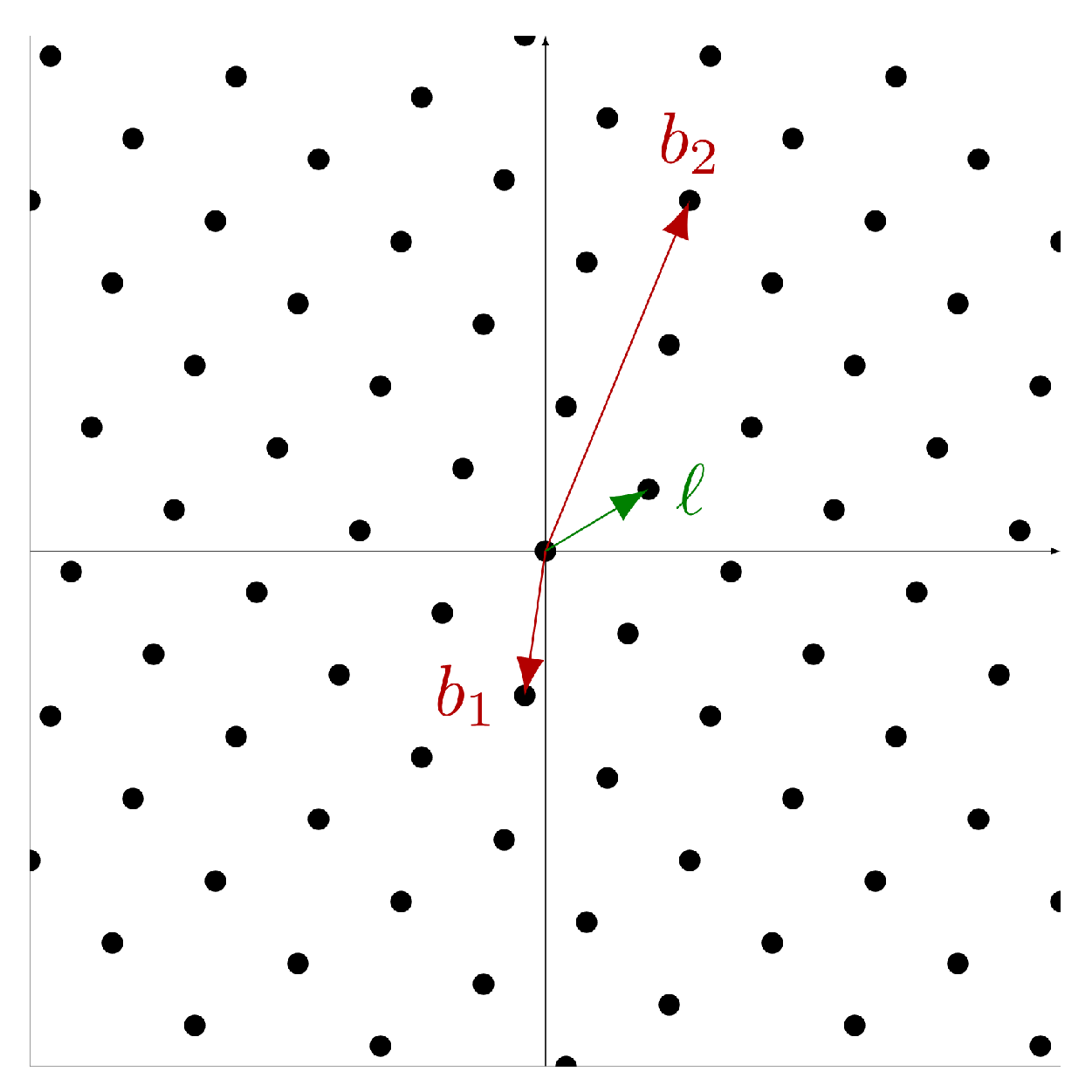
2.1.1. Lattices

Definition 1

(lattice, basis). Let $B=\{b_1,b_2,...,b_m\}$ be a set of linearly independent vectors of ${\mathbb{R}}^n$. Then, the set of all integer linear combinations

$$L\left(B\right)=\left\{\sum _i{a}_i{b}_i\mid a_i\in \mathbb{Z}\right\}\subset {\mathbb{R}}^n$$

is called alatticein ${\mathbb{R}}^n$ generated by B. We furthermore refer to $\{b_1,b_2,...,b_m\}$ as abasisof the lattice L.

An example of a lattice with corresponding basis is shown in Figure 1. We can equivalently generate L via a matrix B containing the basis vectors as column vectors.

Definition 2

(lattice, rank, dimension, full-rank lattice). Let $\{b_1,b_2,...,b_m\}$ be a set of linearly independent vectors of ${\mathbb{R}}^n$. Let B be the $n\times m$ matrix with column vectors $b_1,...,b_m$. Then:

$$L\left(B\right)=\{Bx\mid x\in {\mathbb{Z}}^m\}$$

is called lattice in ${\mathbb{R}}^n$ generated by B. We call m the rank and n the dimension of the lattice. For m equals n, the lattice is called the full-rank lattice.

Observe that the basis underlying a lattice L is not unique. Observe that the lattice generated by the vectors

$$\left(\begin{array}{c}0\\ 1\end{array}\right),\left(\begin{array}{c}1\\ 0\end{array}\right)$$

is ${\mathbb{Z}}^2$, the set of all integer points. ${\mathbb{Z}}^2$ is also generated by the vectors

$$\left(\begin{array}{c}2\\ 1\end{array}\right),\left(\begin{array}{c}1\\ 1\end{array}\right).$$

Figure 2 also illustrates this fact. On the other hand, n linearly independent vectors in ${\mathbb{Z}}^n$ are not necessarily a basis of ${\mathbb{Z}}^n$. As an example, observe that the modified vectors from the example above

$$\left(\begin{array}{c}2\\ 0\end{array}\right),\left(\begin{array}{c}1\\ 1\end{array}\right)$$

do not form a basis of ${\mathbb{Z}}^2$.

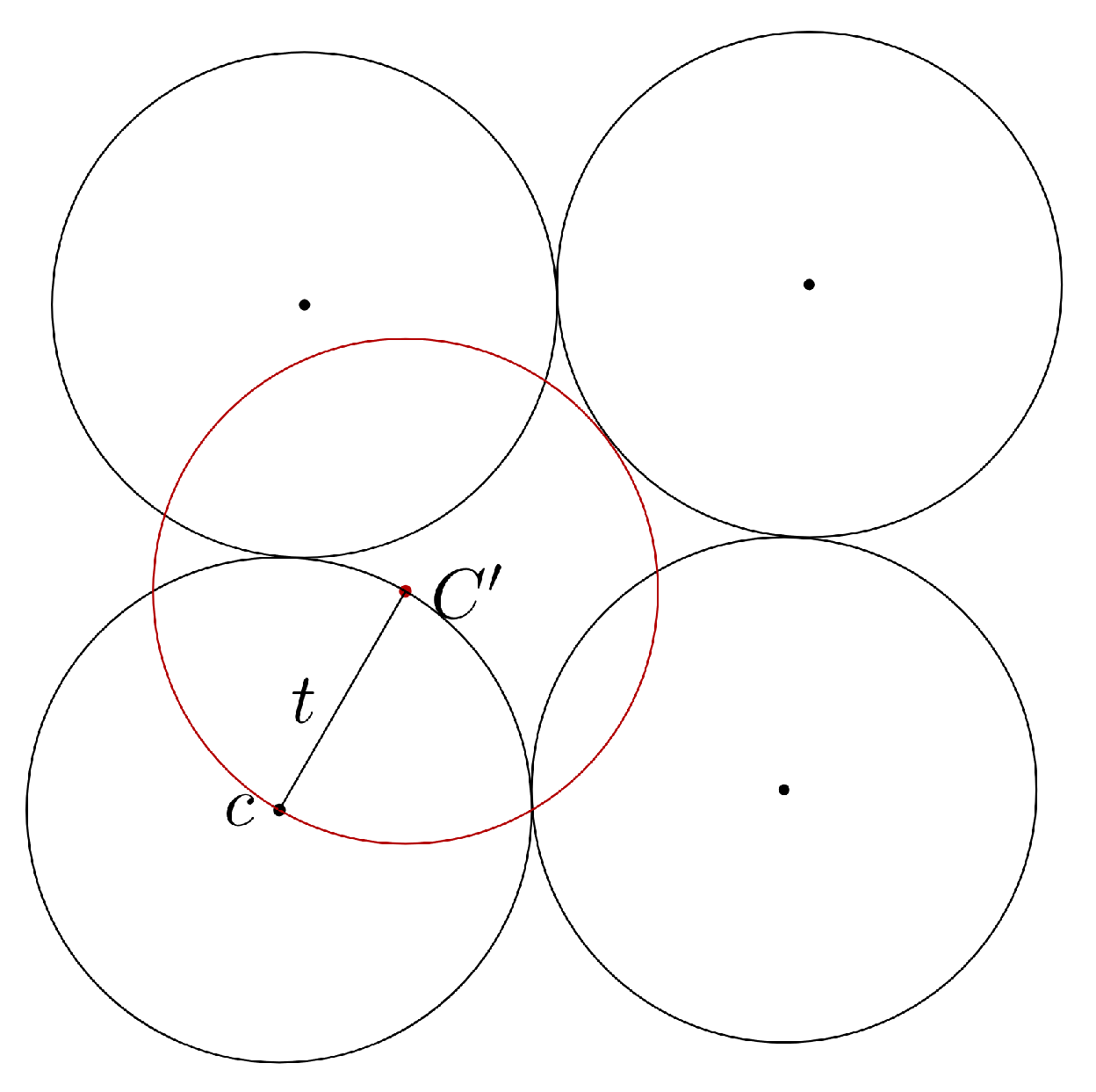
2.1.2. Computational Lattice Problems

The particular structure of lattices allows them to have special mathematical properties. The following computations can be efficiently evaluated using linear algebra algorithms:

• Let $g_1,...,g_k\in {\mathbb{R}}^n$ be a set of vectors generating the lattice L. Calculate a basis $b_1,...,b_m\in {\mathbb{R}}^n$ of L.
• Let L be a lattice. Evaluate whether a given vector c is an element of L.

Other computational lattice problems appear to be generally hard and are - as indicated in the introduction - even believed to be resistant against Shor’s algorithm. Therefore, they are interesting candidates for usage in post-quantum-cryptography. These problems are presented in the following.

Shortest Vector Problem

Let L be a lattice with some basis $B\in {\mathbb{R}}^{n\times m}$ and $\parallel ·\parallel$ some norm. Let $\lambda \left(L\right)$ be the length of the shortest nonzero vector in L. The task of finding $l\in L$ such that $\parallel l\parallel =\lambda \left(L\right)$, i.e., finding any shortest vector of L, is called the shortest vector problem (SVP). Figure 3 illustrates such a shortest vector in a lattice.

2.1.3. Closest Vector Problem

Let L be a lattice with some basis $B\in {\mathbb{R}}^{n\times m}$ and $\parallel ·\parallel$ some norm. Given $q\in {\mathbb{R}}^n$, the task of finding $l\in L$ such that $\parallel l-q\parallel$ is minimal, i.e., find the lattice vector l closest to a given arbitrary vector, is called the closest vector problem (CVP). Figure 4 illustrates a random point with its corresponding closest lattice vector.

2.2. Cryptography Based on Learning with Errors (LWE)

2.2.1. LWE Fundamentals

Learning with Errors

Let ${\mathbb{Z}}_q=\mathbb{Z}/q\mathbb{Z}$ be the ring of integers modulo q. We can naturally form a linear equation system

$$\begin{array}{c}\hfill A·s=b,\end{array}$$

where $A\in {\mathbb{Z}}_q^{n\times m},s\in {\mathbb{Z}}_q^m,b\in {\mathbb{Z}}_q^n$. For example, consider the following system:

$$\begin{array}{c}\hfill A=\left(\begin{array}{cccc}10& 3& 5& 1\\ 4& 1& 1& 2\\ ⋮& ⋮& ⋮& ⋮\\ 3& 1& 1& 5\end{array}\right),b=\left(\begin{array}{c}10\\ 3\\ ⋮\\ 8\end{array}\right)\end{array}$$

Then, the associated equations look like:

$$\begin{array}{cc}\hfill 10·s_1+3·s_2+5·s_3+1·s_4& =10\hfill \\ \hfill 4·s_1+1·s_2+1·s_3+2·s_4& =3\hfill \\ \hfill ⋮\\ \hfill 3·s_1+1·s_2+1·s_3+5·s_4& =8\hfill \end{array}$$

Solving this equation system can be efficiently realized using the Gaussian algorithm. However, adding even only small error values $e\in {\mathbb{Z}}_q^n$ to the equation system yields:

$$\begin{array}{c}\hfill A·s+e=b,\end{array}$$

which renders solving the equation system and retrieving the solution vector s surprisingly hard. This fact is founded in the relation to the hard lattice problems described above, which is presented in a nutshell below.

Decisional LWE

The LWE problem can also be rephrased as a decision problem, usually abbreviated dLWE. Given an LWE sample $(A,b)$ as defined above (s and e are kept secret), the task is to guess whether the values of b have been calculated as $A·s+e$ with small error values e, or whether they have been chosen arbitrarily. Both variants are equivalently hard. The reduction from LWE to dLWE has been proven by Regev ([3], Lemma 4.2), the inverse reduction from dLWE to LWE is trivial.

Linking LWE to Computational Lattice Problems

Consider an LWE problem of the form:

$$\begin{array}{c}\hfill A·s+e=b,\end{array}$$

where $A\in {\mathbb{Z}}_q^{n\times m},b\in {\mathbb{Z}}_q^n$ and small vectors $s\in {\mathbb{Z}}_q^m,e\in {\mathbb{Z}}_q^n$. It is straightforward to solve a concrete LWE instance by solving the closest vector problem. Observe that the closest vector to b is almost always the lattice vector $A·s$ with distance e.

To give an intuition of the relationship between learning with errors and the shortest vector problem, consider the following lattice:

$$\begin{array}{c}\hfill L=\{x\in {\mathbb{Z}}^{m+n+1}\mid (A\mid \mid I_n\mid \mid (-b))·x=0modq\},\end{array}$$

where the ‘$\mid \mid$’ operator denotes concatenation and $I_n$ denotes the $n\times n$ identity matrix. It can be observed that the column vector $(s,e,1)$ is an element of L by verifying that

$$\begin{array}{c}\hfill \left(\begin{array}{ccc}A& I_n& -b\end{array}\right)·\left(\begin{array}{c}s\\ e\\ 1\end{array}\right)=A·s+e-b=b-b=0modq\end{array}$$

holds. It can be shown that the vector $(s,e,1)$ is actually a shortest vector in L and therefore is an SVP solution for L. This means retrieving the vector $(s,e,1)$ directly yields the secret s as well as the error vector e and therefore solves the LWE system.

LWE-Based Encryption Schemes

This section aims to serve as a high-level introduction to LWE-based encryption schemes, so that their basic idea can be easily understood. The following simplified example will only be used to transmit a message consisting of a single bit, but it can be trivially extended to transmit a bitstring of any desired length.

Consider an LWE instance $A·s+e=b$, where $A\in {\mathbb{Z}}_q^{n\times m}$ is chosen uniformly random and $s\in {\mathbb{Z}}_q^m$ and $e\in {\mathbb{Z}}_q^n$ are chosen from an error distribution, i.e., their values are rather small. Let us assume the values A and b are public while the corresponding values s and e are kept secret. The LWE problem then states that it is hard to calculate s or e.

To build the actual encryption scheme, we will randomly sample the additional values $r\in {\mathbb{Z}}_q^n$ as well as errors $e_1\in {\mathbb{Z}}_q^m$ and $e_2\in {\mathbb{Z}}_q$. With that, we construct the equation system:

$$\begin{array}{cc}\hfill u& =A^T·r+e_1\in {\mathbb{Z}}_q^m\hfill \\ \hfill v& =b^T·r+e_2\in {\mathbb{Z}}_q,\hfill \end{array}$$

which can be equivalently represented as:

$$\begin{array}{cc}\hfill \left(\begin{array}{c}u\\ v\end{array}\right)& =\left(\begin{array}{c}{A}^T\\ b^T\end{array}\right)r+\left(\begin{array}{c}{e}_1\\ e_2\end{array}\right)\hfill \end{array}$$

in a compact form.

It is then easy to see that this is also another instance of the LWE problem. With knowledge of $(A,b,u,v)$, it is hard to calculate any of the other values. Furthermore, the decisional LWE problem states that it is even hard to differentiate between the values $u,v$ calculated in the method described above and $u,v^{\prime }$ with some arbitrary value $v^{\prime }$. This is a core part of our encryption system.

For now, let us assume we would just send $(u,v)$ back to the recipient, who (knowing s) could then calculate the value $s^T·u=s^T·(A^T·r+e_1)$. Taking into account that the error values are relatively small, we observe that $s^T·u\approx s^T·A^T·r$ and also that $v=b^T·r+e_2\approx b^T·r\approx {(A·s)}^T·r=s^T·A^T·r$. Thus, neglecting the error values, we find that $s^T·u\approx v$.

This means we have found a way to indirectly transmit about the same value in two separate ways, and we have done so unnoticed by a third person: without knowledge of s, it cannot be deduced how close exactly these values are to each other (dLWE assumption).

The trick is to hide the message in one of these values. When the message is 0, we will just transmit $v^{\prime }=v$. However, in case it is 1, we will transmit $v^{\prime }=v+q/2$ (remember that we are operating on ${\mathbb{Z}}_q$, so this is the value “opposite” to 0). The receiver can then calculate $\mu =v^{\prime }-s^T·u$. If $\mu$ is close to zero (mod q), the message was 0; if it is closer to $q/2$, the message was 1.

Let us summarize the process more formally. Let ${\mathrm{round}}_n(·)$ denote rounding to the nearest multiple of n. For a one-bit message encoded as $\mu \in \{0,\lfloor q/2\rfloor \}$, the ciphertext is $(u,v^{\prime })$ with

$$\begin{array}{cc}\hfill u& =A^T·r+e_1\hfill \\ \hfill v^{\prime }& =b^T·r+e_2+\mu ,\hfill \end{array}$$

from which the receiver can calculate:

$$\begin{array}{cc}\hfill \phantom{=}\mathrm{round}& {}_{\lfloor q/2\rfloor }(v^{\prime }-s^T·u)\hfill \\ \hfill & ={\mathrm{round}}_{\lfloor q/2\rfloor }(b^{T}r+e_2+\mu -s^T(A^{T}r+e_1))\hfill \\ \hfill & ={\mathrm{round}}_{\lfloor q/2\rfloor }({(As+e)}^{T}r+e_2+\mu -s^T{A}^{T}r-s^T{e}_1)\hfill \\ \hfill & ={\mathrm{round}}_{\lfloor q/2\rfloor }({\left(As\right)}^{T}r+e^{T}r+e_2+\mu -{\left(As\right)}^{T}r-s^T{e}_1)\hfill \\ \hfill & ={\mathrm{round}}_{\lfloor q/2\rfloor }(\mu +e^{T}r+e_2-s^T{e}_1)\hfill \\ \hfill & =\mu .\hfill \end{array}$$

For the last equality to hold (and thus, the decryption to succeed), we need the overall effect of the error term $(e^{T}r+e_2-s^T{e}_1)$ to stay below $q/4$. In practice, all candidate schemes use an error distribution and a modulus q where this is not always the case in order to have reasonable ciphertext sizes. The failure probability in all cases is extremely small, so it is usually negligible in practice. However, care must be taken that attackers cannot learn anything about the secret key by intentionally crafting ciphertexts that cause decryption failures.

Flavors of LWE: Ring-LWE and Module-LWE

The sample cryptosystem described above can be trivially extended to encapsulate bitstrings of a fixed length ℓ by running the same protocol ℓ times in parallel. In contrast to the flavors described below, this approach is called Plain LWE (note that even though ${\mathbb{Z}}_q$ is a ring, the term Ring-LWE refers to another approach, see below). A production-ready scheme that uses Plain LWE is Frodo [4]. Because of its simplicity it is considered to have the least potential for attacks. However, this is paid for by communication costs about 15 times higher than with Ring-LWE or Module-LWE. The comparison of Frodo’s public key and ciphertext size to the respective sizes of Kyber and Saber shows this fact. Because of the relatively bad performance, it is not among the NIST standardization finalists (but included as an alternate candidate) and is thus not included in this report. Other variants of LWE can be created by exchanging the underlying algebraic structure. Various flavors have been researched, and we will detail the relevant ones in the following.

Ring-LWE was first proposed by Vadim Lyubashevsky, Chris Peikert and Oded Regev in 2010 [5]. Calculations take place in a polynomial ring $R_q:={\mathbb{Z}}_q\left[x\right]/f\left(x\right)$ for some polynomial $f\left(x\right)$. Therefore, polynomial multiplication is used instead of matrix multiplication.

Module-LWE is a variant that further improves Ring-LWE and was proposed by Adeline Langlois and Damien Stehlé in 2012 [6]. It uses the exact same structure as the sample system detailed above, but the scalars are replaced by ring elements of $R_q$, as defined in the previous paragraph. Consequently, vectors become elements of so-called modules, which are a generalization of vector spaces over rings, hence the name (see

Table 1. Comparison of algebraic structures used in LWE variants.

	Plain LWE	Ring-LWE	Module-LWE
$\mathbf{A}$	${\mathbb{Z}}_q^{n\times m}$	${\mathbb{Z}}_q\left[x\right]/f$	${({\mathbb{Z}}_q\left[x\right]/f)}^{n\times m}$
·	matrix mult.	polynomial mult.	matrix mult.
$\mathbf{s}$	${\mathbb{Z}}_q^m$	${\mathbb{Z}}_q\left[x\right]/f$	${({\mathbb{Z}}_q\left[x\right]/f)}^m$
$\mathbf{b},\mathbf{e}$	${\mathbb{Z}}_q^n$	${\mathbb{Z}}_q\left[x\right]/f$	${({\mathbb{Z}}_q\left[x\right]/f)}^n$

for a comparison).

Most early practical implementations of LWE-based cryptography, such as the NewHope scheme [7], use Ring-LWE. However, it was shown that Ring-LWE possibly provides more attack surface, so that a Ring-LWE scheme is at most as secure as an equally parameterized Module-LWE scheme [8]. For that reason, NIST has decided not to consider Ring-LWE schemes in the third round.

Learning with Rounding

The learning with rounding (LWR) problem is a variant of the LWE problem. Consider a single line of the LWE problem $As+e=b$, where $A\in {\mathbb{Z}}_q^{n\times m}$ is chosen uniformly and $s\in {\mathbb{Z}}_q^m$ and $e\in {\mathbb{Z}}_q^n$ from a small error distribution, i.e.,

$${\left(As\right)}_k+e_k=(a_{k1}·s_1+...+a_{km}·s_m)+e_k=b_k.$$

Instead of sampling and adding a random small error $e_k$, noise is added to the equation by simple rounding. In this case, that means defining a rounding function ${\lfloor ·\rfloor }_p:{\mathbb{Z}}_q\to {\mathbb{Z}}_p$ for some $p<q$ dividing ${\mathbb{Z}}_q$ into p roughly same-sized intervals and mapping an element in ${\mathbb{Z}}_q$ to the index of its corresponding interval. For example, when p and q are both powers of 2, rounding simplifies to mapping an element to its $lo{g}_2\left(p\right)$ most significant bits.

This rounding function can be extended to vectors in ${\mathbb{Z}}_q^n$ by component-wise rounding, i.e., rounding each ${\left(As\right)}_k$ separately. Counter-intuitively, although the noise in LWR is deterministically computed, it is computationally as difficult as solving LWE, i.e., deriving s from A and ${\lfloor A·s\rfloor }_p$ is hard [9]. Just as in the LWE case, variants of LWR can be created by exchanging the underlying structure. For example, the scheme Saber uses Module-LWR.

2.2.2. Kyber

Kyber [10] is a CCA-secure KEM derived from a CPA-secure public-key encryption (PKE) scheme based on Module-LWE. For $n,q\in \mathbb{N}$, the underlying ring is ${\mathcal{R}}_q={\mathbb{Z}}_q\left[X\right]/(X^n+1)$, i.e., the ring of polynomials up to degree $n-1$ with coefficients in ${\mathbb{Z}}_q$. The corresponding module is ${\mathcal{R}}_q^k$ with rank $k\in \mathbb{N}$.

The following primitives are required: a noise space B, where sampling a value from B yields a random small integer value in the range $\{-4,...,4\}$. Additionally, for the KEM construction, secure hash functions $H_1,H_2$ and a secure key derivation function $KDF$ are required.

Internally, the plaintext encrypted by Kyber is a ring element $r\in {\mathcal{R}}_q$. Therefore, the input bitstring $m\in {\{0,1\}}^{256}$ is converted to a ring element $r=toRing\left(m\right)$, i.e., a polynomial, as follows:

$$\begin{array}{c}\hfill \left(\begin{array}{c}0\\ 0\\ 1\\ ⋮\\ 0\\ 1\end{array}\right)\stackrel{toRing}{\to }\left(\begin{array}{c}0\\ 0\\ \lceil \frac{q}{2}\rceil \\ ⋮\\ 0\\ \lceil \frac{q}{2}\rceil \end{array}\right)\iff 0+0·x+\frac{q}{2}·x^2+...+0·x^{n-2}+\frac{q}{2}·x^{n-1}\end{array}$$

It can already be observed that even after having added a vector with small coefficients the original polynomial can easily be reconstructed. The reverse operation $fromRing$ reconstructs a bitstring from a given ring element through coefficient-wise division by $\frac{q}{2}$ and subsequent rounding. The Kyber specification introduces encoding and compression functions, which we have simplified to the $toRing$ and $fromRing$ functions to increase readability and understanding.

Analogously to the general LWE-based encryption scheme described in Section 2.2, the Kyber key generation (Algorithm 1) instantiates a particular LWE problem, $As+e=b$, by generating coefficients A for the linear equation system and sampling a solution vector s as well as an error vector e.

Algorithm 1 Kyber PKE Key Generation: keyGen.

Input: none Generate $A\in {\mathcal{R}}_q^{k\times k}$ Sample $s\in {\mathcal{R}}_q^k$ with coefficients from B Sample $e\in {\mathcal{R}}_q^k$ with coefficients from B Calculate $b=As+e$ Output: public key $pk=(A,b)$, secret key s

The solution vector s functions as the secret key, while A and the vector $b=As+e$ are used as the public key. Calculating s from the public key would be identical to solving an instance of the LWE problem.

The Kyber PKE encryption (Algorithm 2) looks similar to the LWE-based encryption scheme introduced in Section 2.2 expanded to a Module-LWE setting.

Algorithm 2 Kyber PKE Encryption: enc,

Input: public key $pk=(A,b)$, message $m\in {\{0,1\}}^{256}$ Sample $r\in {\mathcal{R}}_q^k$ with coefficients from B Sample $e_1\in {\mathcal{R}}_q^k$ with coefficients from B Sample $e_2\in {\mathcal{R}}_q$ with coefficients from B Calculate $u=A^{T}r+e_1$ Calculate $v=b^{T}r+e_2+toRing\left(m\right)$ Output: ciphertext $c=(u,v)$

With knowledge of the secret value s, the reconstruction of the message m is possible through the corresponding Kyber PKE decryption routine (Algorithm 3).

Algorithm 3 Kyber PKE Decryption: dec

Input: secret key s, ciphertext $c=(u,v)$ Calculate $m^{*}=v-s^{T}u$ Output: message $m=fromRing\left(m^{*}\right)$

Applying the operation $fromRing\left(m^{*}\right)$ reconstructs the original m with very high probability. Indeed, the Kyber encryption scheme is a probabilistic algorithm returning the original message m with very high probability (see

Table 2. Kyber parameter sets with corresponding decryption failure probability $\delta$.

	n	k	q	$\mathit{\delta }$
Kyber512	256	2	3329	$2^{-139}$
Kyber768	256	3	3329	$2^{-164}$
Kyber1024	256	4	3329	$2^{-174}$

for concrete failure probability values), depending on the amount of noise within the sampled vectors.

To construct a CCA-secure KEM from the given PKE, a variant of the Fujisaki–Okamoto transformation (FO-transformation) is used. Fujisaki and Okamoto [11] presented the first generic transformation from asymmetric and symmetric encryption schemes to a secure hybrid encryption scheme. Later, Hofheinz, Hövelmanns and Kiltz [12] extended the work of Fujisaki and Okamoto and presented a generic transformation toolkit, including a transformation of a PKE scheme into a secure KEM. Algorithm 4 shows the Kyber KEM key generation.

Algorithm 4 Kyber KEM Key Generation.

Input: none Generate $\sigma \in {\{0,1\}}^{256}$ Generate $(pk,s)=PKE.keyGen\left(\right)$ Output: public key $pk$, secret key $sk=(s,\sigma )$

In the KEM encapsulation (Algorithm 5), observe that the value r is used in the underlying PKE as a seed for the generation of the otherwise random values during encryption. Although a deterministic public key encryption algorithm is usually not desirable, for a KEM, the receiver needs to be able to repeat the encryption procedure in the same way as the sender. We denote the deterministic version of the encryption routine with given seed r by $PKE.en{c}_r(pk,m)$. Furthermore, the message m is hashed before being fed to the PKE encryption routine.

Algorithm 5 Kyber KEM Encapsulation.

Input: public key $pk$ Generate message $m\in {\{0,1\}}^{256}$ Calculate $(K^{\prime },r)=H_1(H_2\left(m\right)\mid \mid H_2\left(pk\right))$ Calculate $c=PKE.en{c}_r(pk,H_2\left(m\right))$ Calculate $K=KDF(K^{\prime }\mid \mid H_2\left(c\right))$ Output: encapsulation c, shared secret K

The decapsulation routine (Algorithm 6) calculates the required values analogously to the encapsulation routine.

Algorithm 6 Kyber KEM Decapsulation.

Input: public key pk, secret key $sk=(s,\sigma )$, encapsulation c Calculate $H_m=PKE.dec(s,c)$ Calculate $(K^{\prime },r^{\prime })=H_1(H_m\mid \mid H_2\left(pk\right))$ Calculate $c^{\prime }=PKE.en{c}_{r^{\prime }}(pk,H_m)$ If $c=c^{\prime }$ set $K=KDF(K^{\prime }\mid \mid H_2\left(c\right))$ If $c\ne c^{\prime }$ set $K=KDF(\sigma \mid \mid H_2\left(c\right))$ Output: shared secret K

To gain some intuition of how ciphertext validation in Kyber works, have a look at the decryption process as described in detail in Section 2.2. In the Kyber PKE scheme, the message m is embedded within the difference of the vectors v and $s^{T}u$, i.e.,

$$\begin{array}{c}\hfill v-s^T·u=toRing\left(m\right)+(e^{T}r+e_2-s^T{e}_1),\end{array}$$

where $e,e_1,e_2$ are random error vectors. There are a lot of different combinations of values of these error terms that all correspond to the same m. In the KEM, however, the randomness becomes deterministic by deriving it from a chosen r, so there is a unique set of values $(e,e_1,e_2)$ for each m. This property establishes the required CCA-security of the KEM. When an adversary sends a random ciphertext to the decapsulation routine, it will always decipher to a message m, but the probability that the adversary has chosen the specific ciphertext (generated by the correct “random” terms) corresponding to m is negligible.

The Kyber instances with their corresponding parameter choices are shown in Table 2.

2.2.3. Saber

Saber [13] is a CCA-secure KEM derived from a CPA-secure PKE based on Module-LWR. For $n,q\in \mathbb{N}$, the underlying ring is ${\mathcal{R}}_q={\mathbb{Z}}_q\left[X\right]/(X^n+1)$, i.e., the ring of polynomials up to degree $n-1$ with coefficients in ${\mathbb{Z}}_q$. The corresponding module is ${\mathcal{R}}_q^k$ with rank $k\in \mathbb{N}$.

The following primitives are required: a noise space B, where sampling a value from B yields a random small integer value in the range $\{-5,...,5\}$. Additionally, for the KEM construction, secure hash functions $H_1,H_2,H_3$ and a secure key derivation function $KDF$ are required.

Saber’s rounding function does not strictly round down, as we have seen in the general case of LWR in Section 2.2; instead, it rounds to the median of each of the p intervals. (This is basically just the most naive approach for rounding.) This is implemented by adding half of the interval’s length $h\approx \frac{q}{2p}$ and subsequently rounding down, i.e., 

$${\lfloor x\rceil }_p:={\lfloor x+h\rfloor }_p.$$

To implement that efficiently, Saber only uses powers of 2 for the parameters q and p. This simplifies rounding to an addition followed by a bitwise shift.

Like Kyber, the Saber PKE (Algorithms 7–9) is based on the classic LWE-based encryption scheme introduced in Section 2.2. However, error addition is replaced by rounding. This is the only difference to the Kyber PKE presented in Section 2.2.2.

Algorithm 7 Saber PKE Key Generation: keyGen.

Input: none Generate $A\in {\mathcal{R}}_q^{k\times k}$ Sample $s\in {\mathcal{R}}_q^k$ with coefficients from B Calculate $b={\lfloor As\rceil }_p$ Output: public key $pk=(A,b)$, secret key s

Algorithm 8 Saber PKE Encryption: enc

Input: public key $pk=(A,b)$, message $m\in {\{0,1\}}^{256}$ Sample $r\in {\mathcal{R}}_q^k$ with coefficients from B Calculate $u={\lfloor A^{T}r\rceil }_p$ Calculate $v={\lfloor b^{T}r+toRing\left(m\right)\rceil }_p$ Output: ciphertext $c=(u,v)$

Algorithm 9 Saber PKE Decryption: dec

Input: secret key s, ciphertext $c=(u,v)$ Calculate $m^{*}=v-s^{T}u$ Output: message $m=fromRing\left(m^{*}\right)$

Analogously to Kyber, to construct a CCA-secure KEM from the given PKE, a variant of the FO-transformation is used. In fact, the key generation algorithm (Algorithm 10) is completely identical.

Algorithm 10 Saber KEM Key Generation.

Input: none Generate $\sigma \in {\{0,1\}}^{256}$ Generate $(pk,s)=PKE.keyGen\left(\right)$ Output: public key $pk$, secret key $sk=(s,\sigma )$

Again, the KEM construction (Algorithms 11 and 12) is very similar to Kyber. The only structural difference is the absent additional hash function used on the message m.

Algorithm 11 Saber KEM Encapsulation.

Input: public key $pk$ Generate message $m\in {\{0,1\}}^{256}$ Calculate $(K^{\prime },r)=H_2(H_1\left(pk\right)\mid \mid m)$ Calculate $c=PKE.en{c}_r(pk,m)$ Calculate $K=H_3(K^{\prime }\mid \mid c)$ Output: encapsulation c, shared secret K

Algorithm 12 Saber KEM Decapsulation.

Input: public key pk, secret key $sk=(s,\sigma )$, encapsulation c Calculate $m^{\prime }=PKE.dec(sk,c)$ Calculate $(K^{\prime },r^{\prime })=H_2(H_1\left(pk\right)\mid \mid m^{\prime })$ Calculate $c^{\prime }=PKE.en{c}_{r^{\prime }}(pk,m^{\prime })$ If $c=c^{\prime }$ set $K=H_3(K^{\prime }\mid \mid c)$ If $c\ne c^{\prime }$ set $K=H_3(\sigma \mid \mid c)$ Output: shared secret K

The Saber instances with their corresponding parameter choices are shown in

Table 3. Saber parameter sets with corresponding decryption failure probability $\delta$.

	n	k	q	p	$\mathit{\delta }$
LightSaber	256	2	$2^{13}$	$2^{10}$	$2^{-120}$
Saber	256	3	$2^{13}$	$2^{10}$	$2^{-136}$
FireSaber	256	4	$2^{13}$	$2^{10}$	$2^{-165}$

.

2.2.4. Dilithium

Dilithium [14] is a signature scheme based on Module-LWE. For $n,q\in \mathbb{N}$, the underlying ring is ${\mathcal{R}}_q={\mathbb{Z}}_q\left[X\right]/(X^n+1)$, i.e., the ring of polynomials up to degree $n-1$ with coefficients in ${\mathbb{Z}}_q$. The corresponding module is ${\mathcal{R}}_q^l$ with rank $l\in \mathbb{N}$. Additionally, Dilithium requires a secure hash function H.

The key generation (Algorithm 13) is almost identical to Kyber’s key generation. An LWE instance is generated, i.e., a matrix $A\in {\mathcal{R}}_q^{k\times l}$ with $k\in \mathbb{N}$, a secret vector $s\in {\mathcal{R}}_q^l$ and an error term $e\in {\mathcal{R}}_q^k$. As usual, A and b are public, while s is kept private.

Algorithm 13 Dilithium Key Generation: keyGen.

Input: none Generate $A\in {\mathcal{R}}_q^{k\times l}$ Sample $s\in {\mathcal{R}}_q^l$ with small coefficients Sample $e\in {\mathcal{R}}_q^k$ with small coefficients Calculate $b=As+e$ Output: public key $pk=(A,b)$, secret key s

Dilithium’s signing process (Algorithm 14) is probabilistic. In the first step, a random vector $y\in {\mathcal{R}}_q^l$ is sampled. As we will see in the verification process, to achieve correctness, we will use the rounded version of $Ay$ by means of a function $round\left(\right)$. This function takes a given vector of polynomials and rounds each coefficient of every polynomial. The signature is formed by calculating a pair $(z,c)$, where c is formed by hashing the message m and the value $round\left(Ay\right)$. The hash function H maps an input to a polynomial with coefficients in $\{-1,0,1\}$.

Due to the fact that z depending on the secret key, s potentially leads to serious security issues, and z is not output directly. Instead, in order to remove the statistical dependencies between z and s, Dilithium follows a so-called rejection sampling approach. For the details of rejection sampling, we refer to [15,16]. In case z is rendered invalid (’rejected’), the algorithm restarts from step 1.

Algorithm 14 Dilithium Signature generation.

Input: public key $pk=(A,b)$, secret key s, message $m\in {\{0,1\}}^{☆}$ Until z is valid: Sample $y\in {\mathcal{R}}_q^l$ with small coefficients Calculate $w=round\left(Ay\right)$ Calculate $c=H(m\mid \mid w)$ Calculate $z=y+cs$ Output: signature $\sigma =(z,c)$

Given a correct signature $\sigma$, it is possible to recover w using the following calculation:

$$\begin{array}{cc}\hfill round(Az-bc)& =round\left(A\right(y+cs)-(As+e\left)c\right)\hfill \\ \hfill & =round(Ay+Acs-Acs-ce)\hfill \\ \hfill & =round(Ay-ce)\hfill \\ \hfill & =w\hfill \end{array}$$

To indeed recover w, the last step requires $round(Ay-ce)=round\left(Ay\right)$. Since c and e both have small coefficients, their product $ce$ does not influence the outcome of the rounding. In order to verify the signature, we can use a recovered $w^{\prime }$ to recalculate $c^{\prime }=H(m\mid \mid w^{\prime })$ and compare it to the provided signature value c (Algorithm 15). Observe that if z has not been calculated by using the secret key s, i.e., by $z=y+cs$, the terms $Acs$ would not cancel in the equation above leading to an incorrect $w^{\prime }\ne w$. Hence, the value $c^{\prime }$ would be incorrect as well leading to a rejection of the provided signature.

Algorithm 15 Dilithium Verification.

Input: public key $pk=(A,b)$, message $m\in {\{0,1\}}^{☆}$, signature $\sigma =(z,c)$ Calculate $w^{\prime }=round(Az-bc)$ Calculate $c^{\prime }=H(m\mid \mid w^{\prime })$ Output: valid if $c=c^{\prime }$, else invalid

The Dilithium instances with their corresponding parameter choices are shown in

Table 4. Dilithium parameter sets for NIST security levels 2, 3 and 5 with corresponding expected number of needed repetitions #reps of signature generation.

	n	(k,l)	q	#reps
Dilithium 2	256	(4,4)	8380417	4.25
Dilithium 3	256	(6,5)	8380417	5.1
Dilithium 5	256	(8,7)	8380417	3.85

.

2.3. NTRU-Based Cryptography

2.3.1. NTRU Fundamentals

The NTRU Assumption

NTRU is a lattice-based cryptosystem, which was first developed by Hoffstein, Pipher and Silverman in 1996. It originates from the two well-known schemes NTRUEncrypt and NTRUSign. For its abbreviation, “NTRU”, one can find multiple explanation attempts, for example: n-th degree truncated polynomial ring or ’number theorists r us’. As the former indicates, NTRU’s operations take place in the ring of truncated polynomials ${\mathcal{R}}_q={\mathbb{Z}}_q\left[X\right]/(X^n-1)$, where n and q are two positive coprime integers and ${\mathbb{Z}}_q=\mathbb{Z}/q\mathbb{Z}$ denotes the ring of integers modulo q. Therefore, ${\mathcal{R}}_q$ is the ring of all polynomials of degree $<n$ with coefficients in ${\mathbb{Z}}_q$.

Similar to RSA, where it cannot be proven that breaking RSA is as hard as integer factorization, the security of NTRU underlies just a hardness assumption. Let the notation $\stackrel{\mathcal{R}}{\equiv }$ denote congruence in the ring $\mathcal{R}$. The so-called NTRU assumption states that the following task is difficult to solve:

Given $h\in {\mathcal{R}}_q$, find ternary polynomials $f,g\in {\mathbb{Z}}_3\left[X\right]/(X^n-1)$ (a ternary polynomial has coefficients in ${\mathbb{Z}}_3$) such that

$$\begin{array}{c}\hfill f·h\stackrel{{\mathcal{R}}_q}{\equiv }g.\end{array}$$

Later, we will see that this can actually be solved as a shortest vector problem.

NTRU-Based Encryption Schemes

This section will provide an overview of the main theory used to build NTRU cryptosystems. To build a cryptosystem around the NTRU assumption, we need two primes, n and p, as well as an integer, q, which is coprime to both. Furthermore, p is significantly smaller than q; in our case, we always have $p=3$. These integers will define the rings

$$\begin{array}{ccc}\hfill {\mathcal{R}}_q={\mathbb{Z}}_q\left[X\right]/(X^n-1)& \hfill & \hfill {\mathcal{R}}_p={\mathbb{Z}}_p\left[X\right]/(X^n-1)={\mathcal{R}}_3={\mathbb{Z}}_3\left[X\right]/(X^n-1),\end{array}$$

in which the operations take place.

In the first step, we sample two ternary polynomials $f,g\in {\mathcal{R}}_3$, where f needs to be invertible in ${\mathcal{R}}_3$ and ${\mathcal{R}}_q$. Then, we need to calculate said inverses:

$$\begin{array}{ccc}\hfill f_q:=f^{-1}\in {\mathcal{R}}_q& \hfill & \hfill f_3:=f^{-1}\in R_3\end{array}$$

While $f_q$ is used to calculate the public key:

$$\begin{array}{c}\hfill h\stackrel{{\mathcal{R}}_q}{\equiv }{f}_q·g,\end{array}$$

f and $f_3$ serve as the secret key. It is now easy to see that deriving the secret key from the public key provides a solution to the NTRU assumption.

To now encrypt a message $m\in {\mathcal{R}}_3$, we need another random ternary polynomial $r\in {\mathcal{R}}_3$ and calculate the ciphertext as:

$$\begin{array}{c}\hfill c\stackrel{{\mathcal{R}}_q}{\equiv }p·r·h+m=3·r·h+m\end{array}$$

The r ensures that encryption is not deterministic, while multiplication by 3 enables correct decryption, as we are about to see.

The decryption process then consists of two steps. First, we calculate:

$$\begin{array}{cc}\hfill a& =f·c\hfill \\ \hfill & =f·(3·r·h+m)\hfill \\ \hfill & =f·f_q·3·r·g+f·m\hfill \\ \hfill & \stackrel{{\mathcal{R}}_q}{\equiv }3·r·g+f·m\hfill \end{array}$$

The second step is calculated in ${\mathcal{R}}_3$, which ensures that the first term of a vanishes. Multiplying by $f_3$ then leads to the original message m:

$$\begin{array}{cc}\hfill f_3·a& =f_3·(3·r·g+f·m)\hfill \\ \hfill & \stackrel{{\mathcal{R}}_3}{\equiv }m\hfill \end{array}$$

The attentive reader might ask why the condition $p\ll q$ is obligatory, and indeed, this is not clearly evident. The problem lies in the transition between ${\mathcal{R}}_q$ and ${\mathcal{R}}_p$. It is vital for flawless decryption that $a=p·r·g+f·m$ does not only hold true in ${\mathcal{R}}_q$ but also in $\mathbb{Z}\left[X\right]$. To be more precise, if the coefficients of $p·r·g+f·m$ become a reduced mod q, a reduction mod p would not yield m.

In conclusion, the correctness is assured if this calculation yields a polynomial of degree $<n$ and coefficients $<q$. Since $r,g,f,m\in {\mathcal{R}}_p$ have small coefficients, it is sufficient to require $p\ll q$.

Another observable fact is that the decryption process also establishes the possibility to obtain the message m without the knowledge of f. Indeed (according to the NTRU assumption), it is sufficient for an adversary to find any ternary polynomial $\widehat{f}$ such that $\widehat{f}·h$ is again ternary modulo q, since this still ensures that $\widehat{f}·c$ does not become reduced modulo q and the subsequent reduction modulo p would yield m. The authors showed in [17] that in all likelihood the only polynomials with this property are just rotations of f (i.e., polynomials obtained by cyclically rotating the coefficients of f).

Linking NTRU to Computational Lattice Problems

To get an idea of the connection between lattices and NTRU, consider the lattice:

$$\begin{array}{c}\hfill \mathcal{L}=\{(u,v)\in {\mathcal{R}}_q\times {\mathcal{R}}_q\mid u·h\stackrel{{\mathcal{R}}_q}{\equiv }v)\}.\end{array}$$

consisting of every possible solution for a fixed NTRU assumption given $h\in {\mathcal{R}}_q$.

In the following, all calculations are reduced modulo $(X^n-1)$, and we therefore write $u·h=v\mathrm{mod}q$. To find a basis of $\mathcal{L}$, observe that every $(u,v)\in \mathcal{L}$ equivalently fulfills:

$$\begin{array}{c}\hfill u·h-k·q=v\end{array}$$

for some $k\in {\mathcal{R}}_q$. This can be rewritten as:

$$\left(\begin{array}{c}u\\ v\end{array}\right)=\left(\begin{array}{cc}1& 0\\ h& q\end{array}\right)·\left(\begin{array}{c}u\\ -k\end{array}\right)$$

in an equivalent form. Using the coefficients of $u={\sum }_{i=0}^{n-1}{u}_i{x}^i$, $v={\sum }_{i=0}^{n-1}{v}_i{x}^i$, $h={\sum }_{i=0}^{n-1}{h}_i{x}^i$ and $k={\sum }_{i=0}^{n-1}{k}_i{x}^i$, this can be transformed into:

$$\left(\begin{array}{c}{u}_0\\ u_1\\ ⋮\\ u_{n-1}\\ v_0\\ v_1\\ ⋮\\ v_{n-1}\end{array}\right)=\left(\begin{array}{cccccccc}1& 0& \cdots & 0& 0& 0& \cdots & 0\\ 0& 1& \cdots & 0& 0& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1& 0& 0& \cdots & 0\\ h_0& h_1& \cdots & h_{n-1}& q& 0& \cdots & 0\\ h_{n-1}& h_0& \cdots & h_{n-2}& 0& q& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& \ddots & ⋮\\ h_1& h_2& \cdots & h_0& 0& 0& \cdots & q\end{array}\right)·\left(\begin{array}{c}{u}_0\\ u_1\\ ⋮\\ u_{n-1}\\ -k_0\\ -k_1\\ ⋮\\ -k_{n-1}\end{array}\right)$$

Defining $M_h$ as the bottom-left quadrant, it is easy to see that the matrix

$$\left(\begin{array}{cc}{I}_n& 0_n\\ M_h& q·I_n\end{array}\right)$$

defines a basis of the lattice $\mathcal{L}$. It is obvious that $(f,g)\in \mathcal{L}$, and since $f,g\in {\mathcal{R}}_3$, it is also a rather short vector. Furthermore, it can be shown that with overwhelming probability $(f,g)$ is indeed the shortest vector of $\mathcal{L}$. Therefore, being able to solve an SVP also enables finding the secret key of any NTRU cryptosystem.

2.3.2. NTRU

Even though the NIST round three submission of NTRU [18] is mainly based on the generic NTRU encryption scheme we have just seen, it contains a few major differences that need further explanation. The most obvious change regards the underlying polynomial rings. Before, we just considered the two truncated polynomial rings ${\mathcal{R}}_q={\mathbb{Z}}_q\left[X\right]/(X^n-1)$ and ${\mathcal{R}}_p={\mathbb{Z}}_p\left[X\right]/(X^n-1)$ that were both generated by $(X^n-1)$. Instead, we consider polynomial rings that are generated by the three polynomials

$$\begin{array}{ccccc}{\varphi }_1=(X-1)& & {\varphi }_n=\frac{X^n-1}{X-1}& & {\varphi }_1{\varphi }_n=(X^n-1).\end{array}$$

To differentiate the corresponding rings, we introduce the following notation:

$${\mathcal{R}}_k^{\varphi }:={\mathbb{Z}}_k\left[X\right]/\varphi$$

For example, the formerly used ${\mathcal{R}}_3$ is now denoted as ${\mathcal{R}}_3^{{\varphi }_1{\varphi }_n}$.

The key generation (Algorithm 16) mainly consists of the same steps as in the generic NTRU construction. The difference is that sampling and operations take place in different rings and spaces. Note that g is always a multiple of ${\varphi }_1$. Other than that, the step of calculating the inverse $h_q$ is added. All these modifications aim to add another layer of security against forging ciphertexts, as we will see in the decryption step.

Algorithm 16 NTRU PKE Key Generation: keyGen.

Input: none Sample $f\in {\mathcal{R}}_3^{{\varphi }_n}$ Sample $g\in \{{\varphi }_1·v\mid v\in {\mathcal{R}}_3^{{\varphi }_n}\}$ Calculate $f_q=f^{-1}\in {\mathcal{R}}_q^{{\varphi }_n}$ Calculate $h\stackrel{{\mathcal{R}}_q^{{\varphi }_1{\varphi }_n}}{\equiv }g·f_q$ Calculate $h_q=h^{-1}\in {\mathcal{R}}_q^{{\varphi }_n}$ Calculate $f_3=f^{-1}\in {\mathcal{R}}_3^{{\varphi }_n}$ Output: public key h, secret key $sk=(f,f_p,h_q)$

The encryption process (Algorithm 17) only differs in using a lift-function on the message m before encryption. Let ${(m·{\varphi }_1^{-1})}_{{\mathcal{R}}_3^{{\varphi }_n}}$ denote a calculation within the ring ${\mathcal{R}}_3^{{\varphi }_n}$, then:

$$Lift\left(m\right)={\varphi }_1·{(m·{\varphi }_1^{-1})}_{{\mathcal{R}}_3^{{\varphi }_n}}.$$

It is easy to see that $Lift\left(m\right)\stackrel{{\mathcal{R}}_3^{{\varphi }_n}}{\equiv }m$. Now, as a consequence of g and $\widehat{m}$ being multiples of ${\varphi }_1$, the same is true for c.

Algorithm 17 NTRU PKE Encryption: enc.

Input: public key h, message $m\in {\mathcal{R}}_3^{{\varphi }_n}$ Calculate $\widehat{m}=Lift\left(m\right)$ Sample $r\in {\mathcal{R}}_3^{{\varphi }_n}$ Calculate $c\stackrel{{\mathcal{R}}_q^{{\varphi }_1{\varphi }_n}}{\equiv }3·r·h+\widehat{m}$ Output: ciphertext c

The decryption differs the most compared to the general NTRU construction and therefore requires further explanation. In case of a correctly encrypted message m, deciphering takes place in steps 2 and 3. It is not obvious that the calculation in step 2 still yields the same result as in the general NTRU scheme since $f_q$ is the inverse in ${\mathcal{R}}_q^{{\varphi }_n}$ and not in ${\mathcal{R}}_q^{{\varphi }_1{\varphi }_n}$.

Using the fact that g is a multiple of ${\varphi }_1$ and $f_q$ is the inverse of f in ${\mathcal{R}}_q^{{\varphi }_n}$, we can equivalently say

$$\begin{array}{cccc}\hfill g& ={\varphi }_1·v\hfill & \hfill & \mathrm{for}\mathrm{some}v\in {\mathcal{R}}_3^{{\varphi }_n}\hfill \end{array}$$

(1)

$$\begin{array}{cccc}\hfill f·f_q& =1+k·{\varphi }_n\hfill & \hfill & \mathrm{for}\mathrm{some}k\in \mathbb{Z}\left[X\right]\hfill \end{array}$$

(2)

Step 2 then resolves to

$$\begin{array}{cc}\hfill a& =f·c\hfill \\ \hfill & =f·f_q·3·r·g+f·\widehat{m}\hfill & \hfill & \mid \left(2\right)\hfill \\ \hfill & =(1+k·{\varphi }_n)·3·r·g+f·\widehat{m}\hfill & \hfill & \mid \left(1\right)\hfill \\ \hfill & =3·r·g+k·{\varphi }_n·{\varphi }_1·v·3·r+f·\widehat{m}\hfill & \hfill & \mid {\varphi }_1{\varphi }_n\stackrel{{\mathcal{R}}_q^{{\varphi }_1{\varphi }_n}}{\equiv }0\hfill \\ \hfill & \stackrel{{\mathcal{R}}_q^{{\varphi }_1{\varphi }_n}}{\equiv }3·r·g+f·\widehat{m}\hfill \end{array}$$

Finally, we can obtain m in step 3 since $f_3$ is indeed the inverse in the considered ring ${\mathcal{R}}_3^{{\varphi }_n}$ by calculating

$$\begin{array}{cc}\hfill a·f_3& =3·r·g·f_3+f·f_3·\widehat{m}\hfill \\ \hfill & \stackrel{{\mathcal{R}}_3^{{\varphi }_n}}{\equiv }m\hfill \end{array}$$

The first term vanishes since it is a multiple of 3, and as seen before, $\widehat{m}=Lift\left(m\right)\stackrel{{\mathcal{R}}_3^{{\varphi }_n}}{\equiv }m$.

The decryption (Algorithm 18) contains a built-in validation process, which justifies the additional steps. As shown later, this enables the construction of a KEM that avoids re-encryption (in contrast to classic FO-transformation).

The first step validates whether or not c is a multiple of ${\varphi }_1$, which is true for any correctly generated ciphertext, as seen before. In order to verify that r is correctly sampled from ${\mathcal{R}}_3^{{\varphi }_n}$ (step 6 and 7), step 4 and 5 retrieve r using $c,Lift\left(m\right)$ and $h_q$. If any of the validation steps fail, the procedure returns the error vector $(0,0,1)$; otherwise, $(r,m,0)$ is returned.

Algorithm 18 NTRU PKE Decryption: dec.

Input: secret key sk = $(f,f_p,h_q)$, ciphertext c if $c\stackrel{{\mathcal{R}}_q^{{\varphi }_1}}{\not\equiv }0$ return $(0,0,1)$ Calculate $a\stackrel{{\mathcal{R}}_q^{{\varphi }_1{\varphi }_n}}{\equiv }f·c$ Calculate $m\stackrel{{\mathcal{R}}_3^{{\varphi }_n}}{\equiv }a·f_3$ Calculate $\widehat{m}=Lift\left(m\right)$ Calculate $r\stackrel{{\mathcal{R}}_q^{{\varphi }_n}}{\equiv }(c-\widehat{m})·\frac{h_q}{3}$ if $r\in {\mathcal{R}}_3^{{\varphi }_n}$ return $(r,m,0)$ else return $(0,0,1)$ Output: Correct $(r,m,0)$ or error $(0,0,1)$

Constructing the NTRU KEM is now straightforward. The key generation (Algorithm 19) simply calls PKE.keyGen() and samples a random value $\sigma$, which is later used in the decapsulation for implicit rejection.

Algorithm 19 NTRU KEM Key Generation.

Input: none Generate $(h,(f,f_p,h_q))=$ PKE.keyGen() Sample $\sigma \in {\{0,1\}}^{256}$ Output: public key h, secret key $sk=(f,f_p,h_q,\sigma )$

Encapsulation (Algorithm 20) consists of three steps: Random sampling $r,m\in {\mathcal{R}}_3^{{\varphi }_n}$, generating the ciphertext using PKE.enc() and calculating the shared secret K as the hash of r and m with some cryptographic hash function $H_1$.

Algorithm 20 NTRU KEM Encapsulation.

Input: public key h Sample $r,m\in {\mathcal{R}}_3^{{\varphi }_n}$ Calculate $c={\mathrm{PKE}.\mathrm{enc}}_r(h,m)$ $K=H_1(r\mid \mid m)$ Output: encapsulation c, shared secret K

Decapsulation (Algorithm 21) starts with the decryption of c using PKE.dec(). Next, two hashes are calculated, the correct one as a hash of r and m and a decoy as a hash of the sampled values s and c with some cryptographic hash function $H_2$. In case of valid decryption, the former is returned; otherwise, the decoy value is returned.

Algorithm 21 NTRU KEM Decapsulation.

Input: secret key sk = $(f,f_p,h_q,\sigma )$, encapsulation c $(r,m,fail)=$ PKE.dec($(f,f_p,h_q),c$) $k_1=H_1(r\mid \mid m)$ $k_2=H_2(\sigma \mid \mid c)$ if ($fail=0$) set $K=k_1$ else set $K=k_2$ Output: shared secret K

The NTRU submission recommends two different families of parameter sets, which are referred to as NTRU-HRSS and NTRU-HPS. The explanations of this section regard NTRU-HRSS, but the details of both can be found in the algorithm specification [18].

2.3.3. Falcon

Falcon [19] is a signature scheme based on the Gentry–Peikert–Vaikuntanathan (GPV) signature scheme using the NTRU structure [20]. On a very high level, the underlying idea of the GPV framework is as follows. The public key is a full-rank matrix $A\in {\mathbb{Z}}_q^{n\times m}$ (with $m>n$) generating a lattice L, while the secret key is a matrix $B\in {\mathbb{Z}}_q^{m\times m}$ generating a corresponding lattice $L_q^{\perp }$. The lattices L and $L_q^{\perp }$ are orthogonal modulo q, meaning that

$$\forall x\in L,y\in L_q^{\perp }:\langle x,y\rangle =0\mathrm{mod}q.$$

Equivalently, the rows of A and B are pairwise orthogonal, i.e., $B·A^t=0$ mod q.

Given a hash $H\left(m\right)$ of some arbitrary message m and a hash-function H that maps onto L, a valid signature s has to fulfill two properties:

1.

$A·s=H\left(m\right)$ mod q;

2.

$\parallel s\parallel <\beta$ for some boundary $\beta$, i.e., s has to be short.

A solution s satisfying the first property can be easily computed using standard linear algebra; however, additionally considering the second property, finding a valid s is much harder. These requirements are almost identical to the short integer solution problem (SIS), the only difference being that an SIS solution s fulfills $A·s=0$ mod q instead. The SIS problem is average-case-hard and reducible to SVP [21].

However, with knowledge of the secret matrix B, a valid signature s can be efficiently computed. The first step is to find any solution $s^{\prime }$ to the first requirement $A·s^{\prime }=H\left(m\right)$. Afterwards, a sufficiently close vector v in the orthogonal lattice $L_q^{\perp }$ needs to be found. Knowing B, this can be achieved using an efficient CVP approximation algorithm such as Babai’s Algorithm [22] satisfying $\parallel s^{\prime }-v\parallel <\beta$.

Finally, $s=s^{\prime }-v$ forms a valid signature since $A·s=A·s^{\prime }-A·v=H\left(m\right)-0$ due to v being orthogonal to the rows of A.

The overall framework of Falcon is quite similar to GPV and uses the basic idea of the NTRU scheme to generate the required lattices. Similar to NTRU, Falcon’s operations take place in the ring of truncated polynomials ${\mathcal{R}}_q={\mathbb{Z}}_q\left[X\right]/(X^n+1)$, where n and q are two positive coprime integers and ${\mathbb{Z}}_q=\mathbb{Z}/q\mathbb{Z}$ denotes the ring of integers modulo q. Therefore, ${\mathcal{R}}_q$ is the ring of all polynomials of degree $<n$ with coefficients in ${\mathbb{Z}}_q$.

For the key generation (Algorithm 22) a set of four polynomials $f,g\in {\mathcal{R}}_q$ and $F,G\in \mathcal{R}=\mathbb{Z}\left[x\right]/(X^n+1)$ that fulfills

$$\begin{array}{c}\hfill fG-gF=q\mathrm{mod}(X^n+1)\end{array}$$

is needed. Afterwards, analogously to NTRU, we calculate $h=g·f^{-1}\in {\mathcal{R}}_q$. From these polynomials, we can generate the public key matrix $A\in {\mathbb{Z}}_q^{n\times 2n}$ and the secret key matrix $B\in {\mathbb{Z}}_q^{2n\times 2n}$ as

$$\begin{array}{ccc}\hfill A=\left(\begin{array}{cc}1& h\end{array}\right)& \hfill & \hfill B=\left(\begin{array}{cc}g& -f\\ G& -F\end{array}\right),\end{array}$$

where every polynomial is represented as its corresponding matrix (see Section 2.3.1 for notation details).

It is easy to check that

$$\begin{array}{cc}\hfill B·A^t& =\left(\begin{array}{c}g-hf\\ G-hF\end{array}\right)=\left(\begin{array}{c}g-\left(g{f}^{-1}\right)f\\ G-\left(g{f}^{-1}\right)F\end{array}\right)=\left(\begin{array}{c}g-g\\ f^{-1}f(G-g{f}^{-1}F)\end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{c}0\\ f^{-1}(fG-gF)\end{array}\right)=\left(\begin{array}{c}0\\ f^{-1}q\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)modq\hfill \end{array}$$

indeed holds.

Algorithm 22 Falcon Key Generation.

Input: none Sample $f,g\in {\mathcal{R}}_q$ Find $F,G\in \mathcal{R}$ such that $f·G-g·F=q$ mod $(X^n+1)$ Calculate $h=g·f^{-1}$ Output: public key h, secret key $sk=(f,g,F,G)$

To make a Falcon signature probabilistic, a random $r\in {\{0,1\}}^{320}$ is sampled and used to generate the hash $c=H(r\mid \mid m)$ with some cryptographic hash function H. Due to the construction of $A=\left(\begin{array}{cc}1& h\end{array}\right)$, finding an $s^{\prime }$ satisfying property 1 is easy. Since

$$\left(\begin{array}{cc}1& h\end{array}\right)·\left(\begin{array}{c}c\\ 0\end{array}\right)=c$$

holds, we can always use $s^{\prime }={(c,0)}^{\top }$. As described above, we are looking for a vector $v\in L_q^{\perp }$ close to $s^{\prime }$. Falcon does that using a variant of Babai’s algorithm [23]. Then, the difference $s^{\prime }-v$ satisfies properties 1 and 2 and forms a valid signature (Algorithm 23).

To increase security, only the second component of $s={(s_1,s_2)}^{\top }={(c-v_1,-v_2)}^{\top }$ is transmitted, which is already sufficient to verify the validity of s. Due to

$$A·s=\left(\begin{array}{cc}1& h\end{array}\right)·\left(\begin{array}{c}{s}_1\\ s_2\end{array}\right)=s_1+h·s_2=c,$$

we can see that $s_1$ just represents a shift by a small constant.

Algorithm 23 Falcon Signature generation.

Input: secret key sk = $(f,g,F,G)$, message $m\in {\{0,1\}}^{☆}$ Sample $r\in {\{0,1\}}^{320}$ Calculate $c=H(r\mid \mid m)$ Set $s^{\prime }={(c,0)}^{\top }$ Find $v\in L_q^{\perp }$ with $\parallel s^{\prime }-v\parallel <\beta$ Calculate ${(s_1,s_2)}^{\top }=s^{\prime }-v={(c-v_1,-v_2)}^{\top }$ Output: signature $\sigma =(r,s_2)$

Analogously to the signature generation, for verification (Algorithm 24), the message m is hashed together with the provided r. Assuming $s_2$ was correctly generated, the missing value $s_1$ can be calculated by

$$s_1=A·\left(\begin{array}{c}c\\ -s_2\end{array}\right)=c-s_2·h$$

and is declared valid if it is sufficiently small, i.e., $\parallel {(s_1,s_2)}^{\top }\parallel <\beta$.

Algorithm 24 Falcon Verification.

Input: public key h, message $m\in {\{0,1\}}^{☆}$, signature $\sigma =(r,s_2)$ Calculate $c=H(r\mid \mid m)$ Calculate $s_1=c-s_2·h$ Output: valid if $\parallel {(s_1,s_2)}^{\top }\parallel <\beta$, else invalid

The Falcon instances with their corresponding parameter choices are shown in

Table 5. Falcon parameter sets.

	n	q
Falcon-512	512	12,289
Falcon-1024	1024	12,289

.

3. Code-Based Cryptography

3.1. Linear Code Fundamentals

Error-correcting codes are a standard approach to detect and correct communication errors that might happen due to noise during transmission. This technique can be applied to the construction of cryptographic systems where errors are intentionally inserted and can only be corrected by the intended receiver.

3.1.1. Linear Codes

Definition 3

(hamming weight, hamming distance). For a given vector $x=(x_1,\cdots ,x_n)\in {\mathbb{F}}_2^n$, we call

$$weight\left(x\right)=\sum _{i=1}^n{x}_i$$

the hamming weight of x. Note that this simply counts the number of entries equal to 1.

Given another vector $y=(y_1,\cdots ,y_n)\in {\mathbb{F}}_2^n$, we call

$$dist(x,y)=\sum _{i=1}^n\mid x_i-y_i\mid$$

thehamming distance, which denotes the number of bits in which x and y differ.

Definition 4

(inear code). Let $\mathcal{C}$ be a linear subspace of the vector space ${\mathbb{F}}_2^n$ with dimension k. Furthermore, let

$$d=\underset{\begin{array}{c}{c}_i,c_j\in \mathcal{C}\\ c_i\ne c_j\end{array}}{min}dist(c_i,c_j)$$

be the minimum distance of two distinct elements of $\mathcal{C}$.

$\mathcal{C}$ is calledlinear codeor, equivalently, $(\mathbf{n},\mathbf{k},\mathbf{d})-\mathit{c}\mathit{o}\mathit{d}\mathit{e}$. The elements of $\mathcal{C}$ are called codewords.

Elements of an $(n,k,d)$-code $\mathcal{C}$ are binary vectors of length n. However, since $\mathcal{C}$ has dimension k, only k entries can be arbitrarily chosen, and this choice already defines the remaining $n-k$ entries. This means we end up with vectors of length n containing only k bits of non-redundant information. Therefore, it is possible to represent $\mathcal{C}$ as the span of k linear independent codewords $c_1,\cdots ,c_k\in \mathcal{C}$, i.e., 

$$\mathcal{C}=\{G·x\mid x\in {\mathbb{F}}_2^k\},$$

where $G\in {\mathbb{F}}_2^{n\times k}$ with codewords $c_1,\cdots ,c_k$ as columns. G is called generator matrix of $\mathcal{C}$. We can transform G to its standard form (this definition deviates a little from standard literature; however, it is more useful in the context of Classic McEliece). $G^{\prime }={(T^{\top }\mid \mid I_k)}^{\top }$, where $I_k$ is the $k\times k$ identity matrix and $T\in {\mathbb{F}}_2^{(n-k)\times k}$.

Given a generator matrix $G^{\prime }={(T^{\top }\mid \mid I_k)}^{\top }$ in standard form, there is a neat way to check whether a given word $c\in {\mathbb{F}}_2^n$ is a valid codeword, i.e., an element of $\mathcal{C}$. Let $H=(I_{n-k}\mid \mid -T)\in {\mathbb{F}}_2^{(n-k)\times n}$ and $c\in {\mathbb{F}}_2^n$ be a valid codeword, i.e., $c=G·x$ for some $x\in {\mathbb{F}}_2^k$. Then,

$$\begin{array}{cc}\hfill H·c& =H·(G^{\prime }·x)\hfill \\ \hfill & =(H·G^{\prime })·x\hfill \\ \hfill & =\underset{(n-k)+k}{\underbrace{\left(\begin{array}{cccccccc}1& 0& \cdots & 0& -t_{1,1}& -t_{1,2}& \cdots & -t_{1,k}\\ 0& 1& \cdots & 0& -t_{2,1}& -t_{2,2}& \cdots & -t_{2,k}\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1& -t_{n-k,1}& -t_{n-k,2}& \cdots & -t_{n-k,k}\end{array}\right)}}·\underset{k}{\underbrace{\left(\begin{array}{cccc}{t}_{1,1}& t_{1,2}& \cdots & t_{1,k}\\ t_{2,1}& t_{2,2}& \cdots & t_{2,k}\\ ⋮& ⋮& \ddots & ⋮\\ t_{n-k,1}& t_{n-k,2}& \cdots & t_{n-k,k}\\ 1& 0& \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}\right)}}·x\hfill \\ \hfill & =\left(\begin{array}{cccc}{t}_{1,1}-t_{1,1}& t_{1,2}-t_{1,2}& \cdots & t_{1,k}-t_{1,k}\\ t_{2,1}-t_{2,1}& t_{2,2}-t_{2,2}& \cdots & t_{2,k}-t_{2,k}\\ ⋮& ⋮& ⋮& ⋮\\ t_{n-k,1}-t_{n-k,1}& t_{n-k,2}-t_{n-k,2}& \cdots & t_{n-k,k}-t_{n-k,k}\end{array}\right)·x\hfill \\ \hfill & =0\in {\mathbb{F}}_2^{n-k}\hfill \end{array}$$

equals the zero-vector in ${\mathbb{F}}_2^{n-k}$ for any codeword c. Because of this property, H is called the parity check matrix. Indeed, the condition $H·c=0$ holds if and only if c is a valid codeword.

Therefore, a linear code $\mathcal{C}$ can equivalently be defined via its parity check matrix H since $\mathcal{C}$ is exactly the kernel of the map H, so $\mathcal{C}=\{x\in {\mathbb{F}}_2^n\mid H·x=0\}$. This also motivates the following definition.

Definition 5

(syndrome). Let $\mathcal{C}$ be a linear code with parity check matrix H and $x\in {\mathbb{F}}_2^n$ be a vector. We call

$$H·x\in {\mathbb{F}}_2^{n-k}$$

the syndrome of x.

3.1.2. Binary Goppa Codes

A traditional and well-studied family of linear codes are the so-called binary Goppa codes [24]. They were proposed for cryptography in 1978 due to their good security properties and fast decoding capabilities [25].

Definition 6

(binary Goppa code, support, Goppa polynomial). Let ${\mathbb{F}}_{2^m}$ be a finite field for some $m\in \mathbb{N}$ and $g\left(x\right)\in {\mathbb{F}}_{2^m}\left[x\right]$ be an irreducible polynomial of degree $t<2^m$. Let $L=({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n)$ be a sequence of n distinct elements of ${\mathbb{F}}_{2^m}$ which are not roots of $g\left(x\right)$. Then, we define a binary Goppa code $\Gamma (g,L)$ by

$$\Gamma (g,L)=\{c\in {\mathbb{F}}_2^n\mid \sum _{i=1}^n\frac{1}{x-{\alpha }_i}·c_i\equiv 0modg\left(x\right)\}.$$

We call L supportand $g\left(x\right)$ Goppa polynomial.

While we will not delve into the mathematical structure behind binary Goppa codes, it is important to highlight that a given Goppa code depends on its Goppa polynomial and its support. In order to derive the parity check matrix of a given Goppa code $\Gamma (g,L)$, we define

$${\widehat{I}}_i(x,{\alpha }_i):=\frac{1}{x-{\alpha }_i}modg\left(x\right)$$

to be the inverse of $x-{\alpha }_i$ reduced modulo $g\left(x\right)$ for $i\in \{1,...,n\}$. Note that the condition of ${\alpha }_1,\cdots ,{\alpha }_n$ not being roots of g ensures that the inverses $\frac{1}{x-{\alpha }_1},\cdots ,\frac{1}{x-{\alpha }_n}$ exist since, otherwise, $x-{\alpha }_i$ would divide g.

Since ${\widehat{I}}_i(x,{\alpha }_i)$ is already reduced modulo $g\left(x\right)$ and the addition of polynomials with the same degree cannot increase their degree, we can rewrite the defining condition of $\Gamma (g,L)$ in the following way:

$$\begin{array}{c}\hfill \sum _{i=1}^n{\widehat{I}}_i(x,{\alpha }_i)·c_i=0\end{array}$$

Moreover, ${\widehat{I}}_i(x,{\alpha }_i)$ is a polynomial with a maximum degree of $t-1$, i.e., ${\widehat{I}}_i(x,{\alpha }_i)={\sum }_{k=1}^t{\widehat{I}}_{i,k}\left({\alpha }_i\right)·x^{k-1}$. Again, we can rewrite the condition as:

$$\begin{array}{c}\hfill \sum _{i=1}^n{c}_i\sum _{k=1}^t{\widehat{I}}_{i,k}\left({\alpha }_i\right)·x^{k-1}=0.\end{array}$$

From this equation, one can easily derive the parity check matrix $\widehat{H}$ for $\Gamma (g,L)$:

$$\begin{array}{c}\hfill \widehat{H}=\left(\begin{array}{cccc}{\widehat{I}}_{1,1}\left({\alpha }_i\right)& {\widehat{I}}_{2,1}\left({\alpha }_i\right)& \cdots & {\widehat{I}}_{n,1}\left({\alpha }_i\right)\\ {\widehat{I}}_{1,2}\left({\alpha }_i\right)& {\widehat{I}}_{2,2}\left({\alpha }_i\right)& \cdots & {\widehat{I}}_{n,2}\left({\alpha }_i\right)\\ ⋮& ⋮& & ⋮\\ {\widehat{I}}_{1,t}\left({\alpha }_i\right)& {\widehat{I}}_{2,t}\left({\alpha }_i\right)& \cdots & {\widehat{I}}_{n,t}\left({\alpha }_i\right)\end{array}\right)\in {\mathbb{F}}_{2^m}^{t\times n}\end{array}$$

(3)

The inverses in $\widehat{H}$ can then be calculated using n executions of the extended euclidean algorithm (EEA). Applying EEA directly to any $(x-{\alpha }_i)$ and $g\left(x\right)={\sum }_{i=0}^t{g}_i·x^i$ would lead to a simpler version of $\widehat{H}$:

$$\begin{array}{c}\hfill \widehat{H}=\left(\begin{array}{ccccc}1& 0& 0& \cdots & 0\\ g_{t-1}& 1& 0& \cdots & 0\\ g_{t-2}& g_{t-1}& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ g_1& g_2& g_3& \cdots & 1\end{array}\right)\left(\begin{array}{cccc}1& 1& \cdots & 1\\ {\alpha }_1^1& {\alpha }_2^1& \cdots & {\alpha }_n^1\\ {\alpha }_1^2& {\alpha }_2^2& \cdots & {\alpha }_n^2\\ ⋮& ⋮& ⋮& ⋮\\ {\alpha }_1^{t-1}& {\alpha }_2^{t-1}& \cdots & {\alpha }_n^{t-1}\end{array}\right)\left(\begin{array}{cccc}\frac{1}{g\left({\alpha }_1\right)}& 0& \cdots & 0\\ 0& \frac{1}{g\left({\alpha }_2\right)}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & \frac{1}{g\left({\alpha }_n\right)}\end{array}\right)\in {\mathbb{F}}_{2^m}^{t\times n}\end{array}$$

The details of the derivation can be found in [26].

In Classic McEliece, we will always consider a binary version of the parity check matrix $\widehat{H}\in {\mathbb{F}}_{2^m}^{t\times n}$. That means that all elements in ${\mathbb{F}}_{2^m}$ are converted to a column vector representing their binary form of length m. We call the resulting matrix

$$H\in {\mathbb{F}}_2^{mt\times n}$$

the binary parity check matrix.

Theorem 1.

Let $\Gamma (g,L)$ be an $(n,k,d)$ binary Goppa code, where $g\in {\mathbb{F}}_{2^m}\left[x\right]$ has degree t. Then, we can lower-bound the dimension k by

$$k\ge n-mt$$

and the minimum distance d by

$$d\ge 2t+1.$$

Since H is an $mt\times n$ matrix, the corresponding generator matrix G has dimension $n\times k$ with $k\ge n-mt$. The derivation of the lower bound for the minimum distance is not easy to see; that is why we refer to [27] for a detailed proof.

3.1.3. Computational Linear Code Problems

Analogously to lattices, there exist various code-based calculation problems which are considered to be computationally hard and are therefore suitable for cryptographic algorithms.

Given a linear $(n,k,d)$-code $\mathcal{C}\subset {\mathbb{F}}_2^n$ with a random parity-check matrix $H\in {\mathbb{F}}_2^{(n-k)\times n}$ and $q\in {\mathbb{F}}_2^n$, the task of finding the closest codeword $c\in \mathcal{C}$ to q, i.e., the codeword c which minimizes $dist(q,c)$, is computationally hard and is called a syndrome decoding problem.

Due to its structured parity-check matrix, the hardness of the syndrome decoding problem cannot directly be applied to Goppa codes. However, research indicates that distinguishing a Goppa parity-check matrix from a parity-check matrix of a random code is difficult. The parity-check matrix $\widehat{H}$ introduced in Equation (3) gives an intuition of that fact. Observe, that each entry is a polynomial inverse depending on a random Goppa support and a random Goppa polynomial. This Goppa code indistinguishability assumption is the basis for the Classic McEliece cryptosystem, which we will discuss in the following section.

3.2. Classic McEliece

Classic McEliece [28] is a CCA-secure key encapsulation mechanism based on a version of the Niederreiter encryption scheme. A message is represented as an error vector e whose syndrome, i.e., the parity check matrix (public key) applied on e, is used as encryption. Knowing the structure (secret key) of the underlying code, the receiver is able to restore the error vector e from the syndrome using a syndrome decoding algorithm [29].

The Classic McEliece scheme uses binary Goppa codes, which form linear $(n,k,d)$-codes. During key generation (Algorithm 25), Classic McEliece generates a random binary Goppa code $\Gamma (g,L)$. As described above, the code $\Gamma (g,L)$ consists of a Goppa polynomial $g\left(x\right)\in {\mathbb{F}}_{2^m}\left[x\right]$ with degree t for a suitable m and a support L. Then, the corresponding binary parity-check matrix $H\in {\mathbb{F}}_2^{mt\times n}$ is computed and transformed to standard form. H is then published as public key while the Goppa parameters g and L are kept secret. Classic McEliece uses the fact that it is generally infeasible to reconstruct a Goppa code from a given parity-check matrix H.

Algorithm 25 Classic McEliece PKE Key Generation: keyGen.

Input: none Generate random Goppa Code $\Gamma (g,L)$ with Goppa polynomial $g\left(x\right)\in {\mathbb{F}}_{2^m}\left[x\right]$ of degree t Uniform random sequence $L=({\alpha }_1,\cdots ,{\alpha }_n$) of n distinct elements of ${\mathbb{F}}_{2^m}$ Compute corresponding binary parity-check matrix $H\in {\mathbb{F}}_2^{mt\times n}$ Output: public key H, private key $\Gamma (g,L)$.

The idea of Classic McEliece encryption (Algorithm 26) is to send the syndrome $H(c+e)$ of an erroneous codeword $c\in \Gamma (g,L)$ with error $e\in {\mathbb{F}}_2^n$. We can observe that $H(c+e)$ is independent of the concrete codeword c, because $H(c+e)=Hc+He=He$ holds for all codewords. Therefore, we drop c and just calculate $He$. The value e serves as message, and we require it to have weight t, which is defined to be the largest value possible while also guaranteeing correct decryption. Therefore, the size of the message space is $\left(\genfrac{}{}{0pt}{}{n}{t}\right)$. Using the provided parity-check matrix H, the corresponding syndrome $He$ is calculated and sent to the receiver.

Algorithm 26 Classic McEliece PKE Encryption: enc.

Input: public key $H\in {\mathbb{F}}_2^{mt\times n}$, message $e\in {\mathbb{F}}_2^n$ with weight t Compute $C=He\in {\mathbb{F}}_2^{n-k}$ Output: ciphertext C

Knowing the structure of the Goppa code, i.e., the secret Goppa polynomial g and support $({\alpha }_1,\cdots ,{\alpha }_n)$, the receiver is able to reconstruct e from the provided syndrome $C=He$. In order to do that, the given syndrome $C\in {\mathbb{F}}_2^{n-k}$ is extended to the column vector $C^{\prime }=(C,0,\cdots ,0)\in {\mathbb{F}}_2^n$ by appending k zeros. We first observe that

$$\begin{array}{cc}\hfill H(C^{\prime }+e)& =H\left(\right(He,0,\cdots ,0)+e)\hfill \\ \hfill & =H(He,0,\cdots ,0)+He\hfill \\ \hfill & =He+He\hfill \\ \hfill & =0\hfill \end{array}$$

Note that $H(He,0,\cdots ,0)=He$ holds because H is in standard form, i.e., $H=(I_{n-k}\mid \mid -T)$ for some matrix T. The equation above implies that $c=C^{\prime }+e$ is a codeword in our Goppa code $\Gamma (g,L)$. Furthermore, we know there can only be one codeword in $\Gamma (g,L)$ with distance $\le t$ to $C^{\prime }$ since, due to Theorem 1, Goppa codewords have a minimum distance of $2t+1$ (see Figure 5). Since e has weight t, the codeword $C^{\prime }+e$ is the unique codeword with distance $\le t$ to $C^{\prime }$.

Having the secret Goppa parameters, the receiver is able to use a syndrome-decoding algorithm, e.g., Patterson’s Algorithm [30], to find the closest codeword to $C^{\prime }$, obtaining $c=C^{\prime }+e$. Then, simple addition yields $e=C^{\prime }+c$. These steps are summarized in Algorithm 27.

Note that general syndrome decoding is difficult, as seen in Section 3.1. Therefore, a third party without knowledge of the secret Goppa parameters is not able to perform this decryption step.

Algorithm 27 Classic McEliece PKE Decryption: dec.

Input: ciphertext $C\in {\mathbb{F}}_2^{n-k}$, Goppa code $\Gamma (g,L)$ Extend C to $C^{\prime }=(C,0,\cdots ,0)\in {\mathbb{F}}_2^n$ by appending k zeros Find the unique codeword $c\in \Gamma (g,L)$ that is at distance $\le t$ from $C^{\prime }$. If there is no such codeword, return ⊥ Set $e=C^{\prime }+c$ If $\mathrm{weight}\left(e\right)\ne t$ or $C\ne He$, return ⊥ Output: message e

Classic McEliece KEM key generation (Algorithm 28) samples an additional value $\sigma \in {\mathbb{F}}_2^n$. Despite that, the key generation is identical to the key generation of the PKE.

Algorithm 28 Classic McEliece KEM Key Generation.

Input: none Generate random $\sigma \in {\mathbb{F}}_2^n$ Generate $(H,\Gamma (g,L\left)\right)=PKE.keyGen\left(\right)$ Output: public key H, secret key $sk=(\Gamma (g,L),\sigma )$

The family of cryptographic hash functions ${\mathcal{H}}_i$ for $i\in \{0,1,2\}$ is used for both encapsulation and decapsulation. A random vector $e\in {\mathbb{F}}_2^n$ of weight t is sampled and encrypted with a given parity-check matrix H. Additionally, e is hashed to $e_{\mathcal{H}}$. The shared secret K is computed by $K={\mathcal{H}}_1(e,C,e_{\mathcal{H}})$, i.e., a random-looking value depending on e and C (Algorithm 29).

Algorithm 29 Classic McEliece KEM Encapsulation.

Input: public key H Generate random vector $e\in {\mathbb{F}}_2^n$ of weight t Compute $C=PKE.enc(e,H)$. Compute $e_{\mathcal{H}}={\mathcal{H}}_2\left(e\right)$ Compute $K={\mathcal{H}}_1(e,C,e_{\mathcal{H}})$ Output: encapsulation $(C,e_{\mathcal{H}})$, shared secret K

The decapsulation (Algorithm 30) starts with the decryption of a given C, thereby calculating a message candidate e. Assuming a valid input, the original e is obtained. It is clear that by $K={\mathcal{H}}_1(e,C,e_{\mathcal{H}})$ the same shared secret as in the encapsulation is computed.

However, prior to that calculation, the decapsulation process has two means of verifying its input: If decryption fails, the hash value $e_{\mathcal{H}}^{\prime }$ will be based on the random-looking $\sigma$ instead of e. This will ensure that the following comparison will not hold. The obtained message candidate e is verified by checking whether it is indeed a weight-t vector (this happens during PKE.dec). Then, the provided $e_{\mathcal{H}}$ is compared with the computed version $e_{\mathcal{H}}^{\prime }$, thereby checking that the encapsulation was indeed performed based on e as well as the provided public key H and according to the rules of the algorithm.

Algorithm 30 Classic McEliece KEM Decapsulation.

Input: secret key $sk=(\Gamma (g,L),\sigma )$, encapsulation $(C,e_{\mathcal{H}})$ Calculate $e=PKE.dec(C,\Gamma (g,L\left)\right)$ If $e=\perp$ calculate $e_{\mathcal{H}}^{\prime }={\mathcal{H}}_2\left(\sigma \right)$ If $e\ne \perp$ calculate $e_{\mathcal{H}}^{\prime }={\mathcal{H}}_2\left(e\right)$ If $e_{\mathcal{H}}^{\prime }=e_{\mathcal{H}}$ set $K={\mathcal{H}}_1(e,C,e_{\mathcal{H}})$ If $e_{\mathcal{H}}^{\prime }\ne e_{\mathcal{H}}$ set $K={\mathcal{H}}_0(\sigma ,C,e_{\mathcal{H}})$ Output: shared secret K

Encryption and decryption operations are competitively fast compared to lattice-based cryptography; however, the key sizes in Classic McEliece are quite large [31]. Given, for example, the largest parameter set (see

Table 6. Classic McEliece parameter sets using an $(n,k,d)$ Goppa code with error correction capability t.

	n	k	d	t
McEliece348864	3488	2720	129	64
McEliece460896	4608	3360	193	96
McEliece6688128	6688	5024	257	128
McEliece6960119	6960	5413	239	119
McEliece8192128	8192	6528	257	128

), storing the compressed public key H requires $k·(n-k)=6528·(8192-6528)=$ 10,862,592 bits $\approx 1.3$ MB.

The Classic McEliece instances with their corresponding parameter choices are shown in Table 6.

4. Multivariate Cryptography

Multivariate cryptography uses multivariate polynomials, i.e., polynomials in multiple variables, for the construction of key pairs. Its security is based on the assumption that solving a set of multivariate quadratic polynomial equations over a finite field is computationally hard.

4.1. Multivariate Polynomial Fundamentals

4.1.1. Multivariate Polynomial Functions

Definition 7

(multivariate quadratic polynomial function). Let $\mathbb{F}$ be a field. A function $f:{\mathbb{F}}^n\to \mathbb{F}$ is called multivariate function. Let p be a polynomial in the variables $x_1,\cdots ,x_n\in \mathbb{F}$. If f can be represented as $p(x_1,\cdots ,x_n)$, f is called multivariate polynomial function (for finite $\mathbb{F}$, this is possible for any function). If f only contains terms of degree two or less, f is calledmultivariate quadratic polynomial function.

To give an example, the function $f_1(x_1,x_2,x_3)=x_1^2{x}_2+2x_1{x}_2^2+3x_3+4$ is a multivariate polynomial function (of degree 3), while the function $f_2(x_1,x_2,x_3)=x_1^2+2x_1{x}_2+3x_3+4$ is a multivariate quadratic polynomial function. Let $p_1,\cdots ,p_k$ be multivariate quadratic polynomial functions. The vector

$$\mathcal{P}=\left(\begin{array}{c}{p}_1\\ ⋮\\ p_k\end{array}\right)$$

can be interpreted as a function $\mathcal{P}:{\mathbb{F}}^n\to {\mathbb{F}}^k$ by component-wise application and is called polynomial map.

4.1.2. MQ Problem

Let $\mathbb{F}$ be a finite field. Let $p_1,\cdots ,p_k:{\mathbb{F}}^n\to \mathbb{F}$ be multivariate quadratic polynomial functions. Finding a solution $s\in {\mathbb{F}}^n$ to the system of equations    

$$\begin{array}{cc}\hfill p_1\left(s\right)& =0\hfill \\ \hfill & ⋮\hfill \\ \hfill p_k\left(s\right)& =0\hfill \end{array}$$

is called an $\mathcal{MQ}$ (multivariate quadratic) problem [32]. This problem has been proven to be computationally hard.

4.1.3. Multivariate Signature Schemes

Multivariate public-key cryptosystems (MPKC) are constructions where polynomial maps are used to represent public and private keys. However, MPKC constructions are mainly used as digital signature schemes and are not suited for encryption purposes [33].

Let $\mathbb{F}$ be a finite field. The main idea of generating a signature $s\in {\mathbb{F}}^n$ to a given message $m\in {\mathbb{F}}^k$ is to calculate one of possibly many pre-images of the image m under a polynomial map $\mathcal{P}$. This is equivalent to finding a solution s to the system of equations

$$\begin{array}{cc}\hfill p_1\left(s\right)& =m_1\hfill \\ \hfill & ⋮\hfill \\ \hfill p_k\left(s\right)& =m_k\hfill \end{array}\iff \begin{array}{cc}\hfill p_1\left(s\right)-& m_1=0\hfill \\ \hfill & ⋮\hfill \\ \hfill p_k\left(s\right)-& m_k=0,\hfill \end{array}$$

where $\mathcal{P}=\left(p_1,\dots ,p_k\right)$ and $m=\left(m_1,\dots ,m_k\right)$. $\mathcal{P}$ is called a public map and represents the public key. We can design an MPKC scheme in a way that allows finding pre-images under a public map without directly solving the $\mathcal{MQ}$ problem. Usually, this mechanism involves some polynomial map $\mathcal{F}:{\mathbb{F}}^n\to {\mathbb{F}}^k$, which we call the central map. We hide $\mathcal{F}$ by applying the following compositions involving the two affine maps $\mathcal{S}:{\mathbb{F}}^n\to {\mathbb{F}}^n$ and $\mathcal{T}:{\mathbb{F}}^k\to {\mathbb{F}}^k$. The resulting function

$$\mathcal{P}=\mathcal{T}\circ \mathcal{F}\circ \mathcal{S}:{\mathbb{F}}^n\to {\mathbb{F}}^k$$

is the public key to the corresponding secret key $(\mathcal{T},\mathcal{F},\mathcal{S})$. In general, the central map $\mathcal{F}$ requires efficient computation of pre-images. The affine maps $\mathcal{S}$ and $\mathcal{T}$ have to be invertible; therefore, they need to be of full rank.

As mentioned above, a signature s for a given message m is a pre-image of m under $\mathcal{P}$. With knowledge of the decomposition $\mathcal{P}=\mathcal{T}\circ \mathcal{F}\circ \mathcal{S}$, s can be computed by calculating the pre-image of ${\mathcal{T}}^{-1}\left(m\right)$ under $\mathcal{F}$ and subsequent application of $S^{-1}$. To verify a signature s for a message m, we simply need to verify whether $m=\mathcal{P}\left(s\right)$ holds. Note that there could exist multiple valid signatures for a given message m.

The key component of an MPKC is the design of the central map $\mathcal{F}$. Without prior knowledge of the secret key $(\mathcal{T},\mathcal{F},\mathcal{S})$, an attacker cannot distinguish the public map from a randomly generated polynomial map. The complexity of a direct attack is therefore reduced to the difficulty of the $\mathcal{MQ}$ problem. However, observe that the security assumption of this system is stronger than in the case of the $\mathcal{MQ}$ problem due to possible efficient attacks against the central map $\mathcal{F}$. There exists an alternative approach for breaking an MPKC without trying to directly attack the public map. The idea is to find two alternative affine maps that suffice the same criteria of transforming the central map $\mathcal{F}$ into $\mathcal{P}$. Thus, the cryptosystem can be broken by finding alternative private keys which correspond to the same public map. In this context, we need to define a new problem called the $\mathcal{IP}$ problem (Isomorphism of Polynomials) [32].

4.1.4. IP Problem

Let $\mathcal{P}$, $\mathcal{F}$ be two polynomial maps from ${\mathbb{F}}^n$ to ${\mathbb{F}}^k$ with:

$$\begin{array}{cc}\hfill \mathcal{P}& =(p_1,\cdots ,p_k)\hfill \\ \hfill \mathcal{F}& =(f_1,\cdots ,f_k).\hfill \end{array}$$

Assuming two invertible affine transformations $\mathcal{S}:{\mathbb{F}}^n\to {\mathbb{F}}^n$ and $\mathcal{T}:{\mathbb{F}}^k\to {\mathbb{F}}^k$ with

$$\mathcal{P}=\mathcal{T}\circ \mathcal{F}\circ \mathcal{S}$$

exist, finding $\mathcal{S}$ and $\mathcal{T}$ is called an $\mathcal{IP}$ problem, which is also computationally hard [34]. Solving the $\mathcal{IP}$ problem could possibly break an MPKC by finding alternative secret affine functions to a given public map and an arbitrarily chosen central map.

4.2. Rainbow

The Rainbow signature scheme [35] is closely related to arguably the most common multivariate-based signature scheme, namely, Unbalanced Oil and Vinegar (UOV). In order to understand Rainbow, we first need to properly introduce UOV.

The basic idea of UOV consists of dividing the set of variables of the central map $\mathcal{F}$ into two disjoint subsets, which we refer to as oil and vinegar variables. The most important property is that the quadratic polynomials of $\mathcal{F}$ are not allowed to contain cross-terms between two oil variables. UOV has the general advantage of offering fast computations of both public and private keys, as well as a simple structure. A major disadvantage lies in the comparably large key sizes.

The UOV scheme is an MPKC scheme, as described in Section 4.1 with the public map

$$\mathcal{P}=\mathcal{T}\circ \mathcal{F}\circ \mathcal{S}:{\mathbb{F}}^n\to {\mathbb{F}}^k$$

and secret polynomial maps $(\mathcal{T},\mathcal{F},\mathcal{S})$. It is characterized by the integer parameters o and v, specifying the number of oil and vinegar variables, respectively. These parameters define the structure of the central map $\mathcal{F}$ having $k=o$ polynomial functions with $n=o+v$ variables. The central map $\mathcal{F}:{\mathbb{F}}^n\to {\mathbb{F}}^k$ contains k polynomial functions $f_1,\cdots ,f_k$. We restrict those to their homogeneous forms, i.e., omitting constant and linear terms. Then, each $f_r$ has the form:

$$f_r=\sum _{i=1}^v\sum _{j=i}^v{\alpha }_{ij}^{\left(r\right)}{x}_i{x}_j+\sum _{i=1}^v\sum _{j=v+1}^n{\beta }_{ij}^{\left(r\right)}{x}_i{x}_j,$$

where $x_1,\cdots ,x_v$ and $x_{v+1},\cdots x_n$ correspond to the vinegar variables and oil variables, respectively. A central map $\mathcal{F}$ is generated by randomly assigning values to the coefficients ${\alpha }_{ij}^{\left(r\right)},{\beta }_{ij}^{\left(r\right)}$ from $\mathbb{F}$.

The affine transformations $\mathcal{S}$ and $\mathcal{T}$ are also sampled by randomly assigning their coefficients, which is repeated if they turn out not to be invertible. The calculation of pre-images under $\mathcal{F}$ works as follows:

• We randomly assign values to the vinegar variables $x_1,\cdots ,x_v$ (highlighted in red), thus reducing the product between two vinegar variables to constants and the product of an oil and a vinegar variable to a linear term:

  $$f_r=\sum _{i=1}^v\sum _{j=i}^v{\alpha }_{ij}^{\left(r\right)}{x}_i{x}_j+\sum _{i=1}^v\sum _{j=v+1}^n{\beta }_{ij}^{\left(r\right)}{x}_i{x}_j$$
• This results in a linear system of k equations in $n-v=k$ variables, namely, $x_{v+1},\cdots ,x_n$. By applying Gaussian elimination, we solve this system and thereby derive the remaining oil values $x_{v+1},\cdots ,x_n$. In case the system does not have a solution, we repeat the previous step by sampling some other random values for the vinegar variables.

As mentioned in Section 4.1, this MPKC construction is designed in a way that makes it hard to find pre-images under a given public map $\mathcal{P}$; however, knowing the secret decomposition $\mathcal{P}=\mathcal{T}\circ \mathcal{F}\circ \mathcal{S}$ enables an efficient computation of pre-images, i.e., signature generation.

Rainbow generalizes the UOV concept. The Rainbow signature scheme consists of two layers of Oil–Vinegar polynomials, where the second layer includes all variables from the first layer, i.e., the set of vinegar variables from layer two contains all variables of layer one.

A concrete Rainbow instance is defined by an initializing number $v_1$ of vinegar variables for layer one and the number of oil variables for layers one and two, i.e., $o_1$ and $o_2$, respectively. The total number of variables n and the number of equations k can be derived through $n=v_1+o_1+o_2$ and $k=o_1+o_2$. The resulting structure of Rainbow’s central map $\mathcal{F}$ consists of the two layers:

$$\begin{array}{cc}\hfill & \mathrm{Layer}1:\underset{\mathrm{vinegar}\mathrm{variables}}{\underbrace{x_1,\dots ,x_{v_1}}},\underset{\mathrm{oil}\mathrm{variables}}{\underbrace{x_{v_1+1},\dots ,x_{v_1+o_1}}}\hfill \\ \hfill & \mathrm{Layer}2:\underset{\mathrm{vinegar}\mathrm{variables}}{\underbrace{x_1,\cdots ,x_{v_1},x_{v_1+1},\dots ,x_{v_1+o_1}}},\underset{\mathrm{oil}\mathrm{variables}}{\underbrace{x_{v_1+o_1+1},\dots ,x_{v_1+o_1+o_2}}}\hfill \end{array}$$

This construction improves the ratio between the signature size and the message size from $\frac{v+o}{o}$ in the UOV case to $\frac{v_1+o_1+o_2}{o_1+o_2}$ in the two-layer Rainbow case due to $v_1<v$, i.e., signatures are relatively smaller (in practice, this amounts to an about 26% reduction [36]). Due to the reduced number of coefficients needed in the first layer, this also results in a smaller private key. Recent attacks have shown this construction to be vulnerable resulting in a loss of these efficiency gains, see Section 4.2.1.

To generate a concrete key pair (Algorithm 31), the following maps are sampled:

• The secret central map $\mathcal{F}$ consisting of $k=o_1+o_2$ polynomials $f_1,\cdots ,f_k$ of the form

  $$\begin{array}{c}\hfill f_r=\left\{\begin{array}{c}{\displaystyle \sum _{i\le j\in V_1}{\alpha }_{ij}^{\left(r\right)}{x}_i{x}_j+\sum _{i\in V_1,j\in O_1}{\beta }_{ij}^{\left(r\right)}{x}_i{x}_j\mathrm{for}r\in \{1,\dots ,o_1\}}\hfill \\ \\ {\displaystyle \sum _{i\le j\in V_2}{\gamma }_{ij}^{\left(r\right)}{x}_i{x}_j+\sum _{i\in V_2,j\in O_2}{\delta }_{ij}^{\left(r\right)}{x}_i{x}_j\mathrm{for}r\in \{o_1+1,\dots ,o_1+o_2\}}\hfill \end{array}\right.\end{array}$$

  with layer one vinegar indices $V_1=\{1,\cdots ,v_1\}$, layer one oil indices $O_1=\{v_1+1,\cdots ,v_1+o_1\}$, layer two vinegar indices $V_2=V_1\cup O_1$ and layer two oil indices $O_2=\{o_1+1,\dots ,o_1+o_2\}$.
  The coefficients ${\alpha }_{ij}^{\left(r\right)},{\beta }_{ij}^{\left(r\right)},{\gamma }_{ij}^{\left(r\right)},{\delta }_{ij}^{\left(r\right)}$ are randomly chosen from $\mathbb{F}$.
• Two secret randomly chosen invertible affine maps $\mathcal{T}:{\mathbb{F}}^k\to {\mathbb{F}}^k$ and $\mathcal{S}:{\mathbb{F}}^n\to {\mathbb{F}}^n$. Their coefficients are randomly sampled from $\mathbb{F}$ which is repeated if the maps turn out not to be invertible.
• The public key $\mathcal{P}=\mathcal{T}\circ \mathcal{F}\circ \mathcal{S}:{\mathbb{F}}^n\to {\mathbb{F}}^k$.

Algorithm 31 Rainbow Key Generation.

Input: none Sample $\mathcal{S}\in {\mathbb{F}}^n\to {\mathbb{F}}^n$ Sample $\mathcal{F}\in {\mathbb{F}}^n\to {\mathbb{F}}^k$ Sample $\mathcal{T}\in {\mathbb{F}}^k\to {\mathbb{F}}^k$ Calculate $\mathcal{P}=\mathcal{T}·\mathcal{F}·\mathcal{S}\in {\mathbb{F}}^n\to {\mathbb{F}}^k$ Output: public key $\mathcal{P}$, secret key $sk=(\mathcal{T},\mathcal{F},\mathcal{S})$

As described in Section 4.1, a valid signature s of a given message $m\in {\{0,1\}}^{☆}$ of arbitrary length is a pre-image of $H\left(m\right)$ under $\mathcal{P}$, i.e., the equation

$$\mathcal{P}\left(s\right)=H\left(m\right)$$

holds with a suitable cryptographic hash function $H:{\{0,1\}}^{☆}\to {\mathbb{F}}^k$. Since $\mathcal{S}$ and $\mathcal{T}$ are efficiently invertible, finding pre-images under those maps is trivial. Finding pre-images under the central map $\mathcal{F}$ is similar to finding pre-images in a UOV scheme:

• We randomly assign values to the vinegar variables of layer one, i.e., $x_1,\dots ,x_{v_1}$:

  $$\mathrm{Layer}1:\underset{\mathrm{vinegar}\mathrm{variables}}{\underbrace{x_1,\cdots ,x_{v_1}}},\underset{\mathrm{oil}\mathrm{variables}}{\underbrace{x_{v_1+1},\cdots ,x_{v_1+o_1}}};$$
• We solve the resulting linear system of $o_1$ equations to obtain concrete values for the $o_1$ oil variables of layer one;
• The resulting assignment of values for $x_1,\cdots ,x_{v_1+o_1}$ is substituted into the second layer:

  $$\mathrm{Layer}2:\underset{\mathrm{vinegar}\mathrm{variables}}{\underbrace{x_1,\cdots ,x_{v_1},x_{v_1+1},\cdots ,x_{v_1+o_1}}},\underset{\mathrm{oil}\mathrm{variables}}{\underbrace{x_{v_1+o_1+1},\cdots ,x_{v_1+o_1+o_2}}};$$
• We solve the resulting linear system of $o_2$ equations to obtain concrete values for the remaining oil variables of layer two;
• In case one of the linear systems has no solution, we start from the beginning by choosing other random values for the vinegar variables of the first layer.

A valid signature of a message m under $\mathcal{P}$ can be computed by hashing and subsequently finding pre-images under the secret maps $\mathcal{T}$, $\mathcal{F}$ and $\mathcal{S}$ (Algorithm 32).

Algorithm 32 Rainbow Signature generation.

Input: secret key sk = $(\mathcal{T},\mathcal{F},\mathcal{S})$, message $m\in {\{0,1\}}^{☆}$ Calculate $m_H=H\left(m\right)$ Calculate $u={\mathcal{T}}^{-1}\left(m_H\right)$ Find pre-image $u^{-1}$ of u under $\mathcal{F}$ Calculate $s={\mathcal{S}}^{-1}\left(u^{-1}\right)$ Output: signature s

Let $m\in {\{0,1\}}^{☆}$ be a message and $s\in {\mathbb{F}}^n$ a signature. The signature s is accepted if $H\left(m\right)=\mathcal{P}\left(s\right)$ holds; otherwise, it is rejected (Algorithm 33).

Algorithm 33 Rainbow Verification.

Input: public key $\mathcal{P}$, message $m\in {\{0,1\}}^{☆}$, signature $s\in {\mathbb{F}}^n$ Calculate $m_H^{\prime }=\mathcal{P}\left(s\right)$ Calculate $m_H=H\left(m\right)$ Output: valid if $m_H^{\prime }=m_H$, else invalid

The Rainbow instances with their corresponding parameter choices are shown in

Table 7. Rainbow round 3 parameter sets.

	$\mathbb{F}$	${\mathit{v}}_1$	${\mathit{o}}_1$	${\mathit{o}}_2$
Level I	GF(16)	36	32	32
Level III	GF(256)	68	32	48
Level V	GF(256)	96	36	64

.

4.2.1. Rainbow Security Considerations

A recent attack by Ward Beullens [37] in February 2022 has shown a considerable improvement in previously known attacks against Rainbow. The main enhancement arises from the combination of a previously developed rectangular MinRank attack [38] and an improved guessing technique. In order to resist this attack, the Rainbow parameters would be required to even exceed the length of the standard (and better-understood) UOV approach. This essentially renders the preferred usage of Rainbow over UOV questionable since the performance gain is rather small compared to the additional complexity of the scheme.