Adaptive Neural Tracking Control for Nonstrict-Feedback Nonlinear Systems with Unknown Control Gains via Dynamic Surface Control Method
Abstract
:1. Introduction
2. Problem Formulation and Preliminaries
3. Control Law Design and Stability Analysis
3.1. Adaptive Neural Tracking Control Law Design
3.2. Stability Analysis
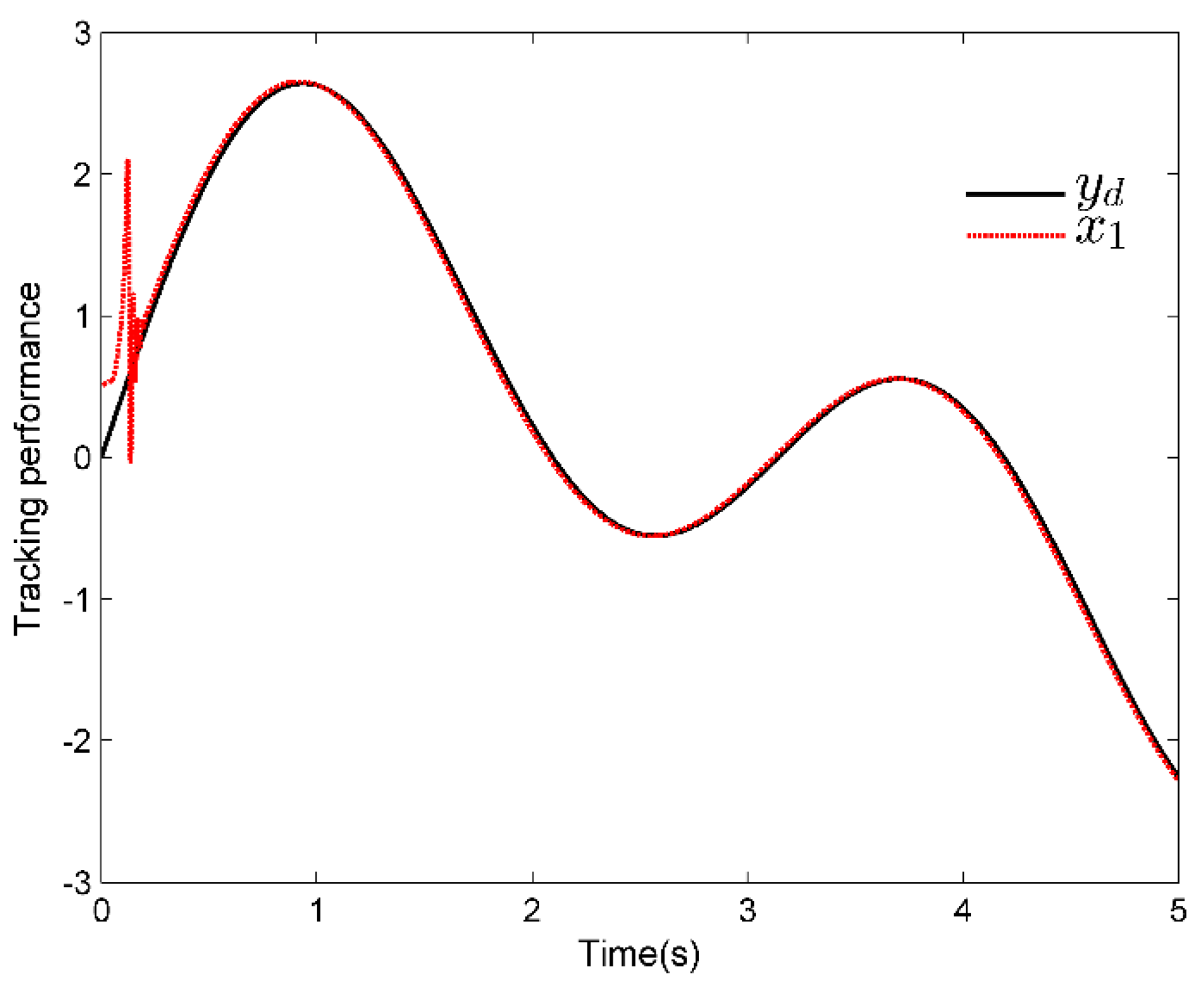
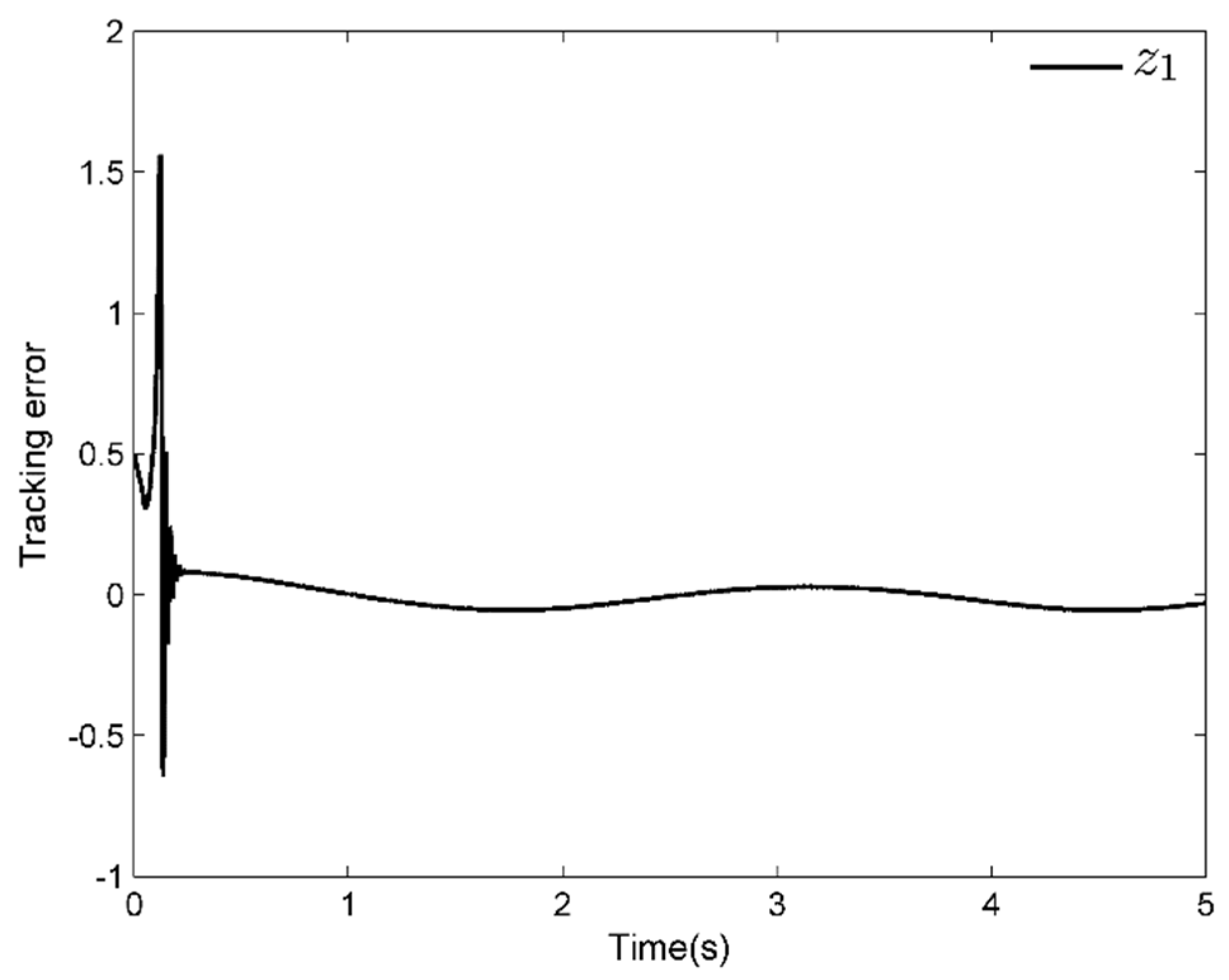
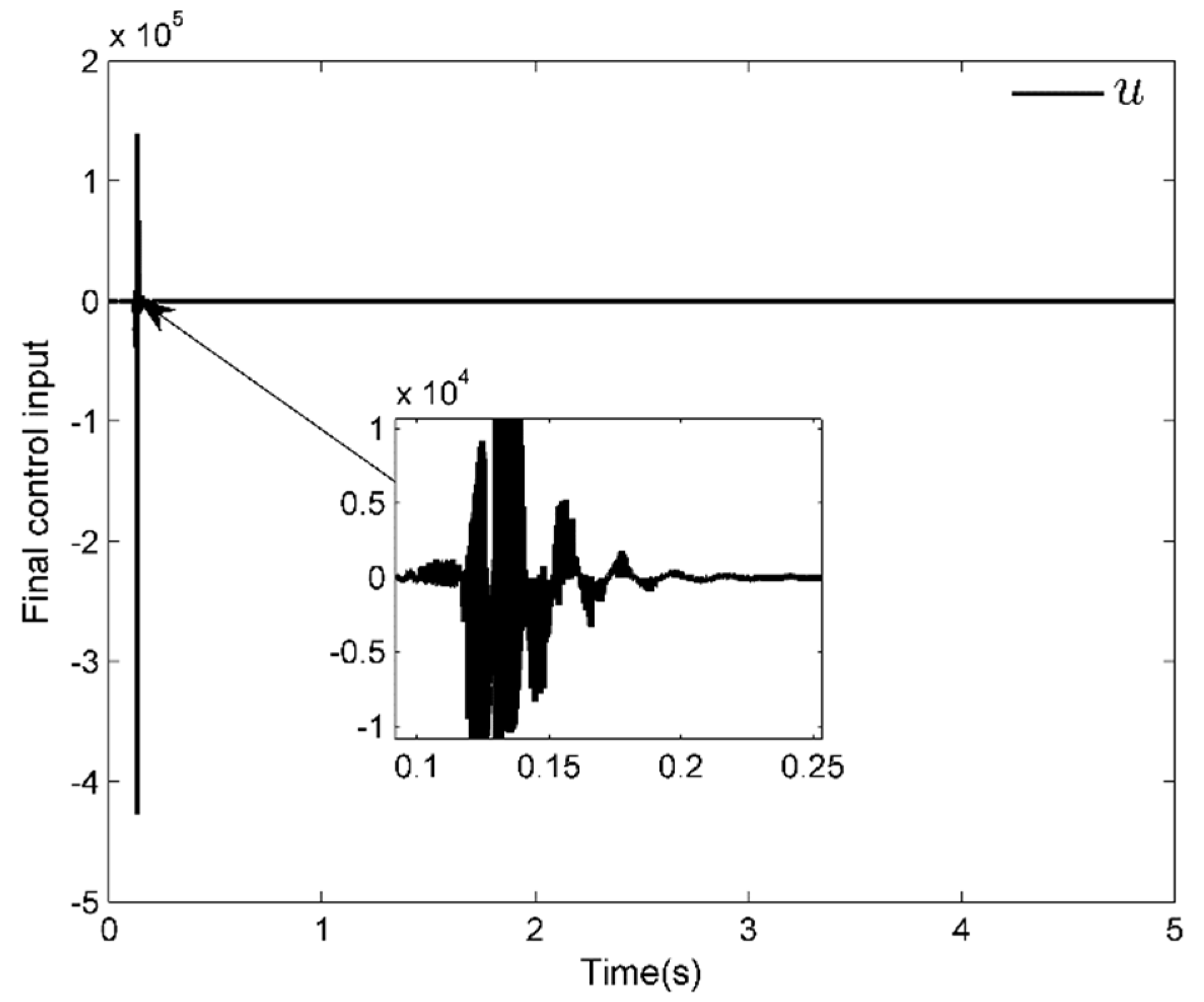
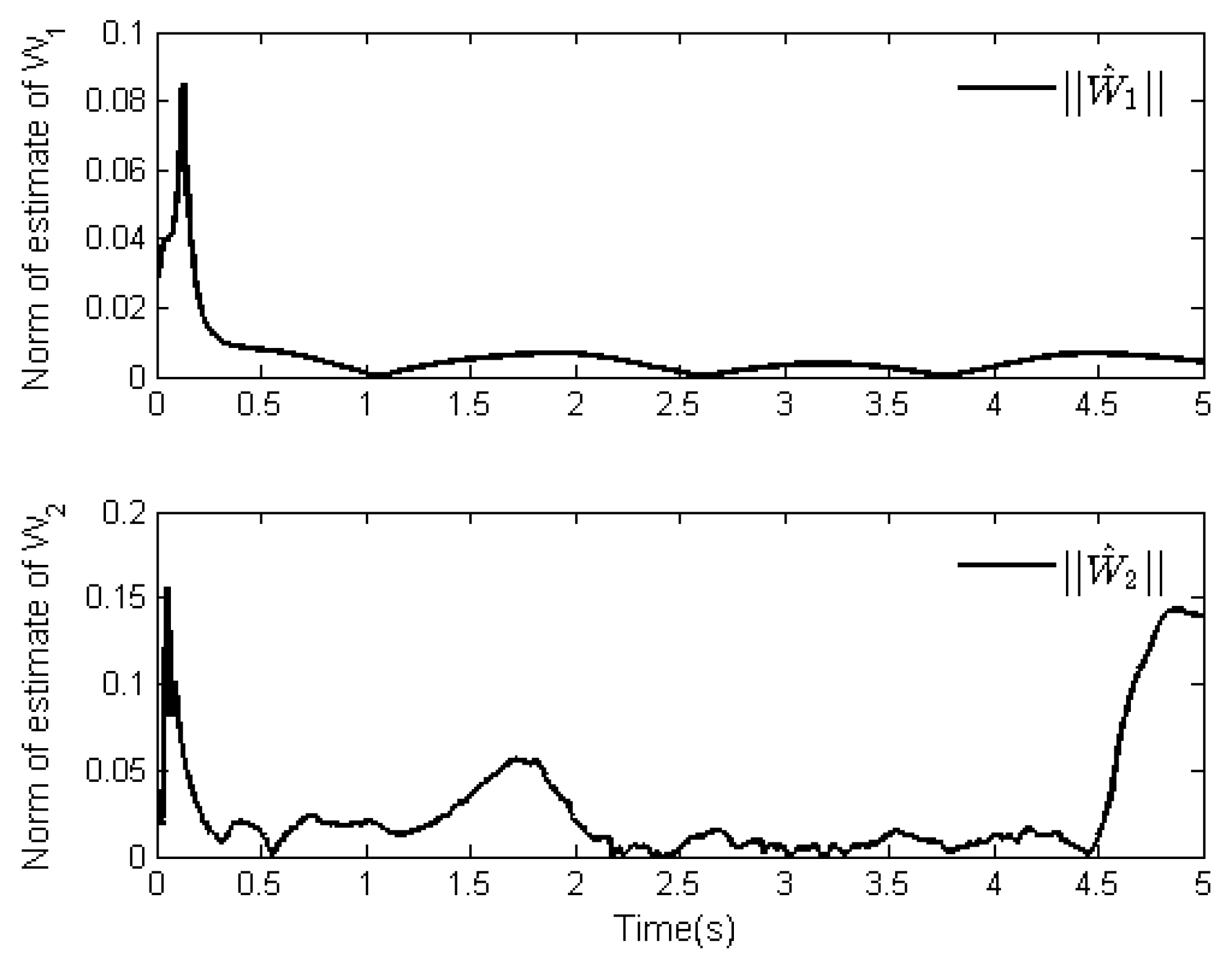
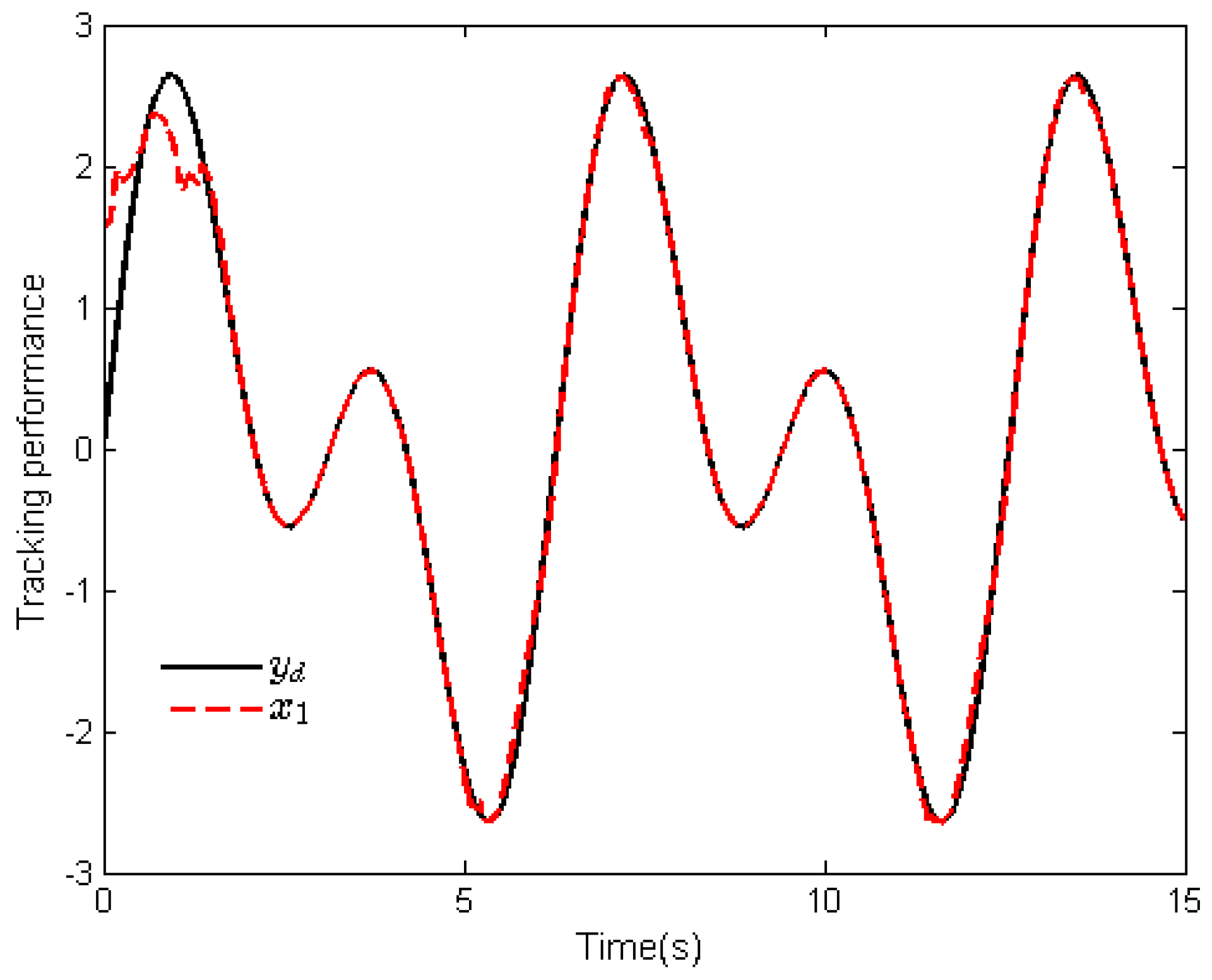
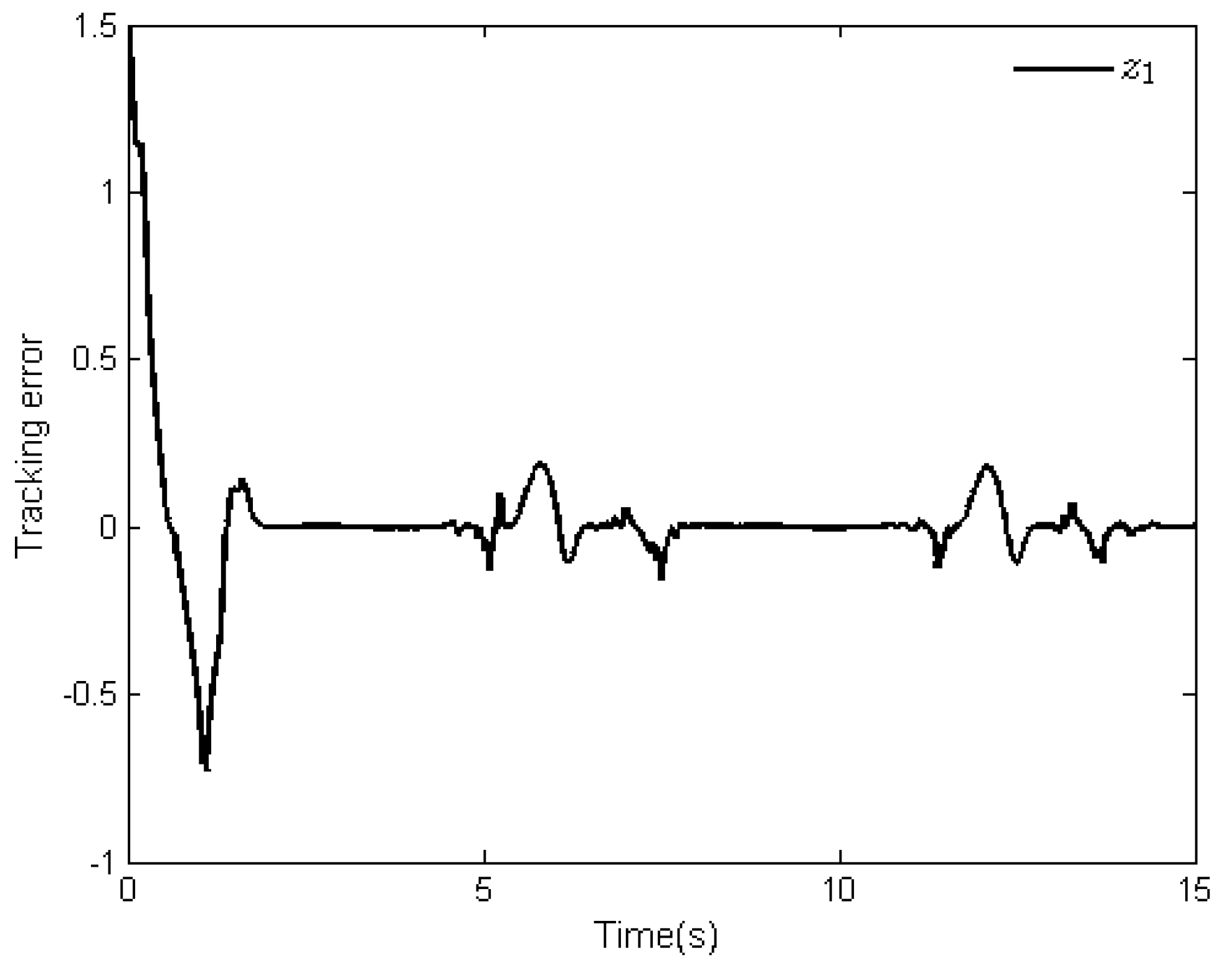
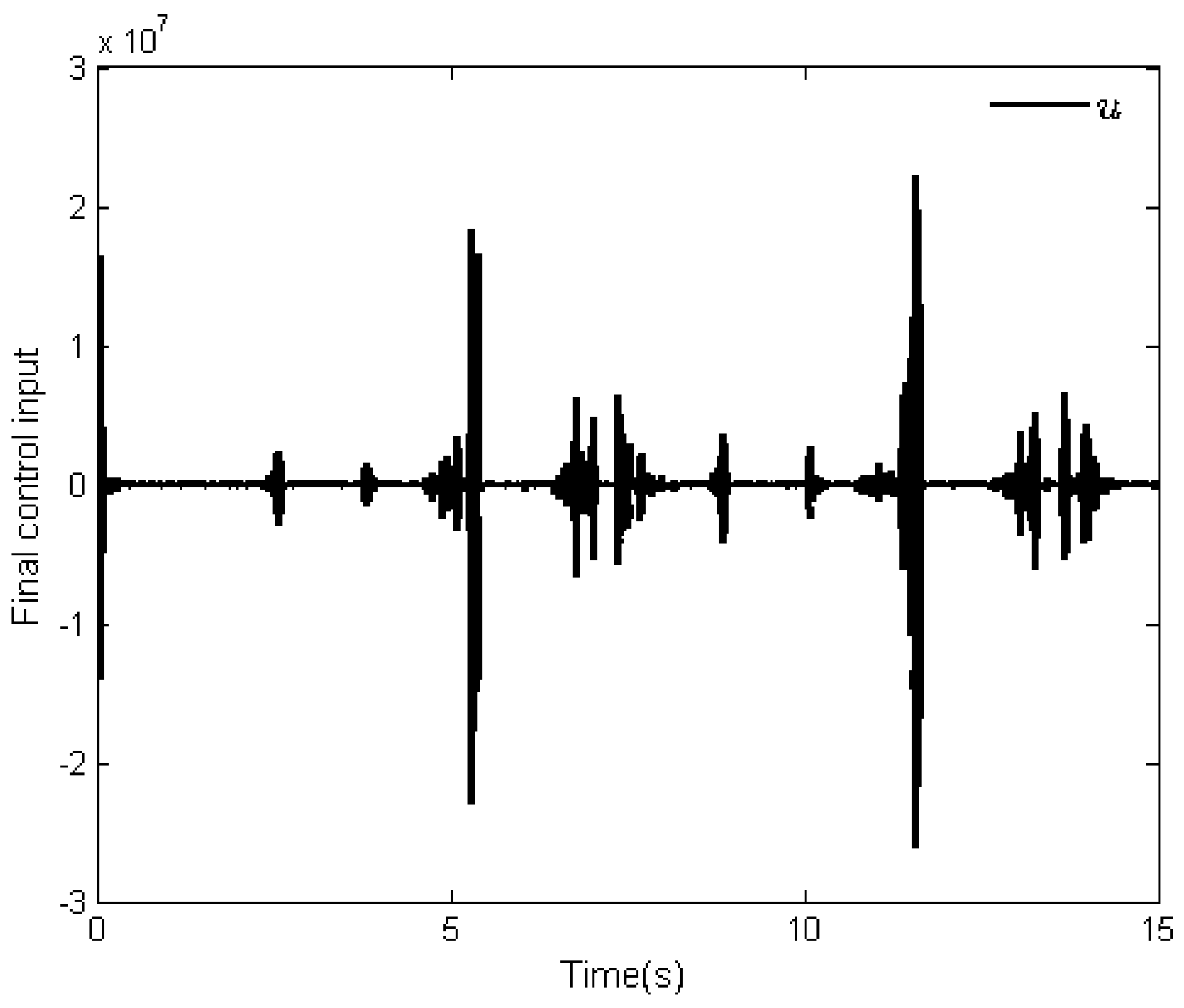
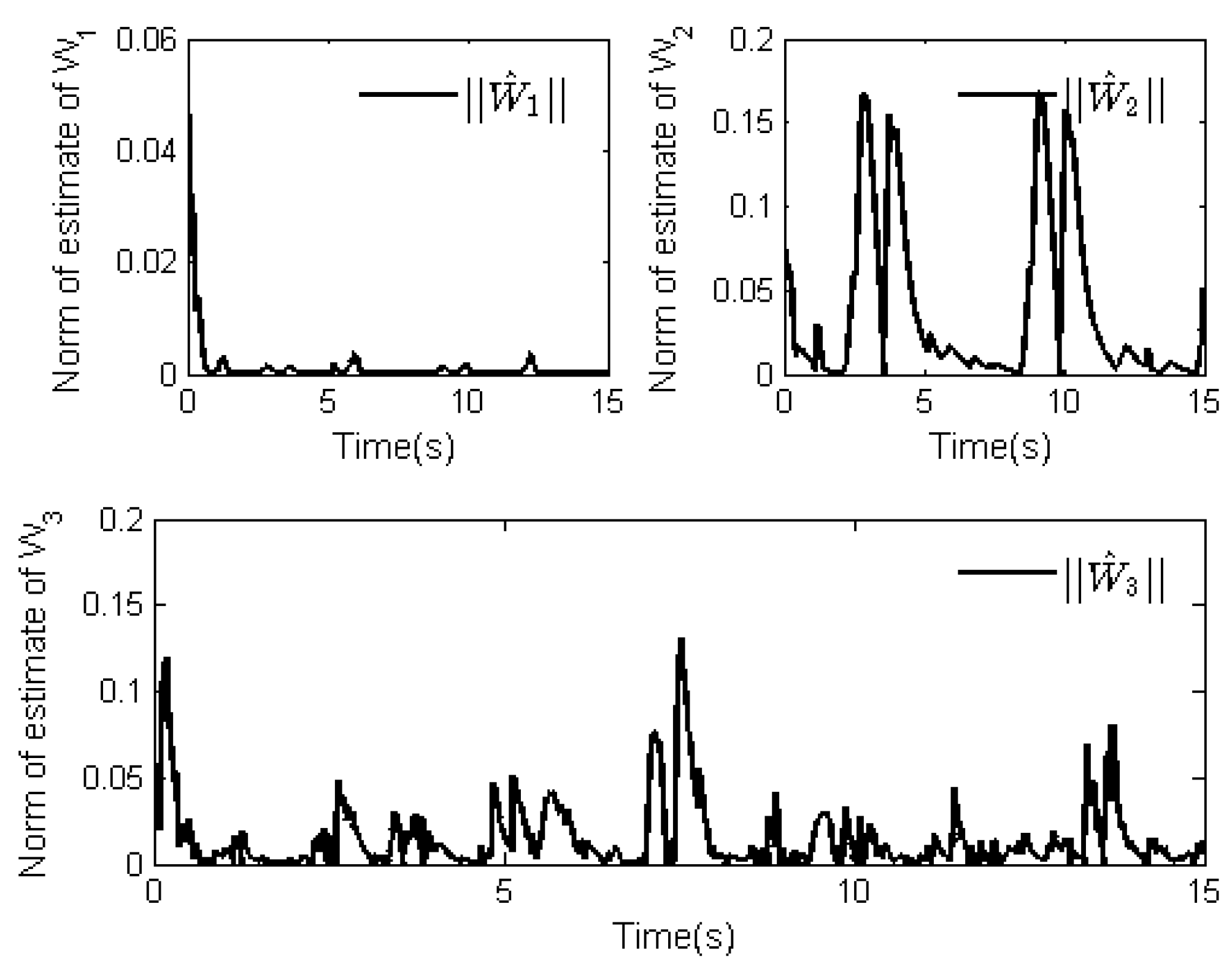
4. Simulation Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, Z.; Yang, Y.; Li, S.; Sun, J. Observer-Based Adaptive Finite-Time Quantized Tracking Control of Nonstrict-Feedback Nonlinear Systems with Asymmetric Actuator Saturation. IEEE Trans. Syst. Man Cybern. Syst. 2022, 50, 4545–4556. [Google Scholar] [CrossRef]
- Zhang, J.; Niu, B.; Wang, D.; Wang, H.; Duan, P.; Zong, G. Adaptive Neural Control of Nonlinear Nonstrict Feedback Systems with Full-State Constraints: A Novel Nonlinear Mapping Method. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Zhang, J.; Tong, S. Adaptive fuzzy output feedback FTC for nonstrict-feedback systems with sensor faults and dead zone input. Neurocomputing 2021, 435, 67–76. [Google Scholar] [CrossRef]
- Yuan, L.; Li, T.; Tong, S.; Xiao, Y.; Gao, X. NN adaptive optimal tracking control for a class of uncertain nonstrict feedback nonlinear systems. Neurocomputing 2022, 491, 382–394. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Q.; Zhao, N.; Wang, L. Fuzzy approximation-based adaptive finite-time control for nonstrict feedback nonlinear systems with state constraints. Inf. Sci. 2021, 548, 101–117. [Google Scholar] [CrossRef]
- Cui, G.; Yang, W.; Yu, J. Neural network-based finite-time adaptive tracking control of nonstrict-feedback nonlinear systems with actuator failures. Inf. Sci. 2021, 545, 298–311. [Google Scholar] [CrossRef]
- Yang, Y.; Niu, Y. Event-triggered adaptive neural backstepping control for nonstrict-feedback nonlinear time-delay systems. J. Frankl. Inst. 2020, 357, 4624–4644. [Google Scholar] [CrossRef]
- Cui, G.; Yu, J.; Shi, P. Observer-Based Finite-Time Adaptive Fuzzy Control with Prescribed Performance for Nonstrict-Feedback Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2022, 30, 767–778. [Google Scholar] [CrossRef]
- Huang, J.-T. Global neuro-adaptive control of nonstrict-feedback systems with unknown control directions and multiple time delays. J. Frankl. Inst. 2020, 358, 533–554. [Google Scholar] [CrossRef]
- Ma, J.; Xu, S.; Ma, Q.; Zhang, Z. Event-Triggered Adaptive Neural Network Control for Nonstrict-Feedback Nonlinear Time-Delay Systems with Unknown Control Directions. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4196–4205. [Google Scholar] [CrossRef]
- Wu, J.; Hu, Y.; Huang, Y. Indirect adaptive robust control of nonstrict feedback nonlinear systems by a fuzzy approximation strategy. ISA Trans. 2021, 108, 10–17. [Google Scholar] [CrossRef]
- Yang, W.; Pan, Y.; Liang, H. Event-triggered adaptive fixed-time NN control for constrained nonstrict-feedback nonlinear systems with prescribed performance. Neurocomputing 2021, 422, 332–344. [Google Scholar] [CrossRef]
- Bi, W.; Wang, T. Adaptive Fuzzy Decentralized Control for Nonstrict Feedback Nonlinear Systems with Unmodeled Dynamics. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 275–286. [Google Scholar] [CrossRef]
- Wang, H.; Kang, S.; Zhao, X.; Xu, N.; Li, T. Command Filter-Based Adaptive Neural Control Design for Nonstrict-Feedback Nonlinear Systems with Multiple Actuator Constraints. IEEE Trans. Cybern. 2021. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, X.; Zhang, S.; Zong, G. Adaptive Neural Backstepping Control Design for A Class of Nonsmooth Nonlinear Systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1820–1831. [Google Scholar] [CrossRef]
- Cao, X.; Shi, P.; Li, Z.; Liu, M. Neural-Network-Based Adaptive Backstepping Control with Application to Spacecraft Attitude Regulation. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 4303–4313. [Google Scholar] [CrossRef]
- Aslmostafa, E.; Ghaemi, S.; Badamchizadeh, M.A.; Ghiasi, A.R. Adaptive backstepping quantized control for a class of unknown nonlinear systems. ISA Trans. 2021, 125, 146–155. [Google Scholar] [CrossRef]
- Meng, F.; Zhao, L.; Yu, J. Backstepping based adaptive finite-time tracking control of manipulator systems with uncertain parameters and unknown backlash. J. Frankl. Inst. 2019, 357, 11281–11297. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, H.; Shi, J.; Huang, Y.; Chen, H.; Guo, K.; Li, Q. An Adaptive Backstepping Sliding Mode Controller to Improve Vehicle Maneuverability and Stability via Torque Vectoring Control. IEEE Trans. Veh. Technol. 2020, 69, 2598–2612. [Google Scholar] [CrossRef]
- Alipour, M.; Zarei, J.; Razavi-Far, R.; Saif, M.; Mijatovic, N.; Dragicevic, T. Observer-Based Backstepping Sliding Mode Control Design for Microgrids Feeding a Constant Power Load. IEEE Trans. Ind. Electron. 2022. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Q.; Hu, C. Adaptive fuzzy command filtered backstepping control for uncertain pure-feedback systems. ISA Trans. 2022. [Google Scholar] [CrossRef]
- Yang, W.; Cui, G.; Ma, Q.; Ma, J.; Tao, C. Finite-time adaptive event-triggered command filtered backstepping control for a QUAV. Appl. Math. Comput. 2022, 423, 126898. [Google Scholar] [CrossRef]
- Deng, X.; Wang, J. Fuzzy-Based Adaptive Dynamic Surface Control for a Type of Uncertain Nonlinear System with Unknown Actuator Faults. Mathematics 2022, 10, 1624. [Google Scholar] [CrossRef]
- Baigzadehnoe, B.; Rahmani, Z.; Khosravi, A.; Rezaie, B. Adaptive decentralized fuzzy dynamic surface control scheme for a class of nonlinear large-scale systems with input and interconnection delays. Eur. J. Control 2020, 54, 33–48. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Zhao, Q.; Li, J.; Wu, Z.-G. Adaptive Neural Dynamic Surface Control with Prespecified Tracking Accuracy of Uncertain Stochastic Nonstrict-Feedback Systems. IEEE Trans. Cybern. 2022, 52, 3408–3421. [Google Scholar] [CrossRef]
- Shi, X.; Cheng, Y.; Yin, C.; Huang, X.; Zhong, S.-M. Design of adaptive backstepping dynamic surface control method with RBF neural network for uncertain nonlinear system. Neurocomputing 2019, 330, 490–503. [Google Scholar] [CrossRef]
- Nussbaum, R.D. Some remarks on a conjecture in parameter adaptive control. Syst. Control Lett. 1983, 3, 243–246. [Google Scholar] [CrossRef]
- Zhao, J.; Tong, S.; Li, Y. Fuzzy adaptive output feedback control for uncertain nonlinear systems with unknown control gain functions and unmodeled dynamics. Inf. Sci. 2021, 558, 140–156. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, X. Adaptive fuzzy command filtering control for nonlinear MIMO systems with full state constraints and unknown control direction. Neurocomputing 2022, 493, 474–485. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, C.; Ge, Y. Adaptive neural network dynamic surface control of uncertain strict-feedback nonlinear systems with unknown control direction and unknown actuator fault. J. Frankl. Inst. 2022, 359, 4054–4073. [Google Scholar] [CrossRef]
- Li, Y.; Yang, G. Observer-based adaptive fuzzy quantizedcontrol of uncertain nonlinear systems with unknown control directions. Fuzzy Sets Syst. 2019, 371, 61–77. [Google Scholar] [CrossRef]
- Ma, Q. Cooperative control of multi-agent systems with unknown control directions. Appl. Math. Comput. 2017, 292, 240–252. [Google Scholar] [CrossRef]
- Rezaee, H.; Abdollahi, F. Adaptive Leaderless Consensus Control of Strict-Feedback Nonlinear Multiagent Systems with Unknown Control Directions. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6435–6444. [Google Scholar] [CrossRef]
- Tong, S.; Li, Y.; Sui, S. Adaptive Fuzzy Tracking Control Design for SISO Uncertain Nonstrict Feedback Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2016, 24, 1441–1454. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, X.; Yuan, Y.; Wei, L.; Xu, B.; Tao, L. Adaptive Neural Tracking Control for Nonstrict-Feedback Nonlinear Systems with Unknown Control Gains via Dynamic Surface Control Method. Mathematics 2022, 10, 2419. https://doi.org/10.3390/math10142419
Deng X, Yuan Y, Wei L, Xu B, Tao L. Adaptive Neural Tracking Control for Nonstrict-Feedback Nonlinear Systems with Unknown Control Gains via Dynamic Surface Control Method. Mathematics. 2022; 10(14):2419. https://doi.org/10.3390/math10142419
Chicago/Turabian StyleDeng, Xiongfeng, Yiming Yuan, Lisheng Wei, Binzi Xu, and Liang Tao. 2022. "Adaptive Neural Tracking Control for Nonstrict-Feedback Nonlinear Systems with Unknown Control Gains via Dynamic Surface Control Method" Mathematics 10, no. 14: 2419. https://doi.org/10.3390/math10142419
APA StyleDeng, X., Yuan, Y., Wei, L., Xu, B., & Tao, L. (2022). Adaptive Neural Tracking Control for Nonstrict-Feedback Nonlinear Systems with Unknown Control Gains via Dynamic Surface Control Method. Mathematics, 10(14), 2419. https://doi.org/10.3390/math10142419




