Scalable Cell-Free Massive MIMO with Multiple CPUs
Abstract
:1. Introduction
1.1. Related Work
- Despite [18] having proved that excellent performance can be achieved when all the APs are connected to a single CPU for joint transmission, it is difficult to let a single CPU control all the APs when the number of APs is large. Moreover, joint transmission requires a single CPU to centralize the signal processing, which puts high demands on the CPU’s processing capacity.
- The traditional precoding and power control of CF-M-MIMO act on the overall APs and UEs, which are difficult to realize in practice. Although a series of studies have proved the superiority of the final results [18,24,25], the complexity of these algorithms grows polynomially with the number of APs or UEs. Moreover, each AP needs to transmit instantaneous CSIs to the CPU, which is also difficult to achieve scalability when there are a large number of APs in the CF-M-MIMO systems.
- We consider a taxonomy with four different implementations of CF-M-MIMO with multiple CPUs, which are classified by different degrees of cooperation among the CPUs. The four different levels of cooperation can be called centralized connectivity, distributed connectivity and complex processing, distributed connectivity and simple processing, and no connectivity, respectively. The difference of these levels is shown in Table 1. We derive novel SE expressions for different levels of multiple CPUs cooperation in the uplink transmission. In addition, unlike most scenarios that specify the number of CPUs participating in the service, we consider a completely user-centric way to select APs.
- We propose a novel signal processing algorithm for cooperation among multiple CPUs. Each CPU processes the local information from its APs, and then transmits these signals to a CPU for final decoding. Based on the generalized Rayleigh quotient, we use simple weighted processing to linearly combine received signals from multiple CPUs with statistical CSIs.
- We compare the performance of different cooperation levels. Monte Carlo simulation results show that our proposed distributed connectivity scheme can achieve scalability with lower backhual burden, and the performance loss is negligible compared to the centralized connectivity scheme.
1.2. Paper Structure
2. System Model
2.1. Channel Estimation
2.2. Uplink Payload Transmission
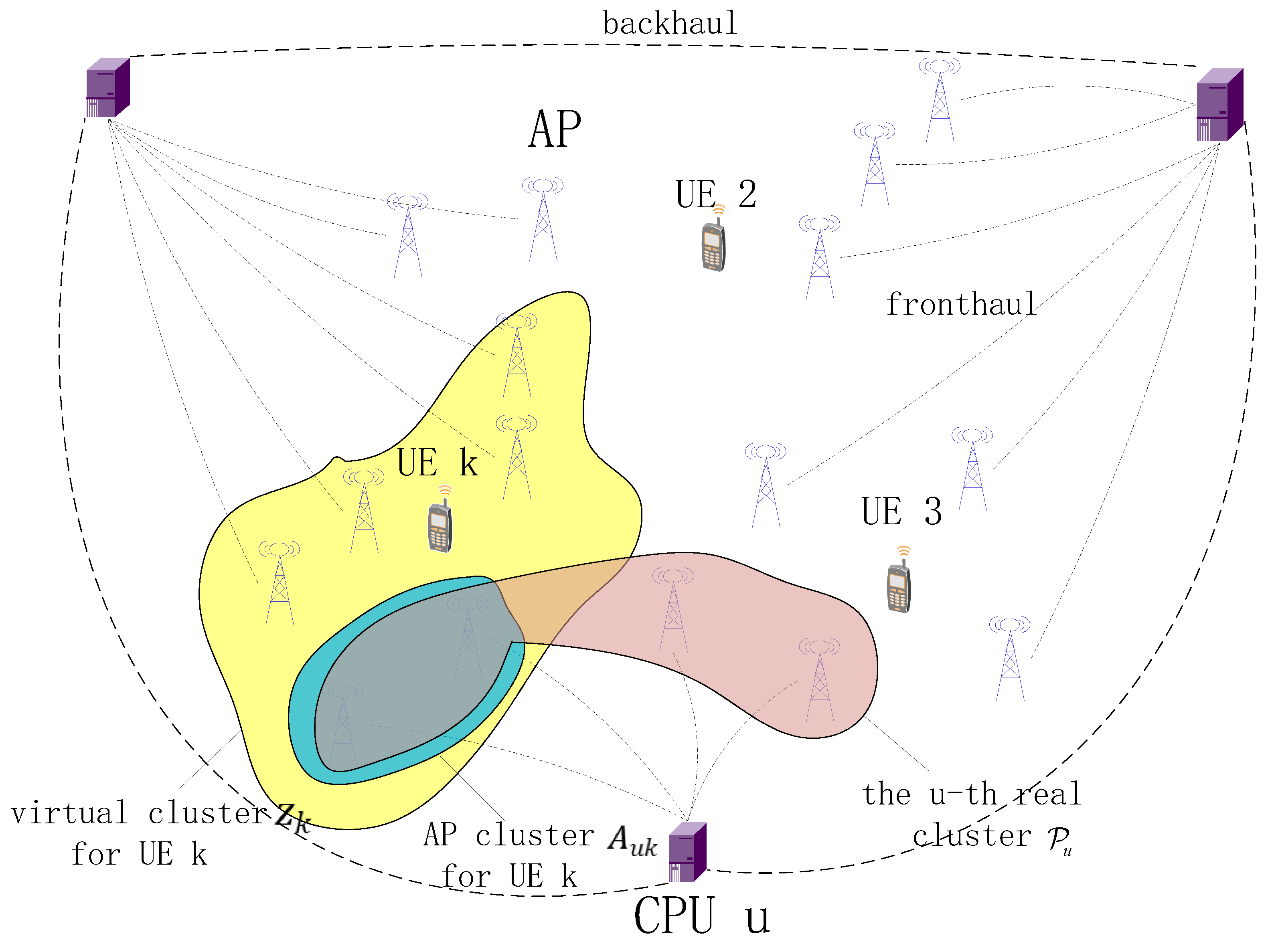
2.3. Dynamic Cooperation Clustering Network
3. Multiple CPUs Cooperative Transmission
3.1. Level 4: Centralized Connectivity
3.2. Level 3: Distributed Connectivity and Complex Processing
| Algorithm 1 Optimization algorithm for Level 3 |
| Input: Channel gain , MMSE combining , noise variance , DCC matrix Output: 1: Initialization: calculate -dimensional vector 2: for u = 1:U do 3: for k = 1:K do 4: if then 5: calculate diagonal matrix 6: update 7: calculate by (23). 8: end if 9: end for 10: end for |
3.3. Level 2: Distributed Connectivity and Simple Processing
3.4. Level 1: No Connectivity
4. Simulation Results
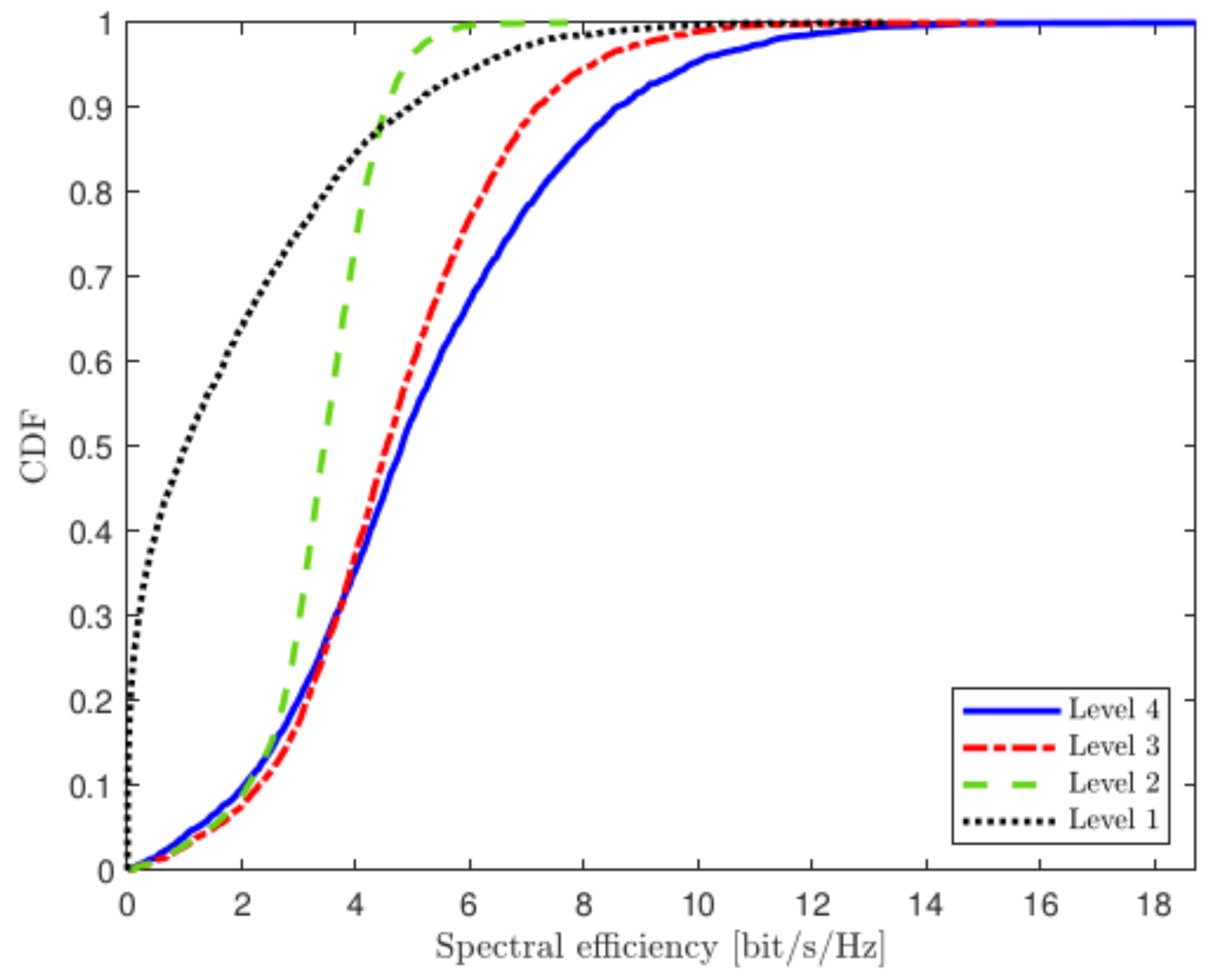
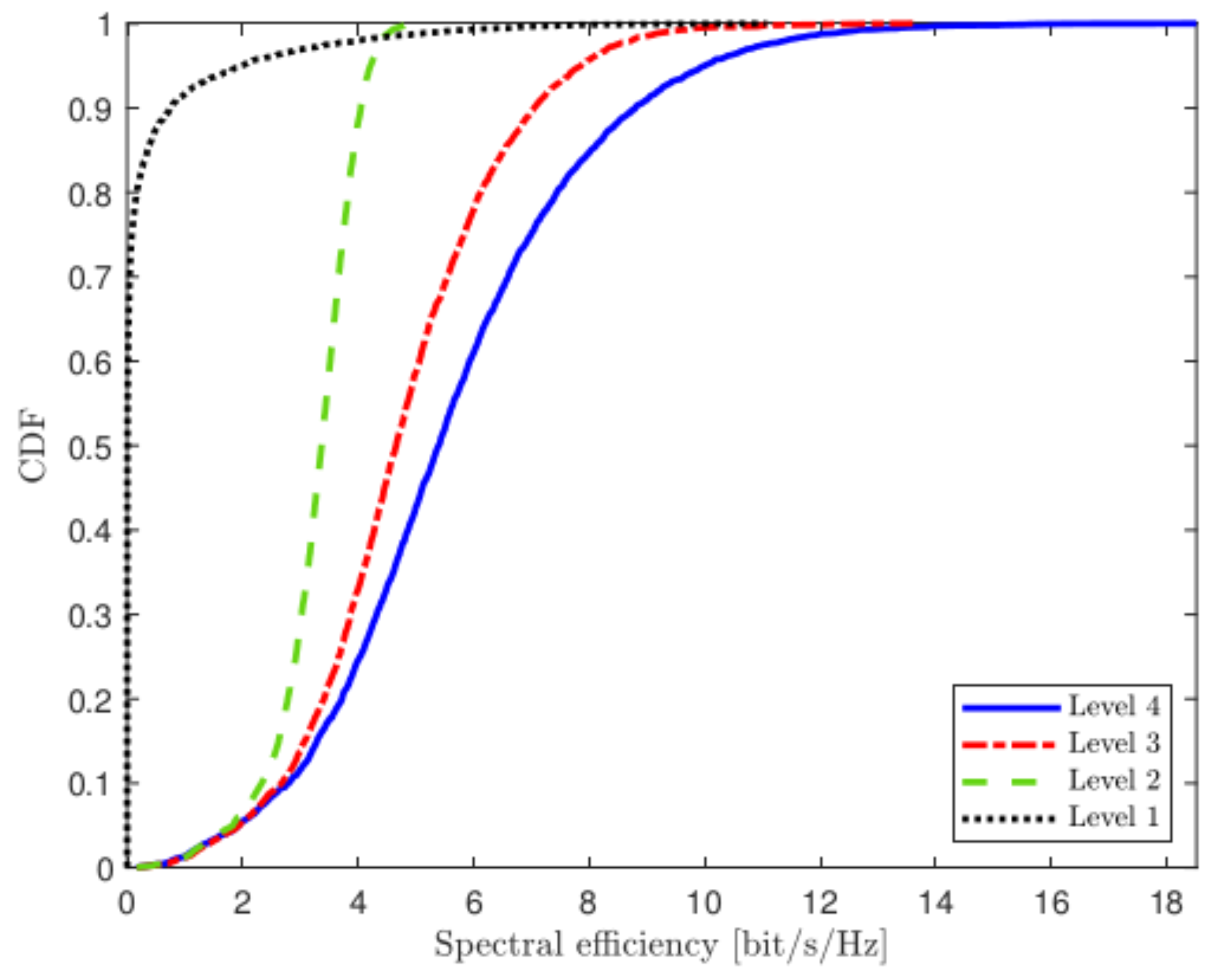
4.1. Uplink Transmission
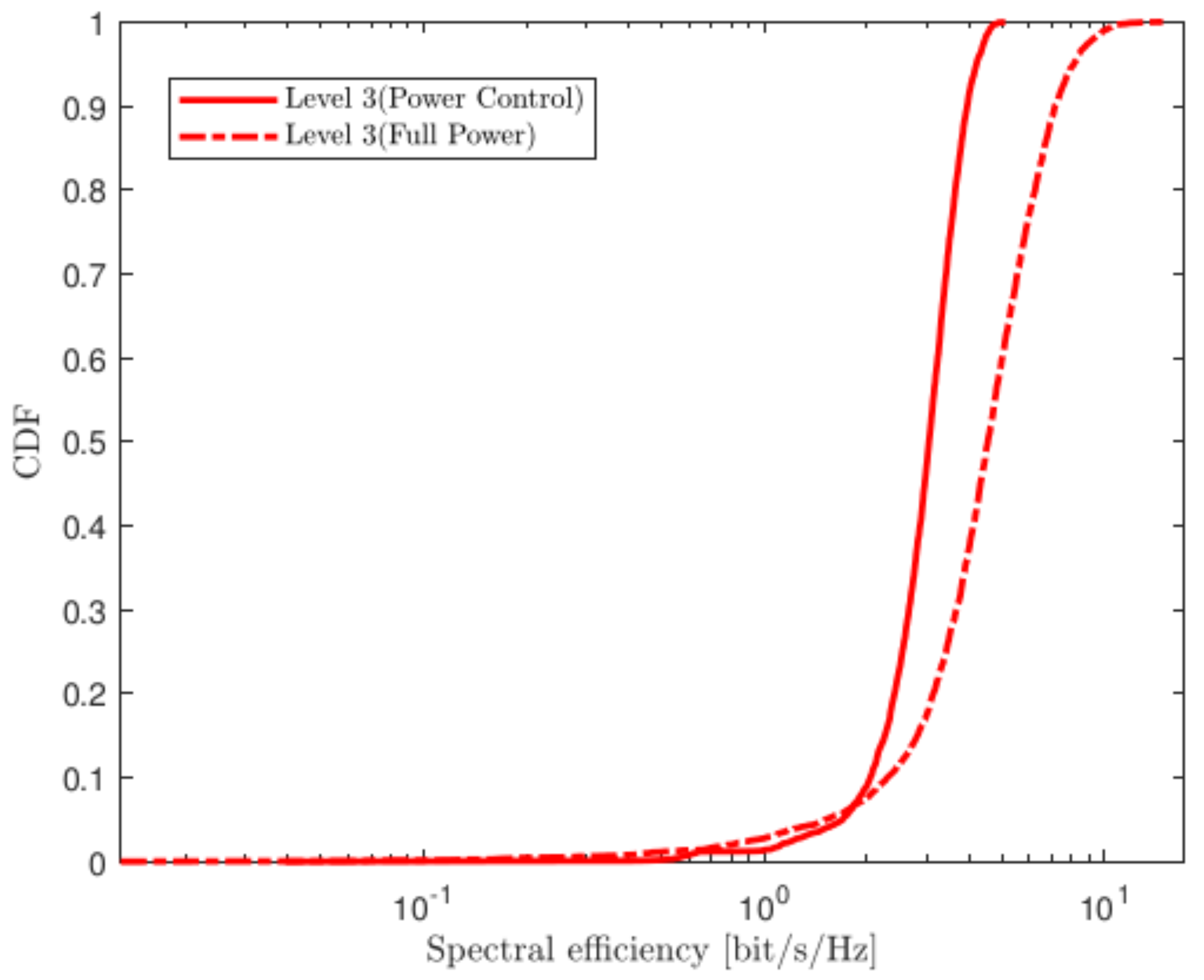
4.2. Power Allocation
4.3. Varying Numbers of CPUs
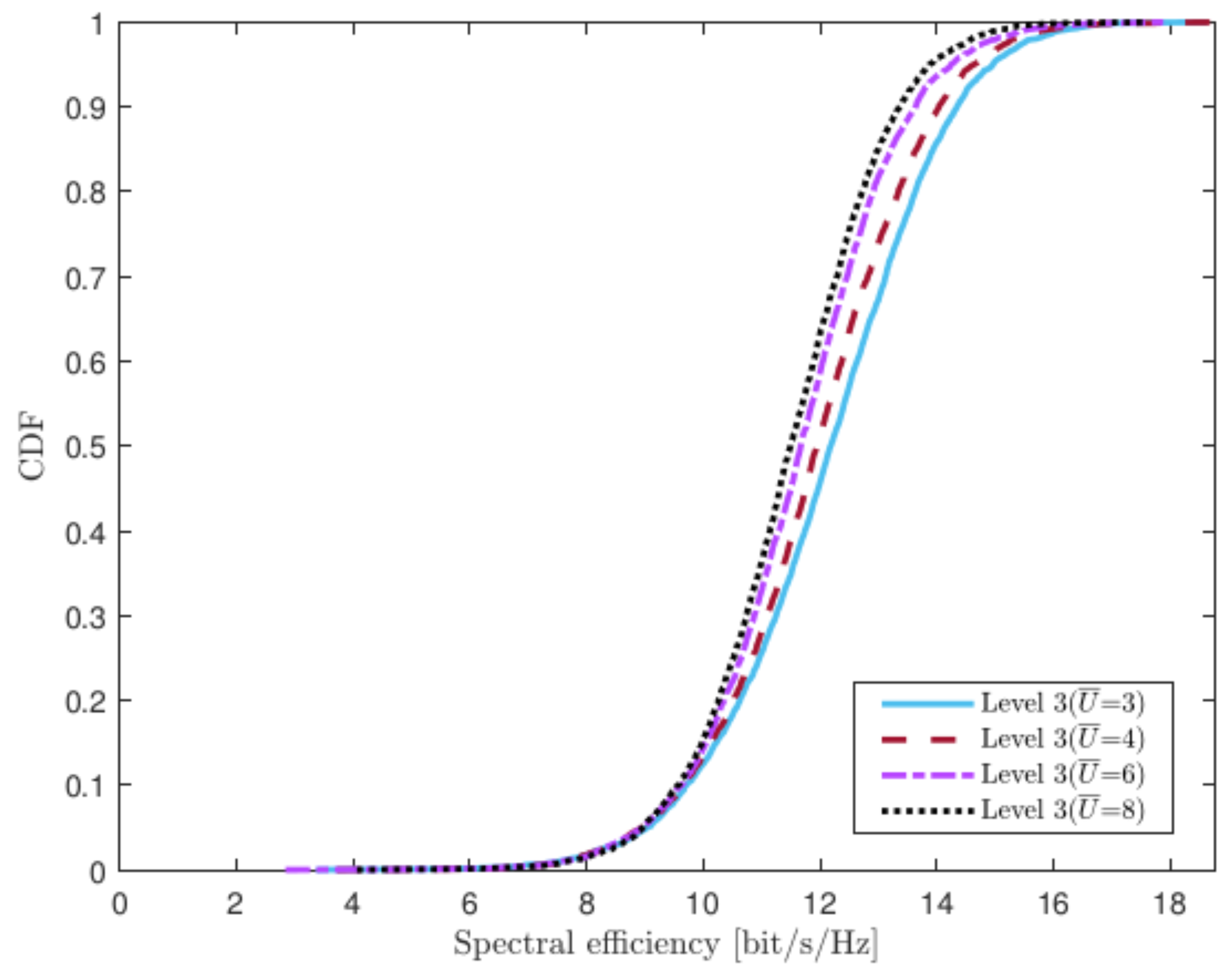
4.4. Varying Numbers of UEs
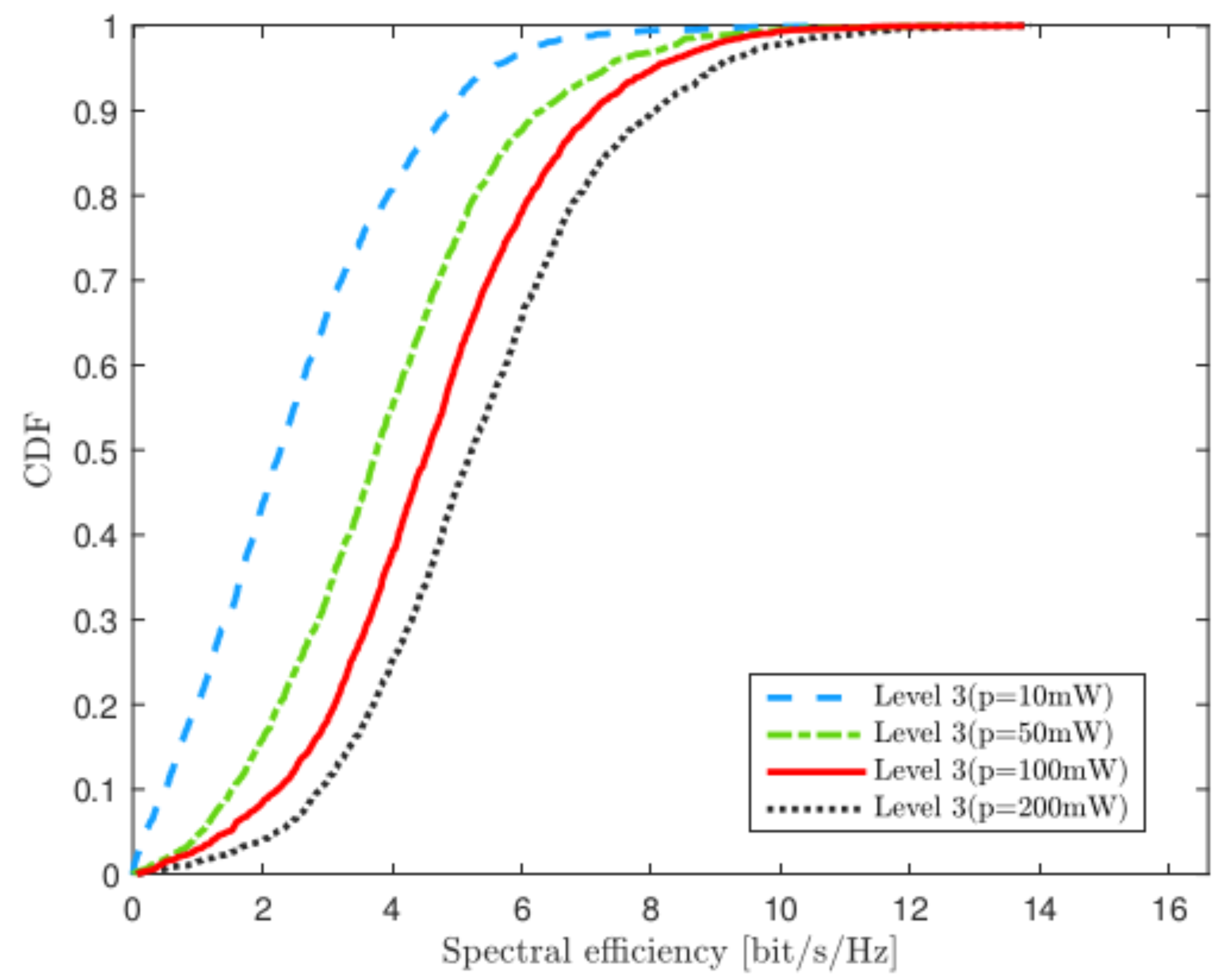
4.5. Varying the Uplink Transmit Power
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Dai, H.; Molisch, A.F.; Poor, H.V. Downlink capacity of interference-limited MIMO systems with joint detection. IEEE Trans. Wirel. Commun. 2004, 3, 442–453. [Google Scholar] [CrossRef]
- Choi, W.; Andrews, J.G. Downlink performance and capacity of distributed antenna systems in a multicell environment. IEEE Trans. Wirel. Commun. 2007, 6, 69–73. [Google Scholar] [CrossRef]
- Andrews, J.G.; Choi, W.; Heath, R.W. Overcoming interference in spatial multiplexing MIMO cellular networks. IEEE Wirel. Commun. Mag. 2007, 14, 95–104. [Google Scholar] [CrossRef]
- Irmer, R.; Droste, H.; Marsch, P.; Grieger, M.; Fettweis, G.; Brueck, S.; Mayer, H.P.; Thiele, L.; Jungnickel, V. Coordinated multipoint: Concepts, performance, and field trial results. IEEE Commun. Mag. 2011, 49, 102–111. [Google Scholar] [CrossRef] [Green Version]
- Lozano, A.; Heath, R.W.; Andrews, J.G. Fundamental limits of cooperation. IEEE Trans. Inf. Theory 2013, 59, 5213–5226. [Google Scholar] [CrossRef] [Green Version]
- Björnson, E.; Kountouris, M.; Debbah, M. Massive MIMO and small cells: Improving energy efficiency by optimal soft-cel coordination. In Proceedings of the 20th International Conference Telecommunication (ICT 2013), Casablanca, Morocco, 6–8 May 2013; pp. 1–5. [Google Scholar]
- Truong, K.T.; Heath, R.W. The viability of distributed antennas for massive MIMO systems. In Proceedings of the 45nd Asilomar Conference Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 2013; pp. 1318–1323. [Google Scholar]
- Björnson, E.; Sanguinetti, L.; Hoydis, J.; Debbah, M. Optimal design of energy-efficient multi-user MIMO systems: Is massive MIMO the answer. IEEE Trans. Wirel. Commun. 2015, 14, 3059–3075. [Google Scholar] [CrossRef] [Green Version]
- Larsson, E.G.; Tufvesson, F.; Edfors, O.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef] [Green Version]
- Marzetta, T.L.; Ngo, H.Q. Fundamentals of Massive MIMO; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Björnson, E.; Larsson, E.G.; Debbah, M. Massive MIMO for maximal spectral efficiency: How many users and pilots should be allocated? IEEE Trans. Wirel. Commun. 2015, 15, 1293–1308. [Google Scholar] [CrossRef] [Green Version]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-free massive MIMO: Uniformly great service for everyone. In Proceedings of the 2015 IEEE 16th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Stockholm, Sweden, 28 June–1 July 2015; pp. 201–205. [Google Scholar]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-free massive MIMO versus small cells. IEEE Trans. Wirel. Commun. 2017, 16, 1834–1850. [Google Scholar] [CrossRef] [Green Version]
- Interdonato, G.; Björnson, E.; Ngo, H.Q.; Frenger, P.; Larsson, E.G. Ubiquitous cell-free massive MIMO communications. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 197. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Björnson, E.; Matthaiou, M.; Ng, D.W.K.; Yang, H.; Love, D.J. Prospective Multiple Antenna Technologies for Beyond 5G. IEEE J. Sel. Areas Commun. 2020, 38, 1637–1660. [Google Scholar] [CrossRef]
- Burr, A.; Bashar, M.; Maryopi, D. Ultra-dense Radio Access Networks for Smart Cities: Cloud-RAN, Fog-RAN and cell-free Massive MIMO. arXiv 2018, arXiv:1811.11077. [Google Scholar]
- Li, S.; Tolbert, L.M.; Wang, F.; Peng, F.Z. Stray inductance reduction of commutation loop in the P-cell and N-cell-based IGBT phase leg module. IEEE Trans. Power Electron. 2013, 29, 3616–3624. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L. Making cell-free massive MIMO competitive with MMSE processing and centralized implementation. IEEE Trans. Wirel. Commun. 2019, 19, 77–90. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, L.D.; Duong, T.Q.; Ngo, H.Q.; Tourki, K. Energy efficiency in cell-free massive MIMO with zero-forcing precoding design. IEEE Commun. Lett. 2017, 21, 1871–1874. [Google Scholar] [CrossRef] [Green Version]
- Björnson, E.; Jorswieck, E. Optimal Resource Allocation in Coordinated Multi-Cell Systems; Now Publishers Inc.: Delft, The Netherlands, 2013. [Google Scholar]
- Kaltenberger, F.; Jiang, H.; Guillaud, M.; Knopp, R. Relative channel reciprocity calibration in MIMO/TDD systems. In Proceedings of the 2010 Future Network & Mobile Summit, Florence, Italy, 16–18 June 2010; pp. 1–10. [Google Scholar]
- Zhou, S.; Zhao, M.; Xu, X.; Wang, J.; Yao, Y. Distributed wireless communication system: A new architecture for future public wireless access. IEEE Commun. Mag. 2003, 41, 108–113. [Google Scholar] [CrossRef]
- Buzzi, S.; D’Andrea, C. Cell-free massive MIMO: User-centric approach. IEEE Commun. Lett. 2017, 6, 706–709. [Google Scholar] [CrossRef]
- Björnson, E.; Hoydis, J.; Sanguinetti, L. Massive MIMO networks: Spectral, energy, and hardware efficiency. Found. Trends Signal Process. 2017, 11, 154–655. [Google Scholar] [CrossRef]
- Sanguinetti, L.; Björnson, E.; Hoydis, J. Toward massive MIMO 2.0: Understanding spatial correlation, interference suppression, and pilot contamination. IEEE Trans. Commun. 2019, 68, 232–257. [Google Scholar] [CrossRef] [Green Version]
- Björnson, E.; Sanguinetti, L. Scalable cell-free massive MIMO systems. IEEE Trans. Commun. 2020, 68, 4247–4261. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhang, J.; Björnson, E.; Ai, B. Local partial zero-forcing combining for cell-free massive MIMO systems. IEEE Trans. Commun. 2021, 69, 8459–8473. [Google Scholar] [CrossRef]
- Interdonato, G.; Buzzi, S. Conjugate beamforming with fractional-exponent normalization and scalable power control in cell-free massive MIMO. In Proceedings of the 2021 IEEE 22nd International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Lucca, Italy, 27–30 September 2021; pp. 396–400. [Google Scholar]
- Nikbakht, R.; Mosayebi, R.; Lozano, A. Uplink fractional power control and downlink power allocation for cell-free networks. IEEE Wirel. Commun. Lett. 2020, 9, 774–777. [Google Scholar] [CrossRef]
- Interdonato, G.; Karlsson, M.; Björnson, E.; Larsson, E.G. Local partial zero-forcing precoding for cell-free massive MIMO. IEEE Trans. Wirel. Commun. 2020, 19, 4758–4774. [Google Scholar] [CrossRef] [Green Version]
- Interdonato, G.; Frenger, P.; Larsson, E.G. Scalability aspects of cell-free massive MIMO. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Nayebi, E.; Ashikhmin, A.; Marzetta, T.L.; Yang, H.; Rao, B.D. Precoding and power optimization in cell-free massive MIMO systems. IEEE Trans. Wirel. Commun. 2017, 16, 4445–4459. [Google Scholar] [CrossRef]
- Nayebi, E.; Ashikhmin, A.; Marzetta, T.L.; Rao, B.D. Performance of cell-free massive MIMO systems with MMSE and LSFD receivers. In Proceedings of the 2016 50th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 6–9 November 2016; pp. 203–207. [Google Scholar]
- Riera-Palou, F.; Femenias, G. Decentralization issues in cell-free massive MIMO networks with zero-forcing precoding. In Proceedings of the 2019 57th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 24–27 September 2019; pp. 521–527. [Google Scholar]
- Aguerri, I.E.; Zaidi, A.; Caire, G.; Shitz, S.S. On the capacity of cloud radio access networks with oblivious relaying. IEEE Trans. Inf. Theory 2019, 65, 4575–4596. [Google Scholar] [CrossRef] [Green Version]
- Biglieri, E.; Proakis, J.; Shamai, S. Fading channels: Information-theoretic and communications aspects. IEEE Trans. Inf. Theory 1998, 44, 2619–2692. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Tataria, H.; Matthaiou, M.; Jin, S.; Larsson, E.G. On the performance of cell-free massive MIMO in Ricean fading. In Proceedings of the 2018 52nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; pp. 980–984. [Google Scholar]
- Adhikary, A.; Ashikhmin, A.; Marzetta, T.L. Uplink interference reduction in large-scale antenna systems. IEEE Trans. Commun. 2017, 65, 2194–2206. [Google Scholar] [CrossRef]
- Nikbakht, R.; Lozano, A. Uplink fractional power control for cell-free wireless networks. In Proceedings of the ICC 2019—2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–5. [Google Scholar]

| Type of CSIs | Level of Computational Complexity | |
|---|---|---|
| Level 4 centralized connectivity | instantaneous CSIs | high |
| Level 3 distributed connectivity and complex processing | statistical CSIs | medium |
| Level 2 distributed connectivity and simple processing | statistical CSIs | low |
| Level 1 no connectivity | − | lowest |
| Each Coherence Block | Statistical Parameters | |
|---|---|---|
| Level 4 | ||
| Level 3 | ||
| Level 2 | − | |
| Level 1 | − | − |
| Computing Combining Vectors | Computing Weighted Vectors | |||
|---|---|---|---|---|
| Multiplications | Divisions | Multiplications | Divisions | |
| Level 4 | − | − | ||
| Level 3 | ||||
| Level 2 | − | − | ||
| Level 1 | − | − | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Sun, Q.; Ji, X.; Chen, X. Scalable Cell-Free Massive MIMO with Multiple CPUs. Mathematics 2022, 10, 1900. https://doi.org/10.3390/math10111900
Li F, Sun Q, Ji X, Chen X. Scalable Cell-Free Massive MIMO with Multiple CPUs. Mathematics. 2022; 10(11):1900. https://doi.org/10.3390/math10111900
Chicago/Turabian StyleLi, Feiyang, Qiang Sun, Xiaodi Ji, and Xiaomin Chen. 2022. "Scalable Cell-Free Massive MIMO with Multiple CPUs" Mathematics 10, no. 11: 1900. https://doi.org/10.3390/math10111900
APA StyleLi, F., Sun, Q., Ji, X., & Chen, X. (2022). Scalable Cell-Free Massive MIMO with Multiple CPUs. Mathematics, 10(11), 1900. https://doi.org/10.3390/math10111900






