A Mathematical Model for Nonlinear Optimization Which Attempts Membership Functions to Address the Uncertainties
Abstract
:1. Introduction
2. Literature Survey
3. Preliminaries
4. An Optimization Model for Fuzzy Nonlinear Programming
4.1. Formulation of the Fuzzy NLP with Equality Constraints
4.2. Computational Procedure
Remark
- A maximum point if starting with the principal major determinant of order then the last principal minor determinants of form an alternating sign pattern starting with
- A minimum point if starting with the principal minor determinant of order then the last principal minor determinants of having the sign of
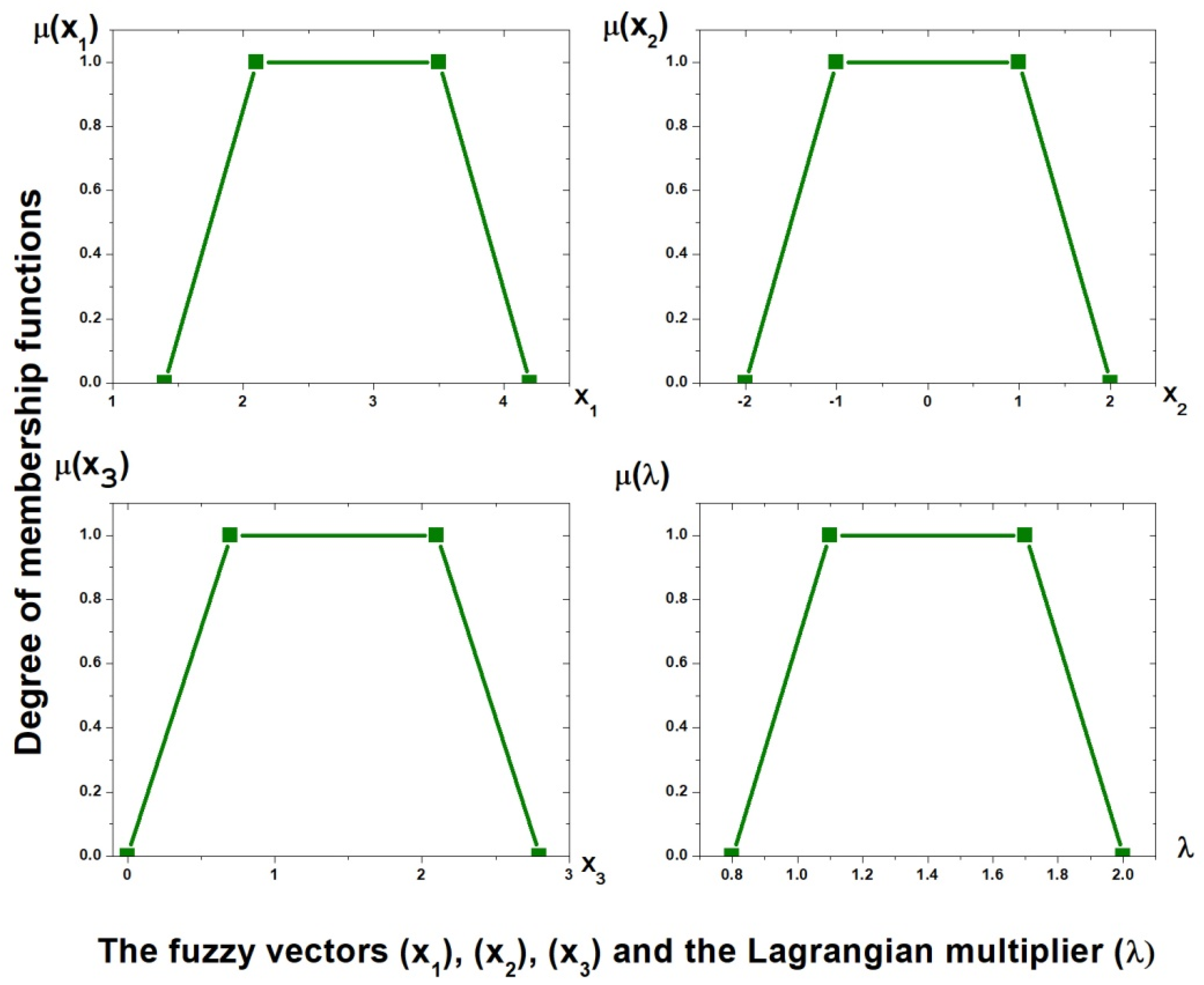
5. Numerical Illustration
5.1. Case (i): NLP with Fuzzy Membership Functions
5.2. Case (ii): The Robust Ranking Approach for NLP with Fuzzy MFs
5.3. Models Performance Evaluation with Different Sets of Inputs
5.4. Comparison Analysis
6. Results and Discussion
- The decision-maker perception, the entire value of the fuzzy NLPP, will be higher than and less than .
- The decision-maker for the entire fuzzy NLPP estimations are going to be bigger than or sufficient to and less than or equivalent to .
- The extent of the favors of the decision-maker for the rest of the estimations of the entire fuzzy NLPP value has frequently been attained as below:
- Here x describes the significance of the entire NLPP, and also the perception of decision-makers for , where
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Information and Control. In Fuzzy Sets; World Scientific: Singapore, 1965; Volume 8, pp. 338–353. [Google Scholar]
- Zimmermann, H.-J. Fuzzy Sets, Decision Making, and Expert Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 10. [Google Scholar]
- Vasant, P.; Nagarajan, R.; Yaacob, S. Fuzzy linear programming: A modern tool for decision making. In Computational Intelligence for Modelling and Prediction; Springer: Berlin/Heidelberg, Germany, 2005; pp. 383–401. [Google Scholar]
- Kheirfam, B.; Hasani, F. Sensitivity analysis for fuzzy linear programming problems with fuzzy variables. Adv. Model. Optim. 2010, 12, 257–272. [Google Scholar]
- Palanivel, K. Contributions to the Study on Some Optimization Techniques in Fuzzy Membership Functions; Bharathidasan University: Trichy, Tamil Nadu, India, 2013. [Google Scholar]
- Palanivel, K. Fuzzy commercial traveler problem of trapezoidal membership functions within the sort of α optimum solution using ranking technique. Afr. Mat. 2016, 27, 263–277. [Google Scholar] [CrossRef]
- Saranya, R.; Palanivel, K. Fuzzy nonlinear programming problem for inequality constraints with alpha optimal solution in terms of trapezoidal membership functions. Int. J. Pure Appl. Math. 2018, 119, 53–63. [Google Scholar]
- Tang, J.; Wang, D. A nonsymmetric model for fuzzy nonlinear programming problems with penalty coefficients. Comput. Oper. Res. 1997, 24, 717–725. [Google Scholar] [CrossRef]
- Tang, J.; Wang, D.; Ip, A.; Fung, R. A hybrid genetic algorithm for a type of nonlinear programming problem. Comput. Math. Appl. 1998, 36, 11–22. [Google Scholar] [CrossRef] [Green Version]
- Fung, R.Y.; Tang, J.; Wang, D. Extension of a hybrid genetic algorithm for nonlinear programming problems with equality and inequality constraints. Comput. Oper. Res. 2002, 29, 261–274. [Google Scholar] [CrossRef]
- Sarimveis, H.; Nikolakopoulos, A. A line up evolutionary algorithm for solving nonlinear constrained optimization problems. Comput. Oper. Res. 2005, 32, 1499–1514. [Google Scholar] [CrossRef]
- Syau, Y.-R.; Stanley Lee, E. Fuzzy convexity and multiobjective convex optimization problems. Comput. Math. Appl. 2006, 52, 351–362. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.-P. Solving fuzzy queueing decision problems via a parametric mixed integer nonlinear programming method. Eur. J. Oper. Res. 2007, 177, 445–457. [Google Scholar] [CrossRef]
- Qin, X.S.; Huang, G.H.; Zeng, G.M.; Chakma, A.; Huang, Y.F. An interval-parameter fuzzy nonlinear optimization model for stream water quality management under uncertainty. Eur. J. Oper. Res. 2007, 180, 1331–1357. [Google Scholar] [CrossRef]
- Kassem, M.A.E.-H. Stability achievement scalarization function for multiobjective nonlinear programming problems. Appl. Math. Model. 2008, 32, 1044–1055. [Google Scholar] [CrossRef]
- Shankar, N.R.; Rao, G.A.; Latha, J.M.; Sireesha, V. Solving a fuzzy nonlinear optimization problem by genetic algorithm. Int. J. Contemp. Math. Sci. 2010, 5, 791–803. [Google Scholar]
- Abd-El-Wahed, W.F.; Mousa, A.A.; El-Shorbagy, M.A. Integrating particle swarm optimization with genetic algorithms for solving nonlinear optimization problems. J. Comput. Appl. Math. 2011, 235, 1446–1453. [Google Scholar] [CrossRef]
- Jameel, A.F.; Sadeghi, A. Solving nonlinear programming problem in fuzzy environment. Int. J. Contemp. Math. Sci. 2012, 7, 159–170. [Google Scholar]
- Michalewicz, Z.; Vignaux, G.A.; Hobbs, M. A nonstandard genetic algorithm for the nonlinear transportation problem. ORSA J. Comput. 1991, 3, 307–316. [Google Scholar] [CrossRef]
- Ilich, N.; Simonovic, S.P. An evolution program for non-linear transportation problems. J. Heuristics 2001, 7, 145–168. [Google Scholar] [CrossRef]
- Hedar, A.-R.; Allam, A.A.; Deabes, W. Memory-Based Evolutionary Algorithms for Nonlinear and Stochastic Programming Problems. Mathematics 2019, 7, 1126. [Google Scholar] [CrossRef] [Green Version]
- Klanšek, U. A Comparison between Milp and Minlp Approaches to Optimal Solution of Nonlinear Discrete Transportation Problem. Transport 2014, 30, 135–144. [Google Scholar] [CrossRef] [Green Version]
- Das, A.; Bera, U.K.; Maiti, M. A profit maximizing solid transportation model under a rough interval approach. IEEE Trans. Fuzzy Syst. 2016, 25, 485–498. [Google Scholar] [CrossRef]
- Das, A.; Lee, G.M. A Multi-Objective Stochastic Solid Transportation Problem with the Supply, Demand, and Conveyance Capacity Following the Weibull Distribution. Mathematics 2021, 9, 1757. [Google Scholar] [CrossRef]
- Ahmadini, A.A.H.; Varshney, R.; Ali, I. On multivariate-multiobjective stratified sampling design under probabilistic environment: A fuzzy programming technique. J. King Saud. Univ.-Sci. 2021, 33, 101448. [Google Scholar] [CrossRef]
- Khan, M.F.; Modibbo, U.M.; Ahmad, N.; Ali, I. Nonlinear optimization in bi-level selective maintenance allocation problem. J. King Saud. Univ.-Sci. 2022, 34, 101933. [Google Scholar] [CrossRef]
- Ali, S.S.; Barman, H.; Kaur, R.; Tomaskova, H.; Roy, S.K. Multi-Product Multi Echelon Measurements of Perishable Supply Chain: Fuzzy Non-Linear Programming Approach. Mathematics 2021, 9, 2093. [Google Scholar] [CrossRef]
- El-Sobky, B.; Abo-Elnaga, Y.; Mousa, A.A.A.; El-Shorbagy, M.A. Trust-Region Based Penalty Barrier Algorithm for Constrained Nonlinear Programming Problems: An Application of Design of Minimum Cost Canal Sections. Mathematics 2021, 9, 1551. [Google Scholar] [CrossRef]
- Gupta, D.; Borah, P.; Sharma, U.M.; Prasad, M. Data-driven mechanism based on fuzzy Lagrangian twin parametric-margin support vector machine for biomedical data analysis. Neural Comput. Appl. 2021, 1–11. [Google Scholar] [CrossRef]
- Lin, L.; Lee, H.-M. Fuzzy nonlinear programming for production inventory based on statistical data. J. Adv. Comput. Intell. Intell. Inform. 2016, 20, 5–12. [Google Scholar] [CrossRef]
- Lu, T.; Liu, S.-T. Fuzzy nonlinear programming approach to the evaluation of manufacturing processes. Eng. Appl. Artif. Intell. 2018, 72, 183–189. [Google Scholar] [CrossRef]
- Saberi Najafi, H.; Edalatpanah, S.A.; Dutta, H. A nonlinear model for fully fuzzy linear programming with fully unrestricted variables and parameters. Alex. Eng. J. 2016, 55, 2589–2595. [Google Scholar] [CrossRef] [Green Version]
- Silva, R.C.; Cruz, C.; Verdegay, J.L. Fuzzy costs in quadratic programming problems. Fuzzy Optim. Decis. Mak. 2013, 12, 231–248. [Google Scholar] [CrossRef]
- Gani, A.N.; Saleem, R.A. Solving Fuzzy Sequential Quadratic Programming Algorithm for Fuzzy Non-Linear Programming. J. Phys. Sci. 2018, 23, 89–96. [Google Scholar]


| Fuzzy Input for Objective Functions’ Coefficient | Fuzy Inputs for Coefficients in Constiants’ and Right Side’s Value | Optimal Objective Value | Solutions | |
|---|---|---|---|---|
| Set-1 | [2,4,7,11]; [6.5,12.3,16,19.98]; [5,9,11.5,15.07] | [4,7,10,13]; [2.5,4.9,7.9,11]; [1.2,3.4,6.7,10.5] and [11.8,14.9,19.2,24.4] | 20.3700 | |
| Set-2 | [0.4,1.13,2.31,5.56]; [16.15,22.39,26.78,29.59]; [5.98,7.99,10.54,13.67] | [1.56,2.67,6.64,9.88]; [2.35,3.89,6.99,8.92]; [5.22,7.41,9.27,10.53] and | 138.5768 | |
| Set-3 | [-3.35,-0.93,-4.11,8.61]; [-5.11,-1.09,-3.11,10.19], [25.98,27.99,30.54,33.67] | [21.05,22.07,26.06,29.08], [12.03,13.09,16.09,18.02], [25.02,27.01,29.07,30.03] and [12,13,14,15] | 0.0178 | |
| Set-4 | [63.89,70.31,79.91,85.13]; [45.11,51.98,63.44,0.97]; [75.21,87.23,90.44,99.92] | [29.68,34.55,39.13,41.45], [12.03,14.09,17.09,19.02], [11.12,12.17,14.19,18.71] and [111.2,122.1,134.9,148.7] | 412.3734 |
| Optimum Values | The Existing Model Is Based on the Conventional Approach | The Proposed Model Is Based on the Conventional Approach in Terms of Fuzziness | The Proposed Model Is Based on the Robust Ranking Approach |
|---|---|---|---|
| 2.8 | |||
| 0 | |||
| 1.4 | |||
| 1.4 | |||
| Min Z | 9.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaliyaperumal, P.; Das, A. A Mathematical Model for Nonlinear Optimization Which Attempts Membership Functions to Address the Uncertainties. Mathematics 2022, 10, 1743. https://doi.org/10.3390/math10101743
Kaliyaperumal P, Das A. A Mathematical Model for Nonlinear Optimization Which Attempts Membership Functions to Address the Uncertainties. Mathematics. 2022; 10(10):1743. https://doi.org/10.3390/math10101743
Chicago/Turabian StyleKaliyaperumal, Palanivel, and Amrit Das. 2022. "A Mathematical Model for Nonlinear Optimization Which Attempts Membership Functions to Address the Uncertainties" Mathematics 10, no. 10: 1743. https://doi.org/10.3390/math10101743
APA StyleKaliyaperumal, P., & Das, A. (2022). A Mathematical Model for Nonlinear Optimization Which Attempts Membership Functions to Address the Uncertainties. Mathematics, 10(10), 1743. https://doi.org/10.3390/math10101743







