Internal Variable Theory in Viscoelasticity: Fractional Generalizations and Thermodynamical Restrictions
Abstract
:1. Introduction
2. Model
- (A)
- Fractional-order internal variable viscoelasticity with constitutive equation of the form that generalizes Equations (1) and (2) such thatThe case where , is trivial, since it leads to Hooke’s law:
- (B)
- Distributed fractional-order internal variable viscoelasticity with a constitutive equation of the form that generalizes the model presented in [1] (p. 36):where is given a constitutive function or distribution. In addition, and denote the relaxation times. In the analysis that follows, we shall assume that Note that Equations (12) and (13) are fractional generalizations of the internal variable model with a continuum of relaxation times, as presented in [1] (p. 36). They also have the form of a distributed-order fractional constitutive equations.
3. Main Results
3.1. Model A
3.2. Model B
4. Examples
- The generalized Zener model;
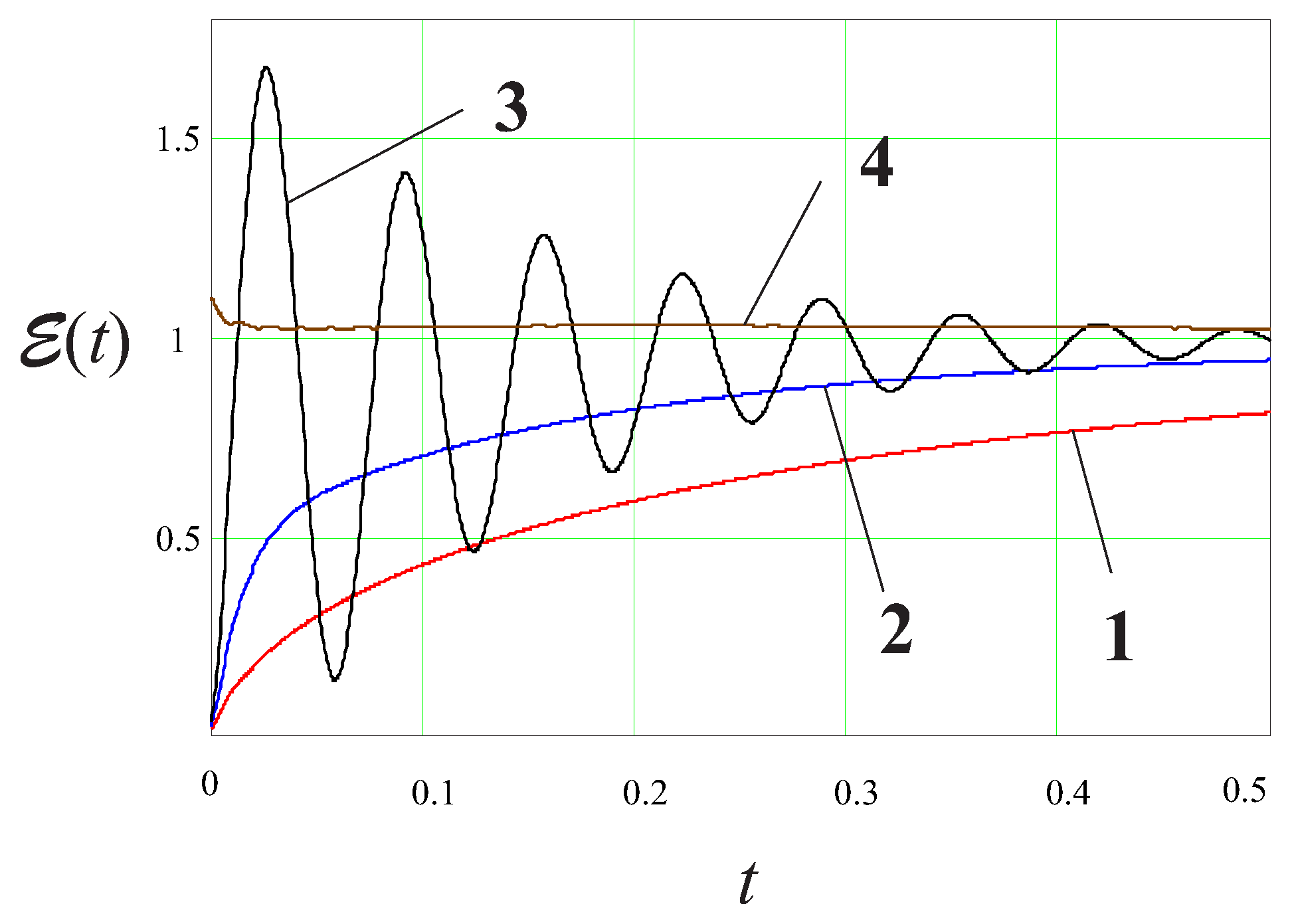
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Banks, H.T.; Kenz, S.H.Z.R. A Brief Review of Elasticity and Viscoelasticity for Solids. Adv. Appl. Math. Mech. 2011, 3, 1–51. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Zhong, D.; Rudykh, S.; Zhou, H.; Qu, S. A Review of Physically Based and Thermodynamically Based Constitutive Models for Soft Materials. J. Appl. Mech. 2020, 87, 110801. [Google Scholar] [CrossRef]
- Atanackovic, T.M. A modified Zener model of a viscoelastic body. Contin. Mech. Thermodyn. 2002, 14, 137–148. [Google Scholar] [CrossRef]
- Hanyaga, A. Internal variable models of Viscoelasticity with fractional Relaxation times. In Proceedings of the DETC’03 ASME Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 2–6 September 2003. [Google Scholar]
- Atanackovic, T.M.; Janev, M.; Pilipovic, S. On the thermodynamical restrictions in isothermal deformations of fractional Burgers model. Phil. Trans. R. Soc. A 2020, 378, 20190278. [Google Scholar] [CrossRef] [PubMed]
- Atanackovic, T.M.; Janev, M.; Pilipovic, S.; Selesi, D. Viscoelasticity of Fractional Order: New Restrictions on Constitutive Equations with Applications. Int. J. Struct. Stab. Dyn. 2020, 20, 2041011. [Google Scholar] [CrossRef]
- Adolfsson, K.; Enelund, M.; Olsson, P. On the Fractional Order Model of Viscoelasticity. Mech. -Time-Depend. Mater. 2005, 9, 15–34. [Google Scholar] [CrossRef]
- Petrovic, L.M.; Zorica, D.M.; Stojanac, I.L.; Krstonosic, V.S.; Hadnadjev, M.S.; Atanackovic, T.M. A model of the viscoelastic behavior of flowable resin composites prior to setting. Dent. Mater. 2013, 29, 929–934. [Google Scholar] [CrossRef] [PubMed]
- Sarcev, I.; Petronijevic-Sarcev, B.; Krstonosic, V.; Janev, M.; Atanackovic, T.M. Modeling the rheological properties of four commercially available composite core build-up materials. Polym. Polym. Compos. 2020, 29, 931–938. [Google Scholar]
- Zink, T.; Kehrer, L.; Hirschberg, V.; Wilhelm, M.; Böhlke, T. Nonlinear Schapery viscoelastic material model for thermoplastic polymers. J. Appl. Polym. Sci. 2022, 139, e52028. [Google Scholar] [CrossRef]
- Maugin, G.A. The saga of internal variables of state in continuum thermo-mechanics (1893–2013). Mech. Res. 2015, 69, 79–86. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Luchko, Y. General Fractional Integrals and Derivatives of Arbitrary Order. Symmetry 2021, 13, 755. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Herrera, I. On dissipation inequalities and linear viscoelasticity. Q. Appl. Math. 1965, 23, 235–245. [Google Scholar] [CrossRef] [Green Version]
- Zorski, H. (Ed.) Foundations of Mechanics; Elsevier, PWN: Amsterdam, The Netherlands; Warsaw, Poland; Berlin, Germany, 1992. [Google Scholar]
- Fabrizio, M.; Morro, A. Mathematical Problems in Linear Viscoelasticity; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Hanyga, A. Physically acceptable viscoelastic models. In Trends in Applications of Mathematics to Mechanics; Hutter, K., Wang, Y., Eds.; Shaker Verlag GmbH: Verlag Aachen, Germany, 2005; pp. 125–136. [Google Scholar]
- Amendola, G.; Fabrizio, M.; Golden, J.M. Thermodynamics of Materials with Memory; Springer: New York, NY, USA; Dordrecht, The Netherlands; Heidelberg, Germany; London, UK, 2010. [Google Scholar]
- Reed, M.; Simon, B. Methods of Modern Mathematical Physics; Academic Press: San Diego, CA, USA, 1980. [Google Scholar]
- Vladimirov, V.S. Equations of Mathematical Physics; Mir Publishers: Moscow, ID, USA, 1981. [Google Scholar]
- Bagley, R.L.; Torvik, P.J. On the fractional calculus model of viscoelastic behavior. J. Rheol. 1986, 30, 133–155. [Google Scholar] [CrossRef]
- Shellhammer, T.H.; Rumesy, T.R.; Krochta, J.M. Viscoelastic properties of edible lipids. J. Food. Eng. 1997, 33, 305–320. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Cohen, A.M. Numerical Methods for Laplace Transform Inversion; Springer Science+Business Media: Boston, MA, USA, 2007. [Google Scholar]
- Konjik, S.; Oparnica, L.; Zorica, D. Waves in fractional Zener type viscoelastic media. J. Math. Anal. Appl. 2010, 365, 259–268. [Google Scholar] [CrossRef] [Green Version]
- Atanackovic, T.; Pilipovic, S.; Selesi, D. Wave propagation Dynamics in a Fractional Zener Model with Stochastic Exication. Fract. Calc. Appl. Anal. 2020, 23, 1570–1604. [Google Scholar] [CrossRef]
- Luchko, Y.; Mainardi, F.; Povstenko, Y. Propagation speed of the maximum of the fundamental solution to the fractional diffusion-wave equation. Comput. Math. Appl. 2013, 66, 774–784. [Google Scholar] [CrossRef]
- Luchko, Y. Fractional wave equation and damped waves. J. Math. Phys. 2013, 54, 031505. [Google Scholar] [CrossRef] [Green Version]
- Atanackovic, T.M.; Janev, M.; Pilipovic, S. Wave equation in fractional Zener-type viscoelastic media involving Caputo–Fabrizio fractional derivatives. Meccanica 2018, 54, 155–167. [Google Scholar] [CrossRef]
- Hristov, J. Prony’s series and modern fractional calculus: Rheological models with Caputo–Fabrizio operator (Chapter 11). In Multi-Chaos, Fractal and Multi-Fractional Artificial Intelligence of Different Complex Systems; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Tarasov, V.E. General Fractional Dynamics. Mathematics 2021, 9, 1464. [Google Scholar] [CrossRef]


| 1 | 1 | 1 | 1 | |||||
| 1 | 1 | 1 | ||||||
| 1 | 1 | 1 | ||||||
| 1 | 1 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atanackovic, T.M.; Dolicanin, C.; Kacapor, E. Internal Variable Theory in Viscoelasticity: Fractional Generalizations and Thermodynamical Restrictions. Mathematics 2022, 10, 1708. https://doi.org/10.3390/math10101708
Atanackovic TM, Dolicanin C, Kacapor E. Internal Variable Theory in Viscoelasticity: Fractional Generalizations and Thermodynamical Restrictions. Mathematics. 2022; 10(10):1708. https://doi.org/10.3390/math10101708
Chicago/Turabian StyleAtanackovic, Teodor M., Cemal Dolicanin, and Enes Kacapor. 2022. "Internal Variable Theory in Viscoelasticity: Fractional Generalizations and Thermodynamical Restrictions" Mathematics 10, no. 10: 1708. https://doi.org/10.3390/math10101708
APA StyleAtanackovic, T. M., Dolicanin, C., & Kacapor, E. (2022). Internal Variable Theory in Viscoelasticity: Fractional Generalizations and Thermodynamical Restrictions. Mathematics, 10(10), 1708. https://doi.org/10.3390/math10101708






