An Extended ORESTE Approach for Evaluating Rockburst Risk under Uncertain Environments
Abstract
:1. Introduction
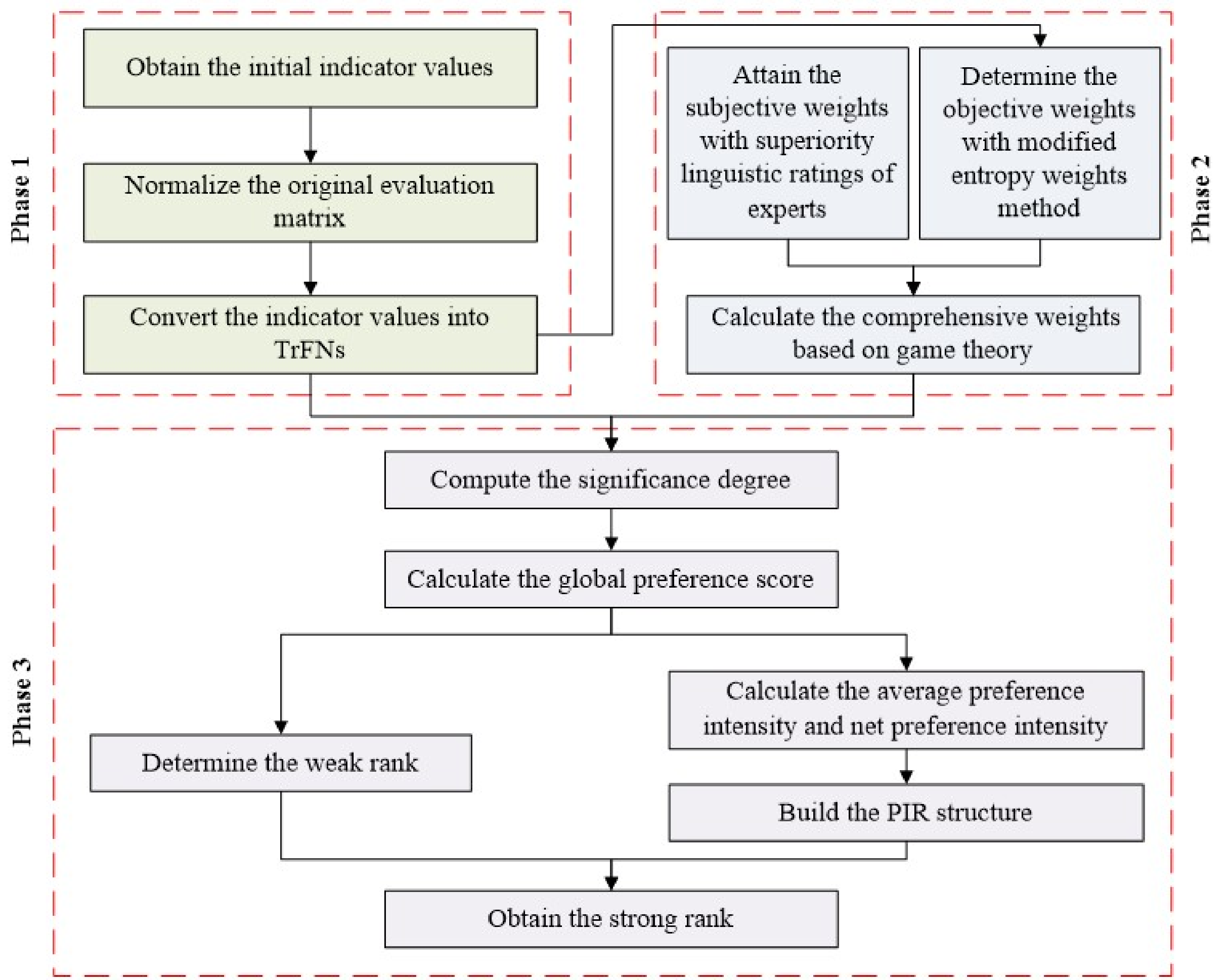
2. Methodology
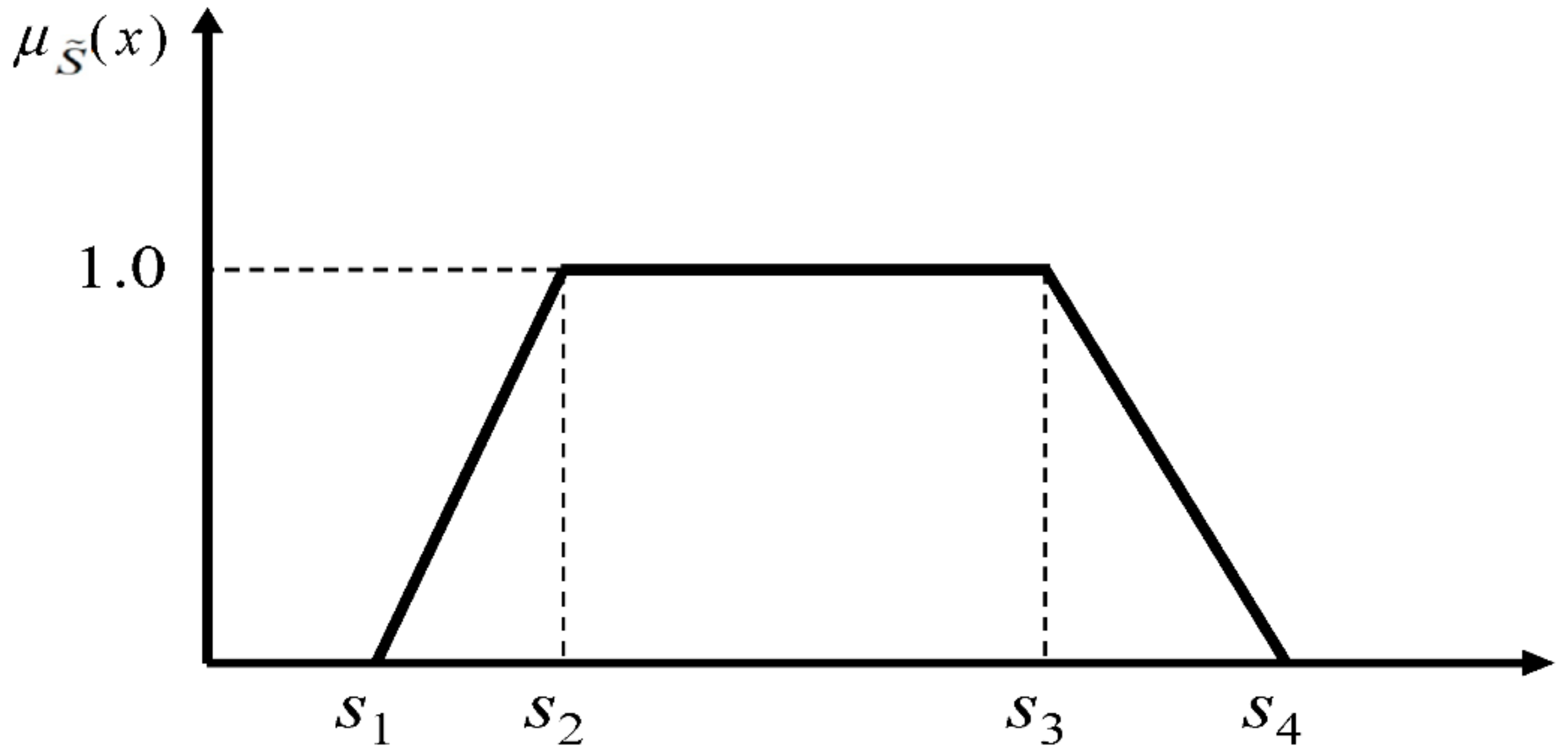
2.1. Trapezoidal Fuzzy Numbers
2.2. Extended ORESTE Method
- (1)
- When , then ;
- (2)
- When , then , where and are two parameters.
3. Case Study
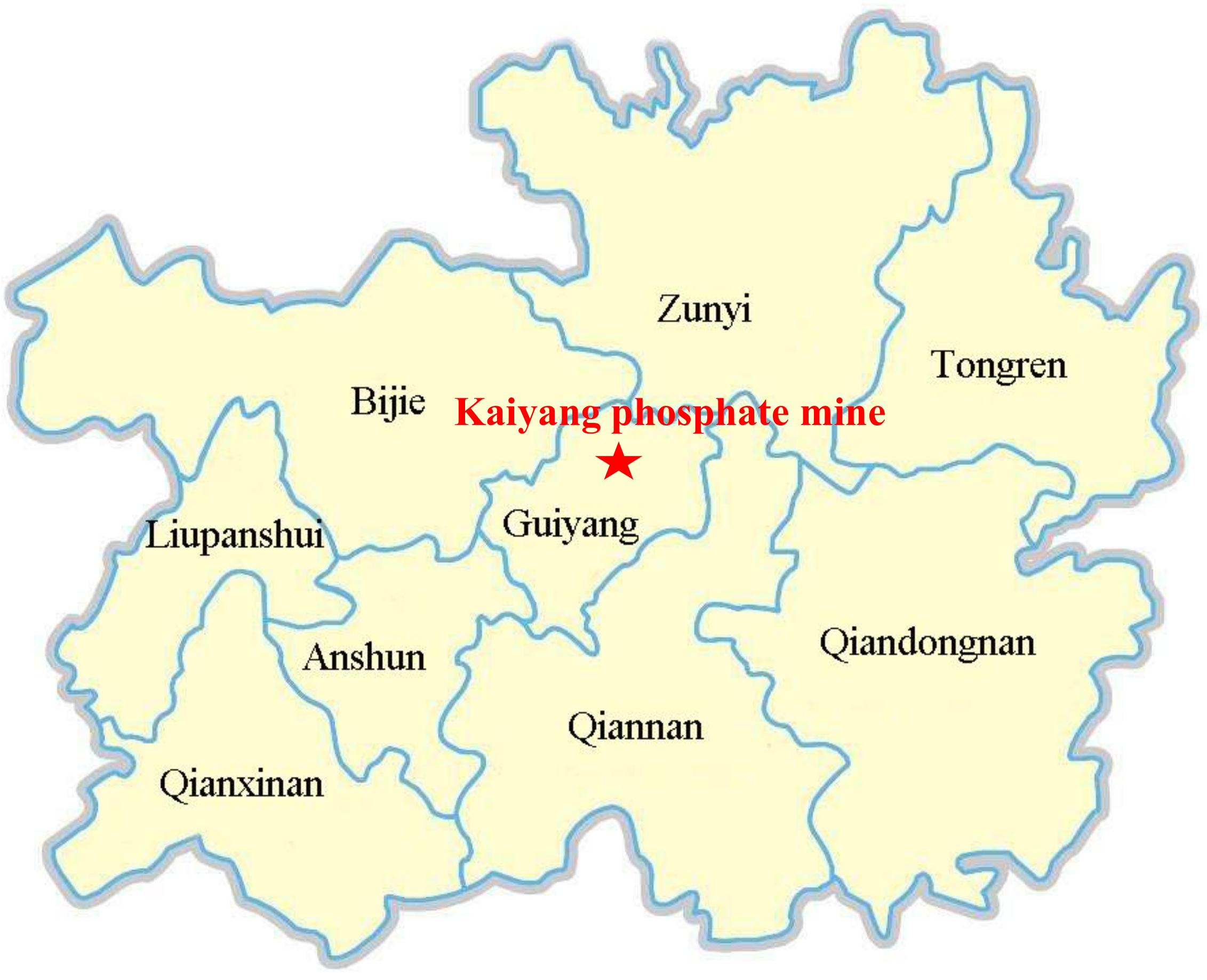
3.1. Project Profile
3.2. Determination of Evaluation Indicators
3.3. Risk Evaluation of Rockburst
4. Discussions
4.1. Comparison Analysis
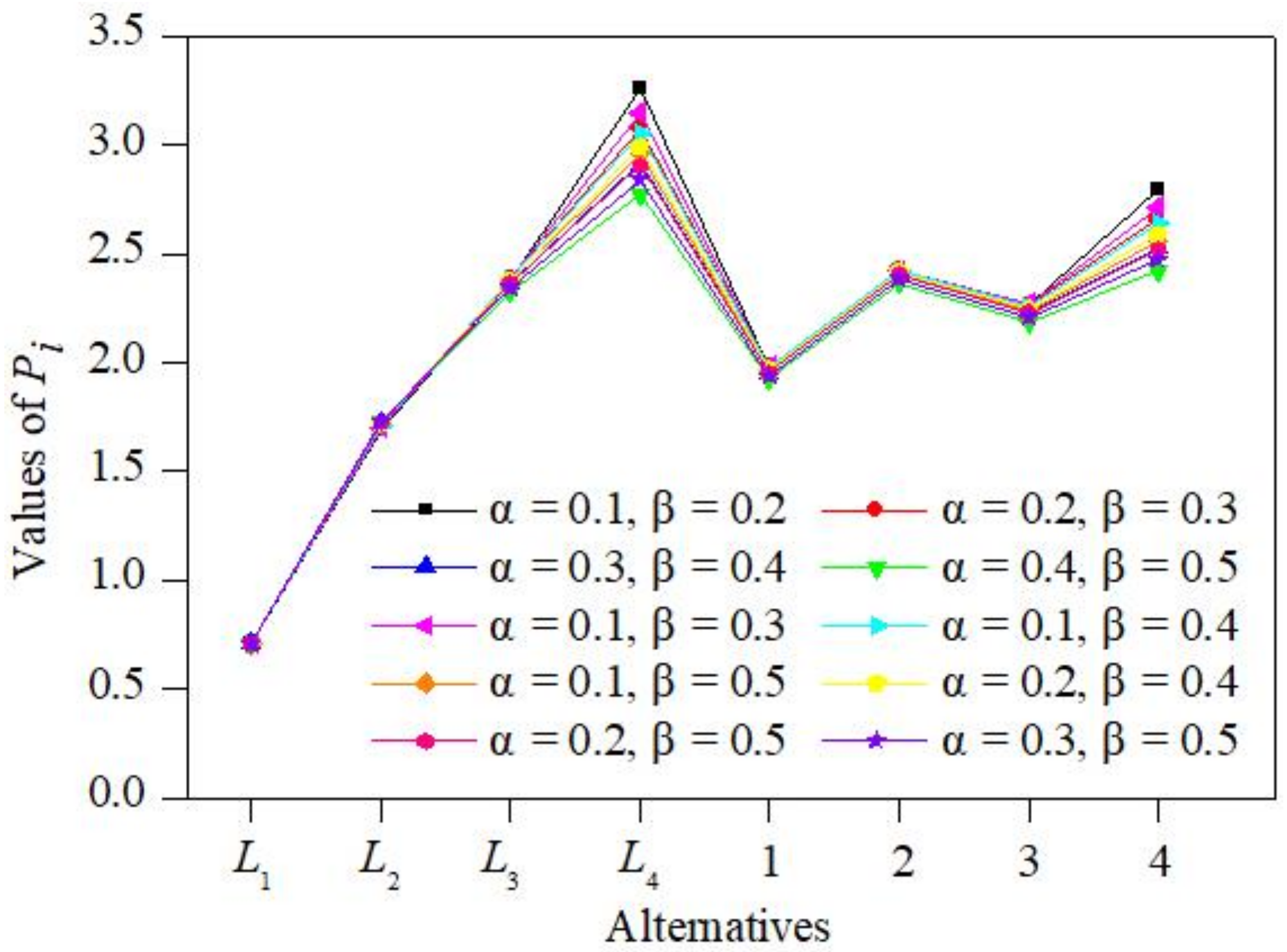
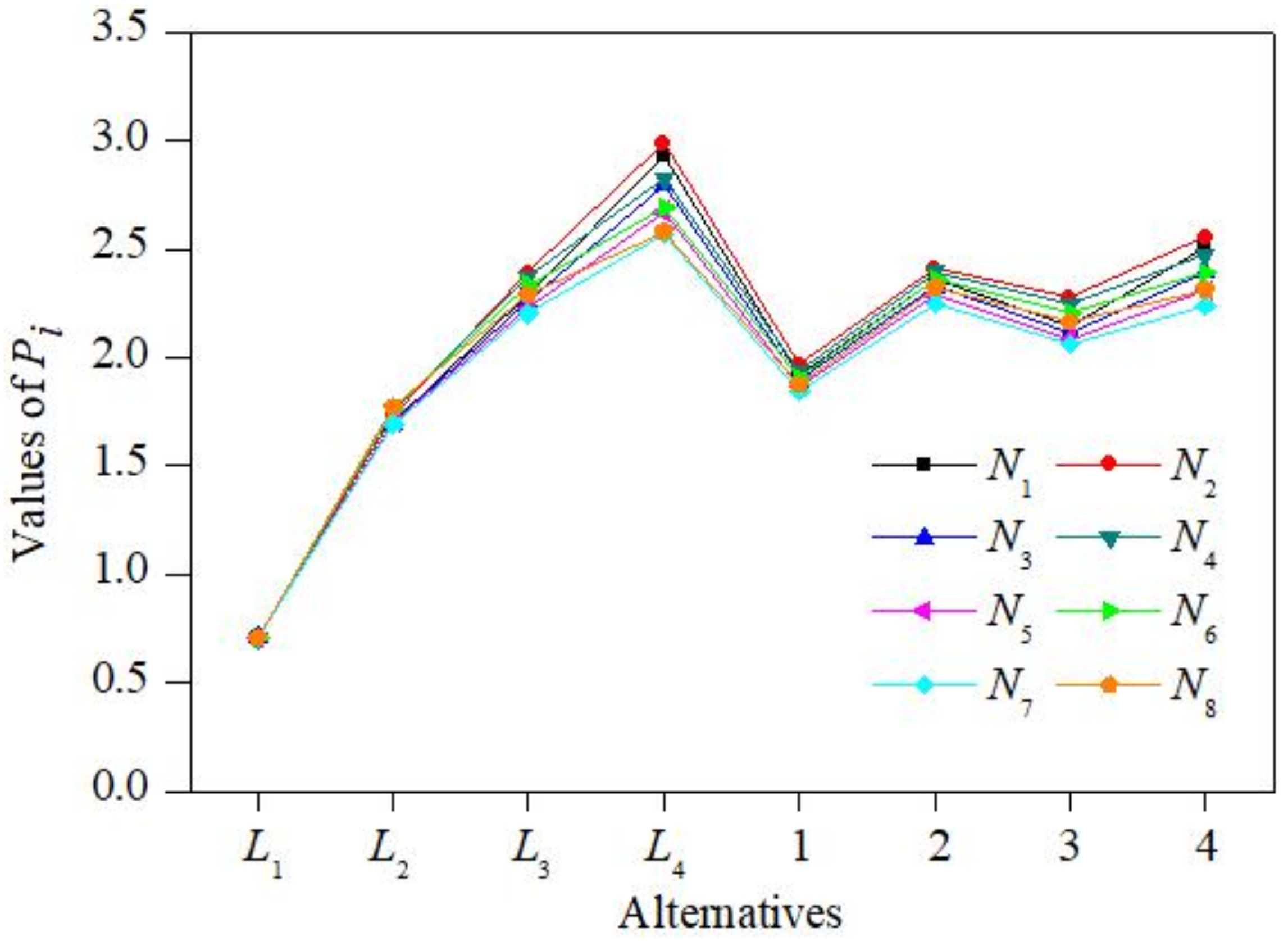
4.2. Sensitivity Analysis
4.3. Managerial Implication
- (1)
- Due to the influence of uncertainty on the evaluation results, some measures should be taken to avoid uncertainty in reality, such as ensuring the high quality of data.
- (2)
- Based on the evaluation results, the areas of high risk should receive more attention. For example, a monitoring system can be installed for the early warning of rockburst.
- (3)
- The technical parameters of rockburst prevention measures can be optimized according to different risk levels. For different risk levels, the prevention measures and their parameters should be different.
- (1)
- The indicator values were expressed by TrFNs after the uncertainty parameters were introduced, which can indicate the uncertain information more reasonably.
- (2)
- Game theory was used to calculate the indicator weights by combining subjective and objective weights, so that the comprehensive weights can be determined more credibly.
- (3)
- The ORESTE approach was extended with TrFNs, which can be used to solve MCDM problems under trapezoidal fuzzy environments.
- (4)
- The proposed methodology was applied to evaluate rockburst risk, and can obtain evaluation results reliably.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ali, S.H.; Giurco, D.; Arndt, N.; Nickless, E.; Brown, G.; Demetriades, A.; Durrheim, R.; Enriquez, M.A.; Kinnaird, J.; Littleboy, A.; et al. Mineral supply for sustainable development requires resource governance. Nature 2017, 543, 367–372. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Zhao, J.; Ju, M.; De Silva, R.V.; Rathnaweera, T.D.; Bandara, A.K. Opportunities and challenges in deep mining: A brief review. Engineering 2017, 3, 546–551. [Google Scholar] [CrossRef]
- Li, D.Y.; Liu, Z.D.; Armaghani, D.J.; Xiao, P.; Zhou, J. Novel ensemble tree solution for rockburst prediction using deep forest. Mathematics 2022, 10, 787. [Google Scholar] [CrossRef]
- Durrheim, R.J. Mitigating the risk of rockbursts in the deep hard rock mines of South Africa: 100 years of research. In Extracting the Science: A Century of Mining Research; Brune, J., Ed.; Society for Mining, Metallurgy, and Exploration: Littleton, CO, USA, 2010; pp. 156–171. [Google Scholar]
- Hedley, D.G.F. A Five-Year Review of the Canada–Ontario Industry Rockburst Project; Special Report SP90; Division Report SP90-064; Canada Centre for Mineral and Energy Technology, Mining Research Laboratory: Ottawa, ON, Canada, 1990. [Google Scholar]
- Shan, Q.Y.; Qin, T. The improved drilling cutting method and its engineering applications. Geotech. Geol. Eng. 2019, 37, 3715–3726. [Google Scholar] [CrossRef]
- Wang, E.Y.; He, X.Q.; Wei, J.P.; Nie, B.S.; Song, D.Z. Electromagnetic emission graded warning model and its applications against coal rock dynamic collapses. Int. J. Rock Mech. Min. Sci. 2011, 48, 556–564. [Google Scholar] [CrossRef]
- Zhou, X.P.; Peng, S.L.; Zhang, J.Z.; Qian, Q.H.; Lu, R.C. Predictive acoustical behavior of rockburst phenomena in Gaoligongshan tunnel, Dulong river highway, China. Eng. Geol. 2018, 247, 117–128. [Google Scholar] [CrossRef]
- Ullah, B.; Kamran, M.; Rui, Y.C. Predictive modeling of short-term rockburst for the stability of subsurface structures using machine learning approaches: T-SNE, K-Means clustering and XGBoost. Mathematics 2022, 10, 449. [Google Scholar] [CrossRef]
- Russenes, B.F. Analysis of Rock Spalling for Tunnels in Steep Valley Sides; Department of Geology, Norwegian Institute of Technology: Trondheim, Norway, 1974. [Google Scholar]
- Barton, N.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. Rock Eng. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Turchaninov, I.A.; Markov, G.A.; Gzovsky, M.V.; Kazikayev, D.M.; Frenze, U.K.; Batugin, S.A.; Chabdarova, U.I. State of stress in the upper part of the earth’s crust based on direct measurements in mines and on tectonophysical and seismological studies. Phys. Earth Planet. Inter. 1972, 6, 229–234. [Google Scholar] [CrossRef]
- Kidybiński, A. Bursting liability indices of coal. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 295–304. [Google Scholar] [CrossRef]
- Lee, S.M.; Park, B.S.; Lee, S.W. Analysis of rockbursts that have occurred in a waterway tunnel in Korea. Int. J. Rock Mech. Min. Sci. 2004, 41, 911–916. [Google Scholar] [CrossRef]
- Tao, Z.Y. Support design of tunnels subjected to rockbursting. In Proceedings of the International Society for Rock Mechanics and Rock Engineering International Symposium, Madrid, Spain, 12–16 September 1988. [Google Scholar]
- Cook, N.G.W.; Hoek, E.; Pretorius, J.P.; Ortlepp, W.D.; Salamon, M.D.G. Rock mechanics applied to study of rockbursts. J. S. Afr. Inst. Min. Metall. 1966, 66, 435–528. [Google Scholar]
- Su, G.S.; Feng, X.T.; Jiang, Q.; Chen, G.Q. Study on new index of local energy release rate for stability analysis and optimal design of underground rock mass engineering with high geostress. Chin. J. Rock. Mech. Eng. 2006, 25, 2453–2460. [Google Scholar]
- Mitri, H.S.; Tang, B.; Simon, R. FE modelling of mining-induced energy release and storage rates. J. S. Afr. Inst. Min. Metall. 1999, 99, 103–110. [Google Scholar]
- Xu, J.; Jiang, J.D.; Xu, N.; Liu, Q.S.; Gao, Y.F. A new energy index for evaluating the tendency of rockburst and its engineering application. Eng. Geol. 2017, 230, 46–54. [Google Scholar] [CrossRef]
- Zhang, C.Q.; Zhou, H.; Feng, X.T. An index for estimating the stability of brittle surrounding rock mass: FAI and its engineering application. Rock Mech. Rock Eng. 2011, 44, 401–414. [Google Scholar] [CrossRef]
- Li, N.; Feng, X.D.; Jimenez, R. Predicting rock burst hazard with incomplete data using Bayesian networks. Tunn. Undergr. Space Technol. 2017, 61, 61–70. [Google Scholar] [CrossRef]
- Li, N.; Jimenez, R. A logistic regression classifier for long-term probabilistic prediction of rock burst hazard. Nat. Hazards 2018, 90, 197–215. [Google Scholar] [CrossRef]
- Pu, Y.; Apel, D.B.; Wang, C.; Wilson, B. Evaluation of burst liability in kimberlite using support vector machine. Acta Geophys. 2018, 66, 973–982. [Google Scholar] [CrossRef]
- Liang, W.Z.; Sari, A.; Zhao, G.Y.; Mckinnon, S.D.; Wu, H. Short-term rockburst risk prediction using ensemble learning methods. Nat. Hazards 2020, 104, 1923–1946. [Google Scholar] [CrossRef]
- Shirani Faradonbeh, R.; Taheri, A. Long-term prediction of rockburst hazard in deep underground openings using three robust data mining techniques. Eng. Comput. 2019, 35, 659–675. [Google Scholar] [CrossRef]
- Xue, Y.G.; Bai, C.H.; Qiu, D.H.; Kong, F.M.; Li, Z.Q. Predicting rockburst with database using particle swarm optimization and extreme learning machine. Tunn. Undergr. Space Technol. 2020, 98, 103287. [Google Scholar] [CrossRef]
- Gong, J.; Hu, N.L.; Cui, X.; Wang, X.D. Rockburst tendency prediction based on AHP-TOPSIS evaluation model. Chin. J. Rock. Mech. Eng. 2014, 33, 1442–1448. [Google Scholar]
- Wang, C.L.; Wu, A.X.; Lu, H.; Bao, T.C.; Liu, X.H. Predicting rockburst tendency based on fuzzy matter-element model. Int. J. Rock Mech. Min. 2015, 75, 224–232. [Google Scholar] [CrossRef]
- Zuo, L.; Zhang, Q.C.; Liu, Y.L.; Yu, Q.; Ding, D.X. Predication model of CW-GT-TODIM for rockburst tendency analysis and its application. World Sci-Tech R. D 2016, 38, 1131–1136. [Google Scholar]
- Xue, Y.G.; Bai, C.H.; Kong, F.M.; Qiu, D.H.; Li, L.P.; Su, M.X.; Zhao, Y. A two-step comprehensive evaluation model for rockburst prediction based on multiple empirical criteria. Eng. Geol. 2020, 268, 105515. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Sanayei, A.; Farid Mousavi, S.; Yazdankhah, A. Group decision making process for supplier selection with VIKOR under fuzzy environment. Expert Syst. Appl. 2010, 37, 24–30. [Google Scholar] [CrossRef]
- Aydin, N. A fuzzy-based multi-dimensional and multi-period service quality evaluation outline for rail transit systems. Transp. Policy 2017, 55, 87–98. [Google Scholar] [CrossRef]
- İç, Y.T.; Yurdakul, M. Development of a new trapezoidal fuzzy AHP-TOPSIS hybrid approach for manufacturing firm performance measurement. Granul. Comput. 2021, 6, 915–929. [Google Scholar] [CrossRef]
- Roubens, M. Preference relations on actions and criteria in multicriteria decision making. Eur. J. Oper. Res. 1982, 10, 51–55. [Google Scholar] [CrossRef]
- Pastijn, H.; Leysen, J. Constructing an outranking relation with ORESTE. Math. Comput. Modell. 1989, 12, 1255–1268. [Google Scholar] [CrossRef]
- Wang, X.D.; Gou, X.J.; Xu, Z.S. Assessment of traffic congestion with ORESTE method under double hierarchy hesitant fuzzy linguistic environment. Appl. Soft Comput. 2020, 86, 105864. [Google Scholar] [CrossRef]
- Kaya, T. Monitoring brand performance based on household panel indicators using a fuzzy rank-based ORESTE methodology. J. Mult.-Valued Log. Soft Comput. 2018, 31, 443–467. [Google Scholar]
- Liu, Z.M.; Wang, X.Y.; Wang, W.X.; Wang, D.; Liu, P.D. An integrated TOPSIS–ORESTE-based decision-making framework for new energy investment assessment with cloud model. Comput. Appl. Math. 2022, 41, 42. [Google Scholar] [CrossRef]
- Liang, W.Z.; Dai, B.; Zhao, G.Y.; Wu, H. Assessing the performance of green mines via a hesitant fuzzy ORESTE–QUALIFLEX method. Mathematics 2019, 7, 788. [Google Scholar] [CrossRef] [Green Version]
- Adali, E.A.; Isik, A.T. Ranking web design firms with the ORESTE method. Ege Acad. Rev. 2017, 17, 243–254. [Google Scholar]
- Pribićević, I.; Doljanica, S.; Momčilović, O.; Das, D.K.; Pamučar, D.; Stević, Ž. Novel extension of DEMATEL method by trapezoidal fuzzy numbers and D numbers for management of decision-making processes. Mathematics 2020, 8, 812. [Google Scholar] [CrossRef]
- Vincent, F.Y.; Chi, H.T.X.; Dat, L.Q.; Phuc, P.N.K.; Shen, C.H. Ranking generalized fuzzy numbers in fuzzy decision making based on the left and right transfer coefficients and areas. Appl. Math. Model. 2013, 37, 8106–8117. [Google Scholar]
- Mahdavi, I.; Heidarzade, A.; Sadeghpour-Gildeh, B.; Mahdavi-Amiri, N. A general fuzzy TOPSIS model in multiple criteria decision making. Int. J. Adv. Manuf. Technol. 2009, 45, 406–420. [Google Scholar] [CrossRef]
- Tseng, M.L.; Lin, Y.H.; Tan, K.; Chen, R.H.; Chen, Y.H. Using TODIM to evaluate green supply chain practices under uncertainty. Appl. Math. Model. 2014, 38, 2983–2995. [Google Scholar] [CrossRef]
- Noordiana, M.I.; Sivakumar, D.M.; Ridzuan, M.M. Selection of natural fibre reinforced composites using fuzzy VIKOR for car front hood. Int. J. Mater. Prod. Technol. 2016, 53, 267–285. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Labs Technol. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Li, X.B.; Mitri, H.S. Evaluation method of rockburst: State-of-the-art literature review. Tunn. Undergr. Space Technol. 2018, 81, 632–659. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, Y.H.; Li, T.J. 1996. Griffith theory and the criteria of rock burst. Chin. J. Rock. Mech. Eng. 1996, 15 (Suppl. 1), 491–495. [Google Scholar]
- Kwasniewski, M.; Szutkowski, I.; Wang, J. Study of Ability of Coal from Seam 510 for Storing Elastic Energy in the Aspect of Assessment of Hazard in Porabka-Klimontow Colliery; Scientific Report; Silesian Technical University: Gliwice, Poland, 1994. [Google Scholar]
- Wang, F.; Li, H. Novel method for hybrid multiple attribute decision making based on TODIM method. J. Syst. Eng. Electron. 2015, 26, 1023–1031. [Google Scholar] [CrossRef]
| Indicators | Risk Levels | |||
|---|---|---|---|---|
| >40 | 26.7–40 | 14.5–26.7 | <14.5 | |
| <2.0 | 2.0–3.5 | 3.5–5.0 | >5.0 | |
| <40 | 40–100 | 100–200 | >200 | |
| >14.5 | 5.5–14.5 | 2.5–5.5 | ≤2.5 | |
| <0.50 | 0.50–0.60 | 0.60–0.75 | >0.75 | |
| 40.0 | 0 | 0 | 14.5 | 0 | |
| 26.7 | 2.0 | 40 | 5.5 | 0.50 | |
| 14.5 | 3.5 | 100 | 2.5 | 0.60 | |
| 0 | 5.0 | 200 | 0 | 0.75 | |
| 13.09 | 1.39 | 10.09 | 1.78 | 0.45 | |
| 23.24 | 5.1 | 165.51 | 5.41 | 0.62 | |
| 15.07 | 2.03 | 103.99 | 1.50 | 0.59 | |
| 29.7 | 6.31 | 290.97 | 5.61 | 0.69 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 0.333 | 0.317 | 0.137 | 0.621 | 0.667 | |
| 0.638 | 0.555 | 0.344 | 0.828 | 0.800 | |
| 1.000 | 0.792 | 0.687 | 1.000 | 1.000 | |
| 0.673 | 0.220 | 0.035 | 0.877 | 0.600 | |
| 0.419 | 0.808 | 0.569 | 0.627 | 0.827 | |
| 0.623 | 0.322 | 0.357 | 0.897 | 0.787 | |
| 0.258 | 1.000 | 1.000 | 0.613 | 0.920 |
| (0.00, 0.00, 0.00, 0.00) | (0.00, 0.00, 0.00, 0.00) | (0.00, 0.00, 0.00, 0.00) | (0.00, 0.00, 0.00, 0.00) | (0.00, 0.00, 0.00, 0.00) | |
| (0.27, 0.30, 0.37, 0.40) | (0.25, 0.29, 0.35, 0.38) | (0.11, 0.12, 0.15, 0.17) | (0.50, 0.56, 0.68, 0.74) | (0.53, 0.60, 0.73, 0.80) | |
| (0.51, 0.57, 0.70, 0.77) | (0.44, 0.50, 0.61, 0.67) | (0.27, 0.31, 0.38, 0.41) | (0.66, 0.74, 0.91, 0.99) | (0.64, 0.72, 0.88, 0.96) | |
| (0.80, 0.90, 1.10, 1.200) | (0.63, 0.71, 0.87, 0.95) | (0.55, 0.62, 0.76, 0.82) | (0.80, 0.90, 1.10, 1.20) | (0.80, 0.90, 1.10, 1.20) | |
| (0.54, 0.61, 0.74, 0.81) | (0.18, 0.20, 0.24, 0.26) | (0.028, 0.031, 0.038, 0.042) | (0.70, 0.79, 0.97, 1.05) | (0.48, 0.54, 0.66, 0.72) | |
| (0.34, 0.38, 0.46, 0.50) | (0.65, 0.73, 0.89, 0.97) | (0.46, 0.51, 0.63, 0.68) | (0.50, 0.56, 0.69, 0.75) | (0.66, 0.74, 0.91, 0.99) | |
| (0.50, 0.56, 0.69, 0.75) | (0.26, 0.29, 0.35, 0.39) | (0.29, 0.32, 0.39, 0.43) | (0.72, 0.81, 0.99, 1.08) | (0.63, 0.71, 0.87, 0.94) | |
| (0.21, 0.23, 0.28, 0.31) | (0.80, 0.90, 1.10, 1.20) | (0.80, 0.90, 1.10, 1.20) | (0.49, 0.55, 0.67, 0.74) | (0.74, 0.83, 1.01, 1.10) |
| Indicators | Linguistic Ratings of Indicators | ||||||
|---|---|---|---|---|---|---|---|
| VH | H | M | FH | H | (3.1, 3.6, 3.8, 4.2) | 0.1883 | |
| H | VH | VH | H | FH | (3.5, 4.0, 4.3, 4.6) | 0.2099 | |
| H | VH | H | FH | H | (3.4, 3.9, 4.1, 4.5) | 0.2037 | |
| FH | FH | VH | VH | H | (3.3, 3.8, 4.2, 4.5) | 0.2023 | |
| H | M | H | H | VH | (3.3, 3.8, 3.9, 4.3) | 0.1959 | |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 0.333 | 0.317 | 0.137 | 0.621 | 0.667 | |
| 0.638 | 0.555 | 0.344 | 0.828 | 0.800 | |
| 1.000 | 0.792 | 0.687 | 1.000 | 1.000 | |
| 0.673 | 0.220 | 0.035 | 0.877 | 0.600 | |
| 0.419 | 0.808 | 0.569 | 0.627 | 0.827 | |
| 0.623 | 0.322 | 0.357 | 0.897 | 0.787 | |
| 0.258 | 1.000 | 1.000 | 0.613 | 0.920 |
| 0.130 | 0.163 | 0.188 | 0.114 | 0.112 | |
| 0.269 | 0.277 | 0.212 | 0.454 | 0.484 | |
| 0.469 | 0.425 | 0.307 | 0.596 | 0.577 | |
| 0.719 | 0.583 | 0.521 | 0.716 | 0.716 | |
| 0.493 | 0.225 | 0.190 | 0.631 | 0.439 | |
| 0.324 | 0.594 | 0.444 | 0.458 | 0.595 | |
| 0.460 | 0.280 | 0.315 | 0.644 | 0.567 | |
| 0.224 | 0.726 | 0.732 | 0.448 | 0.660 |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| 0.198 | 0.000 | 0.000 | 0.000 | 0.024 | 0.000 | 0.000 | 0.010 | |
| 0.333 | 0.136 | 0.000 | 0.000 | 0.091 | 0.057 | 0.033 | 0.079 | |
| 0.510 | 0.312 | 0.176 | 0.000 | 0.256 | 0.170 | 0.198 | 0.164 | |
| 0.254 | 0.080 | 0.012 | 0.000 | 0.000 | 0.069 | 0.007 | 0.090 | |
| 0.342 | 0.144 | 0.065 | 0.002 | 0.156 | 0.000 | 0.094 | 0.022 | |
| 0.312 | 0.114 | 0.011 | 0.000 | 0.064 | 0.064 | 0.000 | 0.086 | |
| 0.417 | 0.229 | 0.162 | 0.071 | 0.253 | 0.097 | 0.191 | 0.000 |
| 0.000 | −0.198 | −0.333 | −0.510 | −0.254 | −0.342 | −0.312 | −0.417 | |
| 0.198 | 0.000 | −0.136 | −0.312 | −0.056 | −0.144 | −0.114 | −0.219 | |
| 0.333 | 0.136 | 0.000 | −0.176 | 0.079 | −0.008 | 0.022 | −0.083 | |
| 0.510 | 0.312 | 0.176 | 0.000 | 0.256 | 0.168 | 0.198 | 0.093 | |
| 0.254 | 0.056 | −0.079 | −0.256 | 0.000 | −0.087 | −0.058 | −0.162 | |
| 0.342 | 0.144 | 0.008 | −0.168 | 0.087 | 0.000 | 0.030 | −0.075 | |
| 0.312 | 0.114 | −0.022 | −0.198 | 0.058 | −0.030 | 0.000 | −0.105 | |
| 0.417 | 0.219 | 0.083 | −0.093 | 0.162 | 0.075 | 0.105 | 0.000 |
| - | O | O | O | O | O | O | O | |
| P | - | O | O | I | O | O | O | |
| P | P | - | O | I | I | I | O | |
| P | P | P | - | P | P | P | P | |
| P | I | I | O | - | O | I | O | |
| P | P | I | O | P | - | I | I | |
| P | P | I | O | I | I | - | O | |
| P | P | P | O | P | I | P | - |
| Authors | Indicators | Evaluation Criteria | Evaluation Results | |||
|---|---|---|---|---|---|---|
| Peng et al. [49] | The intervals of , , and are , , and , respectively. | |||||
| Kidybiński [13] | The intervals of , , and are , , and , respectively. | |||||
| Kwasniewski et al. [50] | The intervals of , , and are , , and , respectively. | |||||
| Tao [15] | The intervals of , , and are , , and , respectively. | |||||
| Wang et al. [28] | The intervals of , , and are , , and , respectively. | |||||
| Authors | Evaluation Methods | Evaluation Results |
|---|---|---|
| Mahdavi et al. [44] | Trapezoidal fuzzy TOPSIS method | |
| Wang and Li [51] | Trapezoidal fuzzy TODIM method | |
| The proposed method | Trapezoidal fuzzy ORESTE method | Weak rank: |
| Strong rank: |
| Value of | Value of | Evaluation Results |
|---|---|---|
| 0.1 | 0.2 | Weak rank: |
| Strong rank: | ||
| 0.2 | 0.3 | Weak rank: |
| Strong rank: | ||
| 0.3 | 0.4 | Weak rank: |
| Strong rank: | ||
| 0.4 | 0.5 | Weak rank: |
| Strong rank: | ||
| 0.1 | 0.3 | Weak rank: |
| Strong rank: | ||
| 0.1 | 0.4 | Weak rank: |
| Strong rank: | ||
| 0.1 | 0.5 | Weak rank: |
| Strong rank: | ||
| 0.2 | 0.4 | Weak rank: |
| Strong rank: | ||
| 0.2 | 0.5 | Weak rank: |
| Strong rank: | ||
| 0.3 | 0.5 | Weak rank: |
| Strong rank: |
| Number | Value of | Value of | Evaluation Results | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | Weak rank: | |
| Strong rank: | |||||||||||
| 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | Weak rank: | |
| Strong rank: | |||||||||||
| 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | Weak rank: | |
| Strong rank: | |||||||||||
| 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | Weak rank: | |
| Strong rank: | |||||||||||
| 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | Weak rank: | |
| Strong rank: | |||||||||||
| 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | Weak rank: | |
| Strong rank: | |||||||||||
| 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | Weak rank: | |
| Strong rank: | |||||||||||
| 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | Weak rank: | |
| Strong rank: | |||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, K.; Liu, Y.; Liang, W. An Extended ORESTE Approach for Evaluating Rockburst Risk under Uncertain Environments. Mathematics 2022, 10, 1699. https://doi.org/10.3390/math10101699
Shi K, Liu Y, Liang W. An Extended ORESTE Approach for Evaluating Rockburst Risk under Uncertain Environments. Mathematics. 2022; 10(10):1699. https://doi.org/10.3390/math10101699
Chicago/Turabian StyleShi, Keyou, Yong Liu, and Weizhang Liang. 2022. "An Extended ORESTE Approach for Evaluating Rockburst Risk under Uncertain Environments" Mathematics 10, no. 10: 1699. https://doi.org/10.3390/math10101699
APA StyleShi, K., Liu, Y., & Liang, W. (2022). An Extended ORESTE Approach for Evaluating Rockburst Risk under Uncertain Environments. Mathematics, 10(10), 1699. https://doi.org/10.3390/math10101699






