A Fuzzy Entropy-Based Group Consensus Measure for Financial Investments ^†

Abstract

This study presents a novel, fuzzy entropy-based approach to the measurement of consensus in group decision making. Here, the basic assumption is that the decision inputs are the ‘yes’ or ‘no’ votes of group members on a financial investment that has a particular expected rate of return. In this paper, using a class of fuzzy entropies, a novel consensus measure satisfying reasonable requirements is introduced for a case where the decision inputs are dichotomous variables. It is also shown here that some existing consensus measures are just special cases of the proposed fuzzy entropy-based consensus measure when the input variables are dichotomous. Next, the so-called group consensus map for financial investments is presented. It is demonstrated that this construction can be used to characterize the level of consensus among the members of a group concerning financial investments as a function of the expected rate of return. Moreover, it is described how a consensus map can be constructed from empirical data and how this map is connected with behavioral economics.

1. Introduction

In group decision making (GDM), the degree of agreement among the group members, i.e., the level of consensus, is a crucial characteristic of the decision-making process. It can be highlighted using an analogy: regarding the decision-making process, the overall evaluation of the decision makers may be considered as some measure of central tendency with which the distribution of a quantitative variable can be characterized. However, these measures do not carry any information about the spread or, in other words, the disagreement of the individual values. This is why we complement the measures of central tendency with some measure of spread. Consensus measures may be regarded as functions that measure how much the inputs from multiple sources agree [1]. Since the concept of consensus and its measurement play an important role in group decision making, it has been intensely studied over the past few decades (see, e.g., [2,3,4,5,6,7,8,9]).

Based on Cabrerizo et al. [10], we can distinguish between hard (1 in case of full consensus, 0 otherwise) and soft consensus measures depending on the range of the function measuring the level of consensus. Bordogna et al. [11] distinguished between the concepts of hard consensus and soft consensus based on the consensus level or linguistic perspectives. In the case of hard consensus, the consensus level needs to have a certain value. For example, the consensus level is 1 when there is a complete consensus (see, e.g., [2,12]). At the same time, soft consensus only requires the consensus level to be within an interval (see, e.g., [13]). According to Guo et al. [13], in the traditional sense, a consensus is a complete and unanimous agreement. The authors of this paper note that owing to the limitations of resources (i.e., time, money, and manpower), it is difficult or even impossible to reach a complete and unanimous consensus. This article presents a method for reaching a soft consensus within a certain level of tolerance.

We should also mention here some seminal articles from the recent literature. In a paper by Gong et al. [14], the authors studied the consistency and consensus modeling of linear uncertain preference relations. A transaction and interaction behavior-based consensus model and its application to optimal carbon emission reduction was presented by Gong et al. in [15]. Tang et al. [16] introduced a method to detect and manage non-cooperative behaviors using a hierarchical consensus model. Yuan et al. [17] proposed a minimum adjustment consensus framework with compromise limits for social network group decision making with incomplete information. Cheng et al. [18] presented a minimum adjustment consensus framework for social network group decision making with incomplete linguistic preference relations. Three two-stage stochastic minimum-cost consensus models with asymmetric adjustment costs were proposed by Li et al. [19].

Herrera-Viedma et al. [20] reviewed soft consensus models and highlighted that there are several ways the decision makers can express their opinions about the possible alternatives. However, dealing with dichotomous input variables is rather rare in the literature. For some exceptions, we refer the reader to the works of Alcantud et al. (see, e.g., [21,22,23]).

In this study, we will concentrate on measuring the degree of agreement among the members of a group in a special case where every group member votes either ‘yes’ or ‘no’. For example, suppose that the board of directors of a company needs to make a decision concerning an investment. In this case, the typical outcome of the decision-making process is the alternative that has the majority among the group members (supposing that this majority exists). For instance, the board of six directors of a company has to decide whether the company invests in a new project that has an expected rate of return r, where $r\in \mathbb{R}$. Every member of the board votes either ‘yes’ or ‘no’. Suppose that for various expected rates of return, we have the votes summarized in

Table 1. Example: votes by board members for various rates of return.

r	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$\overline{x}$
0%	0	0	0	0	0	0	0.0000
2%	1	0	0	0	0	0	0.1667
3%	1	1	0	0	0	0	0.3333
5%	1	1	1	0	0	0	0.5000
8%	1	1	1	1	0	0	0.6667
10%	1	1	1	1	1	0	0.8333
15%	1	1	1	1	1	1	1.0000

, in which $x_i$ is the ith director’s vote; 0 and 1 stand for the ‘no’ and ‘yes’ votes, respectively; and $i=1,2,\dots ,6$.

In Table 1, $\overline{x}$ denotes the arithmetic mean of the inputs, i.e., $\overline{x}=\frac{1}{6}{\sum }_{i=1}^6{x}_i$. In this case, an evident decision-making strategy is based on the value of $\overline{x}$. Namely, the strategy is to invest in the project if $\overline{x}\ge 0.5$ and not invest in the project if $\overline{x}<0.5$. On the one hand, we see that the value of $\overline{x}$ is useful as by using this, we can set a decision threshold and establish a very simple decision-making mechanism. On the other hand, if we look at the inputs for $r=3\%$ and $r=8\%$, we can see that the level of agreement among the decision makers is the same in the sense that the number of votes in the majority is four in both cases. For $r=3\%$, there are two ‘yes’ votes versus four ‘no’ votes, whereas for $r=8\%$, there are four ‘yes’ votes versus two ‘no’ votes. However, the corresponding $\overline{x}$ values do not reflect the equality of the agreement levels in these two cases. This means that the arithmetic mean of the inputs in itself is not an appropriate measure of consensus among the decision makers. Using the proportion of the number of votes in the majority as a measure of the level of agreement seems to be a simple solution to this problem. With this approach, we obtain an index that expresses the level of agreement in the [0.5, 1] interval. A disadvantage of this index is that it is not normalized, i.e., its range is not the unit interval [0, 1]. In this study, we will present a theory of consistent measurement of group consensus in the unit interval.

In the seminal paper by Beliakov et al. [24], a consensus measure is defined as a function $C:{[0,1]}^n\to [0,1]$ that satisfies seven reasonable properties. In our study, we will adapt these requirements to the case where the decision inputs are in the two-element set $\{0,1\}$, and 0 and 1 code the ‘no’ and ‘yes’ votes, respectively. Here, we will utilize fuzzy entropies to build consensus measures. These entropies, just like entropy in physics, can be used to characterize the uncertainty concerning a decision-making situation or a physical system. In other words, we will prove that a fuzzy entropy of the arithmetic mean of the inputs can be regarded as a dissension measure. At the same time, one minus this measure can be treated as a consensus measure, i.e., it satisfies the requirements for a consensus measure in the case where the decision inputs are in the two-element set $\{0,1\}$. It should be emphasized that the proposed consensus measure depends on a fuzzy entropy, which satisfies certain properties. Therefore, this fuzzy entropy can be viewed as a generator of the proposed consensus measure. Here, we will demonstrate that for certain fuzzy entropies, the consensus measures generated by them coincide with some well-known consensus measures.

We will show how the proposed consensus measure can be used to measure the degree of agreement among the members of a group concerning a financial investment that has an expected rate of return $r\in \mathbb{R}$. Of course, we may assume that the value of the consensus measure, among other influencing factors, depends on the value of the expected rate of return r. Here, we will present the idea of the so-called group consensus map for financial investments. This construction expresses the level of consensus among the members of a fixed group concerning financial investments as a function of the expected rate of return. Hence, the group consensus map may be an interesting construction from a behavioral economics perspective. We will outline a procedure based on which the group consensus map can be estimated empirically. Also, we will highlight what the map can tell us about the behavior of the group.

It is worth noting that our approach may also be interesting from organizational and policy-making perspectives. This is due to the fact that in these areas, it is also quite common for decisions to be made based on the dichotomous inputs (i.e., ‘yes’ or ‘no’ votes) of the members of a group.

This paper is structured as follows. In Section 2, we will briefly cover the most important concepts that will be utilized in our study. A fuzzy entropy-based approach to the measurement of consensus for the case where the inputs are dichotomous variables will be presented in Section 3. Here, we will present the requirements for a consensus measure and review some existing consensus measures in light of these requirements. Also, we will adapt the requirements set by Beliakov et al. [24] and show in Section 4 that our consensus measure satisfies these requirements. In Section 5, we will frame our results in a broader context and show the connection between our consensus measure and some existing consensus measures. In Section 6, we will present the idea of a group consensus map for financial investments that is based on the proposed consensus measure, and we will provide an algorithm for estimating it. Lastly, in Section 7, we will summarize our main findings and mention some potential future avenues of research.

2. Preliminaries

Here, we briefly overview some basic concepts that we make use of in our study.

2.1. Continuous-Valued Logical Operations: Strict Triangular Norms, Strong Negations

We will consider the arithmetic operations on the extended real line based on Klement et al. [25] and Grabisch et al. [26]:

$$\begin{array}{c}\frac{1}{0}=\infty ,\frac{1}{\infty }=0,{\mathrm{e}}^{-\infty }=0,{\mathrm{e}}^{\infty }=\infty ,\\ ln\left(0\right)=-\infty ,ln(\infty )=\infty \mathrm{and}0·ln\left(0\right)=0.\end{array}$$

The Archimedean triangular norms (t-norms for short) and their strict class play important roles in continuous-valued logic (for more details, see [25] or [27]). These norms are defined below.

Definition 1.

We say that a continuous t-norm $T:{[0,1]}^2\to [0,1]$ is Archimedean if $T(x,x)<x$ holds for any $x\in (0,1)$.

Definition 2.

We say that a continuous Archimedean t-norm T is a strict t-norm if $T(x,y)<T(x,z)$ whenever $x\in (0,1]$ and $y<z$.

We use the following representation of strict t-norms (see, e.g., Section 5.1 in [25]).

Theorem 1.

A function $T:{[0,1]}^2\to [0,1]$ is a strict t-norm if and only if T is continuous, and there exists a continuous and strictly decreasing function $g:[0,1]\to [0,\infty ]$ with the properties $g\left(1\right)=0$ and $g\left(0\right)=\infty$ such that for any $x,y\in [0,1]$,

$$T(x,y)=g^{-1}\left(g\left(x\right)+g\left(y\right)\right).$$

In Theorem 1, the function g is called an additive generator of the strict t-norm T, which is uniquely determined up to a positive constant multiplier of g.

Later, we utilize the following definition for a strong negation (see, e.g., Definition 1.2 in [28] or Definition 11.3 in [25]).

Definition 3.

We say that a function $N:[0,1]\to [0,1]$ is a strong negation if and only if N satisfies the following requirements:

 (a)

N is continuous       (continuity);

 (b)

N(0) = 1, N(1) = 0      (boundary conditions);

 (c)

N(x) > N(y) for x < y        (monotonicity);

 (d)

N(N(x)) = x for any x ∈ [0, 1] (involution).

Fuzzy Entropies and Fuzziness Measures

A fuzzy set over the universe X is given by a $\mu :X\to [0,1]$ mapping that is called the membership function of the fuzzy set. The value of $\mu \left(x\right)$ expresses the membership degree of $x\in X$ in the fuzzy set in question. Fuzziness measures are used to characterize how much a fuzzy set differs from a crisp set. De Luca and Termini in [29] defined the properties of a quantitative measure $d\left(\mu \right)$ that can be used to characterize the degree of fuzziness of a fuzzy set $\mu$. In their framework, a fuzziness measure $d\left(\mu \right)$ of a fuzzy set $\mu$ should have the following three properties:

P₁ 

$d\left(\mu \right)$ must be 0 if and only if $\mu$ takes on X the values 0 or 1.

P₂ 

$d\left(\mu \right)$ must assume the maximum value if and only if $\mu$ always has the value $\frac{1}{2}$.

P₃ 

$d\left(\mu \right)$ must be greater than or equal to $d\left({\mu }^{*}\right)$, where ${\mu }^{*}$ is any ‘sharpened’ version of $\mu$; that is, any fuzzy set such that ${\mu }^{*}\left(x\right)\ge \mu \left(x\right)$ if $\mu \left(x\right)\ge \frac{1}{2}$ and ${\mu }^{*}\left(x\right)\le \mu \left(x\right)$ if $\mu \left(x\right)\le \frac{1}{2}$.

De Luca and Termini in [29] proposed the measure

$$d\left(\mu \right)=\frac{1}{n}\sum _{i=1}^{n}S\left(\mu \left(x_i\right)\right),$$

(1)

where $x_i$ is an element of a finite set $X=\{x_1,x_2,\dots ,x_n\}$,

$$S\left(x\right)=-\frac{1}{ln\left(2\right)}\left(xln\left(x\right)+(1-x)ln(1-x)\right),$$

(2)

and $x\in [0,1]$ (with the convention $0·ln\left(0\right)=0$). It was proved in [29] that the function $d\left(\nu \right)$, given in Equation (1), satisfies the criteria for a fuzziness measure given in $P_1$–$P_3$. Since the function S in (2) is formally similar to the Shannon entropy, it is often referred to as a fuzzy entropy. We utilize the following definition for a fuzzy entropy.

Definition 4.

We say that a function $F:[0,1]\to [0,1]$ is a fuzzy entropy if F satisfies the following requirements:

(a) 

F is continuous on $[0,1]$.

(b) 

$F\left(0\right)=0$ and $F\left(1\right)=0$.

(c) 

F is strictly increasing on $\left(0,\frac{1}{2}\right)$, and F is strictly decreasing on $\left(\frac{1}{2},1\right)$.

(d) 

$F\left(x\right)$ has a unique maximum at $x=\frac{1}{2}$, and $F\left(\frac{1}{2}\right)=1$.

(e) 

$F\left(x\right)=F(1-x)$ for any $x\in [0,1]$.

It was also demonstrated in [29] that the fuzziness measure given in Equation (1) has the following property:

P₄ 

$d\left(\mu \right)=d\left(\overline{\mu }\right)$, where $\overline{\mu }$ is the ‘complement’ of $\mu$, i.e., the function $\overline{\mu }\left(x\right)$ is given as $\overline{\mu }\left(x\right)=1-\mu \left(x\right)$, where $x\in X$.

It is worth noting that the mapping $N\left(x\right)=1-x$, where $x\in [0,1]$ is a strong negation operation known as the standard or Zadeh negation.

It can be verified (see, e.g., [30]) that if $X=\{x_1,x_2,\dots ,x_n\}$ is a finite set, $\mu :X\to [0,1]$ is the membership function of a fuzzy set on X, and $F:[0,1]\to [0,1]$ is a fuzzy entropy satisfying the properties given in Definition 4, then the measure

$$d_F\left(\mu \right)=\frac{1}{n}\sum _{i=1}^{n}F\left(\mu \left(x_i\right)\right)$$

(3)

satisfies the requirements $P_1$–$P_4$ for a fuzziness measure.

In our study, we will distinguish between the concepts of the fuzziness measure and fuzzy entropy. A fuzziness measure is utilized for measuring how much a fuzzy membership function differs from the characteristic function, whereas a fuzzy entropy is used to generate a fuzziness measure.

We should add that there is an interesting connection between the strict t-norms and fuzzy entropies (see, e.g., [31]). Namely, if $g:[0,1]\to [0,\infty ]$ is an additive generator of a strict t-norm, then based on Theorem 2 in [30], we can see that the function $F_g:[0,1]\to [0,1]$, which is given by

$$F_g\left(x\right)=2g^{-1}\left(\frac{1}{2}\left(g\left(x\right)+g(1-x)\right)\right),$$

satisfies the requirements for a fuzzy entropy given in Definition 4.

3. A Fuzzy Entropy-Based Measure of Group Consensus Concerning a Financial Investment

Let $I\left(r\right)$ denote an investment that has an expected rate of return r, where $r\in \mathbb{R}$. Suppose that in a group of n entities ($n\in \mathbb{N}$, $n\ge 2$), each group member expresses their opinion on an investment $I\left(r\right)$. From now on, $x_i\left(r\right)$ is used to denote the opinion of the ith group member, and $x_i\left(r\right)$ is interpreted as follows:

$$x_i\left(r\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{the}i\mathrm{th}\mathrm{group}\mathrm{member}\mathrm{supports}\mathrm{investing}\mathrm{in}I\left(r\right)\hfill \\ 0,\hfill & \mathrm{if}\mathrm{the}i\mathrm{th}\mathrm{group}\mathrm{member}\mathrm{does}\mathrm{not}\mathrm{support}\mathrm{investing}\mathrm{in}I\left(r\right),\hfill \end{array}\right.$$

where $i=1,2,\dots ,n$. The n-dimensional vector $\mathbf{x}\left(r\right)=\left(x_1\left(r\right),x_2\left(r\right),\dots ,x_n\left(r\right)\right)\in {\{0,1\}}^n$ represents an input vector (opinion vector) of a group. For the sake of simplicity, if r has a fixed value, then we omit it from the notation and use the simplified notations I and $\mathbf{x}=\left(x_1,x_2,\dots ,x_n\right)\in {\{0,1\}}^n$ for the investment $I\left(r\right)$ and input vector $\mathbf{x}\left(r\right)$, respectively.

Suppose that the group decision is modeled using the random variable $Y\left(r\right)$ (Y for short) that has a Bernoulli distribution with the parameter $p\in [0,1]$. That is, $P\left(Y\right(r)=1)=p$ and $P\left(Y\right(r)=0)=1-p$, where $P:\{0,1\}\to [0,1]$ is a probability measure on $\{0,1\}$. Here, the dichotomous variable $Y\left(r\right)$ is the indicator of the group decision such that

$$Y\left(r\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{the}\mathrm{group}\mathrm{supports}\mathrm{investing}\mathrm{in}I\left(r\right)\hfill \\ 0,\hfill & \mathrm{if}\mathrm{the}\mathrm{group}\mathrm{does}\mathrm{not}\mathrm{support}\mathrm{investing}\mathrm{in}I\left(r\right).\hfill \end{array}\right.$$

Under these settings, an obvious decision-making strategy is:

• Invest in $I\left(r\right)$ if $p\ge \frac{1}{2}$.
• Do not invest in $I\left(r\right)$ if $p<\frac{1}{2}$.

The value of the parameter p is unknown but we can estimate it by considering the inputs $x_1,x_2,\dots ,x_n$ as an independent sample on Y. Namely, p can be estimated by

$$\overline{x}=\frac{1}{n}\sum _{i=1}^n{x}_i.$$

Then, with the convention $0·ln\left(0\right)=0$, the entropy of Y, $H\left(Y\right)$, is

$$\begin{array}{cc}\hfill H\left(Y\right)& =-(p{log}_2\left(p\right)+(1-p){log}_2(1-p))\hfill \\ \hfill & =-\frac{1}{ln\left(2\right)}(pln\left(p\right)+(1-p)ln(1-p)),\hfill \end{array}$$

which can be approximated by

$$\widehat{H}\left(Y\right)=-\frac{1}{ln\left(2\right)}(\overline{x}ln\left(\overline{x}\right)+(1-\overline{x})ln(1-\overline{x})).$$

That is, $\widehat{H}\left(Y\right)=S\left(\overline{x}\right)$, where $S\left(x\right)$ is given by Equation (2) for any $x\in [0,1]$. Clearly, the function S meets all the criteria for a fuzzy entropy given in Definition 4. The quantity $S\left(\overline{x}\right)$ can be viewed as a measure of the uncertainty of the group. Here, we also find the following:

• $S\left(\overline{x}\right)=0$ (with the convention $0·ln\left(0\right)=0$) if and only if $x_1=x_2=\cdots =x_n=0$ or $x_1=x_2=\cdots =x_n=1$. That is, there is a maximal agreement among the group members concerning the investment I if and only if $S\left(\overline{x}\right)=0$.
• $S\left(\overline{x}\right)=1$ if and only if $n=2k$ for a $k\in \mathbb{N}$, $k\ge 1$ and k of the inputs are equal to zero and k of the inputs are equal to 1. That is, there is a maximal disagreement among the group members concerning the investment I if and only if $S\left(\overline{x}\right)=1$.

This means that $S\left(\overline{x}\right)$ can be viewed as a dissension measure, whereas $1-S\left(\overline{x}\right)$ can be treated as a consensus measure for the input vector $\mathbf{x}=\left(x_1,x_2,\dots ,x_n\right)\in {\{0,1\}}^n$.

Based on the above line of thinking, more generally, the quantity

$$1-F\left(\frac{1}{n}\sum _{i=1}^n{x}_i\right)$$

can be treated as a degree of agreement (consensus) with respect to the input vector $\mathbf{x}=\left(x_1,x_2,\dots ,x_n\right)\in {\{0,1\}}^n$, where $F:[0,1]\to [0,1]$ is a fuzzy entropy given by Definition 4.

3.1. Consensus Measures

Consensus measures are functions that measure how much the individual inputs of the group members agree with one another. In the seminal paper by Beliakov et al. [24], a consensus measure is defined as a function $C:{[0,1]}^n\to [0,1]$ with the following two basic properties:

(C1)

(Unanimity) For any $a\in [0,1]$, $C(a,a,\dots ,a)=1$.

(C2)

(Minimum consensus for $n=2$) For the special case with two inputs, it holds that $C(0,1)=C(1,0)=0$.

The authors of [24] set the following five reasonable additional requirements that a consensus measure should satisfy:

(C3)

(Symmetry) For any permutation $\pi :\{1,2,\dots ,n\}\to \{1,2,\dots ,n\}$ and input vector $\mathbf{x}=(x_1,x_2,\dots ,x_n)$, $\mathbf{x}\in {[0,1]}^n$, it holds that

$$C(x_1,x_2,\dots ,x_n)=C\left(x_{\pi \left(1\right)},x_{\pi \left(2\right)},\dots ,x_{\pi \left(n\right)}\right).$$

(C4)

(Maximum dissension) For $n=2k$, if k of the inputs are equal to zero and k of the inputs are equal to 1, then $C(0,0,\dots ,1,1)=0$ for all permutations of the input vector.

(C5)

(Reciprocity) For any input vector $\mathbf{x}=(x_1,x_2,\dots ,x_n)$, $\mathbf{x}\in {[0,1]}^n$, it holds that

$$C(x_1,x_2,\dots ,x_n)=C\left(N\left(x_1\right),N\left(x_2\right),\dots ,N\left(x_n\right)\right),$$

where $N:[0,1]\to [0,1]$ is a strong fuzzy negation operator.

(C6)

(Replication invariance) For any input vector $\mathbf{x}=(x_1,x_2,\dots ,x_n)\in {[0,1]}^n$, replicating the inputs does not alter the degree of consensus, i.e.,

$$C\left(\mathbf{x}\right)=C(\mathbf{x},\mathbf{x})=\dots =C(\mathbf{x},\mathbf{x}\dots ,\mathbf{x}).$$

(C7)

(Monotonicity with respect to the majority) For $n=2k$, let half of the inputs be equal and denoted by $\mathbf{a}=(a,a,\dots ,a)$, where $\mathbf{a}\in {[0,1]}^k$. Furthermore, let $\mathbf{x}=(x_1,x_2,\dots ,x_k)$ and $\mathbf{y}=(y_1,y_2,\dots ,y_k)$ be two input vectors, where $\mathbf{x},\mathbf{y}\in {[0,1]}^k$. If $|a-x_j|\le |a-y_j|$ for all $j=1,2,\dots ,k$, then $C\left(\mathbf{a},x_1,x_2,\dots ,x_k\right)\ge C\left(\mathbf{a},y_1,y_2,\dots ,y_k\right)$ holds for any permutation of the inputs.

We should add that if C satisfies (C4), then it also satisfies (C2).

3.1.1. Some Existing Consensus Measures

Without claiming to be comprehensive, here we mention a few well-known consensus measures (for more details, see, e.g, [1,20,24]).

Tastle, Wierman, and Dumdum in [32] considered a Shannon entropy-based measure of consensus for values measured on a Likert scale. Based on [1], for inputs defined over the unit interval $[0,1]$, the consensus measure $C_{TWD}:{[0,1]}^n\to [0,1]$, proposed in [32], can be given by

$$C_{TWD}\left(x_1,x_2,\dots ,x_n\right)=1+\frac{1}{n}\sum _{i=1}^n{log}_2\left(1-|x_i-\overline{x}|\right),$$

(4)

where $\overline{x}$ in Equation (4) denotes the arithmetic mean of the input vector $\mathbf{x}=(x_1,x_2,\dots ,x_n)\in {[0,1]}^n$. According to [24], the consensus measure $C_{TWD}$ given in Equation (4) satisfies properties (C1)–(C6) but does not satisfy property (C7).

The function $C_{\sigma }:{[0,1]}^n\to [0,1]$, which is given by

$$C_{\sigma }\left(x_1,x_2,\dots ,x_n\right)=1-\sqrt{\frac{4}{n}\sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2},$$

(5)

where $\overline{x}$ is the arithmetic mean of the input vector $\mathbf{x}=(x_1,x_2,\dots ,x_n)\in {[0,1]}^n$, is the standard deviation-based consensus measure for this input vector. It can be verified that $C_{\sigma }$ fulfills requirements (C1)–(C6) but does not satisfy property (C7).

Szmidt and Kacprzyk in [33] presented a distance-based consensus measure that can be normalized and adapted to the case where the inputs are in the unit interval. Based on [1], this adaptation of the proposed method results in the following measure:

$$C_{SK}\left(x_1,x_2,\dots ,x_n\right)=1-\frac{2}{n^2}\sum _{\forall i,j|i\ne j}{\left(x_i-x_j\right)}^2,$$

(6)

where $\mathbf{x}=(x_1,x_2,\dots ,x_n)\in {[0,1]}^n$. This measure also satisfies properties (C1)–(C6) but does not satisfy property (C7) (see [24]).

Beliakov, Calvo, and James in [24] proposed the so-called Bonferroni consensus with implication pairs. This consensus measure family is built from aggregation functions and fuzzy implications. The authors of [24] demonstrated that if the aggregation function is the arithmetic mean $M_A$ and the fuzzy implication is the Łukasiewicz implication given by $I_L(x,y)=min(1,1-x+y)$, for any $x,y\in [0,1]$, then the proposed measure satisfies all the requirements ((C1)–(C7)) for a consensus measure. In this case, the measure is

$$C_B^{(M_A,I_L)}\left(x_1,x_2,\dots ,x_n\right)=\frac{4}{n^2}\left(\sum _{i,j=1,i\ne j}^n{I}_L\left(x_i,x_j\right)\right)-\frac{3n-4}{n}.$$

(7)

3.1.2. Requirements for a Measure of Group Consensus on a Financial Investment

In our study, we deal with the special case where inputs are in the two-element set $\{0,1\}$. That is, 0 and 1, respectively, code the ‘no’ and ‘yes’ votes of the group members concerning a financial investment I. Hence, to adapt requirements (C1)–(C7) to our case, we utilize the following definition for a measure of group consensus on a financial investment.

Definition 5.

Let $n\in \mathbb{N}$ and $n\ge 2$. We say that a function $C^{\left(I\right)}:{\{0,1\}}^n\to [0,1]$ is a measure of group consensus on a financial investment I if $C^{\left(I\right)}$ satisfies the following properties:

(C1${}^{*}$)

(Unanimity) For any $a\in \{0,1\}$, $C^{\left(I\right)}(a,a,\dots ,a)=1$.

(C2${}^{*}$)

(Symmetry) For any permutation $\pi :\{1,2,\dots ,n\}\to \{1,2,\dots ,n\}$ and input vector $\mathbf{x}=(x_1,x_2,\dots ,x_n)$, $\mathbf{x}\in {\{0,1\}}^n$, it holds that

$$C^{\left(I\right)}(x_1,x_2,\dots ,x_n)=C^{\left(I\right)}\left(x_{\pi \left(1\right)},x_{\pi \left(2\right)},\dots ,x_{\pi \left(n\right)}\right).$$

(C3${}^{*}$)

(Maximum dissension) For $n=2k$, if k of the inputs are equal to zero and k of the inputs are equal to 1, then $C^{\left(I\right)}(0,0,\dots ,1,1)=0$ for all permutations of the input vector.

(C4${}^{*}$)

(Reciprocity) For any input vector $\mathbf{x}=(x_1,x_2,\dots ,x_n)$, $\mathbf{x}\in {\{0,1\}}^n$, it holds that

$$C^{\left(I\right)}(x_1,x_2,\dots ,x_n)=C^{\left(I\right)}\left(N_s\left(x_1\right),N_s\left(x_2\right),\dots ,N_s\left(x_n\right)\right),$$

where $N_s\left(a\right)=1-a$ is the standard fuzzy negation and $a\in [0,1]$.

(C5${}^{*}$)

(Replication invariance) For any input vector $\mathbf{x}=(x_1,x_2,\dots ,x_n)\in {\{0,1\}}^n$, replicating the inputs does not alter the degree of consensus, i.e., $C^{\left(I\right)}\left(\mathbf{x}\right)=C^{\left(I\right)}(\mathbf{x},\mathbf{x})=\dots =C^{\left(I\right)}(\mathbf{x},\mathbf{x}\dots ,\mathbf{x})$.

(C6${}^{*}$)

(Monotonicity with respect to the majority) For $n=2k$, let half of the inputs be equal and denoted by $\mathbf{a}=(a,a,\dots ,a)$, where $\mathbf{a}\in {\{0,1\}}^k$. Furthermore, let $\mathbf{x}=(x_1,x_2,\dots ,x_k)$ and $\mathbf{y}=(y_1,y_2,\dots ,y_k)$ be two input vectors, where $\mathbf{x},\mathbf{y}\in {\{0,1\}}^k$. If $|a-x_j|\le |a-y_j|$ for all $j=1,2,\dots ,k$, then $C^{\left(I\right)}\left(\mathbf{a},x_1,x_2,\dots ,x_k\right)\ge C^{\left(I\right)}\left(\mathbf{a},y_1,y_2,\dots ,y_k\right)$ holds for any permutation of the inputs.

Notice that since the original property (C2) follows from (C4), we reduced the number of requirements from seven to six such that (C1${}^{*}$) corresponds to (C1) and (C2${}^{*}$)–(C6${}^{*}$) correspond to (C3)–(C7), respectively.

Remark 1.

We should add that the original (C5) criterion in [24] requires that $C(x_1,x_2,\dots ,x_n)=C\left(N\left(x_1\right),N\left(x_2\right),\dots ,N\left(x_n\right)\right)$ holds for a strong negation N. We modified this requirement such that it should hold for the standard fuzzy negation $N_s\left(a\right)=1-a$, where $a\in [0,1]$.

4. A Novel, Fuzzy Entropy-Based Group Consensus Measure and Its Main Properties

Now, we introduce a fuzzy entropy-based mapping and demonstrate that it can be regarded as a measure of group consensus on a financial investment.

Theorem 2.

Let $n\in \mathbb{N}$, $n\ge 2$, and let $\mathbf{x}=\left(x_1,x_2,\dots ,x_n\right)\in {\{0,1\}}^n$ be an input vector of a group of n entities concerning an investment I. Furthermore, suppose that $F:[0,1]\to [0,1]$ is a mapping satisfying the requirements for a fuzzy entropy given in Definition 4. Then, the function $C_F^{\left(I\right)}:{\{0,1\}}^n\to [0,1]$, which is given by

$$C_F^{\left(I\right)}\left(\mathbf{x}\right)=1-F\left(\frac{1}{n}\sum _{i=1}^n{x}_i\right),$$

(8)

satisfies the (C1${}^{*}$)–(C6${}^{*}$) requirements for a consensus measure given in Definition 5.

Proof. 

Proof of (C1${}^{*}$) (Unanimity). Let $a\in \{0,1\}$ and $\mathbf{a}=(a,a,\dots ,a)\in {\{0,1\}}^n$. Then, based on Equation (8), we have

$$C_F^{\left(I\right)}\left(\mathbf{a}\right)=1-F\left(a\right),$$

and noting that $F\left(0\right)=F\left(1\right)=0$ (see property (b) of the fuzzy entropy F given in Definition 4), we readily find that $C_F^{\left(I\right)}\left(\mathbf{a}\right)=1$.

Proof of (C2${}^{*}$) (Symmetry). It trivially follows from the definition of $C_F^{\left(I\right)}$ that for any permutation $\pi$ on the set $\{1,2,\dots ,n\}$ and for any input vector $\mathbf{x}=(x_1,x_2,\dots ,x_n)\in {[0,1]}^n$,

$$C_F^{\left(I\right)}(x_1,x_2,\dots ,x_n)=C_F^{\left(I\right)}\left(x_{\pi \left(1\right)},x_{\pi \left(2\right)},\dots ,x_{\pi \left(n\right)}\right).$$

Proof of (C3${}^{*}$) (Maximum dissension). Let $n=2k$, and suppose that k of the inputs are equal to zero and k of the inputs are equal to 1. This means that $\frac{1}{n}{\sum }_{i=1}^n{x}_i=\frac{1}{2}$, and noting the fact that $F\left(\frac{1}{2}\right)=1$ (see property (d) of the fuzzy entropy F given in Definition 4), we find that $C_F^{\left(I\right)}(x_1,x_2,\dots ,x_n)=0$.

Proof of (C4${}^{*}$) (Reciprocity). Let $\mathbf{x}=(x_1,x_2,\dots ,x_n)\in {\{0,1\}}^n$ be an arbitrary input vector. We need to prove that

$$C_F^{\left(I\right)}(x_1,x_2,\dots ,x_n)=C_F^{\left(I\right)}\left(N_s\left(x_1\right),N_s\left(x_2\right),\dots ,N_s\left(x_n\right)\right)$$

(9)

holds, where $N_s\left(a\right)=1-a$ is the standard fuzzy negation and $a\in [0,1]$. Let $N_s\left(\mathbf{x}\right)$ denote the vector $\left(N_s\left(x_1\right),N_s\left(x_2\right),\dots ,N_s\left(x_n\right)\right)\in {[0,1]}^n$. By taking into account the fact that $F\left(x\right)=F(1-x)$ for any $x\in [0,1]$ (see property (e) of the fuzzy entropy F given in Definition 4), using Equation (8) we obtain

$$\begin{array}{cc}\hfill C_F^{\left(I\right)}\left(N_s\left(\mathbf{x}\right)\right)& =1-F\left(\frac{1}{n}\sum _{i=1}^n{N}_s\left(x_i\right)\right)=1-F\left(\frac{1}{n}\sum _{i=1}^n\left(1-x_i\right)\right)\hfill \\ \hfill & =1-F\left(1-\frac{1}{n}\sum _{i=1}^n{x}_i\right)=1-F\left(\frac{1}{n}\sum _{i=1}^n{x}_i\right)=C_F^{\left(I\right)}\left(\mathbf{x}\right).\hfill \end{array}$$

Proof of (C5${}^{*}$) (Replication invariance). Let $\mathbf{x}=(x_1,x_2,\dots ,x_n)\in {\{0,1\}}^n$ be an arbitrary input vector. Let $k\in \mathbb{N}$, $k\ge 1$ and define the $k·n$-dimensional vector $(\mathbf{x},\mathbf{x},\dots ,\mathbf{x})$ as

$$(\underset{k-\mathrm{times}}{\underbrace{\mathbf{x},\mathbf{x},\dots ,\mathbf{x}}})=(\underset{1}{\underbrace{x_1,x_2,\dots ,x_n}},\underset{2}{\underbrace{x_1,x_2,\dots ,x_n}},\dots ,\underset{k}{\underbrace{x_1,x_2,\dots ,x_n}}).$$

Then, noting Equation (8), we immediately obtain

$$C_F^{\left(I\right)}((\underset{k-\mathrm{times}}{\underbrace{\mathbf{x},\mathbf{x},\dots ,\mathbf{x}}}))=1-F\left(\frac{1}{kn}k\sum _{i=1}^n{x}_i\right)=C_F^{\left(I\right)}\left(\mathbf{x}\right).$$

This means that the function $C_F^{\left(I\right)}$ satisfies property (C5${}^{*}$).

Proof of (C6${}^{*}$) (Monotonicity with respect to the majority). Let $n=2k$ and let half of the inputs be equal and denoted by $\mathbf{a}=(a,a,\dots ,a)$, where $\mathbf{a}\in {\{0,1\}}^k$. Suppose that $\mathbf{x}=(x_1,x_2,\dots ,x_k)$ and $\mathbf{y}=(y_1,y_2,\dots ,y_k)$ are two input vectors, where $\mathbf{x},\mathbf{y}\in {\{0,1\}}^k$, and let $|a-x_j|\le |a-y_j|$ hold for all $j=1,2,\dots ,k$. We aim to show that under these conditions,

$$C_F^{\left(I\right)}\left(\mathbf{a},x_1,x_2,\dots ,x_k\right)\ge C_F^{\left(I\right)}\left(\mathbf{a},y_1,y_2,\dots ,y_k\right)$$

(10)

holds for any permutation of the inputs. We proved that $C_F$ satisfies the symmetry criterion (C2${}^{*}$). Therefore, it is sufficient to show that Equation (10) holds for the $\left(\mathbf{a},x_1,x_2,\dots ,x_k\right)$ and $\left(\mathbf{a},y_1,y_2,\dots ,y_k\right)$ input vectors (i.e., the inputs are in the same order as in Equation (10)). Since $a\in \{0,1\}$, we distinguish the following two cases: (1) $a=0$, and (2) $a=1$.

Case (1): $a=0$. In this case, the condition that $|a-x_j|\le |a-y_j|$ holds for all $j=1,2,\dots ,k$ is equivalent to the condition that $x_j\le y_j$ holds for all $j=1,2,\dots ,k$. Hence, we have

$$0\le \frac{1}{2k}\left(\sum _{i=1}^{k}0+\sum _{i=1}^k{x}_i\right)\le \frac{1}{2k}\left(\sum _{i=1}^{k}0+\sum _{i=1}^k{y}_i\right)\le \frac{1}{2}.$$

(11)

Next, taking into account that the fuzzy entropy F is strictly increasing on $\left(0,\frac{1}{2}\right)$ (see property (c) of the fuzzy entropy F given in Definition 4), based on Equation (11), we find that

$$1-F\left(\frac{1}{2k}\left(\sum _{i=1}^{k}0+\sum _{i=1}^k{x}_i\right)\right)\ge 1-F\left(\frac{1}{2k}\left(\sum _{i=1}^{k}0+\sum _{i=1}^k{y}_i\right)\right),$$

which means that Equation (10) holds.

Case (2): $a=1$. In this case, the condition that $|a-x_j|\le |a-y_j|$ holds for all $j=1,2,\dots ,k$ means that $x_j\ge y_j$ for all $j=1,2,\dots ,k$. Therefore, the following inequality chain holds:

$$\frac{1}{2}\le \frac{1}{2k}\left(\sum _{i=1}^{k}1+\sum _{i=1}^k{y}_i\right)\le \frac{1}{2k}\left(\sum _{i=1}^{k}1+\sum _{i=1}^k{x}_i\right)\le 1.$$

(12)

Since F is strictly decreasing on $\left(\frac{1}{2},1\right)$, Equation (12) implies that

$$1-F\left(\frac{1}{2k}\left(\sum _{i=1}^{k}1+\sum _{i=1}^k{y}_i\right)\right)\le 1-F\left(\frac{1}{2k}\left(\sum _{i=1}^{k}1+\sum _{i=1}^k{x}_i\right)\right),$$

which means that Equation (10) holds. □

5. Connections with Known Consensus Measures

Now, we demonstrate that if the inputs are dichotomous variables, then the following are all special cases of the fuzzy entropy-based consensus measure $C_F^{\left(I\right)}$ given in Equation (8):

(a)

The standard deviation-based consensus measure $C_{\sigma }$ given in Equation (5).

(b)

The consensus measure $C_{SK}$ proposed by Szmidt and Kacprzyk in Equation (6).

(c)

The Bonferroni consensus measure with implication pairs $C_B^{(M_A,I_L)}$ for the case where the aggregation function is the arithmetic mean $M_A$ and the fuzzy implication is the Łukasiewicz implication $I_L$ given in Equation (7).

Let $g:[0,1]\to [0,\infty ]$ be an additive generator of a strict t-norm. As mentioned in Section 2, the function $F_g:[0,1]\to [0,1]$, which is given by

$$F_g\left(x\right)=2g^{-1}\left(\frac{1}{2}\left(g\left(x\right)+g(1-x)\right)\right),$$

(13)

satisfies the requirements for a fuzzy entropy given in Definition 4.

Theorem 3.

Let $n\in \mathbb{N}$, $n\ge 2$; let $\mathbf{x}=\left(x_1,x_2,\dots ,x_n\right)\in {\{0,1\}}^n$ be an input vector of a group of n entities concerning an investment I; and let $g_p\left(x\right)=-ln\left(x\right)$, $x\in [0,1]$ (with the convention $ln\left(0\right)=-\infty$), i.e., $g_p$ is an additive generator of the product t-norm. If the fuzzy entropy $F_{g_p}:[0,1]\to [0,1]$ is induced by $g\left(x\right)=g_p\left(x\right)$, $x\in [0,1]$, according to Equation (13), the standard deviation-based consensus measure $C_{\sigma }$ and the fuzzy entropy-based consensus measure $C_{F_{g_p}}^{\left(I\right)}$ induced by the fuzzy entropy $F_{g_p}$ coincide, i.e., for any $\mathbf{x}\in {\{0,1\}}^n$,

$$C_{F_{g_p}}^{\left(I\right)}\left(\mathbf{x}\right)=C_{\sigma }\left(\mathbf{x}\right).$$

(14)

Proof. 

Using Equation (13), after direct calculation, we find that the fuzzy entropy induced by $g_p$ is

$$F_{g_p}\left(x\right)=2\sqrt{x(1-x)},x\in [0,1]$$

(15)

and using Equation (8), we have that the fuzzy entropy-based consensus measure induced by $F_{g_p}$ is

$$C_{F_{g_p}}^{\left(I\right)}\left(\mathbf{x}\right)=1-2\sqrt{\overline{x}\left(1-\overline{x}\right)},$$

(16)

where $\overline{x}=\frac{1}{n}{\sum }_{i=1}^n{x}_i$. Notice that since $x_i\in \{0,1\}$, $x_i^2=x_i$. Now, using Equation (5), we can write

$$\begin{array}{cc}\hfill C_{\sigma }\left(\mathbf{x}\right)& =1-\sqrt{\frac{4}{n}\sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}=1-2\sqrt{\frac{1}{n}\sum _{i=1}^n\left(x_i^2-2x_i\overline{x}+{\overline{x}}^2\right)}\hfill \\ \hfill & =1-2\sqrt{\frac{1}{n}\sum _{i=1}^n\left(x_i-2x_i\overline{x}+{\overline{x}}^2\right)}=1-2\sqrt{\frac{{\sum }_{i=1}^n{x}_i}{n}-2\overline{x}\frac{{\sum }_{i=1}^n{x}_i}{n}+{\overline{x}}^2}\hfill \\ \hfill & =1-2\sqrt{\overline{x}-{\overline{x}}^2}=C_{F_{g_p}}^{\left(I\right)}\left(\mathbf{x}\right),\hfill \end{array}$$

which means that Equation (14) holds. □

Theorem 4.

Let $n\in \mathbb{N}$, $n\ge 2$; let $\mathbf{x}=\left(x_1,x_2,\dots ,x_n\right)\in {\{0,1\}}^n$ be an input vector of a group of n entities concerning an investment I; and let $g_D\left(x\right)=\frac{1-x}{x}$, $x\in [0,1]$, i.e., $g_D$ is an additive generator of the Dombi t-norms. If the fuzzy entropy $F_{g_D}:[0,1]\to [0,1]$ is induced by $g\left(x\right)=g_D\left(x\right)$, $x\in [0,1]$, according to Equation (13), the following consensus measures both coincide with the fuzzy entropy-based consensus measure $C_{F_{g_D}}^{\left(I\right)}$ induced by the fuzzy entropy $F_{g_D}$:

• The consensus measure $C_{SK}$ proposed by Szmidt and Kacprzyk.
• The Bonferroni consensus measure with implication pairs $C_B^{(M_A,I_L)}$ for the case where the aggregation function is the arithmetic mean $M_A$ and the fuzzy implication is the Łukasiewicz implication $I_L$.

That is, for any $\mathbf{x}\in {\{0,1\}}^n$,

$$C_{F_{g_D}}^{\left(I\right)}\left(\mathbf{x}\right)=C_{SK}\left(\mathbf{x}\right)$$

(17)

and

$$C_{F_{g_D}}^{\left(I\right)}\left(\mathbf{x}\right)=C_B^{(M_A,I_L)}\left(\mathbf{x}\right).$$

(18)

Proof. 

First, we prove that under the conditions of the theorem, Equation (17) holds. Using direct calculation, we find that the fuzzy entropy induced by the function $g_D\left(x\right)=\frac{1-x}{x}$, $x\in [0,1]$, which is an additive generator of the Dombi t-norms, is

$$F_{g_D}\left(x\right)=4x(1-x).$$

(19)

Next, using Equation (8), we have that the fuzzy entropy-based consensus measure induced by $F_{g_D}$ is

$$C_{F_{g_D}}^{\left(I\right)}\left(\mathbf{x}\right)=1-4\overline{x}\left(1-\overline{x}\right),$$

(20)

where $\overline{x}=\frac{1}{n}{\sum }_{i=1}^n{x}_i$. Noting the consensus measure $C_{SK}$ given in Equation (6); the fact that $x_i^2=x_i$ for $i\in \{1,2,\dots ,n\}$; and $x_i-x_j=0$ if $i=j$, we can write

$$\begin{array}{cc}\hfill C_{SK}\left(\mathbf{x}\right)& =1-\frac{2}{n^2}\sum _{\forall i,j|i\ne j}{\left(x_i-x_j\right)}^2=1-\frac{2}{n^2}\sum _{i,j=1}^n\left(x_i^2-2x_i{x}_j+x_j^2\right)\hfill \\ \hfill & =1-\frac{2}{n^2}\sum _{i,j=1}^n\left(x_i-2x_i{x}_j+x_j\right)=1-\frac{2}{n^2}\left(2n\sum _{i=1}^n{x}_i-2\sum _{i,j=1}^n{x}_i{x}_j\right)\hfill \\ \hfill & =1-\frac{4}{n^2}\left(n\sum _{i=1}^n{x}_i-\sum _{i=1}^n\left(\sum _{j=1}^n{x}_i{x}_j\right)\right)=1-\frac{4}{n^2}\left(n\sum _{i=1}^n{x}_i-{\left(\sum _{i=1}^n{x}_i\right)}^2\right)\hfill \\ \hfill & =1-4\left(\overline{x}-{\overline{x}}^2\right)=1-4\overline{x}(1-\overline{x})=C_{F_{g_D}}^{\left(I\right)}\left(\mathbf{x}\right).\hfill \end{array}$$

This means that Equation (17) holds.

Now, we prove that under the conditions of the theorem, Equation (18) also holds. Taking into account Equations (7) and (20), we need to show that

$$1-4\overline{x}\left(1-\overline{x}\right)=\frac{4}{n^2}\left(\sum _{i,j=1,i\ne j}^n{I}_L\left(x_i,x_j\right)\right)-\frac{3n-4}{n}$$

holds. The Łukasiewicz implication $I_L(x,y)=min(1,1-x+y)$, where $x,y\in [0,1]$, satisfies the ordering property, i.e., $I_L(x,y)=1$ if and only if $x\le y$. This means that in the sum

$$\sum _{i,j=1,i\ne j}^n{I}_L\left(x_i,x_j\right)$$

there are as many zero tags as there are $(1,0)$-like pairs among the $(x_i,x_j)$ pairs, where $i,j\in \{1,2,\dots ,n\}$, $i\ne j$. The number of such pairs is equal to the number of zero elements in $\mathbf{x}$ multiplied by the number of non-zero elements in $\mathbf{x}$. Therefore, the number of zero tags in the above sum is

$$\left(n-\sum _{i=1}^n{x}_i\right)\sum _{i=1}^n{x}_i,$$

and so

$$\sum _{i,j=1,i\ne j}^n{I}_L\left(x_i,x_j\right)=n^2-n-\left(n-\sum _{i=1}^n{x}_i\right)\sum _{i=1}^n{x}_i.$$

(21)

Using Equation (21), we can write

$$\begin{array}{cc}\hfill C_B^{(M_A,I_L)}\left(\mathbf{x}\right)& =\frac{4}{n^2}\left(\sum _{i,j=1,i\ne j}^n{I}_L\left(x_i,x_j\right)\right)-\frac{3n-4}{n}\hfill \\ \hfill & =\frac{4}{n^2}\left(n^2-n-\left(n-\sum _{i=1}^n{x}_i\right)\sum _{i=1}^n{x}_i\right)-\frac{3n-4}{n}\hfill \\ \hfill & =4\left(1-\frac{1}{n}-\left(1-\frac{{\sum }_{i=1}^n{x}_i}{n}\right)\frac{{\sum }_{i=1}^n{x}_i}{n}\right)-\frac{3n-4}{n}\hfill \\ \hfill & =1-4\frac{{\sum }_{i=1}^n{x}_i}{n}\left(1-\frac{{\sum }_{i=1}^n{x}_i}{n}\right)=1-4\overline{x}\left(1-\overline{x}\right)=C_{F_{g_D}}^{\left(I\right)}\left(\mathbf{x}\right).\hfill \end{array}$$

This means that Equation (18) holds. □

Remark 2.

It readily follows from Theorem 4 that for any $\mathbf{x}\in {\{0,1\}}^n$,

$$C_{SK}\left(\mathbf{x}\right)=C_B^{(M_A,I_L)}\left(\mathbf{x}\right)$$

(22)

holds, where $n\in \mathbb{N}$, $n\ge 2$.

The values of $C_{F_{g_D}}^{\left(I\right)}\left(\mathbf{x}\right)$, $C_{SK}\left(\mathbf{x}\right)$, $C_B^{(M_A,I_L)}\left(\mathbf{x}\right)$, $C_{F_{g_p}}^{\left(I\right)}\left(\mathbf{x}\right)$, $C_{\sigma }\left(\mathbf{x}\right)$, and $C_{TWD}\left(\mathbf{x}\right)$ computed for the input vectors given in Table 1 are shown in

Table 2. Example: values of various consensus measures for the input vectors given in Table 1.

$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$\overline{x}$	$C_{F_{g_D}}^{\left(I\right)}\left(\mathit{x}\right)$	$C_{SK}\left(\mathit{x}\right)$	$C_B^{(M_A,I_L)}\left(\mathit{x}\right)$	$C_{F_{g_p}}^{\left(I\right)}\left(\mathit{x}\right)$	$C_{\sigma }\left(\mathit{x}\right)$	$C_{TWD}\left(\mathit{x}\right)$
0	0	0	0	0	0	0.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
1	0	0	0	0	0	0.1667	0.4444	0.4444	0.4444	0.2546	0.2546	0.3500
1	1	0	0	0	0	0.3333	0.1111	0.1111	0.1111	0.0572	0.0572	0.0817
1	1	1	0	0	0	0.5000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000
1	1	1	1	0	0	0.6667	0.1111	0.1111	0.1111	0.0572	0.0572	0.0817
1	1	1	1	1	0	0.8333	0.4444	0.4444	0.4444	0.2546	0.2546	0.3500
1	1	1	1	1	1	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000

.

Based on the data in Table 2, we can see that in line with Theorems 3 and 4, the identities $C_{F_{g_p}}^{\left(I\right)}\left(\mathbf{x}\right)=C_{\sigma }\left(\mathbf{x}\right)$ and $C_{F_{g_D}}^{\left(I\right)}\left(\mathbf{x}\right)=C_{SK}\left(\mathbf{x}\right)=C_B^{(M_A,I_L)}\left(\mathbf{x}\right)$ hold.

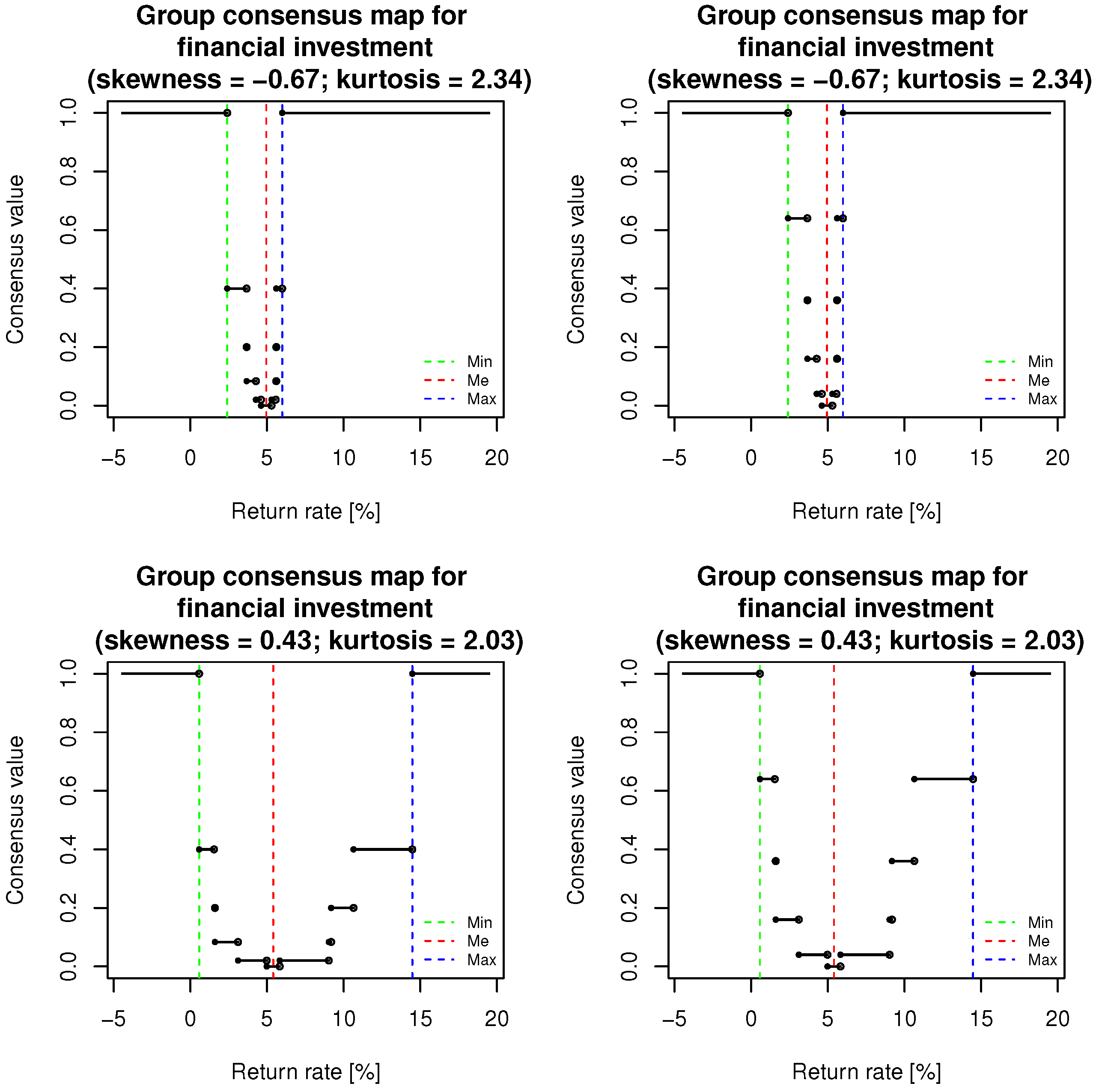
6. Group Consensus Map for Financial Investments

Noting Theorem 2, we have that if $n\in \mathbb{N}$, $n\ge 2$, $\mathbf{x}\left(r\right)=\left(x_1\left(r\right),x_2\left(r\right),\dots ,x_n\left(r\right)\right)\in {\{0,1\}}^n$ is an input vector of a group of n entities concerning an investment $I\left(r\right)$ with an expected rate of return r, and $F:[0,1]\to [0,1]$ is a mapping satisfying the requirements for a fuzzy entropy given in Definition 4, then the function $C_F^{\left(I\right(r\left)\right)}{\{0,1\}}^n\to [0,1]$, which is given by

$$C_F^{\left(I\right(r\left)\right)}\left(\mathbf{x}\left(r\right)\right)=1-F\left(\frac{1}{n}\sum _{i=1}^n{x}_i\left(r\right)\right),$$

(23)

is a consensus measure satisfying the requirements (C1${}^{*}$)–(C6${}^{*}$) given in Definition 5. In practice, there are many factors that can influence the value of the group consensus. Here, ceteris paribus, we concentrate on the impact of the value of the expected rate of return on the value of the consensus measure. Hence, formally, we define the group consensus map for financial investments as a function $M_F:\mathbb{R}\to [0,1]$, which is given by

$$M_F\left(r\right)=1-F\left(\frac{1}{n}\sum _{i=1}^n{x}_i\left(r\right)\right),$$

where $x_i\left(r\right)\in \{0,1\}$ is the input of the ith group member at an expected rate of return $r\in \mathbb{R}$. Here, we assume that the group of n entities is fixed, i.e., for any $r\in \mathbb{R}$, the same group members are involved in the decision-making process. We can assume that if r is sufficiently small, then all the group members vote against the investment, i.e., $x_i=0$ for all $i=1,2,\dots ,n$, and so $M_F\left(r\right)=1$. Similarly, if r is sufficiently large, then all the group members vote in favor of the investment, i.e., $x_i=1$ for all $i=1,2,\dots ,n$, which results in $M_F\left(r\right)=1$. This means we can assume that the $M_F$ function has the following limiting properties:

$$\underset{r\to -\infty }{lim}{M}_F\left(r\right)=1\mathrm{and}\underset{r\to +\infty }{lim}{M}_F\left(r\right)=1.$$

On the other hand, we may also suppose that there exists a $r_0\in \mathbb{R}$ for which the group consensus is minimal. If $r=r_0$, then—roughly speaking—half of the group members vote in favor of and half of them vote against the investment, that is, the value of $M_F\left(r_0\right)$ is close to zero. Since $r_0$ has this semantic meaning, from a behavioral economics point of view, finding the value of $r_0$ may be an interesting task in practice. It is also interesting to consider the shape of the consensus measure curve $M_F\left(r\right)$.

An Algorithm for Estimating the Group Consensus Map

In the following, we outline a simple procedure for empirically estimating the group consensus map. The inputs of the procedure are the expected rate of return $r\in \mathbb{R}$ of a financial investment, and for every decision maker, an investment rate-of-return threshold, which determines the minimum rate of return the decision maker finds an investment attractive enough to invest in. The output of the procedure is the value of the group consensus map at r. The procedure is as follows:

• Inputs:

  –

  $r\in \mathbb{R}$.

  –

  $r_{01},r_{02},\dots ,r_{0n}$, where $r_{0i}$ denotes the investment rate-of-return threshold of the ith group member, $n\ge 2$, $i=1,2,\dots ,n$. $r_{0i}$ represents the rate of return at which the ith decision maker changes his/her decision from acceptance to rejection, and vice versa.

• Step 0: Consider dropping the extreme investment rate-of-return thresholds (i.e., those falling more than 3 standard deviations away from the mean), as they can seriously affect the shape of the map, which we demonstrate later.
• Step 1: Compute $\overline{x}\left(r\right)$ as

  $$\overline{x}\left(r\right)=\frac{{\sum }_{i=1}^{n}I(r_{0i}\le r)}{n},$$

  where $I(r_{0i}\le r)$ is the indicator of the event $\{r_{0i}\le r\}$, i.e.,

  $$I(r_{0i}\le r)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{r}_{0i}\le r\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$
• Step 2: Compute the value of the group consensus map $M_F:\mathbb{R}\to [0,1]$ at r as

  $$M_F\left(r\right)=1-F\left(\overline{x}\left(r\right)\right),$$

  where F is an arbitrarily fixed fuzzy entropy given by Definition 4.
• Output: $M_F\left(r\right)$.

Note that $\overline{x}\left(r\right)$ is a stepwise function, which is non-decreasing in r, and it is none other than the empirical cumulative distribution function estimated from the sample at hand. It is worth noting that there are interesting connections between some statistics of the original sample of investment rate-of-return thresholds and the resulting consensus map. These are as follows:

• Sample median of investment rate-of-return thresholds: At the median, the group consensus map has its global minimum, i.e., the median of the investment rate-of-return thresholds can be treated as the estimate of an $r_0$ value at which $M_F$ is minimal.
• Sample minimum and maximum of investment rate-of-return thresholds: For any $r<min\{r_1,r_2,\dots ,r_n\}$ ($r\ge max\{r_1,r_2,\dots ,r_n\}$, respectively), $\overline{x}\left(r\right)=0$ ($\overline{x}\left(r\right)=1$, respectively) and so $M_F\left(r\right)=1$. This means that at the furthest value of each tail of the investment thresholds’ distribution, the group consensus map reaches its limiting value, i.e., 1, which implies a full consensus.
• Shape parameters of the distribution of investment rate-of-return thresholds: The shape of the group consensus map largely depends on the shape of the distribution of the investment rate-of-return thresholds and the presence of outliers (this is why we suggested dropping these values at the very beginning of the procedure). Where long tails are present in the distribution of the thresholds, the increase in the consensus map is very slow toward its limiting value of 1. Conversely, on the dense side of the distribution, the consensus map increases quite sharply toward 1.

Now, using the simulated investment rate-of-return threshold values from the various distributions, we demonstrate how some summary statistics, such as the minimum, maximum, median, skewness, and kurtosis, of the sample of investment rate-of-return thresholds affect the resulting group consensus map.

The plots in the first row of Figure 1 belong to a sample of 10 investment thresholds simulated from a normal distribution with a mean of 5 and standard deviation of 2, whereas those in the second row were simulated from a ${\chi }^2$ distribution with 5 degrees of freedom. In the first column of Figure 1, we applied the group consensus measure $C_{F_{g_p}}^{\left(I\right)}\left(\mathit{x}\right)=1-2\sqrt{\overline{x}(1-\overline{x})}$, whereas in the second column, the group consensus measure $C_{F_{g_D}}^{\left(I\right)}\left(\mathit{x}\right)=1-4\overline{x}(1-\overline{x})$ was utilized.

Figure 1 shows how the minimum ($Min$), maximum ($Max$), and median ($Me$) statistics of an investment rate-of-return threshold sample affect the corresponding group consensus map. In the intermediate intervals $(Min;Me)$ and $(Me;Max)$, the shape of the group consensus map reflects the shape parameters of the sample. Namely, if atypical values occur (i.e., the distribution is skewed to either side), it is more difficult to reach a full consensus. Although there were no clear outliers in our demonstrative example, it underpinned the importance of Step 0 (i.e., considering dropping the outliers), as the long right tail of the ${\chi }^2$ distribution had a strong impact on the shape of the resulting map plotted in the second row of Figure 1.

7. Conclusions and Future Research Plans

In our study, we introduced a fuzzy entropy-based function and proved that it satisfies six reasonable properties that can be treated as requirements for a consensus measure when the decision inputs are from the two-element set $\{0,1\}$. We demonstrated that our approach can be used to characterize the degree of agreement among the members of a group where each member votes either ‘no’ or ‘yes’ for a financial investment that has a given expected rate of return. As we highlighted, our measure is generated by a fuzzy entropy. If we apply the function $F_{g_D}\left(x\right)=4x(1-x)$ to generate our consensus measure, then the following consensus measures both coincide with the fuzzy entropy-based consensus measure $C_{F_{g_D}}^{\left(I\right)}$ induced by the fuzzy entropy $F_{g_D}$:

• The consensus measure $C_{SK}$ by Szmidt and Kacprzyk.
• The Bonferroni consensus measure with implication pairs $C_B^{(M_A,I_L)}$ for the case where the aggregation function is the arithmetic mean $M_A$ and the fuzzy implication is the Łukasiewicz implication $I_L$.

Furthermore, in the case of applying $F_{g_p}\left(x\right)=2\sqrt{x(1-x)}$ to generate the fuzzy entropy-based consensus measure, we found that it coincides with the standard deviation-based consensus measure $C_{\sigma }$.

Next, we presented the idea of the so-called group consensus map for financial investments. This function expresses the level of consensus among the members of a fixed group concerning financial investments as a function of the expected rate of return. We provided an algorithm for estimating this map using empirical data collected from the decision makers. The resulting group consensus map is an interesting construction from the perspective of behavioral economics, as it describes how the group as a whole behaves. The consensus map helps to identify the following:

• The rates of return that imply the lowest level of consensus and the highest level of dissension.
• The rates of return that imply the highest level of consensus and the lowest level of dissension.
• How the level of consensus evolves regarding other values of the rate of return.

As part of our future research, we would like to study the problem in which the amount of money that could be invested into assets can vary within a certain range. Furthermore, since the choice of the fuzzy entropy affects the fuzzy entropy-based consensus measure, in a future study, we would like to explore the use of various types of fuzzy entropies to see how they impact the consensus map.

The fuzzy entropy-based consensus measure we presented for financial investments can also be adapted to other areas. Therefore, we plan to investigate how the proposed approach can be applied in other fields where group decisions are based on dichotomous inputs. We also plan to validate our approach with more complex, real-life data, and using these data, we would like to compare our method to some existing consensus measures and explore the implications and limitations of the proposed approach. Investigating the weighted version of our consensus measure fell outside the scope of our current research. In a separate study, we plan to derive a weighted version of the proposed measure that could be used to describe the level of agreement in a decision-making process, where each decision maker has a weight $w_i\in (0,1)$ corresponding to the importance of that person’s opinion.