Bipolar Dissimilarity and Similarity Correlations of Numbers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Correlation Functions (Association Measures)
2.2. Similarity and Dissimilarity Functions (Fuzzy Relations)
2.3. Constructing Correlation Functions from Similarity and Dissimilarity Functions
- (a)
- Correlation between x and y is positive if the similarity between x and y is greater than the dissimilarity between them. In the opposite case, the correlation between x and y is negative.
- (b)
- Correlation between x and y is positive if they are “similar” and negative if they are “different”.
3. Results
3.1. Constructing Pearson’s Linear Correlation Coefficient Using Bipolar Dissimilarity Function
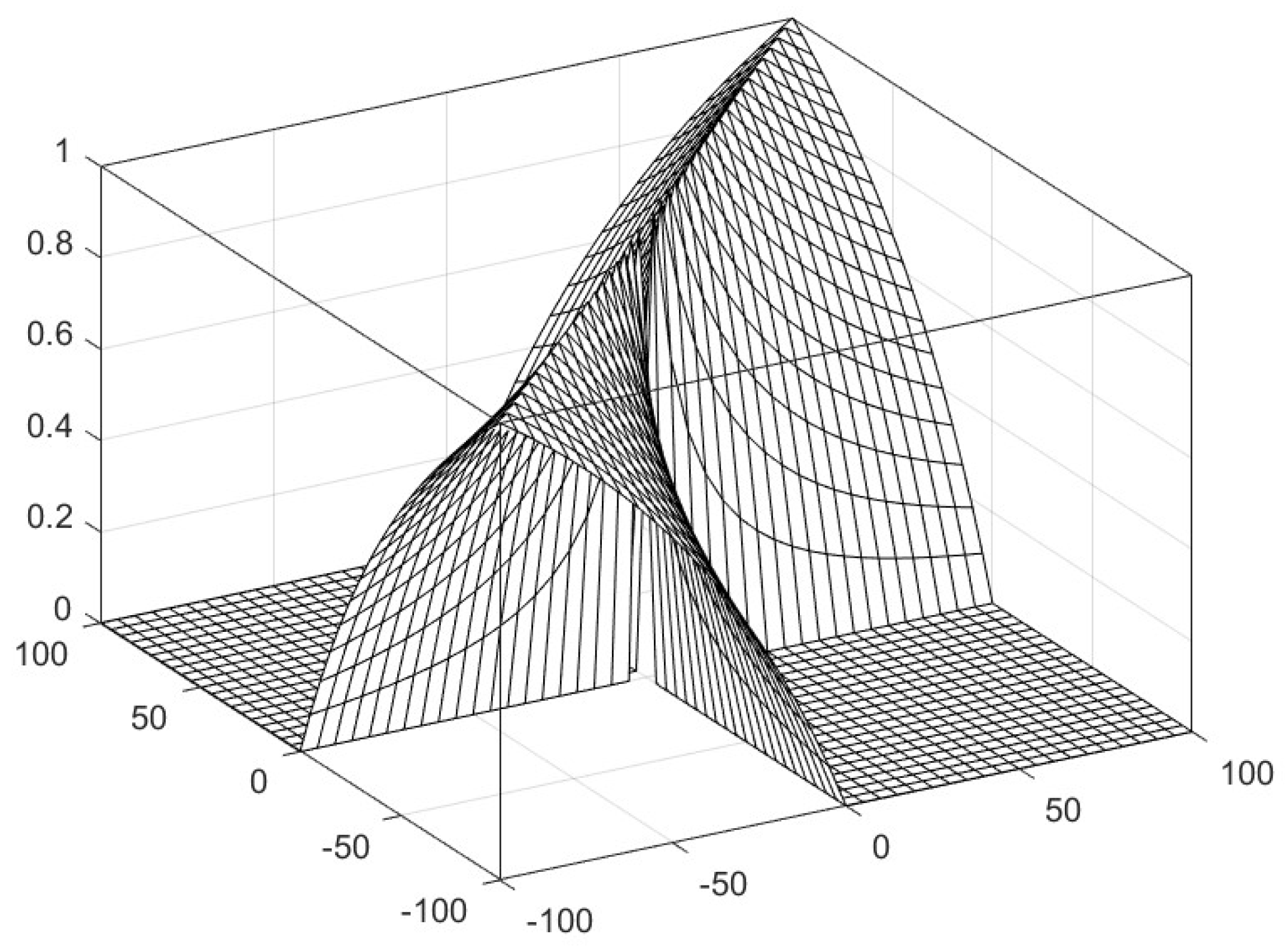
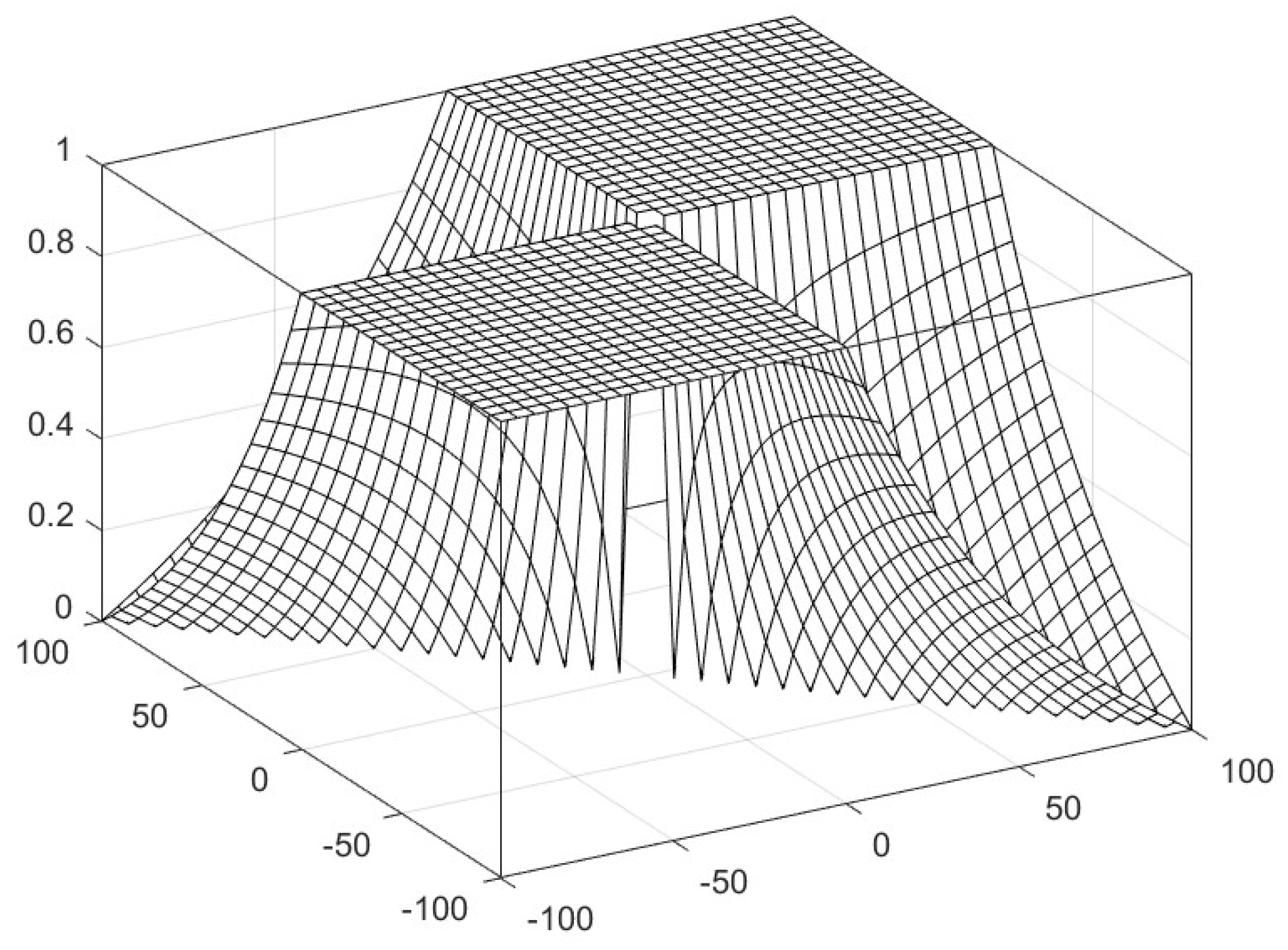
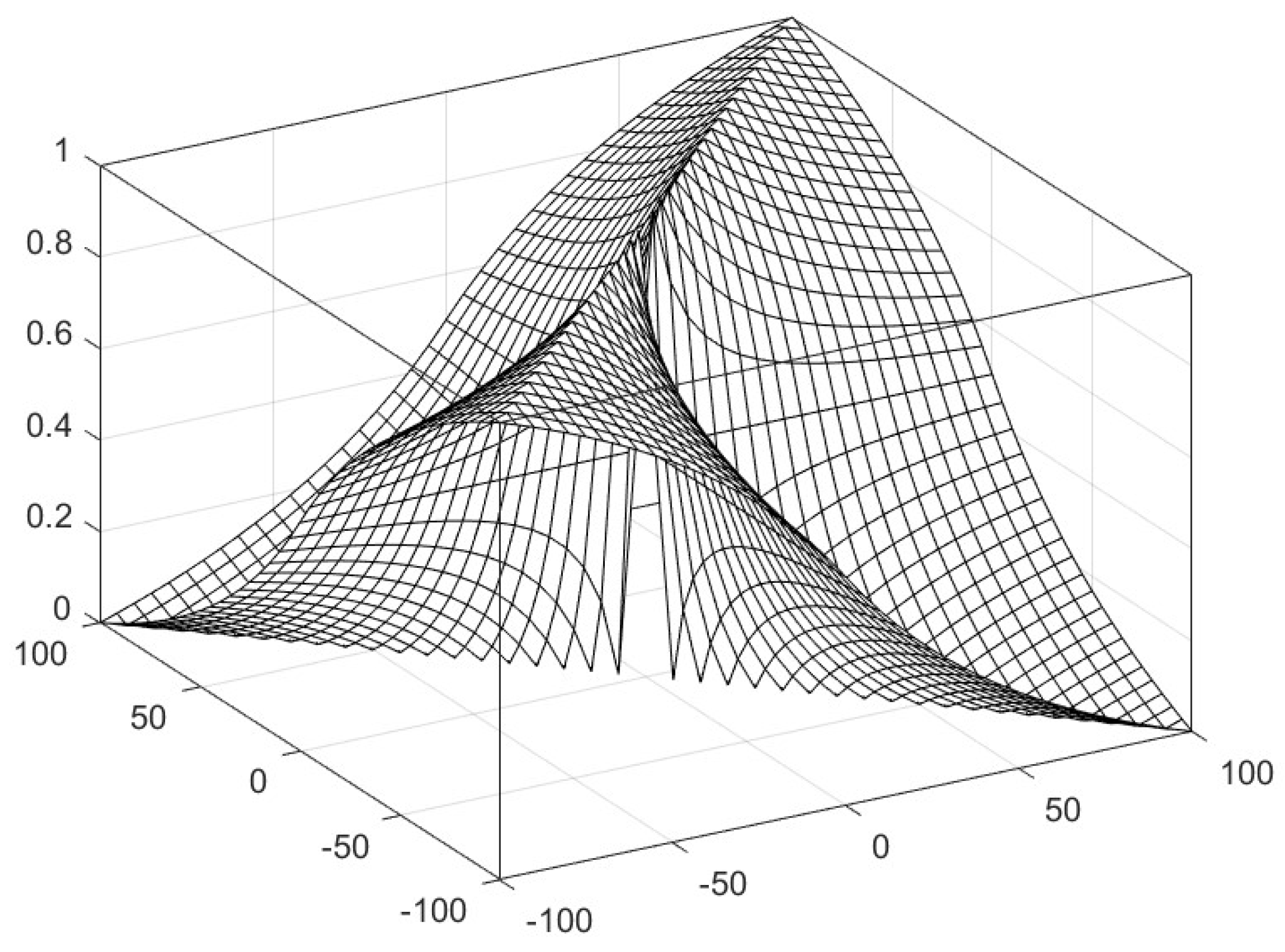
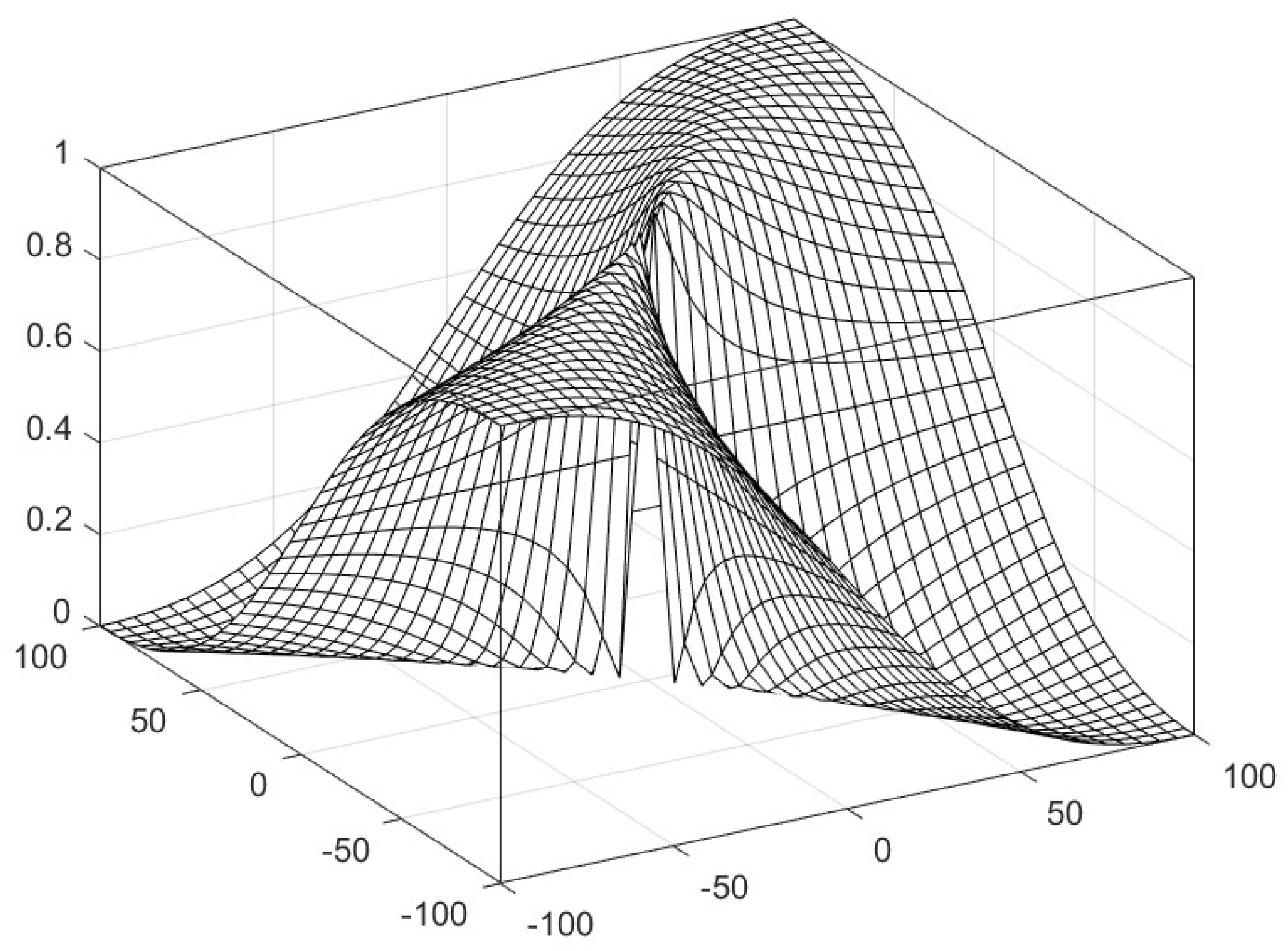
3.2. Non-Bipolar Similarity, Dissimilarity, and Correlation Functions for Real Numbers
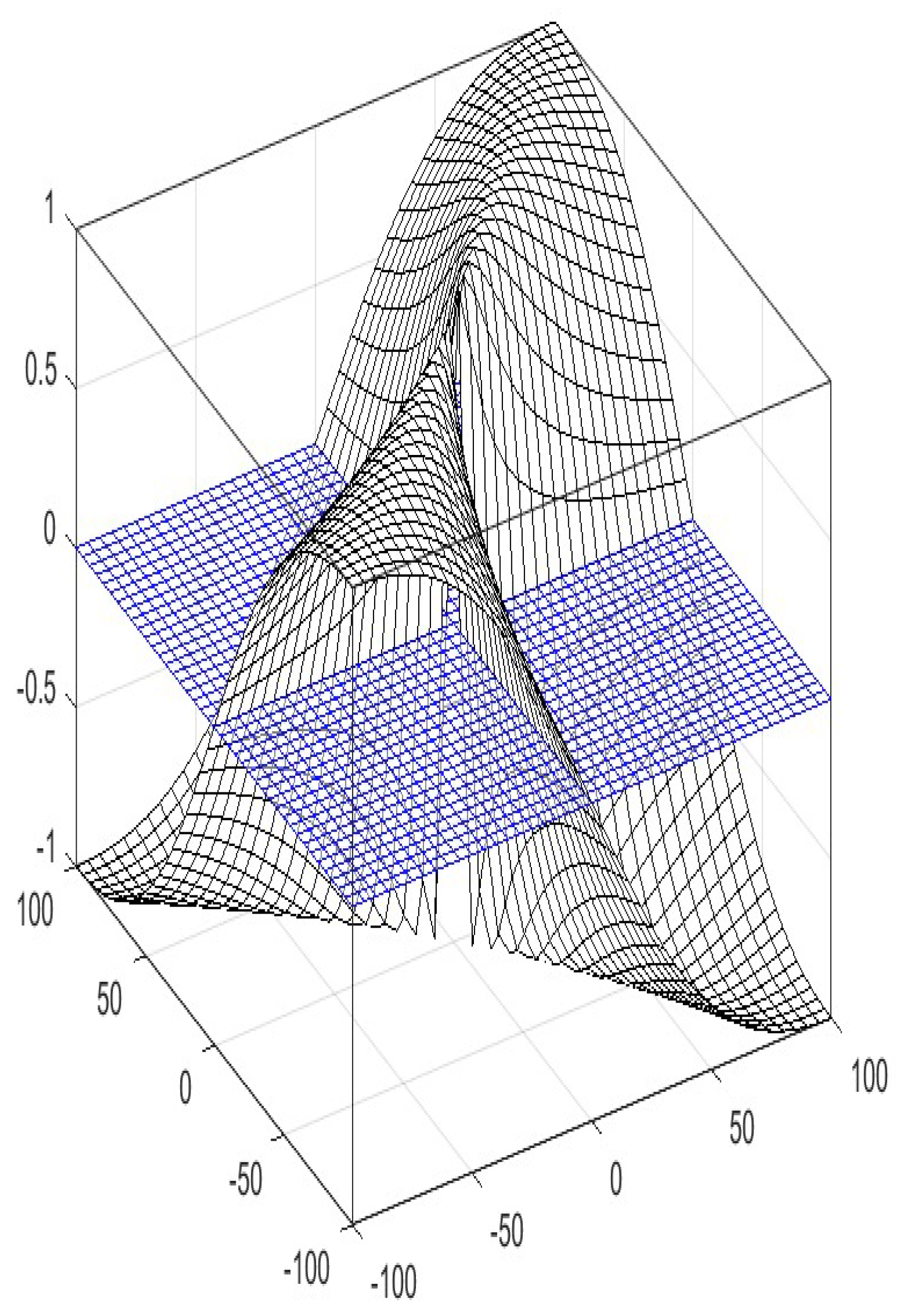
3.3. Bipolar Similarity, Dissimilarity, and Correlation Functions for Real Numbers
4. Bipolar Dissimilarity and Similarity Correlation in Risk Assessment
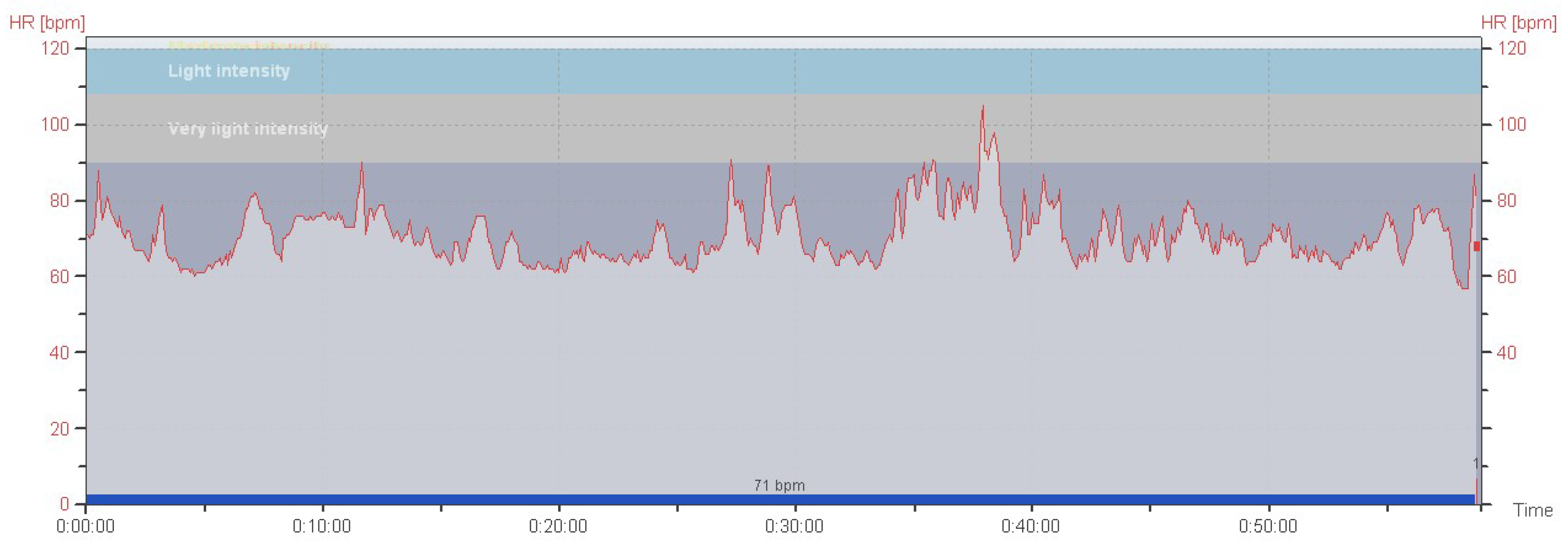
- Measured values (see Figure 6) are stored in a database.
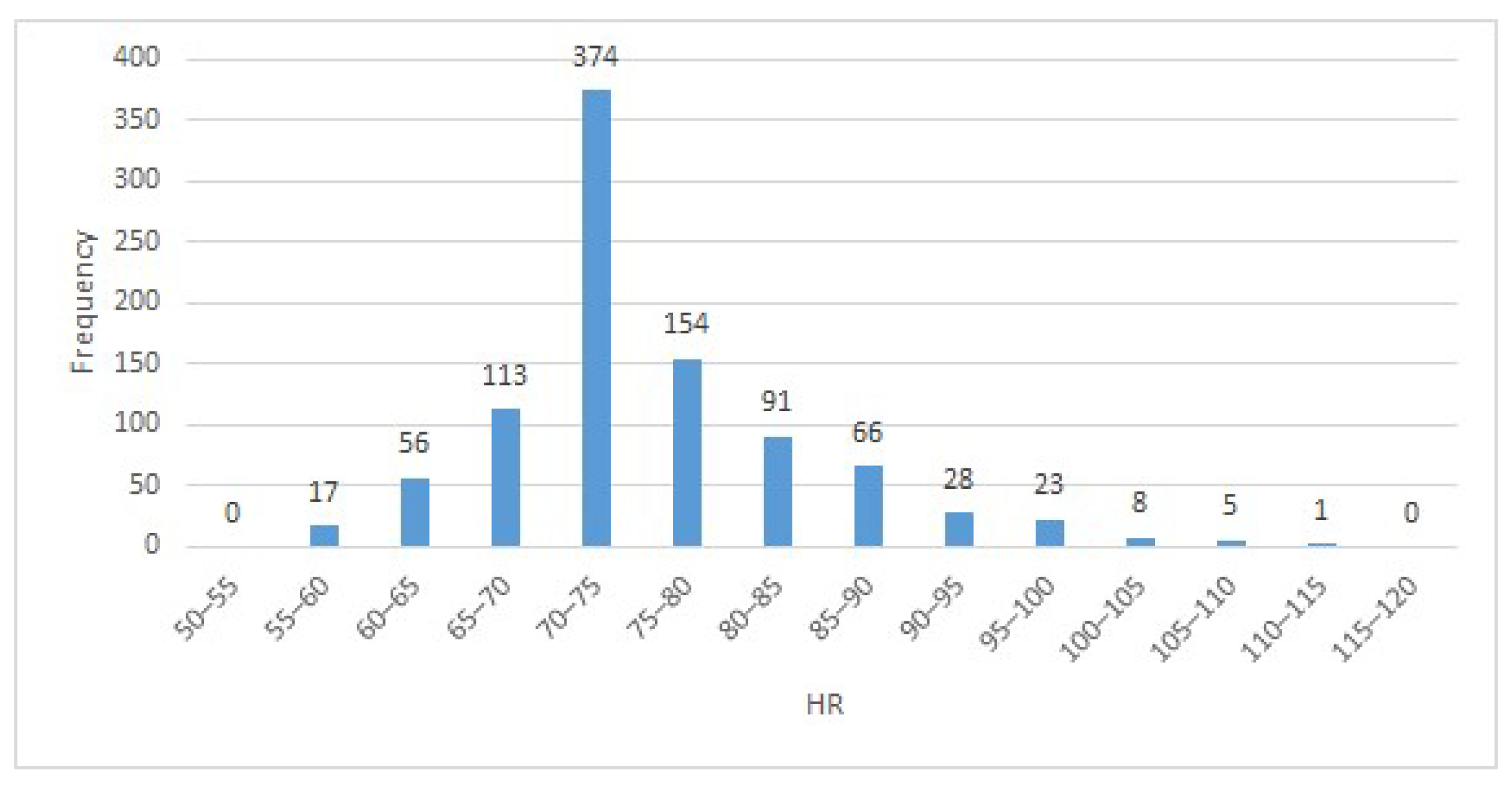
- Histogram is created based on the stored data as illustrated in Figure 7.
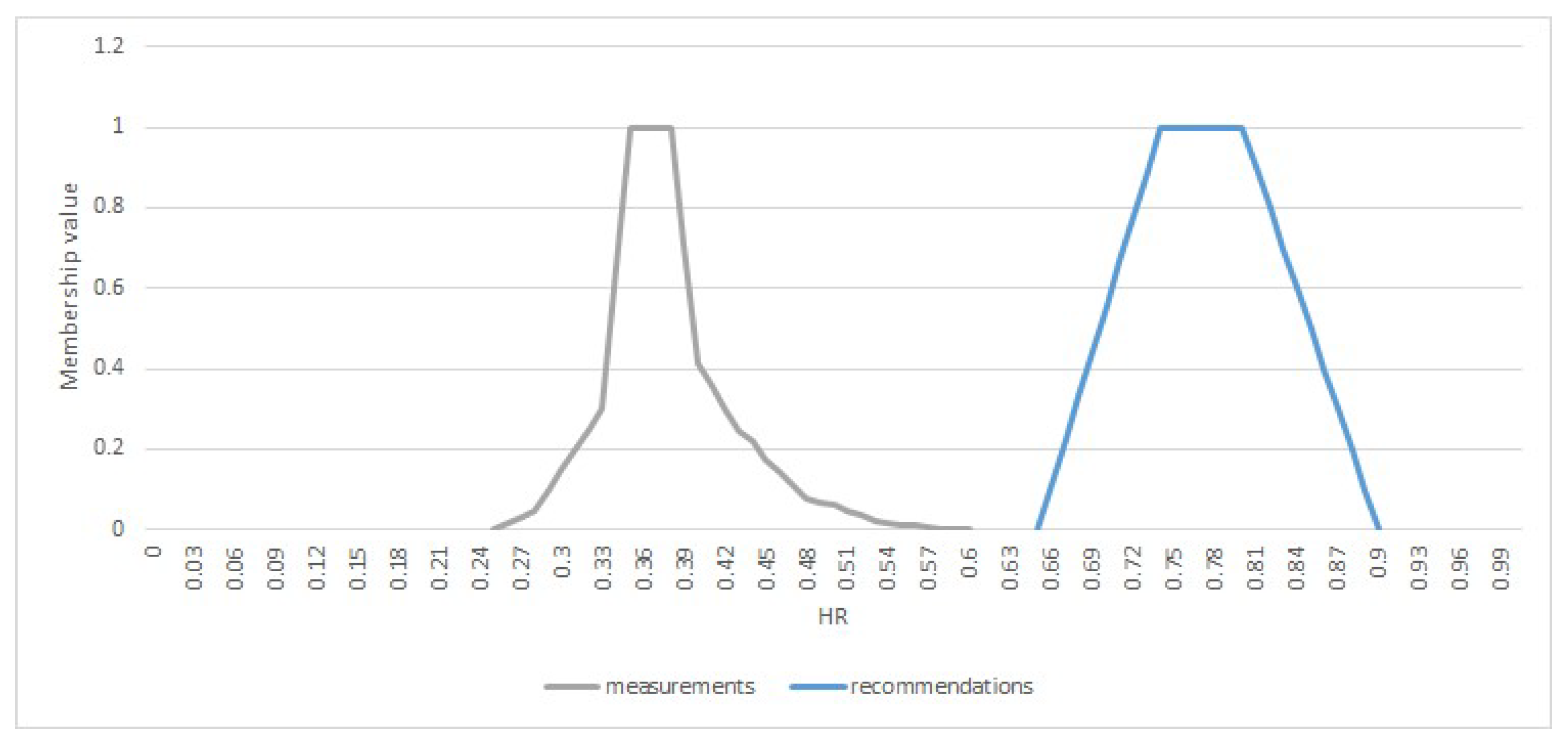
- Fuzzy set is fitted to the histogram, (see in [29]). This set represents the normal reactions of the patient under the same conditions. Medical recommendations for the specific patient should be available in the database as well, or the age- and sex-specific values from the literature can be used instead. Figure 8. shows the fuzzy sets generated based on the measurements and medical recommendations for the above case study.
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bognár, F.; Benedek, P. A Novel Risk Assessment Methodology—A Case Study of the PRISM Methodology in a Compliance Management Sensitive Sector. Acta Polytech. Hung. 2021, 18, 89–108. [Google Scholar] [CrossRef]
- Tóth-Laufer, E.; Takács, M.; Rudas, I.J. Fuzzy Logic-based Risk Assessment Framework to Evaluate Physiological Parameters. Acta Polytech. Hung. 2015, 12, 159–178. [Google Scholar]
- Portik, T.; Pokorádi, L. The summarized weighted mean of maxima defuzzification and its application at the end of the risk assessment process. Acta Polytech. Hung. 2014, 11, 167–180. [Google Scholar]
- Schmucker, K.J. Fuzzy Sets, Natural Language Computations and Risk Analysis; Computer Science Press: Rockville, MD, USA, 1984. [Google Scholar]
- Chen, S.J.; Chen, S.M. Fuzzy risk analysis based on similarity measures of generalized fuzzy numbers. IEEE Trans. Fuzzy Syst. 2003, 11, 45–56. [Google Scholar] [CrossRef]
- Chen, S.-J.; Chen, S.-M. Fuzzy risk analysis based on measures of similarity between interval-valued fuzzy numbers. Comput. Math. Appl. 2008, 55, 1670–1685. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Shang, S.; Qian, W.; Shu, W. A method for fuzzy risk analysis based on the new similarity of trapezoidal fuzzy numbers. Expert Syst. Appl. 2010, 37, 1920–1927. [Google Scholar] [CrossRef]
- Khorshidi, H.A.; Nikfalazar, S. An improved similarity measure for generalized fuzzy numbers and its application to fuzzy risk analysis. Appl. Soft Comput. 2017, 52, 478–486. [Google Scholar] [CrossRef]
- Chutia, R.; Gogoi, M.K. Fuzzy risk analysis in poultry farming using a new similarity measure on generalized fuzzy numbers. Comput. Ind. Eng. 2018, 115, 543–558. [Google Scholar] [CrossRef]
- Gogoi, M.K.; Chutia, R. Similarity measure of the interval-valued fuzzy numbers and its application in risk analysis in paddy cultivation. J. Ambient Intell. Humaniz. Comput. 2021, 1–24. [Google Scholar] [CrossRef]
- Gogoi, M.K.; Chutia, R. Fuzzy risk analysis based on a similarity measure of fuzzy numbers and its application in crop selection. Eng. Appl. Artif. Intell. 2022, 107, 104517. [Google Scholar] [CrossRef]
- Batyrshin, I. Constructing time series shape association measures: Minkowski distance and data standardization. In Proceedings of the 1st BRICS Countries Congress on Computational Intelligence, BRICS-CCI 2013, Porto de Galinhas, Brasil, 8–11 September 2013; IEEE Computer Society Order Number E3194; BMS Part Number CFP1364W-ART. IEEE Computer Society, GPS: Washington, DA, USA, 2013; pp. 204–212. [Google Scholar]
- Batyrshin, I. Association measures and aggregation functions. In Advances in Soft Computing and Its Applications; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8266, pp. 194–203. [Google Scholar]
- Batyrshin, I.Z. On definition and construction of association measures. J. Intell. Fuzzy Syst. 2015, 29, 2319–2326. [Google Scholar] [CrossRef] [Green Version]
- Batyrshin, I.Z. Association measures on [0,1]. J. Intell. Fuzzy Syst. 2015, 29, 1011–1020. [Google Scholar] [CrossRef]
- Batyrshin, I. Association measures on sets with involution and similarity measure. In Recent Developments and New Direction in Soft-Computing Foundations and Applications; Springer International Publishing: Cham, Switzerland, 2016; pp. 221–237. [Google Scholar]
- Batyrshin, I.Z. Data Science: Similarity, Dissimilarity and Correlation Functions. In Artificial Intelligence; Osipov, G.S., Panov, A.I., Yakovlev, K.S., Eds.; LNAI 11866; Springer: Berlin/Heidelberg, Germany, 2019; pp. 13–28. [Google Scholar]
- Batyrshin, I. Towards a general theory of similarity and association measures: Similarity, dissimilarity and correlation functions. J. Intell. Fuzzy Syst. 2019, 36, 2977–3004. [Google Scholar] [CrossRef]
- Batyrshin, I.Z. Constructing correlation coefficients from similarity and dissimilarity functions. Acta Polytech. Hung. 2019, 16, 191–204. [Google Scholar] [CrossRef]
- Yule, G.U. On the association of attributes in statistics: With illustrations from the material of the childhood society, &c. Philos. Trans. R. Soc. Lond. Ser. A 1900, 194, 257–319. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Griffin: London, UK, 1970. [Google Scholar]
- Liebetrau, A.M. Measures of Association; Sage Publications: Thousand Oaks, IA, USA, 1983. [Google Scholar]
- Gibbons, J.D. Nonparametric Measures of Association; Sage Publications: Thousand Oaks, IA, USA, 1993. [Google Scholar]
- Chen, P.Y.; Popovich, P.M. Correlation: Parametric and Nonparametric Measures; Sage: Thousand Oaks, CA, USA, 2002. [Google Scholar]
- Gibbons, J.D.; Chakraborti, S. Nonparametric Statistical Inference, 4th ed.; Dekker: New York, NY, USA, 2003. [Google Scholar]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Geng, L.; Hamilton, H.J. Interestingness measures for data mining: A survey. ACM Comput. Surv. (CSUR) 2006, 38, 1–32. [Google Scholar] [CrossRef]
- Tan, P.N.; Kumar, V.; Srivastava, J. Selecting the right interestingness measure for association patterns. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 32–41. [Google Scholar]
- Tóth-Laufer, E.; Nagy, I. Effect of the Different Membership Function Fitting Methods in Personalized Risk Calculation. In Proceedings of the 22nd IEEE International Conference on Intelligent Engineering Systems 2018 (INES 2018), Las Palmas de Gran Canaria, Spain, 21–23 June 2018; pp. 127–132. [Google Scholar]
- Han, J.; Kamber, M. Data mining: Concepts and techniques, 2nd ed.; Morgan Kaufmann: Amsterdam, The Netherlands, 2006. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batyrshin, I.Z.; Tóth-Laufer, E. Bipolar Dissimilarity and Similarity Correlations of Numbers. Mathematics 2022, 10, 797. https://doi.org/10.3390/math10050797
Batyrshin IZ, Tóth-Laufer E. Bipolar Dissimilarity and Similarity Correlations of Numbers. Mathematics. 2022; 10(5):797. https://doi.org/10.3390/math10050797
Chicago/Turabian StyleBatyrshin, Ildar Z., and Edit Tóth-Laufer. 2022. "Bipolar Dissimilarity and Similarity Correlations of Numbers" Mathematics 10, no. 5: 797. https://doi.org/10.3390/math10050797
APA StyleBatyrshin, I. Z., & Tóth-Laufer, E. (2022). Bipolar Dissimilarity and Similarity Correlations of Numbers. Mathematics, 10(5), 797. https://doi.org/10.3390/math10050797





