Theoretical Study on Non-Improvement of the Multi-Frequency Direct Sampling Method in Inverse Scattering Problems
Abstract
:1. Introduction
2. Two-Dimensional Direct Scattering Problem and the Indicator Function of OSM
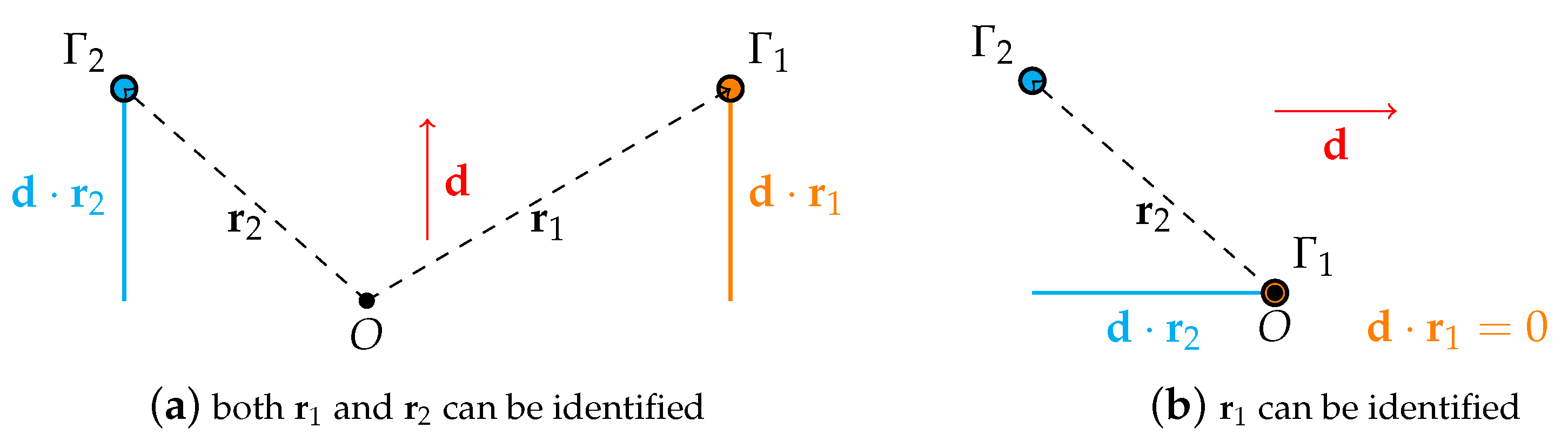
3. Theoretical Reason behind the Non-Improvement of the Multi-Frequency Imaging
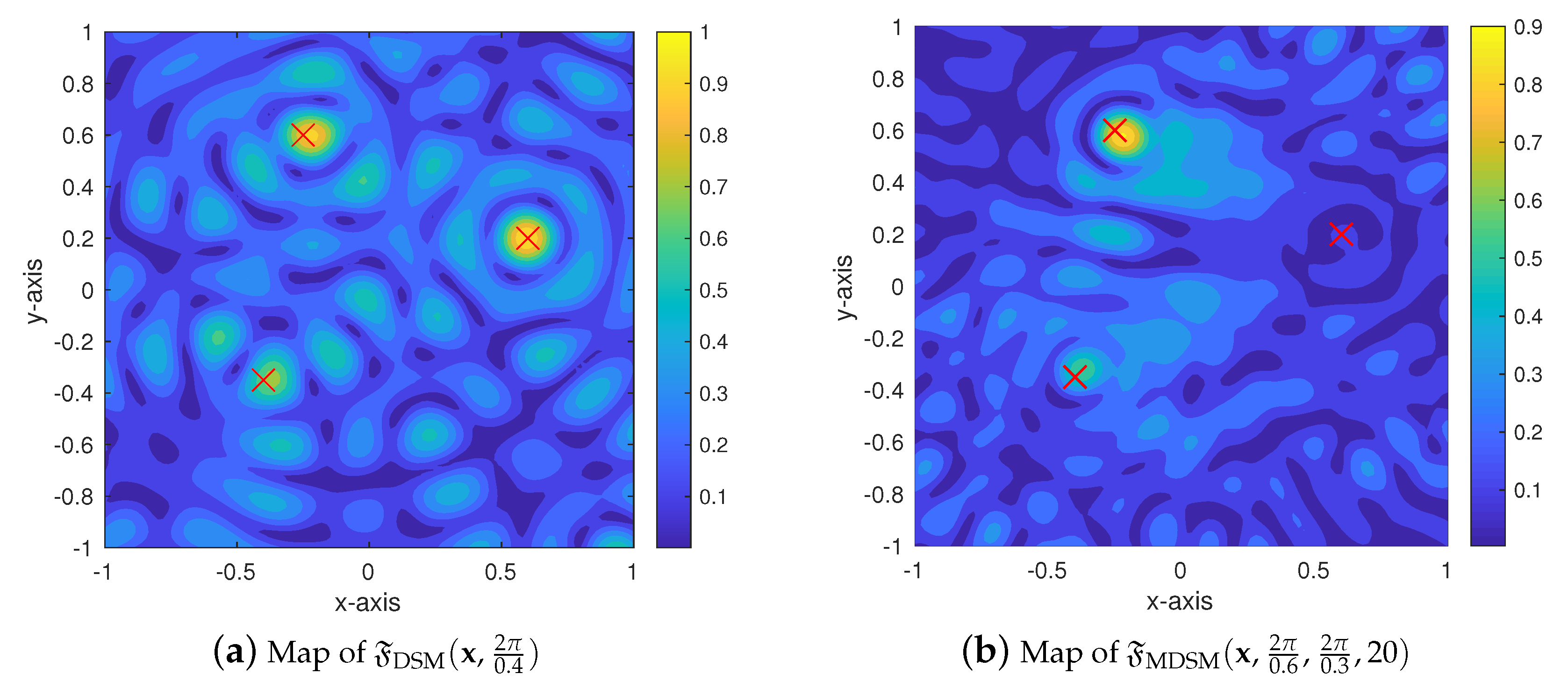
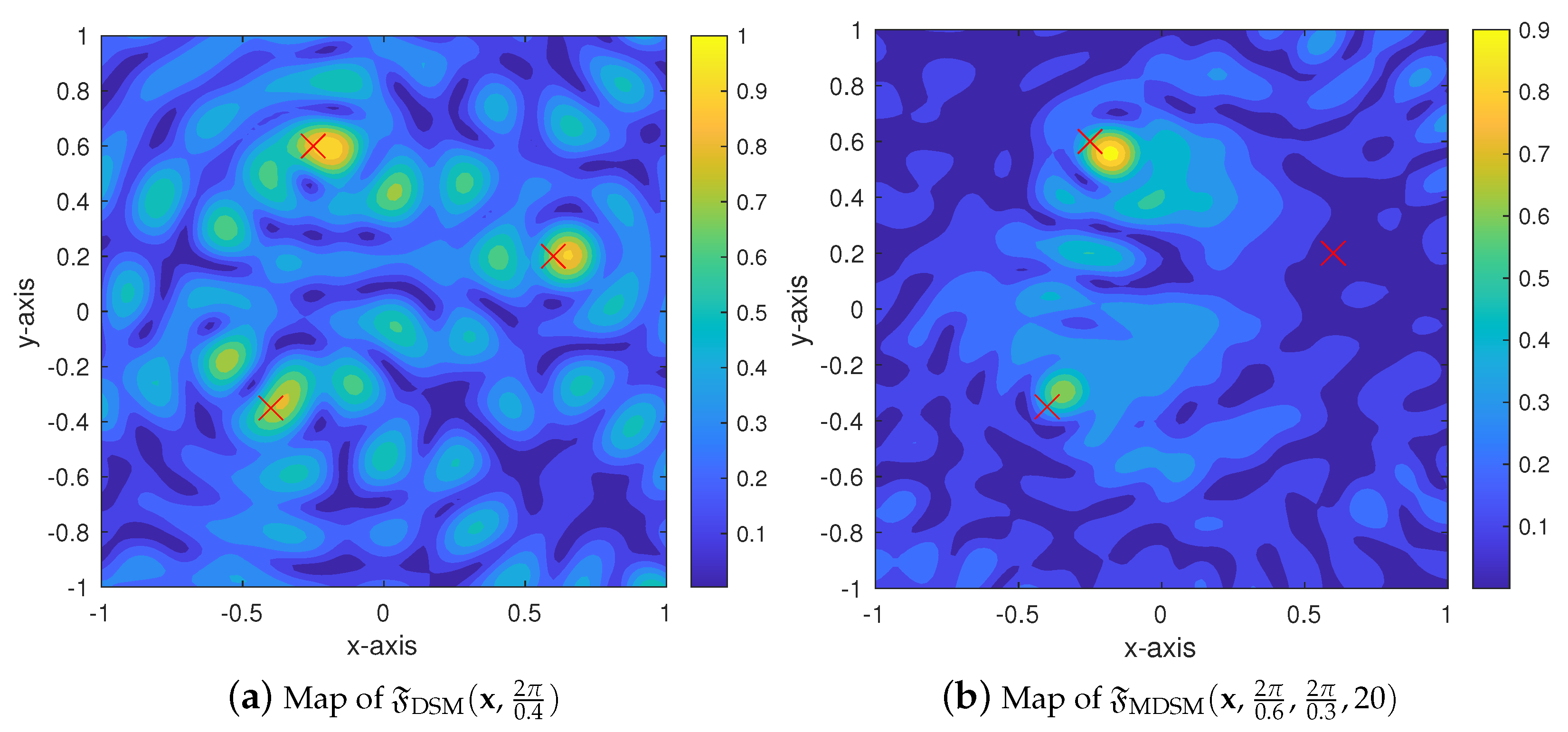
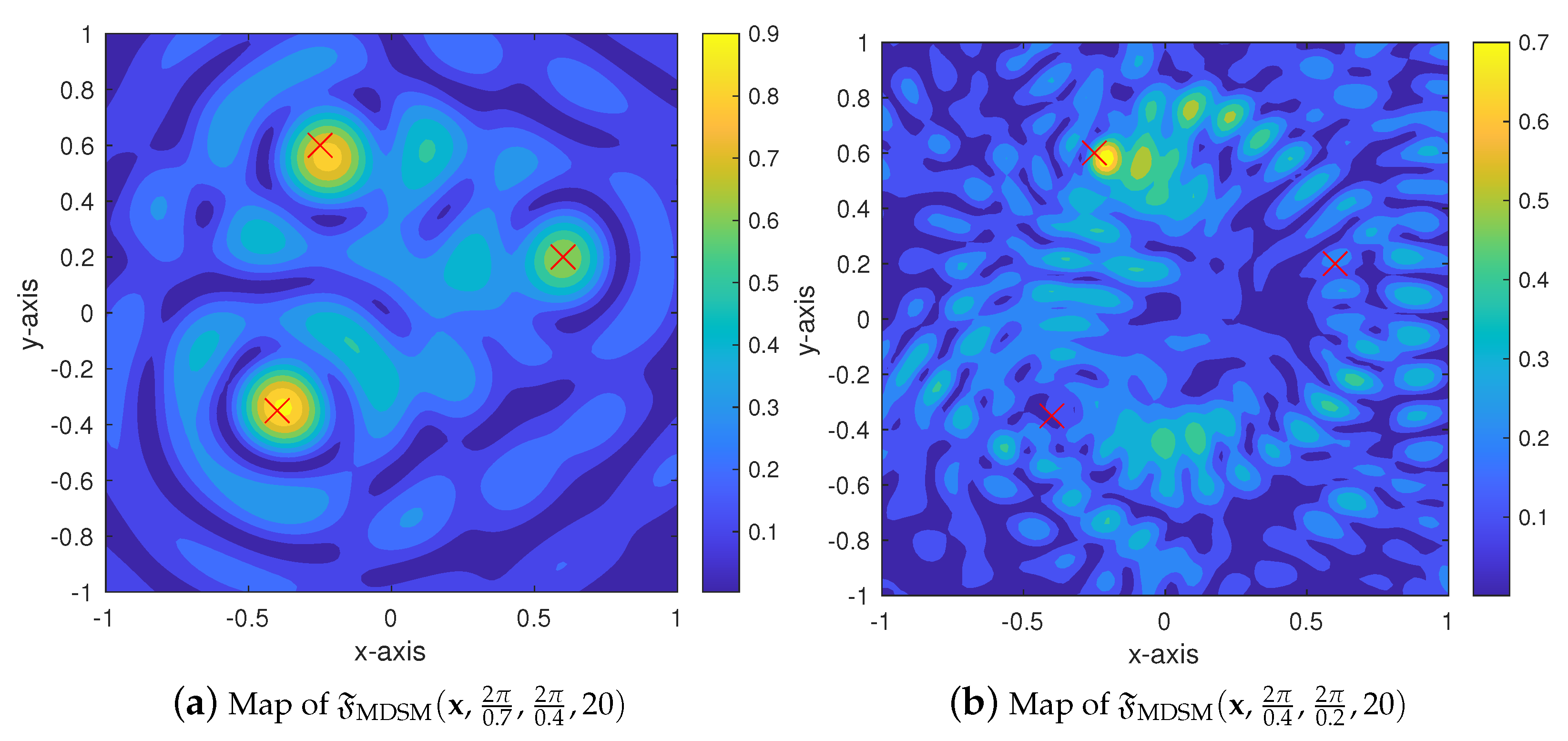
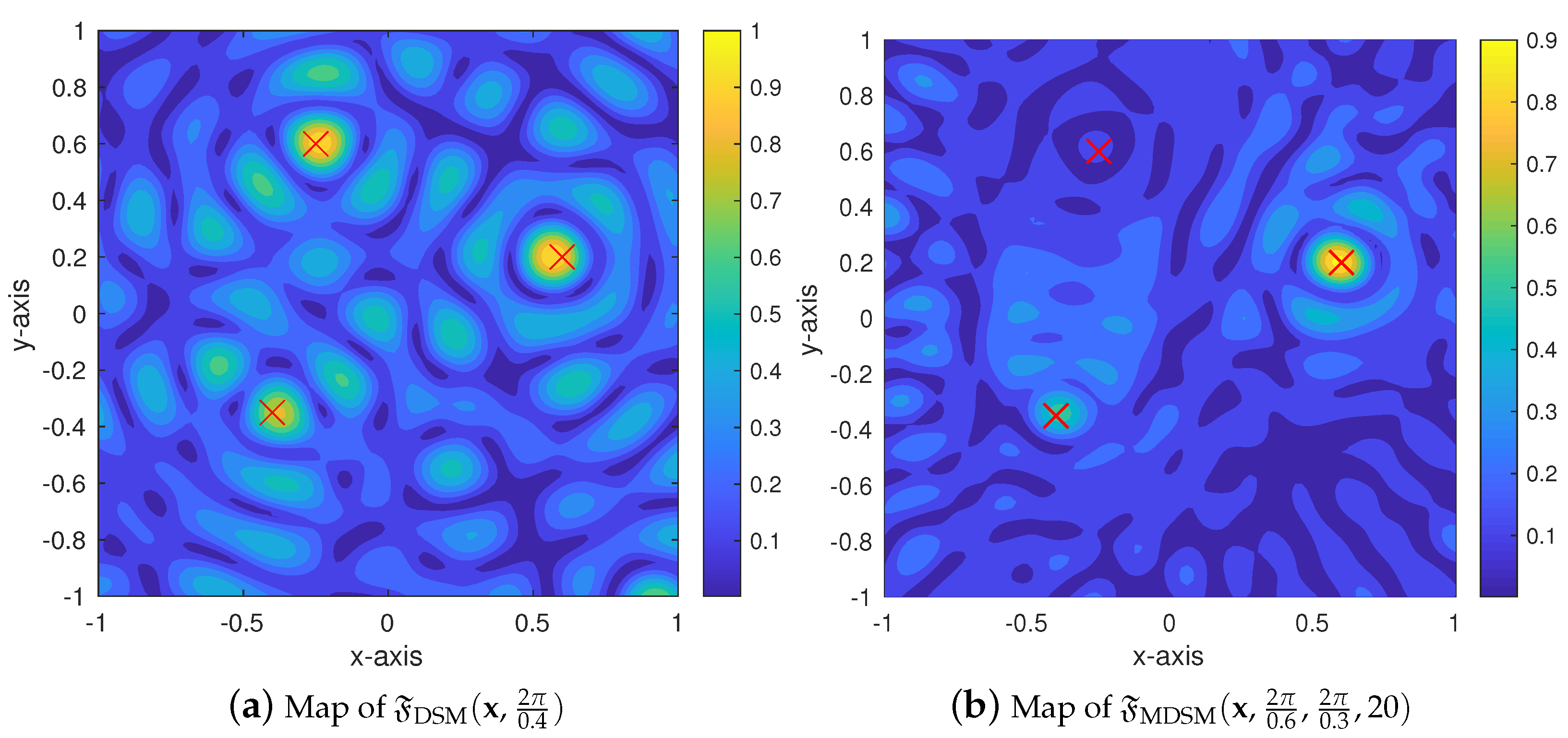
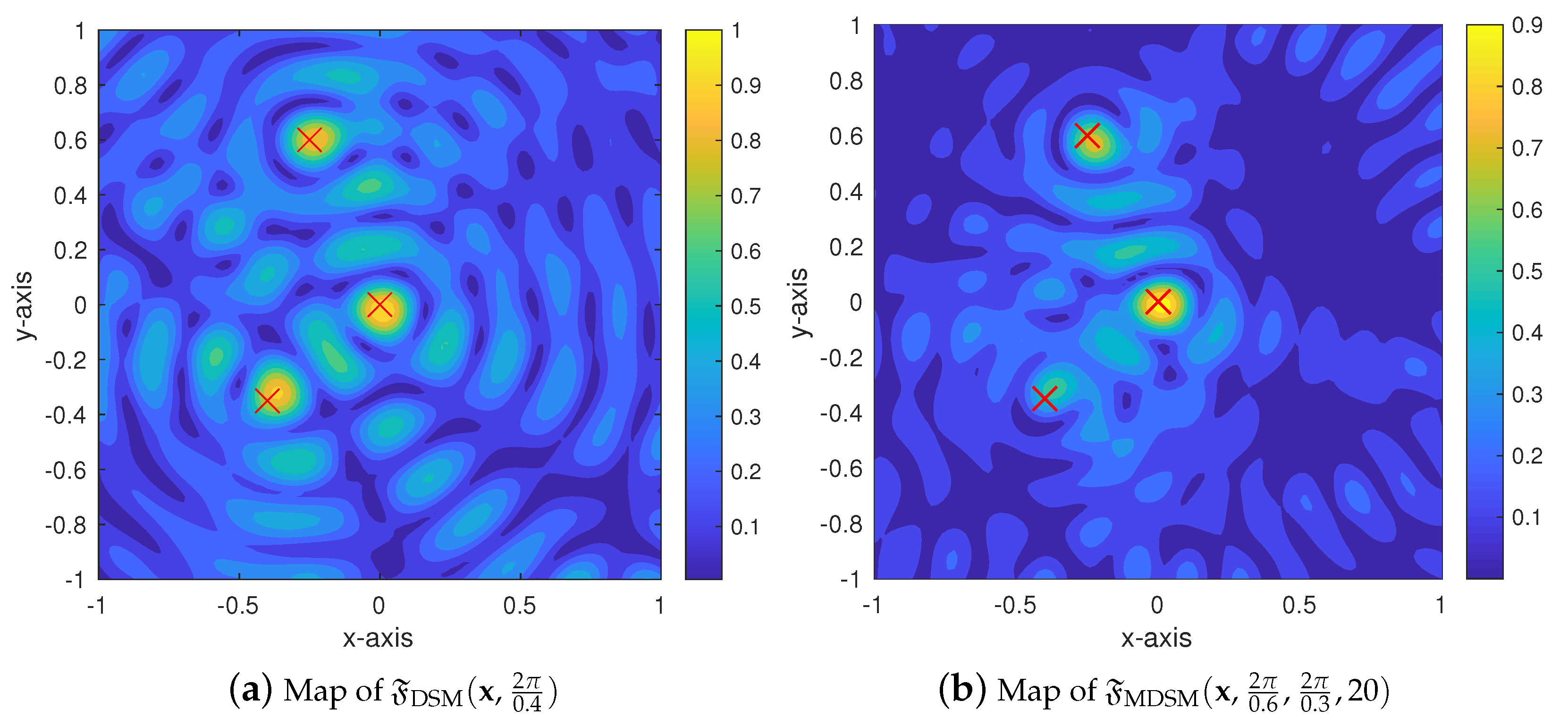
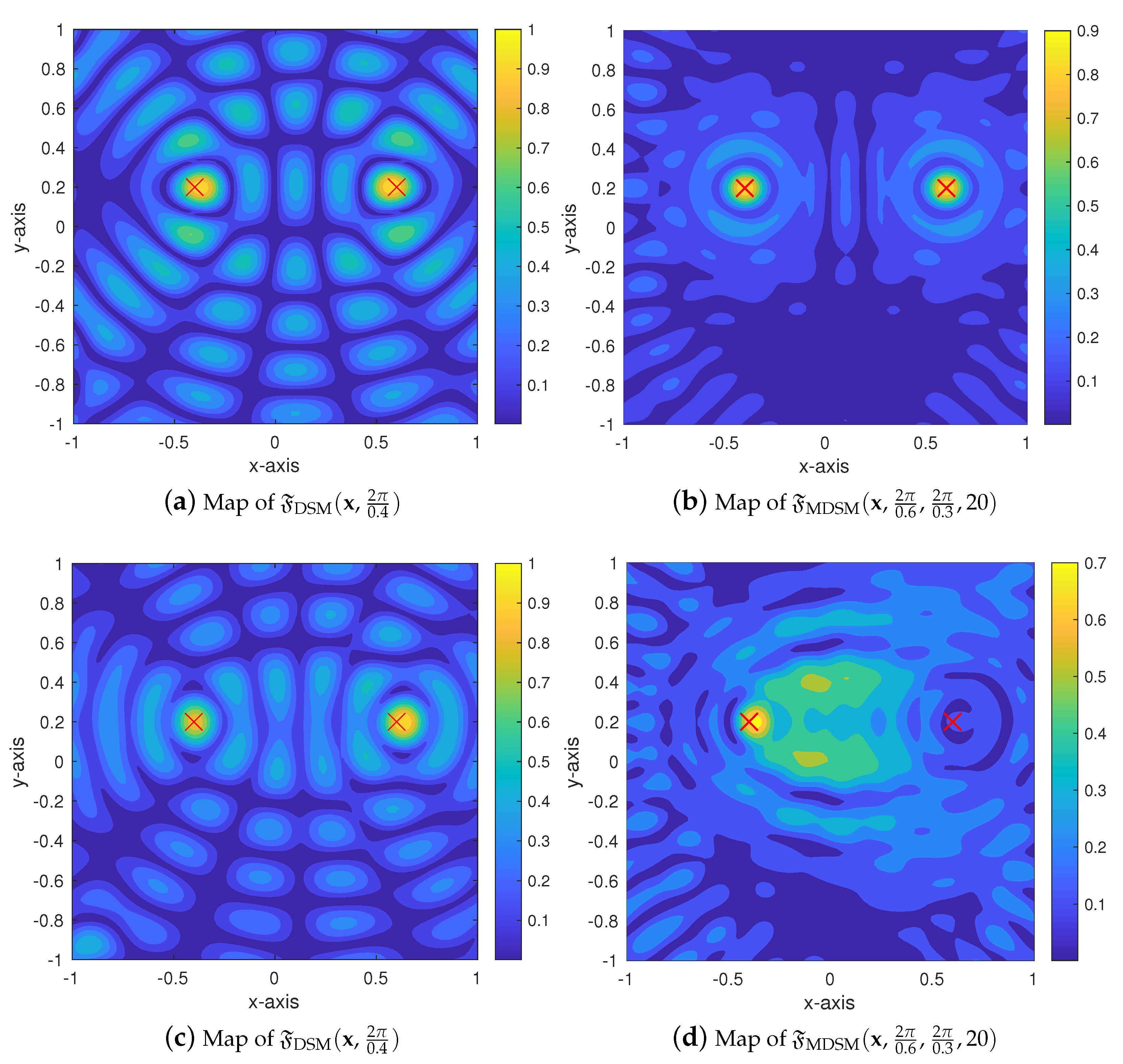
4. Simulation Results and Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ito, K.; Jin, B.; Zou, J. A direct sampling method to an inverse medium scattering problem. Inverse Prob. 2012, 28, 025003. [Google Scholar] [CrossRef]
- Ito, K.; Jin, B.; Zou, J. A direct sampling method for inverse electromagnetic medium scattering. Inverse Prob. 2013, 29, 095018. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Zou, J. A direct sampling method for inverse scattering using far-field data. Inverse Probl. Imag. 2013, 7, 757–775. [Google Scholar] [CrossRef]
- Kang, S.; Lambert, M.; Park, W.K. Direct sampling method for imaging small dielectric inhomogeneities: Analysis and improvement. Inverse Prob. 2018, 34, 095005. [Google Scholar] [CrossRef] [Green Version]
- Kang, S.; Lambert, M. Structure analysis of direct sampling method in 3D electromagnetic inverse problem: Near- and far-field configuration. Inverse Prob. 2021, 37, 075002. [Google Scholar] [CrossRef]
- Chow, Y.T.; Ito, K.; Zou, J. A direct sampling method for electrical impedance tomography. Inverse Prob. 2014, 30, 095003. [Google Scholar] [CrossRef] [Green Version]
- Chow, Y.T.; Ito, K.; Liu, K.; Zou, J. Direct sampling method for diffusive optical tomography. SIAM J. Sci. Comput. 2015, 37, A1658–A1684. [Google Scholar] [CrossRef]
- Kang, S.; Lambert, M.; Park, W.K. Analysis and improvement of direct sampling method in the mono-static configuration. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1721–1725. [Google Scholar] [CrossRef]
- Liu, K.; Xu, Y.; Zou, J. A multilevel sampling method for detecting sources in a stratified ocean waveguide. J. Comput. Appl. Math. 2017, 309, 95–110. [Google Scholar] [CrossRef] [Green Version]
- Liu, K. A simple method for detecting scatterers in a stratified ocean waveguide. Comput. Math. Appl. 2018, 76, 1791–1802. [Google Scholar] [CrossRef]
- Park, W.K. Direct sampling method for retrieving small perfectly conducting cracks. J. Comput. Phys. 2018, 373, 648–661. [Google Scholar] [CrossRef] [Green Version]
- Ahn, C.Y.; Ha, T.; Park, W.K. Direct sampling method for identifying magnetic inhomogeneities in limited-aperture inverse scattering problem. Comput. Math. Appl. 2020, 80, 2811–2829. [Google Scholar] [CrossRef]
- Park, W.K. Direct sampling method for anomaly imaging from scattering parameter. Appl. Math. Lett. 2018, 81, 63–71. [Google Scholar] [CrossRef] [Green Version]
- Ji, X.; Liu, X.; Zhang, B. Phaseless inverse source scattering problem: Phase retrieval, uniqueness and direct sampling methods. J. Comput. Phys. X 2019, 1, 100003. [Google Scholar] [CrossRef]
- Son, S.H.; Lee, K.J.; Park, W.K. Application and analysis of direct sampling method in real-world microwave imaging. Appl. Math. Lett. 2019, 96, 47–53. [Google Scholar] [CrossRef] [Green Version]
- Liu, K. Two effective post-filtering strategies for improving direct sampling methods. Appl. Anal. 2017, 96, 502–515. [Google Scholar] [CrossRef]
- Harris, I.; Nguyen, D.L. Orthogonality sampling method for the electromagnetic inverse scattering problem. SIAM J. Sci. Comput. 2020, 42, B722–B737. [Google Scholar] [CrossRef]
- Ammari, H.; Garnier, J.; Kang, H.; Park, W.K.; Sølna, K. Imaging schemes for perfectly conducting cracks. SIAM J. Appl. Math. 2011, 71, 68–91. [Google Scholar] [CrossRef] [Green Version]
- Park, W.K. Multi-frequency subspace migration for imaging of perfectly conducting, arc-like cracks in full- and limited-view inverse scattering problems. J. Comput. Phys. 2015, 283, 52–80. [Google Scholar] [CrossRef] [Green Version]
- Alqadah, H.F.; Valdivia, N. A frequency based constraint for a multi-frequency linear sampling method. Inverse Prob. 2013, 29, 095019. [Google Scholar] [CrossRef]
- Guzina, B.; Cakoni, F.; Bellis, C. On the multi-frequency obstacle reconstruction via the linear sampling method. Inverse Prob. 2010, 26, 125005. [Google Scholar] [CrossRef] [Green Version]
- Funes, J.F.; Perales, J.M.; Rapún, M.L.; Vega, J.M. Defect detection from multi-frequency limited data via topological sensitivity. J. Math. Imaging Vis. 2016, 55, 19–35. [Google Scholar] [CrossRef]
- Park, W.K. Performance analysis of multi-frequency topological derivative for reconstructing perfectly conducting cracks. J. Comput. Phys. 2017, 335, 865–884. [Google Scholar] [CrossRef] [Green Version]
- Moscoso, M.; Novikov, A.; Papanicolaou, G.; Tsogka, C. Robust multifrequency imaging with MUSIC. Inverse Prob. 2018, 35, 015007. [Google Scholar] [CrossRef] [Green Version]
- Solimene, R.; Ruvio, G.; Dell’Aversano, A.; Cuccaro, A.; Ammann, M.J.; Pierri, R. Detecting point-like sources of unknown frequency spectra. Prog. Electromagn. Res. B 2013, 50, 347–364. [Google Scholar] [CrossRef] [Green Version]
- Park, W.K. Negative result of multi-frequency direct sampling method in microwave imaging. Results Phys. 2019, 12, 859–860. [Google Scholar] [CrossRef]
- Potthast, R. A study on orthogonality sampling. Inverse Prob. 2010, 26, 074015. [Google Scholar] [CrossRef]
- Alzaalig, A.; Hu, G.; Liu, X.; Sun, J. Fast acoustic source imaging using multi-frequency sparse data. Inverse Prob. 2020, 36, 025009. [Google Scholar] [CrossRef] [Green Version]
- Arens, T.; Ji, X.; Liu, X. Inverse electromagnetic obstacle scattering problems with multi-frequency sparse backscattering far field data. Inverse Prob. 2020, 36, 105007. [Google Scholar] [CrossRef]
- Kang, S.; Lambert, M.; Ahn, C.Y.; Ha, T.; Park, W.K. Single- and multi-frequency direct sampling methods in limited-aperture inverse scattering problem. IEEE Access 2020, 8, 121637–121649. [Google Scholar] [CrossRef]
- Kress, R. Inverse scattering from an open arc. Math. Meth. Appl. Sci. 1995, 18, 267–293. [Google Scholar] [CrossRef]
- Ammari, H.; Kang, H.; Lee, H.; Park, W.K. Asymptotic imaging of perfectly conducting cracks. SIAM J. Sci. Comput. 2010, 32, 894–922. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions, with Formulas, Graphs, and Mathematical Tables; Dover: New York, NY, USA, 1996. [Google Scholar]
- Nazarchuk, Z.T. Singular Integral Equations in Diffraction Theory; Mathematics and Applications Series; Karpenko Physicomechanical Institute, Ukrainian Academy of Sciences: Lviv, Ukraine, 1994.



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, W.-K. Theoretical Study on Non-Improvement of the Multi-Frequency Direct Sampling Method in Inverse Scattering Problems. Mathematics 2022, 10, 1674. https://doi.org/10.3390/math10101674
Park W-K. Theoretical Study on Non-Improvement of the Multi-Frequency Direct Sampling Method in Inverse Scattering Problems. Mathematics. 2022; 10(10):1674. https://doi.org/10.3390/math10101674
Chicago/Turabian StylePark, Won-Kwang. 2022. "Theoretical Study on Non-Improvement of the Multi-Frequency Direct Sampling Method in Inverse Scattering Problems" Mathematics 10, no. 10: 1674. https://doi.org/10.3390/math10101674
APA StylePark, W.-K. (2022). Theoretical Study on Non-Improvement of the Multi-Frequency Direct Sampling Method in Inverse Scattering Problems. Mathematics, 10(10), 1674. https://doi.org/10.3390/math10101674




