Operator Calculus Approach to Comparison of Elasticity Models for Modelling of Masonry Structures

Abstract

The solution of any engineering problem starts with a modelling process aimed at formulating a mathematical model, which must describe the problem under consideration with sufficient precision. Because of heterogeneity of modern engineering applications, mathematical modelling scatters nowadays from incredibly precise micro- and even nano-modelling of materials to macro-modelling, which is more appropriate for practical engineering computations. In the field of masonry structures, a macro-model of the material can be constructed based on various elasticity theories, such as classical elasticity, micropolar elasticity and Cosserat elasticity. Evidently, a different macro-behaviour is expected depending on the specific theory used in the background. Although there have been several theoretical studies of different elasticity theories in recent years, there is still a lack of understanding of how modelling assumptions of different elasticity theories influence the modelling results of masonry structures. Therefore, a rigorous approach to comparison of different three-dimensional elasticity models based on quaternionic operator calculus is proposed in this paper. In this way, three elasticity models are described and spatial boundary value problems for these models are discussed. In particular, explicit representation formulae for their solutions are constructed. After that, by using these representation formulae, explicit estimates for the solutions obtained by different elasticity theories are obtained. Finally, several numerical examples are presented, which indicate a practical difference in the solutions.

1. Introduction

The classical linear elasticity provides a description of material behaviour, which is sufficiently accurate for many practical applications. Nonetheless, while modelling such materials, as for example cellular material, fibers and human bones, a more accurate material model describing not only displacement, as in the case of classical elasticity, but also rotations, is required. One the first extension of the classical elasticity towards accounting microeffects of a continuum is related to the so called Cosserat continuum, introduced by Cosserat brothers [1]. After that, several further refinements of the this theory have been proposed by several researchers; see, for example, works of A.C. Eringen [2], and W. Nowacki [3]. After introduction of micro-inertia to the theory of Cosserat brothers, a new theory called the micropolar elasticity has been formed. From the macromodelling point of view, the micropolar elasticity can be used for modelling of masonry structures and objects having similar cellular-like structure.

Modelling of masonry structures in practical engineering is typically empirical-based, i.e., performed by help of empirical formulae and results of experiments. Therefore, the mechanical behaviour of a masonry material is often predicted by simple empirical equations containing basic parameters such as elasticity, compressive, and tensile strengths [4]. Although empirical-based models serve often as a basis for engineering norms, a proper modelling and understanding of material behaviour of masonry structure requires advanced models from continuum mechanics, i.e., theoretical models. Several results related to microscale and mesoscale theoretical models of masonry structures have been presented in recent years [5,6]; see [7] for a comprehensive review of various modelling strategies for masonry structures. From the theoretical point of view, material behaviour can be generally modelled either by help of linear elastic models, or by help of anisotropic models. Although anisotropic models provide a more accurate material description, their use in engineering practice is limited due to high complexity of these models. However, even in the case of linear elastic models, more refined theories of elasticity, such as Cosserat and micropolar theories, are able to account for more complex material behaviour. Nonetheless, practical use of these theories, especially constructing engineering macro-models on their basis, requires a proper theoretical comparison of the elasticity theories for providing a clear guidance on advantages and disadvantages of each theory, which is still lacking. Thus, this paper aims at a formal theoretical comparison on three elasticity models.

Although one of the aims of this paper is performing a formal theoretical comparison of elasticity models, it is important to mention that theoretical models are rarely used in practical engineering, but rather macro-models derived based on theoretical models are more valuable for engineering; see, for example, Refs. [8,9]. Therefore, after performing the a rigorous model comparison by help of quaternionic operator calculus, we discuss several macro-models for Cosserat and micropolar models. These macro-models are based on “simplified”material parameters of Cosserat and micropolar models, which can be easily calculated in engineering practice. The need for such macro-models comes not only from an easier use in engineering practice, but also from the fact, that identifying material constants of Cosserat and micropolar models is not a trivial task; see [10,11] for details.

The paper is organised as follows: Section 2 provides a brief presentation of models of linear elasticity, Cosserat elasticity and micropolar elasticity; Section 3 presents a formal approach to model comparison, which is based on abstract mathematics and relational algebra; finally, Section 4 provides ideas on creating macro-models for using in engineering applications, as well as numerical comparison of various models discussed in this paper.

2. Elasticity Models

In this section, the elasticity models which will be compared in the sequel are shortly summarized. As it is well known, there are several ways for presenting an elasticity model, for example by help of a tensor notation or by help of vectors and matrices. Moreover, very often formulations in terms of secondary variables, such as for example stresses, is preferred over the formulation in terms of primary variables. Evidently, for an objective comparison of models it is necessary to keep a unique style of model formulations. Therefore, all the models presented in this section will follow one style of presentation, which might be different from the original papers and books, where these models were introduced.

2.1. Classical Linear Elasticity

The classical model of linear elasticity is based on the set of three equations; see, for example, Refs. [12,13]:

(i)

Constitutive

$${\sigma }_{ij}=\lambda {\delta }_{ij}{\epsilon }_{kk}+2\mu {\epsilon }_{ij},i,j,k=1,2,3,$$

where ${\sigma }_{ij}$ are components of the stress tensor, ${\epsilon }_{kk}$ is a volumetric strain, ${\epsilon }_{ij}$ are components of the eulerian strain tensor, $\lambda$ and $\mu$ are Lamé coefficients.

(ii)

Strain-displacement relation

$$\epsilon =\frac{1}{2}(\nabla \mathbf{u}+\nabla {\mathbf{u}}^T),$$

where $\mathbf{u}\in {\mathbb{R}}^3$ is the displacement vector.

(iii)

Equilibrium equation

$$\nabla ·\sigma +\rho \mathbf{F}=\rho \ddot{\mathbf{u}},$$

where $\sigma$ is the stress tensor, $\mathbf{F}\in {\mathbb{R}}^3$ is the density of external forces, and $\rho$ is the material density.

By rewriting the equilibrium equation with respect to the displacement vector $\mathbf{u}$, the famous Lamé equation in the static case and absence of body forces is obtained:

$$\mu \Delta \mathbf{u}+(\lambda +\mu )\nabla (\nabla ·\mathbf{u})=0.$$

Finally, let us formulate a complete boundary value problem for the classical linear elasticity:

Problem 1.

Let $\mathsf{\Omega }\subset {\mathbb{R}}^3$ be a bounded simply connected domain with a sufficiently smooth boundary $\mathsf{\Gamma }={\mathsf{\Gamma }}_0\cup {\mathsf{\Gamma }}_1$. A boundary value problem of the linear elasticity is formulated as follows

$$\left\{\begin{array}{c}{\displaystyle \mu \Delta \mathbf{u}+(\lambda +\mu )\nabla (\nabla ·\mathbf{u})=0,}\hfill \\ {\displaystyle \mathbf{u}=\mathbf{g} on {\mathsf{\Gamma }}_0,{\sigma }_{lk}{n}_l={\sigma }_{\left(\mathbf{n}\right)k} on {\mathsf{\Gamma }}_1.}\hfill \end{array}\right.$$

where$\mathbf{g}$is the vector of prescribed displacements on${\mathsf{\Gamma }}_0$,$n_j$are components of the unit outer normal vector,${\sigma }_{\left(\mathbf{n}\right)k}$are given surface forces.

2.2. Cosserat Theory of Elasticity

Following [14], the main equations of Cosserat elasticity are briefly recalled in this subsection. In addition to the displacement vector $\mathbf{u}$ of classical elasticity, Cosserat theory considers also the axial vector of the total rotation $\widehat{\mathit{\psi }}\in {\mathbb{R}}^3$ representing the rigid Cosserat triad. Basic equations of the Cosserat elasticity are given by the set of three equations:

(i)

Constitutive equations

$$\begin{array}{c}{\tau }_{ij}=\lambda {\delta }_{ij}{\epsilon }_{kk}+2\mu {\epsilon }_{ij},{\sigma }_{ij}=2\tau {\gamma }_{ij},\hfill \\ {\displaystyle {\widehat{\mu }}_{ij}=\frac{\alpha }{2}{\delta }_{ij}{\widehat{\kappa }}_{kk}+2\eta {\widehat{\kappa }}_{ij}+2{\eta }^{\prime }{\widehat{\kappa }}_{ji},}\hfill \end{array}$$

where ${\widehat{\mu }}_{ij}$ is the couple stress tensor, ${\widehat{\kappa }}_{ij}$ is the gradient of the total rotation, $\lambda$ and $\mu$ are the Lamé coefficients of classical elasticity, $\eta$, ${\eta }^{\prime }$ are moduli used in the couple stress theory; see [15] for details, $\tau$ denotes the modulus of local rotation, and $\alpha$ denotes the modulus of the volume flux of local rotation. It is important to mention, that the coefficients $\tau$ and $\alpha$ are specific parameters of the Cosserat theory. Additionally, the coefficients $\mu$ and $\tau$ have the same dimensions and thus allowing to introduce the coupling number N:

$$N:=\sqrt{\frac{\tau }{\mu +\tau }},0\le N\le 1.$$

N has the value 0 for classical elasticity and the value 1 for the couple stress theory.

(ii)

Strain-displacement relations. The main difference to the classical elasticity is that additionally to the usual strain tensor ${\epsilon }_{ij}$ and the usual rotation tensor ${\omega }_{ij}$, the relative rotation between the triad and the principal axes of strain is introduced as follows

$${\gamma }_{ij}={\omega }_{ij}-{\psi }_{ij}=-{\gamma }_{ji},$$

which is also represented by the axial vector

$${\widehat{\gamma }}_k=-{\widehat{\omega }}_k-{\widehat{\mathit{\psi }}}_k,\widehat{\gamma }=\frac{1}{2}\nabla \times \mathbf{u}-\widehat{\mathit{\psi }}.$$

(1)

(iii)

Equilibrium equations

$$\begin{array}{c}{\tau }_{ji,j}+{\sigma }_{ji,j}+f_i=0,\hfill \\ 2{\widehat{\mu }}_{ji,j}+2\widehat{{\sigma }_i}+{\widehat{c}}_i=0,\hfill \end{array}$$

where $f_i$ is the coordinate of the body force per unit volume, ${\widehat{c}}_i$ is the coordinate of the body couple per unit volume, ${\tau }_{ij}$ is the symmetric stress tensor, ${\sigma }_{ij}$ is the skew symmetric stress tensor, and ${\widehat{\mu }}_{ij}$ is the couple stress tensor, $\widehat{{\sigma }_i}$ = $\frac{1}{2}{e}_{ijk}{\sigma }_{jk}$, $e_{ijk}$ is the permutation tensor and the comma notation is used to indicate a differentiation with respect to the coordinates.

Next, we write the equilibrium equations of the Cosserat theory in the vector form as follows

$$\begin{array}{ccc}\hfill (\lambda +2\mu ){\nabla }^2\mathbf{u}-\mu \nabla \times (\nabla \times \mathbf{u})-2\tau \nabla \times \widehat{\gamma }+\mathbf{f}& =& 0,\hfill \\ \hfill (\alpha +4\eta +4{\eta }^{\prime }){\nabla }^2\widehat{\mathit{\psi }}-4\eta \nabla \times (\nabla \times \widehat{\mathit{\psi }})+4\tau \widehat{\gamma }+\widehat{\mathbf{c}}& =& 0,\hfill \end{array}$$

where $\mathbf{f}$ is the body force per unit volume, $\widehat{\mathbf{c}}$ is the body couple per unit volume and the vector identity

$${\nabla }^2\mathbf{v}=\nabla (\nabla ·\mathbf{v})-\nabla \times (\nabla \times \mathbf{v})$$

has been used. Next, by substituting (1) into the vector form, we obtain the system of equations with two unknowns

$$\begin{array}{ccc}\hfill (\lambda +2\mu )\nabla (\nabla ·\mathbf{u})-(\mu +\tau )\nabla \times (\nabla \times \mathbf{u})+2\tau \nabla \times \widehat{\mathit{\psi }}+\mathbf{f}& =& 0,\hfill \\ \hfill (\alpha +4\eta +4{\eta }^{\prime })\nabla (\nabla ·\widehat{\mathit{\psi }})-4\eta \nabla \times (\nabla \times \widehat{\mathit{\psi }})-4\tau \widehat{\mathit{\psi }}+2\tau \nabla \times \mathbf{u}+\widehat{\mathbf{c}}& =& 0,\hfill \end{array}$$

Finally, a complete boundary value problem is formulated for Cosserat elasticity:

Problem 2.

Let $\Omega \subset {\mathbb{R}}^3$ be a bounded simply connected domain with a sufficiently smooth boundary $\mathsf{\Gamma }={\mathsf{\Gamma }}_0\cup {\mathsf{\Gamma }}_1$. A boundary value problem of the Cosserat elasticity is formulated as follows

$$\left\{\begin{array}{c}{\displaystyle (\lambda +2\mu )\nabla (\nabla ·\mathbf{u})-(\mu +\tau )\nabla \times (\nabla \times \mathbf{u})+2\tau \nabla \times \widehat{\mathit{\psi }}+\mathbf{f}=0}\hfill \\ (\alpha +4\eta +4{\eta }^{\prime })\nabla (\nabla ·\widehat{\mathit{\psi }})-4\eta \nabla \times (\nabla \times \widehat{\mathit{\psi }})-4\tau \widehat{\mathit{\psi }}+2\tau \nabla \times \mathbf{u}+\widehat{\mathbf{c}}=0,\hfill \\ {\displaystyle \mathbf{u}={\mathbf{g}}_{\mathbf{1}} and \widehat{\mathit{\psi }}={\mathbf{q}}_{\mathbf{2}} on {\mathsf{\Gamma }}_0,}\hfill \\ {\displaystyle t_j=n_i{\tau }_{ij}+n_i{\sigma }_{ij} and {\widehat{m}}_j=n_i{\widehat{\mu }}_{ij} on {\mathsf{\Gamma }}_1,}\hfill \end{array}\right.$$

where$t_j$is the coordinate of the surface force per unit area,${\widehat{m}}_j$is the coordinate of the surface couple per unit area, and$n_i$is the coordinate of the exterior normal.

2.3. Micropolar Model

The Cosserat theory has been extended by including body microinertia effects by Eringen in [2] and therefore, the resulting theory has been named as micropolar theory. The basic equations of the micropolar theory are given by:

(i)

The constitutive equations for a linear micropolar continuum are given as follows [2,11]:

$$\begin{array}{ccc}\hfill {\displaystyle {\sigma }_{ji}}& =& {\displaystyle (\mu +\alpha ){\epsilon }_{ji}+(\mu -\alpha ){\epsilon }_{ij}+\lambda {\delta }_{ij}{\epsilon }_{kk},}\hfill \\ \hfill {\displaystyle {\mu }_{ji}}& =& {\displaystyle (\gamma +ϵ){\kappa }_{ji}+(\gamma -ϵ){\kappa }_{ij}+\beta {\delta }_{ij}{\kappa }_{kk},}\hfill \end{array}$$

where ${\mu }_{ji}$ is the couple stress, ${\sigma }_{ij}$ is the force stress tensor, ${\epsilon }_{ij}$ is the asymmetric tensor of deformation and ${\kappa }_{ij}$ is the torsion flexure tensor, and with $i,j,k=1,2,3$. The six micropolar elastic constants are $\lambda$, $\mu$, $\alpha$, $\beta$, $\gamma$ and $ϵ$.

(ii)

The strain-displacement relations are given by [3]:

$${\epsilon }_{ji}=u_{i,j}-e_{kij}{\phi }_k,{\kappa }_{ji}={\phi }_{i,j},\mathit{\phi }=\frac{1}{2}\nabla \times \mathbf{u}$$

where $u_i$ is the displacement coordinate.

(iii)

Equilibrium equations are given as follows [3]:

$$\begin{array}{c}{\sigma }_{ji,j}+f_i=0,\hfill \\ e_{ijk}{\sigma }_{jk}+{\mu }_{ji,j}+c_i=0,\hfill \end{array}$$

where ${\phi }_i$ is the coordinate of the rotation vector, $f_i$ is the coordinate of the body force per unit volume, $c_i$ is the coordinate of the body couple per unit volume, $\rho$ is the density, $\varrho$ is the rotational inertia and $e_{ijk}$ is the permutation symbol.

Substituting the constitutive equation into the equilibrium equation and defining the deformations, lead to a system of six differential equations; see again [3]. In a compact vector form, these equations have the following form:

$$\begin{array}{c}\hfill (\mu +\lambda )\Delta \mathbf{u}+(\lambda +\mu -\alpha )\nabla (\nabla ·\mathbf{u})+2\alpha \nabla \times \mathit{\phi }+\mathbf{f}=0,\\ \hfill \left(\right(\mu +ϵ)\Delta -4\alpha )\mathit{\phi }+(\beta +\gamma -ϵ)\nabla (\nabla ·\mathit{\phi })+2\alpha \nabla \times \mathbf{u}+\mathbf{c}=0,\end{array}$$

where $\mathbf{f}\in {\mathbb{R}}^3$ is the body forces, $\mathbf{c}\in {\mathbb{R}}^3$ is the body moments, $\mathbf{u}\in {\mathbb{R}}^3$ and $\mathit{\phi }\in {\mathbb{R}}^3$ represents the deformation and rotation of a particle, respectively.

Finally, a complete boundary value problem of the micropolar elasticity is formulated as follows:

Problem 3.

Let $\Omega \subset {\mathbb{R}}^3$ be a bounded simply connected domain with a sufficiently smooth boundary $\mathsf{\Gamma }={\mathsf{\Gamma }}_0\cup {\mathsf{\Gamma }}_1$. A boundary value problem of the Cosserat elasticity is formulated as follows

$$\left\{\begin{array}{c}{\displaystyle (\mu +\lambda )\Delta \mathbf{u}+(\lambda +\mu -\alpha )\nabla (\nabla ·\mathbf{u})+2\alpha \nabla \times \mathit{\phi }+\mathbf{f}=0,}\hfill \\ {\displaystyle (\mu +ϵ)\Delta \mathit{\phi }+(\beta +\gamma -ϵ)\nabla (\nabla ·\mathit{\phi })-4\alpha \mathit{\phi }+2\alpha \nabla \times \mathbf{u}+\mathbf{c}=0,}\hfill \\ {\displaystyle \mathbf{u}={\mathbf{g}}_1 and \mathit{\phi }={\mathbf{g}}_2 on {\mathsf{\Gamma }}_0,}\hfill \\ {\displaystyle t_j=n_i{\sigma }_{ij}+n_i{\tau }_{ij} and l_j=n_i{\mu }_{ij} on {\mathsf{\Gamma }}_1,}\hfill \end{array}\right.$$

where$t_j$is the coordinate of the surface force per unit area,${\tau }_{ij}$is the skew symmetric force stress tensor,$l_j$is the coordinate of the surface couple per unit area, and$n_i$is the coordinate of the exterior normal.

3. Theoretical Model Comparison

The aim of this section is to provide a theoretical basis for a quantifiable comparison of elasticity models introduced in the previous section. Especially, it is important to develop estimates for a “distance” between the models, which will provide the difference between the models not only in general terms as the difference in physical phenomena the models describe, but in terms of specific estimates as well. Moreover, once such estimates are developed, they might be used in practical calculations for simplifying the decision process on choosing a specific model in a concrete situation. Evidently, constructing of such “distance” estimates requires the same theoretical basis for all the models.

In this paper, quaternionic operator calculus is used as a basis for comparative analysis of elasticity models. The choice of quaternionic operator calculus is motivated by the elegance of representation formulae for solutions constructed by help of the well-known operators, which simplifies significantly theoretical analysis of models. Additionally, since quaternionic analysis is a generalisation of the classical complex analysis to ${\mathbb{R}}^3$ and ${\mathbb{R}}^4$, the results for two-dimensional problems are automatically embedded in the construction. Moreover, quaternionic operator calculus has been already used for studying problems of classical elasticity [16], as well as for problems of micropolar elasticity [17]. Finally, in [17] the “distance” estimate for the difference between the micropolar and classical elasticity has been provided, meaning that only representation formulae for the Cosserat theory and related estimates must still be constructed.

3.1. Basics of Quaternionic Analysis

In this subsection, following [16,18], the basics of quaternionic analysis is briefly recalled. Let $1,{\mathbf{e}}_1,{\mathbf{e}}_2,{\mathbf{e}}_3$ be an orthonormal basis of the Euclidean vector space ${\mathbb{R}}^4$. The basis vector ${\mathbf{e}}_0$ is identified with 1. We introduce an associative multiplication of the basis vectors subject to the multiplication rules:

$${\mathbf{e}}_1^2={\mathbf{e}}_2^2={\mathbf{e}}_3^2=-1,{\mathbf{e}}_1{\mathbf{e}}_2=-{\mathbf{e}}_2{\mathbf{e}}_1={\mathbf{e}}_3.$$

This non-commutative product generates the algebra of real quaternions denoted by $\mathbb{H}$. The real vector space ${\mathbb{R}}^4$ will be embedded in $\mathbb{H}$ by identifying the element $\mathbf{a}=(a_0,a_1,a_2,a_3)\in {\mathbb{R}}^4$ with the element

$$\mathbf{a}=a_0+a_1{\mathbf{e}}_1+a_2{\mathbf{e}}_2+a_3{\mathbf{e}}_3\in \mathbb{H}.$$

The real number $\mathbf{Sc}\mathbf{a}:=a_0$ is called the scalar part of $\mathbf{a}$ and $\mathbf{Vec}\mathbf{a}:=a_1{\mathbf{e}}_1+a_2{\mathbf{e}}_2+a_3{\mathbf{e}}_3$ is the vector part of $\mathbf{a}$, or the pure quaternion. The quaternion $\overline{\mathbf{a}}:=a_0-a_1{\mathbf{e}}_1-a_2{\mathbf{e}}_2-a_3{\mathbf{e}}_3$ is the conjugate of $\mathbf{a}=a_0+a_1{\mathbf{e}}_1+a_2{\mathbf{e}}_2+a_3{\mathbf{e}}_3$. The norm of $\mathbf{a}$ is given by $\left|\mathbf{a}\right|=\sqrt{\mathbf{a}\overline{\mathbf{a}}}$ which coincides with the corresponding Euclidean norm of $\mathbf{a}$, as a vector in ${\mathbb{R}}^4$. Finally, the real vector space ${\mathbb{R}}^3$ will be embedded in $\mathbb{H}$ by identifying the element $\mathbf{a}=(a_1,a_2,a_3)\in {\mathbb{R}}^3$ with the corresponding pure quaternion, i.e., $\mathbf{a}=a_1{\mathbf{e}}_1+a_2{\mathbf{e}}_2+a_3{\mathbf{e}}_3\in \mathbb{H}$.

Let $\Omega$ be an open subset of ${\mathbb{R}}^3$ with a sufficiently smooth boundary. An $\mathbb{H}$-valued function is a mapping

$$f:\Omega \to \mathbb{H} with f\left(\mathbf{x}\right)=\sum _{k=0}^3{f}^k\left(\mathbf{x}\right){\mathbf{e}}_k,\mathbf{x}\in \Omega ,$$

where the coordinates $f^k$ are real-valued functions defined in $\Omega$, i.e., $f^k:\Omega \to \mathbb{R}$, $k=0,1,2,3$. Continuity, differentiability or integrability of f are defined coordinate-wisely.

Definition 1.

For continuously real-differentiable functions $f:\Omega \subset {\mathbb{R}}^3\to \mathbb{H}$, which we will denote for simplicity by $f\in C^1(\Omega ,\mathbb{H})$, the operator

$$D:=\sum _{k=1}^3{\mathbf{e}}_k{\partial }_{x_k}$$

is called the Dirac operator.

Additionally, two integral operators is introduced [18]:

Definition 2.

Let $\Omega \subset {\mathbb{R}}^3$, $u\in C(\Omega )$. Then the linear integral operator

$$\left(Tu\right)\left(\mathbf{x}\right):=-\underset{\Omega }{\int }E(\mathbf{y}-\mathbf{x})u\left(\mathbf{y}\right)d{\sigma }_{\mathbf{y}} with E\left(\mathbf{x}\right)=\frac{1}{4\pi }\frac{\overline{\omega }\left(\mathbf{x}\right)}{{\left|\mathbf{x}\right|}^3},\omega \left(\mathbf{x}\right)=\frac{\mathbf{x}}{\left|\mathbf{x}\right|},$$

is called the Teodorescu transform over Ω. We also define the operator

$$\left(F_{\mathsf{\Gamma }}u\right)\left(\mathbf{x}\right):=\underset{\mathsf{\Gamma }}{\int }E(\mathbf{y}-\mathbf{x})d{\mathbf{y}}^{*}u\left(\mathbf{y}\right)$$

that is called Cauchy-Bitsadze operator.

Finally, by using the introduced operators, the Borel-Pompeiu formula can be written in the form

$$\left(F_{\mathsf{\Gamma }}u\right)\left(\mathbf{x}\right)+\left(TDu\right)\left(\mathbf{x}\right)=\left\{\begin{array}{cc}u\left(\mathbf{x}\right),& \mathbf{x}\in \Omega ,\hfill \\ 0,& \mathbf{x}\in {\mathbb{R}}^3\mathsf{\setminus }\overline{\Omega },\hfill \end{array}\right.$$

or shortly $F+TD=I$ for $\mathbf{x}\in \Omega$.

For construction of explicit representation formulae, it is necessary to work with Plemelj projections, and a proper definition of these projections requires the information about the boundary behaviour of the Cauchy-Bitsadze operator:

Theorem 1

(Plemelj-Sokhotzki formulae). Let $u\in C^{0,\beta }(\mathsf{\Gamma },\mathbb{H}),0<\beta \le 1$. Then we have for each regular point ${\mathbf{x}}_0\in \mathsf{\Gamma }$

$$\underset{\begin{array}{c}\mathbf{x}\to {\mathbf{x}}_0\\ \mathbf{x}\in G^{\pm },{\mathbf{x}}_0\in \mathsf{\Gamma }\end{array}}{lim}\left(F_{\mathsf{\Gamma }}u\right)\left(\mathbf{x}\right)=\frac{1}{2}\left[\pm u\left({\mathbf{x}}_0\right)+\left(S_{\mathsf{\Gamma }}u\right)\left({\mathbf{x}}_0\right)\right],$$

where $G^{+}:=G$ and $G^{-}:={\mathbb{R}}^n\mathsf{\setminus }\overline{G^{+}}$, the limit has to be taken as a non-tangential limit, and $S_{\mathsf{\Gamma }}$ is the singular integral operator defined by

$$\left(S_{\mathsf{\Gamma }}u\right)\left(\mathbf{x}\right):=2\underset{\mathsf{\Gamma }}{\int }E(\mathbf{y}-\mathbf{x})d{\mathbf{y}}^{*}u\left(\mathbf{y}\right),\mathbf{x}\in \mathsf{\Gamma }.$$

The limits define the Plemelj projections $P_{\mathsf{\Gamma }}:=\frac{1}{2}(I+S_{\mathsf{\Gamma }})$ and $Q_{\mathsf{\Gamma }}:=\frac{1}{2}(I-S_{\mathsf{\Gamma }})$; see [16] for further details.

For treating boundary value problems of micropolar and Cosserat elasticity, it is necessary to work with modified operators associated with the Dirac operator:

Definition 3.

For continuously real-differentiable functions $f:\Omega \subset {\mathbb{R}}^3\to \mathbb{H}$, which we will denote for simplicity by $f\in C^1(\Omega ,\mathbb{H})$, the operator

$$D_{\alpha }:=\alpha +\sum _{k=1}^3{\mathbf{e}}_k{\partial }_{x_k},\alpha \in \mathbb{C}$$

is called a modified Dirac operator.

Definition 4.

Let $\Omega \subset {\mathbb{R}}^3$, $u\in C(\Omega )$. Then the weakly singular integral operator

$$\left(T_{\alpha }u\right)\left(\mathbf{x}\right):=-\underset{G}{\int }{e}_{\alpha }(\mathbf{y}-\mathbf{x})u\left(\mathbf{y}\right)d{\sigma }_{\mathbf{y}},\mathbf{x}\in \Omega ,$$

is called the modified Teodorescu transform; further, the operator

$$\left(F_{\alpha }u\right)\left(\mathbf{x}\right):=\underset{\mathsf{\Gamma }}{\int }{e}_{\alpha }(\mathbf{y}-\mathbf{x})d{\mathbf{y}}^{*}u\left(\mathbf{y}\right),\mathbf{x}\in {\mathbb{R}}^3\mathsf{\setminus }\overline{\Omega },$$

acting of functions $\mathbf{u}\in C^1(\Omega )\cap C\left(\overline{\Omega }\right)$, is called the modified Cauchy-Bitsadze operator. The kernel $e_{\alpha }$ is given by

$$e_{\alpha }\left(\mathbf{x}\right)=-\frac{1}{{4\pi \left|\mathbf{x}\right|}^3}\left({\alpha \left|\mathbf{x}\right|}^2+\left(i\alpha \right|\mathbf{x}|+1)\sum _{k=1}^3{\mathbf{e}}_x{x}_k\right)e^{-i\alpha \left|\mathbf{x}\right|}.$$

Theorem 2

(Modified Plemelj-Sokhotzki formulae). Let $u\in C^{0,\beta }(\mathsf{\Gamma },\mathbb{H}),0<\beta \le 1$. Then we have

$$\begin{array}{ccc}{\displaystyle \underset{\begin{array}{c}y\to x\in \mathsf{\Gamma }\\ y\in \Omega \end{array}}{lim}\left(F_{\alpha }u\right)\left(x\right)}\hfill & =& {\displaystyle \left(P_{\alpha }u\right)\left(x\right)=\frac{1}{2}\left(I+S_{\alpha }\right)u\left(x\right),}\hfill \\ {\displaystyle \underset{\begin{array}{c}y\to x\in \mathsf{\Gamma }\\ y\in {\mathbb{R}}^n\mathsf{\setminus }\overline{\Omega }\end{array}}{lim}\left(F_{\alpha }u\right)\left(x\right)}\hfill & =& {\displaystyle -\left(Q_{\alpha }u\right)\left(x\right)=-\frac{1}{2}\left(I-S_{\alpha }\right)u\left(x\right),}\hfill \end{array}$$

where the singular integral operator $S_{\alpha }$ is defined by

$$\left(S_{\alpha }u\right)\left(\mathbf{x}\right):=\underset{\mathsf{\Gamma }}{\int }{e}_{\alpha }(\mathbf{y}-\mathbf{x})d{\mathbf{y}}^{*}u\left(\mathbf{y}\right),\mathbf{x}\in \mathsf{\Gamma }.$$

Details of the modified operators and study of their properties can be found in [18].

Important ingredients for the representation formulas which will be used later on in the paper are the mapping properties of the integral operators. These properties have been studied precisely in [16,18]:

$$T:W^{k,p}(\Omega )\to W^{k+1,p}(\Omega ),\mathrm{and} T_{\pm \alpha }:W^{k,p}(\Omega )\to W^{k+1,p}(\Omega ),$$

as well as the facts

$${\partial }_{i}T\mathbf{u}\in W^{k,p}(\Omega ),\mathrm{and} {\partial }_i{T}_{\pm \alpha }\mathbf{u}\in W^{k,p}(\Omega )\mathrm{if} \mathbf{u}\in W^{k,p}(\Omega ),$$

with ${\partial }_i$ denoting partial derivatives w.r.t. coordinate $x_i$, $i=1,2,3$.

3.2. Construction of Representation Formulae

Now the application of the quaternionic operator calculus is used in the formal comparison of elasticity models introduced in Section 2. The strategy follows ideas presented in [17] for the case of micropolar elasticity. Moreover, the use of operator calculus for the classical elasticity has been already presented in the past; see, for example, Refs. [16,18] and references wherein. However, the Cosserat elasticity, as well as comparison of three models, has not been studied yet. To this end, several propositions are presented and theorems for all of three model of elasticity, but new results are only related to the Cosserat elasticity and comparison of three models. Moreover, for shortening the presentation, we will present results for three different elasticity theories immediately in one proposition/theorem. Finally, only Dirichlet boundary conditions will be considered from now on.

We start with the following proposition presenting a hypercomplex reformulation of boundary value problems of three elasticity theories:

Proposition 1.

Let ${\mathbf{u}}_e$ denotes the elasticity solution, ${\mathbf{u}}_c$ denotes the “Cosserat” solution, and ${\mathbf{u}}_m$ denotes the micropolar solution. Considering the displacement fields ${\mathbf{u}}_e,{\mathbf{u}}_c,{\mathbf{u}}_m\in C^2(\Omega )$, the vector of total rotation $\widehat{\mathit{\psi }}\in C^2(\Omega )$ and the micropolar rotations $\mathit{\phi }\in C^2(\Omega )$ as pure quaternions, i.e., $\mathbf{j}=u_1{\mathbf{e}}_1+u_2{\mathbf{e}}_2+u_3{\mathbf{e}}_3$ for $j=\left\{e,c,m\right\}$, $\widehat{\mathit{\psi }}={\widehat{\psi }}_1{\mathbf{e}}_1+{\widehat{\psi }}_2{\mathbf{e}}_2+{\widehat{\psi }}_3{\mathbf{e}}_3$, $\mathit{\phi }={\phi }_1{\mathbf{e}}_1+{\phi }_2{\mathbf{e}}_2+{\phi }_3{\mathbf{e}}_3$, equations of the classical elasticity, Cosserat elasticity, and micropolar elasticity, respectively, can be written as follows

$$DAD{\mathbf{u}}_e=0,$$

(2)

$$\left\{\begin{array}{ccc}{\displaystyle D{N}_{1}D{\mathbf{u}}_c-2\tau \mathrm{Vec}D\widehat{\mathit{\psi }}}& =& 0,\hfill \\ {\displaystyle \left(D-i\sqrt{\frac{\tau }{\eta }}\right)N_2\left(D+i\sqrt{\frac{\tau }{\eta }}\right)\widehat{\mathit{\psi }}-2\tau \mathrm{Vec}D{\mathbf{u}}_c}& =& 0,\hfill \end{array}\right.$$

(3)

$$\left\{\begin{array}{ccc}{\displaystyle D{M}_{1}D{\mathbf{u}}_m-2\alpha \mathrm{Vec}D\mathit{\phi }}& =& 0,\hfill \\ {\displaystyle \left(D-i\sqrt{\frac{4\alpha }{\gamma }}\right)M_2\left(D+i\sqrt{\frac{4\alpha }{\gamma }}\right)\mathit{\phi }-2\alpha \mathrm{Vec}D{\mathbf{u}}_m}& =& 0,\hfill \end{array}\right.$$

(4)

where the operators A, $N_1$, $N_2$, $M_1$, and $M_2$ are defined by

$$\begin{array}{ccc}A\mathbf{w}& :=& {\displaystyle \frac{E-\mu }{E-4\mu }{w}_0-w_1{\mathbf{e}}_1-w_2{\mathbf{e}}_2+w_3{\mathbf{e}}_3,}\hfill \\ N_1\mathbf{w}& :=& -(\lambda +2\mu )w_0-(\mu +\tau )w_1{\mathbf{e}}_1-(\mu +\tau )w_2{\mathbf{e}}_2-(\mu +\tau )w_3{\mathbf{e}}_3,\hfill \\ N_2\mathbf{w}& :=& -(\alpha +4\eta +4{\eta }^{\prime })w_0-4\eta w_1{\mathbf{e}}_1-4\eta w_2{\mathbf{e}}_2-4\eta w_3{\mathbf{e}}_3,\hfill \\ M_1\mathbf{w}& :=& -(\lambda +2\mu -2\alpha )w_0-(\mu -2\alpha )w_1{\mathbf{e}}_1-(\mu -2\alpha )w_2{\mathbf{e}}_2\hfill \\ & & -(\mu -2\alpha )w_3{\mathbf{e}}_3,\hfill \\ M_2\mathbf{w}& :=& -(\alpha +\beta +\gamma )w_0-\gamma w_1{\mathbf{e}}_1-\gamma w_2{\mathbf{e}}_2-\gamma w_3{\mathbf{e}}_3,\hfill \end{array}$$

for a quaternion-valued function $\mathbf{w}=w_0+w_1{\mathbf{e}}_1+w_2{\mathbf{e}}_2+w_3{\mathbf{e}}_3$.

Proof. 

The proof can be done by straight-forward calculations.  □

Next step is reformulating Equations (2)–(4) as operator equations providing the possibility to study directly existence, regularity, stability and uniqueness of Dirichlet boundary value problems. Since the results for the classical elasticity and the micropolar elasticity have been already presented in [16,18], we only briefly summarise these results.

Theorem 3.

The boundary value problem

$$\begin{array}{c}DAD{\mathbf{u}}_e=0, in \Omega ,\hfill \\ {\mathbf{u}}_e=\mathbf{g}, on \mathsf{\Gamma },\hfill \end{array}$$

with $g\in W^{2,k+\frac{3}{2}}\left(\mathsf{\Gamma }\right)$ is uniquely solvable and its solution is given by

$${\mathbf{u}}_e=F_{\mathsf{\Gamma }}\mathbf{g}+T{A}^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{A}^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}{Q}_{\mathsf{\Gamma }}\mathbf{g}.$$

For the case of micropolar elasticity, due to the coupled nature of the problem, a few intermediate steps a used. At first, we the have the following theorem:

Theorem 4.

The system of equations

$$\left\{\begin{array}{ccc}{\displaystyle D{M}_{1}D{\mathbf{u}}_m-2\alpha \mathrm{Vec}D\mathit{\phi }}& =& 0,\hfill \\ {\displaystyle \left(D-i\sqrt{\frac{4\alpha }{\gamma }}\right)M_2\left(D+i\sqrt{\frac{4\alpha }{\gamma }}\right)\mathit{\phi }-2\alpha \mathrm{Vec}D{\mathbf{u}}_m}& =& 0,\hfill \end{array}\right.$$

with Dirichlet boundary conditions

$$\left\{\begin{array}{cccc}{\mathbf{u}}_m\hfill & =& {\mathbf{g}}_1\hfill & on \mathsf{\Gamma },\hfill \\ \mathit{\phi }\hfill & =& {\mathbf{g}}_2\hfill & on \mathsf{\Gamma }\hfill \end{array}\right.$$

is equivalent to the system of operator equations

$$\left\{\begin{array}{ccc}{\mathbf{u}}_m\hfill & =& {\mathbf{A}}_1\mathit{\phi }+{\mathbf{f}}_1,\hfill \\ \mathit{\phi }\hfill & =& {\mathbf{A}}_2{\mathbf{u}}_m+{\mathbf{f}}_2,\hfill \end{array}\right.$$

(5)

where the operators ${\mathbf{A}}_1$ and ${\mathbf{A}}_2$ are defined by

$${\mathbf{A}}_1:=2\alpha T{M}_1^{-1}T\mathrm{Vec}D,{\mathbf{A}}_2:=2\alpha T_{\alpha }{M}_2^{-1}{T}_{-\alpha }\mathrm{Vec}D,$$

together with additional terms ${\mathbf{f}}_1$, ${\mathbf{f}}_2$

$$\begin{array}{ccc}{\displaystyle {\mathbf{f}}_1}\hfill & :=& {\displaystyle F_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_1+T{M}_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{M}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}{Q}_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_1,}\hfill \\ {\displaystyle {\mathbf{f}}_2}\hfill & :=& {\displaystyle F_{\alpha }{\tilde{\mathbf{g}}}_2+T_{\alpha }{M}_2^{-1}{F}_{-\alpha }{\left(\mathrm{tr}{T}_{\alpha }{M}_2^{-1}{F}_{-\alpha }\right)}^{-1}{Q}_{\alpha }{\tilde{\mathbf{g}}}_2,}\hfill \end{array}$$

where ${\tilde{\mathbf{g}}}_1={\mathbf{g}}_1-2\alpha \mathrm{tr}T{M}_1^{-1}T\mathrm{Vec}D\mathit{\phi }$ and ${\tilde{\mathbf{g}}}_2={\mathbf{g}}_1-2\alpha \mathrm{tr}{T}_{\alpha }{M}_2^{-1}{T}_{-\alpha }\mathrm{Vec}D{\mathbf{u}}_m$.

Next, we perform a decoupling of the coupled system of operator Equation (5). Using the representation formula for $\mathit{\phi }$ in the first equation of (5) and correspondingly, the representation formula for ${\mathbf{u}}_m$ in the second equation of (5), the following is obtained:

$$\left\{\begin{array}{cc}\hfill {\mathbf{u}}_m=& {\mathbf{A}}_1\left(F_{\alpha }{\tilde{\mathbf{g}}}_2+T_{\alpha }{M}_2^{-1}{F}_{-\alpha }{\left(\mathrm{tr}{T}_{\alpha }{M}_2^{-1}{F}_{-\alpha }\right)}^{-1}{Q}_{\alpha }{\tilde{\mathbf{g}}}_2+2\alpha T_{\alpha }{M}_2^{-1}{T}_{-\alpha }\mathrm{Vec}D{\mathbf{u}}_m\right)+{\mathbf{f}}_1,\hfill \\ \hfill \mathit{\phi }=& {\mathbf{A}}_2\left(F_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_1+T{M}_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{M}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}{Q}_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_1+2\alpha T{M}_1^{-1}T\mathrm{Vec}D\mathit{\phi }\right)+{\mathbf{f}}_2.\hfill \end{array}\right.$$

By help of the new notations

$$\begin{array}{ccc}{\mathbf{B}}_1\hfill & :=& {\mathbf{A}}_1\left(2\alpha T_{\alpha }{M}_2^{-1}{T}_{-\alpha }\mathrm{Vec}D\right),\hfill \\ {\mathbf{B}}_2\hfill & :=& {\mathbf{A}}_2\left(2\alpha T{M}_1^{-1}T\mathrm{Vec}D\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}{\mathbf{f}}_1^{*}\hfill & =& {\mathbf{f}}_1+{\mathbf{A}}_1\left(F_{\alpha }{\tilde{\mathbf{g}}}_2+T_{\alpha }{M}_2^{-1}{F}_{-\alpha }{\left(\mathrm{tr}{T}_{\alpha }{M}_2^{-1}{F}_{-\alpha }\right)}^{-1}{Q}_{\alpha }{\tilde{\mathbf{g}}}_2\right),\hfill \\ {\mathbf{f}}_2^{*}\hfill & =& {\mathbf{f}}_2+{\mathbf{A}}_2\left(F_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_1+T{M}_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{M}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}{Q}_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_1\right),\hfill \end{array}$$

we finally obtain the following decoupled system

$$\left\{\begin{array}{ccc}{\mathbf{u}}_m\hfill & =& {\mathbf{B}}_1{\mathbf{u}}_m+{\mathbf{f}}_1^{*},\hfill \\ \mathit{\phi }\hfill & =& {\mathbf{B}}_2\mathit{\phi }+{\mathbf{f}}_2^{*}.\hfill \end{array}\right.⟺\left\{\begin{array}{ccc}\left(\mathbf{I}-{\mathbf{B}}_1\right){\mathbf{u}}_m\hfill & =& {\mathbf{f}}_1^{*},\hfill \\ \left(\mathbf{I}-{\mathbf{B}}_2\right)\mathit{\phi }\hfill & =& {\mathbf{f}}_2^{*},\hfill \end{array}\right.$$

(6)

where $\mathbf{I}$ is the identity operator.

Finally, we have the following theorem for the unique solvability of a decoupled problem:

Theorem 5.

For the given boundary conditions ${\mathbf{g}}_{1,2}\in W^{k+\frac{3}{2},2}\left(\mathsf{\Gamma }\right)$ and sufficiently small α, the solution ${\mathbf{u}}_m,\mathit{\phi }\in W^{k,2}(\Omega )$ of decoupled problem (6) is unique, the problem is well-posed, and the solution can be estimated as follows

$$\parallel {\mathbf{u}}_m\parallel \le \parallel {\left(\mathbf{I}-{\mathbf{B}}_1\right)}^{-1}\parallel \parallel {\mathbf{f}}_1^{*}\parallel ,\parallel \mathit{\phi }\parallel \le \parallel {\left(\mathbf{I}-{\mathbf{B}}_2\right)}^{-1}\parallel \parallel {\mathbf{f}}_2^{*}\parallel ,$$

with ${\mathbf{f}}_1^{*}$ and ${\mathbf{f}}_2^{*}$ explicitly given by

$$\begin{array}{cc}{\mathbf{f}}_1^{*}\hfill & =F_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_1+T{M}_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{M}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}{Q}_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_1\hfill \\ \hfill & +2\alpha T{M}_1^{-1}T\mathrm{Vec}D\left(F_{\alpha }{\tilde{\mathbf{g}}}_2+T_{\alpha }{M}_2^{-1}{F}_{-\alpha }{\left(\mathrm{tr}{T}_{\alpha }{M}_2^{-1}{F}_{-\alpha }\right)}^{-1}{Q}_{\alpha }{\tilde{\mathbf{g}}}_2\right),\hfill \\ {\mathbf{f}}_2^{*}\hfill & =F_{\alpha }{\tilde{\mathbf{g}}}_2+T_{\alpha }{M}_2^{-1}{F}_{-\alpha }{\left(\mathrm{tr}{T}_{\alpha }{M}_2^{-1}{F}_{-\alpha }\right)}^{-1}{Q}_{\alpha }{\tilde{\mathbf{g}}}_2\hfill \\ \hfill & +2\alpha T_{\alpha }{M}_2^{-1}{T}_{-\alpha }\mathrm{Vec}D\left(F_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_1+T{M}_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{M}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}{Q}_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_1\right).\hfill \end{array}$$

The results for the Cosserat elasticity will be obtained in the same way, as for the micropolar elasticity, because the type of equations is the same.

Theorem 6.

The system of equations

$$\left\{\begin{array}{ccc}{\displaystyle D{N}_{1}D{\mathbf{u}}_c-2\tau \mathrm{Vec}D\widehat{\mathit{\psi }}}& =& 0,\hfill \\ {\displaystyle \left(D-i\sqrt{\frac{\tau }{\eta }}\right)N_2\left(D+i\sqrt{\frac{\tau }{\eta }}\right)\widehat{\mathit{\psi }}-2\tau \mathrm{Vec}D{\mathbf{u}}_c}& =& 0,\hfill \end{array}\right.$$

with Dirichlet boundary conditions

$$\left\{\begin{array}{cccc}{\mathbf{u}}_c\hfill & =& {\mathbf{g}}_3\hfill & on \mathsf{\Gamma },\hfill \\ \widehat{\mathit{\psi }}\hfill & =& {\mathbf{g}}_4\hfill & on \mathsf{\Gamma }\hfill \end{array}\right.$$

is equivalent to the system of operator equations

$$\left\{\begin{array}{ccc}{\mathbf{u}}_c\hfill & =& {\mathbf{A}}_3\widehat{\mathit{\psi }}+{\mathbf{f}}_3,\hfill \\ \widehat{\mathit{\psi }}\hfill & =& {\mathbf{A}}_4{\mathbf{u}}_c+{\mathbf{f}}_4,\hfill \end{array}\right.$$

(7)

where the operators ${\mathbf{A}}_3$ and ${\mathbf{A}}_4$ are defined by

$${\mathbf{A}}_3:=2\tau T{N}_1^{-1}T\mathrm{Vec}D,{\mathbf{A}}_4:=2\tau T_{\alpha }{N}_2^{-1}{T}_{-\alpha }\mathrm{Vec}D,$$

together with additional terms ${\mathbf{f}}_1$, ${\mathbf{f}}_2$

$$\begin{array}{ccc}{\displaystyle {\mathbf{f}}_3}\hfill & :=& {\displaystyle F_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_3+T{N}_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{N}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}{Q}_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_3,}\hfill \\ {\displaystyle {\mathbf{f}}_4}\hfill & :=& {\displaystyle F_{\alpha }{\tilde{\mathbf{g}}}_4+T_{\alpha }{N}_2^{-1}{F}_{-\alpha }{\left(\mathrm{tr}{T}_{\alpha }{N}_2^{-1}{F}_{-\alpha }\right)}^{-1}{Q}_{\alpha }{\tilde{\mathbf{g}}}_4,}\hfill \end{array}$$

where ${\tilde{\mathbf{g}}}_3={\mathbf{g}}_3-2\tau \mathrm{tr}T{N}_1^{-1}T\mathrm{Vec}D\widehat{\mathit{\psi }}$ and ${\tilde{\mathbf{g}}}_4={\mathbf{g}}_4-2\tau \mathrm{tr}{T}_{\alpha }{N}_2^{-1}{T}_{-\alpha }\mathrm{Vec}D{\mathbf{u}}_c$.

Proof. 

As we have already underlined, the proof of this theorem is identical to the proof of similar results for the micropolar elasticity presented in [17], and therefore, we omit the proof.  □

After decoupling the system of equations of the Cosserat elasticity, the following system of operator equations is obtained:

$$\left\{\begin{array}{ccc}\left(\mathbf{I}-{\mathbf{B}}_3\right){\mathbf{u}}_c\hfill & =& {\mathbf{f}}_3^{*},\hfill \\ \left(\mathbf{I}-{\mathbf{B}}_4\right)\widehat{\mathit{\psi }}\hfill & =& {\mathbf{f}}_4^{*},\hfill \end{array}\right.$$

(8)

where $\mathbf{I}$ is the identity operator, and the operators ${\mathbf{B}}_3,{\mathbf{B}}_4$ are given by

$$\begin{array}{ccc}{\mathbf{B}}_3\hfill & :=& {\mathbf{A}}_3\left(2\tau T_{\alpha }{N}_2^{-1}{T}_{-\alpha }\mathrm{Vec}D\right),\hfill \\ {\mathbf{B}}_4\hfill & :=& {\mathbf{A}}_4\left(2\tau T{N}_1^{-1}T\mathrm{Vec}D\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}{\mathbf{f}}_3^{*}\hfill & =& {\mathbf{f}}_3+{\mathbf{A}}_3\left(F_{\alpha }{\tilde{\mathbf{g}}}_4+T_{\alpha }{N}_2^{-1}{F}_{-\alpha }{\left(\mathrm{tr}{T}_{\alpha }{N}_2^{-1}{F}_{-\alpha }\right)}^{-1}{Q}_{\alpha }{\tilde{\mathbf{g}}}_4\right),\hfill \\ {\mathbf{f}}_4^{*}\hfill & =& {\mathbf{f}}_4+{\mathbf{A}}_4\left(F_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_3+T{N}_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{N}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}{Q}_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_3\right).\hfill \end{array}$$

After that, by studying the mapping properties of operators ${\mathbf{B}}_3,{\mathbf{B}}_4$ and by using the Banach inverse mapping theorem, the following theorem can be proved:

Theorem 7.

For given boundary conditions ${\mathbf{g}}_{3,4}\in W^{k+\frac{3}{2},2}\left(\mathsf{\Gamma }\right)$ and sufficiently small κ, the solution ${\mathbf{u}}_c,\widehat{\mathit{\psi }}\in W^{k,2}(\Omega )$ of decoupled problem (8) is unique, the problem is well-posed, and the solution can be estimated as follows

$$\parallel {\mathbf{u}}_c\parallel \le \parallel {\left(\mathbf{I}-{\mathbf{B}}_3\right)}^{-1}\parallel \parallel {\mathbf{f}}_3^{*}\parallel ,\parallel \widehat{\mathit{\psi }}\parallel \le \parallel {\left(\mathbf{I}-{\mathbf{B}}_4\right)}^{-1}\parallel \parallel {\mathbf{f}}_4^{*}\parallel ,$$

with ${\mathbf{f}}_3^{*}$ and ${\mathbf{f}}_4^{*}$ explicitly given by

$$\begin{array}{cc}{\mathbf{f}}_3^{*}\hfill & =F_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_3+T{N}_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{N}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}{Q}_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_3\hfill \\ \hfill & +2\tau T{N}_1^{-1}T\mathrm{Vec}D\left(F_{\alpha }{\tilde{\mathbf{g}}}_4+T_{\alpha }{N}_2^{-1}{F}_{-\alpha }{\left(\mathrm{tr}{T}_{\alpha }{N}_2^{-1}{F}_{-\alpha }\right)}^{-1}{Q}_{\alpha }{\tilde{\mathbf{g}}}_4\right),\hfill \\ {\mathbf{f}}_4^{*}\hfill & =F_{\alpha }{\tilde{\mathbf{g}}}_4+T_{\alpha }{N}_2^{-1}{F}_{-\alpha }{\left(\mathrm{tr}{T}_{\alpha }{N}_2^{-1}{F}_{-\alpha }\right)}^{-1}{Q}_{\alpha }{\tilde{\mathbf{g}}}_4\hfill \\ \hfill & +2\tau T_{\alpha }{N}_2^{-1}{T}_{-\alpha }\mathrm{Vec}D\left(F_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_3+T{N}_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{N}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}{Q}_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_3\right).\hfill \end{array}$$

3.3. Estimates for the Differences between the Models

Next, following ideas from [17], the theoretical estimates for the pairwise differences of three elasticity models are presented. The main goal is to construct the following estimates

$$\parallel {\mathbf{u}}_e-{\mathbf{u}}_c\parallel ,\parallel {\mathbf{u}}_e-{\mathbf{u}}_m\parallel ,\parallel {\mathbf{u}}_m-{\mathbf{u}}_c\parallel ,\parallel \mathit{\phi }-\widehat{\mathit{\psi }}\parallel ,$$

in $W^{2,1}(\Omega )$ with ${\mathbf{u}}_e$ denoting the elasticity solution, ${\mathbf{u}}_c$ denoting the “Cosserat” solution, and ${\mathbf{u}}_m$ denoting the micropolar solution. The choice of Sobolev space $W^{2,1}(\Omega )$ is motivated by the fact that this is the most popular function space used in engineering applications. Evidently, estimates in other spaces can be straightforwardly constructed.

To construct the estimates, we note that the elasticity solution ${\mathbf{u}}_e$ can be obtained from the “Cosserat” solution and micropolar solution by setting constants $\tau$ and $\alpha$ to zero. Further, representation formulae for $\mathit{\phi }$ and $\widehat{\mathit{\psi }}$ will also be used. Thus, the following estimates are obtained

$$\begin{array}{ccc}\hfill {\displaystyle \parallel {\mathbf{u}}_e-{\mathbf{u}}_c\parallel }& \le & {\displaystyle ∥2\tau T{N}_1^{-1}T\mathrm{Vec}D\left[{\left(\mathbf{I}-{\mathbf{B}}_4\right)}^{-1}{\mathbf{f}}_4^{*}\right]∥,}\hfill \\ \\ \hfill {\displaystyle \parallel {\mathbf{u}}_e-{\mathbf{u}}_m\parallel }& \le & {\displaystyle ∥2\alpha T{M}_1^{-1}T\mathrm{Vec}D\left[{\left(\mathbf{I}-{\mathbf{B}}_2\right)}^{-1}{\mathbf{f}}_2^{*}\right]∥.}\hfill \end{array}$$

(9)

For constructing the remaining two estimates, i.e., $\parallel {\mathbf{u}}_m-{\mathbf{u}}_c\parallel$ and $\parallel \mathit{\phi }-\widehat{\mathit{\psi }}\parallel$, general representation Formulaes (5)–(7) will be used, which lead to the following estimates:

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \parallel {\mathbf{u}}_m-{\mathbf{u}}_c\parallel }& =& {\displaystyle ∥{\mathbf{A}}_1\mathit{\phi }+{\mathbf{f}}_1-{\mathbf{A}}_3\widehat{\mathit{\psi }}-{\mathbf{f}}_3∥\le ∥{\mathbf{A}}_1\mathit{\phi }-{\mathbf{A}}_3\widehat{\mathit{\psi }}∥+∥{\mathbf{f}}_1-{\mathbf{f}}_3∥,}\hfill \\ \hfill {\displaystyle \parallel \mathit{\phi }-\widehat{\mathit{\psi }}\parallel }& =& {\displaystyle ∥{\mathbf{A}}_2{\mathbf{u}}_m{\mathbf{f}}_2-{\mathbf{A}}_4{\mathbf{u}}_c-{\mathbf{f}}_4∥\le ∥{\mathbf{A}}_2{\mathbf{u}}_m-{\mathbf{A}}_4{\mathbf{u}}_c∥+∥{\mathbf{f}}_2-{\mathbf{f}}_4∥.}\hfill \end{array}\right.$$

Hence, the estimates are split into two parts: the part related to boundary conditions via $f_i$, $i=1,2,3,4$, and the part related to the difference in the sought physical quantities. Moreover, because of the coupled nature of the boundary value problems of micropolar and Cosserat elasticity, the estimate for ${\mathbf{u}}_m$ and ${\mathbf{u}}_c$ depends on $\mathit{\phi }$ and $\widehat{\mathit{\psi }}$ and vice versa.

It is important to underline that it would be possible to use representation formulae for the decoupled formulations (6)–(8), which would evidently lead to the following estimates

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \parallel {\mathbf{u}}_m-{\mathbf{u}}_c\parallel }& \le & {\displaystyle ∥{\mathbf{B}}_1{\mathbf{u}}_m-{\mathbf{B}}_3{\mathbf{u}}_c∥+∥{\mathbf{f}}_1^{*}-{\mathbf{f}}_3^{*}∥,}\hfill \\ \hfill {\displaystyle \parallel \mathit{\phi }-\widehat{\mathit{\psi }}\parallel }& \le & {\displaystyle ∥{\mathbf{B}}_2\mathit{\phi }-{\mathbf{B}}_4\widehat{\mathit{\psi }}∥+∥{\mathbf{f}}_2^{*}-{\mathbf{f}}_4^{*}∥.}\hfill \end{array}\right.$$

However, it is more suitable to work with the coupled system for the upcoming discussion.

By using the definitions of operators ${\mathbf{A}}_i$ and terms ${\mathbf{f}}_i$, $i=1,2,3,4$, the following explicit estimates are straightforwardly obtained:

$$\begin{array}{cc}\hfill {\displaystyle \parallel {\mathbf{u}}_m-{\mathbf{u}}_c\parallel \le }& {\displaystyle ∥2T\left(\alpha M_1^{-1}T\mathrm{Vec}D\mathit{\phi }-\tau N_1^{-1}T\mathrm{Vec}D\widehat{\mathit{\psi }}\right)∥+∥F_{\mathsf{\Gamma }}\left({\tilde{\mathbf{g}}}_1-{\tilde{\mathbf{g}}}_3\right)∥}\hfill \\ \hfill & {\displaystyle +∥T{M}_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{M}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}{Q}_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_1-T{N}_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{N}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}{Q}_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_3∥,}\hfill \\ \\ \hfill {\displaystyle \parallel \mathit{\phi }-\widehat{\mathit{\psi }}\parallel \le }& {\displaystyle ∥2T_{\alpha }\left(\alpha M_2^{-1}{T}_{-\alpha }\mathrm{Vec}D{\mathbf{u}}_m-\tau N_2^{-1}{T}_{-\alpha }\mathrm{Vec}D{\mathbf{u}}_c\right)∥+∥F_{\alpha }\left({\tilde{\mathbf{g}}}_2-{\tilde{\mathbf{g}}}_4\right)∥}\hfill \\ \hfill & {\displaystyle +∥T_{\alpha }{M}_2^{-1}{F}_{\alpha }{\left(\mathrm{tr}{T}_{\alpha }{M}_2^{-1}{F}_{\alpha }\right)}^{-1}{Q}_{\alpha }{\tilde{\mathbf{g}}}_2-T_{\alpha }{N}_2^{-1}{F}_{\alpha }{\left(\mathrm{tr}{T}_{\alpha }{N}_2^{-1}{F}_{\alpha }\right)}^{-1}{Q}_{\alpha }{\tilde{\mathbf{g}}}_4∥.}\hfill \end{array}$$

(10)

Analysing the above expressions, it becomes visible that the main difference in between the micropolar model and the Cosserat model is related to the material constants, which are “hidden” in the multiplicative operators $M_1$, $M_2$ and $N_1$, $N_2$, while all other operators are the same. This fact is particularly visible for the boundary part of the estimate. Recall that both models describe displacement of a continuum, it is natural to assume that the displacement boundary conditions ${\tilde{\mathbf{g}}}_1$ and ${\tilde{\mathbf{g}}}_3$ are equal. Thus, the estimate for $∥{\mathbf{f}}_1-{\mathbf{f}}_3∥$ can be simplified to

$$∥{\mathbf{f}}_1-{\mathbf{f}}_3∥\le ∥T\left(M_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{M}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}-N_1^{-1}{F}_{\mathsf{\Gamma }}{\left(\mathrm{tr}T{N}_1^{-1}{F}_{\mathsf{\Gamma }}\right)}^{-1}\right)Q_{\mathsf{\Gamma }}{\tilde{\mathbf{g}}}_1∥,$$

where the non-commutativity of the operators has been taken into account. Further, due to the uniqueness of solution of decoupled problems (6)–(8), it follows that ${\mathbf{u}}_m={\mathbf{u}}_c$ in the case of equal boundary conditions. Therefore, the first summand in the estimate for $\parallel \mathit{\phi }-\widehat{\mathit{\psi }}\parallel$ will depend again on the difference in material constants of both models and the norm of ${\mathbf{u}}_m={\mathbf{u}}_c$. If similar assumptions on the equality of boundary conditions ${\tilde{\mathbf{g}}}_2$ and ${\tilde{\mathbf{g}}}_4$ could be made, then the estimate for $\parallel \mathit{\phi }-\widehat{\mathit{\psi }}\parallel$ would also simplify to the difference in material constants. However, justification of this assumption is not so clear not only from the theoretical point of view, but from the point of view of practical engineering modelling, as well.

The results of this subsection are therefore briefly summarized as:

• The difference between the classical elasticity and the two refined models presented in estimates (9) is controlled by material constants $\tau$ for the Cosserat model and $\kappa$ for the micropolar model. Hence, for $\tau \to 0$ and $\kappa \to 0$ the refined solutions should tend to the elasticity solution.
• The estimates between the micropolar model and the Cosserat model presented in (10) indicates also that the main difference between the models is controlled by the material constants of both models, although the estimates have a more complex structure compared to (9).

Theoretical results presented in this section clearly indicate that material constants of elasticity models play the crucial role in theoretical model comparison and as a result, in a practical engineering modelling, as well. It is also well known that practical identification of material parameters of the micropolar model and the Cosserat model is difficult; see, for example, Refs. [10,11], which limits applicability of these models. To overcome this problem, various engineering approaches for practical calculations of these material parameters and simplified macro-models are used in practice. Some of these macro-models are discussed in the next section.

4. Macro-Models and Numerical Results

In this section, an engineering approach to practical use of the micropolar model and the Cosserat model is discussed. In this way, the two macro-models, namely Cosserat layered rocks and equivalent micropolar continuum, are presented and discussed with respect to practical identification of constants. Moreover, for the sake of a better presentation, only the two-dimensional models will be considered from now on and the constitutive equations for macro-models will be presented in a matrix form. Finally, numerical examples illustrating practical difference between three elasticity models are presented at the end of this section.

4.1. Macro-Models for the Micropolar Elasticity and Cosserat Elasticity

In comparison to the classical elasticity, the Cosserat model and the micropolar model have additional kinematic and static descriptors, which are able to account for the material internal structure. The Cosserat macro-model in this section has a micro- rotation component, while the micropolar model includes both the micro-rotation and skew-symmetric stress. These additional effects of the theories are reflected in new material parameters.

A two-dimensional Cosserat model, which has 4 non-symmetric stress components ${\sigma }_{11}$, ${\sigma }_{22}$, ${\sigma }_{21}$, ${\sigma }_{12}$ and two couple stress components $m_{31}$, $m_{32}$, is often used in rock engineering to model the behaviour of rock masses consisting of a large number of layers. The idea behind this macro-model is to introduce a continuum model in which the layers are virtually smeared across the mass. This construction reduces the computational costs for practical calculations with the model, because when the rock layers are aligned in 1-coordinate direction the moment stress term $m_{32}$ disappears; see [8,19] for the details. Additionally, the Cosserat layered rock model assumes the original Cosserat theory with the additional conjecture that the relative rotation ${\gamma }_{ij}$ can be considered as independent and ignored. The model therefore only considers the effect of micro-rotations in addition to the classical elasticity material strain. The stress-strain relationship is then given in the matrix form as follows:

$$\left(\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{21}\\ {\sigma }_{12}\\ m_{31}\end{array}\right)=\left(\begin{array}{ccccc}{A}_{11}& A_{12}& 0& 0& 0\\ & A_{22}& 0& 0& 0\\ & & G_{11}& G_{12}& 0\\ & symm& & G_{22}& 0\\ & & & & B_1\end{array}\right)\left(\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ {\epsilon }_{21}\\ {\epsilon }_{12}\\ {\kappa }_{31}\end{array}\right),$$

and the material parameters are given by

$$\begin{array}{ccc}{\displaystyle A_{11}=\frac{E}{1-{\nu }^2-\frac{{\nu }^2{(1+\nu )}^2}{1-{\nu }^2+\frac{E}{h{k}_n}}},}\hfill & {\displaystyle A_{22}=\frac{1}{\frac{1-\nu -2{\nu }^2}{E(1-\nu )}+\frac{1}{h{k}_n}},}\hfill & {\displaystyle A_{12}=\frac{\nu }{1-\nu }{A}_{22},}\hfill \\ {\displaystyle \frac{1}{G_{11}}=\frac{1}{G}+\frac{1}{h{k}_s},}\hfill & {\displaystyle G_{11}=G_{12}=G_{21},}\hfill & {\displaystyle G_{22}=G_{11}+G,}\hfill \\ {\displaystyle B_1=\frac{E{h}^2}{12(1-{\nu }^2)}\left(\frac{G-G_{11}}{G+G_{11}}\right),}\hfill \end{array}$$

where the curvatures are ${\kappa }_{31}$, E is the Young’s modulus of the intact layer, $\nu$ is the Poisson’s ratio, h is the layer thickness, G is the shear modulus of the intact layer, $k_n$ and $k_s$ are the joint normal and shear stiffness, respectively.

A macro-model for the micropolar theory has been proposed in [20], where it has been described how a masonry structure can be modelled as a micropolar continuum equivalent to discrete systems of blocks with different geometry. Interlocking bricks are designed to self-lock to the other bricks without the use of mortar. Moreover, this macro-model allows also accounting for independent rotations of individual blocks, which is expected from the micropolar theory. Further, this macro-model includes the parameters for the plain stress classical elasticity solution, which is extended include the skew symmetric tensor ${\tau }_{12}$ and couple stresses ${\mu }_{31}$ and ${\mu }_{32}$. Therefore, the micropolar formulation is able to give results of the relative rotation ($r_3-{\phi }_3$), which measures the effect of the skew symmetric tensor and the micro-rotation ${\phi }_3$. In this 2D micropolar macro-model, the stress-strain relationship is given as follows:

$$\left(\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{12}\\ {\tau }_{12}\\ {\mu }_{31}\\ {\mu }_{32}\end{array}\right)=\left(\begin{array}{cccccc}{A}_{1111}& A_{1122}& 0& 0& 0& 0\\ A_{2211}& A_{2222}& 0& 0& 0& 0\\ 0& 0& A_{1212}& \frac{1}{2}(B_{2121}-B_{1212})& 0& 0\\ 0& 0& \frac{1}{2}(B_{1212}-B_{2121})& -\frac{1}{2}(B_{1212}+B_{2121})+B_{1221}& 0& 0\\ 0& 0& 0& 0& C_{11}& 0\\ 0& 0& 0& 0& 0& C_{22}\end{array}\right)\left(\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ {\epsilon }_{12}\\ r_3-{\phi }_3\\ {\kappa }_{31}\\ {\kappa }_{32}\end{array}\right),$$

(11)

where ${\tau }_{12}$ is the skew-symmetric stress component and $r_3$ is the independent component of the macrorotation tensor, and the material coefficients are given by

$$\begin{array}{ccc}{\displaystyle B_{1212}=\frac{G_{m}dL}{s}{p}_2,}\hfill & {\displaystyle B_{2121}=\frac{Ld{p}_1}{s}\left(\frac{E_m}{2p_3}+G_m\right),}\hfill & {\displaystyle B_{1221}=\frac{G_{m}dL}{s}{p}_1,}\hfill \\ {\displaystyle C_{11}=\frac{E_{m}d{L}^3}{s}{ϵ}_1\left(\frac{1}{32\rho }{p}_1^2+\frac{1}{2}{p}_2^2\right),}\hfill & {\displaystyle C_{22}=\frac{E_{m}d{L}^3}{8s}{p}_1^2{p}_2,}\hfill \end{array}$$

where $G_m$ = $E_m$/(2 × (1 + $\nu$)), is the tangent modulus of the mortar, $E_m$ is the Young’s modulus of the mortar layer, $p_1=b/L$ and $p_2=h/L$ are scale parameters, d is the thickness of the masonry panel, s is the thickness of the mortar layer, L is the length and height of a masonry wall, $p_3=h/b$ is the aspect ratio of a masonry block, h is the height of the block and b is the width of the block. For the case of masonry without interlocking, the matrix coefficients can be written as [20]:

$$\begin{array}{ccc}{\displaystyle B_{1212}=\frac{G_{m}dL}{s}{p}_2,}\hfill & {\displaystyle B_{2121}=\frac{G_{m}dL}{s}{p}_1,}\hfill & {\displaystyle B_{1221}=0,}\hfill \\ {\displaystyle C_{11}=\frac{E_{m}d{L}^3}{8s}{p}_1{p}_2^2,}\hfill & {\displaystyle C_{22}=\frac{E_{m}d{L}^3}{8s}{p}_1^2{p}_2.}\hfill \end{array}$$

Evidently, the stress-strain relationship (11) includes the sub-matrix representing the classical elasticity, namely:

$$\left(\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{12}\end{array}\right)=\left(\begin{array}{ccc}{A}_{1111}& A_{1122}& 0\\ A_{2211}& A_{2222}& 0\\ 0& 0& A_{1212}\end{array}\right)\left(\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ {\epsilon }_{12}\end{array}\right)=\frac{E}{1-{\nu }^2}\left(\begin{array}{ccc}1& \nu & 0\\ \nu & 1& 0\\ 0& & \frac{1-\nu }{2}\end{array}\right)\left(\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ 2{\epsilon }_{12}\end{array}\right)$$

where the Young’s modulus is E, Poisson’s ratio is $\nu$, the Cartesian coordinates system are related to the numbers on the right hand side in the subscript so that 11 = $xx$, 22 = $yy$ and 12 = $xy$.

4.2. Identification of Additional Material Parameters

As it has been mentioned already, the main obstacle in the way of practical use of the micropolar theory and the Cosserat theory is identification of additional material parameters appearing in these theories. Therefore, in this sub-section, a short overview of available results related to identification of material parameters is provided.

Several authors have used theoretical investigations to obtain material parameters of the Cosserat theory and the micropolar theory. In particular, Adomeit determined the couple-stress elastic coefficients of a three-dimensional honeycomb structure from a structural perspective in [21]. Further, Herrmann and Achenbach used couple-stress theory to express the dynamics of a laminated structure and obtained the non-classical material constants based on the geometry and classical elasticity properties in [22]. Additionally, several other authors used an equivalent continuum approach to calculate the material coefficients from structural considerations [23,24,25].

Additionally to theoretical approaches, several experimental studies for identification of additional material parameters have been made in the past by several authors. One of the first experiments for determining the micropolar material coefficients was conducted by Askar in 1972 [26]. Perkins and Thompson used a dynamic test based on couple stress theory to interpret the thickness-dependency of the apparent shear stiffness of an elastic layer of material embedded between two rigid planes [27]. Gauthier and Jahsman were the first to directly attempt to determine all six elastic constants of the linear isotropic micropolar theory through experiments [28,29]. However, they concluded that detection of the micropolar phenomena requires either series of dynamic tests or higher resolution static measurements. Later, Lakes used this conjecture to further develop experiments which are able to determine micropolar elastic constants for materials such as bone, polymeric foams and metallic foams [10]. Additionally, Lakes noted that the micropolar elastic parameters can be related to be more beneficial in terms of the shear modulus, Poisson’s ratio and Young’s modulus as follows [11]:

$$E=\frac{(2\mu +ϵ)(3\lambda +2\mu +ϵ)}{2\lambda +2\mu +ϵ},G=\frac{2\mu +ϵ}{2},$$

$$\nu =\frac{\lambda }{2\lambda +2\mu +ϵ},\mathrm{coupling} \mathrm{number} N={\left[\frac{ϵ}{2(\mu +ϵ)}\right]}^{1/2},$$

$$\mathrm{polar} \mathrm{ratio} P_{\Psi }=\frac{\beta +\gamma }{\alpha +\beta +\gamma },\mathrm{characteristic} \mathrm{length} \mathrm{for} \mathrm{torsion} l_t={\left[\frac{\beta +\gamma }{(2\mu +ϵ)}\right]}^{1/2}$$

$$\mathrm{characteristic} \mathrm{length} \mathrm{for} \mathrm{bending} l_b={\left[\frac{\gamma }{2(2\mu +ϵ)}\right]}^{1/2}.$$

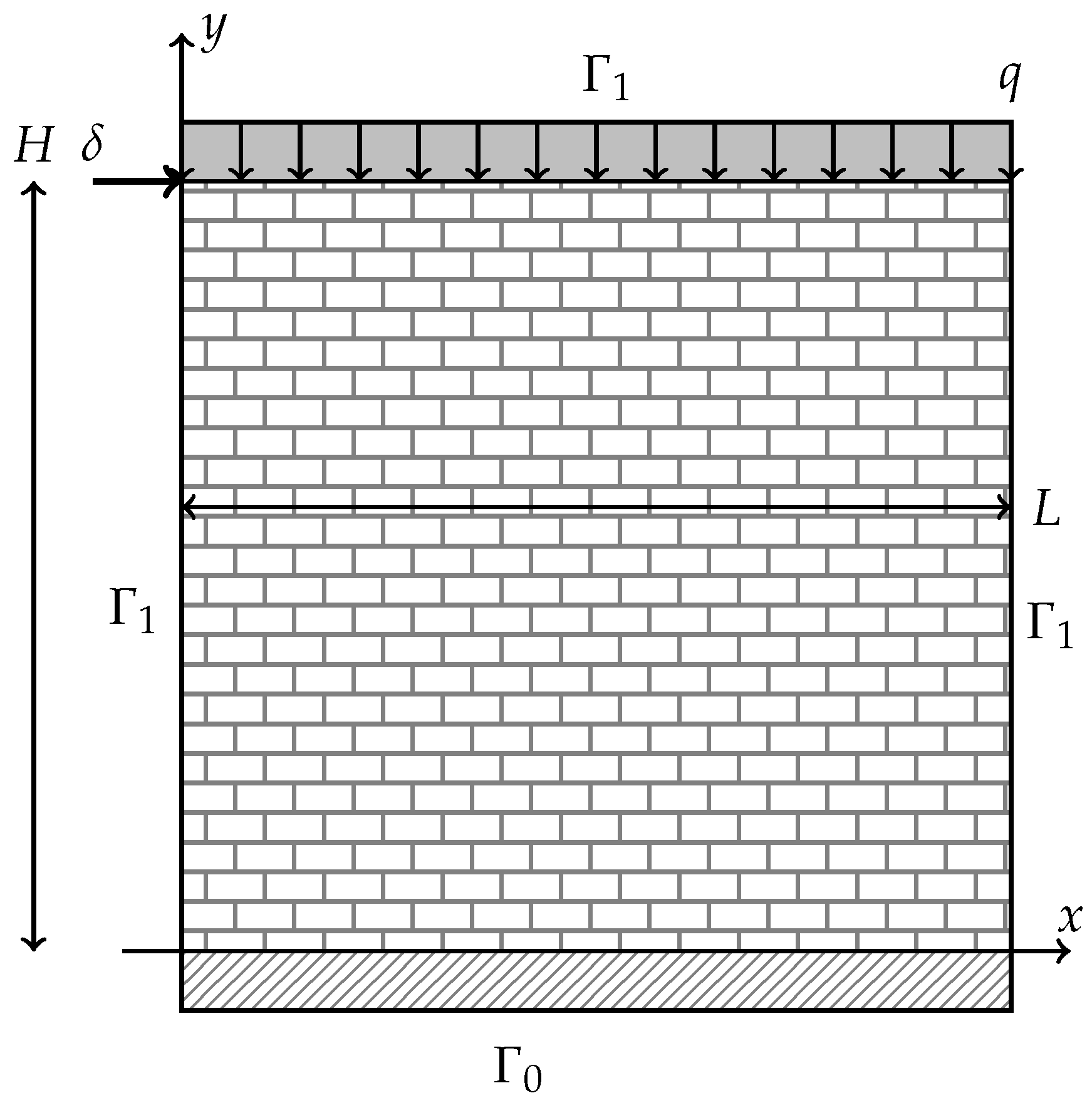
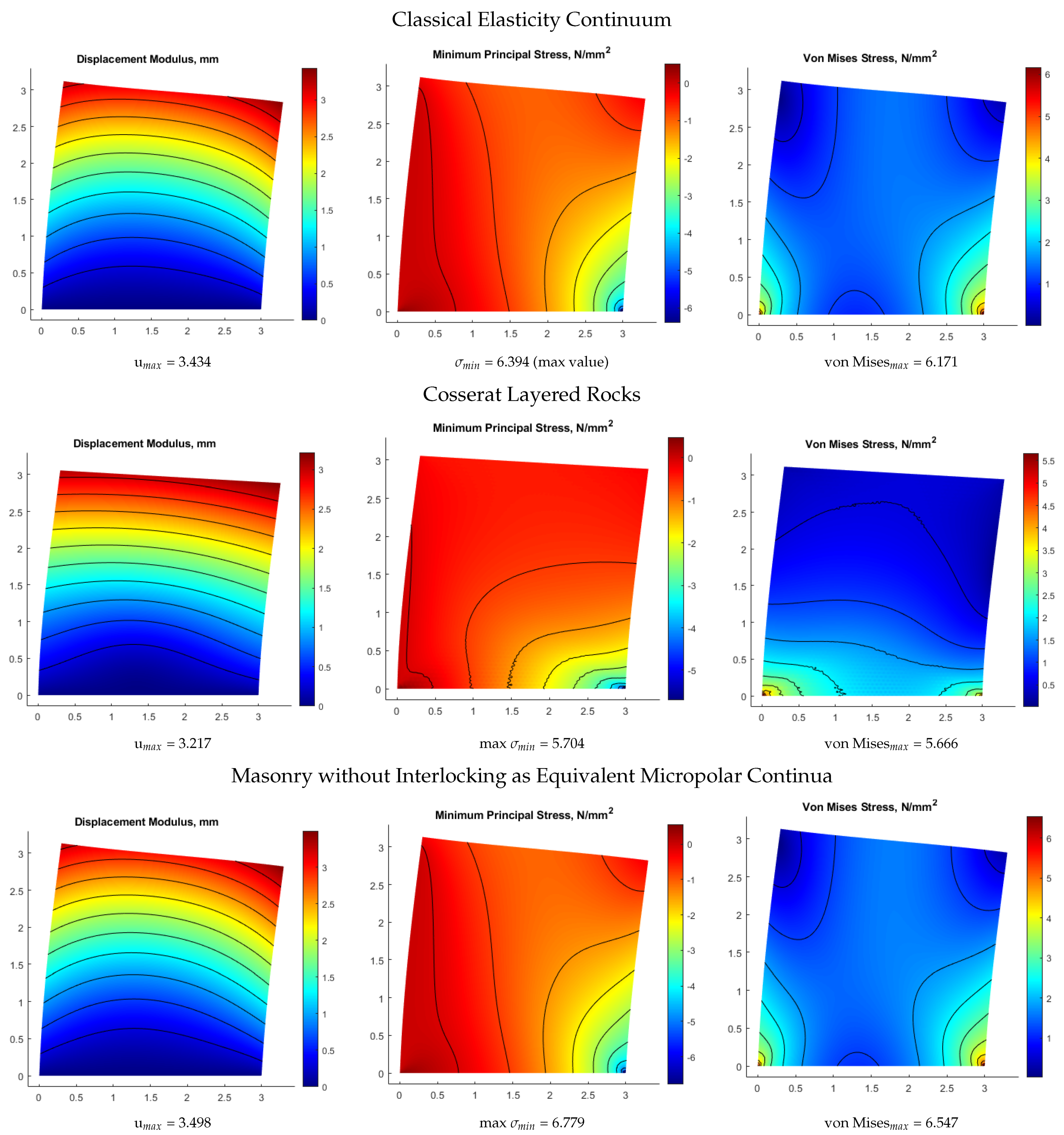
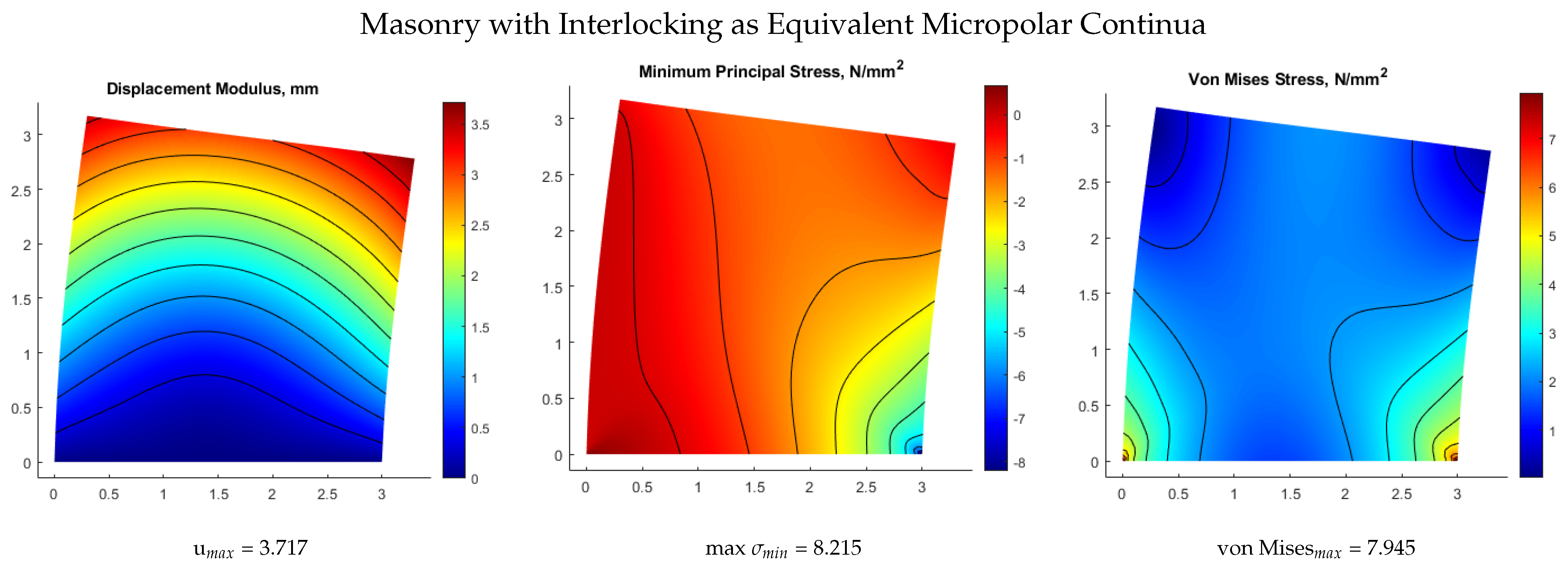
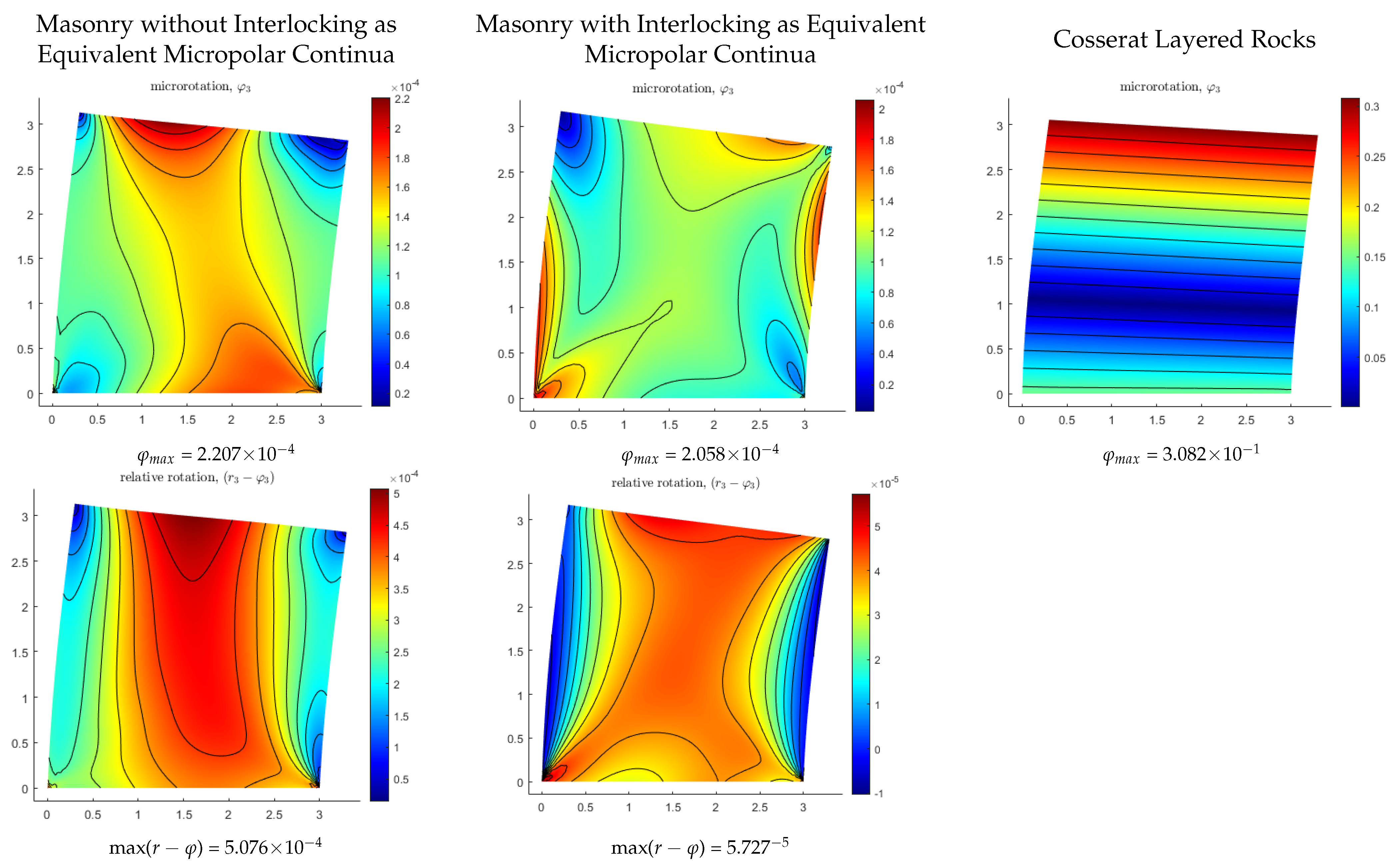
4.3. Numerical Comparison of 2D Micro-Models

In this sub-section, several numerical results related to comparison of the two-dimensional macro-models described in the previous subsections are presented. As a reference example, a wall of the length $L=3$ m and height $H=3$ m is considered, which is subjected to a uniformly distributed load of intensity $q=0.3$ MPa applied to the top of the panel and a point displacement $\delta =0.003$ m applied to the top left corner. The base is fixed in displacements in the x and y directions, and the left and right boundaries are free; see Figure 1.

The following material parameters are chosen for numerical calculations:

• parameters of the classical elasticity: Young’s modulus $E=3655$ MPa and Poisson ratio $\nu =0.15$.
• parameters of the Cosserat model: $h=0.025$ m, $k_n=500$ GPa and $k_s=250$ GPa.
• parameters of the micropolar model: $E_m=780$ MPa, $G_m=\frac{E_m}{2(1+\nu )}$, $d=0.5$ m, $b=0.1$ m and $h=0.025$ m.

The differential equations of the three elasticity theories are solved by using the classical finite element method with triangular quadratic elements with the finest mesh refinement $H/400$ providing elements of the characteristic size $0.0075$ m. The von Mises stress, or the equivalent tensile stress, is chosen as a comparison parameter, because it is typically used in the design of structures for comparing the calculated value to the yield stress of the material. The von-Mises and principal stress are calculated by using an average of the non-symmetric shear stresses ${\sigma }_{21}$ and ${\sigma }_{12}$. Additionally, for relating the numerical results presented in this sub-section with the results of theoretical operator calculus-based estimates provided in Section 3, displacements will be also analysed.

Figure 2 shows the von Mises stresses calculated for different macro-models. As it can be clearly seen from this figure, the stresses observed in the Cosserat layered rocks solution are lower than that of the classical elasticity model, which is expected since the rock layer formulation allow for a weakened horizontal plane allowing for larger displacements. Additionally, the stress profile of the micropolar theory is similar to the one obtained by the classical elasticity, while the Cosserat model provides a slightly different stress profile. The displacement profile is similar for all the models and slightly varies in the magnitude.

Figure 3 presents results of calculations of the relative rotations $r_3-{\phi }_3$ and the micro-rotations ${\phi }_3$ for the Cosserat and mircopolar models. Evidently, micro-rotations ${\phi }_3$ are parallel to the plane of the material layers, which is explained by the applied boundary conditions. The distribution of micro-rotations in the Cosserat layered rock model, micropolar masonry with and without interlocking have major difference. While the micro-rotations in the Cosserat layered rocks formulation runs parallel to the continua, the micro-rotation and relative rotations in the micropolar models tend to resist forces diagonally to the applied loads.

Figure 4 and Figure 5 show further results related to von Mises stress and stress components ${\sigma }_{11}$ and ${\sigma }_{22}$. In particular, Figure 4 shows von Mises stress calculated along the line $y=0$, i.e., in the fixed support. It is important to underline that this result makes sense, since elements of higher regularity are considered and therefore, Sobolev embedding in $C^1$ is satisfied. From these figures, as well as from Figure 2, it is visible that the micropolar model predicts higher stresses in the masonry compared to the classical elasticity. The reason for this is that the models aim to reduce the relative rotations ($r_3-{\phi }_3$) and micro-rotations ${\phi }_3$ with additional stiffness in the formulation. The micro-rotations and relative rotations are less in the interlocked masonry model due to larger rotational stiffness, Figure 3. Higher von Mises stresses are observed in the interlocked masonry walls as a result, Figure 2.

From Figure 4 and Figure 5 it is also visible, that that the values of ${\sigma }_{22}$ in the Cosserat layered rocks model are more concentrated at the bottom of the wall, if compared to the micropolar model and the classical elasticity model. Figure 5 also indicated significant changes in ${\sigma }_{11}$ stress distribution of all three models, which underlines the influence of extra material parameters of the more refined models.

Next for providing further overview of the difference between the three elasticity models, directional strain energies in x and y direction, i.e., normal and tangential strain energy, are calculated:

$$\begin{array}{ccc}\hfill {\displaystyle U_x}& =& {\displaystyle \frac{1}{2}{\int }_v({\sigma }_{11}{\epsilon }_{11}+0.5{\sigma }_{12}{\epsilon }_{12}+0.5{\tau }_{12}{\varphi }_3+{\mu }_{31}{\kappa }_{31})dV,}\hfill \\ \hfill {\displaystyle U_y}& =& {\displaystyle \frac{1}{2}{\int }_v({\sigma }_{22}{\epsilon }_{22}+0.5{\sigma }_{21}{\epsilon }_{21}+0.5{\tau }_{21}{\varphi }_3+{\mu }_{32}{\kappa }_{32})dV.}\hfill \end{array}$$

Table 1. Directional strain energies $U_x$ and $U_y$ in N-m × 10³.

Strain Energy	Classical Elasticity	Cosserat Layered Rocks	Masonry without Interlocking	Masonry with Interlocking
$U_x$	4.502	1.033	7.227	9.586
$U_y$	17.565	18.692	21.374	31.759

shows results of these calculations. From Table 1 and Figure 2, it can be noted that the total strain energy is proportional to the von Mises stress. Additionally, the directional strain components provided in Table 1 indicate the plane of weakness particularly when comparing the directional energy in the classical elasticity continuum and Cosserat continuum.

Finally, the numerical results presented in this section are linked to the theoretical estimates (9) and (10) provided in Section 3. For that purpose,

Table 2. Change in displacements, principal and von Mises stresses for different micro-rotation coefficients in the Cosserat model and its comparison to the micropolar model and the classical elasticity.

Coefficients of ${\mathit{\kappa }}_{31}$ and ${\mathit{\kappa }}_{32}$		$\frac{1}{2}({\mathit{B}}_{2121}-{\mathit{B}}_{1212})$	${\mathit{u}}_{\mathit{max}}$	$max{\mathit{\sigma }}_{\mathit{min}}$	max von Mises
${\mathit{C}}_{11}$	${\mathit{C}}_{22}$		mm	N/mm2	N/mm2
1 × 109	5 × 108	4.536 × 109	3.726	8.240	7.971
1 × 108	5 × 107	4.536 × 109	3.718	8.217	7.948
1 × 107	5 × 106	4.536 × 109	3.717	8.215	7.946
1 × 106	5 × 105	4.536 × 109	3.717	8.215	7.945
1 × 105	5 × 104	4.536 × 109	3.717	8.215	7.945
1 × 104	5 × 103	4.536 × 109	3.717	8.215	7.945
1 × 103	5 × 102	4.536 × 109	3.717	8.215	7.945
1 × 102	5 × 101	4.536 × 109	3.717	8.215	7.945
1 × 101	5 × 100	4.536 × 109	3.717	8.215	7.945
1 × 100	5 × 10−1	4.536 × 109	3.717	8.215	7.945
0	0	4.536 × 109	3.717	8.215	7.945
0	0	0	3.415	6.248	6.029
6.094 × 106	1.219 × 106	4.536 × 109	3.717	8.215	7.945	Micropolar with interlocking
-	-	-	3.434	6.394	6.170	Classical Elasticity

presents results of computing $u_{max}$, $max{\sigma }_{min}$ and maximum von Mises stresses for different values of additional material constants in the macro-model of Cosserat theory. The last two rows of the table show additional computations for the micropolar theory with interlocking and the classical elasticity. As it can be clearly seen from Table 2, the micro-rotation coefficients do not significantly affect the maximum of von Mises stresses unless the coefficients ${\kappa }_{31}$ and ${\kappa }_{32}$ have values of order ${10}^7$ or higher. The values for the coefficient of $\kappa$ used in the numerical example are of order ${10}^6$ (see the row with the micropolar model) and thus do not have a major effect on the stresses. Moreover, the result in Table 2 clearly show that if $\frac{1}{2}(B_{2121}-B_{1212})$ and $-\frac{1}{2}(B_{1212}+B_{2121})+B_{1221}$ are set to 0, then the solution close to the classical elasticity solution, as predicted by estimates (9) and (10). However, it is important to underline that there is still a small difference between these solutions. The reason for this is using of macro-models for computation and not the original differential equations, since the material parameters of the full models are not known.

5. Summary and Conclusions

In this paper, three elasticity theory are discussed and compared: the classical linear elasticity, the Cosserat elasticity, and the micropolar elasticity. The idea of Cosserat and micropolar elasticity is that not only displacements of a continuum are considered, but rotations as well. These theories are expected to describe more accurately materials having cellular structure, or, on a macro level, masonry structures constructed from individual bricks. The obstacle in the way of applying Cosserat and micropolar elasticity in engineering practice is related to additional material constants appearing in these theories. In particular, it is not a trivial task to identify these constants in practice. Therefore, to shed some light on a principal difference between these models, a rigorous quaternionic operator calculus-based analysis of these models is performed and after that we discussed simplified macro-models, which could be used in engineering practice.

Theoretical results presented in this paper are the first of all related to the Cosserat elasticity theory, which has not been considered so far in the setting of quaternionic operator calculus. In this way, explicit representation formulae for the solution of a Dirichlet boundary value problem have been presented, as well as the solvability and uniqueness theorem. Further, several explicit estimates showing the difference between the classical linear elasticity, the Cosserat elasticity, and the micropolar elasticity have been constructed. The main point of these estimate is the fact, that material constant have the biggest influence on the difference between the models. After that the two the general macro-models for the Cosserat elasticity and the micropolar elasticity have been discussed and numerical experiments for these models have been analysed. Numerical results show a difference between the models indicating the tendency of the classical elastic model to underestimate stresses appearing in a structure. The results also indicates Moreover, the results also clearly underline that the material parameters have the major influence on the results of computations with the advanced elasticity models, as it has been predicted by the theoretical estimates. In conclusion, the results of this study indicates that:

• The material constants of micropolar and Cosserat elasticity can be used to introduce anisotropies important for the modeling of masonry structures
• Directional strain energies can be used to identify planes of weakness
• To further evaluate the results of this study, future works should correlate the micropolar and Cosserat material constants to masonry continua based on experiments