Capacity-Oriented Train Scheduling of High-Speed Railway Considering the Operation and Maintenance of Rolling Stock
Abstract
:1. Introduction
- The capacity-oriented train scheduling not only matches train services with the time-space distribution of transportation demand, but also ensures rolling stock maintenance. In this way, we can provide more train services to meet all OD travel demand and ensure the practical operation of rolling stock scheduling.
- A time-space network is designed to describe the operation of rolling stock. Based on this time-space network, an integer programming model is formulated to maximize the number of running arcs, so that we can increase the operating time of rolling stock in rail sections to provide more train services.
- A Lagrangian relaxation-based decomposition algorithm is designed, and it contains two path search sub-algorithms for optimizing the upper and lower bounds corresponding to the relaxation and feasible solutions, respectively. This algorithm can not only solve our model efficiently, but also optimize the quality of train scheduling.
2. Capacity-Oriented Train Scheduling Problem Description
2.1. Time-Space Network Construction
2.1.1. Nodes Construction
2.1.2. Directed Arcs Construction
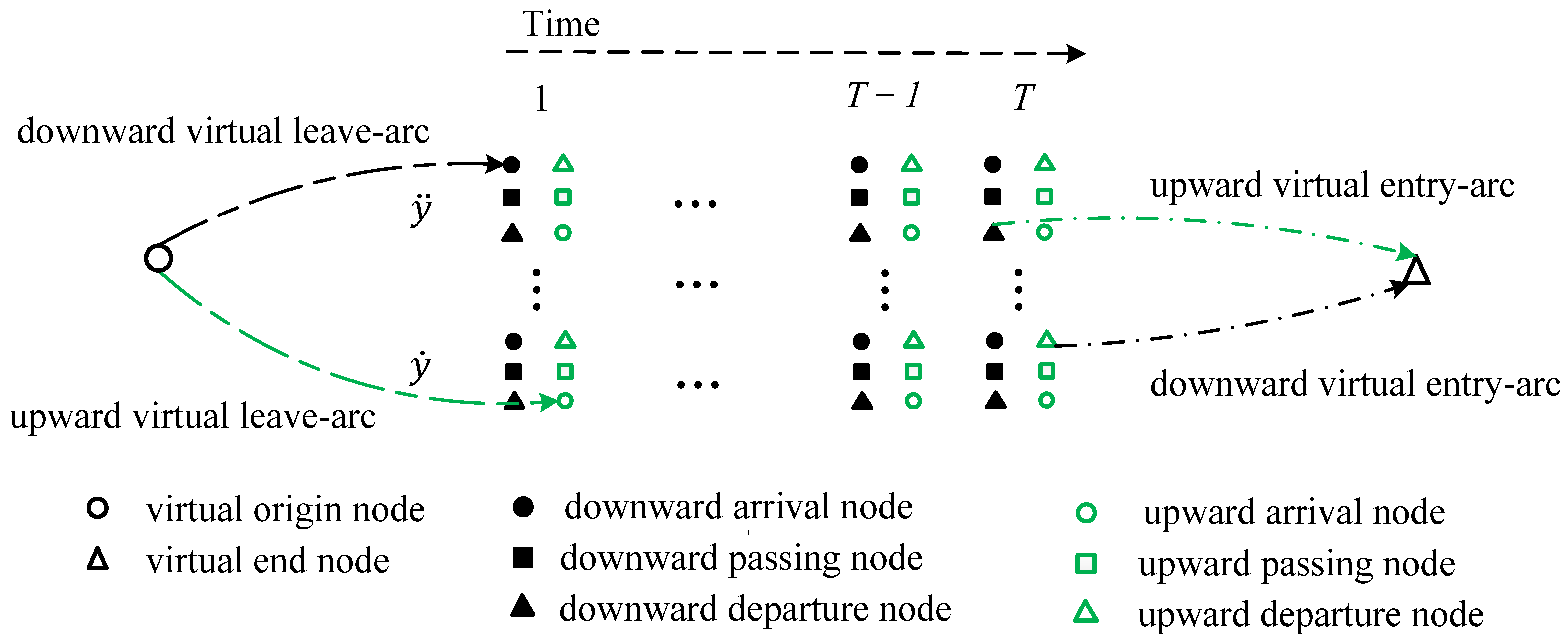
- Virtual arcs
- 2.
- Running arcs in rail sections
- Pass-Pass (P-P for short): when the train does not stop at both the stations and , we construct the pass-pass running arc denoted as from the passing node at station to the passing node at station . This arc means that the train passes through station at time and then passes through station at time , as shown in Figure 2 by the green dotted line with arrows. Obviously, .
- Departure-Pass (D-P for short): when the train stops at station , but passes through station , we construct the departure-pass running arc denoted as from the departure node at station to the passing node at station . This arc means that the train departs from the station at time and then passes through station at time , as shown in Figure 2 by the black dotted line with arrows. In addition, .
- Pass-Arrival (P-A for short): when the train passes through station , but stops at station , we construct the pass-arrival running arc denoted as . from the passing node at station to the arrival node at station . This arc means that the train passes through station at time and then stops at station at time , as shown in Figure 2 by the red dotted line with arrows. In addition, .
- Departure-Arrival (D-A for short): when the train stops at both station and station , we construct the departure-arrival running arc denoted as from the departure node at station to the arrival node at station . This arc means that the train departs from station at time and then stops at station at time , as shown in Figure 2 by the blue dotted line with arrows. In addition, .
- 3.
- Dwell arcs
- 4.
- Stopping sign arcs
- 5.
- Turnaround sign arcs
2.1.3. Time-Space Network Characteristics
- As to the nodes, while the traditional time-space network consists of a set of arrival and passing nodes corresponding to every station and time, we add a kind of nodes called passing nodes. Based on the combination of three nodes, the different types of running arcs are constructed to solve the problem of the running time being affected by stops. Moreover, we set the direction for all nodes. In addition, the sign arcs about stops and turnaround can more directly indicate the changes in state, direction and location of a rolling stock unit over time.
- A continuous path from virtual origin node to virtual end node corresponds to a rolling stock unit’s possible schedule. The running arcs enable the running of a train service, and after the train service, the rolling stock service does not finish, but continues to run another train service, or it goes back to the depot.
2.2. Candidate Stop Plans
2.3. Problem Description and Symbol Definition
2.3.1. Assumptions
- The rail line is a double-track high-speed railway, and both the stations and the depots are regarded as nodes without capacity. The depots are connected to two terminal stations of the rail line, regardless of the path between the station and the depot.
- On the rail line, there are only two terminal stations with turnaround conditions, and all rolling stock units must turn around at these two stations.
- The number of rolling stock units is provided and they are of the same type. In addition, depots are functionally divided into parking depots and maintenance depots. The latter can provide maintenance services.
- The operating time is discretized into a series of equal time intervals, and the time unit is 1 min.
- The transportation demand on this rail line is large enough and the rolling stock units do not have to light run along the track segment (i.e., run with no passengers).
2.3.2. Input and Output
3. Optimization Model of Capacity-Oriented Train Scheduling
3.1. Objective Function
3.2. The Constraints
3.2.1. Constraints Related to the Single Rolling Stock Unit Operation
- Flow balance constraints.
- 2.
- Constraint on the minimum and maximum dwell time at stations in different time periods.
- 3.
- Constraint on the minimum and maximum turnaround time at stations.
- 4.
- Constraint on rolling stock daily maintenance.
- 5.
- Constraint on running time in rail sections.
- 6.
- Constraints on consistency between OD service variables and stop variables.
3.2.2. Association Constraints among Multiple Rolling Stock Units
- Balance constraint on the number of rolling stock units leaving and entering the depot in the morning and evening.
- 2.
- Constraints on arrival and departure intervals.
- 3.
- Constraint on OD service frequency in different time periods.
4. Lagrangian Relaxation Decomposition Model
4.1. Equivalent Minimization Model EM
4.2. Lagrangian Relaxation Decomposition Based on Rolling Stock
5. Algorithm Design Based on Lagrange Relaxation Decomposition
5.1. The Solving Framework of Lagrange Relaxation Decomposition Algorithm
- (1)
- The iteration number reaches its maximum limit .
- (2)
- All sub-gradients are no more than the given standard values .
- (3)
- The number of continuous iterations without improving the lower bound reaches the maximum limit , where the judgment principle of the unimproved lower bound is as follows:where and are the lower bounds of the and iterations, respectively, and ε is the given calculation accuracy.
| Algorithm 1: Algorithm based on Lagrange relaxation decomposition |
| Input: rail line, number of rolling stock, set of alternative stop plans Output: Optimal feasible solution and its upper bound Start Step 1: Initialization Let iteration index , initial multiplier update step size , Lagrangian multipliers . Step 2: Calculate the Lagrangian cost and according to formulations (16) and (17), respectively. Step 3: (Solving the relaxation model RM to achieve a relaxed solution and its lower bound) Achieve a relaxed solution using the relaxation solution generation sub-algorithm introduced in Section 5.2. Search the shortest paths for rolling stock based on the Lagrange cost of arcs one by one in any order. Step 4: (Generating a feasible solution and its upper bound based on the relaxed solution)Achieve a feasible solution using the feasible solution generation sub-algorithm introduced in Section 5.3. Search the shortest paths for rolling stock based on the weights of arcs one by one in ascending priority order. Step 5: The sub-gradient is updated according to formulations (25) to (28). Step 6: (Termination conditions) If all termination conditions are not satisfied, then update the Lagrange multipliers according to formulations (29) to (32), and return to step 2. Otherwise, the procedure is terminated. End |
5.2. Sub-Algorithm of Generating the Relaxed Solution
| Algorithm 2: Single rolling stock shortest path search algorithm based on label idea |
| Input: operation time , node set, arc set, number of rolling stock, candidate stop plan set, stop time parameters, turnaround time parameters Output: Relaxation solution and its upper bound Start Step 1: Initialization Add label to set and let other label sets equal to . Let set , set Step 2: Label checking and updating Select each label in set one by one, execute Select sub-path units from node of label one by one, and execute If , execute Add the label to label set of the node , and set its subordinate nodes , total cost and pre-label . If , execute If the time of the nodes contained in sub-path unit are all within the operation time , execute Calculate the total cost of the sub-path unit and the OD service cost of the stop plan. If , execute Let , , and add label to set . Step 3: Judgment termination condition Let . Find the minimum cost label in and transfer it to and If there is label in and its node is the virtual end point , go to step 4. Otherwise, return to step 2. Step 4: Backtracking primary path and determining all subordinate paths Traceback the path from node of label according to the node and the path unit of pre-label End |
5.3. Sub-Algorithm of Generating Feasible Solution Based on the Relaxed Solution
- Path search is based on the total weights of arcs contained in each path unit. To be exact, it aims to find the path with the minimum total weights of arcs, rather than the path with the minimum total Lagrangian cost of arcs. For simplicity, the symbols and in this section are redefined as the total weights of arcs.
- In order to satisfy the OD service frequency constraints, there are two options when searching a path for the current rolling stock unit. If the generated rolling stock paths have not satisfied the minimum service frequency requirements of each OD, it will select the sub-path unit that is most conductive to improving the OD service frequency according to the greedy principle. Otherwise, when all OD service frequencies in the generated paths have met the requirements, it will select the sub-path unit with the minimum number of stops (i.e., the sub-path unit with minimum total weights of arcs). The matching degree of service OD of each stop plan is calculated as follows:
- In order to satisfy constraints on arrival and departure intervals related to multiple rolling stock units, the restricted arc set is determined in advance. No arcs in the set are allowed to be selected, otherwise the safe headway conflict will occur. The restricted arc set consists of running arcs that are occupied by high priority rolling stock units and the related running arcs that do not conform to their safe interval constraints. Let be denoted as the set of all running arcs selected by the scheduled rolling stock paths, then restrict arc set. can be determined as follows:
- In order to meet the rolling stock maintenance constraint we must ensure that all rolling stock units can enter the maintenance depot within 48 h. Thus, for each rolling stock unit, if it starts from the virtual leave-arc related to the maintenance depot, it can choose any virtual entry-arc to return to the virtual end node. Otherwise, it can only return to the virtual end point by the virtual entry-arc related to the maintenance depot. In this way, we can guarantee that all rolling stock units stay one night every two days at the maintenance depot to receive maintenance.
| Algorithm 3: Heuristic algorithm for generating feasible solutions |
| Input: operation time , node set, arc set, number of rolling stock, candidate stop plan set, dwell time parameters, turnaround time parameters Output: Feasible solution and upper bound Start Step 1: Initialization Let . Rank all rolling stock in ascending order according to their optimal function value in model SRM. The priority order is represented as . Step 2: Search rolling stock path one by one Select rolling stock in priority order , execute Step 2.1: Initialization Add label to set and let other label sets equal to . Let , Step 2.2: Judging the balance between entering and leaving the depot Judge whether the rolling stock starting from the depot with maintenance capability can return to the depot and adjust the virtual arc of returning to the depot. Step 2.3: Restricted arc set updating Update according to the restricted arc set update method. Step 2.4: Label checking and updating Select each label in the set one by one, execute Select sub-path units from node of label one by one, execute If the sub-path unit is not a dwell arc, execute The combination of greedy principle and shortest path principle is used to select the optimal sub-path unit for node . If , execute Add the label to the label set of node , and let , , . If , execute If the time of the nodes contained in is within the time , execute Calculate the total cost of the sub-path unit. If , execute let , and add . Step 2.5: Termination conditions Let . Find the label with the lowest cost in and transfer it to and . If and node is node , go to Step 2.6. Otherwise, return to Step 2.4. Step 2.6: Backtracking primary path and determining all subordinate paths Traceback the path from node of label according to the node and the sub-path unit of pre-label. End |
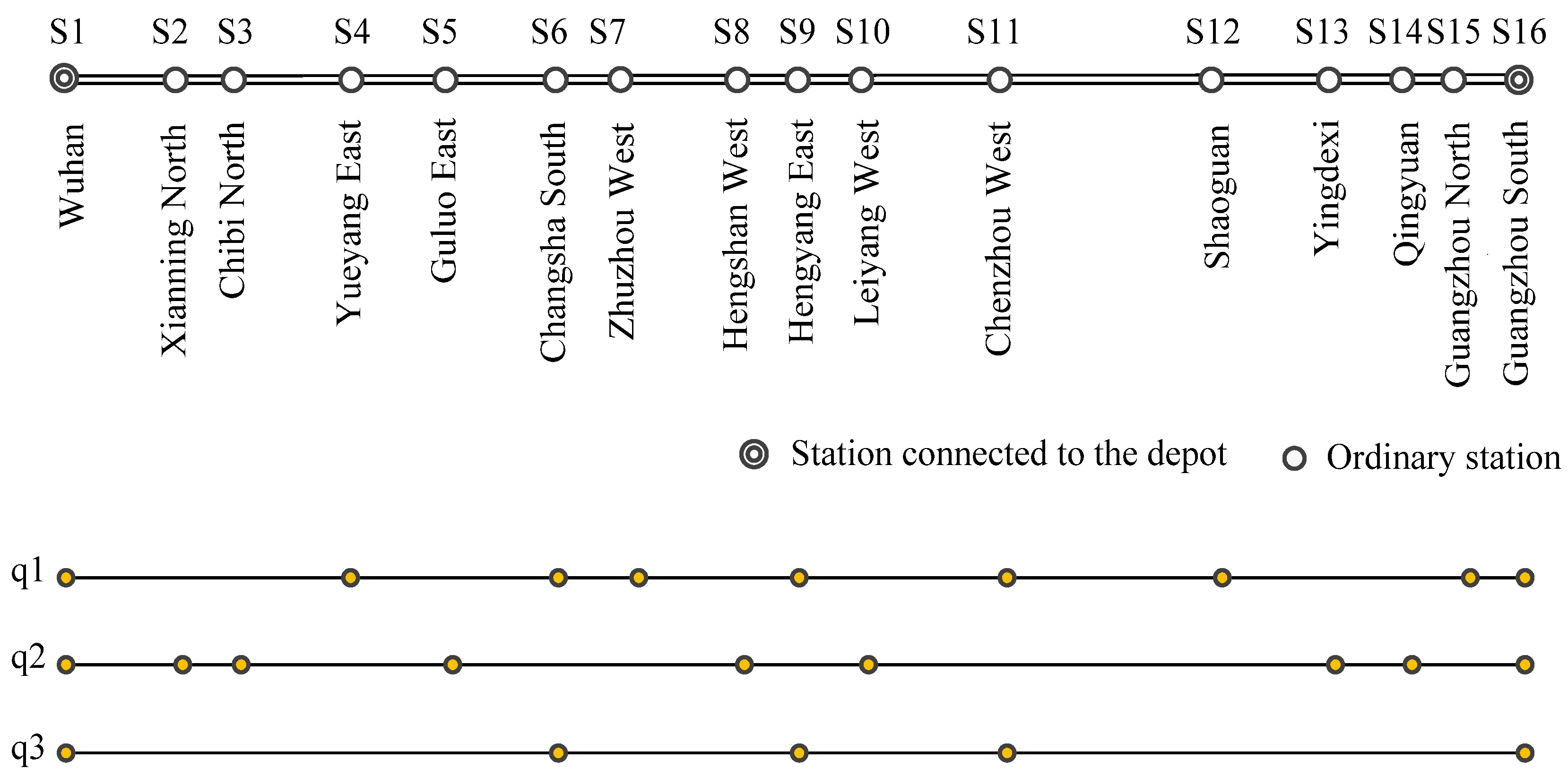
6. Case Study
6.1. Experiment Setup
6.2. Analysis with the Computational Results
- Upper bound (UB): the optimal objective value of model EM. This corresponds to a feasible solution.
- Trans scheduled: the maximum number of trains that can be included in the train timetable.
- Capacity utilization (CU): indicating the transportation capacity in a train timetable which is the ratio of the number of scheduled trains to the ideal number of trains.
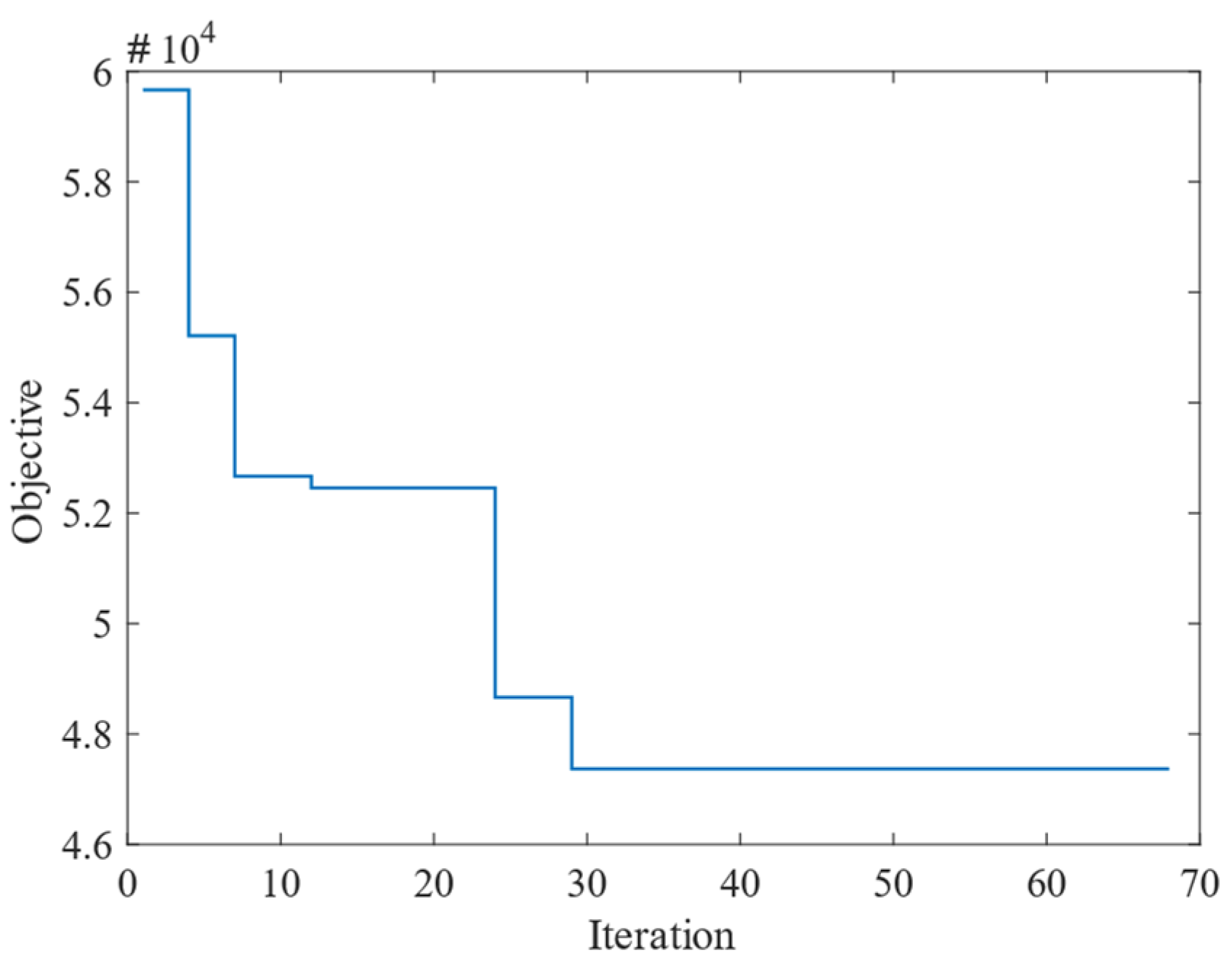
6.2.1. Computational Results
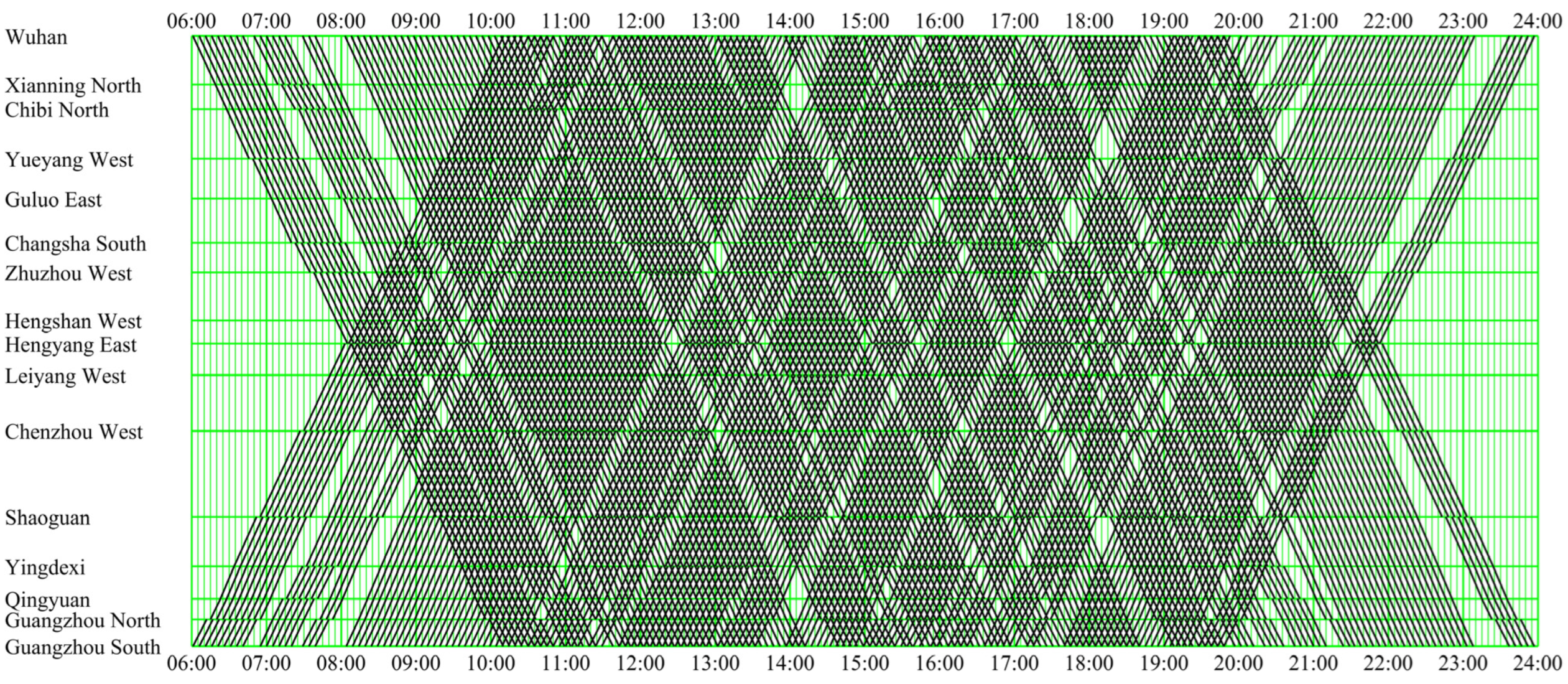
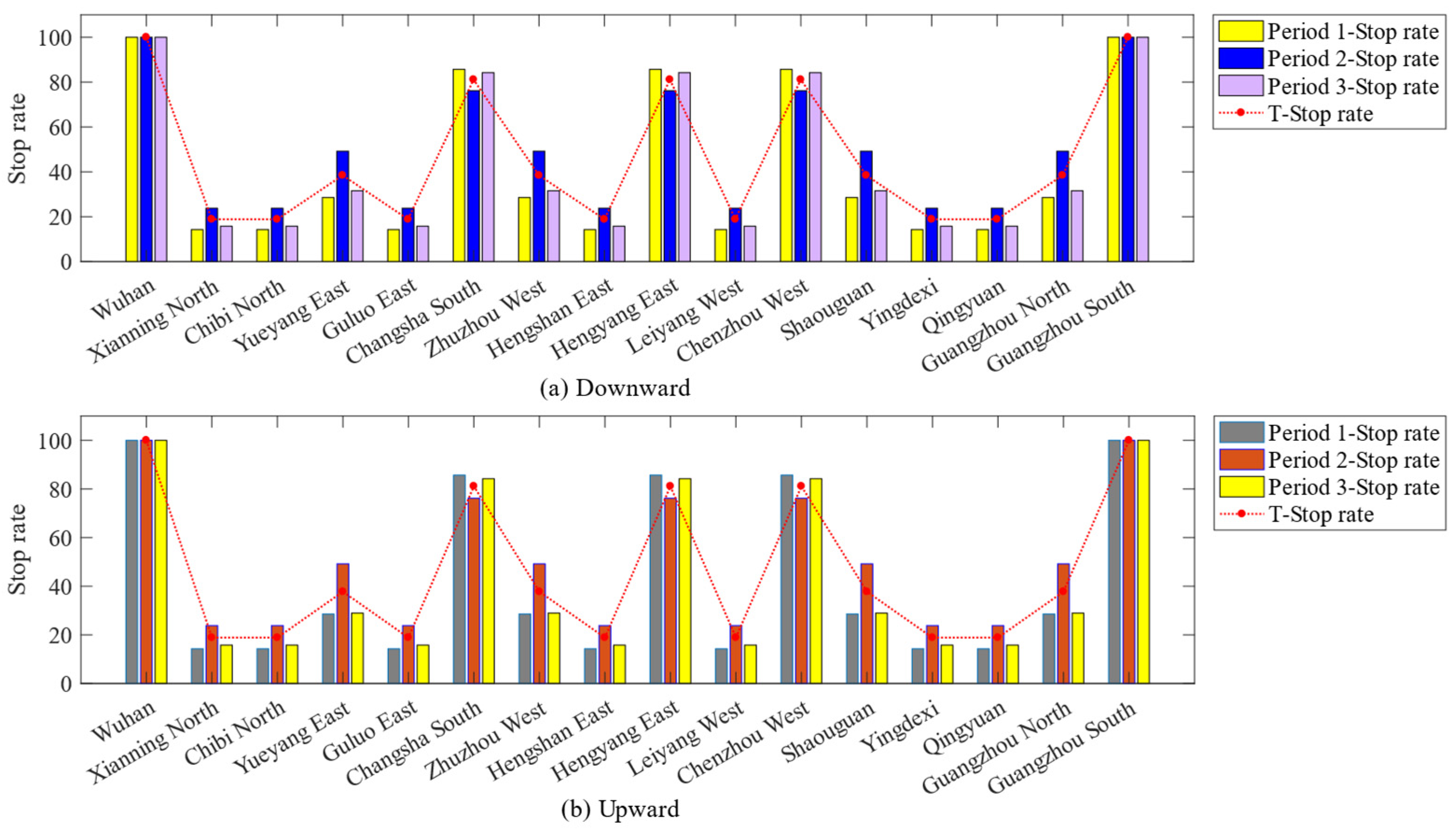
6.2.2. Analysis of the Turnaround Efficiency of Rolling Stock
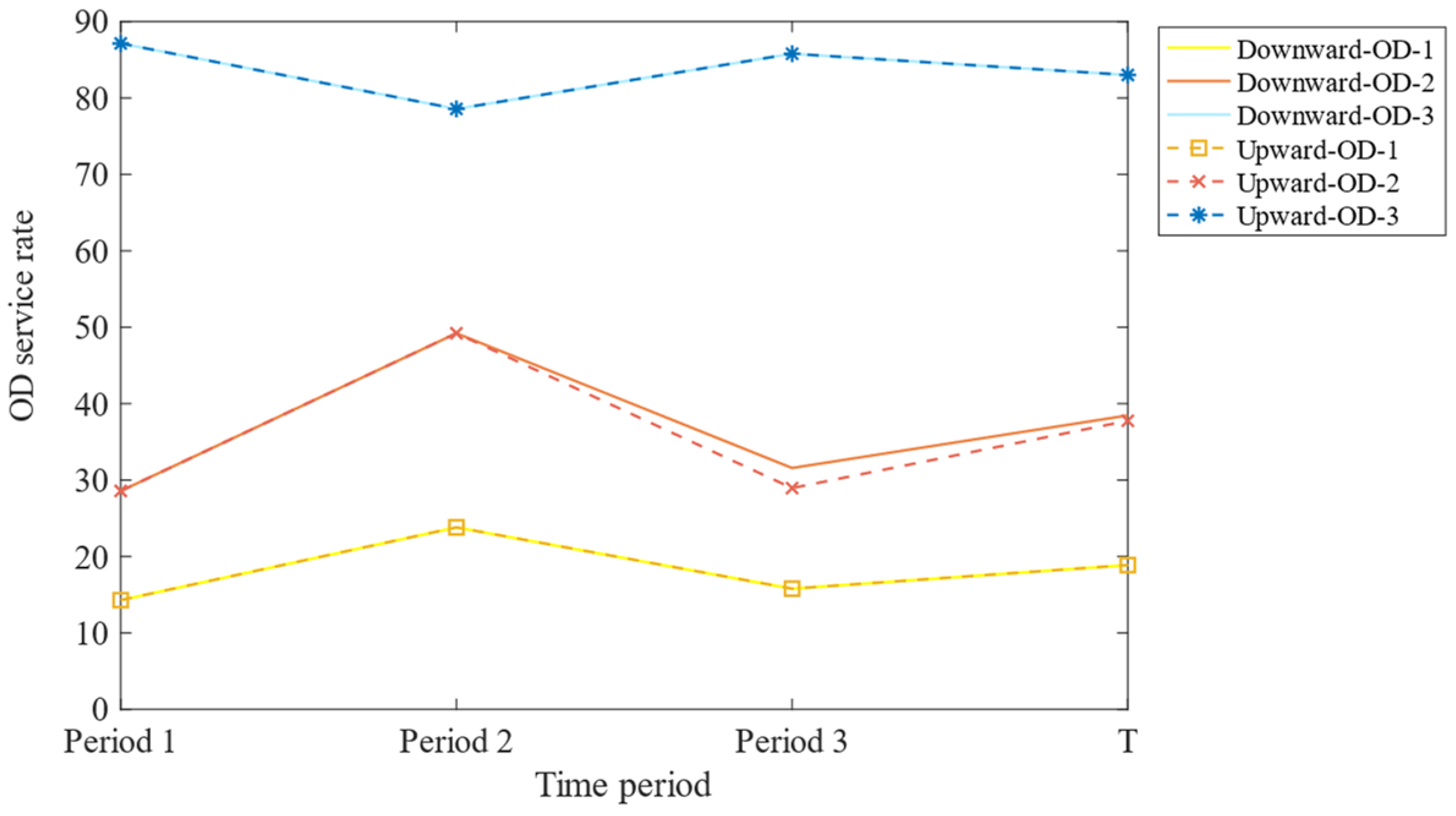
6.2.3. Analysis of OD Service Quality
6.2.4. Analysis of the Quality of Train Services
6.3. Analysis of Sensitivity
6.3.1. Analysis of Sensitivity Based on Rolling Stock Amount
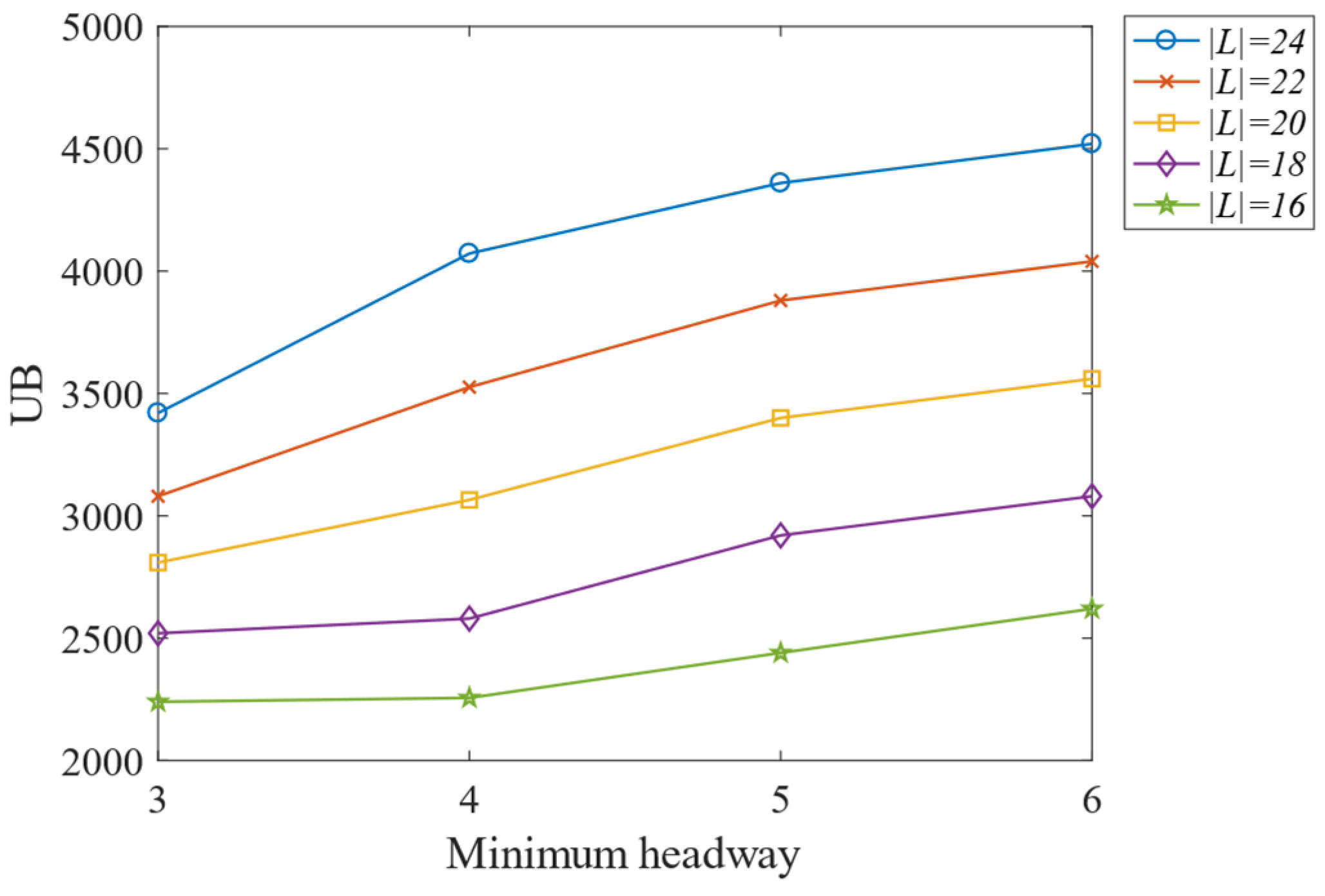
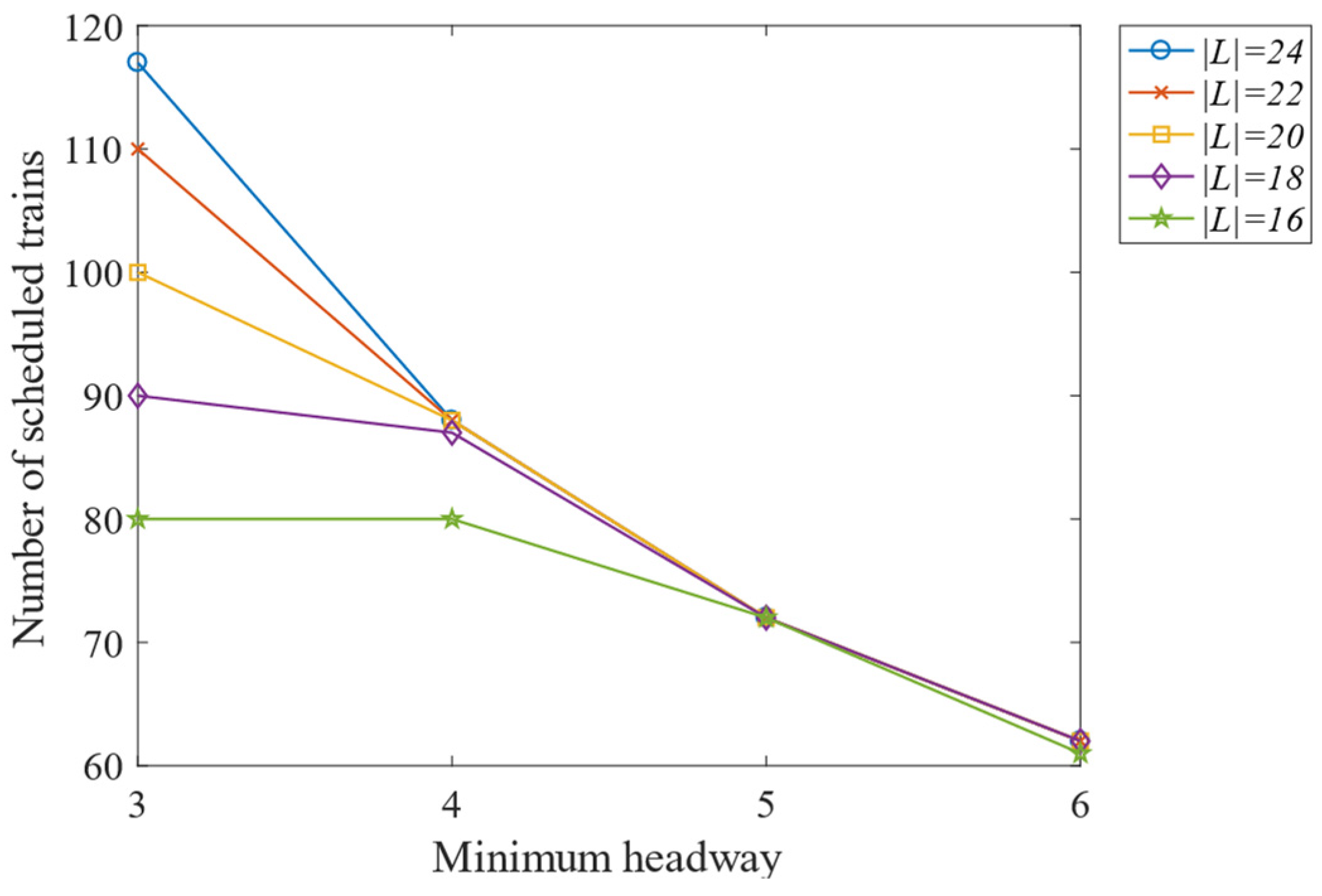
6.3.2. Analysis of Sensitivity Based on Minimum Headway
7. Conclusions and Further Study
- The proposed method is proved to improve the overall transportation capacity by solving a practical instance. The computational results show that we can obtain a saturate train timetable, and the maximum capacity utilization is 91.53%, which closely approximates the expected maximum capacity of the rail line.
- The approach first allows quantifying the impact of rolling stock operations and maintenance aspects into transportation capacity optimization. The optimization result shows that good coordination between train timetable and rolling stock circulation helps improve capacity. Furthermore, the train scheduling can optimize the stop rate and OD service frequency to well match the time-space distribution of passenger demands. Meanwhile, the rolling stock scheduling achieves a high turnaround efficiency and ensures the daily maintenance of rolling stock.
- From a comprehensive sensitivity analysis, increasing rolling stock amounts and reducing the minimum headway are obvious ways to improve capacity. However, the level of rolling stock shortage determines the effect of increasing capacity by reducing the minimum headway. Abundant rolling stock is more beneficial to improvement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Sections | Minimum Running Times/min |
|---|---|
| s1–s2 | 4 |
| s2–s3 | 4 |
| s3–s4 | 6 |
| s4–s5 | 6 |
| Sections | Down Direction | Up Direction | ||
|---|---|---|---|---|
| Time Period 1 | Time Period 2 | Time Period 1 | Time Period 2 | |
| s1–s2 | 5 | 10 | 5 | 10 |
| s1–s3 | 5 | 10 | 5 | 10 |
| s1–s4 | 5 | 10 | 5 | 10 |
| s1–s5 | 5 | 10 | 5 | 10 |
| s2–s3 | 5 | 10 | 5 | 10 |
| s2–s4 | 5 | 10 | 5 | 10 |
| s2–s5 | 5 | 10 | 5 | 10 |
| s3–s4 | 5 | 10 | 5 | 10 |
| s3–s5 | 5 | 10 | 5 | 10 |
| s4–s5 | 5 | 10 | 5 | 10 |
| Parameters | Values | Units |
|---|---|---|
| 240 | min | |
| [1, 119; 120, 240] | min | |
| [] | - | |
| Minimum turn-around time | 10 | min |
| Minimum dwell time | 2 | min |
| Maximum dwell time | 4 | min |
| Minimum turnaround time | 10 | min |
References
- Shi, F.; Wei, T.; Zhou, W.; Luo, X. Optimization method for train diagram of high-speed railway considering the turnover of multiple units and the utilization of arrival-departure tracks. Zhongguo Tiedao Kexue 2012, 33, 107–114. [Google Scholar] [CrossRef]
- Zhou, W.; Qu, L.; Shi, F.; Deng, L. Train scheduling on high-speed rail network based on fixed order optimization. J. Railw. Sci. Eng. 2018, 15, 551–558. [Google Scholar] [CrossRef]
- Cacchiani, V.; Caprara, A.; Toth, P. A column generation approach to train timetabling on a corridor. 4OR 2008, 6, 125–142. [Google Scholar] [CrossRef]
- Xu, X.; Li, K.; Yang, L. Scheduling heterogeneous train traffic on double tracks with efficient dispatching rules. Transp. Res. Part B Methodol. 2015, 78, 364–384. [Google Scholar] [CrossRef]
- Li, K.; Huang, H.; Schonfeld, P. Metro timetabling for time-varying passenger demand and congestion at stations. J. Adv. Transp. 2018, 2018, 3690603. [Google Scholar] [CrossRef]
- Shafia, M.A.; Aghaee, M.P.; Sadjadi, S.J.; Jamili, A. Robust train timetabling problem: Mathematical model and branch and bound algorithm. IEEE Trans. Intell. Transp. Syst. 2011, 13, 307–317. [Google Scholar] [CrossRef]
- Su, S.; Li, X.; Tang, T.; Gao, Z. A subway train timetable optimization approach based on energy-efficient operation strategy. IEEE Trans. Intell. Transp. Syst. 2013, 14, 883–893. [Google Scholar] [CrossRef]
- Bešinović, N.; Goverde, R.M.P.; Quaglietta, E.; Roberti, R. An integrated micro--macro approach to robust railway timetabling. Transp. Res. Part B Methodol. 2016, 87, 14–32. [Google Scholar] [CrossRef] [Green Version]
- Robenek, T.; Maknoon, Y.; Azadeh, S.S.; Chen, J.; Bierlaire, M. Passenger centric train timetabling problem. Transp. Res. Part B Methodol. 2016, 89, 107–126. [Google Scholar] [CrossRef] [Green Version]
- Goerigk, M.; Schöbel, A. Improving the modulo simplex algorithm for large-scale periodic timetabling. Comput. Oper. Res. 2013, 40, 1363–1370. [Google Scholar] [CrossRef]
- Wong, R.C.W.; Yuen, T.W.Y.; Fung, K.W.; Leung, J.M.Y. Optimizing timetable synchronization for rail mass transit. Transp. Sci. 2008, 42, 57–69. [Google Scholar] [CrossRef]
- Kroon, L.G.; Peeters, L.W.P.; Wagenaar, J.C.; Zuidwijk, R.A. Flexible connections in PESP models for cyclic passenger railway timetabling. Transp. Sci. 2014, 48, 136–154. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Zhang, Y.; Zhang, Z.; Yang, L. Optimization of train timetables in high-speed railway corridors considering passenger departure time and seat-class preferences. Transp. Lett. 2022, 1–18. [Google Scholar] [CrossRef]
- Chen, A.; Zhang, X.; Chen, J.; Wang, Z. Joint optimization of high-speed train timetables, speed levels and stop plans for increasing capacity based on a compressed multilayer space-time network. PLoS ONE 2022, 17, e0264835. [Google Scholar] [CrossRef]
- Boroun, M.; Ramezani, S.; Vasheghani Farahani, N.; Hassannayebi, E.; Abolmaali, S.; Shakibayifar, M. An efficient heuristic method for joint optimization of train scheduling and stop planning on double-track railway systems. INFOR Inf. Syst. Oper. Res. 2020, 58, 652–679. [Google Scholar] [CrossRef]
- Lu, C.; Zhou, L.; Chen, R. Optimization of high-speed railway timetabling based on maximum utilization of railway capacity. J. Railw. Sci. Eng. 2018, 15, 32–40. [Google Scholar] [CrossRef]
- Dong, Z.H.A.O.; Siji, H.U. Research of new method of capacity calculation for passenger flow section of high-speed railway. J. China Railw. Soc. 2018, 9, 1–6. [Google Scholar] [CrossRef]
- Harrod, S. Modeling network transition constraints with hypergraphs. Transp. Sci. 2011, 45, 81–97. [Google Scholar] [CrossRef]
- Azadi Moghaddam Arani, A.; Jolai, F.; Nasiri, M.M. A multi-commodity network flow model for railway capacity optimization in case of line blockage. Int. J. Rail Transp. 2019, 7, 297–320. [Google Scholar] [CrossRef]
- Olsson, N.O. Train punctuality analysis in a rolling stock perspective. Transp. Res. Procedia 2020, 47, 641–647. [Google Scholar] [CrossRef]
- Veelenturf, L.P.; Kidd, M.P.; Cacchiani, V.; Kroon, L.G.; Toth, P. A railway timetable rescheduling approach for handling large-scale disruptions. Transp. Sci. 2016, 50, 841–862. [Google Scholar] [CrossRef] [Green Version]
- Liao, Z.; Li, H.; Miao, J.; Corman, F. Railway capacity estimation considering vehicle circulation: Integrated timetable and vehicles scheduling on hybrid time-space networks. Transp. Res. Part C Emerg. Technol. 2021, 124, 102961. [Google Scholar] [CrossRef]
- Giacco, G.L.; Carillo, D.; D’Ariano, A.; Pacciarelli, D.; Marín, Á.G. Short-term rail rolling stock rostering and maintenance scheduling. Transp. Res. Procedia 2014, 3, 651–659. [Google Scholar] [CrossRef]
- Zhong, Q.; Lusby, R.M.; Larsen, J.; Zhang, Y.; Peng, Q. Rolling stock scheduling with maintenance requirements at the Chinese High-Speed Railway. Transp. Res. Part B Methodol. 2019, 126, 24–44. [Google Scholar] [CrossRef] [Green Version]
- Caprara, A.; Fischetti, M.; Toth, P. Modeling and solving the train timetabling problem. Oper. Res. 2002, 50, 851–861. [Google Scholar] [CrossRef]
- Xu, X.; Li, C.L.; Xu, Z. Integrated train timetabling and locomotive assignment. Transp. Res. Part B Methodol. 2018, 117, 573–593. [Google Scholar] [CrossRef]
- Meng, L.; Zhou, X. Simultaneous train rerouting and rescheduling on an N-track network: A model reformulation with network-based cumulative flow variables. Transp. Res. Part B Methodol. 2014, 67, 208–234. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Soumis, F.; Desrosiers, J. A Benders decomposition approach for the locomotive and car assignment problem. Transp. Sci. 2000, 34, 133–149. [Google Scholar] [CrossRef]







| Described Objects | Symbols | Definitions |
|---|---|---|
| Railway network | Set of rail sections | |
| The set of OD | ||
| The set of stations | ||
| Index of station, | ||
| The set of depots | ||
| Parking depot, | ||
| Maintenance depot, | ||
| Set of stations with turnaround capability, | ||
| Rolling stock | Set of rolling stock units | |
| Index of rolling stock unit, | ||
| Total number of rolling stock units | ||
| Time-space network | Set of nodes | |
| Index of time | ||
| Up or down direction of the rail line | ||
| Index of node, | ||
| Set of entry arcs connected with the node | ||
| Set of leave arcs connected with the node | ||
| Arrival node of station at time on direction | ||
| Departure node of station at time on direction | ||
| Passing node of station at time on direction | ||
| Virtual origin node of the rolling stock path, | ||
| Virtual end node of the rolling stock path, | ||
| Set of arcs | ||
| Index of arc, | ||
| Virtual leave-arc connecting to the depot | ||
| Virtual entry-arc connecting to the depot | ||
| Dwelling arc of station in direction at time | ||
| Stopping sign arc of station in direction at time | ||
| Turnaround sign arc of station at time | ||
| Running arc, which means leaving station at time and arriving at station at time | ||
| Set of running arcs, | ||
| Set of dwell arcs, | ||
| Set of running arcs that leave the station at time and enter the section | ||
| Set of running arcs that arrive at the station at time and leave the section | ||
| Parameters | Minimum running time in the section | |
| Additional time for the train decelerating | ||
| Additional time for the train accelerating | ||
| Minimum dwelling time for rolling stock from direction to stop at station within the time period of time | ||
| Maximum dwelling time for rolling stock from direction to stop at station within the time period of time | ||
| Minimum turnaround time of rolling stock in station | ||
| Maximum turnaround time of rolling stock in station | ||
| Train departure interval time | ||
| Train arrival interval time | ||
| Minimum travel time from station to station n | ||
| Maximum travel time from station to station n | ||
| Minimum service frequency of OD | ||
| Other | Infinity | |
| Operating time period | ||
| Time period | ||
| The initial time of a period | ||
| The end time of a period |
| Variables | Definitions |
|---|---|
| 0–1 decision variables, if the rolling stock unit selects arc , then , otherwise | |
| 0–1 variable, if the rolling stock unit serves OD in the time period related to time , , otherwise |
| Lagrange Multipliers | Define Scope | Related Constraints |
|---|---|---|
| Equation (9) | ||
| Equation (10) | ||
| Equation (11) | ||
| Equation (12) |
| Symbols | Meaning |
|---|---|
| Set of labels of node | |
| The index of label, | |
| Node to which label belongs, if | |
| Time of node | |
| Station to which node belongs | |
| Total Lagrangian costs for the path from virtual starting point to node belonging to label | |
| Pre-label of label | |
| Sub-path unit from node to node by stop plan | |
| Total Lagrangian costs of directed arcs in a path unit | |
| Total cost of the served by stop plan | |
| Set of labels have been checked | |
| Set of labels have been checked by the latest updating | |
| Set of temporary storing labels |
| OD | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 | S13 | S14 | S15 | S16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 0 | 27 | 27 | 40 | 27 | 53 | 40 | 27 | 53 | 27 | 53 | 40 | 27 | 27 | 40 | 53 |
| S2 | 27 | 0 | 27 | 0 | 27 | 0 | 0 | 27 | 0 | 27 | 0 | 0 | 27 | 27 | 0 | 27 |
| S3 | 27 | 27 | 0 | 0 | 27 | 0 | 0 | 27 | 0 | 27 | 0 | 0 | 27 | 27 | 0 | 27 |
| S4 | 40 | 0 | 0 | 0 | 0 | 40 | 40 | 0 | 40 | 0 | 40 | 40 | 0 | 0 | 40 | 40 |
| S5 | 27 | 27 | 27 | 0 | 0 | 0 | 0 | 27 | 0 | 27 | 0 | 0 | 27 | 27 | 0 | 27 |
| S6 | 53 | 0 | 0 | 40 | 0 | 0 | 40 | 0 | 53 | 0 | 53 | 40 | 0 | 0 | 40 | 53 |
| S7 | 40 | 0 | 0 | 40 | 0 | 40 | 0 | 0 | 40 | 0 | 40 | 40 | 0 | 0 | 40 | 40 |
| S8 | 27 | 27 | 27 | 0 | 27 | 0 | 0 | 0 | 0 | 27 | 0 | 0 | 27 | 27 | 0 | 27 |
| S9 | 53 | 0 | 0 | 40 | 0 | 53 | 40 | 0 | 0 | 0 | 53 | 40 | 0 | 0 | 40 | 53 |
| S10 | 27 | 27 | 27 | 0 | 27 | 0 | 0 | 27 | 0 | 0 | 0 | 0 | 27 | 27 | 0 | 27 |
| S11 | 53 | 0 | 0 | 40 | 0 | 53 | 40 | 0 | 53 | 0 | 0 | 40 | 0 | 0 | 40 | 53 |
| S12 | 40 | 0 | 0 | 40 | 0 | 40 | 40 | 0 | 40 | 0 | 40 | 0 | 0 | 0 | 40 | 40 |
| S13 | 27 | 27 | 27 | 0 | 27 | 0 | 0 | 27 | 0 | 27 | 0 | 0 | 0 | 27 | 0 | 27 |
| S14 | 27 | 27 | 27 | 0 | 27 | 0 | 0 | 27 | 0 | 27 | 0 | 0 | 27 | 0 | 0 | 27 |
| S15 | 40 | 0 | 0 | 40 | 0 | 40 | 40 | 0 | 40 | 0 | 40 | 40 | 0 | 0 | 0 | 40 |
| S16 | 53 | 27 | 27 | 40 | 27 | 53 | 40 | 27 | 53 | 27 | 53 | 40 | 27 | 27 | 40 | 0 |
| Section | Origin Station | Terminal Station | Minimum Running Time (min) |
|---|---|---|---|
| 1 | Wuhan | Xianning North | 20 |
| 2 | Xianning North | Chibi North | 10 |
| 3 | Chibi North | Yueyang East | 21 |
| 4 | Yueyang East | Guluo East | 17 |
| 5 | Guluo East | Changsha South | 18 |
| 6 | Changsha South | Zhuzhou West | 12 |
| 7 | Zhuzhou West | Hengshan East | 20 |
| 8 | Hengshan East | Hengyang East | 10 |
| 9 | Hengyang East | Leiyang West | 13 |
| 10 | Leiyang West | Chenzhou West | 24 |
| 11 | Chenzhou West | Shaouguan | 36 |
| 12 | Shaouguan | Yingdexi | 21 |
| 13 | Yingdexi | Qingyuan | 14 |
| 14 | Qingyuan | Guangzhou North | 9 |
| 15 | Guangzhou North | Guangzhou South | 11 |
| Parameter | Value | Unit |
|---|---|---|
| 1080 | min | |
| [1–239; 240–599, 600–1080] | min | |
| [] | - | |
| 100 | - | |
| 0.05 | - | |
| 20 | - | |
| 0.005 | - |
| UB | Trains Scheduled | CU | |
|---|---|---|---|
| 80 | 33,400 | 250 | 80.01% |
| 84 | 35,176 | 262 | 83.85% |
| 88 | 36,952 | 274 | 87.69% |
| 92 | 39,576 | 282 | 90.25% |
| 96 | 43,048 | 286 | 91.53% |
| 100 | 47,368 | 286 | 91.53% |
| 120 | 68,968 | 286 | 91.53% |
| Direction | Type | Time Period 1 | Time Period 2 | Time Period 2 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Minimum Value | Average Value | Minimum Value | Average Value | Minimum Value | Average Value | Minimum Value | Average Value | ||
| Downward | OD-1 | 6 | 6 | 15 | 15 | 6 | 6 | 27 | 27 |
| OD-2 | 9 | 12 | 23 | 31 | 9 | 12 | 40 | 55 | |
| OD-3 | 11 | 37 | 30 | 50 | 11 | 33 | 53 | 119 | |
| Upward | OD-1 | 6 | 6 | 15 | 15 | 6 | 6 | 27 | 27 |
| OD-2 | 9 | 12 | 23 | 31 | 9 | 11 | 40 | 54 | |
| OD-3 | 11 | 37 | 30 | 50 | 11 | 33 | 53 | 119 | |
| Stop Plan | Average Train Travel Time/min | D-Value | Number of Stop Plans | |||
|---|---|---|---|---|---|---|
| Down Direction | Up Direction | Down Direction | Up Direction | Down Direction | Up Direction | |
| 249 | 249 | 0 | 0 | 55 | 54 | |
| 249 | 249 | 0 | 0 | 27 | 27 | |
| 229 | 229 | 0 | 0 | 61 | 62 | |
| Origin Station | Number of Train Departures | Number of Rolling Stock Units | ||||
|---|---|---|---|---|---|---|
| Period 1 | Period 2 | Period 3 | T | Departure | Arrival | |
| Wuhan | 42 | 63 | 38 | 143 | 48 | 48 |
| Guangzhou South | 42 | 63 | 38 | 143 | 47 | 47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Li, S.; Kang, J.; Huang, Y. Capacity-Oriented Train Scheduling of High-Speed Railway Considering the Operation and Maintenance of Rolling Stock. Mathematics 2022, 10, 1639. https://doi.org/10.3390/math10101639
Zhou W, Li S, Kang J, Huang Y. Capacity-Oriented Train Scheduling of High-Speed Railway Considering the Operation and Maintenance of Rolling Stock. Mathematics. 2022; 10(10):1639. https://doi.org/10.3390/math10101639
Chicago/Turabian StyleZhou, Wenliang, Sha Li, Jing Kang, and Yu Huang. 2022. "Capacity-Oriented Train Scheduling of High-Speed Railway Considering the Operation and Maintenance of Rolling Stock" Mathematics 10, no. 10: 1639. https://doi.org/10.3390/math10101639
APA StyleZhou, W., Li, S., Kang, J., & Huang, Y. (2022). Capacity-Oriented Train Scheduling of High-Speed Railway Considering the Operation and Maintenance of Rolling Stock. Mathematics, 10(10), 1639. https://doi.org/10.3390/math10101639







