Fundamental Issues of Concept Mapping Relevant to Discipline-Based Education: A Perspective of Manufacturing Engineering

Abstract

This article addresses some fundamental issues of concept mapping relevant to discipline-based education. The focus is on manufacturing knowledge representation from the viewpoints of both human and machine learning. The concept of new-generation manufacturing (Industry 4.0, smart manufacturing, and connected factory) necessitates learning factory (human learning) and human-cyber-physical systems (machine learning). Both learning factory and human-cyber-physical systems require semantic web-embedded dynamic knowledge bases, which are subjected to syntax (machine-to-machine communication), semantics (the meaning of the contents), and pragmatics (the preferences of individuals involved). This article argues that knowledge-aware concept mapping is a solution to create and analyze the semantic web-embedded dynamic knowledge bases for both human and machine learning. Accordingly, this article defines five types of knowledge, namely, analytic a priori knowledge, synthetic a priori knowledge, synthetic a posteriori knowledge, meaningful knowledge, and skeptic knowledge. These types of knowledge help find some rules and guidelines to create and analyze concept maps for the purposes human and machine learning. The presence of these types of knowledge is elucidated using a real-life manufacturing knowledge representation case. Their implications in learning manufacturing knowledge are also described. The outcomes of this article help install knowledge-aware concept maps for discipline-based education.

1. Introduction

This article addresses some fundamental issues regarding concept mapping for discipline-based education. The focus is on manufacturing knowledge representation from the viewpoints of both human and machine learning, and the context is new-generation manufacturing (Industry 4.0, smart manufacturing, and connected factory).

Many authors have studied about how to learn science- and engineering-based subject matters in the early stage of formal education. Accordingly, it has been found that not only knowing about a subject matter, but also doing about it (arguing about scientific theories and findings, suggesting plausible solutions, and so on) can enhance learning [1,2,3,4,5,6,7]. This kind of education (knowing and doing simultaneously) requires integration between theoretical and real worlds following three phases, namely, investigating, evaluating, and developing explanations and solutions. As a result, the learning must be driven by the following activities: (1) Asking questions and defining problems, (2) developing and using models, (3) planning and carrying out investigations, (4) analyzing and interpreting data, (5) using mathematics and computational thinking, (6) constructing explanations and designing solutions, (7) engaging in argument from evidence, and (8) obtaining, evaluating, and communicating information [8]. Having said that, it might not be true that all learners are free from misconceptions [9,10,11,12]. Some efforts are required to help learners overcome misconceptions. When a learner continues her/his science- and engineering-based education at the tertiary level, the abovementioned duality (knower–doer) intensifies due to some predefined educational objectives and outcomes (e.g., the educational objectives and outcomes of the Accreditation Board for Engineering and Technology (ABET) [13]).

Regardless of the level of formal education (school, undergraduate, or graduate level), some motivating factors drive an individual to become a knower and doer simultaneously. The author believes that two of the motivating factors are metacognition and meaningful learning. Metacognition (thinking about thinking) is a higher-order human cognition that allows individuals to monitor and redirect their thinking processes as needed [14,15]. Meaningful learning is perhaps a manifestation of metacognition that emotionally attaches an individual to a learning process, resulting in a concept map (a network of concepts) [16,17,18,19,20]. A remarkable feature of meaningful learning is that it integrates new concepts with existing ones.

Concept map-based education has earned a great deal of attention [20,21,22,23,24,25]. It has spread up to discipline-based education, including manufacturing engineering education [25]. As far as manufacturing engineering education is concerned, concept map-based learning is significant from the viewpoints of both human and machine learning. The significance of concept maps from the viewpoint of human learning in manufacturing evolves due to the advent of learning factory [26,27,28], whereas the significance of concept maps in manufacturing from the viewpoint of machine learning evolves due to the advent of new-generation manufacturing systems [29,30,31]. Thus, as far as the advancement of digital manufacturing is concerned, the construction process of concept maps has become an important issue. A few authors have researched the construction process of concept maps in general. Some of the noteworthy processes are as follows: Semantic gravity-driven concept mapping [21], process, material, automation, and shape universe-based concept mapping [25], focus-question-based concept mapping [32], and weighted concept induction-based concept mapping [33]. The remarkable thing is that the contents of a concept map (intended for human or machine learning) boil down to some propositions. These propositions can be categorized into some types of knowledge [21,31]. Therefore, knowledge-type-aware concept mapping is one of the effective processes of constructing concept maps. For this perspective, this article is written.

Accordingly, this article aims to provide more insights into the general categorization of knowledge and its representation using concept maps from the perspectives of manufacturing engineering education. Therefore, this article must describe the fundamental issues of manufacturing engineering knowledge and its ICT-based representation from the perspectives of human and machine learning. It must define the knowledge types from a domain-neutral perspective (i.e., epistemology). Lastly, it must elucidate how to accommodate the knowledge types into the learning activities in manufacturing engineering education through the formation of concept maps. Therefore, the rest of this article is organized as follows. Section 2 presents the fundamental issue underlying concept mapping in manufacturing engineering. Section 3 provides a knowledge classification method for organizing the manufacturing engineering-relevant contents for concept mapping. Section 4 analyzes a manufacturing engineering-relevant concept map using the proposed knowledge classification. Section 5 concludes this study.

2. Fundamental Issues Regarding Manufacturing Knowledge Representation

The previous section states that concept mapping in manufacturing is significant from both human and machine learning perspectives. The significance in terms of human learning evolves due to the advent of a concept called learning factory [26,27,28], whereas the significance in terms of machine learning evolves due to the advent of a concept called new-generation manufacturing systems [29,30,31]. On the other hand, the concept of learning factory is heavily linked to the concept of new-generation manufacturing systems. Thus, before eliciting the fundamental issues of manufacturing knowledge representation using concept maps, the relevant aspects of new-generation manufacturing systems must be elucidated. Accordingly, this section presents some of the fundamental issues relevant to knowledge representation that center around new-generation manufacturing systems.

Manufacturing (or production) systems have continuously been evolving under the influence of information and communication technology. As a result, a concept of new-generation manufacturing systems has been evolved, which is referred to as Industry 4.0, smart manufacturing, connected factory, Society 5.0, Made in China 2025, and alike [26,27,28,29,30,31,34,35,36,37,38,39,40]. The primary goal is to achieve an active collaboration among hardware devices (e.g., machine tools, robots, measuring instruments), software systems (CAD/CAM, ERP, and SCM systems), and human resources on a real-time basis by exchanging the required data, information, and knowledge [34,35,36,37,38,39,40]. For achieving this goal, a set of relevant technologies has been introduced, namely, human-cyber-physical systems, digital twins, and the Internet of things [26,27,28,29,30,31,34,35,36,37,38,39,40]. Numerous authors have studied these technologies. For example, Zheng et al. [31] reviewed Industry 4.0 and provided a system architecture where the data intensiveness of design, monitoring, machining, control, and scheduling are classified into four layers—namely, sensor and actuator deployment, data collection, big data analysis, and big data-driven decision-making. The layers are organized in the order of edge (where an activity occurs), fog (cyber-physical-human-integrated systems), and cloud (an ICT infrastructure for collecting and disseminating information from/to a wide range of stakeholders). Koren et al. [34] described how to modify the reconfigurable manufacturing systems in order to accommodate the functionalities of Industry 4.0 [29,32]. They have emphasized that the human-cyber-physical systems or the systems that reside in the fog (the mid-wear between edges and cloud) must be populated with the contents called digital twin (computable virtual abstraction of real objects, processes, and phenomena). Ullah [30,38] and Ghosh et al. [40] described that there are three kinds of digital twins, namely, object twin, process twin, and phenomenon twin. Among these twins, phenomenon twin is the most challenging twin to construct because the construction of phenomenon needs stochastic dynamical systems-based formulation and user-defined technique to capture the dynamics of the underlying phenomenon [38,40]. However, Industry 4.0 or smart manufacturing is perhaps in its infancy. A great deal of research lies ahead. For example, what the best architecture of new-generation manufacturing systems should be is not known yet. Some authors consider that network-based architecture is suitable for smart manufacturing [41]. Other authors consider that hierarchical architecture is suitable for smart manufacturing [42]. Some authors consider that a shift to system modeling-centric activities from (current) document meeting-centric activities is needed for smart manufacturing from both syntax [43] and semantic [44] viewpoints. Some authors consider that manufacturing decision-relevant data, information, and knowledge must be organized using bio-inspired computational frameworks for machine learning [40,41,42,43,44,45]. From the human learning viewpoint, on the other hand, manufacturing engineering-relevant educational contents can be organized in ABET-centric means [46] or other e-learning-centric means [47,48]. No matter the intended use (machine learning or human learning), or the level of sophistication (data, information, model, knowledge, simulation, and digital twin), the manufacturing engineering-relevant contents must be represented by concept maps. The reason is as follows.

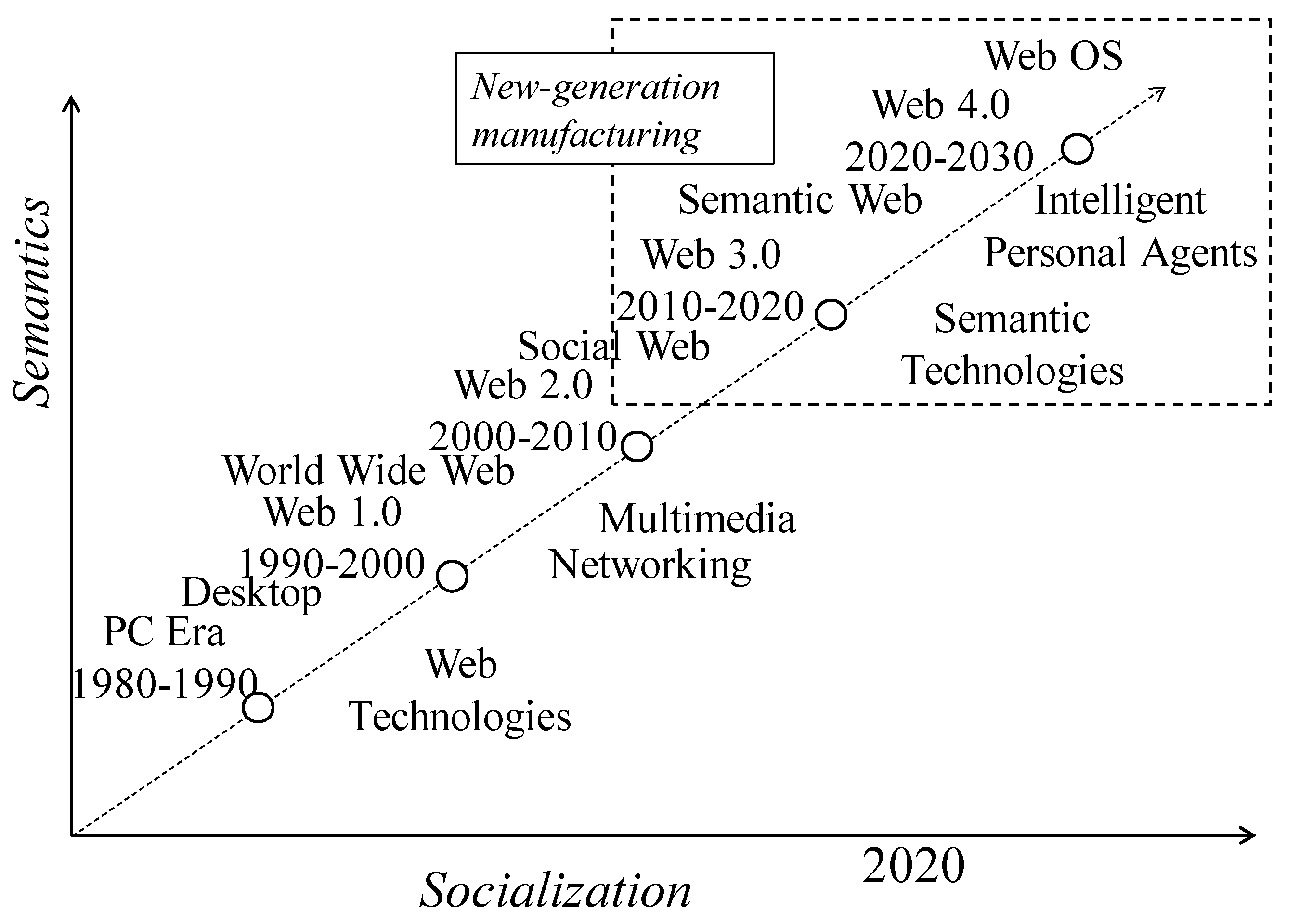
Consider the evolution of web technology [49,50], as schematically illustrated in Figure 1. As seen in Figure 1, the evolution of web technology entails two dimensions. One of the dimensions is socialization, and the other is semantics (meaning of the contents). At the initial stage of web technology (Web 1.0), the communication was mainly one-way, where the users could only read the contents available on the web through the Internet. The next era (Web 2.0) materialized two-way communication, adding a functionality called writing on top of reading. This era dominates current web-based practices. The degree of socialization and semantics in these two eras has been limited. In order to increase this degree, the semantics of the contents must be increased. This leads to a concept called the semantic web [49]. Centering this new technology (semantic web), the web has been transforming into a new era called Web 3.0/4.0 [50]. The ultimate goal is to materialize personal intelligent devices. To achieve this, the contents originated in different information silos (e.g., big-data coming from different domains) must be integrated. The integration requires “meaning base” of a piece of content on top of the content itself. As a result, ontology-driven data structures of content preparation for the semantic web has evolved [51]. 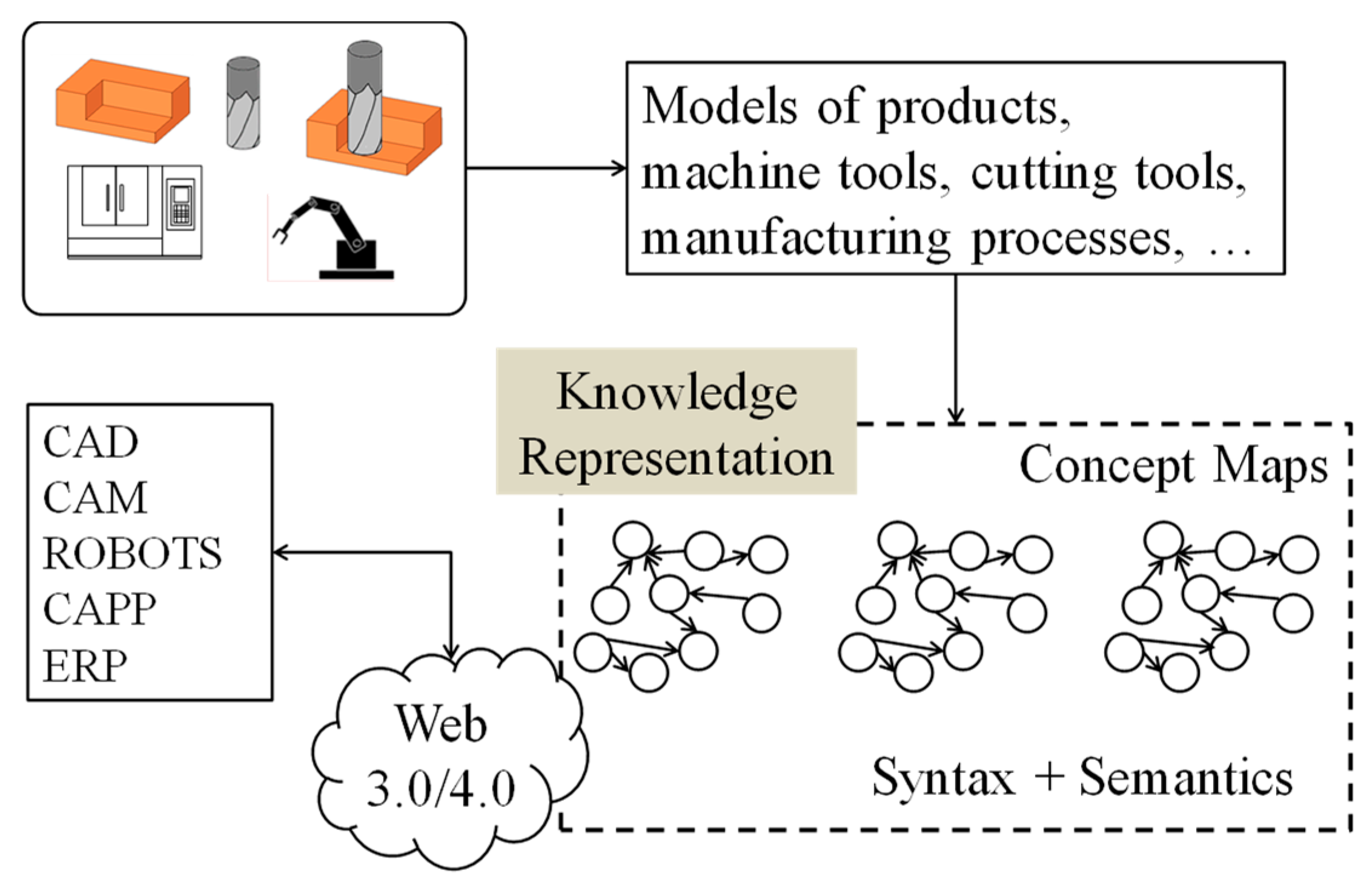Thus, new-generation manufacturing is moving toward an era where the content preparation points out a scenario, as shown in Figure 2. As seen in Figure 2, in the era of Web 3.0/4.0, the manufacturing contents (i.e., different types of experimental and sensor data, models of products, machine tools, cutting tools, manufacturing processes, scheduling, and models of different manufacturing phenomena) will incorporate both the contents (syntax) and their meaning (semantics). The current trend shows that a user-defined description of the meaning of the content must be incorporated along with the content itself [25,26,30,40,45,52]. The description is inclined more toward user-defined linguistic expressions (soft) than toward predefined ontology (hard). This softness in expressing semantics leads to concept map-oriented content preparation. This means that for new-generation manufacturing, concept mapping [19,20,21,32] becomes a default choice, no matter the content type of contents (model, data, knowledge, and alike) [25,26,30,40].

Apart from the issue of concept map-based content preparation for new-generation manufacturing, it (new-generation manufacturing) entails some other fundamental issues because the systems involved in new-generation manufacturing are supposed to operate as open systems. As such, independent domains might be linked as an ad hoc basis. As a result, the contents originated at unknown sources can be shared for reuse. At the same time, the contents might be altered without prior notification. 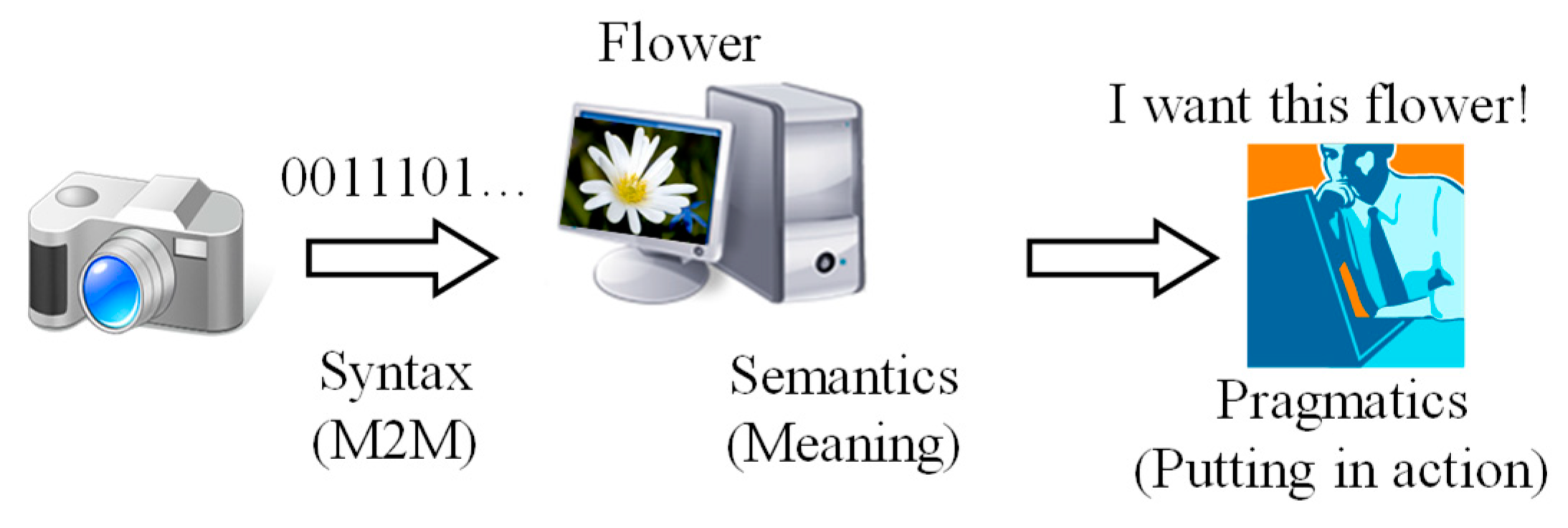This incorporates one more issue, called pragmatics [45], with syntax and semantics, as schematically illustrated in Figure 3. The contents relevant to syntax mean codified contents for machine-to-machine (M2M) communication; the contents relevant to semantics mean what does the content mean to the stakeholders. The contents relevant to pragmatics, on the other hand, must ensure that whether or not the contents are trustworthy to put into action. For the sake of better understanding, the concept of pragmatics is shown along with syntax, which are schematically illustrated in Figure 4 using an arbitrary example (i.e., the example of flower). Thus, manufacturing system developers must consider these three aspects while preparing the contents using semantic web-embedded concept maps. Now, one of the ways to tackle pragmatics, along with syntax and semantics, is to rely on the epistemic nature of the contents. This leads to a knowledge-type-aware concept map construction process. Before describing the general process of a knowledge-type-aware concept map construction process, the epistemic classification of knowledge and their origin must be articulated. This issue is described in the following section.

3. Epistemic Classification of Knowledge

In general, a piece of knowledge is a proposition that is “justified true belief”. Notably, a piece of knowledge means facts, principles, theories, and practices that are accumulated by learning; both cognitive reflections and direct experiences of individuals or groups can contribute to articulate a piece of knowledge [26]. Numerous authors have classified knowledge in different ways. From the viewpoint of an organization, knowledge is categorized into two categories, explicit knowledge and tacit knowledge [53,54]. Explicit knowledge can be formally represented for reuse, whereas tacit knowledge cannot be represented explicitly, because it is in possession of an individual or a group of individuals working in an organization (e.g., the skill to operate a machine tool). Based on semantic gravidity, knowledge can be classified into four types, namely, novice knowledge, theoretical knowledge, practical knowledge, and professional knowledge [21]. However, the author believes that epistemology (the branch of philosophy that deals with the origin and nature of knowledge) [55] is perhaps the best inspiration for classifying knowledge. Immanuel Kant [56] proposed one of the well-recognized epistemic classifications of knowledge. Kant considered both idealistic and realistic arguments of knowledge formation and proposed that there are three main types of knowledge, namely, analytic a priori, synthetic a priori, and synthetic a posteriori knowledge, as schematically illustrated in Figure 5. Analytic a priori knowledge means the knowledge gained by defining things (e.g., all bachelors are unmarried males; a triangle has three sides; feed rate is the velocity at which a cutting tool is advanced against the workpiece; and alike). Thus, analytic a priori knowledge is always true (i.e., tautology). On the other hand, synthetic a priori knowledge is the knowledge that is gained by using a mathematical deduction. Some of the examples of synthetic a priori knowledge are as follows: 7 + 4 = 11; p = the summation of included angles of a triangle is equal to 180°; the theoretical maximum surface roughness height of a turned surface is given as $R_t=125\left(f^2/r_{ϵ}\right)$ μm, where f is the feed rate (mm/rev) and $r_{ϵ}$ nose radius (mm) of the cutting tool; and alike. Synthetic a priori knowledge is true within the relevant context. For example, p is true when the triangle is drawn on a planner surface, not on a curved surface. The same argument is valid for $R_t=125\left(f^2/r_{ϵ}\right)$ μm, i.e., it is true only when the relevant assumptions are obeyed. The other Kantian category of knowledge is called synthetic a posteriori knowledge. This category of knowledge evolves from real-world experience (or experimentation) (e.g., bachelors are rich; an apple is good for health; the feed force is less than the cutting force; and alike). As a result, synthetic a posteriori knowledge can be proven true, partially true, partially false, and even false, i.e., it is true for a stakeholder but may not necessarily be true for others (i.e., it is a matter of fact).

However, Kantian knowledge is based on the fact that a human being is primarily a knower, as shown in Figure 5. As mentioned in the first section of this article, a human being can be a knower and doer at the same time. In the doer mode, a human being remains pragmatic and gives priority to her/his preferences and judgment, even though everything is not clearly known in terms of other forms of knowledge. The knowledge gained in pragmatic mode can be of two types. One of the types evolves in the analytic mode. It is referred to as meaningful knowledge as if it is the outcome of meaningful learning. It thus injects new concepts, as it is the result of an individual’s preference: “It seems to me that….” For example, consider the following proposition: “A cutting tool having an oval cross-sectional area performs better than a cutting tool having a circular cross-sectional area while removing material around sharps corner of a workpiece in milling.” This is an outcome of meaningful learning because it injects a new cutting tool (oval-shaped tool) to solve a problem (remove material in the sharp corners of a workpiece). This proposition cannot be proven true or false until there is a piece of supportive synthetic a priori or synthetic a posteriori knowledge available. As far as manufacturing is concerned, this type of knowledge can dominate other types of knowledge. The other type of knowledge in doer mode is defined as skeptic knowledge. It evolves in the synthetic mode. It may or may not inject new concepts. It is directly related to other types of knowledge. Skeptic knowledge often leads learners to ponder a course of action to study further. Thus, it is somehow linked to other types of knowledge; that is, it is a purposeful interpretation of an individual based on other available pieces of knowledge. For example, consider the following proposition: “Reduce feed rate to ensure a better surface finish.” It is a piece of skeptic knowledge and helps take a course of action (e.g., optimize a material removal process), even though the rationale is somewhat informal. However, when skeptic knowledge is directly related to a piece of meaningful knowledge, the skepticism regarding it (meaningful knowledge) manifests the skepticism regarding skeptic knowledge. At the same time, it follows other concept maps as a part of further study regarding the subject matter. It means that skeptic knowledge acts as a tool for enhancing meaningful learning among learners. This is exemplified in the next section.

Nevertheless, other than the analytic a priori knowledge, all the types of knowledge mentioned above can be proven false. This means that a learner, either a human being or a machine, can set a strategy to verify or validate whether or not a given piece of knowledge is true before using it. The strategy will depend on the type of knowledge. For example, if the type of knowledge is synthetic a priori, the learner is supposed to find out the deductive steps and relevant definitions (analytic a priori knowledge) to determine the truthfulness of it. If the type of knowledge is synthetic a posteriori, the learner is supposed to find out the rationales and integrity of the relevant experimental results or experience to determine the truthfulness of it. If the type of knowledge is meaningful knowledge, then the learner must identify the innovative process that leads to the conclusion (meaningful knowledge) or identify the analytical or experimental processes that lead to the meaningful knowledge. If the type of knowledge is skeptic knowledge, then the learner must extract the pieces of relevant pieces of background knowledge (analytical a priori, systematic a priori, synthetic a posteriori, or meaningful knowledge) that helped the knowledge formulator to conceive the skeptic knowledge for taking actions.

4. Concept Map Creation and Analysis

Having described the fundamental issues and types of knowledge, it is time to create and analyze a concept map containing manufacturing engineering contents.

It is worth mentioning that many authors have studied subject matter-based educational needs and relevant ICT infrastructures from the viewpoint of new-generation manufacturing [25,46,57,58,59,60]. Some authors have emphasized a particular type of knowledge structure and its transformation [61] for the sake of active learning and teaching. Some authors have emphasized concept map-based content preparation [25] for enhancing meaningful learning in manufacturing [16,17,18,19,20,21]. In addition, many concept maps carrying both theoretical and empirical knowledge of manufacturing can be found in [25,30,31,40]. Some of them are for human learning [25], and some of them are for machine learning [30,31].

However, the concept map-based learning performances of some undergraduate engineering students have been reported in [25]. One of the remarks made by the learners is about the size of the concept map (large size makes the content less attractive and cumbersome). Another important observation made by the learners is that some of the concepts are controversial, and, thereby, difficult to comprehend, even though excellent illustrations and references are embedded in the concept maps. As a result, the central theme of meaningful learning (avoiding memorization [16,17,18,19,20,21]) gets affected. The root cause of this is perhaps the presence of synthetic a posteriori knowledge, meaningful knowledge, and skeptic knowledge in the concept map. This means that some of the concepts may appear to be analytic a priori, but they are meaningful knowledge or even skeptic knowledge. In this case, the instructor may put more effort into explaining these pieces of knowledge so that the learners avoid memorization or seek other reference materials to grasp the real meaning or counterexamples. As a result, knowledge-aware concept mapping can make the maps systematic and comprehensible to learners. At the same time, the instructor can carry out the teaching activities in a more systematic manner.

For example, a relatively small concept map is constructed based on the concept map of a turning (a widely used manufacturing process) shown in [25]. For the sake of better understanding, a well-known subject matter—the shear plane theory of a material removal process—is considered, as illustrated in Figure 6. Mechanical or manufacturing engineering students learn the shear plane theory (Figure 6) at the undergraduate level, which is an oversimplified model of chip formation in material removal processes [62]. The symbols shown in Figure 6 have their usual meaning. Numerous propositions can represent the knowledge underlying the contents shown in Figure 6. Each proposition should be based on a type of knowledge described in the previous section. The number of propositions depends on the individual who formulates those.

Figure 7 shows a screen-print of the semantic web constructed to represent the knowledge underlying Figure 6. It can be accessed through the Internet from the URL shown in [63]. The icons shown in the nodes called “here” have links to the illustrations shown in Figure 6. If needed, other contents (video clip and other concept maps) can be linked to the appropriate nodes of the concept map shown in Figure 7. Since there are no experimental facts associated with Figure 7, there are no propositions regarding the synthesis a posteriori knowledge in Figure 7. Synthetic a posteriori knowledge relevant to turning can be found in the concept maps reported in [25,30,45].

The concept map shown in Figure 7 boils down to the following propositions.

(1)

The components of two balancing forces (illustrated in Figure 6) act while removing materials in the form of a chip from a workpiece.

(2)

Workpiece materials become the chip from a plane called shear plane due to the action of a cutting tool.

(3)

The chip forms by maximizing the shear force, resulting in the included angle ∠ABE (illustrated in Figure 6) equal to π/4.

(4)

Shear force acts along the shear plane.

(5)

The included angle ∠ABE is equal to ϕ + τ − α based on the geometric relationships among the three pairs of forces illustrated in Figure 6.

(6)

Two balancing forces (illustrated in Figure 6) can be represented by three pairs of forces, where each pair consists of two orthogonal components.

(7)

Cutting force acts in the direction of cutting velocity.

(8)

Cutting force is a component of one of the three pairs of forces (illustrated in Figure 6).

(9)

The shear plane angle is given as ϕ = π/4 + (α − τ).

Consider the first proposition: The components of two balancing forces (illustrated in Figure 6) act while removing materials in the form of the chip from a workpiece. It is a piece of synthetic a priori knowledge because it comes from a mathematical deduction that two forces must act along a line but in the opposite directions to maintain a balance. This is true because the external forces acting on the workpiece makes a static balance; otherwise, the workpiece may move out from the holding devices.

Consider the second statement: Workpiece materials become the chip from a plane called shear plane due to the action of a cutting tool. This proposition is a sophisticated form of knowledge because it entails two forms of knowledge, namely, analytic a priori knowledge and meaningful knowledge. If the proposition is rewritten using two propositions, then this duality of knowledge can be understood. For example, consider the following two propositions: (2-1) Workpiece materials become the chip due to the action of a cutting tool; and (2-2) Workpiece materials become the chip from a plane called shear plane. Proposition 2-1 is a piece of analytic a priori knowledge because it just defines the manufacturing process (chip formation is necessary for achieving material removal in machining), as well the role of a cutting tool. On the other hand, the other proposition (proposition 2-2) is a piece of meaningful knowledge. The reason is that one has considered this concept (shear plane) to explain chip formation. Chip formation can occur from a region (not a plane) [62]. This means that the idea of the shear plane is somewhat controversial at this point. As far the knowledge-aware construction of concept maps is concerned, the map shown in Figure 7 needs revision, avoiding the mixing of the types of knowledge.

Consider the third proposition: The chip forms by maximizing the shear force, resulting in the included angle ∠ABE (illustrated in Figure 6) equal to π/4. It is also a piece of meaningful knowledge because a new concept is injected (maximizing the shear force) to set the value of the angle ∠ABE. There are other ways to perceive this case. For example, one can consider instead that “minimizing energy” is the phenomenon that takes place while removing the chip from a workpiece during machining [62]. Therefore, comprehending this knowledge requires some effort from the learner’s side and making it compressible requires efforts from the instructor’s side.

Consider the fourth proposition: Shear force acts along the shear plane. It is a piece of analytic a priori knowledge that defines the concept of shear force with respect to shear plane. Even though this proposition is a piece of analytic a priori knowledge, it is coupled with another concept (shear plane) that also needs to be defined. Since the concept of shear plane refers to a piece of meaningful knowledge, the comprehension regarding the shear force creates an amount of fuzziness among the learners. Therefore, this piece of knowledge creates what can be referred to as fuzzy circularity. Therefore, both concepts (shear force and shear plane) must be handled with care during the process of learning and teaching.

Consider the fifth proposition: The included angle ∠ABE is equal to ϕ + τ − α based on the geometric relationships among the three pairs of forces illustrated in Figure 6. It is a piece of synthetic a priori knowledge because ∠ABE = ϕ + τ − α is deduced from the geometric relationships shown in Figure 6. Therefore, if the learns can follow the steps used in the deduction, the validity of the proposition becomes clear to them. The instructor may set some exercises for the learners to master the steps.

Consider the sixth proposition: Two balancing forces (illustrated in Figure 6) can be represented by three pairs of forces, where each pair consists of two orthogonal components. It is a piece of synthetic a priori knowledge because, from a mathematical point of view, a planner force can be deduced into two orthogonal components. Regarding the three pairs of forces, the following comments can be made. Consider, for example, the force acting between the cutting tool surface and the chip (Figure 6). Whenever an object slides against another, friction force occurs, and its magnitude depends on the surface condition (coefficient of friction) and the force acting normal to the sliding surfaces. This kind of explanation is deductive truth that relates basic knowledge of physics and engineering science. The same arguments hold for the other two pairs of forces. Therefore, there is no problem treating proposition 6 as a piece of synthetic a priori knowledge.

Consider the seventh proposition: Cutting force acts in the direction of cutting velocity. It is a piece of analytic a priori knowledge because it defines cutting force; that is, a force that acts in the direction of cutting velocity. Even though this proposition is a piece of analytic a priori knowledge, it is coupled with another concept (cutting velocity) that also needs to be defined. Therefore, this piece of knowledge creates a circularity. This time it does not entail fuzzy circularity, unlike the case for proposition 4. This time, it is rather a simple circularity. Nevertheless, both concepts (cutting force and cutting velocity) deserve explanation with respect to each other, requiring extra care from both the learner’s and instructor’s sides.

Consider the eighth proposition: Cutting force is a component of one of the three pairs of forces (illustrated in Figure 6). It is a piece of synthetic a priori knowledge because, from the knowledge of mathematics (vector algebra), it is clear that a planner force can be decomposed into orthogonal components.

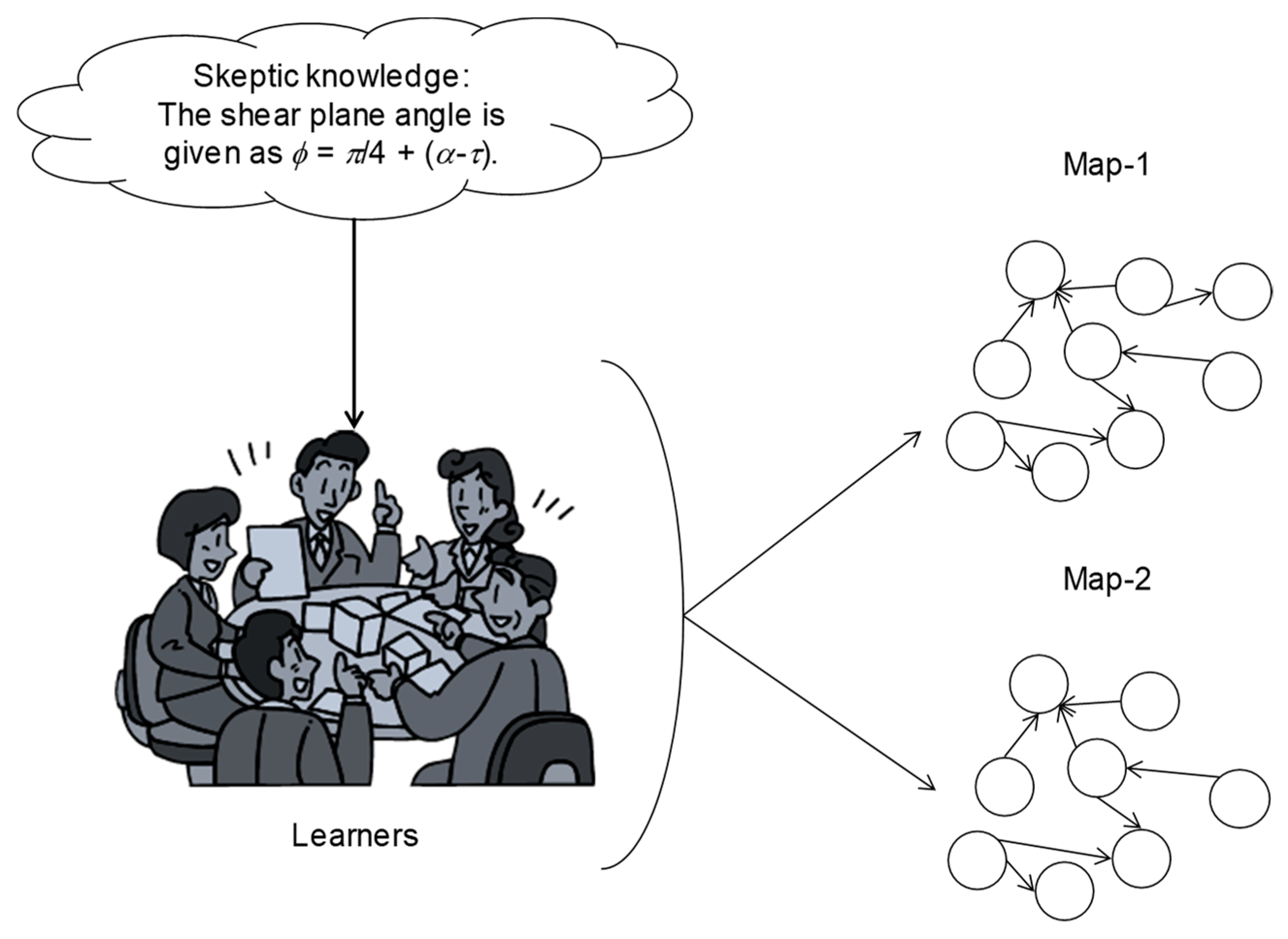
Consider the last proposition: The shear plane angle is given as ϕ = π/4 + (α − τ). It is a piece of skeptic knowledge, though it seems a piece of synthetic a priori knowledge. The reasons are two-fold. The first reason is its epistemic nature, and the other reason is its ability to trigger other learning activities that can incorporate other concept maps. This is schematically illustrated in Figure 8. As seen in Figure 8, at least two new concept maps, denoted as Map-1 and Map-2, can evolve due to this piece of skeptic knowledge. While pursuing Map-1, the link of the proposition 9 (skeptic knowledge) with other propositions can be considered. It is directly related to propositions 2, 3, and 4, which entail meaningful knowledge. Since a great deal of skepticism is already associated with propositions 2, 3, and 4, as described above, proposition 9 is automatically subjected to a great deal of skepticism. Therefore, learners can seek other pieces of meaningful knowledge (say, “the chip forms by minimizing energy at the shear please”) [62]. In this case, the included angle ∠ABE (illustrated in Figure 6) will no longer be equal to π/4, resulting in a relationship other than ϕ = π/4 + (α − τ). If so, new pieces of knowledge (say, ϕ = π/4 + 0.5(α − τ)) may evolve [62]. This results in a new concept map, denoted as Map-1. Consider the concept map Map-2. The learning activity can also be directed toward incorporating some pieces of synthetic a posteriori knowledge (experimental facts). In this case, the apparent learning activities are as follows. According to Figure 6, the ratio between the thicknesses of the undeformed material before chip formation and deformed material after chip formation (denoted as r) is equal to sin(ϕ)/cos(ϕ − α). An experiment can be carried out to know r for a predefined α (rake angle). If these experimentally determined values of r and ϕ are input in r = sin(ϕ)/cos(ϕ − α), the value of ϕ can be calculated. This calculated value can be compared to the theoretical one, ϕ = π/4 + (α − τ). Thus, proposition 9 (skeptic knowledge) leads to some learning activities to know about the nature of machining from different points of view, to see whether or not the associated meaningful knowledge can be trusted. In other words, proposition 9 can enhance discipline-based education.

5. Conclusions

Though concept mapping has contributed to different levels of education, its construction and deployment processes require a great deal of study. As far as manufacturing engineering is concerned, both learning factory and human-cyber-physical systems (i.e., human and machining learning) have opened new opportunities for concept maps and brought new challenges as well. The proposed types of knowledge (analytic a priori, synthetic a priori, synthetic a posteriori, meaningful, and skeptic knowledge) can help exploit the abovementioned opportunities and tackle the challenges. This is clear from the contents presented in the previous few sections.

In order to educate students with the basic knowledge of material removal (a common topic that all manufacturing engineering students study at undergraduate degree level), a nine proposition-based concept map has been introduced. The map represents knowledge of the shear plane theory of material removal. All types of knowledge are integrated into the map, except synthetic a posteriori knowledge. The remarkable thing is that the learning process directs the learners to form new concept maps, wherein the not-yet-included type of knowledge (in this case, synthetic a posteriori knowledge) is likely to appear. This directs the whole learning process in the direction of meaningful learning.

Instead of the presented concept map, a concept map without embedding synthetic a priori knowledge can be considered for the same purpose (educating students with the basic knowledge of material removal) and can be observed whether or not the learners propose another concept map that incorporates synthetic a priori knowledge. This means that there is enough room for further investigations showing the education capability of concept maps and, thereby, meaningful learning, while offering manufacturing engineering education.