An Extended Constructive Alignment Model in Teaching Electromagnetism to Engineering Undergraduates
Abstract
:1. Introduction
2. Proposed Model
2.1. Entry Survey
2.2. The Three-Level Learning Objectives
- Gauss’s Law for electrostatic fields and Maxwell’s first equation.
- Gauss’s Law for magnetostatic fields and Maxwell’s second equation.
- Faraday’s Law for time-varying electric fields and Maxwell’s third equation.
- Ampere’s Law for time-varying electromagnetic fields and Maxwell’s fourth equation.
- Plane wave solution.
- Poynting theory, electromagnetic power, basic electromagnetic radiation principles, and their applications.
2.3. Three-Level Assessment and Evaluation Methods
2.4. Student Self-Assessment and Instructor Assessment Rubrics
3. Discussion
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- As of now, after completing my undergraduate degree, I am planning on:
- Doing graduate studies
- Working in the industry
- Doing my own thing, for example, painting, carving, sculpture
- If I can get one thing out of this course it would be:
- Nothing, I registered just because it is required. I have a different subject interest.
- Try this subject and see whether I should pursue this for my graduate studies
- Learn how things work and apply it at work
- While registering for this course
- I knew/heard this course it very mathematics and physics intensive
- Oops, I did not know that. But I can catch up quickly.
- Oh no, why? Engineers don’t need math or physics.
- We all learn in different ways. But if I have to choose one, that I learn quickly by
- Watching and feeling
- Watching and thinking
- Doing and feeling
- Doing and thinking
- Knock on wood, but if my performances at exams are not satisfactory
- I will sue the instructor. I am exceptional, and it is always the instructor’s fault.
- It might be a bad day. I want to write a make-up exam.
- I get nervous at exams. If so I will do an extra project or a presentation, whichever it takes to show my actual knowledge.
Appendix B
- A spherical charge cloud with volume charge density and radius , is located at the origin of a spherical coordinate system. Determine the electric flux density and electric field intensity at a distance such that,
- An infinite length of a wire contains a line charge density of . Choosing a suitable coordinate system, calculate the electric field intensity at a radial distance from the wire.
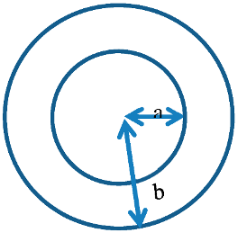
- Two hollow spheres are located at the origin of a spherical coordinate system. Surface of the inner sphere carries a total charge of and the surface of the outer sphere carries a total charge of The space between the spheres is filled with air.
- Find the electric field intensity at a radial distance
- Calculate the potential difference between the two spheres
- How much of a capacitance is developed between the two spheres?
Appendix C

Appendix D
- A 15W EM radiator is isotopically radiating energy equally in all directions. Your task is to calculate the surface area of a dish antenna located 15 m from the radiator to collect 1W of power.
- What should be the radiating surface for the above radiator? …………………………………………………………………….
- Calculate the average power density 15 m from the radiator. ………………………………………………………………………….
- If the goal is to collect 1W at the receiver, what should be the surface area of the receiver……………………………………………………………………
- What should be the radius of the above dish ……………………………………….
- If the above dish was replaced by a parabolic antenna with the same radius, will the power collected will increase or decrease?
References
- Hadzigeorgiou, Y.; Garganourakis, V. Using Nikola Tesla’s story and his experiments as presented in the film “The Prestige” to promote scientific inquiry: A report of an action research Project. Interchange 2010, 41, 363–378. [Google Scholar] [CrossRef]
- Hadzigeorgiou, Y.; Klassen, S.; Froese-Klassen, C. Encouraging a “romantic understanding” of science: The effect of the Nikola Tesla story. Sci. Educ. 2012, 21, 1111–1138. [Google Scholar] [CrossRef]
- Hadzigeorgiou, Y. Imaginative science education. In The Central Role of Imagination in Science Education; Springer International: Cham, Switzerland, 2016. [Google Scholar]
- Airasian, P.; Cruikshank, K.A.; Mayer, R.E.; Pintrich, P.; Raths, J.; Wittrock, M.C. A Taxonomy for Learning, Teaching, and Assessing: A Revision of Bloom’s Taxonomy of Educational Objectives; Anderson, L.W., Krathwohl, D.R., Eds.; Allyn and Bacon: Boston, MA, USA, 2001; ISBN 978-0-8013-1903-7. [Google Scholar]
- Biggs, J.B. Enhancing teaching through constructive alignment. High. Educ. 1996, 32, 347–364. [Google Scholar] [CrossRef]
- Biggs, J.B. What the student does Teaching for enhanced learning. High. Educ. Res. Dev. 1999, 18, 1–19. [Google Scholar] [CrossRef]
- Biggs, J. Aligning Teaching and Assessment to Curriculum Objectives; Imaginative Curriculum Project, LTSN Generic Centre: York, UK, 2003. [Google Scholar]
- Biggs, J.B. Teaching for Quality Learning at University: What the Student Does; McGraw-Hill: Maidenhead, UK, 2011; ISBN 9780335242757. [Google Scholar]
- Bloom, B.S.; Engelhart, M.D.; Furst, E.J.; Hill, W.H.; Krathwohl, D.R. Taxonomy of Educational Objectives: The Classification of Educational Goals. Handbook I: Cognitive Domain; David McKay Company: New York, NY, USA, 1965. [Google Scholar]
- Brooks, J.; Brooks, M. In Search of Understanding: The Case for Constructivist Classrooms; ASCD: Virginia, VA, USA, 1993. [Google Scholar]
- Cain, A.; Grundy, J.; Woodward, C.J. Focusing on Learning through Constructive Alignment with Task-Oriented Portfolio Assessment. Eur. J. Eng. Educ. 2018, 43, 569–584. [Google Scholar] [CrossRef]
- Cobb, P. Theories of knowledge and instructional design a response to Colliver. Teach. Learn. Med. 2002, 14, 52–55. [Google Scholar] [CrossRef]
- Knaack, L. A Practical Handbook for Educators: Designing Learning Opportunities; De Sitter Pubns: Whitby, ON, Canada, 2011; ISBN-13: 978-1897160473. [Google Scholar]
- Smith, C. Design–focused evaluation. Assess. Eval. High. Educ. 2008, 33, 631–645. [Google Scholar] [CrossRef]
| Topic | Learning Objective(s) | Assessment Method(s) | Evaluation Method(s) |
|---|---|---|---|
| 1. Gauss’s Law for electrostatic fields and Maxwell’s first equation. | Low: By the end of this chapter students are expected to explain Maxwell’s first equation and its implications. | Conference, Self-assessment | A quiz Presentation, Case study |
| Medium: By the end of this chapter students will be able to apply Maxwell’s first equation to solve real-world physics problems. | Self-assessment quiz, Question and answer, I am in the fog about … | Exam problem, Quiz | |
| High: By the end of this chapter students are expected to design a basic static charge dust collector using Maxwell’s first equation. | Chart it out, Concept map | Group project (2-3 students), A term paper Project report | |
| 2. Gauss’s Law for magnetostatic fields and Maxwell’s second equation. | Low: By the end of this chapter students will be able to discuss the practical implications of Maxwell’s second equation. | Discussion, Conference | Short presentation, Quiz, Short essay |
| Medium: By the end of this chapter students will be able to solve problems related to Maxwell’s second equation. | Self-assessment quiz, I am in the fog about, Operation outline | Exam questions, Quizzes | |
| High: By the end of this chapter students will be able to create a computer software model of Earth’s magnetic system. | Chart it out, Ticket out the door, Concept map | Problem based project, Research report, Research paper | |
| 3. Faraday’s Law for time-varying electric fields and Maxwell’s third equation. | Low: By the end of this chapter students are expected to describe Faraday’s law and its implications. | Discussion, Conference | Quiz Short, presentation |
| Medium: Upon completing this chapter students are expected to compute values for real-world problems based on Faraday’s law. | Self-assessment quiz, I am in the fog about, Operation outline | Exam questions, Quizzes | |
| High: By the end of this chapter students will be able to build an electromagnetic inductor to demonstrate Faraday’s law. | Ticket out the door, Concept map | Experiment, Prototype building | |
| 4. Ampere’s Law for time-varying electromagnetic fields and Maxwell’s fourth equation. | Low: By the end of this chapter students are able to define Ampere’s law and its implications. | Ticket out the door | Presentation, Short quiz answers, Short essay |
| Medium: By the end of this chapter students are able to calculate values for a real-world application using Ampere’s law. | Self-assessment quiz, I am in a fog about, Question and answer | Exam questions, Quizzes | |
| High: by the end of this chapter students are expected to construct an electromagnet with given specifications based on Ampere’s law. | Conference, Ticket out the door, Concept map | Short project, Live demonstration, Presentation of a prototype | |
| 5. Plane wave solution. | Low: By the end of this chapter students are able to state the plane wave solution. | Ticket out the door | Presentation, Short essay, Short quiz |
| Medium: By the end of this chapter students are able to manipulate the plane wave solution and apply it in a real-world problem. | Self-assessment quiz, Questions and answers, Operations outline | Exam questions, Quizzes | |
| High: By the end of this chapter students will be able to synthesize plane wave electromagnetic propagation in computer software. | Chart it out, Ticket out the door, Concept map | Project, Demonstration, Video presentation | |
| 6. Poynting theory, electromagnetic power, basic electromagnetic radiation principles, and their applications. | Low: By the end of this chapter students will be able to identify the appropriate concepts used in real-world EM wave propagation applications. | Ticket out the door, Discussion | Presentation, Essay |
| Medium: By the end of this chapter students will be able to analyze the real-world EM applications using appropriate concepts. | Self-assessment quiz, I am in the fog about, Operations outline | Exam questions, Long answer quizzes, Summary paper | |
| High: By the end of this chapter students are expected to integrate EM concepts and implement a solution to a real-world problem. | Conference, I am in the fog about, Concept map | Prototype building, Video presentation, Term paper, Presentation |
| Evaluation Method | Percentage |
|---|---|
| Quizzes | 10% |
| Homework | 15% |
| Exams (3 including the finals) | 25% |
| Projects (6 mini projects) | 50% |
| Topic | Unsatisfactory | Needs Development | Satisfactory | Excellent |
|---|---|---|---|---|
| Gauss’s Law for electrostatic fields and Maxwell’s first equation. | I can neither both explain, apply nor design an application based on Maxwell’s first equation. | I can explain Maxwell’s first equation. But I can neither apply nor design an application based on it. | I can explain and apply Maxwell’s first equation. But I cannot design an application based on it. | I can explain, apply and design an application using Maxwell’s first equation. |
| Gauss’s Law for magnetostatic fields and Maxwell’s second equation. | I can neither discuss the implications, solve problems nor create an application based on Maxwell’s second equation. | I can discuss the implications of Maxwell’s second equation. But I can neither solve problems nor create an application using it. | I can discuss and solve problems using Maxwell’s second equation. But I cannot create an application based on it. | I can discuss the implications, solve problems and create an application based on Maxwell’s second equation. |
| Faraday’s Law for time-varying electric fields and Maxwell’s third equation | I can neither describe, compute nor build an application based on Faraday’s law. | I can describe Faraday’s law. But I can neither compute nor build an application based on it. | I can describe and compute values for a practical problem. But I cannot build an application. | I can describe, compute and build an application to demonstrate Faraday’s law. |
| Ampere’s Law for time-varying electromagnetic fields and Maxwell’s fourth equation. | I can neither, define, calculate values nor construct an application using Ampere’s law. | I can define Ampere’s law. But I cannot calculate values or construct an application. | I can define and calculate values for problems, using Ampere’s law. But I cannot construct an application. | I can define, calculate values and construct an application based on Ampere’s law. |
| Plane wave solution. | I can neither state, manipulate nor synthesize plane wave solution. | I can state plane wave solution. But I cannot manipulate or synthesize it. | I can state and manipulate plane wave solution. But I cannot synthesize it. | I can state, manipulate and synthesize plane wave solution. |
| Poynting theory, electromagnetic power, basic electromagnetic radiation principles, and their applications. | I can neither identify, analyze nor integrate practical applications of EM wave propagation concepts. | I can identify EM concepts for real-world scenarios. But I can neither analyze nor integrate concepts. | I can identify and analyze EM concepts for real-world scenarios. But I cannot integrate those for implementations. | I can identify, analyze and integrate EM appropriate EM concepts to implement solutions. |
| Topic | Unsatisfactory | Needs Development | Satisfactory | Excellent |
|---|---|---|---|---|
| Gauss’s Law for electrostatic fields and Maxwell’s first equation. | Student can neither both explain, apply nor design an application based on Maxwell’s first equation. | Student can explain Maxwell’s first equation. But the student can neither apply nor design an application based on it. | Student can explain and apply Maxwell’s first equation. But the student cannot design an application based on it. | Student can explain, apply and design an application using Maxwell’s first equation. |
| Gauss’s Law for magnetostatic fields and Maxwell’s second equation. | Student can neither discuss the implications, solve problems nor create an application based on Maxwell’s second equation. | Student can discuss the implications of Maxwell’s second equation. But the student can neither solve problems nor create an application using it. | Student can discuss and solve problems using Maxwell’s second equation. But the student cannot create an application based on it. | Student can discuss the implications, solve problems and create an application based on Maxwell’s second equation. |
| Faraday’s Law for time-varying electric fields and Maxwell’s third equation | Student can neither describe, compute nor build an application based on Faraday’s law. | Student can describe Faraday’s law. But the student can neither compute nor build an application based on it. | Student can describe and compute values for a practical problem. But the student cannot build an application. | Student can describe, compute and build an application to demonstrate Faraday’s law. |
| Ampere’s Law for time-varying electromagnetic fields and Maxwell’s fourth equation. | Student can neither, define, calculate values nor construct an application using Ampere’s law. | Student can define Ampere’s law. But the student cannot calculate values or construct an application. | Student can define and calculate values for problems, using Ampere’s law. But the student cannot construct an application. | Student can define, calculate values and construct an application based on Ampere’s law. |
| Plane wave solution. | Student can neither state, manipulate nor synthesize plane wave solution. | Student can state plane wave solution. But the student cannot manipulate or synthesize it. | Student can state and manipulate plane wave solution. But the student cannot synthesize it. | Student can state, manipulate and synthesize plane wave solution. |
| Poynting theory, electromagnetic power, basic electromagnetic radiation principles, and their applications. | Student can neither identify, analyze nor integrate practical applications of EM wave propagation concepts. | Student can identify EM concepts for real-world scenarios. But the student can neither analyze nor integrate concepts. | Student can identify and analyze EM concepts for real-world scenarios. But the student cannot integrate those for implementations. | Student can identify, analyze and integrate EM appropriate EM concepts to implement solutions. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maxworth, A. An Extended Constructive Alignment Model in Teaching Electromagnetism to Engineering Undergraduates. Educ. Sci. 2019, 9, 199. https://doi.org/10.3390/educsci9030199
Maxworth A. An Extended Constructive Alignment Model in Teaching Electromagnetism to Engineering Undergraduates. Education Sciences. 2019; 9(3):199. https://doi.org/10.3390/educsci9030199
Chicago/Turabian StyleMaxworth, Ashanthi. 2019. "An Extended Constructive Alignment Model in Teaching Electromagnetism to Engineering Undergraduates" Education Sciences 9, no. 3: 199. https://doi.org/10.3390/educsci9030199
APA StyleMaxworth, A. (2019). An Extended Constructive Alignment Model in Teaching Electromagnetism to Engineering Undergraduates. Education Sciences, 9(3), 199. https://doi.org/10.3390/educsci9030199





