Abstract
Science, technology, engineering, and mathematics (STEM) education has become a new trend in international education curriculum reform. This study analyzed the teaching of seven subjects and performance indicators by collecting data from literature of diversified fields, proficiency training courses, and syllabi of construction management curricula provided by Taiwanese higher education institutions. Research incorporated both qualitative and quantitative methods. Qualitative approaches comprised a literature review and in-depth interview with experts; the quantitative approach was the fuzzy Delphi method, which was used to identify the syllabus constructs of major subjects and rate their performance indicators of secondary subjects. Interpretive structural modelling helped construct a systemic structure and relationships among different types of subjects to analyze curriculum frameworks and systematize teaching models. This study can be referenced to design syllabi for systemic courses in departments of construction engineering and management to educate future construction engineers at higher education institutions.
1. Introduction
The construction industry is critical to the building infrastructure of a country and is highly related to economic development and the lives of the public. Because construction projects involve diverse works, the industrial environment of construction is more complicated compared with other industries, and its characteristics of project management are unique. Conventional models of teaching have been adopted by the universities and colleges in Taiwan, yet such models fail to keep pace with technological development. The construction industry is vital for building a country’s infrastructure and is closely associated with a country’s economic development and the lives of the public. Because construction projects involve numerous types of work, the working environment in the construction industry is more complicated than those in other industries, and the characteristics of construction project management (CPM) are unique. Taiwan’s higher education adopts a conventional teaching model to teach CPM, failing to keep pace with technological advancements. In recent years, countries around the world have placed an increased emphasis on promoting access to education for traditionally underrepresented groups and also to improve the quality of STEM education [1,2]. STEM education has become a new trend in international education curriculum reform. It is an interdisciplinary educational method that integrates science, technology, engineering, and mathematics, emphasizing experiences obtained in real-life situations. Moreover, STEM education can be combined with cooperative learning, inquiry-based teaching, science and technology teaching, numerous assessment skills, and other learning strategies to encourage learners to understand STEM and investigate and integrate STEM topics for additional applications [3].
Rapid change in science and technology is changing the skills that countries expect from individuals today [4,5]. In addition to STEM education, cultivating future CPM personnel’s innovation ability, ethics and law literacy, and leadership and execution is vital in university-level CPM education to equip students with the professional skills and competence to adapt to the workplace. In general, government officials and professors in university construction engineering departments may not have experience with engaging in construction projects or dealing with the pressure of managing construction operations; therefore, they cannot clearly identify problems in various aspects of the industry. Educators teach construction and engineering students from their own perspectives, teaching that students should have a global vision and should learn from diversified channels; however, courses focusing on the integration of the various aspects of construction (e.g., mechanics, management, legal affairs, and social science) are lacking.
Because of the stressful competition in the construction industry, few people with practical experience care about construction education. Although the basic duties of a university teacher in Taiwan comprise teaching, research, and service, most teachers regard academic research as their primary work because it allows them to pursue academic career advancement. However, the criteria for excellence for teachers in Taiwan differ from those for engineers in the professional industry. Teachers on campus emphasize theory over practices; hence, the students whom they teach often require re-education after entering the workplace and typically exhibit inadequate innovation ability, ethical and law literacy, and leadership and execution ability. This study summarized existing research on the STEM education of CPM personnel and reviewed the practical courses required in the industry. The next section presents a literature review on related ability indices, namely those on the academic performance in construction and engineering subjects and on creative thinking. Furthermore, the STEM-related competencies focus on “discerning patterns and relationships” in the data to understand the evidence that they collect [6].
The rest of the paper is organized as follows. Section 2 reviews previous studies concerning STEM education and related issues in the latest literature. Section 3 develops a mathematical model to deal with the fuzzy Delphi method and interpretive structural modelling (ISM). Section 4 discusses the analysis and test results. Finally, Section 5 provides the conclusions and some suggestions for future research.
2. Literature Review
School science subjects are playing an increasing role in guiding students towards dealing with issues and concerns confronting everyday life and making them aware of future careers. However, students’ motivation to learn through school science and their unwillingness to pursue science-related careers has been recognized as a problem. Several influencers that play a role in promoting students’ aspirations in science studies and possible science careers have been identified [7,8]. Xiang, Yalan, and Yu (2017) compared the goals of talent cultivation in Chinese and other international CPM schools, determining that schools overseas focus more on cultivating comprehensive qualities in students rather than merely professional knowledge and abilities. International schools require students to receive comprehensive education on multifarious subjects and to develop professional awareness, self-learning abilities, and self-improving abilities. Additionally, schools overseas focus more on linking school education and professional qualifications, emphasizing that the qualification requirements of the profession can be satisfied through learning and that learning serves as a basis of future project management [9]. In this section, several course-related CPM personnel ability indices are summarized to measure CPM personnel’s core competency, creative thinking, and STEM education.
2.1. Core Competency Requirements for CPM Personnel
In this new era of ongoing technological developments and rapidly evolving knowledge, innovative thinking ability is essential for individuals to succeed in the future. The construction industry is no exception. The construction industry shoulders the responsibility of civil engineering and infrastructure projects and is, therefore, closely related to economic development and people’s lives. The construction industry is relatively unsusceptible to the influences of other industries but has a strong potential for stimulating the development of other industries; therefore, it is commonly considered a leading industry. It can increase the demands of upstream and downstream industries, thereby stimulating national economic growth. University lecturers share the common goal of helping students develop scientific literacy; it is crucial that the students develop scientific literacy in order to improve their learning performance in science courses, the ability to understand instructions from their teachers and be capable of understanding the surrounding world, taking personal, workplace, and community decisions and acting as informed citizens appreciating scientific norms and the moral issues associated with science [10,11]. From the perspective of construction, related industries and professions include construction plants, professional subcontractors, material suppliers, machinery leasing industry, test and inspection units, construction companies, architects, technician firms, and engineering consulting companies. CPM is a management process of technology integration that involves specific construction projects in a specific industrial environment. The scientific management and control of the entire process of construction projects, which often involve fields such as construction engineering, highway, bridge, and tunnel engineering, railway engineering, and port and waterway engineering, require diversified, complicated technological backgrounds and foundations. Construction management is an interdisciplinary subject that involves technology and management, exhibiting complex features.
2.2. Creative Thinking Instruction
Creativity plays a vital part in shaping the future of a country. Scientific creativity as domain-specific creativity has been identified as one of the most important contributing factors to the advancement of human civilization [12,13]. At present, China is undergoing a new phase of industrialization and urbanization, which entails multifarious large-scale construction projects. Along with continual globalization, internationalization has become an inevitable path the Chinese construction industry must follow. The ability to handle international affairs and to perform comprehensive construction management have become paramount in university students [9]. Taiwan is also under this influence. The 21st century is characterized by drastic changes. Rapid development and dissemination of information technologies as well as the increasingly accelerated pace of social diversification are reshaping the world. Humankind is facing the third industrial revolution, an era of knowledge economy where victory is determined by brainpower. Innovative thinking, creative thinking, and problem-solving abilities are currently all basic abilities essential for future global citizens. Innovation can be considered a process of knowledge production, exploitation, and dissemination. The cultivation of creativity and innovation capacity is not only the prerequisite of the knowledge economy but also a highlight of future education. The key points are as follows: 1. creativity is a key foundation in the current knowledge economy era and 2. creativity cultivation should be redirected to education. Interactions are crucial to students’ learning of innovation; they help students determine their advantages and disadvantages. Through interactions with peers, students can ask themselves “Can I do this?” instead of “Am I better than other people?” [14]. In this era of ongoing technological development and rapid knowledge evolution, innovative thinking ability constitutes a key foundation for individuals to face the new world. This is also true in the construction industry. Although CPM is a historic discipline, engineers continue to exert creativity in actual construction projects. The results of previous research indicated that enhancing innovative thinking abilities can bring positive influences to organizations and educate teams to achieve specific goals through collaboration [15,16].
Jianxia Cao and Akinori Nishihara (2012) proposed the following approaches for creative thinking instruction. Brainstorming [17,18] as follows:
- Jones (2011) regarded brainstorming as the most direct and common approach to training creative teaching abilities; it was the sudden appearance of ideas and aesthetic feeling, which would stimulate the partners to induce resonance [19];
- Attribute listing: Attribute listing was to list old thoughts, ideas, and principles for recombination or modification to become novel. The creation of new products was mostly the remodeling of old objects, and the remodeling was to change the attributes;
- Morphological analysis: Attribute listing stressed modification, while morphological analysis paid attention to combinations;
- Synectics: Developed by Gordon, synectics utilized analogy and metaphor for helping thinkers analyze problems so as to form various points of view; and
- Reviews of 6 w: It was intended to review current regulations or products from six angles of (1) Why? (2) What? (3) Who? (4) When? (5) Where? and (6) How?
2.3. Science, Technology, Engineering, and Mathematics Education for CPM Personnel
Every country’s education system is its basis for progress and the groundwork for its future. Changes happen very slowly in education, since education systems are some of the largest and most complex systems in every society and are impossible to change overnight [20]. During curricular reforms across Europe, another chance appeared towards increasing learners’ interest in science education, particularly in relation to future job selection in the field of natural sciences and technology [21]. Amid growing concerns about the future of the U.S. economy and workforce, educators and policymakers alike have increasingly emphasized the need to expand the number of students interested in, qualified for and actually pursuing careers in STEM education [22]. The integration of science, technology, engineering and mathematics, known as STEM education, is a growing area in developed and developing countries (United Nations Educational, Scientific and Cultural Organization) [23,24]. From this point of view, mathematics education has an important role in training well-equipped individuals with the skills and knowledge required in the 21st century [5]. The interdisciplinary integration of science, technology, engineering, and mathematics (STEM) education has received substantial attention in recent years; reports by the National Science and Technology Council of the United States and United States President’s Council of Advisors on Science and Technology have indicated a trend of STEM-based talent cultivation in the United States. The United States’ primary purpose for promoting STEM education is likely to enhance its citizens’ science and mathematics literacy, thereby substantially increasing the results of science and technology competency tests. Economic growth in Taiwan is mainly driven by the manufacturing sector, which includes the construction industry.
The development of skilled labor is a crucial factor for future competitiveness in the manufacturing sector. Specifically, the annual number and proportion of higher education graduates from STEM fields are common indices worldwide for assessing a nation’s future competiveness. Science and technology education in the United States transformed first from craft education to science and technology education and, more recently, to quasi-engineering and STEM education. STEM education is promoted among CPM personnel to develop project design, STEM integration, and problem solving abilities. In the United States, a general call for reform has been raised for the teaching and learning of science, technology, engineering, and mathematics (STEM). The increased concern for student achievement and interest in STEM fields was a result of international comparisons. It was determined that the United States was losing ground in the competitive labor market, falling behind in the creation of new and innovative ideas, and students in the United States were underperforming compared with their international peers in mathematics and science [25].
The STEM subject areas could also be integrated for reasons other than international comparison concerns. Many science topics require proficiency in mathematics in order to understand concepts and processes, while mathematics devoid of its scientific context could be seen as a subject worthy of study only for its own sake.
2.4. Summary of Competencies for CPM Personnel
This study focused on developing a curriculum aimed at cultivating talent in individuals with an engineering background and management expertise. Given that construction projects have become activities with low added value, talent cultivated through this curriculum is expected to elevate added value and increase the profit margins in the construction industry to enable personnel to become competent professional managers or even top executives who can be responsible for the future integration of the construction industry. Seven areas were summarized after related literature, STEM educational programs, existing curriculum design programs for businesses and public servants, examination subjects for CPM departments in Taiwan, certified civil engineering technologist examinations, and the civil engineering category of the civil service examination had been reviewed (Table 1).

Table 1.
Competencies to be developed in CPM personnel training courses.
However, it is from the nexus of these two core subjects that technological and engineering innovations often arise. So, while the label “STEM” may have originated due to international concerns, the grouping of these subjects was more natural than simply sharing urgency for improvement [26]. Thus, following the international trend to implement STEM education for CPM personnel can widely attract talent. Encouraging students to major in science, technology, engineering, and mathematics and continually increasing investments in the education of these four fields can cultivate students’ scientific and technological literacy, thereby enhancing their global competitiveness. The implementation of STEM education substantially assists international students (who major in science or technology) in professional work and internships.
3. Methodology of Research
A mixed design was adopted in this study to conduct a qualitative and quantitative investigation. The qualitative investigation involved research and data collection through a literature review, participatory observations, interviews, focus group meetings, and a case study. For the quantitative investigation, multi-criteria decision-making and its applications were adopted. First, the fuzzy Delphi method was employed to prioritize the planned courses. Subsequently, an interpretive structural modeling (ISM) method was employed to transform course elements into graphic presentations of transitive hierarchy; the course sequence could be planned based on these presentations.
3.1. Fuzzy Delphi Method
The Delphi method is a structured decision support technology. Its purpose is to obtain relatively objective information and opinions through independent and subjective judgments of multiple experts in the process of information collection. A fuzzy set is a class of objects with a continuum of grades of membership. Such a set is characterized by a membership (characteristic) function which assigns to each object a grade of membership ranging between zero and one [27]. The fuzzy Delphi method was proposed by Ishikawa et al. [28,29]. The fuzzy Delphi method is derived from the conventional Delphi method; in the conventional Delphi method, the consensus value that represents expert opinion is only a concept of mean. In fact, an undetermined functional relationship exists in expert consensus, which can vary from geometric mean, maximum mean, minimum mean, and harmonic mean to arithmetic mean depending on the consensus function. As for the selection of fuzzy membership functions, previous research was usually based on a triangular fuzzy number, a trapezoidal fuzzy number and a Gaussian fuzzy number. In the real world, human beings face many decision making problems, including ones with conflicting criteria. Multiple-criteria decision making (MCDM) was developed to provide assistance to decision makers in choosing among alternatives [30,31]. The Delphi technique has been used in various fields of study, including program planning, needs assessment, policy determination and resource utilization, to develop a full range of alternatives, explore or expose underlying assumptions, as well as to correlate judgments in many disciplines [32]. As the Delphi method presents the advantage of anonymous decision-making from experts in industries, government, and universities, it is applied at the modeling stage [33].
This study applied the two triangle fuzzy numbers method and the Gray statistics method theory to solving the group decision. This research applied fuzzy decision making (FDM) for the screening of alternate factors. The fuzziness of common understanding of experts could be solved by using the fuzzy theory, evaluated on a more flexible scale. The efficiency and quality of questionnaires could be improved. Thus, more objective evaluation factors could be screened through the statistical results. The FDM steps are as follows [34,35]:
Step 1: A fuzzy expert questionnaire was designed to investigate all items. Experts were asked to provide a possible interval value for each evaluated item. The minimum (maximum) of the interval value indicated the most conservative (optimistic) cognitive value of the evaluated item in question.
Step 2: For each evaluated item i, the most conservative and optimistic cognitive values provided by all experts were calculated. Outliers that were at least twice the standard deviation away from the mean were eliminated. Among the remaining values, the minimum , geometric mean , and maximum of the most conservative cognitive values, and the minimum , geometric mean , and maximum of the most optimistic cognitive values were calculated separately.
Step 3: Based on the calculation results from Step 2, a triangular fuzzy number for the most conservative cognitive value for evaluation item i was calculated as , and that of the most optimistic cognitive value was calculated as (Figure 1).
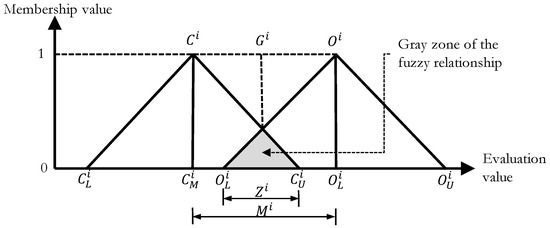
Figure 1.
Jeng’s triangular fuzzy number structure [35].
Step 4: The following method was adopted to determine whether the experts’ opinions had reached a consensus.
If no overlapping was observed between two triangular fuzzy numbers (i.e., ), a consensus range was determined among the interval values of the experts’ opinions, suggesting that all opinions converged within this range. Therefore, the importance level of consensus is obtained as the arithmetic mean of and (1):
If overlapping was observed in the two triangular fuzzy numbers (i.e., ) and the gray zone () was narrower than the range between the arithmetic mean of the experts’ optimistic cognitive values and that of their conservative cognitive values (), no consensus range existed among the expert opinion interval values. In addition, the two experts who provided extreme values (the most conservative value in optimistic cognition and most optimistic value in conservative cognition) did not deviate sufficiently from the other experts in their opinions to cause opinion divergence. The importance level of consensus of evaluation item i equaled the fuzzy set obtained by calculating the mix of fuzzy relationships between the two triangular fuzzy numbers. The quantified score of that fuzzy set with maximum membership value was obtained using (2) and (3):
If overlapping was observed in the two triangular fuzzy numbers (i.e., ) and the gray zone () was wider than the range between the arithmetic mean of the experts’ optimistic cognitive values and that of their conservative cognitive values (), no consensus section existed among the expert opinion interval values. In addition, the two experts who provided extreme values (the most conservative value in optimistic cognition and most optimistic value in conservative cognition) deviated sufficiently from the other experts in their opinions to cause opinion divergence. Evaluation items that did not converge were presented to the experts for reference. Steps 1–4 were repeated for all items and the questionnaire was distributed repeatedly until all items had converged. The consensus value for each item was then calculated. Microsoft’s EXCEL software function tool was used in this study to perform the calculation model and verification of fuzzy Delphi, which was also used to calculate the matrix calculus on next section.
3.2. Interpretive Structural Modelling (ISM) Definition
ISM is a structural modeling technique that can be used to analyze interrelationships between elements to produce a holistic and concrete diagram of the structural hierarchy of the said interrelationships. The primary concept of this technique was first proposed by Warfield as a social system engineering method. This technique divides a complex system into several subordinate systems and their constituent elements. A comprehensive multilevel structural hierarchy based on empirical experience and computer descriptions can be automatically generated. Warfield (1974) indicated that when the structural level of a system increases, its complexity level increases accordingly. By using ISM-based mathematical operations, objective and scientific structural diagrams can be obtained. Initially, ISM involved calculating binary matrices (correlation matrices) by using individual or group psychology models; relevant relations are indicated by element values [36]. Recent studies have extensively applied this technique to analyze key factors of project management [37].
A multilevel hierarchical structure model intuitively and clearly reflects the structural relationships between various elements in a system. ISM is a convenient method that does not require difficult mathematical theories. Thus, it can easily be understood by system analysis personnel. The reachability matrix, T, reflects the extent to which the vertices of a directed graph can be reached after passing a certain amount of path. Through logical operations of an adjacency matrix that represents a directed graph, a reachability matrix can be obtained. By breaking down the reachability matrix, a complex system can eventually be decomposed into a multilevel hierarchy with clear levels. ISM has a wide range of applications and plays a critical role in revealing system structure, particularly analyzing the content structure of teaching resources and the teaching process model in question. In addition, ISM is a relatively modern and specialized research method for the quantitative research of educational computing [38,39].
The calculation method of ISM involves performing hierarchical analysis and correlation interpretation of a complex system by using correlative structures. In practice, n elements in a system constitutes a set, S. Assume that S = {s1,s2,s3…,sn} and its cross product is defined as S × S = {(si, sj) | si, sj S}, the equation must simultaneously satisfy reflexivity, symmetry, and transitivity. The calculation steps are described as follows.
3.3. Calculation Steps of ISM
Step 1: Establish the correlation diagram or adjacency matrix of the elements
Step 2: Calculate the reachable matrix
The incidence matrix was established according to
B = D + I
Through the operations in Step 1, adjacency matrix D is added to identity matrix I and proceeds toward exponentiation through the Boolean Algebra rule. This operation process is repeated until the matrix result no longer changes. When the equation has been satisfied, the matrix with the lowest power is determined as the reachable matrix [40]. The power of B is obtained in sequence in Microsoft Excel until the result has been satisfied as = . A reachable matrix is obtained and abbreviated as M. When B = D + I, subjecting B to exponentiation with ≥(k − 1) power does not change the result; at this time, k is a dimension of D (6):
B* = Bk = Bk+1
M is the reachable matrix, which has a transitive relationship with element correlation matrix B. When M() = 1, a path exists between node ; by contrast, when 0, no path exists between node . After calculation, = = ( = = ) is obtained, indicating that the matrix values gradually attain consistency.
Step 3: Convert the reachable matrix to a hierarchy matrix
The reachable matrix contains the concepts of reachability set R() and priority set A(). Reachability set R() refers to the ith element that can reach matrix M and is extracted from elements that have a relationship value of 1 based on horizontal calculations. Priority set A() refers to the ith element that can reach matrix M and is extracted from elements that have a relationship value of 1 based on vertical calculations. These relationships can be expressed as follows:
Based on the aforementioned reachable matrix, the reachability set, antecedent set, and common set of all elements can be identified. By conducting area decomposition and interlevel decomposition on the reachability matrix, a multilevel hierarchical structure model of the system can be established [41]. ISM is suitable for establishing, deriving, and revising relatively large models and is capable of determining the interrelationships between elements based on graphic theories [42]. Furthermore, ISM facilitates the transformation of vague ideas and viewpoints to structural relationship models where all elements are presented in matrices for subsequent analysis. This method enables experts to express more ideas and suggestions, which can then be amalgamated and categorized based on factor definitions, thereby ensuring the comprehensiveness and soundness of the model and the generation of a hierarchical structure diagram [41].
4. Discussion
In this study, nine CPM curriculum design experts were invited for in-depth interviews and to form a decision-making team. Three of these experts were senior engineers and curriculum design experts from the government (coded as G), three were professors of academic CPM departments (coded as S), and the remaining three were instructors of CPM courses who had conducted training in the industry (coded as I). Table 2 lists the analysis and test results. Decision choices for multi-criteria decision-making are determined by expert groups, but too many expert opinions are not easy to converge. Therefore, we only collected experts from Taiwan.

Table 2.
Analysis of experts’ consensus values.
All nine experts possessed adequate knowledge of the research topic and quantitative methods. Based on a literature review, seven training courses with related competencies were developed, as summarized in Section 2. A questionnaire was subsequently developed and distributed to all nine experts to be completed individually.
4.1. Statistical Analysis Using the Fuzzy Delphi Method
Table 2 indicates that among the seven training courses, leadership and execution (S5) was the most critical in terms of experts’ consensus values (8.31), followed sequentially by innovation (S6; 8.22) and ethics and law (S7; 7.91).
Table 3 details the fuzzy membership test results of the experts’ ratings and overall ranking. Thus, curriculum design for CPM personnel should emphasize leadership and execution, innovation, and ethics and law.

Table 3.
Analysis of test results of fuzzy membership of experts’ ratings.
In particular, the importance of project management should be highlighted in the leadership and execution and innovation courses. Because CPM personnel are frequently engaged in high-budget construction projects, training courses should require personnel to pay special attention to the quality and safety of such projects and should deter them from engaging in corrupt practices.
4.2. Analysis of ISM Statistics
First, paired comparisons of the experts’ opinions on the seven training areas were conducted to determine whether causal relationships existed. The experts were asked to mark correlated areas and leave uncorrelated areas blank when completing the questionnaire. An adjacency matrix was derived from the results (Figure 2).
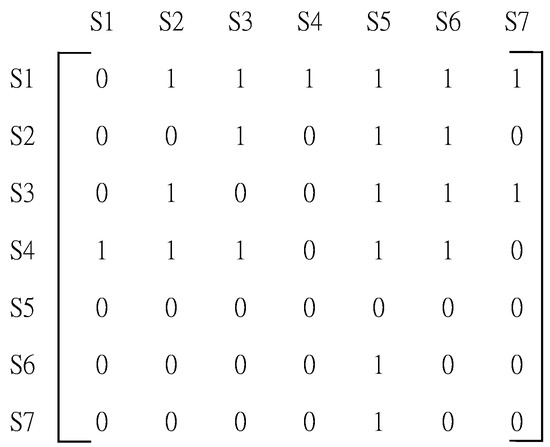
Figure 2.
Adjacency matrix D.
The adjacency matrix was subsequently converted to a reachable matrix by using graph theory [36]. A self-referential causal relationship matrix (B) was created by adding identity matrix I to the aforementioned adjacency matrix D (Figure 3).
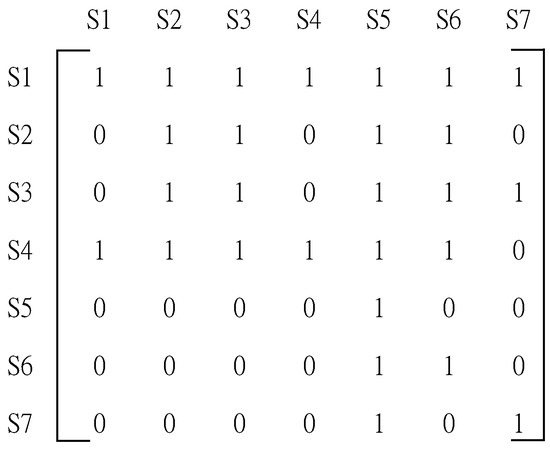
Figure 3.
Self-referential causal relationship matrix B.
In this study, an adjacency matrix was incorporated into an identity matrix, and repeated calculation and convergence were conducted through ISM to generate a reachability matrix (Figure 4).
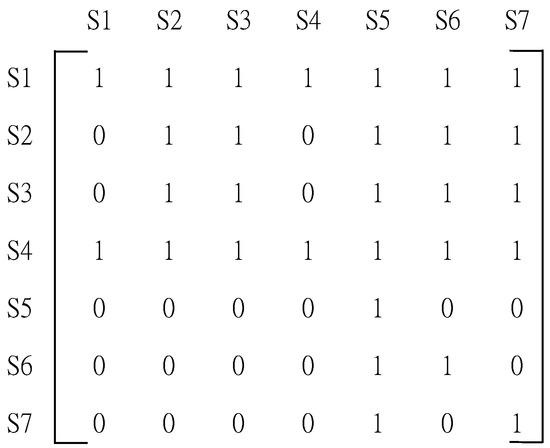
Figure 4.
Reachability matrix.
The basic concept of ISM is to extract the compositional elements of a problem through creative techniques. In this study, when analyzing teaching concepts, the conceptual elements of teaching and learning were extracted through the decision-making process of teaching and learning. Subsequently, computer technologies and mathematical and scientific tools such as directed graphs and matrices were applied to process information concerning the elements and their interrelationships. Finally, textual descriptions were added to clarify the levels and overall structure of the problem in question, thereby further enhancing understanding of said problem. To obtain clearer teaching structure diagrams, computer calculations were performed. The relationship matrix of teaching concept analysis was input and calculated using the reachable matrix to produce an interpretive structure model. ISM analysis results were obtained; the relationships between the reachability set and antecedent set warranted further investigation (Table 4, Table 5, Table 6 and Table 7).

Table 4.
First-order extraction.

Table 5.
Second-order extraction.

Table 6.
Third-order extraction.

Table 7.
Fourth-order extraction.
From R() A() R(), the first-level element set was obtained as ; the rows and columns corresponding to in the reachable matrix were crossed out. In a similar vein, the second-, third-, and fourth-level element sets were obtained as , , and , respectively. After the analysis, the hierarchical matrix diagram was converted to a hierarchical transitive relationship diagram (Figure 5).
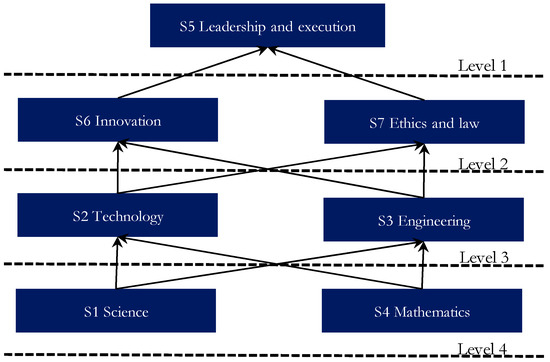
Figure 5.
Hierarchical structure diagram of curriculum design courses for CPM personnel.
Figure 5 illustrates the learning hierarchy and learning paths of CPM personnel’s training. STEM education comprises the most basic courses in the education of CPM personnel; science and mathematics serve as the basis for teaching design, and technology and engineering serve as level 3 subjects. After basic courses have been completed, those of innovation and ethics and law should be implemented. The learning hierarchy and learning paths generated in this study can cultivate the skills of CPM personnel with leadership and execution skills.
5. Conclusions
CPM personnel’s curriculum design should emphasize leadership and execution, innovation, and ethics and law. In particular, the importance of project management should be highlighted in leadership and execution and innovation courses. CPM personnel must grasp the actual situation of a project operation by being actively involved in the execution process and exploring crucial details; they must visit the construction site in person to fully understand the situation. Professional ethics are abstract concepts that are difficult to measure or transcribe as doctrines. CPM personnel are constantly involved in high-budget construction projects. Civil engineering and building industries in Taiwan have long faced depression and an unhealthy professional culture. Hence, the current situation constitutes a suitable opportunity for related personnel to collectively enhance professional engineering ethics. The implementation of an ethics and law course could prevent corruption and enhance construction quality and safety. The importance of professional STEM education should be highlighted in college education and professional and technologist examinations. The importance ranking of the aforementioned seven areas of CPM personnel’s curriculum design summarized in this study and their teaching sequence based on correlations within courses and teaching designs could serve as a reference for the government and construction industries in developing curriculum design programs. In the dilemma faced by global construction engineering personnel training, the model developed by this research can be used as a reference for other universities to revise teaching order. Subsequent studies are recommended to further investigate detailed course items in these learning areas and the arrangement of learning hours, or perform weighted analysis or other forms of learning performance evaluation.
Author Contributions
Conceptualization, W.-L.H.; Study process of the paper was conducted mainly by W.L.H. and H.-L.L.; Formal Analysis, Y.-S.C.; Writing-Review & Editing Y.-C.S.; Project Administration, T.-Y.C.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Grout, I. Remote laboratories as a means to widen participation in stem education. Educ. Sci. 2017, 7, 85. [Google Scholar] [CrossRef]
- Hite, R.; Milbourne, J. A proposed conceptual framework for k–12 stem master teacher (stemmate) development. Educ. Sci. 2018, 8, 218. [Google Scholar] [CrossRef]
- Tsai, H.-Y.; Chung, C.-C.; Lou, S.-J. Construction and development of istem learning model. Eurasia J. Math. Sci. Technol. Educ. 2018, 14, 15–32. [Google Scholar] [CrossRef]
- Yıldırım, B.; Selvi, M. An experimental research on effects of stem applications and mastery learning. Eğitimde Kuram ve Uygulama 2017, 13, 183–210. [Google Scholar] [CrossRef]
- Yıldırım, B.; Sidekli, S. Stem applications in mathematics education: The effect of stem applications on different dependent variables. J. Balt. Sci. Educ. 2018, 17, 200–214. [Google Scholar]
- Asghar, A.; Huang, Y.-S.; Elliott, K.; Skelling, Y. Exploring secondary students’ alternative conceptions about engineering design technology. Educ. Sci. 2019, 9, 45. [Google Scholar] [CrossRef]
- Palmer, T.A.; Burke, P.F.; Aubusson, P. Why school students choose and reject science: A study of the factors that students consider when selecting subjects. Int. J. Sci. Educ. 2017, 39, 645–662. [Google Scholar] [CrossRef]
- Kotkas, T.; Holbrook, J.; Rannikmäe, M. A theory-based instrument to evaluate motivational triggers perceived by students in stem career-related scenarios. J. Balt. Sci. Educ. 2017, 16, 836–854. [Google Scholar]
- Xiang, G.; Yalan, D.; Yu, Y. Discussion on the impact of international evaluation on development of construction management professional education. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 5655–5662. [Google Scholar] [CrossRef]
- Shi, W.-Z.; Wang, J. Comparison on views of nature of science between math and physics students. J. Balt. Sci. Educ. 2017, 16, 77–85. [Google Scholar]
- Torres, J.; Vasconcelos, C. Nature of science and models: Comparing portuguese prospective teachers’ views. Eurasia J. Math. Sci. Technol. Educ. 2015, 11, 1473–1494. [Google Scholar]
- Siew, N.M.; Chin, M.K. Design, development and evaluation of a problem-based with cooperative module on scientific creativity of pre-schoolers. J. Balt. Sci. Educ. 2018, 17, 215–228. [Google Scholar]
- Hu, W.; Shi, Q.Z.; Han, Q.; Wang, X.; Adey, P. Creative scientific problem finding and its developmental trend. Creat. Res. J. 2010, 22, 46–52. [Google Scholar] [CrossRef]
- Chang, C.-Y.; Lin, P.-L. The relationship between science achievement and self-concept among gifted students from the third international earth science olympiad. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 3993–4007. [Google Scholar]
- Birinci, C.M. Teacher in reggio emilia approach: Educational needs and views. Eurasia J. Math. Sci. Technol. Educ. 2017, 14, 279–290. [Google Scholar] [CrossRef]
- Canman, D. İnsan Kaynakları Yönetimi; Yargı Yayınevi: Ankara, Turkey, 2000. [Google Scholar]
- Hu, R.; Wu, Y.-Y.; Shieh, C.-J. Effects of virtual reality integrated creative thinking instruction on students’ creative thinking abilities. Eurasia J. Math. Sci. Technol. Educ. 2016, 12, 477–486. [Google Scholar]
- Cao, J.; Nishihara, A. Understand learning style by eye tracking in slide video learning. J. Educ. Multimed. Hypermedia 2012, 21, 335–358. [Google Scholar]
- Jones, R.M. Development of Attitudes of Children toward Coastal Environment Themes Survey: Exploring Attitudes of Louisiana Middle School Students. Master’s Thesis, Louisiana State University, Baton Rouge, LA, USA, 2011. [Google Scholar]
- Flogie, A.; Lakota, A.B.; Aberšek, B. The psychosocial and cognitive influence of ict on competences of stem students. J. Balt. Sci. Educ. 2018, 17, 267–276. [Google Scholar]
- Bílek, M. Intercultural learning: Challenges for current science education. J. Balt. Sci. Educ. 2018, 17, 532–534. [Google Scholar]
- LaForce, M.; Noble, E.; Blackwell, C. Problem-based learning (PBL) and student interest in stem careers: The roles of motivation and ability beliefs. Educ. Sci. 2017, 7, 92. [Google Scholar] [CrossRef]
- UNESCO Office Jakarta; Regional Bureau for Science in Asia and the Pacific. Annual Report 2010. Unesco Office Jakarta. Available online: http://unesdoc.unesco.org/images/0019/001921/192108e.pdf (accessed on 5 December 2018).
- EL-Deghaidy, H.; Mansour, N.; Alzaghibi, M.; Alhammad, K. Context of stem integration in schools: Views from in-service science teachers. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 2459–2484. [Google Scholar] [CrossRef]
- Augustine, N.R. Rising above the gathering storm: Energizing and employing america for a brighter economic future. Retrieved March 2005, 19, 2008. [Google Scholar]
- Bicer, A.; Capraro, R.M.; Capraro, M.M. Integrated stem assessment model. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 3959–3968. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Ishikawa, A.; Amagasa, M.; Shiga, T.; Tomizawa, G.; Tatsuta, R.; Mieno, H. The max-min delphi method and fuzzy delphi method via fuzzy integration. Fuzzy Set Syst. 1993, 55, 241–253. [Google Scholar] [CrossRef]
- Hsieh, H.-N.; Hou, C.-Y.; Chou, C.-Y. Smart city strategy refined with public participation in the case of hsinchu city, taiwan. ICIC Express Lett. Part B Appl. 2015, 6, 619–626. [Google Scholar]
- Su, C.-H.; Hsaio, K.-C. Developing and evaluating gamifying learning system by using flow-based model. Eurasia J. Math. Sci. Technol. Educ. 2015, 11, 1283–1306. [Google Scholar]
- Ho, S.-Y.; Chen, W.-T.; Hsu, W.-L. Assessment system for junior high schools in taiwan to select environmental education facilities and sites. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 1485–1499. [Google Scholar] [CrossRef]
- Shyr, W.-J. Developing the principal technology leadership competency indicators for technical high schools in k-12 in taiwan. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 2085–2093. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Cheng, A.-C.; Hsueh, S.-L.; Qu, D. Dahp expected utility based evaluation model for management performance on interior environmental decoration–an example in taiwan. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 8257–8265. [Google Scholar] [CrossRef]
- Hsieh, H.-N.; Chou, C.-Y.; Chen, Y.-Y.; Hou, C.-Y. Applying a fuzzy delphi method to construct intelligent city indicators: A case study of taichung. ICIC Express Lett. Part B Appl. 2014, 5, 1693–1699. [Google Scholar]
- Jeng, T.-B. Fuzzy Assessment Model for Maturity of Software Organization in Improving Its Staff’s Capability. Master’s Thesis, National Taiwan University of Science and Technology, Taipei City, Taiwan, 2001. [Google Scholar]
- Warfield, J.N. Developing interconnection matrices in structural modeling. IEEE Trans. Syst. Man Cybern. 1974, 1, 81–87. [Google Scholar] [CrossRef]
- Liu, H.-L. Planning wetland ecology-based outdoor education courses in taiwanese junior high schools. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 3261–3281. [Google Scholar] [CrossRef]
- Wu, Y.; Bian, Q. Research on the drivers of cost control in hydropower construction project. ICIC Express Lett. Part B Appl. 2012, 3, 1603–1608. [Google Scholar]
- Lee, Y.-C.; Shiau, Y.-C.; Hsu, W.-L. Applying interpretive structure modeling on the interactive correlations on factor analysis in natural and cultural scenic area at taiwan. Artif. Life Robot. 2015, 21, 37–42. [Google Scholar] [CrossRef]
- Warfield, J.N. Societal Systems: Planning, Policy, and Complexity; John Wiley & Sons: Hoboken, NJ, USA, 1976. [Google Scholar]
- Sage, A.P. Methodology for Large-Scale Systems; McGraw-Hill College: Hightstown, NJ, USA, 1977. [Google Scholar]
- Warfield, J.; Ayiku, M. Sociotechnical modeling for developing nations. SCIMA 1989, 18, 25–40. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).