1. Statement of the Myth
Mathematics is a central discipline in the school curriculum. As a consequence, it is important that the teaching and learning of mathematics be held to a high standard. However, it has frequently been remarked that in our K–12 school system, this high standard is not generally met. There are two aspects of this. One focuses on student knowledge and performance—students seem to have little knowledge of the subject and can do very little with what they do have [
1] (Chapter 5). The other concerns the student experience. Mathematics is a subject full of wonder and beauty, but students in secondary school rarely experience that [
2,
3].
Interestingly, it is concern about the first that has led to the second. Worry about student knowledge and performance has led to the construction of a curriculum that is narrow in scope and technical in character. There is little room for wonder and beauty in such a design.
In my own teaching experience, I find this problem to be particularly pronounced at the secondary level. In elementary school, the curriculum is more open, more flexible, and there is more time for “play,” certainly in the hands of a mathematically “playful” teacher. At university, the overall agenda is the encounter with “real” mathematics, where wonder and beauty is there for the “taking,” but again this needs a mathematically “giving” teacher. However, at the secondary level the emphasis seems to me to be quite definitely on the preparation of students for college and university, most particularly for calculus, and for some reason we have interpreted that mandate at a purely technical level. Hanna [
4] (p. 20) tracks some of the origins of this.
Why have we settled for such a sterile experience for our students and our teachers? This is justified, explicitly or implicitly, by the claim that our hand is forced by the nature of the discipline—that in mathematics a sufficient technical base must be put in place before the “real” subject can be tackled. In this regard, mathematics is different from other disciplines such as biology, history, English and the creative arts; in those subjects the student can learn by playing with the same kinds of questions, structures and works of art that the professionals work with and talk about. This is not the case in mathematics. This brings us to the statement of the myth.
The Myth. The narrow technical character of the school math curriculum is a necessary consequence of the nature of the subject itself. The curricula of other subjects are based on the investigation, discussion and enjoyment of sophisticated questions, narratives and creative works of interest to professionals in the field. Analogous works exist in mathematics but these are not yet accessible to school students. The reasons for this are found in what is a fundamental difference in nature between mathematics and other disciplines.
2. The Community of Disciplines
My objective here is to situate mathematics as a member of a community of disciplines, and I begin by asking what exactly mathematics is. G.H. Hardy, in his 1940 “apology” for being a mathematician, said [
5] (p. 40), “A mathematician, like a painter or a poet, is a maker of patterns. If his patterns are more permanent than theirs, it is because they are made with
ideas.” Since that time, there have been many restatements of this idea; mine is that
mathematics is the abstract study and creation of structure. Of course Hardy need not have stopped at painters and poets; any scholar or analyst, from literary criticism to neuroscience to urban design, is engaged in the study and creation of structure. What sets mathematics apart is the abstract level at which it works—it studies structure for its own sake. That is what gives it both its purity and sense of beauty, and its unexpectedly wide applicability to the many different kinds of questions we ask about the world we live in. I recall that, as a young man, it was this purity that attracted me to mathematics.
Structures can be simple or complex. Some mathematical structures, for example the multiplication of integers or fractions, are fairly simple, though still quite rich. Others are more complex or sophisticated, and multiplication offers a good example of this in its generalization to integers modulo n, complex numbers, transformations and ultimately group theory.
Sophisticated structures are hard to understand; to work productively with them requires a lot of what is often called “play”—kicking around different kinds of concrete realizations, looking at things from different angles, extracting components to see how they fit together. To succeed in such play, you have to be able to hold in your mind and work with a number of different things at once (it has been suggested that in mathematics this number might be as high as five). Now, to manage that, you cannot keep track of everything in your conscious mind, and that means you have to make certain things “automatic.” Think of a juggler keeping five balls in the air. The conscious mind must keep track of some aspects of the five trajectories, but it certainly cannot handle them all; hours of practice are needed to internalize the routine. What is the nature of that practice? Quite simply, you learn to juggle by juggling—perhaps with fewer balls.
What is true for juggling is true of any discipline that works with sophisticated structures, and that pretty well covers all the fields of study in today’s academic landscape. In our high schools we see this in almost every classroom. In biology class they talk about the complex ecological effects of deforestation; in history class they discuss the reasons for the decline of empires, in drama they study
Cat on a Hot Tin Roof, and in English they read
Wuthering Heights, all activities that work with a sophisticated structure and are of great interest to professionals in the discipline. But this is not what things look like in the math classroom. Jo Boaler reflects on this dichotomy:
There are other indications that math is different from all other subjects. When we ask students what math is, they will typically give descriptions that are very different from those given by experts in the field. Students will typically say it is a subject of calculations, procedures, or rules. But when we ask mathematicians what math is, they will say it is the study of patterns that is an aesthetic, creative, and beautiful subject. Why are these descriptions so different? When we ask students of English literature what the subject is, they do not give descriptions that are markedly different from what professors of English literature would say.
Her juxtaposition of English and mathematics works well for me, as in the school curriculum these are the two disciplines that sit at the centre of the school program. English also has a strong generative component typically lacking in school mathematics. Students in English understand that they are expected to write creatively, but in math class they will claim that it is unfair to be asked to solve a problem they have not seen before. To discover why these two subjects differ in such a significant manner, I take a closer look at the nature of the high school mathematics curriculum.
3. The High School Math Curriculum
It is not hard to get a sense of the nature of the high school math curriculum. One can sit in a classroom for a few periods, or read a few sections in one of the many textbooks, or consult the official curriculum document. All such documents begin with general discussions of process, but the realized curriculum is more often what is detailed in the specific expectations and examples. In
Figure 1 I give an example of this.
Clearly, a mathematician would never simply “use technology to investigate linear, quadratic, and exponential models for this relationship.” Rather, he or she would begin by thinking about how the data were generated and what physical processes were at work. In fact, that thinking leads to quite a wonderful story and as a way of seeing what is missing in the Ministry description, I will summarize it.
It turns out that my then PhD student, Nathalie Sinclair, and I generated that very data in 1998 in a Grade 12 class [
7]. First of all, the data were taken by the students themselves from a real tire. They pumped the tire up, drilled the hole, and monitored the fall of pressure over, not 30 min, but an entire hour. What did we do for that hour? We talked about what might be going on and how you might build a model for the emerging dataset, and that took us into a discussion of the shape of the curve. Even during the first 10 min, when we had only three data points, we had a discussion about whether we should get a straight line or a curve that would get flatter as time went on. That brought us up against this mysterious concept of air pressure. We could “feel it” clearly enough by putting our fingers against the hole, but how were we to mathematize it? We finally agreed that this pressure should be less when there was less air inside “pushing” the air out, but how on earth might we get a precise hold on this apparently complex phenomenon?
Because of that perplexing discussion, they were ripe to be surprised [
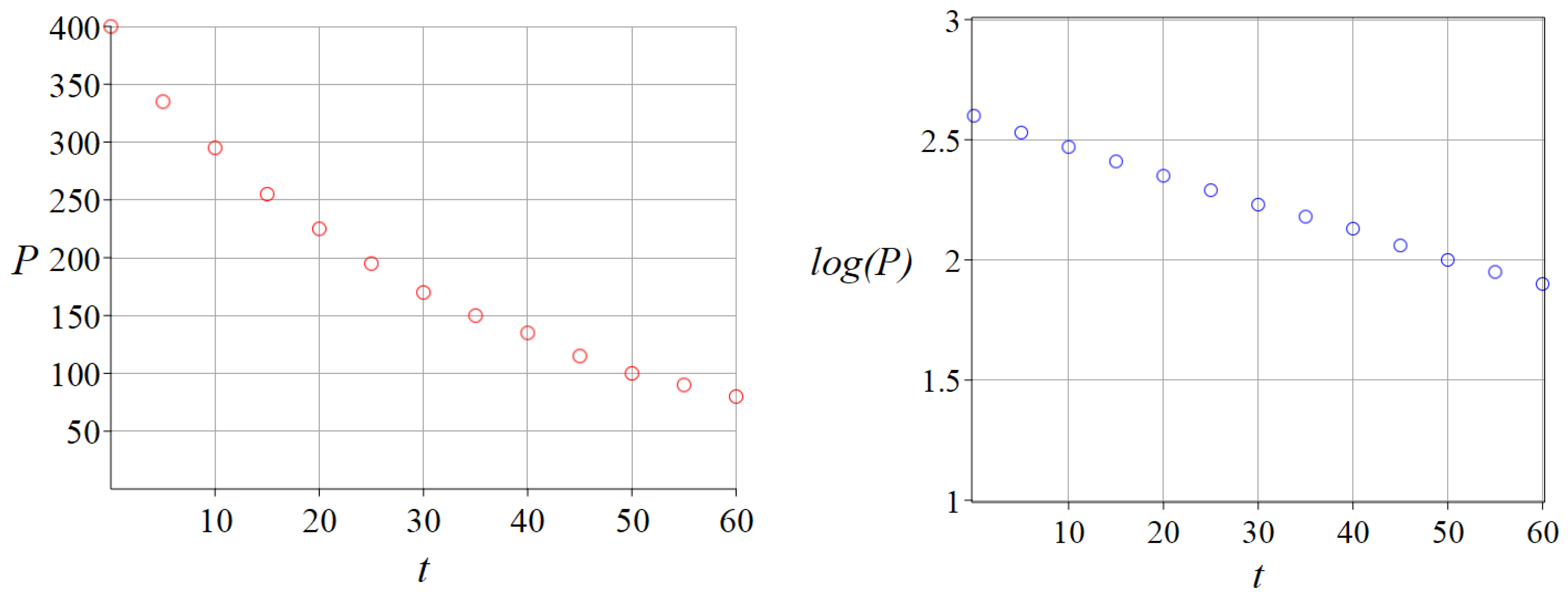
8]. We suggested that it was perhaps not complicated at all, but that the molecules of air were simply scooting around the inside of the tire, bouncing off whenever they hit the inner surface of the tire, except for those rare cases in which they encountered the hole instead and then they passed right through into the outside air. So the pressure against the finger was simply the normal punch of the speeding molecules that escaped from the tire. With that memorable clarifying insight, the students were ready to observe that the flow rate must be proportional to the number of molecules inside the tire, leading directly to the exponential model
. To evaluate the parameters
A and
r we could use Excel to fit the dataset with an exponential curve, but this is really too good an opportunity not to use a log plot. We take the logarithm of the
P-data and plot that against time and what we get (
Figure 2) is a visual treat.
The straight line in
Figure 2 is a visual verification of our exponential model, one that a simple exponential fit would not accomplish nearly so well. It is all the more memorable for being generated by the students’ own hands. At this point we could (and eventually did) fit a linear equation to the data and exponentiate that to arrive at the
P-equation. As I recall, though, even before that, I printed out a copy of the log
P-graph, gave the students rulers and had them estimate the slope and intercept and construct from these an equation for the line. When they exponentiated
that, they had constructed a truly “hands-on” version of the
P-equation.
What had this activity, which occupied two 75-min class periods, accomplished? It gave the students a hands-on engagement with a sophisticated structure, talking about it, engaging it in different ways, and performing a mathematical analysis. Of most importance it was an activity that a mathematician would find interesting and it began with the question that the mathematician would first ask:
what exactly is going on here? There is a sense in which the problem in
Figure 1 does invite the reader to investigate which model might be more “realistic,” but the set-up and the context are completely misleading, and it would require an unusual teacher, with experience, time and additional resources, to construct from the given activity a truly mathematical investigation.
4. The Wisdom of the Past
To understand what to do with all this, I need to connect these ideas with the writings that have most influenced my teaching life. I begin with Alfred North Whitehead, whose 1929 book
The Aims of Education was the bible throughout my early teaching years.
There is only one subject-matter for education, and that is Life in all its manifestations. Instead of this single unity, we offer children—Algebra, from which nothing follows; Geometry, from which nothing follows; Science, from which nothing follows; History, from which nothing follows; a Couple of Languages, never mastered; and lastly, most dreary of all, Literature, represented by plays of Shakespeare, with philological notes and short analyses of plot and character to be in substance committed to memory. Can such a list be said to represent Life as it is known in the midst of the living of it?.
Here Whitehead is clearly not denigrating algebra or the plays of Shakespeare, but he despairs of the narrow technical version that typically dominates the classroom. Whitehead certainly understands the critical role that technical mastery plays in learning and indeed in any creative enterprise, but it must be properly situated in what he calls the Rhythm of Education [
9] (Chapter II). There he identifies three stages of learning: Romance, Precision and Generalization. To some extent, all our learning proceeds through these stages in order, such that, roughly speaking, the child is dominated by Romance, the youth by Precision, and the adult by Generalization. In practice, however, the stages cycle continuously like eddies in the fast-flowing stream of life (and indeed at different times we can all be children or adults).
The first stage of Romance is one of ferment, novelty and mystery, of hidden possibilities and barely justifiable leaps. This stage, in its fullness, motivates the second stage, in which we strive for comprehension and mastery—ideas must be tamed and organized, requiring care, honesty and restraint. Finally, the third stage is essentially a return to Romance, but now with the technique acquired at stage two. Our ideas have new power because we have harnessed them. The great fruit of this ultimate stage of learning is wisdom: the capacity to handle knowledge. The central point that Whitehead makes is that the discipline of stage two must not be imposed until the fullness of stage one has properly prepared the student. Failing that, the knowledge that is obtained will be inert and ineffective. That often seems to be the case for the knowledge that students bring into my first-year university course.
I now turn to John Dewey; among his influential writings, it is his 1934 book,
Art as Experience, that for me has unlocked the mysteries of education. Here, Dewey constructs an entire theory of the aesthetic around individual experience; in effect he calls us to be artists in all our interactions, and the canvas upon which we paint is our own experience.
The word “aesthetic” refers, as we have already noted, to experience as appreciative, perceiving and enjoying. It denotes the consumer’s rather than the producer’s standpoint. It is Gusto, taste; and, as with cooking, overt skillful action is on the side of the cook who prepares, while taste is on the side of the consumer, as in gardening there is a distinction between the gardener who plants and tills and the householder who enjoys the finished product.
Dewey’s main thesis is that the aesthetic experience is jointly constructed between painter and viewer, performer and audience, that both are called to be artists in a shared experience. For me this captures the essential character of the teacher–student relationship; I as teacher am the gardener, the student is the householder and we are working together to create beauty, and that means that we
both have our hands in the earth. Seymour Papert warns that this cannot happen unless the activity brought into the classroom has meaning for the student:
The important difference between the work of a child in an elementary mathematics class and that of a mathematician is not in the subject matter (old fashioned numbers versus groups or categories or whatever) but in the fact that the mathematician is creatively engaged in the pursuit of a personally meaningful project. In this respect a child’s work in an art class is often close to that of a grown-up artist.
In my own work I have little experience with art class, but I do have some experience with drama, and there I find a parallel between the response of the student and the teacher to the work being studied and constructed. I do not think it is unreasonable to strive for comparable harmony in the mathematics class.
In mathematics, aesthetic considerations are regarded as significant in the quest for truth and they infuse every aspect of a mathematician’s life [
8]. Nathalie Sinclair’s marvellous book
Mathematics and Beauty [
12] discusses the different ways in which aesthetic considerations impact the mathematician’s work, the motivational—what structures are worth investigating; the generative—how we come to understand the workings of the structure; and the evaluative—choosing the best among different possible approaches or analyses [
12] (part III). Of these, the generative role has perhaps been the most fascinating to me: how beauty and wholeness can be a reliable guide in our search for the correct path. Poincare [
13] famously wrote that this link between beauty and truth worked through the unconscious and was fundamental to the discovery process. Papert [
14] took up this theme in a wonderful essay in his quest to use technology to show the process at work in the activity of children. His ideal classroom is built around what he earlier described as projects:
This project-oriented approach contrasts with the problem approach of most mathematics teaching: a bad feature of the typical problem is that the child does not stay with it long enough to benefit much from success or from failure. Along with time-scale goes structure. A project is long enough to have recognizable phases—such as planning, choosing a strategy of attempting a very simple case first, finding the simple solution, debugging it and so on. And if the time scale is long enough, and the structures are clear enough, the child can develop a vocabulary for articulate discussion of the process of working towards his goals.
This certainly fits my own recent work, and I find myself paying considerable attention to the question of what structures are the right ones to bring into a class of students at various grade levels. Barabe and Proulx call Papert’s project-oriented approach a complete rebuild, “
une reconstruction complète” of school mathematics [
15] (p. 26), defining the mathematics curriculum itself not in terms of content but as the activity or experience of the students.
5. A Complete Rebuild
What mathematicians do is seek to understand the structure of complex systems. As I have said, what sets them apart from other scientists and humanists and artists is that they work on an abstract level.
My proposal here is that the mathematics curriculum should be built around structurally rich activities, of which the tire-pressure investigation is an example. Of course, technical procedures such as completing a square or simplifying will be practised, but they should arise organically as part of a greater investigation. I will give three reasons for this proposal. First, that is what mathematics is, and if we are going to do something else in high school we should be honest and give the course another name. Secondly, mathematical activities have beauty and integrity and such experiences are fundamental to human nature. Thirdly, if we ask what capacities our students will need in their future lives, the answer is that these are not the completion of a square and the simplification of , but are rather the investigation of complex structures.
The current mathematics curriculum does not have this character. Indeed, it might best be described as a collection of fragments;
Figure 1 is an example of such a fragment. These fragments are of course hopeful components of beautiful sophisticated structures, but those structures hardly ever appear in the classroom. Those few students who choose to take the time to play with the fragments and talk about them and build castles with them can have the wonderful experience, often over subsequent years, of seeing those structures emerge, but for most students the fragments remain a mysterious rite of passage (but passage to what?).
If fragments occupy one end of the experience spectrum, wholeness lies at the other, and Whitehead’s Life and Rhythm, Dewey’s aesthetic and Papert’s projects are about the wholeness of the student experience. Another aspect of wholeness, quite relevant to my emphasis on the creative arts, is found in an observation by Geoffrey Vickers that the loss of an organic connection between science and art is recent and unnatural. He bemoans
the sad history of Western culture which, over the last two centuries, has so narrowed the concepts of both Science and Art as to leave them diminished and incommensurable rivals,—the one an island in the sea of knowledge not certified as science; the other an island in the sea of skill not certified as art… Moreover the two words “Ars” and “Scientiae” not only embraced virtually all skill and knowledge, but also overlapped each other’s territory without offense.
This passage came my way at an important moment in my life, and supported my desire to move forward into the aesthetic. The cultural forces that Vickers is talking about are precisely those that have bent our school curricula to the grim task of preparing the students for a STEM future in a technologically-driven society. The irony is that employers who are hiring in the STEM disciplines are now more interested in the so-called complementary traits, the five C’s: creativity, critical thinking, collaboration, cooperation and care [
1].
The prospect of a complete rebuild poses three operational questions. Are teachers ready for it? Are students ready for it? Are the architects of the curriculum ready for it?
The teachers. A high school Math Head I have been working with asked recently: “Where are we going to find the teachers for this? The teacher candidates I work with do not understand how to play with mathematics.” I feel that there is some change here. In my own interaction with math faculty at the Faculties of Education, I find that they understand what needs to be done and are working as hard as they can in their courses to accomplish this. In my experience, where things have gone wrong for their students is more often in the BA and BSc classrooms, which “cover” material at a rate that is manageable by perhaps the top 30% of the class but reduce the remaining 70% to the anxious experience of memorizing context, leaving little time for play. Often our future high school teachers are recruited from that 70%.
The students. There is a wide range of evidence ([
2,
11,
17] that students of all ages are aesthetic beings and are capable of more creative endeavours than we credit them with. Even so, there will always be great heterogeneity in the level of activity students can handle. For this reason, considerable attention is being paid to the construction of tasks providing a low mathematical floor (requiring minimal prerequisite knowledge), and a high mathematical ceiling (offering opportunities to explore more complex concepts and relationships and more varied representations) [
8] (p. 236). Boaler discusses such activities:
Low floor, high ceiling tasks allow all students to access ideas and take them to very high levels. Fortunately, low floor, high ceiling tasks are also the most engaging and interesting math tasks with value beyond the fact that they work for students of different prior achievement levels…Such teaching, though demanding, is also extremely fulfilling for teachers, especially when they see students who lack confidence and were previously low-achieving take off and soar.
Some students will be ready and eager to roll the task right up onto the stage of Precision; others who might not yet have the right analytical tools can still play and wonder on the stage of Romance. Indeed “wonder” is a magical word and Sinclair and Watson [
18] have a marvellous book review in which they play with its two shades of meaning. In terms of the student’s future, it is worth observing that few of them will ever need to complete a square or simplify
However, they
will often need to arrive at an understanding of the workings of a complex structure, perhaps every time they change jobs. If we can keep that firmly in mind in our assessment of the value of an activity, that might help to expand our viewpoint.
The curriculum. Papert comments that “it is possible for children to do creative mathematics (that is to say: to
do mathematics) at all stages of their scholastic lives … but a great deal of creative mathematical work by adult mathematicians is necessary to make it possible” [
11] (p. 250). That creative work is the construction of a collection of activities that engage the students in the process of doing mathematics, that is, in grappling with the structure of a complex system with interacting parts. A curriculum based on the investigation of such structures is a different kind of curriculum than the one we currently have; it has different methods and different objectives—indeed, it has a whole different structure. Moving to such a curriculum is a huge step and I do not see it happening at the secondary level until a good body of activities has been fashioned and played with in the classroom. Where are we to look to find these activities?––to mathematics, of course, and the structures that mathematicians work with. Many of these will be found in the tertiary classroom and can be adapted to work at the secondary level.
An example from my linear algebra course is our study of the Hamming error-correction code. The heart of that two-week unit is the isomorphism between the code and the wonderful “hat game,” first brought to my attention by the remarkable Richard Hoshino. The winning strategy for that game is available to anyone who understands the coding algorithm. For example, consider the 15-hat game. I call for 15 volunteers from the class to sit around a table and I put hats on each of them, red or blue, determined in each case by the flip of a coin. They all can see the colour of the other 14 hats but not their own. Each player is given a piece of paper on which they are to write RED, BLUE or PASS. The team as a whole wins if at least one person writes the colour of her hat, and no one writes the wrong colour. PASS does not count either way. The team can of course get together beforehand and decide on a strategy. The amazing result is that the strategy derived from the coding algorithm will win with probability 15/16. One reason this result is so surprising is that it is clearly the case that every time a colour is written on the paper it must be wrong 50% of the time. (An accessible example is the three-hat game––students can find a strategy that wins 3/4 of the time.)
The point is that while the interaction between the hat game and error-correcting codes can be analysed by working with the structures of linear algebra, it can also be understood in a more elementary way, in this case using binary arithmetic—perfect for the senior secondary level. Even within that framework, the structure is sophisticated and requires considerable play. However, when you “get it,” it snaps into place and you have this wonderful feeling—I understand!
6. Summing Up
I want school mathematics to give students a
whole mathematical experience. Not only is such a curriculum “true to the nature of the discipline” [
3] (pp. 22–23), it also responds to the needs of the student both now and in the future. In their student lives, they need beauty and wholeness as much as anything else, and in their future lives they need the experience of coming to grips with sophisticated structures of different kinds.
However, such a curriculum really is different in kind and its challenges are substantial. We need writers with an artistic core who have mathematical and pedagogical skills; we need teachers who are prepared to reimagine what it means to be a classroom mathematics teacher and are willing to spend time workshopping promising activities; and we need students who are “game” to embark on mathematical play.
Such changes at the secondary level would have profound implications before and after. At the elementary level there is a rapidly developing body of work providing and supporting creative tasks that can engage children in play and develop their mathematical thinking. In some ways, things are more relaxed at this level as students are farther away from the urgency to prepare for tertiary mathematics. The main challenge here appears to be the knowledge and experience of many of the teachers, and there are calls for better training and resources, for example to help teachers understand the importance of structured play [
19]. At the tertiary level, significant changes are needed as well [
2]. Instructors will need to understand that their students have some real experience with mathematical play but will need more time in which to do it.
What, then, of the myth? Other than in the classrooms of exceptional teachers (and I am fortunate to have worked with a number of these), the mathematics we find in today’s schools is narrow and technical, an entirely legitimate offspring of the curriculum documents and standard textbooks. This is far from the character of the discipline itself and bears little resemblance to the activity of mathematics. Mathematics is different from other disciplines in the precision of its language and the consequent possibility of a complete understanding of its ideas. Yet that in no way requires a fragmented learning experience at the school level; indeed, young students are naturally holistic as learners and need Romantic experiences to propel them onto the stage of Precision. It is particularly important that school nurture them along this path.
Last week I brought a recently developed unit [
20] into a 2-h grade 11/12 class. The objective was to understand why we have 12 notes in an octave; indeed, what remarkable property of the number 12 is at play here (why not 10 or 15?)? We ranged over a broad array of activities, involving frequencies, harmonies, and the nature of perception—for example, how good are we at distinguishing notes of slightly different frequencies? The answer is that we are amazingly good. Indeed, using a tone generator the students discovered that the brain has the power to distinguish between an eardrum vibrating at 2000 oscillations per second and one with a vibration of 2010. The more you think about that, the more extraordinary that seems to be. That is experience. That is Life! Our students are hungry for it.