Abstract
In this article, we ask the question of what it takes for targeted efforts to be reasonably successful in altering students’ misconceptions and unproductive beliefs and ensuing myths about mathematics as a discipline and a school subject and about themselves in relation to mathematics, so as to pave the way for satisfactory learning. We attempt to answer this question through the analysis of three cases of upper secondary school students, who all struggled with mathematics-related difficulties due to myths resulting from misguided beliefs, erroneous proof schemes, or mistaken interpretations of the didactical contract, the three theoretical constructs we employ in the study. We describe how specially educated teachers, so-called “mathematics counsellors”, taking part in a professional development program conducted by the authors, were able, firstly, to identity these students, then to diagnose more precisely the nature of their difficulties, and finally to design targeted interventions in order to assist the students in actually overcoming (parts of) their difficulties and eventually dispelling some of the myths they were influenced by. We further offer an analysis of the elements responsible for the success of these interventions. More precisely, we identify five such elements. Finally, we zoom in on the role and intricate connectedness of the three theoretical constructs mentioned above.
1. Introduction and Background
Since 2012, we have designed and been in charge of an in-service program providing particularly interested Danish upper secondary school mathematics teachers with professional development in the didactics of mathematics. The purpose has been to educate them to become so-called “maths counsellors”, i.e., teachers who are able to help students with mathematics-specific learning difficulties to overcome or reduce these, by teaching the prospective counsellors to detect such students, to diagnose the nature of their difficulties, and to design interventions meant to assist the students in counteracting them [1]. Several upper secondary schools in Denmark now employ such maths counsellors to assist the increasing number of students who experience difficulties with mathematics or mathematics-related subjects. The typical maths counsellor has a master’s degree in mathematics and has taught at least five years in upper secondary school mathematics programs. Typically, the teachers who enter the maths counsellors program do so on their own initiative, with, of course, the approval of their school management—as opposed to having been pointed out by the school to undertake this type of further education, which in our experience seldom functions well. Hence, the teachers who enter the program are experienced teachers, who know that the program is rather demanding but are enthusiastic about making a difference for students who experience difficulties with mathematics.
From the perspective of designing such an educational program, the important thing for us was to offer these future maths counsellors first-hand encounters with relevant research literature from the field of mathematics education and to assist them in applying this literature as an essential tool for their future detections, diagnoses, and interventions so as to make their practice research-based. To this end, the program attempts to strike a delicate balance between theory and practice, where the counsellors have to apply their newly gained knowledge, insights, and abilities towards actual students who have been identified as having mathematics-specific learning difficulties. This means that, for the duration of the program, which is three semesters, the counsellors work part-time with a good handful of students who possess difficulties related to, at least, one of the three themes of the program. These themes are: mathematical concepts and concept formation; mathematical reasoning, proofs, and proving; and mathematical models and modelling. For each of the three semesters, the counsellors are to produce a written project report, accounting for their work with the students identified (i.e., detected and invited to participate) and, more precisely, discussing their detection of these students, their diagnosis of the students’ mathematics-related difficulties, and the design, implementation, and assessed effects of the intervention designed for these students by the maths counsellors. It is also part of the report to account for the specific ways the undertakings just mentioned have been informed by the research literature studied. It is in the cases reported by the maths counsellors, all of whom have been supervised by us, that we have found inspiration for the present article.
As mathematics educators, we are—and were—of course aware of the significant impact of the myths resulting from students’ misconceptions and misguided beliefs about what mathematics is, both as a scientific discipline and as a school subject, on their learning of mathematics (cf. Section 2). Yet, during the last five years in our work with the maths counsellors, we have not only seen how students are under the spell of myths about mathematics and how several results from the research literature are reproduced in students’ non-productive mathematics-related perceptions and views, but we have also witnessed the positive effects of the targeted efforts by the maths counsellors in our program to counteract such misguided student conceptions. The question we ask ourselves in this article, then, is what conditions are necessary and sufficient for effective counteraction to actually occur, i.e., what does it take for such targeted efforts to be reasonably successful in altering the students’ misconceptions and unproductive beliefs and dispelling the myths they uphold so as to pave the way for satisfactory learning? Clearly, it is not enough to merely tell the students that their (mis)conceptions are responsible for the difficulties they experience in mathematics. They must be brought to realize this themselves on the basis of their own experience. But how to achieve this?
Below, we provide three authentic, empirical, and illustrative cases as a basis for our attempt to answer these questions. In all three cases, the efforts of the maths counsellors did in fact help the students overcome some of their difficulties, to a greater or lesser extent, by engaging them in activities that altered (or at least broadened) their conceptions of mathematics into more constructive ones regarding mathematics as a discipline and as a school subject, thus dispelling, at least partly, some of the myths that governed their view of mathematics. The three cases were structured according to, although not necessarily restricted to, one of the following three myth-generating or generated misguided conceptions that we have seen with a great many students:
- Students’ conception of mathematics as a set of basically meaningless disconnected procedures that have to be memorized, and the consequences such a perception may have once the students begin to invent their own rules concerning mathematical procedures in order to create at least local meaning in what they are supposed to do.
- The interplay between students’ everyday experiences and conceptions and their conceptions regarding mathematics, and in particular what happens when everyday conceptions interfere with and influence their mathematical work and reasoning in a negative manner.
- Students’ conception of mathematical instruction as a decade-long training of what they perceive as essentially the same procedures and methods used over and over again, and the potential consequences such a conception may have for students’ self-efficacy.
Before we move on to presenting the three cases, however, we outline a selection of theoretical constructs from mathematics education research of relevance to the cases presented, in particular pertaining to student beliefs and how non-productive specimens of these may constitute “stumbling blocks” for the students’ learning of mathematics. We also briefly address methodological aspects concerning the cases reported and the data presented therein. Upon elaborating on the three cases, we finish with a slightly more general discussion of what it takes to dispel myths by counteracting destructive student misconceptions of mathematics and of how the described efforts of the maths counsellors may be considered as constructive “existence proofs” in this regard.
2. Theoretical Constructs Related to Student Beliefs
For an overall definition of beliefs, we adhere to a definition by Philipp in the second NCTM handbook on research in mathematics education. He describes beliefs as “lenses through which one looks when interpreting the world” [2] (p. 258) and further defines beliefs as:
Psychologically held understandings, premises, or propositions about the world that are thought to be true. Beliefs are more cognitive, are felt less intensely, and are harder to change than attitudes. Beliefs might be thought of as lenses that affect one’s view of some aspect of the world or as dispositions toward action. Beliefs, unlike knowledge, may be held with varying degrees of conviction and are not consensual. Beliefs are more cognitive than emotions and attitudes.[2] (p. 259)
It is a widely held conviction that, in order to change students’ behavior, teachers’ practices, and both parties’ approaches to mathematics, their beliefs first have to change, because beliefs act as filters that affect what we see, and because we have difficulty seeing what we do not already believe [3].
Mathematics education literature offers various attempts to organize notions of mathematics-related beliefs. We shall rely on the tripartition put forward by Op’t Eynde, de Corte, and Verschaffel [4] with an extension due to Jankvist [5]. On the basis of an extensive literature review, Op’t Eynde and colleagues propose that students’ mathematics-related beliefs may be:
- Beliefs about mathematics education: (a) beliefs about mathematics as a subject; (b) beliefs about mathematical learning and problem solving; (c) beliefs about mathematics teaching in general
- Beliefs about the self: (a) self-efficacy beliefs; (b) control beliefs; (c) task-value beliefs; (d) goal-orientation beliefs
- Beliefs about the social context: (a) beliefs about the norms in their own class ((a1) the role and the functioning of the teacher; (a2) the role and the functioning of the students); (b) beliefs about the socio-mathematical norms in their own class [4] (p. 28)
Clearly, two of the foci of the present article, namely, students’ beliefs that mathematics is a set of disconnected procedures and beliefs about the relationship between the discipline of mathematics and everyday life, fall outside this tripartition. Rather, such beliefs would fall inside what Thompson refers to as the “conception of the nature of mathematics”, which covers “conscious or subconscious beliefs, concepts, meanings, rules, mental images, and preferences concerning the discipline of mathematics” [6] (p. 132). The same is true of several of the student beliefs identified by Schoenfeld:
- Mathematics problems have one and only one right answer.
- There is only one correct way to solve any mathematics problem—usually the rule the teacher has most recently demonstrated to the class.
- Ordinary students cannot be expected to understand mathematics; they expect to simply memorize it and apply what they have learned mechanically and without understanding.
- Mathematics is a solitary activity, done by individuals in isolation.
- Students who have understood the mathematics they have studied will be able to solve any assigned problem in five minutes or less.
- The mathematics learned in school has little or nothing to do with the real world.
- Formal proof is irrelevant to the processes of discovery or invention. [7] (p. 359)
Against this background, Jankvist [5] extends the tripartition by Op’t Eynde and colleagues with a fourth component of beliefs about mathematics as a discipline (cf. Figure 1).
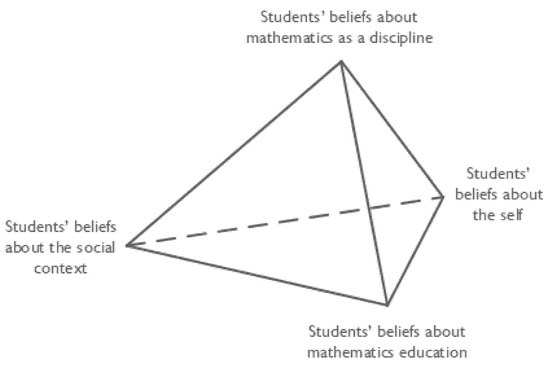
Figure 1.
Students’ mathematics-related beliefs as made up by a basis of their beliefs about mathematics education, the social context and the self (triangle) [4], and their beliefs about mathematics as a discipline (the point above the triangle resulting in a tetrahedron) [5].
The mathematics education literature often mentions students’ beliefs about mathematics or about the nature of mathematics and, occasionally, beliefs related to aspects of the discipline of mathematics [8]. However, as shown by Jankvist, such phrases often cover very different aspects of students’ mathematics-related beliefs [9]. Jankvist defines beliefs about mathematics as a discipline to include “students’ beliefs about mathematics as a pure science, an applied science, a system of tools for societal practice as well as the philosophical and epistemological nature of mathematical concepts, theories, etc.” [5] (p. 45). Jankvist argues for placing the component of mathematics as a discipline outside the triangle in Figure 1, as opposed to turning this into a square, since this fourth component may well be rather different from the beliefs about mathematics as a school subject (1a in the tripartition by Op’t Eynde and colleagues). Still, if students are to alter non-productive beliefs about mathematics as a discipline, this can usually only happen “in the interplay between their social context (class), their mathematics education, and their self, which is to say the triangle making up the base of the tetrahedron” [5] (p. 45). Whether or not this does actually happen is of course a different question. Under the assumption that, when students have been exposed to mathematics education for years, they should have formed an idea about the nature of mathematics, Kloosterman asked American high school students what they would answer if an out-of-space alien turned up and asked them what mathematics is [10]. To his surprise, the students were generally incapable of providing answers and would in general begin to talk about whether they liked mathematics or not, why they needed to learn it, etc. Kloosterman concluded: “The nature of mathematics as a discipline is not an issue that United States high school students think about” [10] (p. 258) and that “students have a hard time separating the activities in a mathematics class from the nature of the discipline itself” [10] (p. 264). When the students were pressed to talk about the nature of mathematics, they mentioned “that mathematics can be used to solve a variety of problems and that it involves numbers” and they often mentioned “the procedural nature of mathematics but almost never mention deduction or proof” [10] (p. 258). This example illustrates characteristic myths about mathematics as well as the mutual influence between the components of, for example, beliefs about mathematics education and beliefs about mathematics as a discipline.
Another construct that we shall take into account is that of the didactical contract (DC). This forms part of Brousseau’s theory of didactical situations and concerns students’ interaction with the didactical environment (or the milieu) [11]. Brousseau says that the “student learns by adapting herself to a milieu which generates contradictions, difficulties, and disequilibria, rather as human society does. This knowledge, the result of the student’s adaptation, manifests itself by new responses which provide evidence for learning” [11] (p. 30). The students’ interaction with the environment can be guided by the teacher or the teacher’s expectations (the situations in which this takes place are termed “didactical”), and/or be a result of the students’ genuine interest in mathematics stimulated by the environment (taking place in situations referred to as “adidactical”). The teachers’ expectations and classroom norms, as well as the students’ expectations of the teacher’s role and activities, are described as a result of a didactical contract between teacher and students. The contract is often implicit and tacit, albeit unavoidable, and is typically based on years of classroom experience on the part of both teachers and students. It guides the actors’ behavior and mutual expectations, as described by the EMS Education Committee’s “solid findings” article on the topic:
The DC is the set of reciprocal obligations and ‘sanctions’ which each partner in the didactical situation imposes or believes to have imposed with respect to the knowledge in question, explicitly or implicitly, on the other; or are imposed, or believed by each partner to have been imposed on them with respect to the knowledge in question. The DC is the result of an often implicit “negotiation” of the mode of establishing the relationships for a student or group of students, a certain educational environment, and an educational system.[12] (p. 54)
Students’—and teachers’—mathematics-related beliefs are of course likely to affect the didactical contract, or at least the parties’ perception of it. Similarly, a given didactical contract can, in itself, affect and give rise to—or suppress—certain mathematics-related beliefs in the students.
The final theoretical construct, which we shall make use of in our analyses below, is Harel’s and Sowder’s proof schemes: “A person’s (or a community’s) proof scheme consists of what constitutes ascertaining and persuading for that person (or community)” [13] (p. 809). Overall, a proof scheme belongs to one of three classes, each composed of different subclasses. The first class consist of what Harel and Sowder call external conviction proof schemes, which may be manifested as an authoritarian proof scheme, e.g., that something is held to be true because the teacher or the textbook or some other authority says so, as a ritual proof scheme, e.g., that a geometry proof in the USA must have a two-column format, or a non-referential symbolic proof scheme, e.g., that a proof must display symbols and symbolic manipulations, which do not carry any meaning for the learners. The second class consist of the empirical proof schemes, which are either inductive proof schemes, e.g., you are being convinced by one or several specific empirical examples, or by what is perceived as a “crucial” generic example, or perceptual proof schemes, e.g., when a conjecture is validated on the basis of rudimentary mental “images that consist of perceptions and a coordination of perceptions but lack the ability to transform or to anticipate the results of a transformation” [14] (p. 255). Finally, the deductive proof schemes are those with which we are familiar from the discipline of mathematics, such as direct proof, including axiomatic proofs, proof by contradiction, proofs by mathematical induction, combinatorial proofs, etc., all governed by logical deduction from a local or global set of premises.
Of course, a given student’s proof scheme—or conviction scheme, as we might prefer to call it, since the notion actually concerns what it takes to convince a person—may in some way be affected by that student’s beliefs. If a student perceives mathematics as a natural science in the same way as, say, physics, then that student might not only be content with, but insist on empirical examples as proof of a general mathematical statement. However, the underlying reason for such misguided beliefs and insufficient proof schemes and the resulting myths may indeed also be due to an inadequate didactical contract. Conversely, students’ proof or conviction schemes will inevitably affect their beliefs about mathematics and their positions with regard to the didactical contract. Following our analyses of the three cases, we shall return to the intricate relationships between students’ beliefs, proofs schemes, and perceptions of the didactical contract. First, however, we shall turn to a brief discussion of the methodological aspects surrounding the three cases.
3. Methodological Aspects
The core of this article is a presentation and analysis of three cases, i.e., a case study. A case study is not a presentation of singular specimens but of cases of something. For a specimen to be a case, it has to be an exemplary prime instance of a larger class of specimens, which share a number of characteristic traits and properties in certain respects, whereas they may differ in several other respects. Oftentimes, it is difficult to convincingly demonstrate that a given specimen does indeed deserve to be considered a case, since this requires scrutiny of all the specimens in the class supposedly represented by the alleged “case”, at least in principle. Such a demonstration is a beyond the scope of any journal article. So, the readers usually have to take the authors’ word for the exemplarity of an alleged case whilst being offered access to all the raw data on the basis of which the case has been selected.
In the present context, the cases have been selected—by us—from a large pool of some 50 students who have been chosen (out of around 700 students) as focus students by the prospective mathematics counsellors participating in our professional development program for upper secondary mathematics teachers. All these students have been described in the reports written by the teachers who worked with them in the program, and our selection rests on careful reading of all these reports. It is our best judgment that the traits and properties represented by the three case students are indeed found to manifest degrees in the entire student population, but we cannot prove it in an article such as this. Therefore, our conclusion and discussion must necessarily take a qualitative form when it comes to the generalizability of the findings we are going to present.
In each of the three cases, upon firstly having detected the students to be worked with and next having attempted to “diagnose” the individual student’s mathematics-specific difficulties, the maths counsellors, under our supervision, designed interventions, inspired by or based upon the mathematics education theoretical constructs that they had studied as part of the program. These interventions took place during the middle part of one semester, i.e., they typically had a duration of three months and seldom comprised more than ten 40–80-min sessions with the students. (All quotations have been translated into English by us.)
In order to provide a bit more of a background to the three cases we are going to present in the next section, we shall briefly outline the structure of Danish upper secondary school. Danish non-vocational upper secondary education—to which the cases belong—typically takes three years, corresponding to grades 10–12 (ages 16–18/19) (even though there is, in fact, also a two-year option). The three-year upper secondary school is organized in three different streams, a general academically oriented stream, called stx, a technology- and science-oriented stream, called htx, and a commerce and business-oriented stream called hhx. All students have to study mathematics for at least one year, called C level. Many students (and soon all) must study mathematics for two years, called B level, whereas a somewhat smaller (but not small) segment of the student population study mathematics for all three years, called A level. In principle, a given level is supposed to be the same across the different streams, but, as there is a great diversity in content and approach in the three streams, they should not be taken to be identical, even though the label is the same. Students will have to take a national exam in mathematics according to the level at which they have chosen to study mathematics.
4. First Case: Mathematics as Disconnected Procedures
In the Spring of 2015, two teachers, Tina Rosendahl and Henrik Kærgaard, worked with a second-year student, with the pseudonym Christian, in the technology/science stream (called htx) of Danish upper secondary school [15]. The teachers knew Christian from a course in programming, where he had shown a clear understanding of the logical aspects involved. However, from Christian himself and from a colleague who taught him before, they learned that he was close to a failing grade in his mathematics course. This led the two prospective maths counsellors to further investigate the case of Christian. They wanted to find out what he thought of mathematics, both as a school subject and a discipline, and what his perceptions of logic and mathematical truth were. Hence, they designed a diagnostic interview in order to uncover some of his mathematics-related beliefs that might have acted as stumbling blocks and destructive myths in his learning of mathematics. The teachers found that Christian felt alright with mathematical topics which he immediately could see as having a practical application, e.g., calculation with percentages, whereas he saw no relevance of trigonometry. When performing simple arithmetical computations on specific numbers, e.g., involving addition, multiplication, and parentheses, Christian experienced no difficulties but, when presented with a simple algebraic task in a symbolic domain, he exclaimed: “I hate algebra. Because it’s full of ‘cheaters’” [15] (p. 147). Asked about the history of mathematics, Christian showed some knowledge concerning counting and computations as he replied “... counting with stones, later the abacus” [15] (p. 146). When asked about the hierarchy of arithmetical operations, he suggested that “... someone had invented it” and provided the following account of it: “[when] multiplying, you calculate with larger numbers to begin with. Then you want to reduce them first, so you take the simple part and pluses and minuses afterwards. Parentheses are often like… what’s inside them is more important. You always ‘frame’ what’s more important” [15] (pp. 146–147). On the basis of the interview, the two prospective maths counsellors diagnosed Christian as having a conception of mathematics as a subject “consisting of an incomprehensible swarm of weird and incoherent mnemonic rules that make no sense” [15] (p. 147). Because of this, he seemed to have convinced himself that he could not understand or do mathematics at the level required and might as well give up. In other words, he was under the spell of a destructive myth.
Taking the above as their point of departure, the teachers designed an intervention with the purpose of making Christian realize that, in fact, in mathematics you only have to memorize a very few rules, and then you are able to deduct most of the rest of what you need. The main idea for the intervention was to present Christian with a small handful of algebraic conventions and axioms, allowing him to make sense of and familiarize himself with these through a number of little exercises. This was to be followed up by some more complex tasks designed to enable him to come to grips with selected basic algebraic operations and results. The teachers hoped that Christian would then realize that these results did not drop down from the skies but followed directly from the axioms initially introduced through a process of logical reasoning. On the basis of different theoretical constructs, including Brousseau’s notion of didactical and adidactical situations [11] and Hanna’s notion of proofs that not only prove but also explain [16], the teachers designed a three-session intervention. In the first session (in which we were observers), Christian worked with the hierarchy of the arithmetical operations and had to multiply symbolic expressions, the results illustrating areas of quadrilaterals, e.g., (a + b)∙(c + d) corresponding to a quadrilateral with sides a + b and c + d. In the second session, Christian, among other things, was asked to deduce the formula for a squared binomial, (a + b)2 = a2 + b2 + 2ab, again supported by figures showing the corresponding squares and rectangles. In the third session, he had to work with the power conventions and rules. Upon being asked to deduce that a0 = 1, Christian uttered: “Oh, I’ve seen that on the Internet, you just have to accept that it is 1. I once asked a third year student about it, and he said that the proof was like really long” [15] (p. 177). As the math counsellors explain, once Christian was told that in less than two minutes he would have made this proof himself, he looked rather suspicious. Yet, applying the previously deduced power rules, he was indeed able to do so. At the end of the session, Christian was asked to respond to the fact that he had just deduced all the power rules and that the only mnemonic rules he had applied were some basic axioms and the hierarchy of the arithmetic operations. He was rather baffled—although obviously also proud of his accomplishments.
As a consequence of the intervention, the two teachers observed in class how Christian’s attitude to the subject of mathematics changed. He now believed that it was actually possible for him to understand and learn something and he became determined to get as far as possible within the last few months of the school year. In a final exam project in mathematics that year, Christian received the grade 7 (corresponding to a C on the ECTS scale, where he used to score F or E). One year later, the maths counsellors interviewed Christian again in his final year in high school, in order to assess possible long-term effects of the intervention. He said:
I have come to view the solving of mathematics tasks in a different way. The same is true of programming. I’ve begun considering what possibilities I have for getting help, when there is something I can’t figure out—as opposed to giving up, which is what I would have done before. I still prefer to solve the tasks by myself. When something is difficult, I have now learned that I can address the task by simplifying it—place things in a sequence and take them bit by bit, instead of looking at everything in one big hotchpotch. [...] I found out that mathematics is simpler than I thought prior to the intervention. I can now remember how the formulae [rules] are connected. Actually, I’m going to have some math as part of my chosen higher education program, where I’ll be studying ICT technology. [...] I’ve always known that there was some kind of logic in mathematics, only I hadn’t found it. Now I have. [...] After the intervention, I have gained the courage to pursue a higher education degree, where I have to apply mathematics. Before, I believed that I suffered from dyscalculia. You made me see mathematics in a completely different way. Now I know that I’m not innumerate.[17]
It seems fair to claim that this intervention actually dispelled some of the myths that used to ruin Christian’s relationship with mathematics.
5. Second Case: Everyday Conceptions in Mathematics
The two teachers and prospective maths counsellors Mette B. Lomholt and Morten S. Larsen followed Student A, as they called her, closely throughout her three years in the technical branch of upper secondary school where she took mathematics and physics at the highest possible level, Lomholt and Larsen being her teachers in these subjects [18,19]. They specifically intervened towards her learning difficulties during the last semester of her second year and the first semester of her third year.
Student A believed that mathematics is completely focused on numerical computations and that mathematics tasks are prompts to rush off to do some computations as quickly as possible, a myth that, in the beginning, completely governed her relationship with mathematics. Whenever she was unsure of what to do—which was often—she would begin guessing at random or throw herself head over heels into some aimless plan. So, it was largely a matter of chance whether or not the computations she undertook had any bearing on the questions posed in the tasks. One consequence of her beliefs about mathematics was that, for ordinary students, independent thinking is neither necessary nor desirable when dealing with mathematics. She was very hostile to and afraid of tasks that either do not require any computations or place computations in contexts involving symbolic calculations. She was particularly reluctant to engage in tasks requiring reasoning in an algebraic or a geometric environment.
Based on A’s response to a large variety of test questions of different kinds, the teachers first realised that her understanding and skills in algebraic contexts were very weak, in fact to such an extent that this perturbed her ability to reason mathematically. For example, when asked to consider the equation 38x + 72 = 38x, she wrote “You cannot add ‘pure’ numbers and ‘x-numbers’. It’s like adding pears and bananas. So, you cannot reduce the equation any further” [18] (p. 78). After having made several (actually legal) transformations of another equation, she finished by writing “1x = x ⇒ 0”, where it is not completely clear what the inference is supposed to be. She knew that x⋅x = x2 but not that d⋅d = d2. When examining or making statements involving formulae, she had a strong preference for working with specific numbers rather than with symbolic expressions. She was neither able to interpret, nor convinced by, conclusions obtained by manipulating formulae or expressions. When asked whether it is true that the volume of a cube is multiplied by 8 if all edge lengths are multiplied by 2, she wrote V = s⋅s⋅s and then said, “I don’t think that the new volume is eight times as large” [18] (p. 94). She maintained this response when prompted to write V’ = (2s)⋅(2s)⋅(2s) = 8s3. When asked whether it is true that if one halves the diameter of a circle then both the area and the circumference of the new circle are half those of the original circle, respectively, she was convinced that the answer is “yes”, even though she was able to correctly state the formulae for the area and circumference of a circle. The teachers invited her to make drawings representing doubling the edge lengths of a square and of a cube, which she was hardly able to do. After having been assisted by the teachers in making the drawings and then asked to interpret them, she was not convinced that they show that the area and the volumes are multiplied by 4 and 8, respectively. As the teachers wrote: “She is algebraically convinced but remains uncomfortable with drawings, at least when chequered or diced patterns are involved.” [18] (p. 95) In other words, A was a strong believer in the “law” that if something in a context is doubled, then everything is doubled, which is a marked instance of the over-generalization of proportionality, as previously studied [20,21].
Against this background and considering similar experiences with A in her physics class, the teachers concluded that in addition to algebraic reasoning, A’s difficulties were largely to do with mathematical modelling in situations involving proportionality, scaling, ratio, rate, and speed. This was further reflected in her fear of units and unit conversion, especially in physics. So, they designed a three-week intervention program in which A was invited to work on a large variety of modelling-oriented tasks involving these notions. In the design of these intervention activities, the maths counsellors relied on Lesh’s and Doerr’s theoretical construct of model-eliciting activities [22]. A was asked to formulate hypotheses concerning formula-specific relationships and afterwards test these by using manipulative materials such as Lego blocks. As particularly regards the doubling of the edge lengths of squares and cubes, A assembled and disassembled the blocks numerous times, eventually convincing herself of the squaring of the area and cubing of the volume, whilst stating “This is a shaking experience” [18] (p. 144). At the end of the intervention program, A had made considerable progress, even though there was still room for further progress. She could make drawings on her own initiative, try to interpret and make sense of tasks before attempting to solve them, and no longer believed that proportionality rules the world, that mathematics consists in numerical computations, and that symbolic calculations have nothing to do with numbers or with the world outside mathematics.
As the teachers observed, their relative success in changing A’s beliefs about the nature of mathematics and mathematical activity and in strengthening her mathematical competencies would not have been possible had she not been willing to invest a non-negligible amount of time and effort and to endure frustration over an extended period of time. Another key point in the story of A is that the achieved improvements of her mathematical understanding and competencies rested on the maths counsellors’ targeted and sustained efforts of trying to uncover the roots of A’s learning difficulties in mathematics and eventually to dispel some of the myths she was under.
6. Third Case: Long-Standing Training of Procedures
In the fall of 2016, three teachers, Christian Wejdemann, Karl-Kristian Bjerregaard, and Flovin Næs, worked with a second-year student in the general stream (called stx) of Danish upper secondary school [23]. Rikke (the pseudonym given by the teachers) was a conscientious student, a bit quiet in her behavior, and reluctant in showing her mathematical work to others. Her attainment level was usually assessed to around 4 or 7 (D or C on the ECTS scale). In her homework assignments as well as in the math counsellors’ testing and subsequent interviewing of her, she displayed difficulties in relation to recognizing and classifying functions according to their type (e.g., linear functions, power functions, exponential functions, etc., in modelling contexts), a key component of upper secondary mathematics education in Denmark. She was offered the opportunity to take part in a four-session intervention related to aspects of mathematical modelling, where she would have to apply different types of functions as means for mathematizing real-world problem situations. At first, Rikke was reluctant to take part in this intervention, but eventually she agreed, on the condition that she could do it together with a classmate. As part of these sessions, the two students first had to pair verbal descriptions of problem situations with the correct graphical representations out of several options, and next to pair formula-based expressions of functions with graphical representations.
The following task and Rikke’s problems in tackling it clearly illustrate her misconceptions in relation to identifying function types and also provide an entry point to some of her mathematics-related beliefs that were seen to act as stumbling blocks in her mathematical work. The verbal description of the problem situation was: “At 7 p.m., Axel’s body temperature is the usual 37 degrees Celsius. He then becomes very ill, and in the following time period [unspecified] his body temperature rises by 1.5 degrees per hour; y denotes Axel’s body temperature, and x denotes the number of hours after 7 p.m. on the night in question.” The two students then had to decide whether this verbal description corresponded to linear growth, growth by a power law, or to exponential growth. Rikke’s first conjecture was that the situation could be described by an increasing exponential function and that this was due to the fact that Axel’s body temperature rose by 1.5 degrees per hour. Rikke produced a (correct) table of five corresponding x- and y-values. Still, she insisted that this resulted in exponential growth. The maths counsellors then asked her to calculate more values and eventually to plot them on a piece of graph paper. Once she had completed this, she exclaimed:
- Rikke: This is pretty linear!
- Teacher: Why does this surprise you?
- Rikke: Because normally, when we have something that grows per time unit, then it is an exponential function. [23] (p. 228)
As it turns out, Rikke practiced a strategy of spotting clue words and other triggers, e.g., a phrase like “per time unit”, and then based her choice of function type on this. Also, the maths counsellors discovered that she generally did not believe in her own calculated values for sample points. Rather, she attempted to choose a graphical representation based on the formula expression (if possible), often leading to an incorrect choice. During the third session, the maths counsellors interviewed Rikke about this, and in the process uncovered a central belief of hers.
- Rikke: I think it is because there are so many different ways to calculate it, and then you begin to doubt [...]. I often think about if what I do is actually correct. [...]
- Teacher: Is it the same in other subjects, i.e., that you feel this insecurity, or is it peculiar to mathematics?
- Rikke: In biotechnology, for example, we also calculate and solve problems sometimes. But there you get insecure because it is difficult, and the others think so too. So you are more in it together, finding it hard. And then we can ask the teacher. But in maths, which is a very important subject, and I have it at A level… there are other factors involved, I think.
- Teacher: But biotech is also important and at A level.
- Rikke: Yeah, I know that, but, in biotech, we are all working together on tasks that are pretty hard, and which we haven’t tried before, whereas we’ve had mathematics since forever. Biotech is new in a completely different way, and we don’t have the same background knowledge as we do in math. In biotech everything is new, and we all have to learn the same, from the same ‘beginning’, if you can say that.
- Teacher: Is it that you feel it is worse in math because you ought to be able to do it, since you’ve studied maths for so many years?
- Rikke: Yes, I think so, and then I get insecure, if there is something I can’t figure out. Then I think, ‘fuck, it’s going to affect my grades’ or something. I feel stupid.
- Teacher: In math, the pressure of expectations is greater in some way?
- Rikke: Yeah, a little I think. It seems like the expectations are a little greater, and that you should be able to do everything in math, I think.
- Teacher: Are these expectations from the teacher? The classmates? Or the textbook? Where do they stem from?
- Rikke: All of the above, kind of… Now, you are in upper secondary school and you are supposed to be able to do it.
- Teacher: A final question. In the final national written exams in mathematics, B level and A level, how many students do you think fail these?
- Rikke: Not very many.
- Teacher: Make a guess. In percentage.
- Rikke: Maybe 5%.
- Teacher: No, actually it is a lot higher. I’m not saying this to scare you, but rather to deal with your idea that ‘everybody is able to do maths’ and ‘we’ve had it for such a long time, so we ought to be on top of it’. Math is hard and it is very different in upper secondary school. So, you need to view it in the same way as you view biotech. [23] (pp. 238–239)
As part of the final session of the intervention, the maths counsellors emphasized the need for Rikke to trust the methods she had been introduced to, e.g., to calculate supporting points in order to determine the type of growth at issue and to dare to experiment more as part of her mathematical problem tackling. Upon the completion of the intervention, the maths counsellors gave Rikke a test where she was invited to do a number of tasks alone in a room while being video-filmed. Although Rikke by no means was able to correctly answer all tasks presented to her, the maths counsellors did document a significant change in her approach to a task. To a larger extent, she now applied a strategy by which she tried to arrive at a formula expression informed by calculations based on the verbal task description. Once having obtained a formula expression, she would even sometimes control it by performing calculations and see if these matched the previous ones based on the verbal descriptions. Some time after the intervention, Rikke offered her thoughts about it in an email to the maths counsellors:
Hi.I’d like to thank you for the opportunity to participate in the intervention. It was a way for me to come to think about and view math in a different way than what I’ve done before. [...] in the beginning it did in fact put my self-confidence on trial, but that has changed, of course. [...] I truly feel that my motivation for raising my hand in various subjects has grown. I am now more daring, even if what I say sometimes turns out to be wrong. In principle, I have come to trust myself more than I did before. It’s not that my attitude towards math has changed as such, since I’ve always liked maths. But the sessions with you guys made me desire to be taught more math, simply because I now feel more confident in the subject. I’m also more confident now in my own approach to solving tasks—if you see what I mean. I don’t wait for my classmates to confirm that they have used the same approach as I did—now I actually trust myself, what I do, and what I know. Cooperation with my classmates in maths—I feel—has also changed to my advantage, if I may say so. The methods you provided me with in the sessions made me trust myself, without all the time needing to seek confirmation that what I’m doing is right. [...] You told me that maths has a high failure rate—this has made me aware that I’m not the only one who finds maths hard sometimes, and that I’m not alone in this.Since I now have some tools and other ways of seeing mathematical relationships, I also have more appetite for doing cranky tasks on my own. I’ve learned to turn my insecurity into something positive, so I look at [mathematical] relationships from different angles and use my calculations to arrive at results that I myself believe in. An important point, I think, is not always just restricting yourself to the basics [rules, formulas, etc.], but to do experiments, make some calculations. For example, for exponential functions there is a certain formula, a certain way the graph has to look, and some requirements that have to be fulfilled. Previously—as I believe you also noticed—I restricted myself to considering a mathematical relationship solely based on the information given [in the task] and the basics and used that to decide whether a function is exponential, linear, and so on. This didn’t always work so well for me [...]. You taught me that with different tools and methods you can easily determine the relationship, without initially being able to see it on the basis fof the given information. [...] I can definitely use these experiences and my newly acquired tools and methods from the intervention in my everyday maths classes. And I want to say that I’m quite positively surprised at what I’ve actually gained from all of this.I hope you can use my answer for something.Rikke[23] (pp. 256–257)
At least two of Rikke’s myths about mathematics were dispelled by this intervention, namely, that, when you have received teaching of mathematics for 10 years, you should have grasped it by then, and that the ingredients required to deal with a mathematics tasks are based on surface features.
7. Analysis of the Three Students’ Beliefs
Christian was a student who had come to believe that mathematics is a subject that is out of reach in terms of understanding, at least for him. His own encounters with the subject had failed, also according to his previous teachers, and he accepted this and in fact agreed. He acknowledged that it is potentially possible for others to learn and do mathematics, but unfortunately not for him. He believed to be operating under a didactical contract saying that most of mathematics needs to be memorized and learnt by rote, because the subject makes no sense from a logical point of view. In particular, things related to algebra and geometry appeared almost as “abracadabra” to him. Still, he did accept that some aspects of mathematics can be of practical importance.
As the reader will notice, some of Christian’s views coincide with Schoenfeld’s list of students’ counterproductive beliefs about mathematics [7]. Christian’s “beliefs about mathematics as a discipline” were misguided, and this affected this “beliefs about mathematics education”—hence in the tetrahedron of Figure 1, we are dealing with the edge between these two vertices—because he did not see the subject of mathematics as concerning reasoning and logic, but rather as an arbitrary collection of mnemonic rules. This, however, had consequences for his negative “beliefs about the self”. Seen in this light, it may not be so strange that Christian performed poorly in mathematics. Also, considering that he did not suffer from more general cognitive disabilities, since he did well in his programming class, it seems fair to infer that his difficulties in relation to mathematics in large part stemmed from his counterproductive beliefs and the myths that created them.
The maths counsellors chose to invest efforts in making it clear to him that mathematics is a discipline of reasoning rather than of rote learning. They decided to focus on a topic about which Christian uttered fear and contempt, namely algebra, and did so with the hope that if he could come to grips with the fundamentals of algebra, this might have a spillover effect into other topic areas. Because algebra apparently had caused Christian so much trouble, they decided to begin with the most elementary symbol conventions, rules, and manipulations of symbolic expressions and formulae. They established a local axiomatization of algebra, which could and would form the basis for Christian’s mathematical work as part of the intervention. They supplemented the algebraic manipulations, e.g., of the formula for a squared binomial, with drawings in order to—hopefully—provide a meaning to and plausibility of the axiomatic rules. In so doing, they hoped to convince Christian that he could learn to obtain mathematical conclusions, that he actually could do mathematics.
The intervention was a success—as mentioned, we witnessed part of it. Christian experienced that he was actually able to do mathematics, not just memorize it, but perform reasoning and carry out deductions of his own. Moreover, the things he had to do made sense to him. The two maths counsellors hit the nail on its head with their design of the intervention. Christian got to realize and experience that people—people like himself—can in fact be brought to understand mathematics. He experienced that one can act mathematically and activate mathematical processes—and, not least, he experienced a set of rules (axioms), the ones on which the intervention was based, that he could make sense of and relate to. This not only changed his attitude towards mathematics and his behavior in relation to the subject, but also boosted his self-confidence in general.
Concerning Student A, it is difficult to say whether her beliefs and the myths she were under primarily concerned “mathematics as a discipline” or “mathematics education”, although we lean towards the latter. This was not least due to the fact that she considered mathematics to be a subject dealing mainly with computations. In fact, she expressed almost fear—or “math anxiety” [24]—when having to perform any type of mathematical reasoning or algebraic manipulation. From a didactical contract perspective, Student A knew that she was required to do this as part of mathematics, but she was very reluctant to embark on such undertakings.
These were the symptoms that the teachers noticed at first and the reason why they offered Student A to participate in the interventions in the first place. During the course of the interventions, the teachers uncovered some of her more deeply rooted mathematical stumbling blocks, namely, her conceptual difficulties related to proportionality, scaling, ratio, and volume, especially in relation to tasks involving mathematical modelling. A dominant aspect of A’s difficulties was her reliance on an empirical proof scheme, a proof scheme which, on the one hand, was one source of her troubles but, on the other hand, turned out also to be a source of inspiration in the attempts to reconcile this proof scheme with the deductive proof scheme. Through the design of a number of model-eliciting activities, the teachers sought to provide meaning to Student A in relation to the concepts involved. She was to gain experience—also of a concrete and empirical nature—of what happens to proportions and ratios when the constituents, including units, change. As part of the intervention, it became clear that what was actually essential was to draw on her belief that mathematical convictions must be empirically founded, if she was not to simply doubt her own calculations. We admit that this seems rather extreme and we have not encountered a similar case, neither before nor after Student A.
Rikke was a student who was embarrassed by the fact that she did not do as well in mathematics as she, according to her own beliefs, thought she ought to, since she had been learning mathematics for 10 years already. Furthermore, she believed that she was one of only a very few students who was performing somewhat poorly. These beliefs mainly correspond to the edge of the tetrahedron connecting the vertices “beliefs about mathematics education” and “beliefs about the self”, although there are also links to the vertex “beliefs about the social context”. Rikke was concerned about her academic appearance and worked hard to avoid exposing her difficulties to other students and to her teachers. She was also concerned—in fact even nervous—about her grades in mathematics, which was probably one reason why she was rather reluctant to participate in the intervention in the first place.
Unlike the other two cases, we do not see clear links to “beliefs about mathematics as a discipline”. An interesting aspect of Rikke’s case was her perception of her biotechnology class. Since this subject was new to all students, it was okay to find it hard and difficult—in contrast to mathematics. This seems to constitute a rather peculiar version of the didactical contract, one that relates to the entire school system as opposed to just her current mathematics class. From a slightly different perspective, Rikke could be considered to show elements of “math anxiety” [24]. Her teacher’s approach to this was to inform her that the number of students who actually fail mathematics in upper secondary school is much higher than she imagined, indicating to her that not only she, but many students at this level actually do find mathematics difficult and hard.
Rikke was selected for intervention because of her marked lack of ability to choose the correct type of function in tasks about mathematical modelling. On closer inspection, the teachers found that her choice of functions relied on certain “trigger words”. On the one hand, this was of course due to Rikke’s insufficient understanding of different representations of functions, including her limited ability to make conversions between these [25]. On the other hand, it might also partly be explained by her perception of the didactical contract as requiring her to be able to immediately “guess” the correct function type on the basis of some superficial features of the task description. She simply believed that, in mathematics, there is no need to think and reflect about one’s choice. From a proof scheme perspective, Rikke was markedly dependent on an external conviction scheme of the authoritarian type, which was also evident from the fact that she constantly sought confirmation from both teacher and classmates in everything she did in mathematics. As part of the intervention, the mathematics counsellors attempted to move her towards a more empirical conviction scheme, demonstrating to her why and how it is okay to “experiment’” to some extent, as part of carrying out mathematical processes, and that she herself could in fact do this—which, as her letter illustrates, she actually came to realize. Although the trees did not grow to the sky, Rikke did become more capable of switching between different representations of functions and used this to correctly select functions from the types at her disposal. Another outcome of the intervention was that Rikke began to take the initiative in mathematics classes, both in relation to her own problem-solving and modelling and when collaborating with other students. Finally, we should like to call attention to the fact that Rikke’s letter to the teachers actually shows a very high degree of self-reflection and an explicit acknowledgement of myths having been dispelled—which again underlines the impact of the intervention.
8. Discussion of the Efficacy of the Interventions
What, then, are the elements responsible for the success of the interventions described? As we see it, these are mainly five.
Firstly, satisfactory boundary conditions, an organizational framework, and exterior practical circumstances must be in place. The (upper secondary) schools and their management have to support and facilitate the initiative. They must acknowledge that many students need this kind of assistance and they must agree to cater for education to teachers that enables them to actually do it. This implies that teachers must be provided with a research-based insight that allows them to carry out both diagnoses and interventions in addition to identifying the students in need of assistance. Not least, sufficient time must be allotted to teachers and students for undertaking the tasks in the interventions.
Secondly, well-founded diagnostic work must be done by the teachers in order to uncover the roots of the students’ misguided conceptions of mathematics, i.e., which are the misconceptions of the didactical contract or the unproductive beliefs, etc., that foster destructive myths and should be “blamed” for the students’ mathematics-related difficulties. To increase the likelihood of successful and productive diagnostic work, this must be grounded in pertinent mathematics education research. If the diagnoses are only superficial and merely point to the symptoms of the misconceptions rather than to their roots, then the following interventions are likely to be much less effective than they could be.
Thirdly, clever interventions have to be designed, i.e., interventions which, to a sufficient degree, capture and address significant elements of the problems diagnosed with the specific student(s). Interventions, too, have to be research-based as much as possible but they cannot be so to the same extent as the preceding diagnosis. This is because research tells us much more about mathematical learning and learning difficulties than about successful teaching, which is much more dependent on the setting, context, and conditions within which it takes place and, above all, on the students being taught. So, teachers have to be very inventive in combining research findings with their own intervention designs targeting the specific students with whom they work. Surely, there is an element of luck involved in this enterprise.
Fourthly, not only the teachers, but also the students have to be prepared to invest the necessary amounts of effort and time. The interventions are only likely to work if the students cooperate and are willing to engage in the designed activities in the manner intended by the teachers. In other words, students and teachers have to come to an agreement on a didactical contract for the intervention. In order for this to happen, a significant degree of mutual trust between the students and the teachers have to be established.
Fifthly and finally, if the four elements just mentioned are present, including the element of luck in relation to the intervention design, it is not unlikely that the intervention may have a number of positive spillover effects, especially in the form of generalizability of the experiences. For instance, in the case of Christian, even though the intervention concerned basic algebra, the increased self-confidence that he acquired alongside his improved understanding of algebra positively affected his entire life with the subject of mathematics. Similarly, a spillover from Rikke’s intervention was that she, too, began to trust herself in the social context of doing mathematics.
The three cases in unison illustrate that even though the five elements listed above are undoubtedly somewhat demanding, they are not insurmountable. In terms of time invested, the interventions for both Christian and Rikke lasted less than three months. For Student A, the intervention was a lengthier one, as the two teachers met with her more or less regularly over a period of one year. Still, the cases illustrate quite clearly that, although these three students’ misconceptions and unproductive beliefs were the products of 10 years or more of mathematics teaching and learning, something effective could actually be done about them in a markedly smaller timespan, both in absolute and in relative terms. However, we have to admit that we do not know much about the long-term duration of the documented changes. Yet, the changes lasted long enough to be significant throughout students’ remaining years in upper secondary school, including their final exams.
The theoretical constructs that we have applied in our analyses of the case study of the three students are those of students’ mathematics-related beliefs, proof schemes, the didactical contract. Although these three constructs are usually not perceived as directly related to each other, they are indeed rather closely connected in the sense that misguided beliefs may cause misconceptions of the didactical contract and vice versa and that erroneous or rudimentary proof schemes may stem from a mistakenly construed didactical contract. An obvious question to ask is, of course, why the didactical contract goes awry? We can think of two main reasons for this. Firstly, the mathematics teacher may possess, him- or herself, misguided mathematics-related beliefs, e.g., in relation to mathematics as a discipline. Secondly, even though the teacher actually knows how to construe the didactical contract in a reasonable, sensible, and productive fashion, the possibilities, e.g., of a practical or financial nature, for actually implementing it are not present to the degree needed. Which of these two reasons are to blame for the misguided and destructive conceptions of Christian, Student A, and Rikke is not to say, especially since their misconceptions are the results of 10 or more years of mathematics education, with different teachers, at different schools, etc. Still, as singular instances and taken together, the cases of these three students illustrate the connectedness of the theoretical constructs of beliefs, proof schemes, and didactical contract. In fact, a separate study of the interconnectedness of these three constructs would be of both theoretical and practical importance. Unfortunately, this goes beyond the scope of the present article but does deserve to be taken up at a later point in time.
9. Conclusions
The question we set out to answer in this article was: what does it takes for targeted efforts to be reasonably successful in altering students’ misconceptions and unproductive beliefs and dispelling myths so as to pave the way for satisfactory learning? We have tried to answer this question by way of a study of three cases in which it proved possible to design and implement such targeted efforts with a reasonable degree of success. We have further tried to identify the factors that were responsible for the achievements obtained, obtaining the five elements presented in the previous section. A common trait of these elements is that it is necessary to pay serious attention to the substantive aspects of the teaching and learning of mathematics, rather than being content with its superficial features.
It is clear that the efforts described did not rest on implementing a fixed, one-size-fits-all template of detection, diagnosis, and intervention to all students in all situations. Even though mathematical learning and mathematical learning difficulties do indeed have some universal constituents, which have been uncovered by research, they also manifest themselves very differently in different students. The specific combination and realization of misconceptions and unproductive—or even destructive—mathematics beliefs and myths held by a student is typically particular to that student. This has to be reflected in the interventions put in place to help a student overcome his or her difficulties, and some degree of “a lucky hand” is necessary for a successful outcome.
Acknowledgments
We want to thank the mathematics counsellors educated in our program at Roskilde University, not only the seven teachers who have provided us with the three cases discussed in the present article, but all the 72 who have completed the program so far, for giving us access to unique first-hand experiences with students as well as with cases and data like the ones presented here.
Author Contributions
This article has been written jointly and integratedly by the two authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jankvist, U.T.; Niss, M. A framework for designing a research-based ‘math counsellor’ teacher programme. Educ. Stud. Math. 2015, 90, 259–284. [Google Scholar] [CrossRef]
- Philipp, R.A. Mathematics teachers’ beliefs and affect. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F.K., Jr., Ed.; Information Age Publishing: Charlotte, NC, USA, 2007; pp. 257–315, ISBN-13: 978-1-59311-587-6. [Google Scholar]
- Parajes, M.F. Teachers’ beliefs and educational research: Cleaning up a messy construct. Rev. Educ. Res. 1992, 62, 307–332. [Google Scholar]
- Op’t Eynde, P.; de Corte, E.; Verschaffel, L. Framing students’ mathematics-related beliefs. In Beliefs: A Hidden Variable in Mathematics Education? Leder, G.C., Pehkonen, E., Törner,, G., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002; pp. 13–37. ISBN 1-4020-1058-3. [Google Scholar]
- Jankvist, U.T. Changing students’ images of “mathematics as a discipline”. J. Math. Behav. 2015, 38, 41–56. [Google Scholar] [CrossRef]
- Thompson, A.G. Teachers’ beliefs and conceptions: A synthesis of the research. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; Macmillian Publishing Company: New York, NY, USA, 1992; pp. 127–146. ISBN 0-02-922381-4. [Google Scholar]
- Schoenfeld, A.H. Learning from instruction. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; Macmillian Publishing Company: New York, NY, USA, 1992; pp. 334–370. ISBN 0-02-922381-4. [Google Scholar]
- Spangler, D.A. Assessing students’ beliefs about mathematics. Arith. Teacher 1992, 40, 148–152. [Google Scholar]
- Jankvist, U.T. Using History as a ‘Goal’ in Mathematics Education. Ph.D. Thesis, Roskilde University, Roskilde, Denmark, August 2009. Published as no. 464 in Tekster fra IMFUFA. Available online: http://milne.ruc.dk/imfufatekster/pdf/464.pdf (accessed on 18 April 2018).
- Kloosterman, P. Beliefs about mathematics and mathematics learning in the secondary school: Measurement and implications for motivation. In Beliefs: A Hidden Variable in Mathematics Education? Leder, G.C., Pehkonen, E., Törner, G., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002; pp. 247–269. ISBN 1-4020-1058-3. [Google Scholar]
- Brousseau, G. Theory of Didactical Situations; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997; ISBN 0-7923-4526-6. [Google Scholar]
- Education Committee of the European Mathematical Society. What are the reciprocal expectations between teacher and students? Solid findings in mathematics education on didactical contract. Newsl. Eur. Math. Soc. 2012, 84, 53–55. [Google Scholar]
- Harel, G.; Sowder, L. Toward comprehensive perspectives on the learning and teaching of proof. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F.K., Jr., Ed.; Information Age Publishing: Charlotte, NC, USA, 2007; pp. 805–842, ISBN-13: 978-1-59311-589-0. [Google Scholar]
- Harel, G.; Sowder, L. Students’ proof schemes: Results from an exploratory study. In Research in College Mathematics Education III; Schoenfeld, A.H., Kaput, J., Dubinsky, E., Eds.; AMS: Providence, RI, USA, 1998; pp. 234–283. ISBN 978-0-8218-0882-5. [Google Scholar]
- Rosendahl, T.; Kærgaard, H.N.L. Udvikling af Matematikforståelse—Hos Elever Med Snublesten; Diploma Report; Roskilde University: Roskilde, Denmark, January 2016. [Google Scholar]
- Hanna, G. Some pedagogical aspects of proof. Interchange 1990, 21, 6–13. [Google Scholar] [CrossRef]
- Rosendahl, T.; Kærgaard, H.N.L. Udvikling af matematikforståelse med elevens egen logik. In Matematikvejledning i Gymnasiet; Niss, M., Jankvist, U.T., Eds.; Frydenlund: Frederiksberg, Denmark, 2018. [Google Scholar]
- Lomholt, M.B.; Larsen, M.S. Matematikvejledning i htx—Forsøg Med, og Refleksioner over, Identifikation, Diagnosticering og Intervention over for Elever Med Særlige Vanskeligheder i Matematik; Diploma Report; Roskilde University: Roskilde, Denmark, January 2014. [Google Scholar]
- Lomholt, M.B.; Larsen, M.S. A’s historie. In Fra snublesten til Byggesten—Matematikdidaktiske Muligheder; Niss, M., Jankvist, U.T., Eds.; Frydenlund: Frederiksberg, Denmark; pp. 98–121. 2016; ISBN 978-87-7118-609-3. [Google Scholar]
- Van Dooren, W.; De Bock, D.; Janssen, D.; Verschaffel, L. The linear imperative: An inventory and conceptual analysis of students’ overuse of linearity. J. Res. Math. Educ. 2008, 39, 311–342. [Google Scholar] [CrossRef]
- De Bock, D.; Van Dooren, W.; Verschaffel, L. Students’ over-use of linearity: An exploration in physics. Res. Sci. Educ. 2011, 41, 389–412. [Google Scholar] [CrossRef]
- Lesh, R.; Doerr, H.M. (Eds.) Beyond Constructivism, Models and Modeling Perspectives on Mathematics Problem Solving, Learning, and Teaching; Lawrence Erlbaum Associates, Publishers: Mahwah, NJ, USA, 2003; ISBN 0-8058-3822-8. [Google Scholar]
- Wejdemann, C.; Bjerregaard, K.-K.; Næs, F.T.N. Matematikvejlederuddannelsen—Afsluttende Rapport; Diploma Report; Roskilde University: Roskilde, Denmark, January 2017. [Google Scholar]
- Fennema, E.; Sherman, J.A. Fennema-Sherman mathematics attitudes scales: Instruments designed to measure attitudes toward the learning of mathematics by females and males. J. Res. Math. Educ. 1976, 7, 324–326. [Google Scholar] [CrossRef]
- Duval, R. A cognitive analysis of problems of comprehension in a learning of mathematics. Educ. Stud. Math. 2006, 61, 103–131. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).