Abstract
Fuzzy logic dates back to 1965 and it is related not only to current areas of knowledge, such as Control Theory and Computer Science, but also to traditional ones, such as Philosophy and Linguistics. Like any logic, fuzzy logic is concerned with argumentation, but unlike other modalities, which focus on the crisp reasoning of Mathematics, it deals with common sense reasoning; i.e., with approximate reasoning. Although the teaching of logic has formed part of mainstream education for many years, fuzzy logic is a much more recent inclusion. In this paper we emphasize the desirability of having illustrative examples related to students’ everyday activities, such as sports, in order to introduce fuzzy logic in higher education. Taking an example from cycling, we show, step by step, how to model an approximate reasoning regarding the choice of a ratio (a combination of freewheel and chainring) in order to advance more or less with each rotation of the pedals. Led by this example, a number of alternatives attending to the formal representation of the premises and the ways of inferring a plausible conclusion are analyzed. The choices made between alternatives are justified. We show that the conclusion inferred in the example is consistent with the models selected for premises and fuzzy inference and similar to that concluded by a human being.
1. Introduction. Fuzzy logic and education
Disciplines that are subject to being taught are shaped over time. There are the ever-present areas, such as Mathematics, Philosophy, Linguistics or Physics, and other more recent ones, such as Psychology or Logic. Even with relatively few years of autonomy in education, Logic includes traditional areas, such as Aristotle×s syllogistic, and other more innovative ones, such as Zadeh’s fuzzy logic. In effect, a modern development of logic is fuzzy logic. Since 1965, as quoted in [14], it has garnered increasing credibility and dissemination. Institutionally, formal logic is taught in the schools of Philosophy, Mathematics and, more recently, in Computer Science.
Although fuzzy logic is a recent field, its subject matter is related not only with current areas, but also with traditional ones. Even though fuzzy logic’s prominence is due mainly to its role in modern control systems, vagueness has influenced the philosophical debate since ancient times. Thus, Aristotle highlighted the philosophical dimension of the formal study of vagueness relating the future contingent phrases (‘Tomorrow there will be a sea battle’, a statement that today is neither true nor false) with discussions on free will. Old areas of Mathematics, such as topology, measurement theory or algorithms, have been also ‘fuzzified’. But certainly, the closest relationship with fuzzy logic is with Advanced Computing. Therefore, fuzzy logic has to do with at least two areas whose teaching has long been institutionalized, Mathematics and Philosophy, but also with a more recent one, Computer Science.
Fuzzy logic has not remained a mere theory; on the contrary, it has given rise to manufactured products, of industrial or domestic use. Therefore, and this case is not too frequent in the history of science, it is a theory that has achieved its own technology. From this point of view, fuzzy logic is not only a scientific matter but also a tool with which to do things; i.e. an applied logic.
Like any logic, fuzzy logic is concerned with argumentation. But unlike others, such as bivalent logic, which deals with precise arguments from Mathematics, fuzzy logic deals with common sense reasoning; i.e. with approximate reasoning [15]. While crisp arguments are characteristic of mature stages of our cognitive development, individuals come across common argumentation from childhood [3]. Thus, a three-year-old child may argue with some difficulty about a statement of elementary geometry involving crisp reasoning, but he/she will almost certainly be able to decide reasonably, and without apparent effort (using an argument rather implicit than explicit), on whether or not he/she wants fewer vegetables or whether or not he/she want more cookies, ‘fewer’ and ‘more’ being approximate quantifiers.
In adolescence, the student will have to study numerous subjects and, to successfully face this task, will have to develop skills involving the management of imprecision: heuristics for learning and data memory techniques (e.g. mnemonics rules), strategies for relating different information, reasoning by analogy to find solutions based on similar, previously solved cases, etc. These tasks involve implicit rather than explicit, approximate rather than crisp reasoning. Furthermore, in each specific area, many arguments have inaccurate and incomplete data, requiring approximation and tuning. This type of argumentation will be abundant in the areas of Social Sciences [2] and Humanities and also, somewhat surprisingly, not infrequent in Physics: experiments are sometimes verified to a degree; laws frequently include not all, but the majority of cases, etc. In mathematics, fuzzy logic is more appropriate than bivalent logic for representing the intuition underlying mathematical proofs, often requiring vague natural language verbalization until the concept is grasped [1,8].
Finally, at university, the student may wish to become acquainted with fuzzy logic in order to increase his/her knowledge of logic, his/her cultural skills or to acquire an instrument for solving problems or performing tasks in the setting of other disciplines; i.e., using fuzzy logic as an instrumental tool.
Fuzzy logic has recently undergone an extraordinary popularization and scientific dissemination in several mass media. The adjective ‘fuzzy’ gained wide popularity at least in two different prominent media: reporting and advertising. The advertisement as a ‘propaganda’ of the ‘fuzzy’ label has been favoured by the stamp of the fuzzy logic brand as a synonym for reliability and innovation in consumer products such as washing machines, video cameras or tensiometers. Thus, it has become common to see certain well-known trademarks including labels such as ‘made with fuzzy logic’ or ‘fuzzy-logic-controlled’ into their products. The scientific dissemination of fuzzy logic has been encouraged by the robustness of its solutions and the ease of its management. This has given rise to an increasing number of textbooks, which include chapters devoted to fuzzy logic, not only in the field of Logic itself, but also in Computing, Analytical Philosophy and Linguistics. References to fuzzy logic in books on Social Sciences (Education, Psychology, Sociology, Anthropology) also abound, especially those dealing with methodological aspects, as this logic provides an adaptive and efficient analysis of aspects such as subjectivity or instability, characteristics of their subject matter.
The increasing presence of fuzzy logic in scientific, cultural, educational, commercial and technological fields demands a kind of literacy in the basic principles of approximate reasoning. In this task it would be useful to have good examples in order to introduce the basics of fuzzy logic in a rigorous, but at the same time, enjoyable way. With this in mind, this paper is organized as follows. In Section 2 we introduce the basics fuzzy logic, emphasizing the differences with boolean logic and probability. In 3 we illustrate, step by step, how to model an example of approximate reasoning in cycling using fuzzy logic, considering that education should encourage students with intuitive examples, and that the lessons must be proportionate to the age of pupils. Finally, the conclusions and references close this work.
2. Boolean logic, probability and fuzzy logic
One of the most relevant features that define us as human beings is that of possessing the capability to reason. Traditionally, the science of reasoning is deductive logic, since Aristotelian deductive logic was associated to syllogism. A syllogism is a logical argument in which a quantified statement (the conclusion) follows from other two quantified statements (the premises). Both the premises and the conclusion are made up of precise statements and the only quantifiers admitted are all and some (in their positive and negative forms). Valid syllogisms are those in which the conclusion follows unequivocally from premises; i.e., if the syllogism is correct, there is no counterexample making the premises true and the conclusion false. A typical example of valid syllogism is:

This example comes from Mathematics, the science par excellence of precise reasoning. As Rowland puts in [10], Mathematics as a final or finished product is usually performed as a timeless and exact knowledge, leaving aside any trait of ambiguity or vagueness in its expression. But although the justificatory context of Mathematics seems to be accurate, the discovery context is peppered with several kinds of vagueness, as the same author shows. Beyond that, crisp reasoning has severe limitations. Many statements employed in every-day arguments are imprecise or vague. For example, along the lines of the Aristotelian syllogistic modes, from the premises:

it is not strictly possible to derive any conclusion. Two factors are relevant in precluding a conclusion: (1) the first and the second premise include uncovered quantifiers in the Aristotelian syllogistic (almost, few) and (2) there is no perfect matching between the words representing the middle term, even if ‘healthy’ and ‘salutary’ are synonyms. However, using common sense, most people would say that some conclusion can be reached from the premises: in particular, among others, that ‘Few young people use drugs’.
Imprecise or approximate reasoning play an important role in our daily lives and it would seem imperative to deal with it. Traditionally, several logics are devoted to dealing with the imprecision; two of the most successful are probabilistic logic and, more recently, fuzzy logic. Although both focus on imprecision, their subject of study and objectives are different. Loosely speaking, one can say that while probability deals with uncertainty, fuzziness addresses vagueness. We shall now go on to examine this.
There are four types of sentences relating determinate/indeterminate, crisp/vague. Focusing on these, a sentence can be classifiable as (a) determinate and crisp, (b) indeterminate and crisp, (c) vague and determinate, (d) vague and indeterminate. An example of (a) is ‘A triangle has three angles’. An example of (b) is ‘I throw a die and it is a multiple of 3’. An example of (c) is ‘Swallowing about 30 grams of Amanita Phalloides is lethal’. An example of (d) is ‘Athletes are tall’. Although we shall not focus specifically on (a) and (c) examples, we shall point to a difference between them. Both (a) and (c) are true, but in a different way: while (a) is a necessary truth—it follows from the definition of triangle, (c) is, however, a contingent or experimental truth; i.e., almost everyone who swallows 30 grams of Amanita is endangering his/her life, but there may be people who exhibit a particular tolerance or weakness to the poison, with more or less than 30 g being required to cause death. For the purpose of differentiating fuzziness from probability, the relevant examples are (b) and (d).
While (b) is an example of a probabilistic statement, (d) is an example of a vague sentence: they help us to distinguish between probability and fuzziness. Returning to the aforementioned sentence, ‘I throw a die and it is a multiple of 3’, we can note that if the die is perfect (not manipulated or misconstrued), each of its faces has a 1/6 probability of coming out and, as probability is an additive measure, the probability of ‘getting a multiple of 3’ can be calculated as follows:
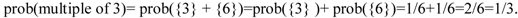
Thus, ‘getting a multiple of’ 3 is an indeterminate sentence, not an imprecise or vague one [13]. Before throwing the dice we don’t know if we are going to get a multiple of 3 or not, but afterwards, the outcome can be only true or false. No other alternative is possible. Someone may argue that we can also say that the probability that an athlete is a tall person is high. This is true. But what seems really difficult is to assign a single value between 0 and 1 to that statement.
Unlike the sentence ‘get a multiple of 3’, the phrase ‘Athletes are tall’ is vague. Although we can substitute the height of each athlete for a precise measurement, the sentence is vague because there are individuals named as ‘tall and ‘not tall’ by different people. Vague individuals are ‘borderline cases’; i.e., cases not firmly true or false. Furthermore, for the same person, an individual may be tall enough for some sports (hockey) but not for others (basketball). Only if we know the sport that he or she is involved in can we reasonably say if he or she is tall or not. Vague predicates are context-dependent.
‘Young’, ‘tall’ or ‘happy’ are all examples of vague meanings, but fuzzy logic focuses only on vague predicates that are measurable. ‘Youth’ and ‘height’ are measurable, but not ‘happiness’ (at least not in the same way). A measurable vague predicate P can be represented by a curve (a function), fP. The curve determines the degree to which a given object satisfies certain property or not. Graded properties are represented by fuzzy sets. A fuzzy set over a universe X is defined by its generalized membership function, usually denoted by µP(x), representing the compatibility to attribute the property P to a given element x or, in other interpretation, the possibility to soundly attribute P to x. In this latter sense, as Zadeh noted in [16], it is said that a vague predicate is characterized by its possibility distribution, i.e., by the specification of the degree to which each element of the universe is compatible with the meaning of the predicate. By way of example, in the universe U=[0, 10], the vague predicate ‘small’ can be represented by the following possibility distribution:
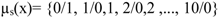
i.e., the compatibility of 0 with the predicate ‘small number’ is 1 or, in an alternative way, the possibility of calling 0 a ‘small number’ is 1, …, and so on.
Vague properties, unlike crisp ones, are not an all or nothing matter. There is no universal definition of ‘young’, as there is for a ‘triangle’. ‘Triangle’ induces a perfect classification of geometric figures: something is either a triangle or it is not. But vague predicates, such as ‘young’ or ‘tall’, can be used differently depending on the context. Thus, evaluating an individual as ‘young’ perhaps will vary depending on whether we are talking about a competitive chess player or a teacher; a person is not categorized as ‘tall’ in the same way for a basketball team as for a cycling team. Depending on the context, the representation of the meaning of ‘young’ or ‘tall’ may vary, even slightly. But in each case, its representation is precise. Fuzzy logic is a matter of degree, but it is a precise logic of imprecision.
Consider the difference between the representation of a vague predicate and a crisp one. For example, in the universe U=[0, 10], the crisp predicate P= greater or equal to five has only one possible use and the curve (membership function, f) representing it will be (Figure 1):
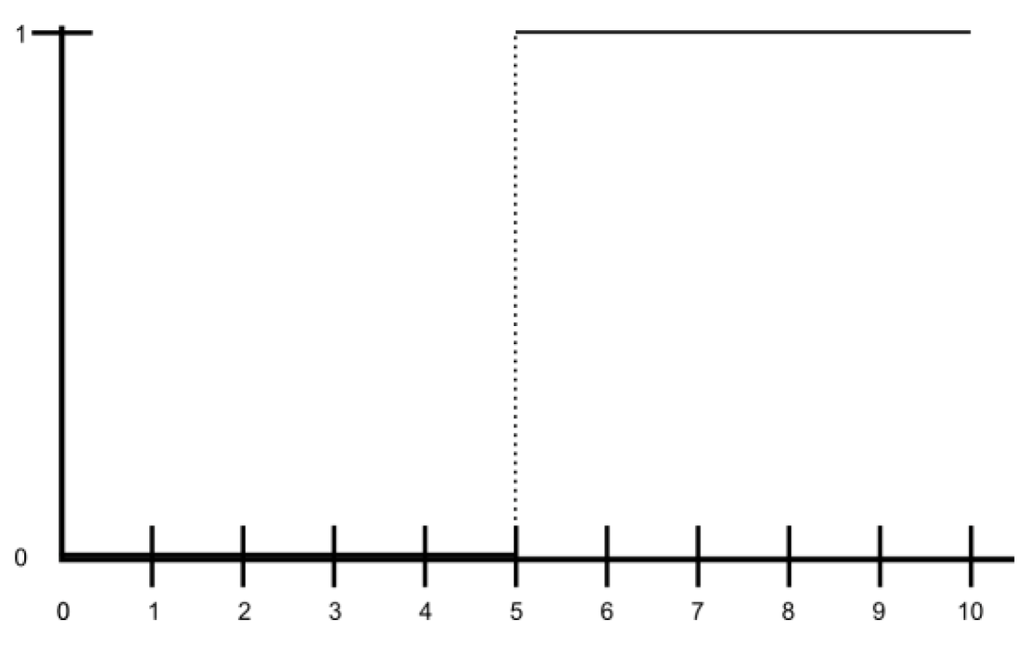
Figure 1.
Representation of the predicate greater or equal to five.
i.e., 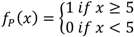
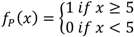
configuring a two-step function.
In contrast, in the universe U=[0, 100] the vague predicate P’=old can be used or interpreted slightly differently. The following are three different curves that can be consistently used attending to the meaning of ‘old’ (Figure 2):
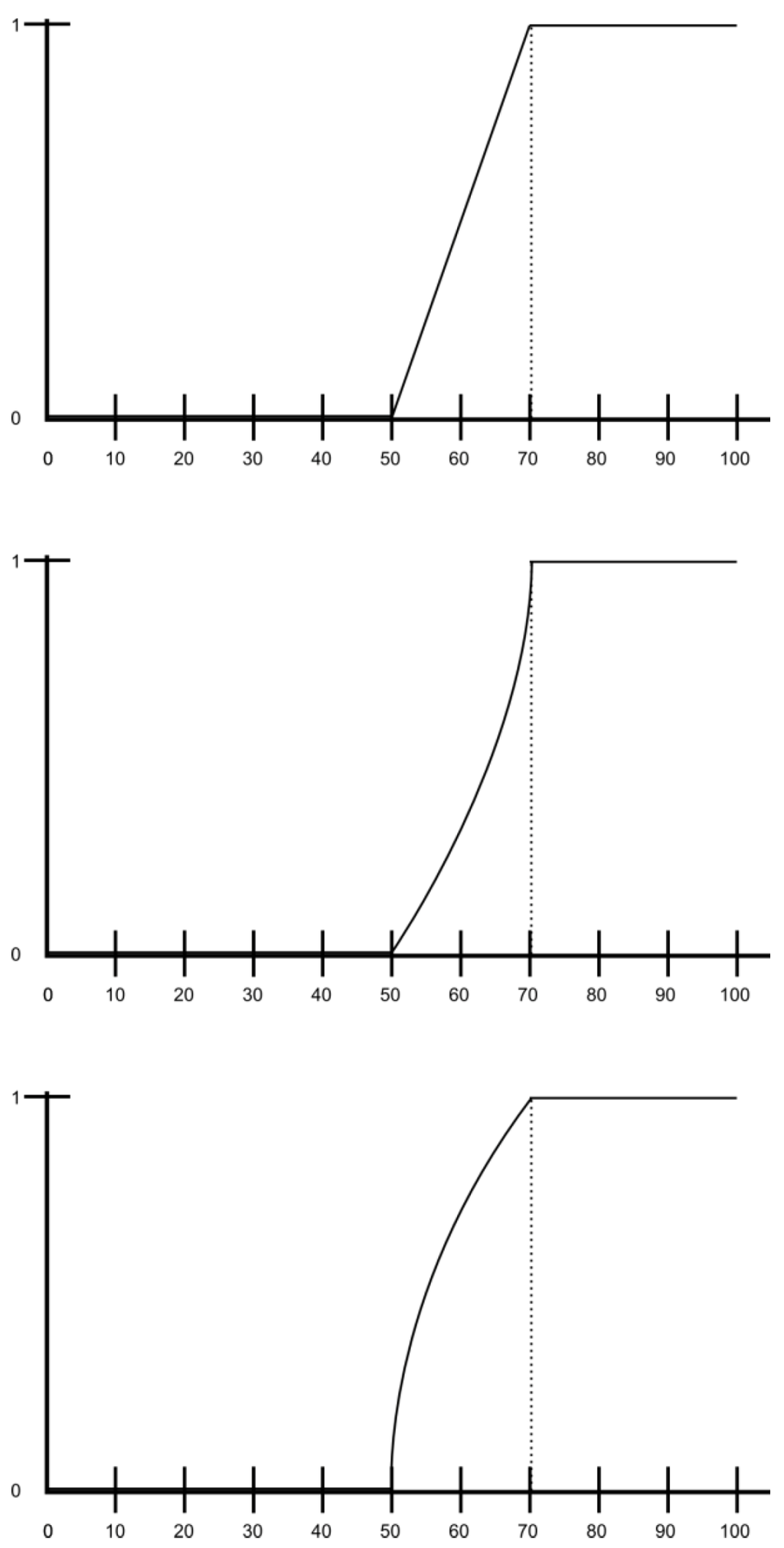
Figure 2.
Representations of the predicate old.
The curve shows that if you are below 50, then you are not old. If you are over 70, you are old. Between 50 and 70 years, the curve increases but differently in the three representations: if Peter is 62 years old, the degree of compatibility of his age with the first curve for ‘old’ is greater than with the second and lower than with the third. But in all cases, albeit with slight differences, the curves show the degree in which ‘Peter is young’ considering only his numerical age (62).
Fuzzy sets may be conjoined, disjoined or negate. Let us look at an example of conjunction (˄). Let F be the fuzzy set =around 5 kilos (F) and S=around 6 kilos (S). Both predicates are represented by the following membership functions (µF, µS).
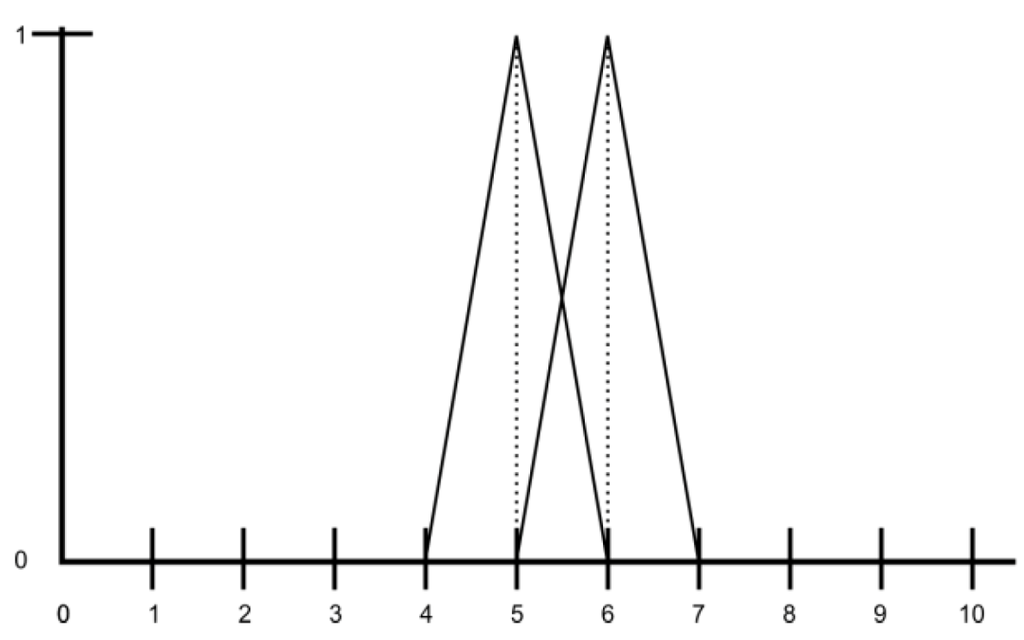
Figure 3.
Representation of the predicates around 5 kilos and around 6 kilos.
We can ask for an object whose weight is around 5 and 6 kilos. That is a conjunction. In the theory of fuzzy sets, the copula can be represented by the min connective, i.e, fF˄S(x)=min(fF(x), fS(x)). Thus, the new sentence will be represented by this new function (Figure 4):
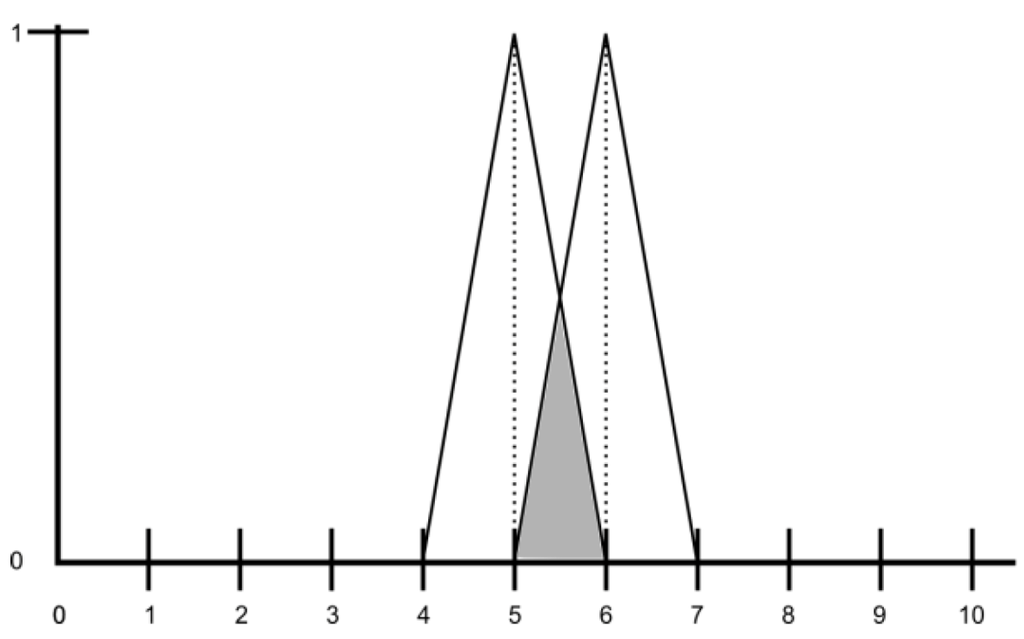
Figure 4.
Representation of the predicate around 5 and 6 kilos.
showing the compatibility of a given weight with the predicate around 5 and 6 kilos. The new representation is consistent with common sense: an object of 5.5 kilos is around 5 and 6 kilos with a greater degree than an object of 4.7 kilos. Note that, unlike probability, fuzzy logic is not additive. Thus, the compatibility of an object being ‘around 5 and 6 kilos’ is not the sum of the compatibility of that object being around 5 kilos and being around 6 kilos (it will be considerably greater).
Fuzzy logic shows its suitability for dealing with inexact or vague predicates not only in everyday cases, but also in scientific knowledge—including mathematical knowledge—approaching cases, where not everything is classifiable as ‘black and white’ [7]. Vagueness and fuzzy logic has gained increasing prominence in the contemporary scientific landscape. There are over 280,000 papers in the scientific literature with the label ‘fuzzy’ in the title. There are over 22,383 papers listed in Math.Sci.Net database alone. There are 25 journals with ‘fuzzy’ in the title and close to 25,000 patents in USA and Japan built on fuzzy technologies. Fuzzy logic has proved useful in managing approximate reasoning, in both theoretical and applied spheres and, thus, should be taught in higher education; particularly, in degrees in Mathematics and Computer Science.
In the setting of Polya’s contribution [9], we appreciate teaching science topics through examples. Examples should illustrate familiar situations, even if they are complex. Toy examples included in textbooks usually do not show the complexity underlying the matters approached and, consequently, the worth of the theory used to solve them. The example that we will develop in this paper is intended to be both complex and familiar, and aims to overcome the deficiencies alluded to above.
The example that we will introduce below is drawn from the world of sport and, in particular, from cycling. It is aimed at beginners in approximate reasoning; in particular, for students of Philosophy, Mathematics and Computer Science. The example will be developed step by step, explaining alternatives and elections. I agree with Garrido [6] regarding the relevance of adapting the educative material to the audience; of adjusting the level and manner of introducing fuzzy logic to pupils. What follows is an attempt towards a contribution to this task.
3. Teaching the basics of fuzzy logic through an example (by way of cycling)
Anyone who has been cycling has, either, consciously or unconsciously, reasoned along the lines of: ‘To go fast, I have to switch to a very small freewheel and a large chainring’. As any cyclist knows, the bicycle speed depends on the ratio transmitted to the chain; i.e., on the number of teeth on the freewheel and on the number of teeth on the chainring. The reasoning, informally stated above, is actually an enthymeme: it hides some premise. More specifically, the rule that makes it possible to reach the conclusion using the information included in the premise (the ratio used) is omitted. An explicit representation of the argument is as follows:
Premises:
- P1: On a bicycle, with a small freewheel and a large chainring, I go fast.
- P2: I selected a very small freewheel and a very large chainring.
Conclusion:
- C: I go very fast.
To perform a formal model of this reasoning, fuzzy logic must to provide:
- A representation of the vague lexicon included in the premises (in bold): ‘On a bicycle, with a small freewheel and a large chainring, I go fast and ‘I selected a very small freewheel and a very large chainring’.
- A method for inferring a conclusion. As a conclusion follows from imprecise premises, it must be approximate, providing information according to what the premises do (‘I go really fast’)
No doubt about the imprecise character of the premises. ‘Very’, is a linguistic label, generally an adverb of quantity that qualifies the meaning of the adjectives (small, large) that they modify. In effect, the bike does not move forward without any shade of meaning; but advances ‘little’, ‘a lot’, ‘really fast’, ... the freewheels are not ‘big’ or ‘small’ exclusively, but ‘very big’, ‘small enough’,…; that is the usual way to refer to our choice of gear. We need this granularity to explain why we are going slow, very slow, fast or very fast. And to represent these singularities we resort to fuzzy logic.
3.1 Preliminaries
In order to model a problem involving vague language adequately, we must consider the following specificities:
Vague predicates are context dependent and represented by a generalized membership function.
Vague predicates are quite common in natural language and they contrast with crisp predicates, which are timeless, generally belonging to the world of mathematics, an ideal realm of pure thoughts where everything is or is not—thus, the number 3 is prime or not; a triangle is scalene or it is not, etc. On the contrary, ordinary language (the language we use to communicate) is full of words that cannot be defined completely, once and for all, without regard to context.
Crisp predicates often lack context or have a quite general context: e.g., in the universe of natural numbers, 7 is a prime number regardless of whether we refer to a subset or to another subset of 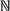 . Vague predicates, nevertheless, are contextual, local. Thus, considering the same route, a chainring of 52 teeth will be small for a professional cyclist and large for an amateur cyclist. Even a single ratio can be qualified by one cyclist as large or small depending on whether it is used in a flat time trial or in a hilly time trial.
. Vague predicates, nevertheless, are contextual, local. Thus, considering the same route, a chainring of 52 teeth will be small for a professional cyclist and large for an amateur cyclist. Even a single ratio can be qualified by one cyclist as large or small depending on whether it is used in a flat time trial or in a hilly time trial.
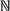 . Vague predicates, nevertheless, are contextual, local. Thus, considering the same route, a chainring of 52 teeth will be small for a professional cyclist and large for an amateur cyclist. Even a single ratio can be qualified by one cyclist as large or small depending on whether it is used in a flat time trial or in a hilly time trial.
. Vague predicates, nevertheless, are contextual, local. Thus, considering the same route, a chainring of 52 teeth will be small for a professional cyclist and large for an amateur cyclist. Even a single ratio can be qualified by one cyclist as large or small depending on whether it is used in a flat time trial or in a hilly time trial. Fuzzy logic provides models for representing vagueness in context. By way of example, in the universe U=[0, 6], ‘numbers less than 3’ and ‘numbers far from 3’ would be represented as follows Figure 5):
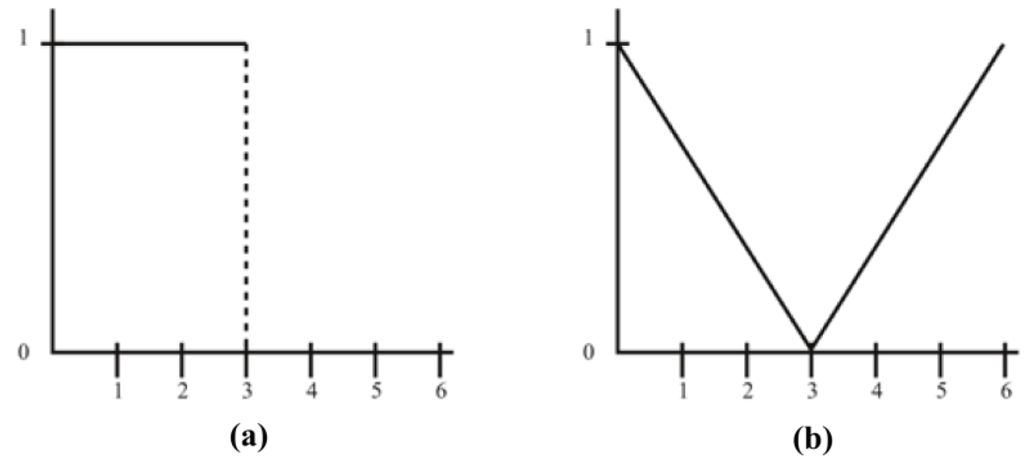
Figure 5.
(a) Numbers less than 3. (b) Numbers far from 3, U=[0,6]
But note that, considering another universe, U = [0, 9], while the representation of the predicate ‘numbers less than 3’ does not change (‘less than’ is a crisp predicate), the representation of ‘numbers far from 3’ is altered, as shows the right figure below. In effect, you can check that the figures for ‘far from 3’ mismatch in the range 3-6 (Figure 6).
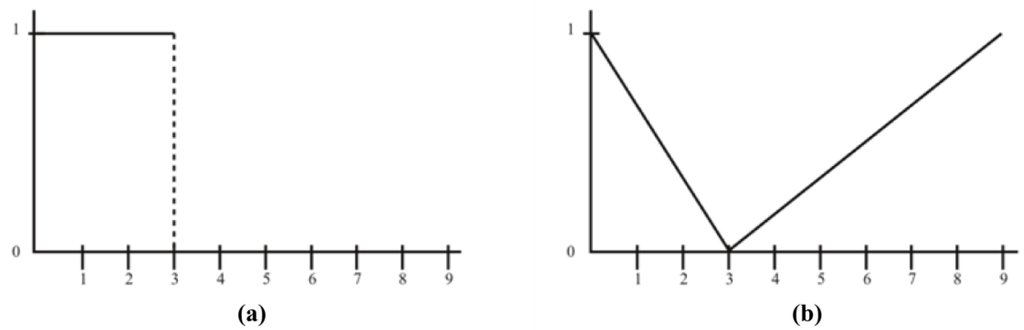
Figure 6.
(a) Numbers less than 3. (b) Numbers far from 3, U=[0,9]
The figures show graphically that while crisp predicates are context independent, vague predicates are always sensitive to the universe of reference. While crisp predicates classify the world in black and white, vague predicates put objects on a gray scale.
Just as a crisp predicate is characterized by its precise membership function (1 or 0 values), a vague predicate is represented by a generalized membership function; i.e., by the attribution of degrees of membership to the elements of the universe of reference. Thus, the generalized membership function that corresponds to the vague predicate ‘numbers far from 3’, U=[0, 6], can be recovered by the top figure and can be summarized as follows:
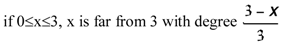
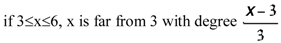
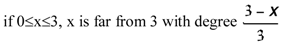
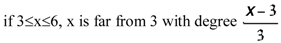
Considering only the integer values, the meaning of the imprecise predicate ‘number far from 3’ is represented by the following set of element-value pairs:
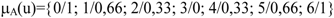 i.e.: 0 is far from 3 with degree 1; 1 is far from 3 with degree 0,66; 2 is far from 3 with degree 0,33… The fuzzy set ‘number far from 3’ (A) is characterized by the membership function μA, representing the degree to which each element of the universe of discourse is compatible with what the vague predicate means. But one may ask why to propose this representation and not others, such as the following:
i.e.: 0 is far from 3 with degree 1; 1 is far from 3 with degree 0,66; 2 is far from 3 with degree 0,33… The fuzzy set ‘number far from 3’ (A) is characterized by the membership function μA, representing the degree to which each element of the universe of discourse is compatible with what the vague predicate means. But one may ask why to propose this representation and not others, such as the following:
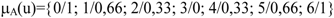
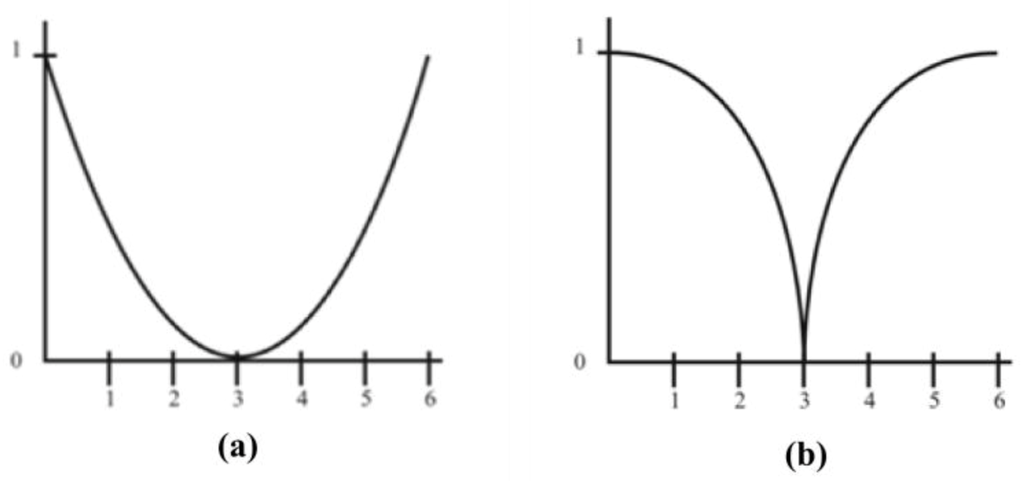
Figure 7.
Other representations of the predicate ‘numbers far from 3’.
We can see that while Figure 7 (a) relativizes the distance, Figure 7 (b) seems to accentuate it. Figure 6 (b) represents perhaps the most balanced interpretation. If two representations of the same predicate disagree significantly, then refereeing would be required. Refereeing will be based on: (a) checking that the universe of discourse is the same; (b) performing an experiment that yields evidence about what is the best or most appropriate representation; (c) speaking about the admissible interpretations of the predicate, in order to provide the more faithful representation of its meaning (commonly understood as its use). So, if a person says that there are few road accident victims in a weekend and another says there are many, one must note that both assess the problem in the same context (i.e., in the context of last year, the last weekend, compared with industrial accidents, etc.). If, even using the same context, serious divergences emerge, we must collect data to fully address the discussion. Once the data are known, it is possible to appeal to rationality: nobody in their right mind would say, at this moment in Spain, that 2, for example, constitutes a large number of accidents in one weekend, and nobody can judiciously justify that 60 are very few. There are bands of road accidents (e.g., 10, 15,) that have no clear assessment. For such cases, a level of agreement is required in order to reach a consensus about what the phrase ‘Few road accidents in one weekend’ means.
Complex sentences accept several valuations.
Once we have a way to represent the imprecise meaning of simple sentences with fuzzy sets, we may ask how to evaluate complex sentences; i.e., how to make negations, disjunctions, conjunctions or conditionals from atomic sentences. There are several ways to negate, aggregate or condition vague sentences, which we now go on to examine.
A fuzzy negation operator n is a function n: [0,1] → [0,1] that is strictly decreasing (n(a)>n(b), if a<b), continuous, and which satisfies the classical conditions of limit (n(1)=0; n(0)=1) and involution (n(n(a))=a. If a1-a2=n(a2)-n(a1) for all a1, a2 ∈[0, 1], n(a)=1-a is the only negation. If that condition is not met, there are other negation operators. For example, if we represent the meaning of the predicate ‘small’ in U = [0, 1] by the following membership function:
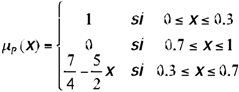
its negation (not_small) could be characterized by,
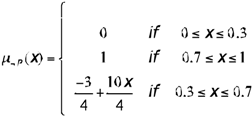
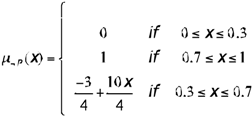
or by 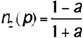
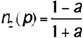
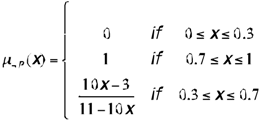
Graphically (Figure 8):
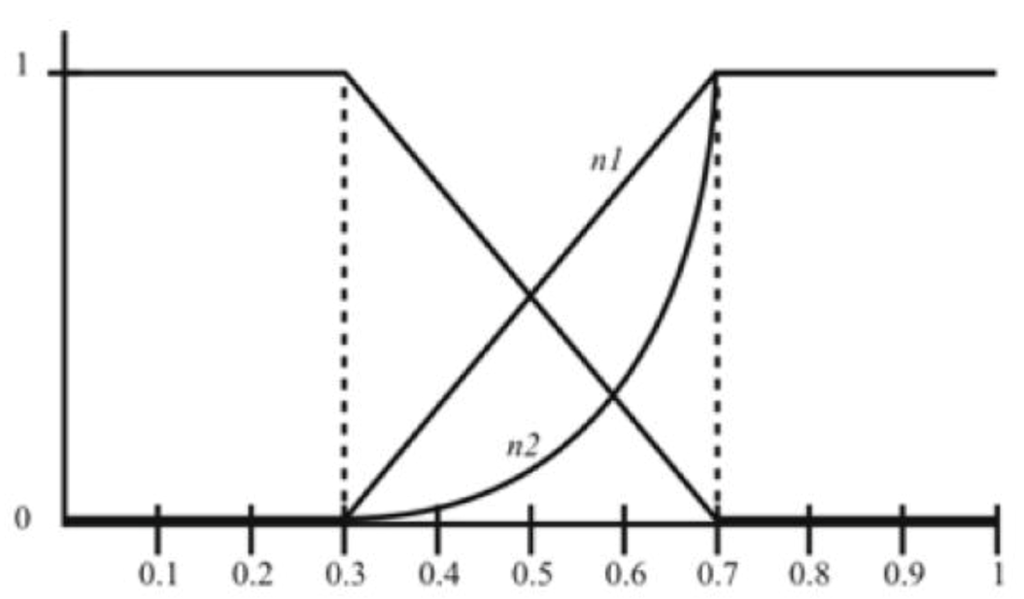
Figure 8.
Several negation functions.
There are also several ways to intersect or join fuzzy sets. Choosing one of the alternatives depends on the meaning of the sentences under conjunction or disjunction. Thus, taking the first example, if the sentences denote situations that are independent between themselves, as occurs in ‘He was climbing the pass using a small freewheel’ and ‘He was well hydrated’, the use of the min connective to conjoin and the max connective to disjoin is advisable. But if the information is mutually influenced, as in ‘I was climbing the pass using a small freewheel’ and ‘I was climbing the pass using a big chainring’, then the use of the product connective for conjunction and the sum minus product connective for disjunction is more adequate. Indeed, it would seem to be plausible to say that if a cyclist uses a small freewheel, with degree 0.8, and he is (badly) hydrated, with degree 0.3, the confidence of gaining greater speed should be reduced to the poor hydration level. In turn, we know that, for speed, the choice of the freewheel teeth and the election of the chainring teeth are both in interdependence. Therefore, if someone chooses a small freewheel, with degree 0.8 (very small), and a large chainring with degree 0.3 (slightly larger), the prevision for achieving a certain speed are slightly below that the degree of the chainring (0.24), because, as it is little big, does not favour the expectations generated by selecting a small freewheel. Therefore, there are several ways to conjoin and to disjoin. The following are some of the most frequently used t-norms and t-conorms:

Table 1.
Types of t-norms and t-conorms.
| Name | Notation | Definition |
|---|---|---|
| bounded | T0 | Max(0,a+b-1) |
| S0 | Min(1, a+b) | |
| product | T1 | a×b |
| S1 | a+b-a×b | |
| min/max | T2 | min(a,b) |
| S2 | max(a,b) |
Two fuzzy sets are also related if one conditions the other. A fuzzy conditional is usually a straightforward generalization of the typical ways in which the classic material conditional can be defined. Depending on which definition is selected, two principal families can be distinguished: S-conditionals and R-conditionals.
S-conditionals generalize the classical definition a→b≡¬a˅b replacing ˅ with a t-conorm S and ¬ with a fuzzy complement. It follows that a→b ≡ S(n(a), b). If we take n(a)=1-a, then S(n(a), b)=S(1-a, b). If we substitute S with a quoted union, we obtain the conditional Lukasiewicz conditional: IL(a, b)=min(1, 1-a+b); if S is max, we obtain the Kleene-Dienes conditional: IK(a, b)=max(1-a, b).
The family of R-conditionals are obtained by generalization: a→b ≡ sup{x∈[0, 1] | a˄x≤b}. Replacing ˄ with the product, we obtain the Goguen’s conditional:
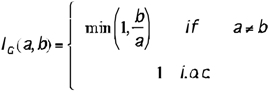
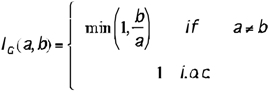
If we use T(a, b)=max(0, a+b-1), we obtain the Lukasiewicz conditional.
Since conditional operators are designed based on t-norms and t-conorms, there are a wide variety of them. There are up to 40 and there is empirical evidence to diagnose their suitability for different interpretations of the meanings of fuzzy conditional sentences. A. Sobrino and S. Fernández [11] have developed an extraction system for conditional rules, applying the same to a book of music. The method conjectures the conditional operator that best reflects the meaning of the conditional sentence. For example, when information between antecedent and consequent interacts and, thus, it is non-commutative, as in ‘The more severe the trial, the greater the sentence’ the Kleene-Dienes alternative would seem to be a suitable choice: a→b=max(1-a, b). But if the information contains a certain symmetry, as happens in ‘If the measure of a piece is incomplete with respect to its extent, the latter must to provide the value of the time remaining, completing the symmetry of the whole’, then the appropriate election would be the Mamdani operator: a→b=min(a, b), as min(a, b)=min(b, a). The examples resorted to show fuzzy logic as a matter of approximation, design and experimentation. Approximation, as evaluating the meaning of the sentences is a matter of degree; design, as we endeavour to adapt the formal models to the peculiarities of the vague meaning; and, experimentation, as it is the use of those sentences which determines which model(s) from those available is/are most appropriate.
Fuzzy inference allows different modalities.
Once we know how to assess complex fuzzy propositions, let us not go on to see how the values are transmitted from propositions-premises to a proposition-conclusion. There are several modalities of approximate inference [5]:
- Compositional inference
- Inference by analogy or compatibility
- Interpolative inference
The most common way to formalize vague reasoning is the so-called compositional inference or generalized Modus Ponens, which we shall refer to in order to model the example employed in the present study.
But first we shall briefly review the other two modes of inference.
In the inference by analogy, using a similarity measure, we calculate the degree to which the perception or fact named by the premise satisfies the antecedent of the rule. This degree is transferred to the conclusion. In schematic form:

Table 2.
Scheme of inference by analogy.
| If X is A then Y is C |
| A’ is γ compatible with (or similar to) A |
Hausdorff’s distance is frequently used to define the similarity as the inverse of that distance.
The interpolative inference (Figure 9) arises generalizing the fuzzy relation ‘to be between’ applied to rules that define paradigmatic or prototypical examples:
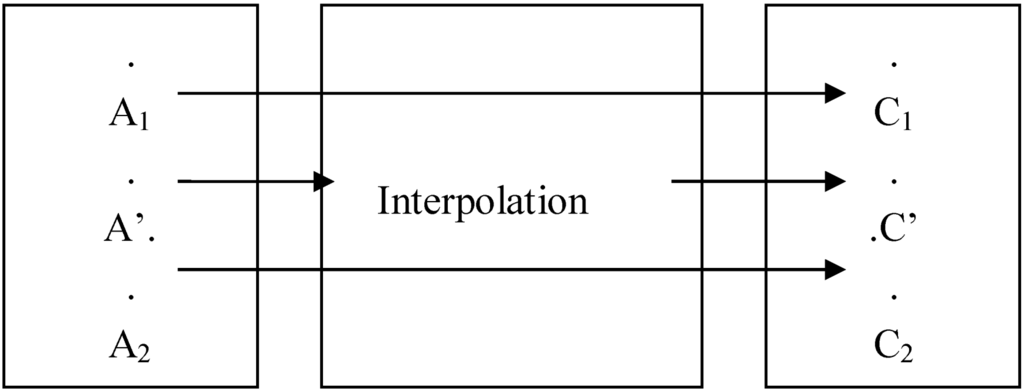
Figure 9.
Schema of interpolative inference.
i.e., interpolation enables us to conclude that C’ is between C1 and C2 to approximately the same extent that A’ is between A1 and A2.
While models by analogy use a simple rule, the interpolative reasoning requires two or more rules to provide information with which to generate a conclusion. In this regard, it also differs from the compositional inference, which will be described below.
Compositional rule of inference or generalized Modus Ponens matches the following schema:

Table 3.
Compositional rule of inference.
| Perception or fact | X is A* |
where A* is similar to A and the rule, if correct, should conclude one D* similar to D.
Which of these forms of approximate reasoning should be used to model the example used in the present study? There is no sense in using interpolative reasoning: there are not two rules, but only one. We are led, therefore, to choose between the inference by analogy and the compositional inference. In reasoning by analogy, the compatibility between the fact and the antecedent of the rule is established. In the compositional inference, as its name indicates, we compound or mix the fact and the rule in order to provide a conclusion. Both methods would seem to be suitable for modelling our example. Here we will choose the compositional rule of inference, as it is more traditional. We now go on to consider the above quoted schema in more detail.
The rule ‘if X is A then Z is D’ is valued as a fuzzy conditional linking the condition (A) and the conditioned by the premise (D):
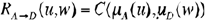 where C is the most appropriate conditional operator relating the meaning of A and D. The perception or fact X is A* is represented by a value that will be the extent to which X is consistent with what A* means. Since there are two premises, the value of the fact or perception is conjoined with each of the possibilities that offer the rule using the most appropriate t-norm. The highest of these values is ascribed to the conclusion. In summary:
where C is the most appropriate conditional operator relating the meaning of A and D. The perception or fact X is A* is represented by a value that will be the extent to which X is consistent with what A* means. Since there are two premises, the value of the fact or perception is conjoined with each of the possibilities that offer the rule using the most appropriate t-norm. The highest of these values is ascribed to the conclusion. In summary:
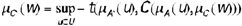 for a continuous t-norm T and for all w.
for a continuous t-norm T and for all w.
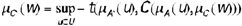
3.2 Numerical Models for representing the example
Let us now see how to model the example used in the present study, taking the caveats referred to in the above paragraphs into account. We recall:
Given the premises:
- P1: On a bicycle, with a small freewheel and a large chainring, I go fast.
- P2: I selected a very small freewheel and a very large chainring.
we can ask what conclusion can be expected.
First, we have to represent the information involved in the premises. Let SF be the predicate ‘small freewheel’ and LC, ‘large chainring’. Suppose we have agreed that SF and LC are well defined by the following possibility distributions.

Table 4.
Proposition of the antecedent of the rule, premise_1.
| μSF(x)= {12/0.9; 16/0.6; 20/0.4; 24/0.1} |
| μLC(y)= {33/0.1; 52/0.9} |
12, 16, 20 and 24 being the number of teeth of the freewheel, and 33 and 52 the number of teeth of the chainring.
Let GF be the predicate ‘go fast’, represented by the following possibility distribution:

Table 5.
Consequence of rule, premise_1.
| μGF(z)= {3/0.1; 6/0.5; 9/0.9} |
where 3, 6 are 9 are the meters moved forward with each revolution of the chainring.
First, we have to combine the information ‘small freewheel’ and ‘large chainring’. As freewheels and chainrings interact to achieve more or less speed, we use the t-norm product to represent the conjunction thereof. This combination of freewheels and chainrings gives rise to a ‘big ratio’ (BR) μSF(x) × μLC(y)=μBR(x,y) and its values are reflected in the following table:

Table 6.
Conjunction of propositions that are the antecedent of the rule.
| μBR(x,y) | 12 | 16 | 20 | 24 |
|---|---|---|---|---|
| 33 | 0.09 | 0.06 | 0.04 | 0.01 |
| 52 | 0.81 | 0.0.54 | 0.36 | 0.09 |
Now we can calculate the values of the conditional clause ‘If I select a big ratio, I go fast’, μBR→GF(w). First, we analyze the rule we intend to model interpreting the meaning and the dependence or independence of their predicates, choosing the most appropriate conditional operator. In this case, ‘If I select a big ratio, I go fast’, can be interpreted as:
- I select a big ratio and I go fast.
- Or I do not select a big ratio or I go fast
- Or I do not select a big ratio, or I do and I go fast.
- Or I do not select a big ratio or I go at a speed proportional to the ratio selected.
1 shows a case where the material conditional is satisfied: the condition and the conditioned are true but exclude the hypothetical character of the antecedent and, thus, the possibility that the condition does not hold. The other three cases do include this feature. 2 show the traditional interpretation: either the antecedent is met or it is not. 3 add some kind of completeness: either the antecedent fails, or the antecedent and the consequent are satisfied. Lastly, 4 say that either the antecedent fails or the consequent is proportional, depending on the degree of satisfaction of the antecedent. For our example, 3 or 4 may be appropriate interpretations. 3 is a sound interpretation as it expresses the congruence between ‘go fast’ and ‘big ratio’ quite well and because, if the condition is given, the interaction between the condition and the conditioned can be calculated by the t-norm product. It is not a good choice if the condition is poorly satisfied and if the difference with the degree of satisfaction of the conditioned is large; in such a case, the conditional tends to be true, not owing to any consistency between the values of the condition and the conditioned, but because, as the condition is weakly true, the conditional tends to be true. 4 is also an acceptable option as, in an approximate scenario, we must conclude in proportion to the available information. The moral: not always there is just one single model to choose and not always will the choice selected be optimal for all cases. Thus we have to decide in a justifiable manner between alternatives not fully disjoint. Here we provide a number of reasons for choosing between two options: the conditional operator (a→b)=1-a+a×b, known as the Reichenbach operator, or the Gaines operator, defined by:
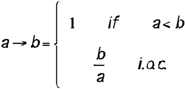
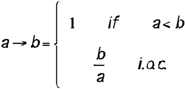
Supposing we decided on the first (i.e., the definition by Reichenbach). According to this choice:

Table 7.
Premise_1 (Rule).
| μBR→GF(w) | 12-33 | 12-52 | 16-33 | 16-52 | 20-33 | 20-52 | 24-33 | 24-52 |
|---|---|---|---|---|---|---|---|---|
| 3 | 0.919 | 0.0.271 | 0.9406 | 0.514 | 0.964 | 0.676 | 0.991 | 0.919 |
| 6 | 0.955 | 0.595 | 0.97 | 0.74 | 0.98 | 0.82 | 0.995 | 0.955 |
| 9 | 0.9181 | 0.919 | 0.994 | 0.946 | 0.996 | 0.964 | 0.999 | 0.991 |
These values should show the congruence between the speed selected and the progress made (3, 6, 9 are the advanced meters).
Once the value of the rule has been determined, let us now go on to see how to calculate the value of the perception or fact. The truth value of the fact is a modification of the value of the antecedent of the rule: compared with it, the only difference is that the adjective (small) is qualified by the adverb ‘very’ (‘very small freewheel’) and, once again, ‘big’ is qualified by ‘very’ (‘very big chainring’)—i.e., we perceive a very small freewheel and a very big chainring. In fuzzy logic, we know that if an element satisfies a predicate P in a degree, satisfies the predicate ‘very_P’ to a less extent. There is agreement that the square function captures this intuition; i.e., if μP(u)=x, μvery_P(u)=x2. Taking into account this definition:
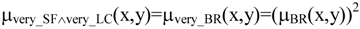
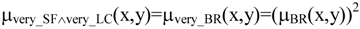

Table 8.
Premise_2 (Rule).
| μvery_BR(x,y) | 12 | 16 | 20 | 24 |
|---|---|---|---|---|
| 33 | 0.0081 | 0.0036 | 0.0016 | 0.0001 |
| 52 | 0.6561 | 0.2916 | 0.1295 | 0.0081 |
We have values for the rule and for the perception or fact. What value should be passed on to the conclusion? Answering this question involves composing the values of the table denoting the meaning of the fact with the values shown in the table above representing the meaning of the rule. Following Zadeh’s rule, we obtain A* with the composition sup-T. In [13], Trillas et al. have proved that, if we use the Reichenbach conditional to model the rule (and that was our choice), the only t-norm that ensures consequences in the sense of Tarski is the bounded one; i.e.,
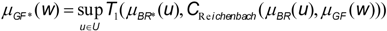
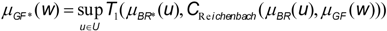
Performing the calculus that the above formula suggests, we obtain the following values for μA*(w):

Table 9.
Conclusion.
| μGF*(w)= {3/0; 6/0.251; 9/0.5751} |
If we analyse the results, we can see that the values for 3 and 6 are very close to the square of the values of μGF for these same elements. The value for 9 is the most divergent (it should be around 0.81 and, in fact, it is 0.5751). How can be expressed this answer? This matter is called, in the realm of fuzzy logic, ‘linguistic approximation’ and there are different techniques for solving it. Generally speaking, we can check that the obtained set μGF* is more similar to one that ideally represent ‘go very fast’ than to any other, and that is precisely the conclusion that a rational agent draws from the premises. The conclusion is approximate because the reasoning is so too; there is nothing special about it.
This is an example of approximate reasoning with truths degree. By so doing, fuzzy logic is a multiple-valued multiple-logic; i.e., it is a family of infinitely-valued logics.
But people reason, rather than with degrees, with linguistic expressions as those founded in the example above: ‘low speed’, ‘go fast’, etc. Is it possible to represent and manage the reasoning of our example-guide with this kind of linguistic labels? The answer is yes. Let us now go on to see how.
3.3 Linguistic Models
Let us agree that the knowledge relating speed and progress of a bicycle is showed by the following rules:
- If the freewheel is small and the chainring is large, the progress made is remarkable
- If the freewheel is medium and the chainring is medium, the progress made is moderate
- If the freewheel is large and the chainring is small, little progress is made.
Let us agree that these rules can be represented as the following figures show (Figure 10):
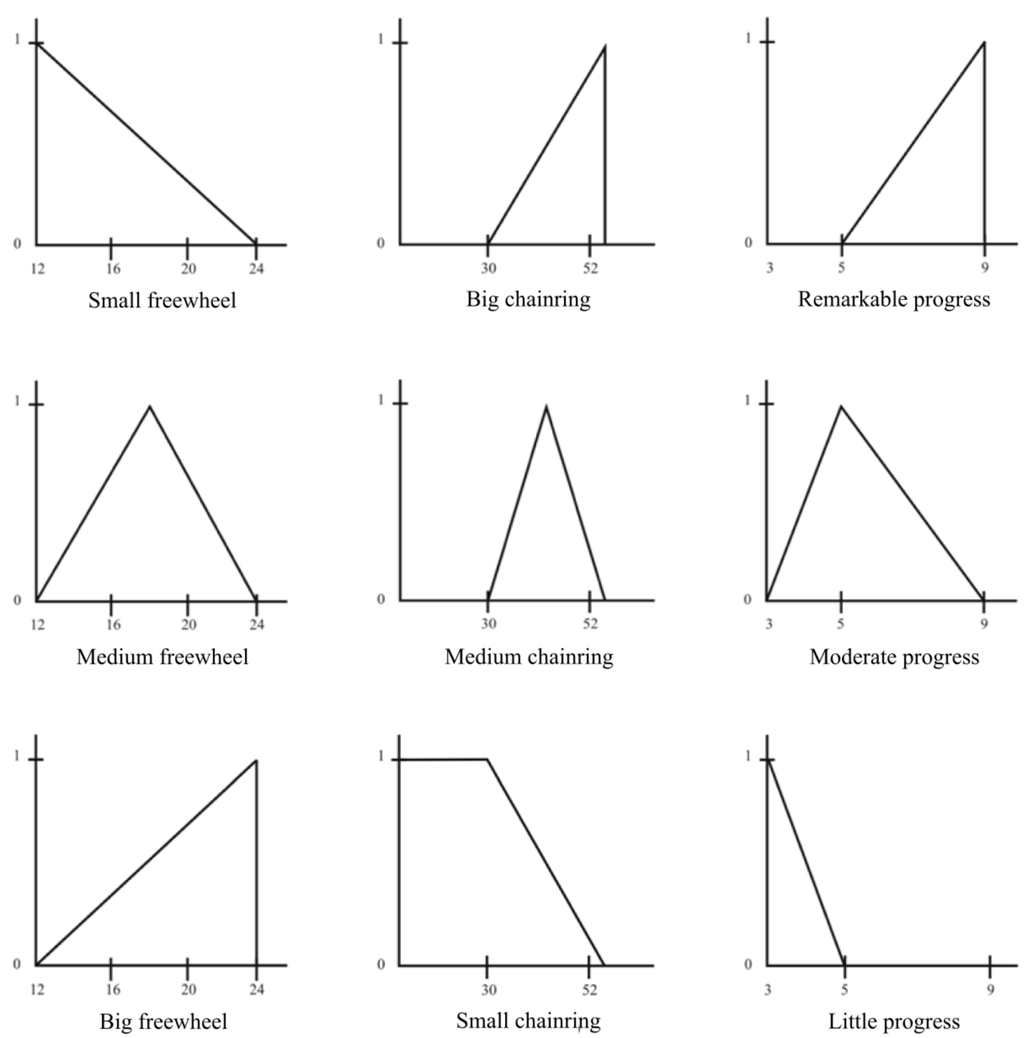
Figure 10.
Graphical representation of the fuzzy terms involved in the rules.
where 12, 16, etc., are the number of teeth of the freewheel; 30, 52 are the number of teeth of the chainring and 3, 6, 9 are meters of forward progress.
Suppose we observe that the bike has 16 teeth in the freewheel and 52 teeth in the chainring. What is the expected progress? To make this example more straightforward and illustrative, we use the t-norm min to draw the conclusion, even though we argue previously that that choice was not entirely appropriate. In each figure, we represent the conditions of the problem and, immediately after, we move the minimum value to the conclusion (Figure 11).
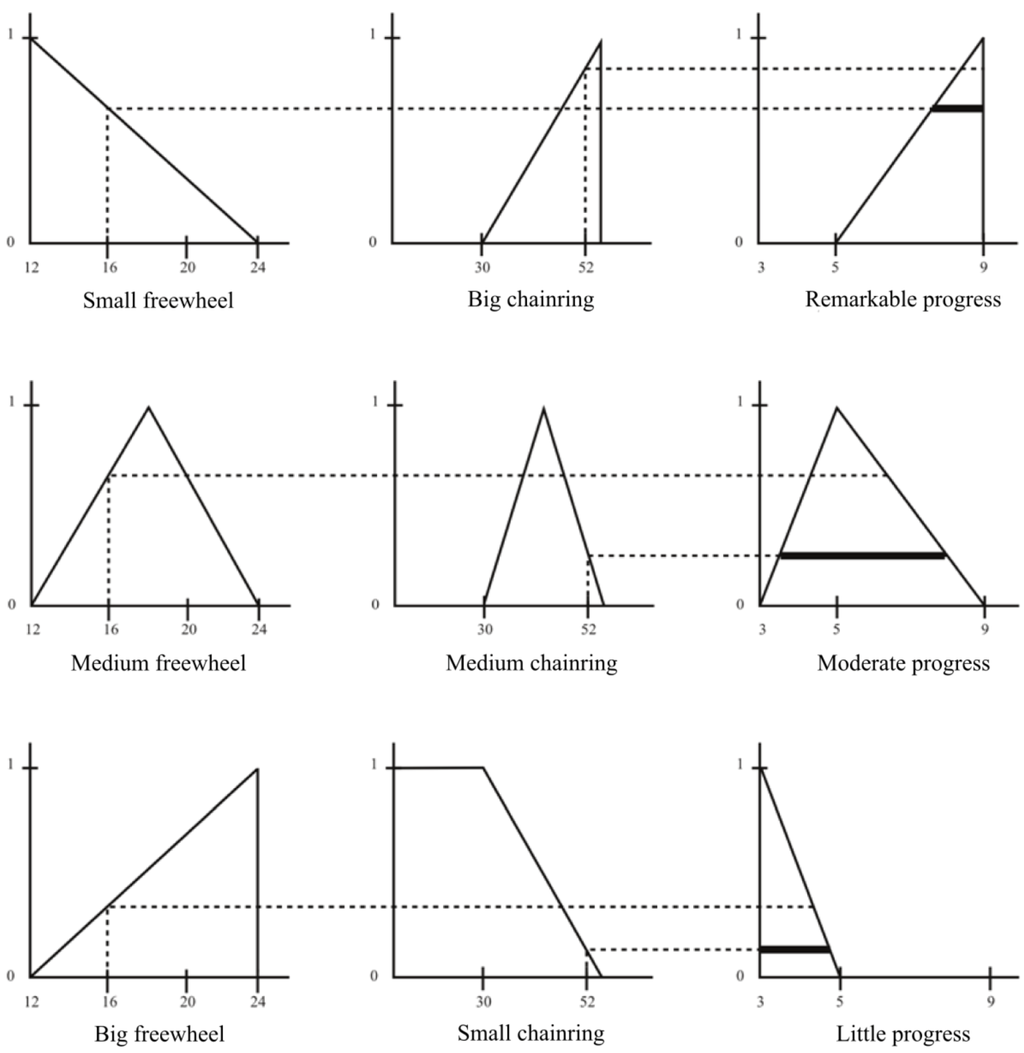
Figure 11.
Graphical representations of the rules using the t-norm min.
Finally, among the min values we choose the supreme:
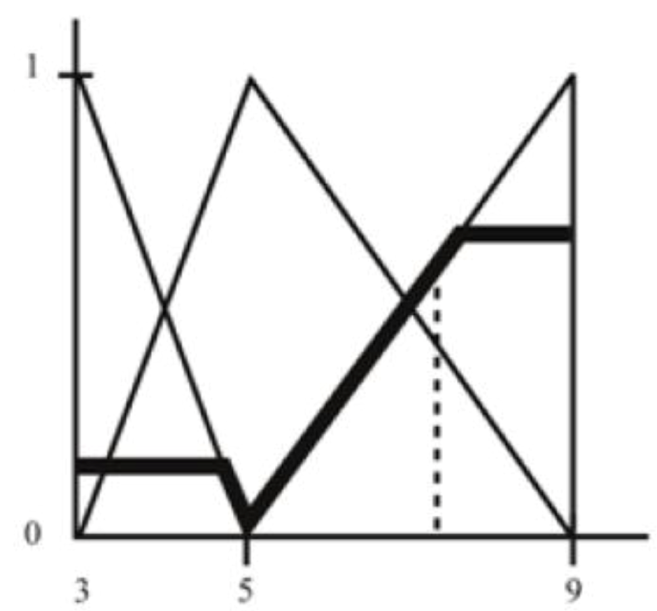
Figure 12.
Centre of area.
Note that the centre of the area (Figure 12) dividing the figure highlighted in bold in two equal parts falls within the label ‘progress a lot’. This conclusion matches the observation and provides a solution to the problem using a fuzzy interval as result (the progress would be between 5 and 9 meters).
4. Conclusions
The role of classical logic in teaching is unquestionable, as is stressed by the ASL (Association for Symbolic Logic) Committee on Logic and Education in [12]. The role of fuzzy thinking in student thinking is profitable even when the mathematical problems seem not to be fuzzy, as Zazkis pointed out in [18]. In this paper we have shown the expediency of literacy in fuzzy logic in higher education, motivated by the increasing relevance of fuzzy logic, as shown by its popularity and dissemination, not only in academia, but also in commercial activities, as evidenced by the success of its applications. In this regard, we believe that selecting stimulating examples can be significant. Teaching fuzzy logic through an example should exemplify how the premises are modelled, which alternatives are taken between the possible choices to model it, and how the conclusion follows from premises in a degree of truth proportional to the truth of the latter. In this work we develop an example for handling approximate reasoning on how to select a suitable gear ratio to attain a certain speed by pedalling.
The example-guide developed in this paper shows that fuzzy logic is an adequate tool for managing approximate reasoning, providing plausible solutions to problems that, like those concerned with the decisions individuals take when cycling in order to make significant or little progress, are verbalized in an inexact or vague manner. Therefore, in its linguistic version, is an example of computing with words [17]. Fuzzy logic is shown as a tool for solving puzzles that occur with some frequency in everyday settings, being commonplace or relevant, but still lacking a precise specification (either because we cannot provide it or because, even being able to do so, we do not require more precision), furnishing solutions in terms of plausible conclusions.
By modelling the example-guide of this work, we have attempted to conduct an exercise in logical analysis of the sentences including vague words, in the tradition inaugurated by M. Black in [4] and in the style employed by G. Polya in [9].
Acknowledgements
Thanks to the reviewers for their helpful suggestions.
This work is dedicated to my teachers E. Trillas and S. Termini, who introduced me to the fascinating world of fuzzy logic.
This work was supported by the Spanish Ministry for Economy and Innovation and by the European Regional Development Fund (ERDF/FEDER) under grant TIN2011-29827-C02-02.
References
- Alsina, C.; Trillas, E. Fuzzy Sets and Mathematical Education. Learn. Math. 1991, 11, 16–19. [Google Scholar]
- Balkir, Z.G.; Alniacik, U.; Apaydin, E. Fuzzy logic in legal education. Turk. Online J. Dist. Educ. 2011, 12, 60–69. [Google Scholar]
- Beth, E.W.; Piaget, J. Epistemologie mathematique et psychologie; Paris P.U.F.: Paris, France, 1961. [Google Scholar]
- Black, M. Vagueness: an exercise in logical analysis. Philos. Sci. 1937, 4, 427–455. [Google Scholar]
- Cross, V.V.; Sudkamp, T.A. Similarity and Compatibility in Fuzzy Set Theory; Physica-Verlag: Berlin, Germany, 2002. [Google Scholar]
- Garrido, A. AI and Mathematical Education. Educ. Sci. 2012, 2, 22–32. [Google Scholar] [CrossRef]
- Kosko, B. Fuzzy thinking: the new science of fuzzy logic; Hyperion Books: New York, NY, USA, 1993. [Google Scholar]
- Lee, B.-S.; Kang, M.-K. Fuzzy Concept and Mathematics Education. J. Korean Soc. Math. Educ., Ser. D., Res. Math. Educ. 1997, 1, 75–85. [Google Scholar]
- Polya, G. How to solve it: a new aspect of mathematical method; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Rowland, T. Well Maybe Not Exactly, but It×s Around Fifty Basically? Vague Language in Mathematics Classrooms. In Vague Language Explored; Cutting, J., Ed.; Palgrave. MacMillan, 2007; pp. 79–96. [Google Scholar]
- Sobrino, A.; Fernández, S. Hacia una lógica fuzzy experimental. In XII Congreso Español de Tecnologías y Lógica Fuzzy; Jaén, 2004; pp. 651–656. [Google Scholar]
- The ASL Committee on Logic and Education. Guidelines for Logic Education. Bull. Symbolic. Logic. 1995, 1 (1), 4–7. [CrossRef]
- Trillas, E.; Alsina, C.; Terricabras, J.M. Introducción a la lógica borrosa; Ariel: Barcelona, Spain, 1995. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Logic and Its Application to Approximate Reasoning; IFIP Congress: Stockoholm, Sweden, 1974; pp. 591–594. [Google Scholar]
- Zadeh, L.A. Fuzzy sets as a basis for theory of possibility. Fuzzy. Syst. Rep. Lett. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Logic = Computing With Words. IEEE Trans. Fuzzy Syst. 1996, 4, 103–111. [Google Scholar] [CrossRef]
- Zazkis, R. Fuzzy Thinking in Non-fuzzy Situations: Understanding Students’ Perspective. Learn. Math. 1995, 15, 39–41. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).