Characteristics of Effective Mathematics Teaching in Greek Pre-Primary Classrooms

Abstract

Limited evidence exists on how teachers contribute to student learning gains in early childhood education. This study draws on the Dynamic Model of Educational Effectiveness (DMEE) and investigates the impact of teacher factors on pre-primary students’ mathematics achievement. It also examines whether the five proposed dimensions—frequency, quality, focus, stage, and differentiation—can clarify the conditions under which these factors influence learning. Using a stage sampling procedure, 463 students and 27 teachers from Greek pre-primary schools were selected. Mathematics achievement was assessed at the beginning and end of the school year, while external observations measured the DMEE factors. Analysis of observation data using multi-trait multilevel models provided support for the construct validity of the measurement framework. Teacher factors explained variation in student achievement gains in mathematics. The added value of using a multidimensional approach to measure the functioning of the teacher factor was identified. Implications of the findings are drawn.

1. Introduction

The pursuit of educational quality has remained a key concern for scholars in the field of educational effectiveness (Chapman et al., 2016; Creemers et al., 2013; Lindorff et al., 2020; Sammons, 2009), acknowledging that education should produce positive learning outcomes across various domains and subject areas. In recent times, the critical role of quality Early Childhood Education (ECE) is more and more emphasized due to its contribution in promoting students’ holistic development (Fuller et al., 2017; Pramling, 2022; Shuey & Kankaraš, 2018) and subsequent academic success (Balladares & Kankaraš, 2020; Dimosthenous et al., 2020; Eliassen et al., 2023; Sammons et al., 2008a, 2008b, 2017). Student achievement is influenced by factors operating at multiple levels, a finding consistently supported by effectiveness studies across various countries (Teddlie & Reynolds, 2000). Specifically, achievement gains are shaped by variables at four distinct levels: the education system, the school, the classroom/teacher, and the individual student (Scheerens, 2013). As learning primarily unfolds through interactions between teachers and students, as well as among students within the classroom setting, factors at both the student and teacher levels are considered to have a direct impact on student learning outcomes (e.g., Scheerens & Bosker, 1997; Townsend, 2007). Moreover, research in both pre-primary and primary education has shown that teacher-related factors play a more significant role than school-level factors in accounting for differences in student achievement, affecting both cognitive outcomes (Kyriakides & Creemers, 2009; Michaelidou, 2025) and affective outcomes (R. D. Muijs et al., 2014). Also, these studies refer to generic teacher factors, as they can be implemented and have an impact on student learning regardless of the types of outcome (e.g., cognitive, metacognitive, psychomotor, emotional) (e.g., Dierendonck, 2023; Katsantonis, 2025; Kyriakides & Creemers, 2008; Mejía-Rodríguez & Kyriakides, 2022; Seidel & Shavelson, 2007) and the educational phase (pre-primary, primary, and secondary) (Kyriakides & Creemers, 2008; Scheerens, 2013). Within this framework, a quantitative synthesis of 167 studies exploring the impact of teaching factors on student achievement indicated that the teacher-related variables proposed by the Dynamic Model of Educational Effectiveness (DMEE) (Creemers & Kyriakides, 2008) were moderately linked to student achievement, regardless of whether the learning outcomes assessed were cognitive, affective, or psychomotor in nature. Numerous empirical studies and meta-analyses emphasize the moderate yet consistent association between teacher factors of the DMEE and student achievement across various educational contexts, with most studies conducted in European countries. Notably, a study in Ghana found that teacher factors provided a more compelling explanation for achievement variation than in any European context (Azigwe et al., 2016).

Given that most effectiveness studies have concentrated on examining the contribution of generic teacher factors in promoting students’ learning outcomes within primary and/or secondary education, a growing need has emerged for further research investigating the effectiveness of teaching factors in enhancing student learning progress in ECE. A recent synthesis of 160 teacher effectiveness studies indicates that most studies were carried out in primary (57.5%) and secondary schools (39.4%) (Kyriakides et al., 2021b). Despite being limited, two studies revealed that teaching factors of DMEE have an impact on cognitive learning outcomes in pre-primary classrooms, both of which were conducted in Cyprus (Kyriakides & Creemers, 2009; Michaelidou, 2025). Therefore, more evidence is required to assess the generalizability of these results and to gain a better understanding of how teachers can effectively promote student learning outcomes in ECE and other educational contexts.

Against this backdrop, the current study is grounded in the DMEE, widely recognized as one of the most recent theoretical frameworks in Educational Effectiveness Research (EER) (Heck & Moriyama, 2010; Sammons, 2009), and seeks to address the identified research gap by exploring the impact of DMEE teacher-related factors on mathematics learning outcomes among ECE students in Greece. Therefore, this study seeks to contribute both theoretically and practically to the field of ECE by investigating the impact of specific teaching characteristics on the development of cognitive learning outcomes in mathematics among ECE students in Greece. This focus is particularly relevant given that recent research continues to highlight early mathematics skills as strong predictors of later academic achievement (ten Braak et al., 2022; Watts et al., 2024). Children who fail to acquire foundational skills in numeracy, geometry, and algebra at an early age often face persistent challenges, with achievement gaps tending to widen over time (Getenet & Beswick, 2023; Vogel et al., 2023). This underscores the importance of ensuring that ECE programs provide all students with a core body of mathematical knowledge essential for advanced skill development. Furthermore, the present study aims to explore the added value of employing five dimensions to assess the functioning of teacher-related factors within the DMEE. The proposed measurement framework emphasizes the importance of considering both quantitative and qualitative aspects of how teacher factors operate when developing a model of effective teaching in ECE. Accordingly, the following section outlines the theoretical framework of the study by presenting an overview of the DMEE teacher factors and the five dimensions used to evaluate their functioning. Then, the research questions of the study are pointed out (see Section 3).

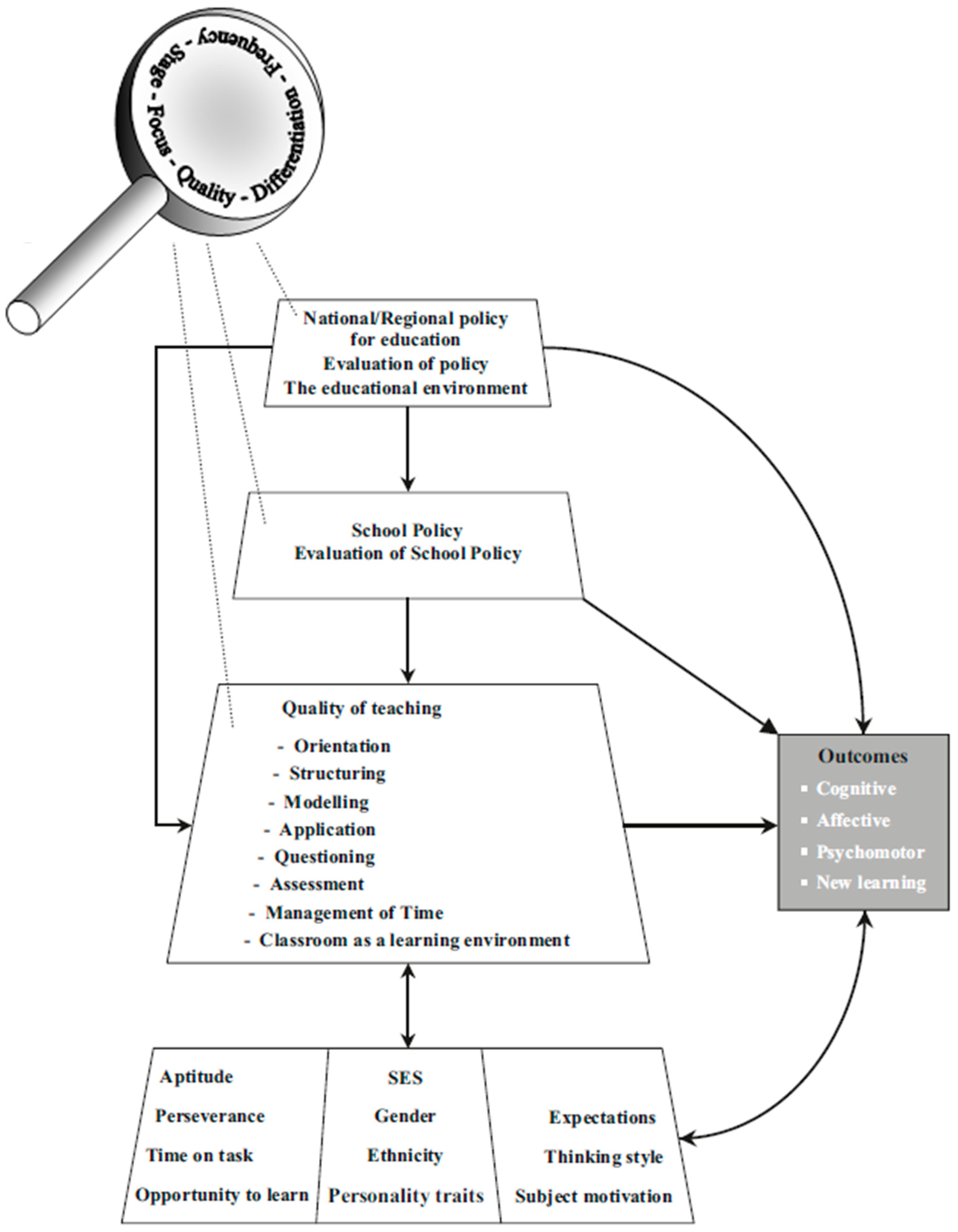
2. The Theoretical Framework of the Study: An Overview of the Dynamic Model of Educational Effectiveness at the Teacher Level

Over the last four decades, several teacher-related factors have been identified in research as having a positive association with student learning outcomes (e.g., Brophy & Good, 1986; Creemers, 1994; Doyle, 1986; R. D. Muijs et al., 2014; D. Muijs & Reynolds, 2001). These factors are not limited to a single approach to learning and teaching but rather encompass a broad spectrum of teacher behaviors that integrate elements from various approaches (Kyriakides et al., 2013; Scheerens, 2013; Seidel & Shavelson, 2007). This study draws on the DMEE, which identifies eight factors describing teachers’ observable instructional behaviors found to be associated with student learning outcomes: orientation, structuring, questioning, modeling, application, time management, the teacher’s role in creating a learning environment, and assessment. In Figure 1, an illustration of the DMEE factors at each level is provided.

2.1. Teacher-Level Factors

At the teacher level, the DMEE draws from major learning theories, including behaviorism, cognitivism, constructivism, and human/motivation theories (Creemers & Kyriakides, 2008). The model recognizes a specific type of teacher behavior as a factor not only when there is empirical evidence linking it to student achievement, but also when a particular learning theory—supported by some empirical validation—can explain the mechanisms through which that behavior influences learning. For instance, the inclusion of orientation as a teacher factor is grounded in motivation theories that shed light on how it enhances student engagement and learning outcomes. Similarly, application was considered a teacher factor due to insights from cognitive load theory. Additionally, constructivist theories were taken into account in defining the main elements of the three factors of DMEE (i.e., modeling, assessment, and orientation). Creemers and Kyriakides (2008) clarified these choices when they introduced the DMEE, explaining the rationale behind the inclusion of each teacher factor (for a detailed review, see Creemers & Kyriakides, 2008).

It can be argued that the DMEE arose from a critical evaluation of educational effectiveness models developed in the 1990s (e.g., Creemers, 1994; Scheerens, 1992; Stringfield & Slavin, 1992) and builds upon key findings from teacher effectiveness research (e.g., Brophy & Good, 1986; Doyle, 1986; R. D. Muijs et al., 2014; D. Muijs & Reynolds, 2001; Rosenshine & Stevens, 1986), emphasizing the importance of a theory-driven and evidence-based approach to enhancing educational quality (Creemers et al., 2013; Panayiotou et al., 2016). Over the past two decades, substantial evidence has affirmed the validity of the DMEE, with more than 21 empirical studies—primarily conducted in Europe—demonstrating the influence of teacher factors on student learning outcomes. Additional support for the DMEE’s validity at the teacher level has also emerged from studies in countries outside Europe, including Canada, the Maldives, and Ghana (e.g., Azigwe et al., 2016; Kyriakides et al., 2013). A brief overview of each teacher factor is provided below (for further details, see Creemers & Kyriakides, 2008).

(1)

Orientation. This factor refers to teacher behavior aimed at presenting the objectives of a specific task, lesson, or series of lessons, and/or encouraging students to identify the reasons behind a given activity. Such practices are intended to enhance the perceived relevance and meaning of tasks, thereby promoting students’ active engagement in the learning process (e.g., De Corte, 2000; Paris & Paris, 2001). Consequently, orientation tasks should occur at various points throughout a lesson or sequence of lessons—such as the introduction, core, and conclusion—and across lessons aimed at achieving different types of objectives. It is expected that teachers will support their students to develop positive attitudes towards learning. Therefore, effective orientation tasks are those that are clear to students and encourage them to identify the goals of the activity. Teachers should also consider all students’ perspectives on why a specific task, lesson, or series of lessons is conducted.

(2)

Structuring. Rosenshine and Stevens (1986) asserted that student achievement is enhanced when teachers deliver instructional content actively and structure it using the following essential strategies: (a) beginning with overviews and/or reviewing objectives, (b) outlining the content to be covered and signaling transitions between lesson segments, (c) emphasizing key ideas, and (d) summarizing main points at the lesson’s conclusion. Summary reviews are also important for student achievement, as they help integrate and reinforce the learning of essential concepts (Brophy & Good, 1986). These structuring strategies do more than aid memorization; they enable students to understand information as a coherent whole by recognizing the connections between its parts. Additionally, student achievement tends to be higher when information is repeatedly presented and key concepts are reviewed (Leinhardt, 1989). The structuring factor further encompasses teachers’ ability to gradually increase lesson difficulty (Creemers & Kyriakides, 2006; Krepf & König, 2022). By scaffolding learning in this way, teachers help students begin tasks that are accessible and manageable, fostering their confidence and motivation. As students build their understanding and skills, the tasks become more complex, sustaining their interest and encouraging deeper cognitive involvement and the development of advanced skills (L. W. Anderson & Krathwohl, 2001; Zeitlhofer et al., 2024).

(3)

Questioning. D. Muijs and Reynolds (2001) assert that effective teaching involves frequent questioning and engaging students in discussions. While research on question difficulty yields inconsistent findings (Redfield & Rousseau, 1981), the developmental level of students determines the appropriate complexity of questions. Studies indicate that about 75% of questions should seek correct answers (L. M. Anderson et al., 1979), with the remainder aiming for substantive responses rather than no response (L. M. Anderson et al., 1979; Brophy & Good, 1986). Recent studies and meta-analyses emphasize the importance of balancing factual questions with higher-order prompts that promote reasoning and exploration in mathematics (Kokkinou & Kyriakides, 2022; Kyriakides et al., 2013; Orr & Bieda, 2025). Many classrooms focus mainly on questions that have only one correct answer. Research indicate that incorporating 30–40% process questions—such as those that invite explanations or predictions—can foster deeper mathematical thinking (Björklund et al., 2020). In addition, high-order questioning has been found to be more effective in promoting students’ critical thinking than low-order questions, which primarily target basic knowledge and comprehension (Barnett & Francis, 2011; Kyriakides et al., 2020; Pollarolo et al., 2023). The type of questions posed should align with the instructional context: basic skills instruction benefits from quick, accurate responses. At the same time, complex content calls for more challenging questions that may not have a single correct answer. Brophy (1986) highlights that evaluating question quality should consider frequency, teaching objectives, and timing. Moreover, a mix of product questions (requiring specific responses) and process questions (demanding explanations) is essential, with effective teachers leaning towards more process questions (Evertson et al., 1980; D. Muijs & Reynolds, 2001). Drawing on findings from studies examining teacher questioning skills and their link to student achievement, this factor is defined in the DMEE by five elements related to the type of question asked, the time given for student responses, and the quality of feedback provided—whether the question is answered or remains unanswered (Creemers & Kyriakides, 2006). Firstly, teachers are encouraged to use a combination of product questions—which typically elicit a single correct response—and process questions, which require students to give more elaborate explanations (Askew & Wiliam, 1995; Scheerens, 2013). Second, the length of the pause after questions is considered, with expectations that it varies depending on the question’s level of difficulty. Third, question clarity is assessed by examining the extent to which students understand what is expected of them, that is, what the teacher wants them to do or discover. Fourth, the appropriateness of the question’s difficulty level is evaluated. Optimal question difficulty should vary according to the context. For example, basic skills instruction requires a great deal of drill and practice, and thus necessitates frequent, fast-paced review, in which most questions are answered rapidly and correctly. However, when teaching complex cognitive content or trying to get students to generalize, evaluate, or apply their learning, effective teachers usually raise questions that may have no single correct answer at all (R. D. Muijs et al., 2014). Specifically, most questions should prompt correct answers. In contrast, the remaining questions should encourage substantive, overt responses (even if incorrect or incomplete), rather than no response at all (Alexander et al., 2022; Brophy & Good, 1986; Kyriakides et al., 2021b). Fifth, the manner in which teachers handle student responses is analyzed: correct answers should be acknowledged as such (not necessarily by the teacher). When students provide partially correct or incorrect answers, effective teachers recognize the accurate parts and, if there is potential for improvement, work to elicit more accurate responses (Rosenshine & Stevens, 1986). These teachers maintain engagement with the original respondent by rephrasing the question or providing clues, rather than ending the interaction by supplying the answer themselves or asking another student to respond (Alexander et al., 2022; R. D. Muijs et al., 2014; Kyriakides et al., 2018b).

(4)

Modeling. While research on teaching higher-order thinking skills and problem-solving has a long history, these teaching and learning activities have gained unprecedented focus over the past two decades due to policy priorities emphasizing new educational goals. As a result, researchers have investigated the extent to which the modeling factor is linked to student learning outcomes (R. D. Muijs et al., 2014). Numerous studies on teacher effectiveness indicate that effective teachers are expected to assist students in using specific strategies or developing their own approaches to solving various types of problems (Grieve, 2010). Consequently, students are encouraged to cultivate skills that support the organization of their own learning, such as self-regulation and active learning (Kraiger et al., 1993). In defining this factor, the DMEE considers not only the characteristics of modeling tasks provided to students but also the teacher’s role in aiding students to devise problem-solving strategies. Teachers can either demonstrate a straightforward method for solving a problem or encourage students to articulate their own approaches, using these student-generated strategies as a foundation for modeling. Recent research suggests that the latter approach may more effectively promote students’ ability to apply and refine their own problem-solving strategies (Aparicio & Moneo, 2005; Gijbels et al., 2006; Kyriakides et al., 2020; Polymeropoulou & Lazaridou, 2022).

(5)

Application. Drawing on cognitive load theory—which suggests that working memory has limited capacity and can only retain a certain amount of information at a time (Kirschner, 2002; Paas et al., 2003)—each lesson should incorporate application activities. Effective teachers facilitate student learning by providing opportunities for practice and application through seatwork or small-group tasks (Borich, 1996; R. D. Muijs et al., 2014). Beyond simply counting the number of application tasks, the application factor examines whether students are merely asked to repeat previously covered material or whether the tasks require engagement at a more complex level than the lesson itself. It also considers whether application tasks serve as foundations for subsequent teaching and learning steps. Additionally, this factor addresses teacher behaviors related to monitoring, supervising, and providing corrective feedback during application activities. When students work independently or in groups, effective teachers circulate to track progress and offer assistance and constructive feedback (Hattie & Timperley, 2007; Yang et al., 2021).

(6)

Classroom as a learning environment. This factor encompasses five key elements that enable teachers to establish a supportive and task-focused learning environment: teacher-student interaction, student-student interaction, the way students are treated by the teacher, the level of competition among students, and the degree of classroom disorder. Research on classroom environment highlights the first two elements—teacher-student and student-student interaction—as central components in assessing classroom climate (e.g., Cazden, 1986; Den Brok et al., 2004; Harjunen, 2012). However, the DMEE emphasizes examining the types of interactions present in the classroom, rather than focusing on students’ perceptions of their teacher’s interpersonal behavior. Specifically, the DMEE focuses on the immediate effects of teacher actions in fostering relevant interactions, as learning occurs through these interactions (Kyriakides et al., 2021b). Therefore, the model aims to assess how effectively teachers promote on-task behavior by encouraging such interactions. The remaining three elements pertain to teachers’ efforts to establish an efficient and supportive learning environment (R. D. Muijs et al., 2014; Walberg, 1986). These are evaluated by observing teacher behaviors in setting rules, encouraging students to respect and follow them, and maintaining these rules to sustain an effective classroom environment.

(7)

Assessment. Assessment is considered an essential component of teaching. In particular, formative assessment has been identified as one of the most significant factors linked to effectiveness across all levels, especially within the classroom (e.g., Christoforidou & Kyriakides, 2021; De Jong et al., 2004; Hopfenbeck, 2018; Panadero et al., 2019; Shepard, 1989). Consequently, the information collected through assessment is expected to help teachers identify students’ learning needs and evaluate their own instructional practices. Beyond the quality of assessment data—specifically their reliability and validity—the DMEE focuses on the extent to which the formative, rather than summative, purpose of assessment is realized. This factor also encompasses teachers’ skills across all key phases of the assessment process—planning and constructing tools, administering assessments, recording results, and reporting—and emphasizes the dynamic interplay among these phases (Black & Wiliam, 2009; Christoforidou et al., 2014; Christoforidou & Kyriakides, 2021; Kyriakides et al., 2024a).

(8)

Management of time. Building on a critical analysis of earlier educational effectiveness research models, the DMEE emphasizes that efficient time management is a key indicator of effective classroom management. Carroll’s model (Carroll, 1963), a foundational framework in EER, defined student achievement—or learning effectiveness—as a function of the actual time required for learning relative to the time spent on learning (i.e., quantity of instruction). However, Carroll’s model does not address how learning occurs. More recent frameworks, such as Creemers’ comprehensive model (Creemers, 1994), highlight ‘opportunity to learn’ and ‘time on task’ as crucial factors influencing educational outcomes. These factors, operating at various levels, are strongly connected to student engagement. Thus, effective teachers are expected to cultivate and maintain an environment that maximizes engagement and optimizes learning time (e.g., Creemers & Reezigt, 1996; Scheerens, 2013; Wilks, 1996). Recognizing the limitations of earlier models of EER, the DMEE argues that concepts like time/opportunity and quality are somewhat vague but can be clarified by examining other instructional characteristics linked to learning outcomes. For example, the DMEE argues that effective teachers should organize and manage the classroom to function as an efficient learning environment, thereby maximizing student engagement. Towards this direction, the amount of instructional time used per lesson is considered, as well as how well that time fits within the overall schedule. Moreover, this factor focuses on whether students remain on task or become distracted, and whether teachers effectively address classroom disruptions without wasting teaching time. It also assesses how time is allocated across different lesson phases based on their importance and the distribution of time among various student groups. Consequently, time management is considered as a critical indicator of a teacher’s ability to manage the classroom effectively.

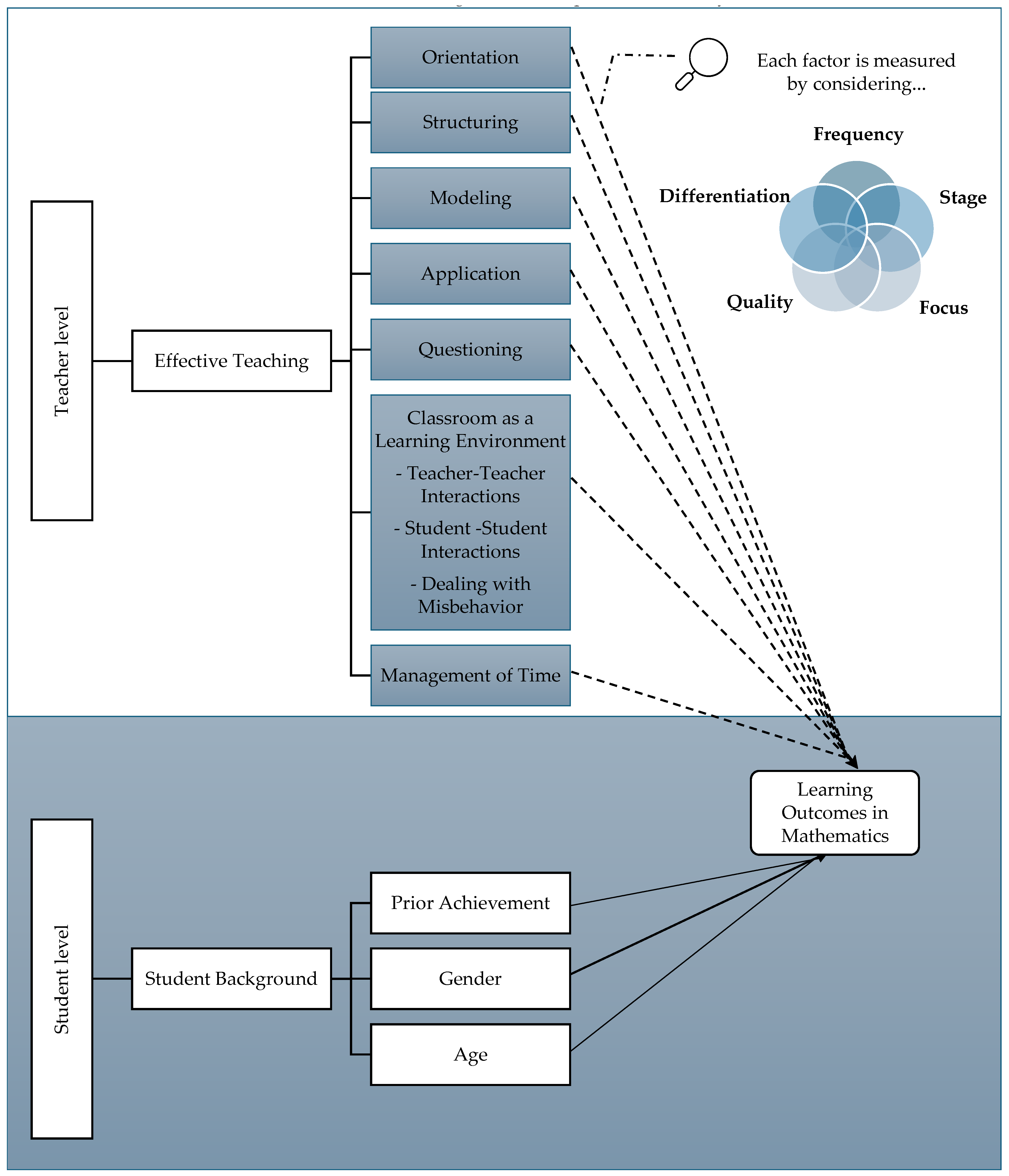
2.2. Using a Multidimensional Approach to Measure the Functioning of Teacher Factors

In most effectiveness studies, a clear distinction is rarely made between the different aspects of an effectiveness factor that have been found to be associated with student achievement (Creemers et al., 2010; Scheerens, 2016). This highlights the need for researchers to clearly specify how each factor was measured and to identify the particular aspects that were found to be associated with student achievement. For instance, one study (Reezigt et al., 1999) testing the validity of the comprehensive model of educational effectiveness (Creemers, 1994) assessed school evaluation policy by measuring the frequency of evaluations, revealing both beneficial and adverse effects of this factor on student learning outcomes. Conversely, another study focused on how school evaluation data was used and found that schools employing evaluations for formative purposes were more effective than others (Demetriou & Kyriakides, 2012). It could be argued that contradictory findings regarding the impact of school evaluation in these two studies stem from their different focuses: one emphasized the frequency dimension of the factor, while the other concentrated on its specific qualitative characteristics. Thus, one of the essential characteristics of the DMEE is its attempt to define effectiveness factors by using the following five measurement dimensions: frequency, focus, stage, quality, and differentiation. The proposed measurement framework recommends assessing each factor not only by quantifying its occurrence within the system, school, or classroom but also by evaluating specific aspects of its operation, taking into account its qualitative characteristics. The significance of addressing each dimension is discussed in the following section.

(1)

Frequency. Frequency represents a quantitative method for assessing the functioning of each effectiveness factor by determining how often an activity related to that factor occurs within a system, school, or classroom. It is assumed that measuring frequency enables researchers to gauge the importance teachers place on each factor (Creemers & Kyriakides, 2008). To date, the most effective studies have focused solely on this dimension, likely because it is the simplest way to measure a factor’s functioning. For example, to assess the frequency dimension of the structuring factor, researchers might count the number of structuring tasks during a lesson or the total time spent on such tasks. However, the DMEE contends that relying solely on a quantitative approach is insufficient, especially given that the relationship between the frequency of each factor and student achievement may be nonlinear. For instance, a curvilinear relationship is expected between the frequency of teacher assessment and student learning outcomes, as excessive emphasis on assessment may reduce actual teaching and learning time. In contrast, the absence of any assessment prevents teachers from adapting instruction to students’ needs (Creemers & Kyriakides, 2006; van Geel et al., 2023; Wolterinck et al., 2022). Therefore, the additional four dimensions, which explore qualitative aspects of each factor’s functioning, should also be taken into account.

(2)

Focus. The focus dimension considers both the specificity of activities linked to a factor’s functioning and the number of objectives each activity is intended to achieve. Specifically, the DMEE acknowledges that tasks associated with a factor’s functioning are purposeful and do not occur by chance. For example, when teachers ask students to complete an application task, they likely aim to achieve specific goals through that activity, such as practicing a particular algorithm to solve a quadratic equation, recognizing its use in various problem types, or identifying different representations of a concept. This means that researchers measuring the qualitative aspects of a factor’s functioning should strive to identify the intended purposes of each activity, acknowledging that an activity may aim to fulfill one or multiple objectives. The importance of the focus dimension stems from research showing that when all activities target a single purpose, the likelihood of achieving that goal is high, but the overall effect of the factor may be limited because other potential purposes and synergies remain unaddressed (Kyriakides et al., 2021b; Schoenfeld, 1998). Conversely, if all activities aim to achieve multiple purposes, there is a risk that specific objectives may not be addressed thoroughly enough to be successful (R. D. Muijs et al., 2014; Pellegrino, 2004). The second aspect of the focus dimension involves the specificity of activities, which can range from very specific to more general. For example, in relation to the orientation factor, a task may prompt students to reflect on the reasons behind a specific task, lesson, or sequence of lessons. The DMEE assumes that assessing the focus dimension—both in terms of activity specificity and the number of goals a teacher aims to achieve—helps determine whether an appropriate balance is struck. In the case of orientation, effective teachers are expected to provide not only particular orientation tasks (e.g., why we are estimating the perimeter of this shape) but also more general ones (e.g., why we study geometry) to support student learning outcomes and foster positive attitudes toward learning (Kyriakides et al., 2021b).

(3)

Stage. The stage at which tasks associated with a factor take place is also examined; the factors need to be sustained over an extended period to ensure they exert a continuous, direct or indirect, influence on student learning (Creemers, 1994). This assumption is partly grounded in findings from evaluations of programs aimed at improving educational practice, which show that the impact of such interventions depends, in part, on the duration of their implementation within a school (Gray et al., 1999; Kyriakides et al., 2021a, 2024b; Slater & Teddlie, 1992). For instance, structuring tasks are not expected to occur solely at the beginning or the end of a lesson but should be distributed across its various stages. Similarly, orientation tasks should not be confined to a single lesson but extended throughout the entire school year to sustain student motivation and maintain active engagement in learning. Although measuring the stage dimension provides insights into the continuity of a factor’s presence, the specific activities associated with the factor may vary over time (Creemers, 1994). Hence, employing the stage dimension to assess a factor’s functioning enables us to determine the degree of consistency at each level, as well as the flexibility in applying the factor throughout the study’s duration.

(4)

Quality. This dimension pertains to the intrinsic characteristics of a specific factor, as outlined in the literature. Its importance in measuring a factor’s functioning stems from the fact that effectiveness can vary; research has shown that only particular activities linked to a factor positively influence student learning outcomes. For example, in terms of orientation, the measurement of dimension quality refers to the properties of the orientation task, specifically whether it is clear to students and whether it has any impact on their learning. In particular, teachers may present the reasons for performing a task simply because they have to do it as part of their teaching routine, without having much effect on student participation. In contrast, others may encourage students to identify the purposes that can be achieved by performing a task and therefore increase their students’ motivation towards a specific task/lesson/or series of lessons. Another example, when considering the quality of the application tasks, the appropriateness of each task is measured by looking at the extent to which the students are asked simply to repeat what they already covered with their teacher or whether the application task is more complex than the content covered in the lesson, perhaps even being used as a starting point for the next step in teaching and learning. The extent to which application tasks are used as starting points for learning can also be seen as an indication of the impact that application tasks have on students.

(5)

Differentiation. Differentiation refers to the extent to which activities associated with a factor are carried out consistently for all individuals involved (e.g., students, teachers, and schools). Adapting instruction and related activities to the specific needs of each individual or group is expected to improve the effective implementation of the factor and ultimately maximize its impact on student learning outcomes. While differentiation might be considered a characteristic of an effectiveness factor, it has been intentionally treated as a distinct dimension for measuring each effectiveness factor, rather than being included within the quality dimension (see Kyriakides et al., 2021b). This distinction highlights the importance of recognizing and addressing the unique needs of each student or group. The DMEE asserts that it is difficult to deny that individuals of all ages learn, think, and process information differently. One approach to differentiation involves teachers tailoring their instruction to meet the individual learning needs of students, which are influenced by factors such as gender, socioeconomic status (SES), ability, thinking style, and personality type (Goyibova et al., 2025; Jiang & Yang, 2022; Kyriakides, 2007; Zajda, 2024). For example, effective teachers tend to provide low-achieving students with more active instruction and feedback, greater redundancy, and smaller instructional steps that lead to higher success rates (Brophy, 1986; Creemers & Kyriakides, 2006; Zeng, 2025). Importantly, the differentiation dimension does not suggest that different students are expected to reach different goals. Instead, adopting policies to address the unique needs of various groups of schools, teachers, or students is intended to ensure that all can achieve the same educational objectives. This perspective is supported by research that focuses on advancing both quality and equity in education (e.g., Kelly, 2014; Kyriakides et al., 2018a). Therefore, by treating differentiation as a distinct measurement dimension, the DMEE aims to support schools where teaching practices are maladaptive and assist teachers in implementing differentiation that does not hold back lower achievers or increase individual differences (Anastasou & Kyriakides, 2024; Caro et al., 2016; Kokkinou & Kyriakides, 2022; Kyriakides et al., 2019; Perry et al., 2022; Scherer & Nilsen, 2019; Tan et al., 2023). In conclusion, we argue for adopting a multidimensional perspective when examining the contribution of specific teaching practices. Additionally, an integrated approach to defining teaching quality is employed, drawing upon prior studies that have utilized the DMEE framework. To address the research questions presented in the next section, this study is grounded in the theoretical framework depicted in Figure 2, which incorporates both student-level and teacher-level effectiveness factors. Teaching quality is defined through seven of the eight teacher-level factors outlined in the DMEE, except of assessment, which was not measured in the present study. For practical reasons, it was only possible to use the observation instruments developed by Creemers and Kyriakides (2012) to measure the teacher factors of the DMEE and not the student and teacher questionnaires, which were designed in order to generate data on the assessment factor (see Christoforidou et al., 2014; Christoforidou & Kyriakides, 2021; Kyriakides et al., 2024a). It is important to note that these factors of DMEE are considered as multidimensional constructs assessed across the five dimensions previously described, aiming to determine their impact on students’ learning outcomes in mathematics. Furthermore, selected student background variables—namely prior achievement in mathematics, age, and gender—were included to examine their predictive validity in accounting for variations in student achievement (see Figure 2, which presents the study’s theoretical framework).

3. Research Aim

The study presented here aims to test the two main assumptions of the DMEE at the teacher level. First, it aims to identify the impact of teacher factors on the learning of ECE students in mathematics. To the author’s knowledge, so far only two studies have investigated the impact of teacher factors of DMEE on student learning outcomes in ECE, both conducted in Cyprus. Considering that the DMEE conceptualizes teacher factors as generic, there is a clear need for research across different countries and educational phases—especially in ECE—to empirically test this assumption. Such studies can help determine the extent to which each factor explains variation in ECE student achievement. Secondly, the study aims to investigate whether the five proposed dimensions for measuring teacher factors can effectively identify the conditions under which these factors impact student learning in ECE. By exploring the added value of these five measurement dimensions, more comprehensive strategies to enhance teaching quality in ECE may be developed (Creemers et al., 2013). Accordingly, the study reported here was designed to address the following three main research questions:

• To what extent can the five dimensions proposed by the DMEE be used to measure in a valid and reliable way each teacher factor of the model?
• Which teacher factors (if any) of DMEE explain variation in student achievement in mathematics?
• To what extent does the use of all five dimensions to measure each factor help us to explain a larger variance of student achievement in mathematics?

4. Methods

4.1. Measuring Students’ Achievement in Mathematics

Student achievement in mathematics was evaluated at the start and conclusion of the 2020–2021 school year through two criterion-referenced performance tests. In particular, a battery of performance tests originally developed for a value-added assessment study in mathematics (Kyriakides, 2002) was employed. These assessments targeted essential concepts in early mathematics development (Hachey, 2013; Knaus, 2017; Linder et al., 2011), measuring students’ knowledge and skills in numeracy, measurement, geometry, probability, and statistics—areas all included in the national curriculum of Greece1 (Ministry of Education, Religious Affairs and Sports, 2003). Evidence about the validity of the battery of mathematics tests was provided by studies conducted in Cypriot pre-primary schools (e.g., Kyriakides, 2002; Kyriakides & Creemers, 2009; Michaelidou, 2025). However, since this battery of tests was administered for the first time in the Greek context, modifications to the test were deemed necessary to ensure alignment with the recent Greek curriculum. The modifications were employed with the assistance of six pre-primary teachers and two pre-primary coordinators in Greece regarding the extent to which the battery of tasks covered the mathematics curricula for pre-primary level and the extent to which the items were in line with their practices (e.g., context of the items, type of questions, difficulty level of the language used, time given) and took into account the abilities of students to understand what they are expected to do. Empirical support for both the content and face validity of the tests was generated. It is important to note that a detailed specification table for both pre- and post-mathematics tests was developed (18 items were included in each test). A number of common tasks (n = 10) were incorporated into both assessments to ensure consistency and comparability of the tests. In contrast, the level of difficulty in the post-mathematics test was progressively increased. The students participating in the study were asked to complete several criterion-referenced tasks (e.g., students were given a picture with two carpets and were asked to color the widest one) related to each objective of the aforementioned mathematical areas, and all student responses were scored according to a scoring scheme.

Due to the abovementioned modifications, the psychometric characteristics of the modified test were assessed. Specifically, the Extended Logistic Model of Rasch (Andrich, 1988) was applied to analyze the data gathered at both the beginning and end of the 2020–2021 school year. For each test, the analysis of student achievement data demonstrated that the scales possessed satisfactory psychometric properties. More precisely, the indices for both student (case) and item separation exceeded 0.80, indicating adequate separability of each scale (Wright, 1985). Additionally, the infit and outfit mean square statistics for each scale were close to one, with corresponding infit and outfit t-scores approximately zero. Each analysis further revealed that all item infit values ranged between 0.87 and 1.09, confirming a good fit to the Rasch model (Keeves & Alagumalai, 1999). For each student, two separate scores reflecting their mathematics achievement at the beginning and end of the school year were generated based on the Rasch person estimates. Importantly, no student achieved a perfect score nor scored zero on either test. Furthermore, in each test, fewer than 4% of students scored above 80% of the maximum score, and fewer than 6% scored below 10%. These results indicate the absence of ceiling and floor effects in the achievement data.

4.2. Measuring Quality of Teaching

External observations were conducted to evaluate all teacher factors of the DMEE, except of assessment. In particular, two observation instruments (i.e., one high and one low inference) created by Creemers and Kyriakides (2012) were utilized to measure the teacher factors and their respective dimensions. These instruments have been utilized by various research teams to test the core assumptions of the DMEE at the teacher level, providing evidence supporting the construct validity of each instrument (for a review, see Kyriakides et al., 2021b). On the one hand, the high-inference instrument captures the DMEE’s seven teacher-level factors (except the assessment factor) and consists of 40 statements reflecting teacher behaviors during teaching. The observer is expected to complete a Likert scale to indicate how often each type of teacher behavior is observed. The high-inference instrument is completed after the lesson and requires the observer to have a high degree of judgment (Creemers & Kyriakides, 2008). On the other hand, the low-inference instrument, which is filled out during the lesson, constrains such interpretations by focusing on more readily observable behaviors. The low-inference instrument takes into account the five measurement dimensions of teacher factors of DMEE (i.e., frequency, focus, stage, quality, and differentiation). In particular, observers are expected to report not only on how frequently tasks associated with these factors take place but also on the period during which each task takes place and its focus. An emphasis on measuring specific aspects of the quality dimension of each factor (e.g., the type of questions raised, and the type of feedback provided to students’ answers) can also be identified (Creemers & Kyriakides, 2008). In this study, five members of the research team in Greece conducted the observations. All observers were PhD holders or candidates with a background in early childhood education. They underwent a five-day training course led by an expert familiar with both low- and high-inference observation tools. The training involved studying the observation manual, practicing coding with videotaped lessons, and receiving guidance on coding factors and dimensions to ensure consistency across observers. Four 40 min video lessons were used for coding practice, each followed by a one-hour group discussion. Observers then completed an inter-rater reliability test using a 40 min lesson. The observers attained a minimum inter-rater reliability of 75% agreement with master-coded ratings (These were initially developed in order to measure the factors in primary schools, and the research team had to adapt them to the context of pre-primary classrooms). Each class was visited three times, with three mathematics lessons observed per teacher during the whole school year. For each observational instrument, the Cronbach’s alpha reliability coefficient for each scale exceeded 0.83 (i.e., 0.84 up to 0.91), and the inter-rater reliability coefficient (ρ²) was higher than 0.82 (i.e., 0.83 up to 0.89).

A one-way analysis of variance confirmed that the data from each scale were generally at the teacher level. Finally, separate multi-trait multilevel models were applied for each DMEE factor to examine the extent to which data from the two observation methods reliably measured each factor across the five DMEE dimensions. The key results from these models, which support the validity of the instruments, are presented in the first part of the results section and provide answers to the first question of this study.

5. Results

This section is divided into two parts. The first part focuses on the validity of the two observation instruments used to measure the functioning of the teacher factors in the DMEE and addresses the first research question. The second part presents the results of multilevel regression analyses of student achievement in mathematics, aiming to answer the second and third research questions.

5.1. Using Five Dimensions to Measure Each Teacher Factor: Testing the Validity of the Proposed Measurement Framework

DMEE posits that each teacher factor can be measured through five dimensions; thus, separate Confirmatory Factor Analyses (CFA) were conducted for each factor, in order to address the first research question of the study. Specifically, the analyses assessed whether data obtained from two different observation methods (i.e., low-inference and high-inference observations) could measure each factor of the model in a valid and reliable manner, in line with the five proposed DMEE dimensions. In the case of the orientation factor, each relevant observed variable was linked to one of the five trait factors, representing a specific dimension of teachers’ orientation skills, as well as to one method factor corresponding to the data collection method (i.e., high-inference or low-inference observation instrument). The uniqueness of each observed variable was assumed to be uncorrelated. Figure 3 illustrates the model used to determine whether the orientation factor of DMEE can be represented by the five dimensions (traits) through the items of the two observation instruments (methods). It was found that this factor can be represented by all dimensions through the items of both observation instruments. Specifically, it was found to be represented by frequency (i.e., the number of orientation tasks that take place in a typical lesson as well as how long each orientation task takes place), focus (i.e., whether an orientation task may refer to a part of a lesson, to the whole lesson, or even to a series of lessons), stage (i.e., it is expected that orientation tasks will take place in different parts of a lesson or series of lessons (e.g., introduction, core, ending of the lesson) and in lessons that are expected to achieve different objectives), quality (i.e., the properties of the orientation task, especially to whether it is clear for the students and whether it has any impact on their learning) and differentiation (i.e., it is assumed that effective teachers are those who provide different types of orientation tasks to students by taking into account differences in the personal and background characteristics of their students, teaching objectives, and organizational and cultural context of their school/classroom). From Figure 3, several observations emerge: individual standardized loadings on trait and method factors indicate the convergent validity of the observed variables. High loadings on trait factors (above 0.65) combined with low loadings on method factors (below 0.35) demonstrate good convergent validity. The standardized loadings on traits can be interpreted as validity coefficients for each measure. Additionally, there was no evidence of strong general method effects.

Similar multi-trait multi method models were used for each factor of the DMEE.

Table 1. Goodness-of-fit indices for the optimal Structural Equation Models employed to assess the validity of the proposed framework for measuring each teacher-level factor of the DMEE.

SEM Models	X2	d.f.	CFI	RMSEA	X2/d.f.
Orientation
(1) 5 correlated traits, 2 correlated methods	118.7	69	0.945	0.03	1.72
Questioning
(1) 5 correlated traits, 2 correlated methods	126.3	69	0.948	0.04	1.83
Application
(1) 5 correlated traits, 2 correlated methods	116.6	69	0.952	0.03	1.69
Modeling
(1) 4 correlated traits, 2 correlated methods	119.4	73	0.949	0.03	1.63
Management of Time
(1) 5 correlated traits, 2 correlated methods	117.3	69	0.953	0.02	1.70
Structuring
(1) 5 correlated traits, 2 correlated methods	120.8	69	0.956	0.02	1.75
Classroom as a Learning Environment
(Teacher-student relations, Student-student relations)
(1) 2 correlated second order, 2 correlated methods	118.0	69	0.955	0.02	1.71
Dealing with Misbehavior
(1) 5 correlated traits, 2 correlated methods	127.0	69	0.951	0.04	1.84

displays the key results from the CFA models used to analyze the multi-trait-multimethod matrix (MTMM) for each DMEE factor, excluding assessment. In particular, it presents the fit indices of the first-order factor model, which emerged as the best-fitting model to describe each factor. Overall, these findings support the construct validity of the five measurement dimensions for most of the effectiveness factors studied. The only exceptions that were identified reveal the difficulty of treating differentiation and quality as two distinct dimensions (i.e., traits) in the case of modeling, since a four-trait and two-method model was found to fit better than the theoretical model (i.e., the five-trait and two-method model). Moreover, the findings of this study suggest that the classroom as a learning environment should not be treated as a single effectiveness factor. Instead, it comprises two interrelated but distinct factors: the quality of relationships among students and the quality of teacher–student relationships. Table 1 presents the fit indices for each of these factors separately, supporting this distinction. Moreover, the comparison of CFA models for each factor confirmed both convergent and discriminant validity of the five measurement dimensions proposed by the DMEE. Convergent validity was evidenced by relatively high standardized loadings on trait factors (above 0.63), whereas standardized loadings on method factors were comparatively low (below 0.36). These results reinforce the appropriateness of employing multi-method approaches to enhance measurement and construct validity, thereby providing more substantial support for the reliability of the findings derived from subsequent analyses.

5.2. Searching for Teacher Factors Associated with Student Achievement in Mathematics

A multilevel regression analysis (with students nested within teachers) was conducted to address the second research question and to identify which teacher factors explain variations in student achievement in mathematics. Since Greek pre-primary teachers teach mathematics in a single class, it was not possible to treat the class and the teacher level as two separate levels. Most schools in our sample had only one class of pre-primary students. Therefore, the three-level model (students within teachers within schools) was not found to fit better than the student within the teacher model, which was found to fit better than any other two-level models.

Table 2. Parameter Estimates and (Standard Errors) for the Multilevel Analyses of Student Achievement in Mathematics.

	Final Mathematics Achievement (Dependent Variable)
Factors	Model 0	Model 1	Model 2a	Model 2b	Model 2c	Model 2d	Model 2e
Fixed part (Intercept)	17.41(1.02) ***	11.21 (1.01) ***	9.85 (1.03) ***	9.87 (1.02) ***	10.24 (1.04) ***	9.56 (1.03) ***	10.21 (1.02) ***
Student Level
Prior achievement		0.61 (0.02) ***	0.59 (0.03) ***	0.58 (0.03) ***	0.57 (0.03) ***	0.57 (0.03) ***	0.58 (0.03) ***
Sex (boys = 0, girls = 1)		0.15 (0.13)	0.16 (0.14)	0.14 (0.12)	0.10 (0.11)	0.17 (0.15)	0.19 (0.16)
Age (in years)		−0.08 (0.24)	−0.07 (0.25)	−0.08 (0.28)	−0.08 (0.26)	−0.09 (0.26)	−0.07 (0.27)
Teacher Level
Freq Structuring			0.38 (0.16) **
Freq Orientation			0.32 (0.14) *
Freq Questioning			0.27 (0.13) *
Freq Application			0.14 (0.14)
Freq Modeling			0.18 (0.15)
Freq Management of time			0.31 (0.14) *
Freq Teacher-student relation			0.36 (0.15) **
Freq Student-student relation			0.34 (0.14) **
Freq Misbehavior			0.35 (0.16) *
Stage Structuring				0.24 (0.09) **
Stage Orientation				0.25 (0.11) *
Stage Questioning				0.19 (0.09) *
Stage Application				0.17 (0.08) *
Stage Modeling				0.20 (0.09) *
Stage Management of time				0.25 (0.11) *
Stage Teacher-student relations				0.13 (0.11)
Stage Student-student relation				0.24 (0.11) *
Stage Misbehavior				0.22 (0.10) *
Focus Structuring					0.29 (0.12) **
Focus Orientation					0.14 (0.13)
Focus Questioning					0.24 (0.11) *
Focus Application					0.19 (0.08) **
Focus Modeling					0.17 (0.08) *
Focus Management of time					0.14 (0.09)
Focus Teacher-student relation					0.16 (0.07) *
Focus Student-student relation					0.18 (0.09) *
Focus Misbehavior					0.09(0.08)
Quality Structuring						0.29 (0.11) **
Quality Orientation						0.26 (0.10) **
Quality Questioning						0.34 (0.12)**
Quality Application						0.28 (0.13) *
Quality Management of time						0.33 (0.14) **
Quality Teacher-student relations						0.29 (0.12) **
Quality Student-student relation						0.28 (0.11) **
Quality Misbehavior						0.28 (0.12) *
Dif/tion Structuring							0.12 (0.08)
Dif/tion Orientation							0.21 (0.10) *
Dif/tion Questioning							0.19 (0.09 )*
Dif/tion Application							0.21 (0.09)*
Dif/tion Management of time							0.13 (0.11)
Dif/tion Teacher-student relation							0.20 (0.09) *
Dif/tion Student-student relation							0.15 (0.09)
Dif/tion Misbehavior							0.16 (0.09)
Quality Modeling including differentiation							0.17 (0.08) *
Variance components
Class	20.20%	17.31%	13.25%	12.09%	12.58%	10.80%	12.19%
Student	79.80%	32.99%	32.65%	32.61%	32.62%	32.60%	32.61%
Explained		49.70%	54.10%	55.30%	54.80%	56.60%	55.20%
Significance test
X2	2654.53	2165.82	1918.22	1868.62	1936.92	1853.52	1962.52
Reduction		488.71	247.6	297.2	228.9	312.3	203.3
Degrees of freedom		1	7	8	6	8	5
p-value		0.001	0.001	0.001	0.001	0.001	0.001

* p < 0.05, ** p < 0.01, *** p < 0.001. For each alternative model 2 (i.e., models 2a–2e), the reduction is estimated in relation to the deviance of model 1.

presents the results from the multilevel regression analysis (students within teachers) of final mathematics achievement. The second column displays the results of the empty model (i.e., the model without any explanatory variables). The variance at each level was statistically significant at the 0.05 level, indicating that the teacher effect accounted for 20% of the variance. This finding aligns with results from teacher effectiveness studies carried out in multiple countries (see Kyriakides et al., 2021b). In the next step, explanatory variables at the student level were added to the empty model. The likelihood ratio test (χ²) indicated a significant improvement between the empty model and Model 1 (p < 0.001), supporting the selection of Model 1. Key observations from the results presented in the second column for Model 1 include: first, Model 1 accounts for approximately 50% of the total variance in student achievement in mathematics, with the majority of this explained variance occurring at the student level; and second, prior knowledge was the only student-level variable significantly associated with student achievement.

Table 2 presents five distinct versions of Model 2. In each version, the factor-trait scores derived from the SEM models—corresponding to one of the five dimensions used to measure each teacher factor in the DMEE—were added to Model 1. The fit of each of these five models was compared to Model 1, with the likelihood ratio test (χ²) indicating a significant improvement for all versions (p < 0.001). This suggests that variables representing the five measurement dimensions of teacher factors significantly influence student achievement in mathematics. More specifically, the results in column 3 (Model 2a), which examine the frequency dimension, show that all factors except modeling and application explain variation in student mathematics achievement. Model 2b indicates that the stage dimension of all factors—except for time management—has a statistically significant effect on student achievement at the 0.05 level. Regarding the focus dimension (Model 2c), six factors (structuring, questioning, application, modeling, teacher-student interactions, and student interactions) were found to be associated with gains in mathematics achievement. Model 2d’s results reveal that the quality dimension of all DMEE factors has a statistically significant effect on student achievement at the 0.05 level. Notably, Model 2d explains more variance than any other Model 2 version, underscoring the importance of measuring the quality dimension to capture the impact of teacher factors on mathematics achievement. Finally, the differentiation dimension (Model 2e) shows that four factors—questioning, orientation, teacher-student interactions, and managing misbehavior—along with the modeling factor (which relates to both quality and differentiation dimensions), are significantly associated with student achievement.

At the next stage of the analysis, the third research question was addressed, and the extent to which the use of all five dimensions was identified in an attempt to explain a larger variance of student achievement in mathematics. Specifically, we sought to determine how much additional variance could be explained when considering the effects of the frequency dimension of teacher factors alongside at least one other dimension. To achieve this, four alternative models were developed, each combining the frequency dimension with another dimension of the DMEE factors (i.e., model 3a: frequency and focus; model 3b: frequency and stage; model 3c: frequency and quality; and model 3d: frequency and differentiation). Each alternative model was compared with Model 2a, which includes only the frequency dimension. The likelihood statistics for each comparison supported the inclusion of multiple dimensions, showing a statistically significant improvement at the 0.05 level. Additionally, all alternative models explained more variance than the model considering only the frequency dimension. Notably, the model incorporating all five dimensions (Model 4) accounted for the greatest amount of variance and demonstrated the best fit among all models. Importantly, this model explained over 80% of the variance at the teacher level (16.6% out of 20.2%) in student mathematics achievement, indicating that considering all five dimensions is essential to maximize explained variance at the teacher level. However, none of the models explained more than approximately 65% of the total variance overall, which may be due to the limited number of student-level factors (only three) included in the analysis.

6. Discussion

Examining the impact of each proposed factor on student achievement, the findings generally reaffirm the important role of teacher factors. Specifically, the factors identified by the DMEE were found to be associated with student achievement in mathematics, a core subject within the Greek ECE curriculum. These results align with previous research conducted in different educational contexts (e.g., Kyriakides & Creemers, 2008, 2009; Konstantopoulos, 2011; Michaelidou, 2025; Panayiotou et al., 2014), which emphasized the generic nature of these factors. It is essential to acknowledge that a significant amount of variance in mathematics achievement exists at the student level and is associated with students’ background characteristics, including prior academic performance. Furthermore, the findings are consistent with earlier effectiveness studies conducted in Cyprus, which demonstrated that gender was not significantly associated with mathematics achievement at the end of pre-primary education (e.g., Kyriakides & Creemers, 2009; Michaelidou, 2025). This study provides additional support for the impact of teacher factors as proposed by the DMEE, reinforcing their generic nature and the premise that these factors contribute to student learning outcomes across different contexts. The findings also expand upon those of Kyriakides and Creemers (2009) by demonstrating the predictive validity of these factors in a new context, where all examined factors were significantly associated with mathematics achievement.

Furthermore, the study indicates that the DMEE offers a valuable theoretical framework for future research aimed at validating key characteristics of effective teaching in ECE. Specifically, the findings support the construct validity of the five measurement dimensions for most teacher-level effectiveness factors. In line with previous studies (e.g., Kyriakides & Creemers, 2008, 2009), the results emphasize the importance of measuring both quantitative and qualitative aspects of teacher factors, challenging earlier research that focused primarily on frequency as the only measurement dimension. The added value of employing all five dimensions—frequency, quality, focus, stage, and differentiation—to measure teacher factors is underscored, as these dimensions collectively explain greater variation in student achievement gains across outcomes. Notably, some factors did not demonstrate a statistically significant relationship with student achievement when assessed solely by their frequency dimension but showed significant effects when other dimensions were considered. For instance, although the frequency dimension of modeling and application was not linked to mathematics achievement, its quality dimension had a statistically significant impact on student achievement in mathematics. This underscores the importance of examining not only the quantity of effective teaching practices but also their qualitative attributes. It suggests that relying exclusively on frequency measures could lead to erroneous conclusions about a factor’s impact and result in underestimating the explanatory power of teacher factors.

Future research that supports and expands upon these findings may provide more precise directions for linking effectiveness research with educational practice and school improvement efforts. More specifically, at the policy level, future studies could offer clearer guidance on how to effectively bridge educational effectiveness research with classroom practice and broader school improvement initiatives. Although the Greek educational system is highly centralized, there is currently no national policy—across ECE, primary, or secondary education—specifically addressing characteristics of effective teaching that Greek teachers are expected to promote. In this context, the findings of this study have the potential to inform national policy on teaching quality in ECE. Studies such as the one reported in this paper may also support policymaking efforts in this direction, particularly if the generalizability of the current results is explored further in other subject areas, such as language, beyond the mathematics focus of this study. Given that the teacher-level factors examined are considered to be generic, replication studies in different subjects and across educational levels—including primary and secondary education—are essential. Such efforts would contribute to a more comprehensive understanding of the quality of teaching across the Greek education system. In practice, the current study could contribute to enhancing teachers’ skills, enabling them to become more effective in supporting and promoting students’ learning outcomes. In addition, from the perspective of teacher professional development (TPD), such research has the potential to significantly inform the design of targeted TPD programs that are grounded in empirical evidence and oriented toward sustainable practice improvement. In particular, teachers may be encouraged not only to consider the frequency with which they employ various teaching practices (e.g., structuring, modeling, application) but also to reflect critically on the quality, stage, focus, and differentiation dimensions associated with these practices. TPD programs in the field of ECE could benefit from integrating these dimensions, shifting the emphasis from merely increasing the use of “effective” practices to cultivating teachers’ pedagogical judgment about how and when to implement them. For instance, educators may be guided to not only increase the number of structuring and orientation tasks but also to deploy them strategically across different phases of a lesson or over a sequence of lessons. Such a shift underscores the pedagogical relevance of the stage dimension, which may contribute not only to explaining variations in student achievement but also to informing individualized action plans for professional growth. Moreover, should future studies confirm the critical role of differentiation, there would be further impetus for TPD programs to prepare teachers to meet the diverse learning needs of their students more effectively. In the context of ECE, differentiation is especially pertinent, as this developmental stage often necessitates early intervention and individualized support to address emerging learning profiles (Berber et al., 2024; Eikeland & Ohna, 2022; Kyriakides & Creemers, 2009). Therefore, future research on the generalizability of these findings could not only strengthen the validity of the DMEE framework but also provide actionable insights for teachers and educational stakeholders, fostering more targeted, responsive, and impactful teaching practices within early childhood settings.

7. Research Limitations and Suggestions for Further Research

The present study aimed to address a notable gap in the literature; however, several limitations should be acknowledged. First, the research was conducted exclusively in Greece with data from students aged 4 to 6 years, which limits the generalizability of the findings. Future studies should seek to replicate these results with larger samples and across different age groups, both within Greece and internationally. Additionally, this study focused primarily on the influence of teacher factors on cognitive outcomes, specifically mathematics achievement. Expanding future research to explore the effects of teacher factors on a broader range of cognitive and affective outcomes—such as socioemotional and motor skills—would provide a more holistic perspective. Moreover, the study examined the short-term effects of teacher factors using data collected at two points within a single academic year, employing an exploratory design that limited the ability to infer causal relationships. Employing longitudinal designs with multiple measurement points over several years in future research would better capture both short- and long-term effects of teacher factors. Such approaches would offer deeper insights into the dynamic relationship between teacher practices and diverse student populations. Lastly, although the current study demonstrated the importance of incorporating all five dimensions to explain differences in student achievement, only approximately 65% of the total variance was accounted for. This may be attributed to the fact that only three student-level factors were considered (see Section 5), as collecting background data is particularly challenging in ECE due to the young age of the students. However, by collecting data on student background factors, including socioeconomic status (SES), ethnicity, home learning environment, and opportunities to learn, future research may investigate the impact of teacher factors on promoting not only quality but also equity in education (Kyriakides et al., 2018a). This would allow for the examination of potential differential effects of teacher-level factors based on students’ backgrounds and contribute to a deeper understanding of individual differences. Ultimately, such an approach could help promote improved learning outcomes for all students.