Using Game-Based Learning for Engaging with Determinants in Mathematics Education at the University Level

Abstract

Practising the calculation of determinants is important in linear algebra. A pioneering study involving 580 first-year university students evaluated the impact of game-based learning in higher mathematics education. The participants formed two groups: an experimental group of 279 students and a control group of 301. The experimental group students played the non-digital educational card game DETerminator, designed to help students learn and practise calculating determinants in small square matrices. In contrast, the control group received no intervention, allowing for a clear outcome comparison. Students in the experimental group worked in smaller teams during didactic gameplay sessions that involved solving matrix-determinant problems in a competitive and collaborative classroom setting, enhancing their understanding through interaction and teamwork. The objective of this paper is to provide a detailed presentation of the DETerminator game and showcase its integration as an effective teaching tool for practising essential concepts and theorems related to determinants. Moreover, a quasi-experiment was conducted to explore how incorporating game-based learning can lead to successful and enjoyable mathematical education experiences for students. We used a quantitative approach to assess the effectiveness of the card game on academic achievement. At first, a pre- and post-test design was employed with the experimental group of 279 participants to evaluate the short-term effects of game-based learning. The Wilcoxon test was utilised for hypothesis testing, revealing a large effect size of 0.63. Moreover, the results from related midterm exam problems were statistically analysed to obtain the medium-term impact. The outcomes were compared using the Mann–Whitney U-test. The results demonstrated that the experimental group statistically outperformed the control group, but achieving a small effect size of 0.16, with a mean score of 3.14 out of 7 on the designated midterm exam tasks, compared to the control group’s mean score of 2.5. The small effect size suggests that, although the intervention had a positive effect, it is worth considering what other options there are for increasing the medium-term effect. A Likert-scale questionnaire was used to evaluate students’ attitudes towards the game. Our findings show the importance of incorporating game-based learning strategies in mathematics education at the university level, especially for enhancing students’ proficiency in key topics such as the determinant of a matrix.

1. Introduction

The integration of new methods for learning mathematics in higher education is of paramount importance. Innovative teaching techniques can significantly contribute to a deeper understanding, especially of complex mathematical concepts and relationships (Debrenti, 2025). Game-based learning (GBL) is one of the active learning methodologies still in use today, and it has come a long way from simple card games (CGs) and simulations to modern digital platforms and technologies. Definitions of GBL mostly emphasise that it is a type of gameplay with defined learning outcomes (Plass et al., 2015), and GBL aims to use the fun nature of games for learning purposes (Connolly et al., 2012; Mikrouli et al., 2024). According to the current understanding of the game-based learning strategy, it exploits the experiential and motivational potential of games in the learning process. Researchers emphasise that games have a special place in learning—including in higher education—because of their ability to enhance learners’ motivation, evoke positive emotions, and stimulate deep cognitive processing (Vlachopoulos & Makri, 2017). This process involves selecting relevant information, organising it into a coherent structure and integrating it with prior knowledge. Moreover, the researchers identify three learning outcomes when integrating games into the learning process: cognitive, behavioural, and affective (Vlachopoulos & Makri, 2017). Stenros (2017) points out that game-based learning is not simply the application of playful elements in the learning environment but an approach in which the specific rules, goals and dynamics of the game encourage learners to participate and learn. This may include elements of serious games and gamification, which aim to make the learning process more enjoyable and engaging (Schrader, 2022). This approach of GBL thus focuses on the learning experience and emphasises the engaging and enjoyable nature of game-based activities to promote effective learning.

In this paper, we present a game-based learning experiment implemented in a real educational environment with 580 first-year university students. A sad trend in recent years is the high drop-out rate of students, which is most pronounced in the first two semesters. The introduction of GBL has open aim of reducing drop-outs and improving learning outcomes at both universities that participated in the implementation of this research. To implement GBL, a game with playful elements on the topic of determinants was needed to support the learning process. Such a game was not previously available. The non-digital card game used in the experiment is based on the well-known UNO^® game; this was adapted and modified to create a new game: the DETerminator card game. To ensure the replicability of the experiment, we describe the game in detail, including the didactic and game design guidelines that guided the creation of DETerminator.

2. Literature Review

2.1. A Brief History of Determinant

A determinant is a scalar associated with a square matrix. The concept of the determinant began to take shape in the 17th and 18th centuries and reached its modern form in the 19th century, thanks to the combined efforts of several mathematicians. A famous Japanese mathematician, Seki Kowa (also known as Seki Takakazu), was the first to propose the idea of the $2\times 2$ determinant in 1683 (Majima, 2013). About the same time, somewhere between 1678 and 1713, Gottfried Wilhelm Leibniz used the concept of determinants in solving systems of linear equations. He recognised that a certain property of the coefficient matrix of linear equations, which we now call the determinant, was essential for determining solvability (Knobloch, 2013). Both Seki Kowa and Leibniz not only discovered the idea of the determinant as a unique scalar, but they also understood many elementary properties of determinants. These properties included how to expand a determinant using any row or column, known today as the Laplace expansion, and how to determine which terms in the expansion are positive and which are negative. Therefore, the concept of the determinant appeared in Japan and Germany at almost exactly the same time.

In the 18th and 19th centuries, the theory of determinants gained many applications and became an important branch of mathematical research. Gabriel Cramer is known for Cramer’s Rule, which uses determinants to solve systems of linear equations. He published this result in 1750 (Hedman, 1999). Étienne Bézout significantly contributed to the theory of determinants, connecting to polynomials and matrix theory. Carl Friedrich Gauss’s work in linear algebra, with the method of Gaussian elimination, also advanced the development of the theory of determinants, even though he did not use the term determinant himself. Augustin-Louis Cauchy, who published his work in 1812, was the first to use the term determinant and made significant contributions to formalising the theory of determinants (Muir, 2018). Arthur Cayley’s work greatly influenced the development of determinants and matrix theory. He is known for the Cayley-Hamilton theorem, which connects determinants and matrices. Cayley introduced a pair of vertical lines to denote the determinant (the square matrix is between the vertical lines) (Burton, 2011).

2.2. The Importance of Determinant

The concept of the determinant is central in linear algebra and its various applications. One of its primary uses is in determining whether a matrix is invertible. Determinants also play an important role in solving systems of linear equations. Determinants help us understand the behaviour of linear transformations, including scaling, rotating, and shearing in multidimensional spaces. In geometry, determinants are used, for example, to compute the areas, volumes, and hypervolumes of various geometric shapes. They can describe how a transformation alters the scale of an object (Lay et al., 2016). In multivariable calculus, the Jacobian determinant is vital for changing variables in multiple integrals, ensuring accurate transformations of coordinate systems (Thomas et al., 2005). Determinants are also important in eigenvalue problems, because they help to determine the characteristic polynomial of a matrix (Lay et al., 2016). Eigenvalues are crucial in many applications across physics and engineering. Furthermore, the determinant is involved in differential equations, providing insights into the behaviour of dynamic systems. It is a powerful tool in stability analysis, helping to ascertain the nature of equilibrium points. The Wronskian determinant is used in solving higher-order differential equations because it provides a way to check the linear independence of the solutions, which is essential for writing down the general solution (Blanchard et al., 2012). In the field of control theory, determinants are utilised to design and analyse control systems. They are essential in computer graphics for operations like changing the perspective and modelling complex transformations. Moreover, determinants are used in economics for input-output analysis, which examines the interactions between different sectors of the economy (Miller & Blair, 2022). In statistics, a variance–covariance matrix is a square matrix that contains the variances and covariances associated with several variables. In multivariate statistical analyses, such as MANOVA (Multivariate Analysis of Variance) and discriminant analysis, the determinant of the variance–covariance matrix is often used. It plays a key role in the computation of test statistics and in the assessment of the equality of variance–covariance matrices across different groups (Barker, 1984).

The list above is far from exhaustive. The concept of determinants is used in various fields of science, showing that it plays a fundamental role, and not limited to mathematical theory and applications. Its versatility and utility across disciplines underscore the profound significance of this mathematical concept.

2.3. Benefits of UNO^® Card Games

The card game UNO^®, which celebrated 50 years in 2021 and is a registered trademark of Mattel Corporation, is a great game with remarkable didactical potential (Meyrath et al., 2024). UNO^® is a non-cooperative, multiplayer strategy game where players aim to be the first to discard all of their cards (Benson, 2022). The popularity of UCGs (UNO^® Card Games) can be attributed to several factors. The game’s rules are simple and easy to learn. Players can quickly start and enjoy the game. The moderate duration of each round makes it perfect for quick and fun sessions. The game offers exciting gameplay with various action cards that can reverse the direction of play, skip turns, or force players to draw extra cards, ensuring a constantly engaging and dynamic experience. UNO^® has a compact size, making it highly portable, so it can be played almost anywhere, whether at home, during travel, or at social gatherings. Numerous variations of UNO^® exist, featuring different rules, card quantities, and player limits, each found in various countries around the globe (Ramadhan et al., 2015).

UCGs are social games. These games unite people and provide a fun and shared experience. Despite its simplicity, the game involves strategic elements because players must decide the best times to play their cards, keeping the game interesting and competitive. The game is suitable for all age groups, making it a favourite among families, as both young and older players can enjoy it. The combination of competition and luck adds to the excitement because success depends not only on strategy but also on the draw of the cards, so it creates a balanced and enjoyable gameplay. The variety of card combinations and player strategies ensures that each game is unique, providing endless entertainment. Moreover, UCG is an inclusive game. Players can play effectively at different levels the game. Since luck plays a big role, even inexperienced players have a chance to win. Moreover, alliances between players do not play a significant role. The game’s outcome is unknown in advance, as players who almost win may not win. The inclusive nature of UCG is enhanced by its adaptability to specific needs. People with speech and hearing impairments can easily play it. Some colour-blind people can also play, as the cards use very distinct colours. In addition, there are special UNO^® card packs with symbols to distinguish colours or with a tactile Braille writing system (Meyrath et al., 2024).

The UCG can be used for various didactic purposes. For example, Dunac and Demir (2013) reported that they involved high school science students in their experiment, using a modified UCG created by a teacher and a student to help their conceptual understanding of different energy transformations. The results show that the UCG activity helped the students better understand the physical phenomenon of energy transformations. The students experienced conceptual gains over traditional teaching and learning practices. Mahartika et al. (2020) presented a modification of UCG, the Chemuno card game, designed to help students memorise the periodic table of chemical elements. The game is based on the principle of the chemical triangle, which combines macroscopic, submicroscopic, and symbolic representations. The purpose of the game is to help students more easily understand and remember the properties and locations of chemical elements in the periodic table. Researchers have found that the game effectively improves the students’ knowledge and motivation to learn chemistry. Another chemistry UCG is the Salt-UNO card game created by Redzuan and Tien (2023). The authors conclude that the Salt-UNO card game is suitable for teaching the topic of salt in Grade 4 chemistry in Malaysia.

There are many options for using UCGs to support language teaching. Lukas et al. (2020) created a UCG game variant (U-NO-ME) for English vocabulary development. Their research aimed to explore the potential of the U-NO-ME card game as an educational game to enhance vocabulary acquisition in first-grade students. The results showed that the students’ perceptions of the U-NO-ME card game were positive because it improved students’ memory retention and stimulated their motivation to learn. Muslimin and Harintama (2022) used UCG to teach English (as a foreign language) and develop correct sentence formation. They reported that the modified UNO English card game can overcome errors and difficulties in descriptive writing and motivate learners well. Nurhalimah and Ahmad (2023) examined the effect of using UCG in learning Arabic. The game aimed to improve students’ understanding of Arabic texts, and researchers found that using UCG had a positive impact on student comprehension skills, leading to improved scores in reading comprehension tests. Supper (2023) showed a modified version of the UNO^® game, which was used to teach anthropology students at the university level, aiming to provide participants with their first ethnographic research project experience.

Of course, the classic UNO^® card game is a great maths learning tool for all ages, from preschoolers starting with number recognition to university students working on harder concepts. Demaine et al. (2014) have investigated original UCGs from the viewpoint of algorithmic combinatorial game theory and analysed the computational complexity of UCG variants. The researchers have proved that even a single-player version of UNO^® is NP-complete. The Maths UNO adaptations are not official, commercially available games, but teachers, educators, or parents often create ideas to add mathematical content to the classic UNO^® game. These adaptations are often adapted to the learning environment and the needs of the learners and implemented with self-made cards. For example, on the Teachers Pay Teachers (TPT) website, many teachers share their own Maths UNO games on various topics, such as multiplication, division, fractions, etc., for preschool and primary school children. For example, Chong et al. (2022) experimentally demonstrated that the non-digital Intego card game, a variant of the UCG, can effectively develop numeracy skills in primary school children of year 8 in integer operations. Their study results showed that the game effectively increased students’ numeracy skills and that participants had positive attitudes towards it. UCGs can also be used to teach the basics of set theory, and using UCGs to learn probability can help students understand the theory and application of probability through concrete, practical examples (Meyrath et al., 2024). A systematic literature review identified 41 records between January 1980 and June 2025 that the original UNO^® game or UNO-type games have been used as learning media in mathematics education (Szilágyi et al., 2025).

There is a clear trend that different variants of UNO^® have been effective GBL tools in recent years. The good practices listed above inspired the creation of the DETerminator card game, which is a UCG, a Maths UNO game for university practice.

3. The DETerminator Card Game for Determining Determinants

The DETerminator UCG was created during a collaboration between two Hungarian universities. Preparatory work started in the autumn of 2023 at the Budapest University of Economics and Business. The game took four months to create and fine-tune at the University of Miskolc. The first live test with a large number of students took place in the spring semester of the academic year 2023/2024 at the Budapest University of Economics and Business with 279 students and the participation of teachers from both universities.

3.1. Description of the DETerminator Card Game

The basic idea of the educational game DETerminator was inspired by an official and popular UNO^® variant, the UNO ALL WILD!^® card game. In many aspects, we did not alter the original game; for example, the cards were made with the same four base colours as in UNO^®. However, a significant difference is that the cards feature determinants instead of integers. We retained certain types of action cards, but we also created new ones. In the DETerminator deck, all action cards are four-coloured. We also modified the original game’s rules to better meet the educational objectives of the DETerminator game. The complete DETerminator card deck consists of 104 cards. On 80 coloured base cards, there are square matrices whose determinants can be determined with some routine. In addition to these, there are 24 action cards in the deck. The base cards have yellow, green, blue, and red backgrounds. Each base card features a square matrix placed in a white ellipse tilted at a 45-degree angle, with 10 matrices per colour. Each base card comes in two copies. The determinants on the cards can be calculated in the head using the expansion theorem and the rules regarding the operational properties of the determinants. For example, blue cards are shown in Figure 1.

We aimed to ensure that the tasks in the DETerminator game are varied but not overly difficult. By setting the optimal level of challenge, the game provides an appropriate difficulty level, which allows the flow experience to develop. Tasks that are too easy can make the game boring, while those that are too difficult can make it frustrating. The difficulty level of the tasks on the cards is not uniform. Easier tasks can quickly provide a sense of achievement and help with engagement, while more complex tasks, which require synthesising several theoretical results, aim to maintain interest.

3.2. Didactic and Game Design Elements

We have considered that the game’s name can significantly impact its reception and success. An attractive and eye-catching name helps to capture the attention of potential players. Liberman et al. (2004) have found that the game’s name influences how players think and act; it serves as a framework that influences both game interpretation and decision-making. A well-chosen name reflects the purpose and theme of the game, improves player motivation, enhances the gaming experience, and fits generational needs. The name DETerminator meets these requirements. An important aspect of the development was to keep the fun and competitive nature of classic UNO so that learning is fun and enjoyable for players.

In designing the card game, we followed the guidelines of Kalmpourtzis (2019), 54 design principles in 13 classes of Laine and Lindberg (2020), and the five principles of educationally rich mathematical games of Russo et al. (2023). The DETerminator game is aimed at first-year undergraduate students who are learning about the concept and properties of the determinant during their studies. One of the main criteria of game-based education is goal orientation; didactic games used in GBL must have clear educational goals that align with curricular requirements. It is important that games are not only fun but also aim to develop specific mathematical skills or concepts. The didactic aim of the DETerminator game is to practise the rules for determining the determinant of a square matrix and to reinforce the skills of calculation in the head. The game was designed considering the age, mathematical knowledge, and interests of the target group. The topic of the game is directly related to the curriculum being taught; accordingly, the mathematical content of the game is relevant and in line with curricular expectations. The challenge in the DETerminator game is the same as the UNO^® challenge: be the first to get rid of all the cards. An important didactic feature of Maths UNO games is content coherence, i.e., the cards and the game mechanics should be consistent with the learning objectives. Given that the DETerminator focuses on calculating the determinant, each card contains a related mathematical operation (sometimes many operations) that players must solve to progress.

The DETerminator didactic game enables different learning styles. The game involves students interacting with each other and teachers. The game can be played with competitive and cooperative elements, ensuring that individual performance and group work are equally valued. The learning phase takes place when the cards containing the determinants are laid down, because when a card is laid down, the player has to say out loud what the value of the determinant on the played card is. Control is the teacher, who is present as the player and checks the correctness of the value. Combining visual and auditory cues helps players learn and implement strategies effectively. DETerminator is a competitive game, but cooperation is allowed and a good idea during the first few games for didactic aims. Teacher involvement provides immediate feedback, which is a crucial element for a successful learning process. The game’s adaptability to different learning styles creates a motivating and fun environment that fosters student engagement and interest in the educational content. The criteria for follow-up and evaluation are also implemented. During the game, participants receive immediate and consistent feedback on correct or incorrect answers provided by the teacher participating in the game. After the game, the acquired and practised skills are tested and evaluated, and feedback is given to the players to help track progress. During the development, we balanced skill and luck: while incorporating elements of chance can make a game more exciting, the outcome should primarily depend on the player’s maths skills and knowledge. This balance ensures that the game remains fair and educational.

A didactic game’s social and emotional aspects are as important as mathematical tasks and relationships. Effective maths games encourage players to cooperate, share strategies, and discuss problem-solving methods. This not only deepens understanding but also promotes the development of social skills and teamwork, making the learning experience more meaningful and enjoyable. The engagement and motivation factors of the players help the learning process. Enticing and captivating games help maintain learners’ interest and motivate students to persist in problem-solving through a common game, a sense of accomplishment, or progress. Encouraging risk-taking allows students to try different strategies without fear of negative consequences, fostering knowledge. Using different sets of action cards and the opportunity to change determinants in the deck, we provided ways to change the parameters of the game so that it could evolve and remain challenging.

3.3. Cards in the Deck

The DETerminator deck, designed for engaging gameplay, consists of 104 cards. These cards are divided into different suits and types, with each suit featuring number-value cards in four colours: red, blue, green, and yellow. Each colour has number cards from 0 to 9, and there are two of each in the deck.

We implemented a Java application that generates and manages card decks with integrated LaTeX functionality. The application involves several components and features. It allows users to create new cards and decks that display mathematical formulas. The export and printing functions allow users to save the LaTeX-rendered cards in pdf or editable txt format. In DETerminator, players can test their knowledge and improve their counting skills by identifying 44 different determinants on 40 cards. The card deck includes the determinants of 25 2 × 2 matrices and 19 3 × 3 matrices. Some cards contain more than one determinant, allowing students to solve different computational problems and perform operations between determinants.

Table 1. Determinants in the DETerminator deck.

Value	Red Cards	Blue Cards	Yellow Cards	Green Cards
0	$\left|\begin{array}{cc}4& 2\\ 14& 7\end{array}\right|$	$\left|\begin{array}{ccc}1& 2& 3\\ 7& 4& 5\\ 2& 4& 6\end{array}\right|$	$\left|\begin{array}{cc}2& 4\\ 5& 10\end{array}\right|$	$\left|\begin{array}{cc}0& e\\ 0& \pi \end{array}\right|$
1	$\left|\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right|$	$\left|\begin{array}{cc}3& -8\\ -4& 11\end{array}\right|$	$\left|\begin{array}{cc}3& 2\\ 7& 5\end{array}\right|$	$\left|\begin{array}{ccc}1& 0& 0\\ 3& 2& 1\\ 4& 1& 1\end{array}\right|$
2	$\left|\begin{array}{ccc}9& 4& 1\\ 3& 1& 0\\ 4& 2& 0\end{array}\right|$	$\left|\begin{array}{cc}-\pi & -1\\ 3& {\displaystyle \frac{1}{\pi }}\end{array}\right|$	$\left|\begin{array}{cc}10& 2\\ 14& 3\end{array}\right|$	$\left|\begin{array}{cc}\sqrt{2}& 0\\ 0& \sqrt{2}\end{array}\right|$
3	$\left|\begin{array}{ccc}1& 0& 0\\ \pi & 3& 0\\ e& \sqrt{3}& 1\end{array}\right|$	$\left|\begin{array}{ccc}3& 0& 0\\ 0& 2& 7\\ 0& 1& 4\end{array}\right|$	$\left|\begin{array}{ccc}0& -1& 0\\ 3& 5& 2\\ 6& 2& 5\end{array}\right|$	$\left|\begin{array}{ccc}0& 0& 1\\ 2& 1& 5\\ 1& 2& -1\end{array}\right|$
4	$\left|\begin{array}{ccc}7& 0& 2\\ -1& 0& 4\\ 5& 0& 8\end{array}\right|+\left|\begin{array}{ccc}-1& 3& 4\\ 0& 2& 5\\ 0& 0& -2\end{array}\right|$	${\left(\left|\begin{array}{cc}-6& 2\\ 5& -2\end{array}\right|\right)}^2$	$\left|\begin{array}{ccc}0& 4& 4\\ -1& 5& -2\\ 0& 4& 5\end{array}\right|$	$\left|\begin{array}{cc}{\displaystyle \frac{1}{3}}& -1\\ 2& 6\end{array}\right|$
5	$3·\left|\begin{array}{cc}2& 2\\ 6& 7\end{array}\right|-\left|\begin{array}{cc}7& 5\\ 4& 3\end{array}\right|$	$\left|\begin{array}{ccc}0& 2& 1\\ 5& 2& 1\\ 0& 3& 1\end{array}\right|$	$\left|\begin{array}{cc}\sqrt{25}& 0\\ 0& 1\end{array}\right|$	$\left|\begin{array}{cc}1& 0\\ 0& 1\end{array}\right|+4·\left|\begin{array}{ccc}-1& 0& 0\\ 0& 1& 0\\ 0& 0& -1\end{array}\right|$
6	$\left|\begin{array}{ccc}1& 9& 0\\ 0& 1& 0\\ 8& 4& 6\end{array}\right|$	$\left|\begin{array}{cc}-\sqrt{2}& 5\\ -2& \sqrt{8}\end{array}\right|$	$\left|\begin{array}{cc}{log}_2{2}^6& 10\\ 0& 1\end{array}\right|$	$\sqrt{6}·\left|\begin{array}{cc}\sqrt{2}& 0\\ 0& \sqrt{3}\end{array}\right|$
7	$\left|\begin{array}{cc}-2& 3\\ 3& -8\end{array}\right|$	$\left|\begin{array}{ccc}1& 0& 0\\ {\left({\displaystyle \frac{1}{2}}\right)}^3& 7& 0\\ 5& -6& 1\end{array}\right|$	$\left|\begin{array}{cc}-7& \sqrt{49}\\ -7& 6\end{array}\right|$	$\left|\begin{array}{ccc}3& 2& 1\\ 0& 1& 0\\ 5& -1& 4\end{array}\right|$
8	$\left|\begin{array}{ccc}6& -5& 2\\ 16& 7& 4\\ 0& 1& 0\end{array}\right|$	$\left|\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& 2\end{array}\right|$	$\left|\begin{array}{cc}-2& 0\\ 0& -4\end{array}\right|$	$\left|\begin{array}{cc}6& 2\\ 11& 5\end{array}\right|$
9	$\left|\begin{array}{cc}ln1& -3\\ 3& 7\end{array}\right|$	$\left|\begin{array}{cc}2& 3\\ 3& 6\end{array}\right|·\left|\begin{array}{cc}3& 4\\ 3& 5\end{array}\right|$	$\left|\begin{array}{cc}0& 3\\ -3& 0\end{array}\right|$	$\left|\begin{array}{ccc}1& 0& 0\\ 2& 3& 0\\ -1& 4& 3\end{array}\right|$

shows the determinants on the cards.

The calculation and properties of the determinant of the matrix are discussed in several sources, for example, in Strang (2023). Properties of determinants are essential for determining the value of a determinant with minimal calculations. These properties involve the elements of the matrix as well as row and column operations, making it easier to compute the determinant’s value efficiently.

Table 2. Properties of determinants and their frequency in the DETerminator deck.

Property	Description of the Property	Cards	Frequency
Cofactor Expansion	The determinant can be expanded using any row or column. Choosing a row or column with more zeros can simplify the calculations.	R2, R6, R8, B3, B5, Y3, Y4, G1, G3, G7, G9	11
Triangular Property	If the elements above or below the main diagonal are equal to zero, then the value of the determinant is equal to the product of the elements of the diagonal of the matrix.	R1, R3, R4, B7, B8, Y6, Y8, G5, G6, G9	10
Zero Rows or Columns	If a matrix has a row or column of zeros, its determinant is zero. This property makes it easy to quickly determine whether the matrix is singular.	R4, G0	2
Linearly Dependent Rows/Columns	If a determinant contains two or more linearly dependent rows or columns, then the value of the determinant is zero.	B1, G0	2
Row or Column Multiplication	If you multiply a row (or column) by a scalar, the determinant is multiplied by that scalar as well.	R5, G5, G6	3
Determinant of Products	The determinant of the product of two matrices is equal to the product of their determinants.	B4, B9	2
Row and Column Swapping	Swapping two rows (or columns) of a matrix multiplies the determinant by −1.	Y3, Y4, G7	3

displays the features that can be practised with the DETerminator deck, along with the corresponding cards associated with each feature. Cards can be identified using Table 1; for instance, R3 refers to a card from the red series with a determinant value of 3. In creating the deck of cards, we aimed to incorporate a range of tasks that were not overly challenging. Since the game requires players to calculate the value of the determinant mentally, we employed determinants’ properties that facilitate quick mental calculations.

The game becomes even more exciting and varied with the inclusion of special action cards, which encourage social interaction and strategic thinking. There are 24 action cards in the deck with six different action card types, as seen in Figure 2. We kept three of the original UNO^® action cards:

• Draw Two: The next player must draw two cards and miss their turn.
• Reverse: Changes the direction of play.
• Skip: The next player is skipped.

We develop for DETerminator three new action card types which add an exciting twist to the traditional UNO^® rules:

• Draw Three: The next player must draw three cards and miss their turn.
• Get Rid of a Card: If this card is played, the player must give one of the cards in his hand to a fellow player.
• Four-Leaf Clover: This is a multifunctional card with the following three options:
  • Choose a Colour: Similar to a Wild card in the original UNO deck, allowing the player to select the next colour to be played.
  • Start a Round-Robin: Each player passes their hand to the next player, based on the current direction of play, adding an element of surprise and strategy.
  • Replace the Entire Cards in One Player’s Hand: This could be a powerful move, letting a player swap their hand with the other player’s hand, which can extremely change the course of the game.

Action cards are four-coloured, which means that once they are played, the play can be continued with any colour card. The only exception is if the four-leaf clover is played by a player and the colour request is chosen from the multi-function card options. Then, the game continues according to the requested suit. The four-leaf clover is the only card type in the deck that can be used to request a new colour.

3.4. Game Mechanics

DETerminator is a fun and fast-paced card game that provides entertainment and significant educational potential for players. The game is specifically designed for groups of 4–10 players. With more players, there are more opportunities for tactics, as there are more aspects to consider: the number of cards in other players’ hands, the cards they have dealt, and the combinations of cards in their own hands. With more players, there is more laughter, humour, and fun. Ramadhan et al. (2015) confirmed that UNO^® is best to play with four, five, or six players. At this number, each player has the opportunity to play often enough to make the game more exciting than if there were fewer than four or more than six players. We played with 8–9 players, because the number of students was very high. The playing time for a party was usually 20–25 min. An average of three games can be played in sixty minutes.

The game starts with a dealer who deals seven cards to each player from a deck of 104 cards. The remaining cards form the draw pile and are placed face down in the centre of the table. The first card of the discard pile is chosen and placed face up near the draw pile. The game begins with a selected starting player. He/she discards one of their cards first. Each subsequent player must match the top card of the discard pile either by colour or by determinant value with the card they discard. They must announce the determinant value aloud when they discard it. If a player has multiple cards of the exact same colour and value (e.g., two red 7s), they can discard them all at once. Players can also use special action cards that provide different rules and opportunities during the game. The game goes around, and players take turns placing their cards in the discard pile. If a player has only one card left, they must say “DET” or draw two penalty cards. The first player to get rid of all cards wins. Figure 3 illustrates the flow of a player’s turn in the DETerminator card game.

In play, players sometimes can stop the game by throwing down a card that matches both the colour and number on the top card in the discard deck, even if it is not their turn. This form of play, often called the “challenging” or “interrupting” rule, adds a lively and fast-paced feeling to the game. It is a little hard to master for starters, but players who have some experience with the game find that it makes things more thrilling and less predictable.

4. Research Objectives and Research Questions

The primary objective of this study is the evaluation of the effectiveness of the DETerminator card game as a tool for teaching the calculation of determinants to first-year university students. By employing a quasi-experimental research design alongside exploratory research and a mix of quantitative methods, the research aims to assess the impact of GBL on students’ learning process, engagement, and motivation in the context of learning mathematical concepts related to determinants and their properties. The research collected quantitative feedback from students regarding their experiences and perceptions of using the DETerminator card game, providing valuable information on the effectiveness of the learning process. The research aims to contribute to the existing knowledge on GBL by demonstrating the effectiveness of this innovative learning tool in higher mathematics education.

We sought to answer the following research questions:

• RQ1: How effective is the DETerminator card game in teaching first-year university students to calculate determinants immediately after use and in the medium term?
• RQ2: What is the extent of improvement in first-year university students’ performance in calculating determinants when using the DETerminator card game compared to traditional teaching methods?
• RQ3: How do first-year university students evaluate their learning experience after the use of the DETerminator card game?

5. Research Methodology

5.1. General Background

This experiment was carried out at a Hungarian university in the capital in the spring semester of 2024. The 580 students in this study attended lectures by the same instructor concurrently at the Budapest University of Economics and Business (BUEB).

5.2. Teaching and Learning Methods in the Experiment

Figure 4 shows the pyramidal model of our experiment. The pyramid approach to education is an all-encompassing framework designed to create and enhance effective learning environments. The learning pyramid model was developed by Dale (1946). He studied different levels and methods of learning, and the pyramid model helped to illustrate how different teaching methods affect the effectiveness of learning. The base of the pyramid represents the least effective methods, while the top represents the best methods, such as teaching others or hands-on experience. Research shows that reading manuals or instructions and listening to lectures are the least effective ways to learn new skills. In contrast, the most effective ways of learning include doing something concrete or simulating a real task (Lee et al., 2023; Wróblewska & Okraszewska, 2020). The pyramidal model in Figure 4 is a visual representation that shows the applied teaching methods and their main properties. It is structured with the most passive learning methods at the base and the most active and engaging GBL method at the top.

Four teaching/learning methods were defined for the experiment. The first two are the frontal lecture and practical sessions in traditional university education. Generally, throughout a semester, students were introduced to the concept of determinants and their properties in a 90 min frontal lecture, followed by a 90 min practical session a few days later. This arrangement was applied to both groups (580 students) involved in our experiment for the first and second levels of learning.

Two weeks later, the experimental group (279 students) participated in other activities. In the third level of learning, they participated in an optional 90 min online lesson. One day before the in-person part, we had a lecture on the Microsoft Teams (Microsoft Corporation, Redmond, WA, USA) platform, during which we reviewed concepts, properties, calculation tips, and tricks concerning determinants. Then, we briefly demonstrated the cards of the DETerminator deck to the students.

In the next step, we tested the DETerminator deck with 279 students from BUEB during project week as part of an optional course. We conducted an on-site GBL session, during which participants played the DETerminator card game in small groups facilitated by teachers. This was a three-hour gameplay session, during which approximately 90 students participated simultaneously each hour, supervised by 10 instructors. Each student played for a minimum of 60 min. The DETerminator gameplay session represented the fourth level of learning.

During project week, there is a break in the traditional curriculum at BUEB. During this week, students work independently or in small groups on projects related to their courses at home, and they also have the opportunity to take extra courses at the university. The Let’s Play Mathematics! course was one of these connecting to the economics mathematics course, meaning that students voluntarily signed up to participate in the course, which we created specifically for the purpose of conducting the experiment, with all the necessary official permits in place. The participants of the Let’s Play Mathematics! course formed the experimental group. In this group, the traditional lecturer–student roles were replaced by the role set of more knowledgeable students. The lecturers were present in the collaborative learning space more like peers, their primary task being the internalisation of knowledge through play. Since there is a break in teaching during the project week, we have not had the opportunity to organise traditional task-solving sessions for the members of the control group. We conducted the experiment with this limitation, given that we measured the short-term effects of GBL only in the experimental group.

5.3. Research Design and Tools

In our quantitative research, we used a quasi-experimental design. In the experiment, we implemented several methods to comprehensively investigate the learning processes and effectiveness of the new didactic game, as seen in

Table 3. Events of the research for the members of the experimental group.

Event	Type	Venue	Duration
Frontal theoretical lecture	On-site	Classroom environment	90 min
Frontal practical session	On-site	Classroom environment	90 min
Optional course	Online	Microsoft Teams	90 min
Pre-test	Supervised online	Classroom environment, Microsoft Forms	30 min
DETerminator gameplay session (Let’s Play Mathematics course)	On-site	Classroom environment	60 min
Post-test	Supervised online	Classroom environment, Microsoft Forms	30 min
Questionnaire	Online	Microsoft Forms	15 min
Midterm exam	On-site	Classroom environment	45 min

.

To assess the short-term effects, we utilised a pre-test and post-test design. The first step was writing a pre-test, which allowed us to evaluate the participants’ knowledge and skills regarding the subject matter. These initial data served as a reference point for comparison. All students of the experimental group participated in a technologically assisted assessment process during the in-person session at the same time. They completed a pre-test using Microsoft Forms (Microsoft Corporation, Redmond, WA, USA), a digital platform that allows efficient and accurate data collection. The duration of the pre-test was 30 min. Details of the pre-test tasks can be found in Appendix A.1. The use of technology continued as the students completed the post-test, also in the Microsoft Forms application, ensuring a streamlined and effective assessment process. Details of the post-test tasks can be found in Appendix A.2. The pre- and post-tests used in the experiment were validated during the autumn semester with the participation of 50 students at the BUEB. The validation process is detailed in Appendix A.3.

We also asked the students to complete a feedback survey, also in Forms. Likert scale tests offer a reliable and efficient way to quantitatively analyse subjective data. Likert scales give respondents the opportunity to express their opinions and attitudes in a more nuanced way rather than just a yes/no response. Since the response options are distributed on a scale, it reduces the tendency to give extreme answers and helps to obtain a more balanced picture of respondents’ opinions. During the research, participants’ opinions and attitudes were measured using a 15-question survey, which employed a 5-point Likert scale. Based on the collected data, we conducted descriptive statistics to understand the overall response patterns. We also performed a correlation analysis to identify potential relationships between the questions. Additionally, we assessed the reliability of the scale using Cronbach’s alpha for the entire set of questions. The questions of the questionnaire are presented in Section 6.3.

One week later, after the DETerminator GBL session, students wrote the midterm papers on-site at the university using the traditional paper-based method. The results of the experimental group were compared with those of the control group to assess the effects of the complex treatment involving GBL. The midterm exam tasks can be found in Appendix A.4.

During the experiment, the experimental group received 150 min more treatment, as shown in Figure 4. The first 30 min of the 90 min online lecture were devoted to reviewing the mathematical rules shown in Table 2, while the remaining 60 min were spent explaining the gameplay and rules of the DETerminator game. The primary goal of the online session was to ensure that the participants in the experimental group understand the gameplay and the rules of the game. By organising the online session, we were able to ensure that no additional explanation of the game was necessary after the groups were formed. It is important to emphasise that no additional knowledge was passed on during the online session, and the determinants on the cards were not calculated. We considered it necessary to separate the presentation of the game from the GBL activity itself because the 279 students were divided into three groups to participate in the game session. This saved us a significant amount of time because the participants arrived in the room already knowing the rules of DETerminator. In our opinion, the extra time does not affect the short-term effects of GBL, as this was only measured in the experimental group. However, we should note that the extra time spent on revision may have affected the results of the mid-term measure.

5.4. Participants

Students from the Faculty of Finance and Accounting of the Budapest University of Economics and Business participated in the experiment. In the second semester of the academic year 2023/2024, 1212 students participated in first-year economic mathematics, one of the topics of which is linear algebra. The curriculum deals with matrices, determinants and their applications in economics. 580 students participated in the study. There were 279 participants in the experimental group and 301 in the control group. In our experiment, the experimental and control groups attended the same lecture. During the semester, they were introduced to the same concepts, the same theorems, and the same problems.

The students range in age from 18 to 23, with some taking the economic mathematics course not for the first time.

Table 4. Gender distribution in the total sample.

	Participants
	Experimental Group		Control Group		Total
Gender	N	%	N	%	N	%
Female	205	73.48	149	49.5	354	61.03
Male	74	26.52	152	50.5	226	38.97
Total	279	100.00	301	100.00	580	100.00

illustrates the breakdown of participants by gender for the total sample.

The experimental group has a higher proportion of females (73.48%) than males (26.52%). However, this proportion does not bias the results because it is generally observed that female enrolment is higher in programmes related to business, such as business administration and management, business informatics, economics, or finance and accounting, compared to technical or natural science fields. Women outnumber men in undergraduate enrolment in a majority of OECD countries (Mead, 2023). For the control group, the proportion of women and men is almost equal.

Table 5. Number of participants per group and BA programme.

	Participants
	Experimental Group		Control Group		Total
BA Program	N	%	N	%	N	%
Business Administration and Management (BM)	133	47.67	97	32.23	230	39.66
Finance and Accounting (FA)	88	31.54	124	41.20	212	36.55
Human Resources (HR)	55	19.71	80	26.58	135	23.28
Business Informatics (BI)	3	1.08	0	0.00	3	0.51
Total	279	100.00	301	100.00	580	100.00

displays the distribution of the entire sample across various BA programmes.

In the experiment, students from the Bachelor of Business Administration and Management, Bachelor of Finance and Accounting, Bachelor of Business Informatics, and Human Resources BA programmes participated. Given that the curricula are the same for all four BA programmes, the practical classes are mixed with students from the different undergraduate courses.

In the previous semesters, we had GBL activities. We observed that among the H5P applications edited in Moodle, the most popular among the students was the card game. GBL helped students to understand and master the concepts. The good experiences inspired the creation of the card game DETerminator. To implement the GBL experiment, we ran a practical course, called Let’s Play Mathematics, in which we played and tested the DETerminator card game. During the course, students formed ten small groups. Ten facilitators supervised the play: eight lecturers from the Budapest University of Economics and Business and two from the University of Miskolc. As this was an intensive weekly course, we did not have more opportunities to run additional courses. The course was taken by 279 students who formed the experimental group. Members of the experimental group volunteered for the game-based educational experiment.

Table 6. Gender distribution across BA programmes in the experimental group.

	Experimental Group
	Female		Male		Total
BA Program	N	%	N	%	N	%
Business Administration and Management (BM)	78	27.96	55	19.71	133	47.67
Finance and Accounting (FA)	75	26.88	13	4.66	88	31.54
Human Resources (HR)	52	18.64	3	1.08	55	19.71
Business Informatics (BI)	0	0.00	3	1.08	3	1.08
Total	205	73.48	74	26.52	279	100.00

shows the distribution of the experimental group by BA programmes and gender.

Eight experienced instructors selected ten practice classes, which formed the control group for the experiment. The control group members did not participate in the Let’s Play Mathematics courses but agreed to participate in the pedagogical experiment. The control group consisted of 301 students, as the practice lessons had an average of 29–31 students.

Table 7. Gender distribution across BA programmes in the control group.

	Control Group
	Female		Male		Total
BA Program	N	%	N	%	N	%
Business Administration and Management (BM)	29	9.63	68	22.59	97	32.23
Finance and Accounting (FA)	66	21.93	58	19.27	124	41.2
Human Resources (HR)	54	17.94	26	8.64	80	26.58
Total	149	49.5	152	50.5	301	100.00

shows the distribution of the control group by BA programmes and gender.

5.5. Ethics

Participants were fully informed of the research objectives and procedures at the outset and consented to voluntary participation. To ensure anonymity, participant data were recorded and analysed using codes instead of names. Participation was entirely voluntary, and all planned activities were completed. The study maintained the ethical standards outlined in the BUEB Code of Ethics.

6. Data Analysis and Results

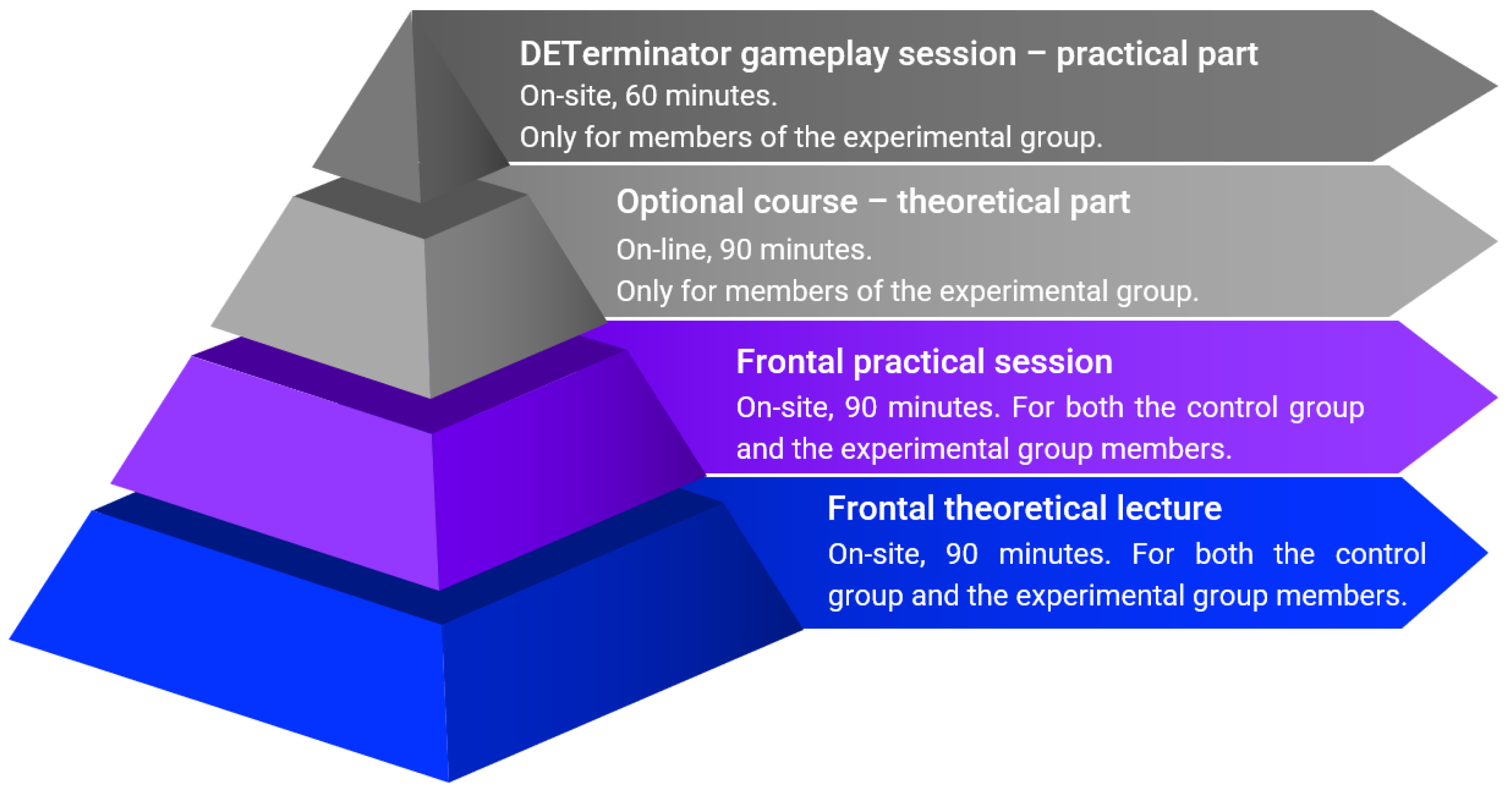
This section presents the data collected during the experiment and the statistical analysis of the data.

6.1. Pre- and Post-Tests

The pre- and post-tests were evaluated using the Microsoft Forms application, which was used to collect the data based on the pre-set correct answers. The resulting data sets were imported separately and then merged into the Microsoft Excel (Microsoft Corporation, Redmond, WA, USA) platform. The statistical calculator DATAtab (DATAtab e.U., Graz, Austria) was used for data analysis. The 279 participants in the experimental group completed pre- and post-tests; descriptive statistics for these are presented in

Table 8. Descriptive statistics for pre-test and post-test.

	Pre-Test	Post-Test
N	279	279
Mean (M)	4.38	5.82
Median	5	6
Mode	6	6
Standard Deviation (SD)	1.78	0.49
Minimum	0	3
Maximum	6	6
Median Absolute Deviation (MAD)	1	0

. Both tests consisted of six questions, each worth one point.

The mean score notably increased from 4.38 to 5.82, indicating that the overall performance of the participants improved considerably after the GBL session. This positive trend is supported by the median, which grows from 5 to 6. The standard deviation decreased from 1.78 to 0.49, demonstrating that the scores became less varied, i.e., the results of the participants were more closely clustered around the mean post-intervention. The minimum score increased from 0 in the pre-test to 3 in the post-test, which is particularly noteworthy, as it highlights that even the lowest-performing individuals showed signs of improvement. The median and the maximum score remained constant at 6, indicating that high achievers maintained their performance level. The reduction in the median absolute deviation from 1 to 0 suggests that the participants became more homogenous in terms of their scores, reflecting an overall increase in proficiency across the board. The descriptive statistical data indicate a clear improvement in performance from the pre-test to the post-test. Based on the data analysis of the pre-test and post-test results, it can be concluded that the DETerminator GBL intervention had a positive and measurable effect on student learning outcomes.

Hypothesis testing was used to determine if there is a statistically significant difference between the results of the pre-test and the post-test. To answer the research question RQ1, the following hypotheses were formulated:

• Null hypothesis:
  The post-test results are equal to or lower than the pre-test results.
• Alternative hypothesis: The post-test results are greater than the pre-test results.

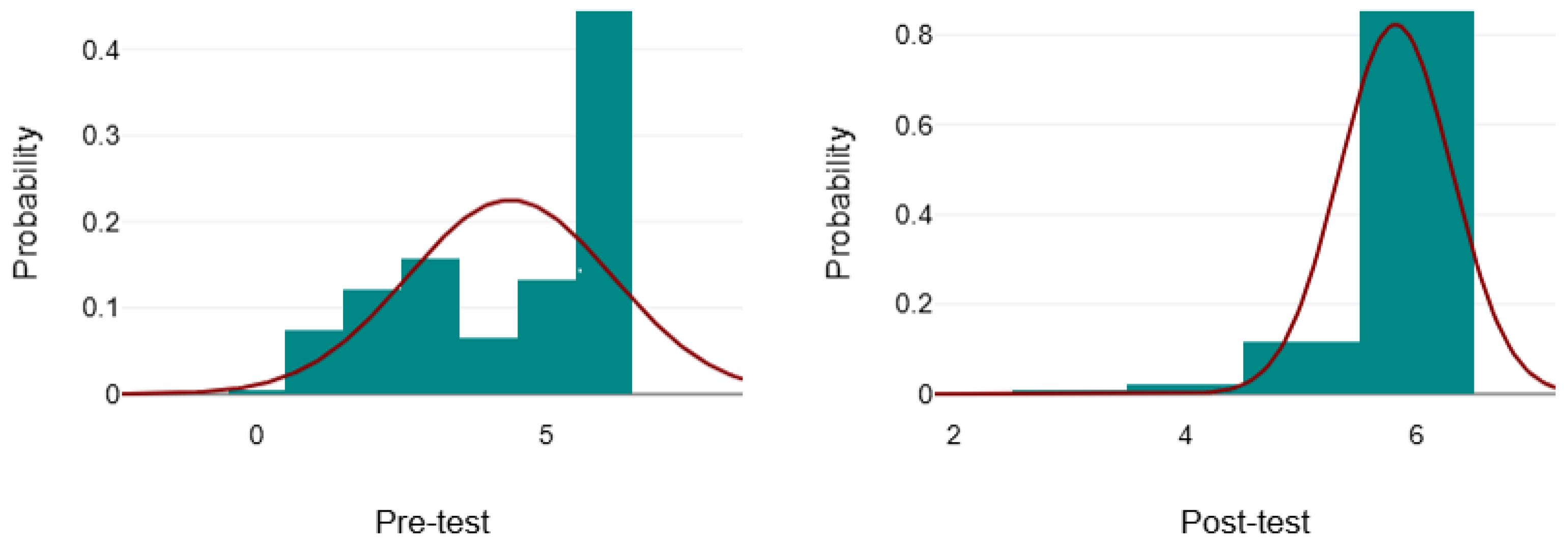
The histograms of the pre-test and post-test data are shown in Figure 5. The left histogram represents the pre-test results, while the right histogram shows the post-test results, illustrating the changes in distribution and central tendency following the GBL intervention.

It was checked whether the normality condition was met. We used four different statistical tests to check the normality (see

Table 9. Different statistical tests to check the normality.

	Pre-Test		Post-Test
	Statistics	p	Statistics	p
Kolmogorov–Smirnov	0.26	<0.001	0.5	<0.001
Kolmogorov–Smirnov (Lilliefors)	0.26	<0.001	0.5	<0.001
Shapiro–Wilk	0.81	<0.001	0.42	<0.001
Anderson–Darling	21.3	<0.001	74.34	<0.001

). Low p-values, that is, less than 0.05, indicate that the data differ significantly from a normal distribution. In our case, all four tests indicate that the data differ significantly from the normal distribution. This means that we should proceed with statistical methods for hypothesis testing that do not assume the normality of the data.

Due to the failure of the normality assumptions, we used the Wilcoxon test to compare the pre-test and post-test results. The Wilcoxon test is a suitable choice because it is a non-parametric method, i.e., it does not assume that the data follows a normal distribution. The Wilcoxon test is designed for paired data, which is relevant in this context since we are analysing the differences between the same participants’ pre-test and post-test scores. This test accounts for the individual paired differences, providing a robust analysis even in the presence of outliers (Sheskin, 2011). By utilising the Wilcoxon signed-rank test, we statistically evaluate whether the differences observed between the pre-test and post-test scores are significant, testing our hypotheses.

We calculated the Wilcoxon test ranks for the pre-test and post-test datasets. The results are summarised in

Table 10. Wilcoxon test ranks for the pre-test and the post-test.

	N	Mean Rank	Sum of Ranks
Negative Ranks	151	84.5	12,759.5
Positive Ranks	10	28.15	281.5
Equal	118
Total	279

.

The analysis of the Wilcoxon test ranks comparing pre-test and post-test scores reveals significant trends in student performance following the DETerinator GBL session. A total of 279 participants were evaluated. Among them, 151 individuals exhibited negative ranks (Pre-test < Post-test), indicating that their post-test scores were higher than their pre-test scores. This significant majority suggests an improvement in performance for these students after the intervention, which is a positive outcome. Only 10 participants demonstrated positive ranks (Pre-test > Post-test), meaning their post-test scores were lower than their pre-test scores. The average rank for those who improved was 84.5, while the average rank for those who declined was significantly lower at 28.15. This disparity between the number of negative and positive ranks highlights a generally favourable impact of the instructional strategy employed. Additionally, 118 participants showed equal scores on both assessments (Pre-test = Post-test), indicating no change in their performance. The findings suggest that a significant proportion of students benefited from the GBL intervention.

Table 11. Wilcoxon signed-rank test results for pre-test and post-test.

	W	z	p	r
Pre-test–Post-test	281.5	−10.6	<0.001	0.63

presents a more detailed statistical analysis of these results. The Wilcoxon test statistic (W) is 281.5, indicating the sum of ranks associated with the positive differences. The standardised z-score of −10.6 reinforces the significance of the results, while the p-value of less than 0.001 confirms that the changes in scores are statistically significant, leading us to reject the null hypothesis. Finally, the effect size (r) of 0.63 reflects a large effect, suggesting that the GBL intervention had a meaningful overall impact on the participants’ learning outcomes. Note that the effect size is considered large if $r>0.5$ (Steyn, 2020).

6.2. Midterm Exam

The midterm exam results were manually entered into a Microsoft Excel spreadsheet and then imported into the DATAtab application for data analysis. The scores of the tasks related to determinants in the midterm exam were collected and analysed for all 580 participants. Descriptive statistics are presented in

Table 12. Descriptive statistics for midterm exam scores.

	Control Group	Experimental Group
N	301	279
Mean (M)	2.5	3.14
Median	3	3
Mode	3	3
Standard Deviation (SD)	1.8	1.62
Minimum	0	0
Maximum	6	7
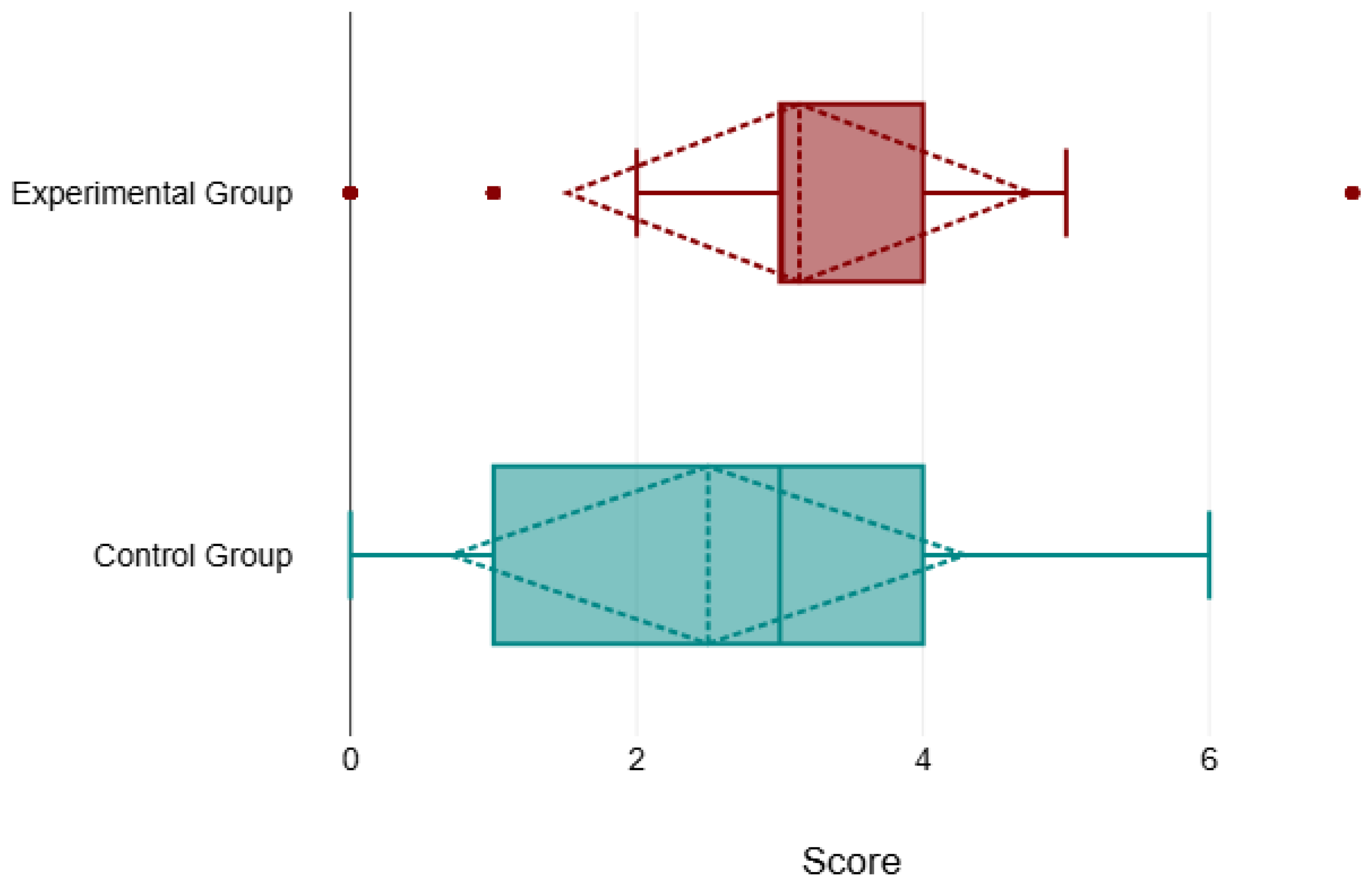
Median Absolute Deviation (MAD)	2	1

, and Figure 6 illustrates the essential features of the midterm exam scores for both groups.

The mean score for the Control Group is 2.5, which is notably lower than the Experimental Group’s mean score of 3.14. Both groups share the same median score of 3. When examining the mode, both groups display a most frequent score of 3, this score was the most common among participants across both datasets. However, the standard deviation reveals a difference: the Control Group has a higher standard deviation of 1.8 compared to the Experimental Group’s 1.62. This higher standard deviation for the Control Group implies that scores are more widely dispersed from the mean, highlighting greater variability in individual performance compared to the more consistent scores of the Experimental Group. Looking at the range of scores, both groups have a minimum score of 0, signifying that some participants did not score any points. The maximum score for the Control Group is 6, whereas the Experimental Group reached a maximum score of 7; there was a higher peak performance within the Experimental Group. Furthermore, analysing the MAD reveals that the Control Group has a MAD of 2, which is higher than the Experimental Group’s MAD of 1. So, the scores in the Control Group not only vary more widely from the mean but also show greater inconsistency around the median.

The descriptive statistics show that the experimental group performed a bit better overall compared to the control group. Statistical testing must be performed to further validate this conclusion. The following hypotheses were formulated to answer research question RQ2:

• Null hypothesis: There is no difference between the experimental and control groups with respect to the dependent variable.
• Alternative hypothesis: There is a difference between the experimental and control groups regarding the dependent variable.

None of the samples are normally distributed (see

Table 13. Different statistical tests to check the normality.

	Control Group		Experimental Group
	Statistics	p	Statistics	p
Kolmogorov–Smirnov	0.18	<0.001	0.24	<0.001
Kolmogorov–Smirnov (Lilliefors)	0.18	<0.001	0.24	<0.001
Shapiro–Wilk	0.89	<0.001	0.9	<0.001
Anderson–Darling	11.38	<0.001	12.47	<0.001

), and their sizes are different and independent of each other. Because of these conditions, a non-parametric statistical method, the Mann–Whitney U-test was used to compare the performance of the experimental and control groups.

Table 14. Mann–Whitney U-test results.

	U	z	Asymptotic p	Exact p	r
Mann–Whitney U-test	34,356	−3.89	<0.001	<0.001	0.16

shows the results of the Mann–Whitney U-test. The U statistic value is 34,356. This number represents the number of times a score from one group ranks higher than a score from the other group. The current U statistic suggests there is a notable difference in the ranking of scores between the two groups. The z-statistic is −3.89. This value indicates the standardised deviation of the U statistic from the mean. The asymptotic p-value is <0.001, which is significantly below the conventional alpha level of 0.05, providing strong evidence to reject the null hypothesis. Moreover, the exact p-value is also <0.001. Its consistency with the asymptotic p-value further confirms the statistical significance of the findings. The effect size (r) is calculated to be 0.16, which is a small effect size (Steyn, 2020). So, the Mann-Whitney U-test results indicate a significant difference between the experimental group and the control group at the 5% significance level.

6.3. Questionnaire

In the questionnaire, different categories of questions are distinguished to obtain a comprehensive picture of general mathematical attitudes, experiences with the DETerminator game, the benefits of the game, and the possibilities for development. In addition to collecting demographic data, Category I questions focused on participants’ attitudes towards mathematics learning (Q1–Q3) and game-based learning (Q4–Q6). Category II questions were specifically related to game-based learning with the DETerminator game (Q7–Q12) and opinions about the DETerminator card game (Q13–Q15). The questions and the percentage distribution of responses received from the 279 participants are presented in

Table 15. Results of Category I of the questionnaire with the descriptive statistical data.

No.	Question	1	2	3	4	5	M	SD
Q1	Do you usually enjoy learning maths?	14%	13.6%	26.9%	23.3%	22.2%	3.26	1.32
Q2	Do you find learning maths interesting?	10.4%	10%	16.8%	30.5%	32.3%	3.64	1.31
Q3	How important do you find learning mathematics?	2.5%	7.9%	23.3%	28.7%	37.6%	3.91	1.07
Q4	How interested are you in game-based teaching methods?	0.7%	2.2%	10.4%	25.8%	60.9%	4.44	0.82
Q5	Would you welcome opportunities for game-based learning in other topics in your university mathematics courses?	1.1%	1.1%	5.4%	21.5%	71%	4.60	0.74
Q6	Do you think using new forms of teaching in mathematics is necessary?	1.4%	2.2%	10%	25.8%	60.6%	4.42	0.86

and

Table 16. Results of Category II of the questionnaire with the descriptive statistical data.

No.	Question	1	2	3	4	5	M	SD
Q7	How easy did you find the questions in the pre-test?	2.2%	12.5%	45.9%	25.1%	14.3%	3.37	0.95
Q8	How easy did you find the questions in the post-test?	2.2%	5.7%	30.8%	41.2%	20.1%	3.71	0.92
Q9	How much of a game did the learning process feel like with the DETerminator game?	0.4%	2.5%	10.8%	32.6%	53.8%	4.37	0.8
Q10	When writing the post-test, how much did the learning phase between the two tests help?	0.4%	1.8%	10.8%	30.5%	56.6%	4.41	0.78
Q11	Do you think the DETerminator card game makes learning the technique of calculating the determinant easier?	1.1%	3.6%	11.5%	24.4%	59.5%	4.38	0.90
Q12	Did you enjoy learning during the DETerminator game?	0.7%	3.2%	11.1%	25.4%	59.5%	4.40	0.86
Q13	Do you think the determinants on the game cards are effective for learning?	0.7%	2.2%	11.1%	24%	62%	4.44	0.83
Q14	How did you like the graphic design of the game?	0.7%	1.4%	10.4%	27.6%	59.9%	4.44	0.79
Q15	If there was an online version of the DETerminator game, would you play it before the midterm exam?	0.7%	4.3%	7.5%	25.1%	62.4%	4.44	0.86

, together with descriptive statistical data.

The questions presented in Category II focus on students’ experiences and perceptions of the DETerminator card game as a learning tool for understanding the concept and properties of the determinant in mathematics. Each question aims to gauge various aspects of the learning process, including perceived difficulty, enjoyment, effectiveness, and preferences for future engagement with the game.

Table 15 provides a clear overview of the results from Category I of the questionnaire, showing the distribution of responses for each question alongside the mean (M) and standard deviation (SD). The data presented in Table 15 reflect the students’ responses regarding their perceptions of learning mathematics and the potential to incorporate game-based teaching methods into their education. Each question provides insight into the students’ attitudes toward mathematics, interest in innovative teaching methods, and overall engagement with the subject. The first question (Q1), which enquires about students’ enjoyment of learning mathematics, reveals a diverse range of opinions. With a mean score of 3.26, students are slightly inclined toward enjoying math, but nearly 40% of respondents either disagree or express a neutral stance. This indicates that while some students find satisfaction in studying mathematics, a significant number do not, highlighting the necessity for educators to explore pedagogical strategies that foster enthusiasm and engagement in this subject. In evaluating the second question (Q2) concerning the interest in learning mathematics, the responses skew more positively, with a mean score of 3.64. Approximately 62.8% of students report some level of agreement with the statement that they find learning mathematics interesting. This suggests an optimistic attitude among students about the content, even if the interest varies among individuals. The results imply that while some strategies may work effectively for a majority, educators should remain mindful of those who may still struggle with engagement. The third question (Q3) addresses the perceived importance of mathematics in students’ lives or future careers, scoring a mean of 3.91. The high percentage of students recognising its importance reinforces the idea that students appreciate the subject’s relevance and are likely aware of its applications in various fields. This understanding presents an opportunity for educators to connect the material more directly to real-world applications, potentially enhancing the enthusiasm and perceived relevance of the subject.

Question four (Q4) showcases an impressive mean score of 4.44 regarding students’ interest in game-based teaching methods, with an overwhelming 60.9% of respondents expressing strong approval. This indicates a strong inclination towards engaging teaching styles that involve gaming components. The positive reception towards game-based learning methods highlights a shift in educational expectations, wherein students are more receptive to innovative instructional approaches that could enhance their learning experiences. The fifth question (Q5) emphasises students’ willingness to integrate game-based learning across various fields, yielding a high mean of 4.60. An astounding 71% of respondents strongly endorse this idea. Finally, the sixth question (Q6) in Category I regarding the necessity of new teaching methods in mathematics garnered a mean score of 4.42, further illustrating students’ eagerness for change. With over 60% of respondents agreeing that innovative teaching strategies are essential, it becomes evident that students recognise that traditional methods may not suffice to effectively meet their learning needs.

Overall, the data of Category I reveal that while students have a strong foundation of interest in and recognition of the importance of mathematics, they also clearly call for engaging, modernised instructional methods. The revealed preference for game-based teaching indicates that students are not just passive learners but active participants inclined to embrace innovative approaches.

In Category II (see Table 16), the first two questions (Q7 and Q8) assessed students’ perceptions of the difficulty of questions presented in a pre-test and a post-test. For Q7, regarding the pre-test, the mean score is 3.37, indicating that students found the pre-test questions to be moderately easy, with 45.9% selecting the neutral option (3) and 25.1% feeling that the questions were easy (4). The response distribution shows several students found them challenging, as indicated by the 14.3% who strongly agreed (5) that they found it easy. In Q8, the post-test received a higher mean score of 3.71, suggesting that students perceived these questions to be easier than those in the pre-test. This improvement may imply that the learning experience facilitated by the DETerminator game effectively prepared students to face questions more confidently. Question 9 explicitly addresses how much of a game-like experience the learning process felt while using the DETerminator. A strong mean score of 4.37 indicates that 53.8% of participants felt that the learning process felt very much like a game, with a minimal percentage rating it below neutral. Question 10 evaluates how beneficial the learning phase between the two tests was, with a mean score of 4.41. The fact that 56.6% rated this as highly beneficial reveals that the students appreciated the learning phase, recognising its role in consolidating their knowledge. The next question (Q11) investigates the perceived ease of learning the technique of calculating determinants through the DETerminator card game, garnering a mean score of 4.38. The majority (59.5%) agreed strongly that the game made mastering the calculation process easier. Following up, Question 12 directly asks students about their enjoyment while using the DETerminator game. With a mean score of 4.40, the results reveal a high level of enjoyment, suggesting that the game not only serves an educational purpose but also creates a positive atmosphere for learning maths, a subject often viewed as dry or daunting by students.

In Question 13, students evaluate the effectiveness of the determinants presented on the game cards for their learning. A mean of 4.44, with 62% affirming their effectiveness, further emphasises that the materials used within the game were well-received and believed to be effective learning aids. Question 14 assesses the game’s graphic design, obtaining another mean score of 4.44. A significant 59.9% rated the design highly, indicating that the visual aspects of the game contributed positively to their learning experience, potentially making the game more appealing and engaging. Lastly, Question 15 queries students’ interest in an online version of the DETerminator game for revision purposes before the midterm exam. With a mean score of 4.44 and 62.4% expressing a strong desire to use it, the results suggest that students are willing and enthusiastic about supplemental learning tools.

The standard deviation values in Table 16 suggest that the responses generally exhibit low variability. This indicates that students had similar perceptions about the DETerminator game and their learning experiences. The low standard deviations typically point to a strong consensus regarding the game’s effectiveness as an educational tool. The data from Category II confirm that the DETerminator card game is an effective educational tool that enhances students’ learning enjoyment and comprehension of mathematical concepts when calculating determinants. The high mean scores across various questions indicate that students found the game engaging, enjoyable, and beneficial for learning. Additionally, the positive feedback on the game’s structure, its perceived effectiveness, and students’ willingness to use it further suggest that GBL approaches can significantly improve educational outcomes in university mathematics.

Table 17. Item-total statistics.

Item	Corrected Item-Total Correlation	Interpretation	Cronbach’s Alpha If Item Deleted
Q1	0.55	strong correlation	0.91
Q2	0.59	strong correlation	0.91
Q3	0.66	very strong correlation	0.9
Q4	0.56	strong correlation	0.9
Q5	0.66	very strong correlation	0.9
Q6	0.64	very strong correlation	0.9
Q7	0.4	good correlation	0.91
Q8	0.43	good correlation	0.91
Q9	0.62	very strong correlation	0.9
Q10	0.64	very strong correlation	0.9
Q11	0.72	very strong correlation	0.9
Q12	0.77	very strong correlation	0.9
Q13	0.75	very strong correlation	0.9
Q14	0.57	strong correlation	0.9
Q15	0.69	very strong correlation	0.9

summarises the item-total statistics, and Figure 7 shows the correlation heatmap.

The Cronbach’s alpha is 0.91. This value is very high, as Cronbach’s alpha ranges from 0 to 1. A value of 0.91 suggests that the questions are highly consistent and reliable. Generally, a Cronbach’s alpha above 0.7 is considered acceptable, above 0.8 is considered good, and above 0.9 is considered excellent. The value 0.91 falls into the excellent category, indicating that the items consistently measure the underlying construct. This level of reliability enhances the validity of the results and confirms that the survey is robust. When interpreting the results of a Cronbach’s alpha analysis, we are interested in the corrected item-total correlation and the Cronbach’s alpha when each item is omitted. Essentially, it is about assessing the internal consistency of your scale and how each item contributes to it. This is what the Table 17 tells us. A high correlation here means that the item aligns well with the total score of the other items, contributing significantly to the scale’s internal consistency. Q3, Q5, Q6, Q9, Q10, Q11, Q12, Q13, and Q15 items exhibit very strong correlations, indicating they align particularly well with the overall measured construct and are reliable indicators of the underlying variable. Q1, Q2, Q4, and Q14 items demonstrate strong positive correlations with the total score, implying they contribute positively to the overall internal consistency of the scale. Q7 and Q8 items have lower corrected item-total correlations compared to others, suggesting that while they still contribute to the scale, their relationship with the total score is not as strong. This is not coincidental, as these two questions were for pre- and post-test questions, not for game-based learning.

The Pearson correlation analysis indicates several significant relationships between the questions. The Pearson correlation coefficient (r) tells about the strength and direction of the linear relationship between the questions. We have made the correlation matrix, which includes both the correlation coefficients and the associated p-values for each pair of questions (Q1 to Q15). The p-values indicate whether the correlation coefficients are statistically significant. A p-value $<0.05$ typically shows a statistically significant correlation. In our case, most of the correlations have p-values less than 0.001, indicating strong statistical significance. The data were analysed to find 5 strong ($\left|r\right|>0.7$) and 16 medium correlations ($0.3\le \left|r\right|<0.7$), as seen in Figure 7. The correlation between Q11 and Q13 (r = 0.85, $p<0.001$) is remarkably high, indicating a strong positive relationship. Similarly, Q12 and Q13 (r = 0.80, $p<0.001$) demonstrate another strong positive correlation. The correlation between Q12 and Q11 (r = 0.76, $p<0.001$) reflects a strong positive relationship between these two survey questions. On another note, the correlation between Q2 and Q3 (r = 0.79, p < 0.001) shows these questions are related. Lastly, the correlation of Q2 and Q1 (r = 0.77, p < 0.001) is also strong.

7. Discussion and Answer to Research Questions

Our study investigated the effectiveness of a GBL intervention, employing the non-digital DETerminator card game, in enhancing university students’ understanding and calculation skills related to determinants. The results show a significant positive impact of GBL on both short-term and medium-term learning outcomes, coupled with overwhelmingly positive student feedback. This discussion section delves deeper into these findings and, at the same time, answers the research questions.

7.1. Answer to Research Question RQ1

The effectiveness of the DETerminator card game was evaluated in the experiment based on short- and medium-term changes in students’ knowledge and skills related to determinants. Our answer to the research question RQ1 is the following:

• To measure the short-term effectiveness, a pre-test and a post-test were administered to the experimental group (students who played the DETerminator game). The results indicated a significant improvement in students’ scores from the pre-test (mean of 4.38) to the post-test (mean of 5.82). This shift indicates that after the intervention with the game, they performed more proficient calculations of the determinants and conceptual practices on the topic. The use of the Wilcoxon signed-rank test further confirmed that this improvement was statistically significant, with a p-value of less than 0.001, rejecting the null hypothesis and indicating that the game-based learning approach had a positive impact. The effect size of 0.63 indicates that the intervention had a large and meaningful effect on student performance.
• To assess medium-term effectiveness, the performance of the experimental group was compared to that of the control group during a midterm exam, which included problems related to determinants. The experimental group achieved a mean score of 3.14 out of 7, compared to the control group’s mean score of 2.5. The Mann–Whitney U-test indicated a moderate difference between the two groups, with a p-value of less than 0.001 and an r-value of 0.16.

The improvement can be attributed to several factors inherent in the game’s design. The competitive and collaborative aspects fostered active engagement and peer learning, while the immediate feedback provided by instructors during gameplay ensured a continuous cycle of learning and refinement. The varied difficulty levels of the determinant problems on the cards facilitated a gradual increase in challenge, allowing students to build confidence and skills progressively. Our results align with the literature emphasising the positive impact of GBL on motivation and cognitive engagement (Balaskas et al., 2023; Francisco, 2023; Jääskä et al., 2022; Szilágyi et al., 2025).

The results of the experiment for the medium-term effect suggest that the DETerminator GBL approach fostered a deeper and more lasting understanding of the concepts rather than merely superficial memorisation. The observed difference, though minor, still holds practical significance, indicating that GBL can contribute to better long-term retention in mathematics. The smaller effect size may also indicate a need for reinforcement activities after the initial GBL intervention to maximise long-term retention. The smaller effect size observed in the medium-term outcomes suggests an opportunity for further enhancement of student learning through reinforcement activities following the GBL intervention. While the non-digital DETerminator card game effectively improved students’ understanding of determinants in the short term, the small effect size indicates that additional measures might be necessary to ensure the retention of this knowledge over time. Reinforcement activities, such as follow-up problem-solving sessions, review games, online GBL, or collaborative group activities, could help consolidate the skills and concepts students acquired during the game. These activities would not only serve to refresh students’ memories but also reinforce their understanding by providing further opportunities for practice and application of their mathematical skills in varied contexts. Such ongoing engagement is crucial in mathematics education, where concepts build upon one another, and a solid foundation is essential for tackling more complex topics. Integrating spaced repetition techniques, where students revisit the concepts at strategically spaced intervals, could significantly enhance long-term retention of knowledge. Incorporating various types of activities (both individual and collaborative) may also cater to different learning preferences, ensuring that all students can effectively reinforce their understanding.

Our findings suggest that the integration of the non-digital DETerminator card game into the mathematics curriculum not only improves immediate learning outcomes but also may promote superior retention of knowledge relative to traditional teaching methods. The clearly better performance measured in the short term and the moderate effect observed in the medium term show that the game theory approach can be an effective didactic tool in learning determinants. Our result confirms that the DETerminator game leads to rapid knowledge acquisition in the initial period, while in the longer term, it may have a positive but more moderate effect.

7.2. Answer to Research Question RQ2

RQ1 is primarily concerned with evaluating the effectiveness of the DETerminator card game in terms of immediate knowledge gain and how well students retain that knowledge over time. It assesses both short-term (through pre-tests and post-tests) and medium-term (through midterm exam performance) outcomes. RQ2 specifically examines the degree of improvement in student performance while using the complex treatment with the DETerminator card game versus those who were taught through traditional methods. It is more focused on measuring the comparative outcomes of the two teaching strategies rather than assessing effectiveness on its own.

The comparative results from the midterm exam, which included problems related to determinants, indicated that students who engaged with the card game outperformed their peers who received conventional instruction. This difference in performance illustrates that the DETerminator card game not only enhanced students’ immediate understanding but also contributed to their ability to retain and apply that knowledge effectively in a testing scenario. The statistical analysis utilising the Mann–Whitney U-test highlighted this significant difference, with a p-value of less than 0.001, so the improvement was not due to chance. The results demonstrate that the DETerminator card game has a statistical significance in enhancing first-year university students’ performance in calculating determinants compared to traditional teaching methods.

The results of measuring medium-term effects can be influenced by a number of factors, which make it difficult to interpret the results and identify causal relationships. In the case of the experiment, the different treatment times may have been a contributing factor, although we should note that no additional knowledge has been transferred to those who participated in the experimental group. The extra online session focused mainly on the rules of the DETerminator game. At the same time, we shall also point out that the midterm exam is a significant milestone in terms of completing the Economic Mathematics course, so students in both the experimental and the control groups were motivated to answer the questions to the best of their ability. For this reason, we believe that the difference in performance can be attributed to the complex treatment involving GBL sessions.

7.3. Answer to Research Question RQ3

The questionnaire results indicated that students found the DETerminator game to be an enjoyable and effective learning tool. A significant portion of participants expressed that the game made learning the techniques for calculating determinants easier, with 59.5% of respondents agreeing strongly with this statement. The majority of students reported high levels of enjoyment while participating in the game, with a mean response of 4.40, suggesting that the game not only facilitated learning but also created a positive and engaging atmosphere. The sense of fun and competition encouraged by the game likely contributed to enhancing their motivation and reducing anxiety typically associated with studying mathematics.

Students also acknowledged the effectiveness of the game’s content, with 62% affirming that the determinants presented on the game cards were beneficial for their learning. This demonstrates that students not only enjoyed the gaming experience but also recognised its educational value, reinforcing the importance of integrating GBL into the mathematics curriculum. The feedback indicated that students positively valued the opportunity to work collaboratively while playing the game, which fostered social interaction and teamwork. This collaborative aspect enhanced their understanding of mathematical concepts, supporting the notion that active engagement through GBL significantly benefits educational outcomes. First-year university students in this survey overwhelmingly evaluated their learning experience with the DETerminator card game positively, highlighting its effectiveness in making learning enjoyable and meaningful. The DETerminator game not only succeeded in improving their understanding of determinants but also contributed to creating a more engaged and motivated classroom environment.

The overwhelmingly positive student feedback obtained through the questionnaire further reinforces the findings. The high mean scores across various questions related to enjoyment, perceived usefulness, and perceived ease of learning strongly suggest that the DETerminator game created a positive and engaging learning experience. This accords with existing research emphasising the motivational effects of GBL and, above all, how it fosters both internal motivation and enjoyment of learning as well (Connolly et al., 2012). The online implementation of the game was generally well supported by respondents, clearly indicating that this area is worth focusing on in future developments.

8. Conclusions, Limitations, and Future Plans

Numerous studies have highlighted the positive impact of GBL methods on student performance, participation, and motivation (Costa et al., 2025; Debrenti, 2024; Szilágyi et al., 2025). Mathematical didactic CGs are a promising method for improving mathematical skills and promoting active learning. Educational games combine enjoyment and learning to meet educational goals (Taş & Bolat, 2023). The sophisticated designs of these games engage learners, creating an enjoyable and dynamic learning experience (Zhelal & Kaymak, 2023). The analysis of didactic games highlights a critical concern: many of these games fail to deliver an entertainment experience like that of traditional entertainment games familiar to players. However, engaging learners is crucial, as high levels of engagement are associated with improved motivation, increased participation, and better retention of information (Dele-Ajayi et al., 2016). By integrating captivating narratives, appealing visuals, and mechanics similar to popular entertainment games, didactic games can create an immersive environment that actively engages users. Such engagement not only sustains interest but also enhances the practical application of knowledge, making the learning process more meaningful. When students find a didactic game both enjoyable and effective, they are more likely to immerse themselves in the content and invest the necessary effort to master the material. Therefore, it is essential for developers of educational games to provide the entertainment aspect of the game, ensuring that the learning experience is not only informative but also enjoyable. Striking this balance between fun and education can ultimately lead to more effective teaching tools that resonate with students and drive positive learning outcomes.

When developing the DETerminator educational game, we took into account the recommendations in the literature (Kalmpourtzis, 2019; Laine & Lindberg, 2020; Russo et al., 2023), and our many years of experience as educators helped us in the process of developing the card game. The success of the DETerminator game can be attributed to its thoughtful design, which successfully balanced the fun and engaging elements of the UNO game with the rigour of mathematical problem-solving. The varied difficulty levels of the tasks, combined with action cards that introduced unexpected challenges and strategic elements, enhanced the learning experience. The clear alignment between the game’s mechanics and the learning objectives, along with the structured feedback mechanisms, created a strong foundation for successful learning.

The results of this study provide substantial evidence supporting the integration of the DETerminator didactic CG into university mathematics education. The DETerminator game proved a highly effective tool for teaching determinants, enhancing both short-term and medium-term learning outcomes and fostering positive student attitudes towards learning mathematics.

While the study offers compelling evidence for the efficacy of the DETerminator GBL intervention, certain limitations warrant consideration. The quasi-experimental design, while pragmatic, restricts the ability to make causal inferences. The sample was also drawn from the bachelor’s degree programmes of one university, which may limit the generalisability of the findings to other contexts. Another limitation of this pilot study is the voluntary nature of participation in the game-based learning condition, which may have introduced self-selection bias. Students who opted in might have been more motivated, open to experimentation, or confident in their abilities compared to those in the control group, potentially influencing outcomes independently of the intervention itself (Heckman, 1979). While baseline comparisons did not reveal major demographic or performance differences between groups, unobserved factors cannot be ruled out. This is a common challenge in educational innovation studies where participation is not randomly assigned (Hernán & Robins, 2020). We therefore interpret our findings as preliminary and exploratory, rather than causal, and emphasise that they provide an initial indication of the potential of game-based approaches. Future studies should address this limitation through designs that reduce selection bias, such as random assignment or quasi-experimental approaches (e.g., propensity score matching or covariate adjustment), to strengthen causal inference and ensure robustness of results (Stuart, 2010).

The experimental group received 150 min more treatment. Most of it was spent with the preparation for the game session and the game itself. We acknowledge that a significant limitation in measuring medium-term effects is the lack of additional traditional-style educational sessions organised for the control group for an extra 150 min. This makes it difficult to fully measure the effect of the intervention and compare it with traditional educational methods. We were not authorised to organise mandatory extra activities for members of the control group. If the experiment is repeated, it is particularly important to ensure that this restriction is lifted.

Further research could also focus on exploring the long-term retention of knowledge, comparing the GBL approach to other active learning strategies, and developing more sophisticated methods of assessing the impact of GBL on higher-order thinking skills. While limitations exist, the findings suggest that GBL holds considerable promise for improving the effectiveness and engagement of mathematics education at the university level. Further research aimed at addressing the identified limitations and exploring the various facets of GBL within different contexts is needed to fully realise its potential. Investigating the role of different game mechanics (e.g., collaboration vs. competition) on learning outcomes would also be beneficial.

It is a well-known fact that the number of educational digital games is growing steadily every year to support mathematical learning (Debrenti, 2024). According to Dienes (2015), using activities, games, and concrete experiences as the foundation of learning mathematics can make the process more engaging and enjoyable. We believe that incorporating digital tools that enhance efficiency can further enrich this joyful experience, helping students understand mathematical concepts more effectively through interactive and hands-on approaches. These games help students learn different topics independently or in multiplayer versions and make learning more motivating. The positive reception of Determinator by students encouraged us to start developing an online version. We developed the DET digital game, which is an online version of DETerminator that can even be played in multiplayer mode. The DET game works now in the beta stage, where it is being tested and refined. Our future plans include comparing the effectiveness of digital and non-digital game versions, as well as conducting student testing using a combination of the two.