Reforming First-Year Engineering Mathematics Courses: A Study of Flipped-Classroom Pedagogy and Student Learning Outcomes
Abstract
1. Introduction
- What contradictions (“tensions”) emerge when students participate in a flipped-classroom approach in a first-year engineering mathematics course?
- How do students develop confidence, competence, and knowledge while navigating these contradictions (“tensions”) within a flipped-classroom setting?
2. Theoretical Framework and Research Background
2.1. Theoretical Framework Background
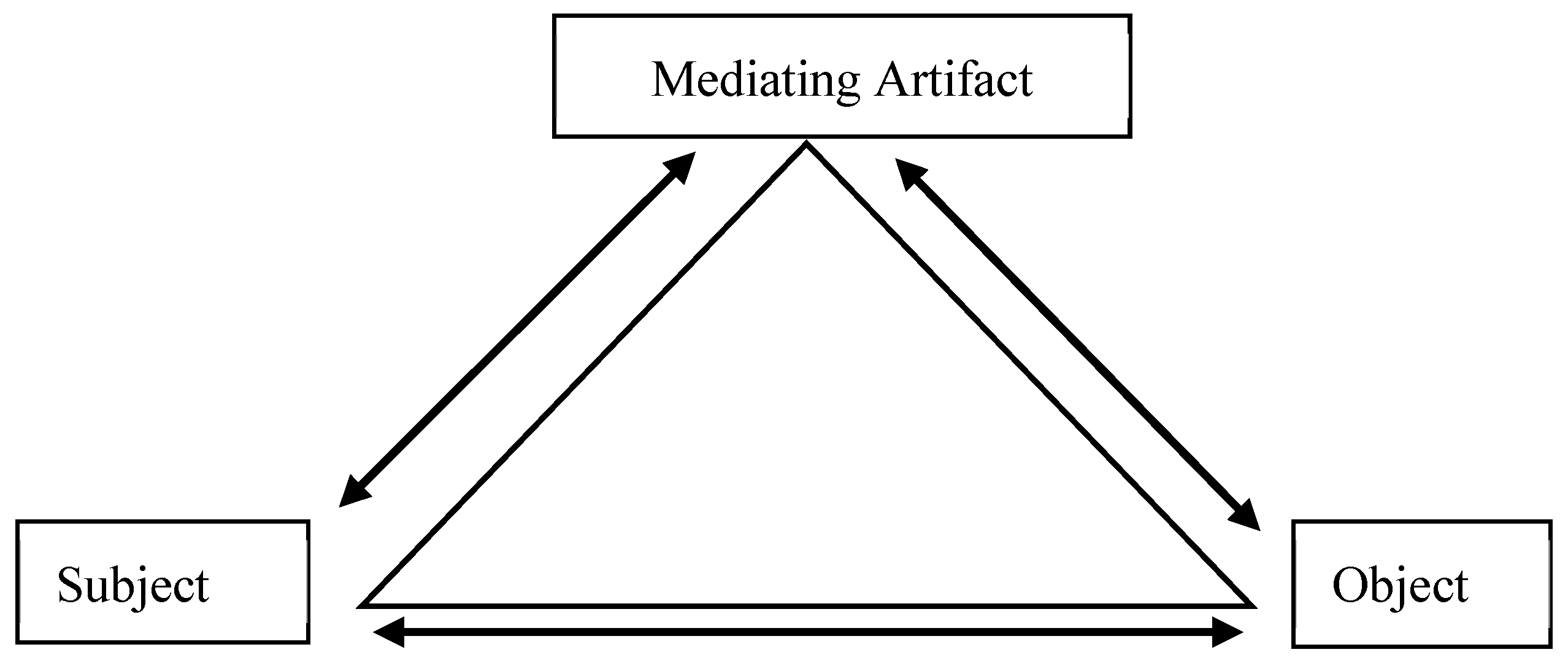
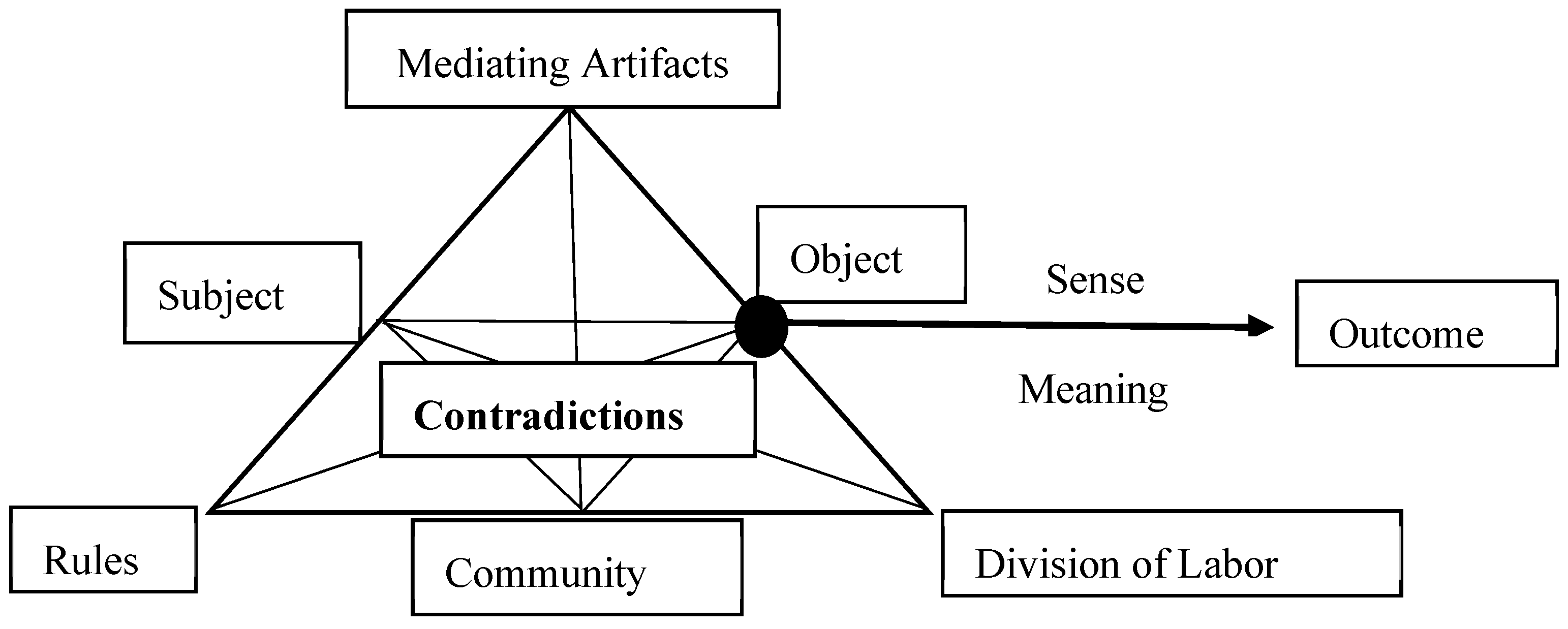
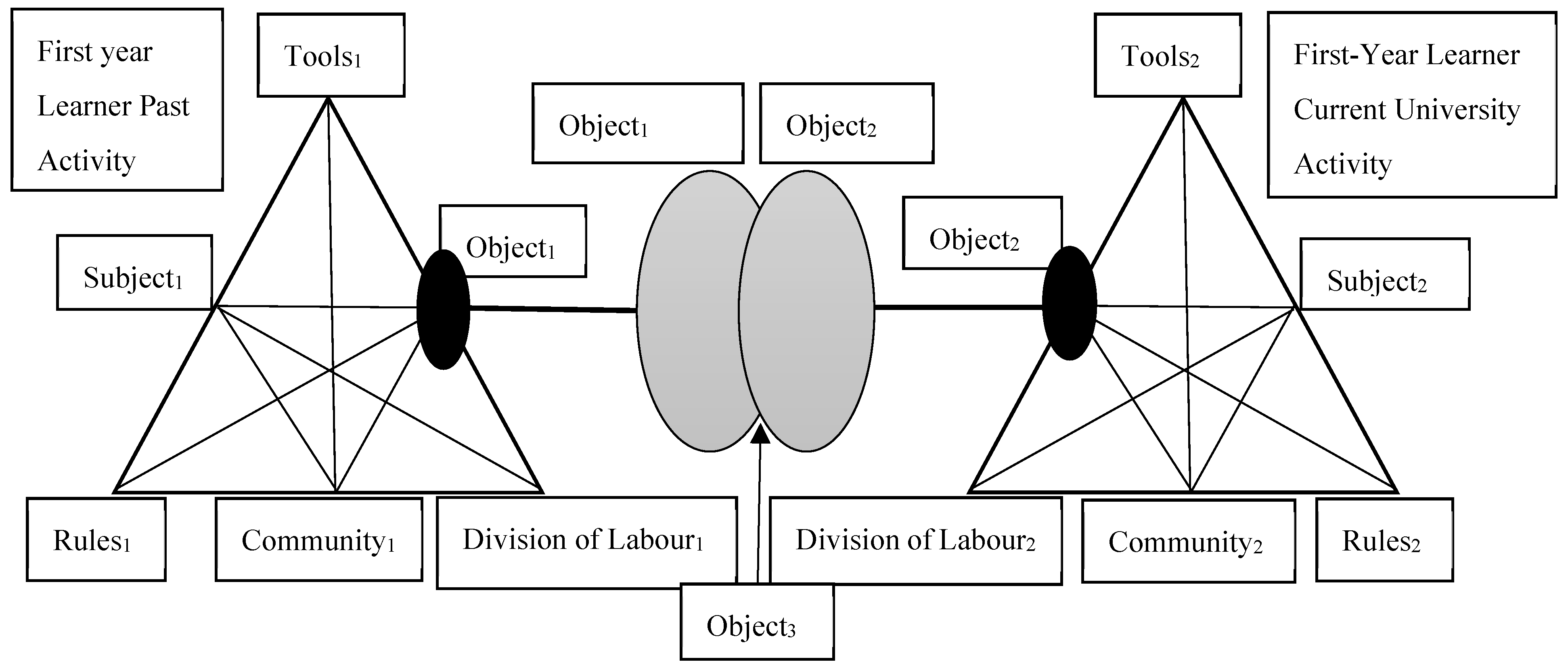
2.2. Activity System in the Context of Study
2.3. Contradictions
2.4. First-Year Teaching–Learning Approaches
2.5. Research Problem and Background
3. Materials and Methods
3.1. Ethics
3.2. Participants’ Backgrounds
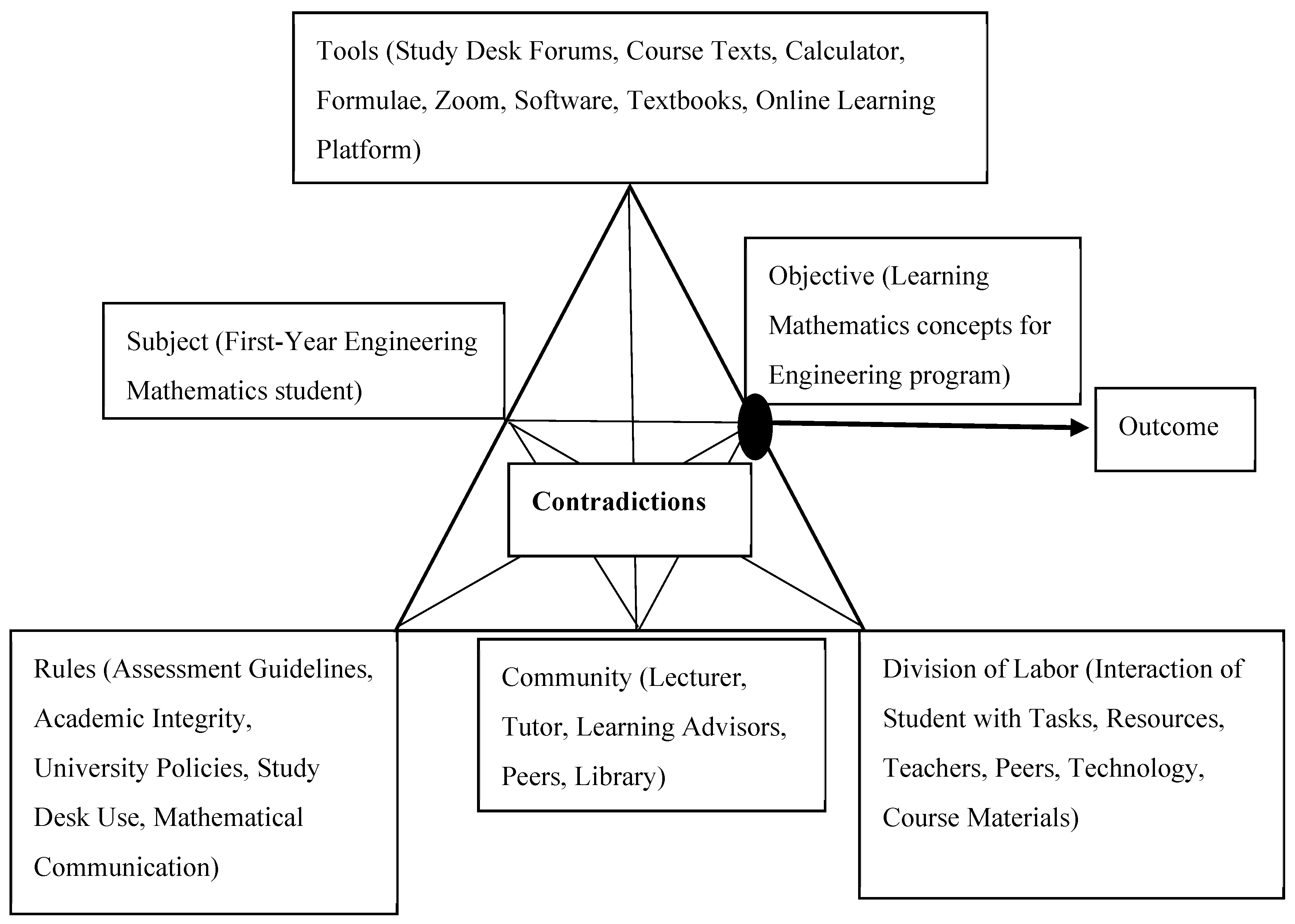
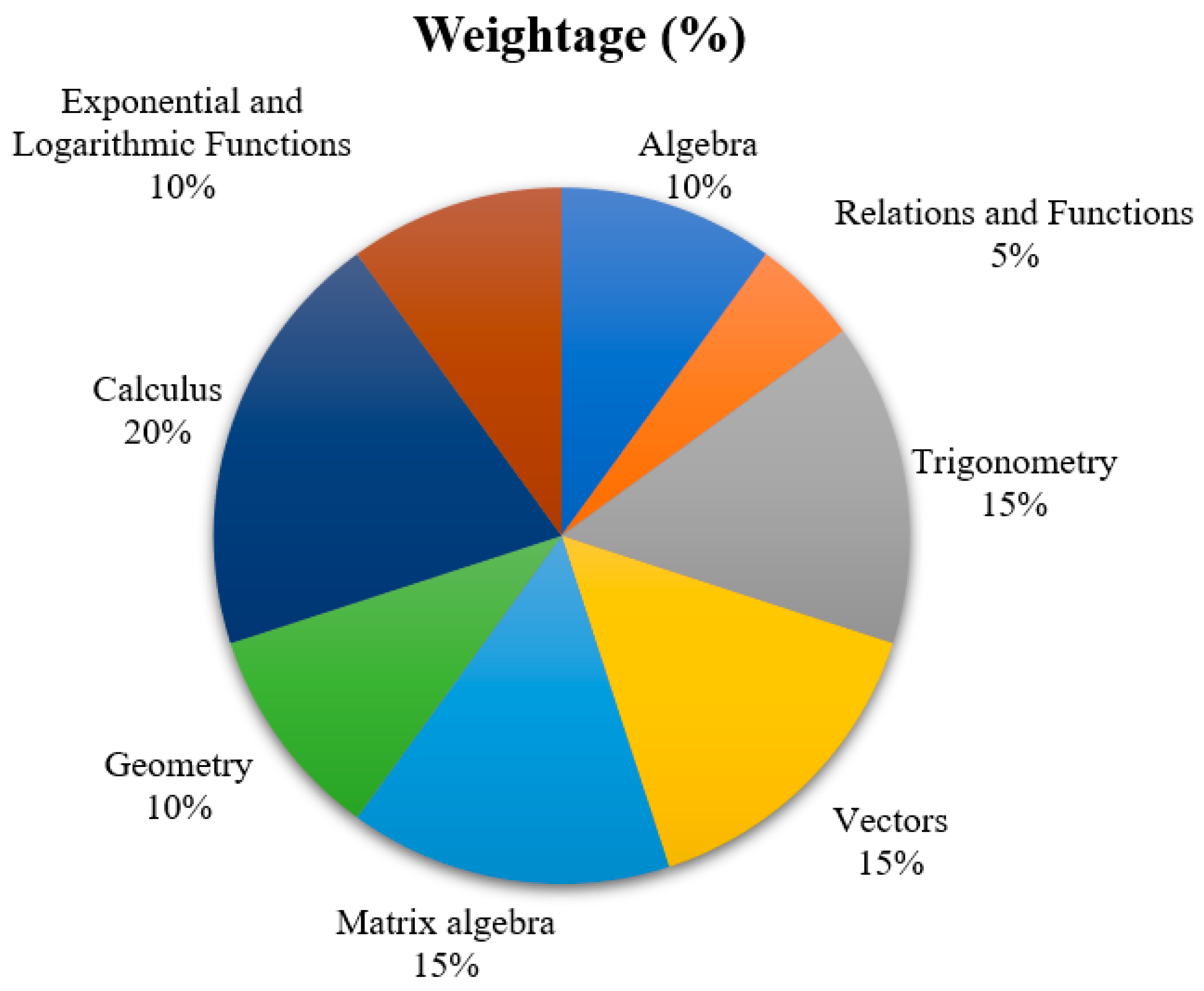
3.3. Course Rationale and Mathematical Concepts
3.4. Methodology
4. Results and Discussion
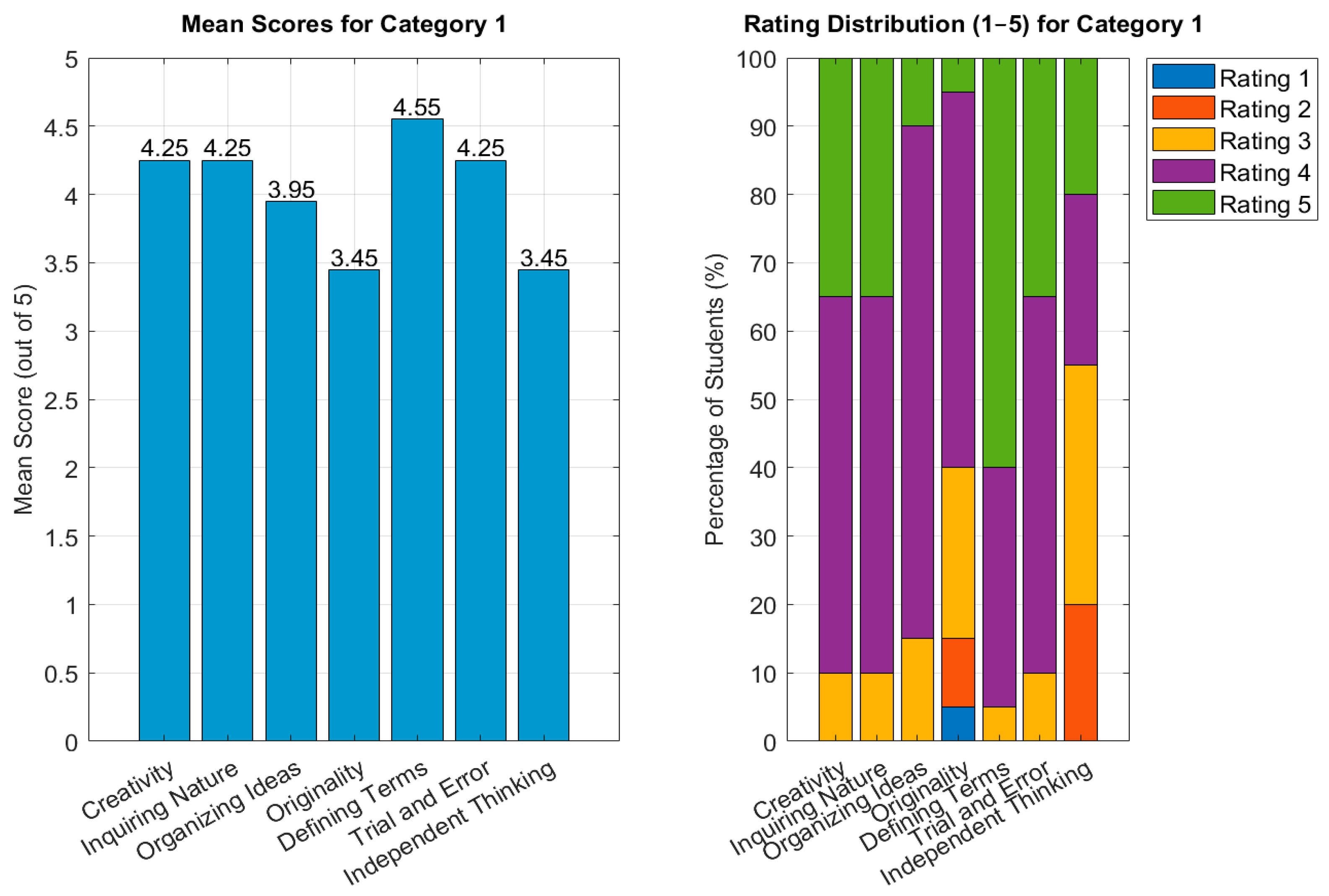
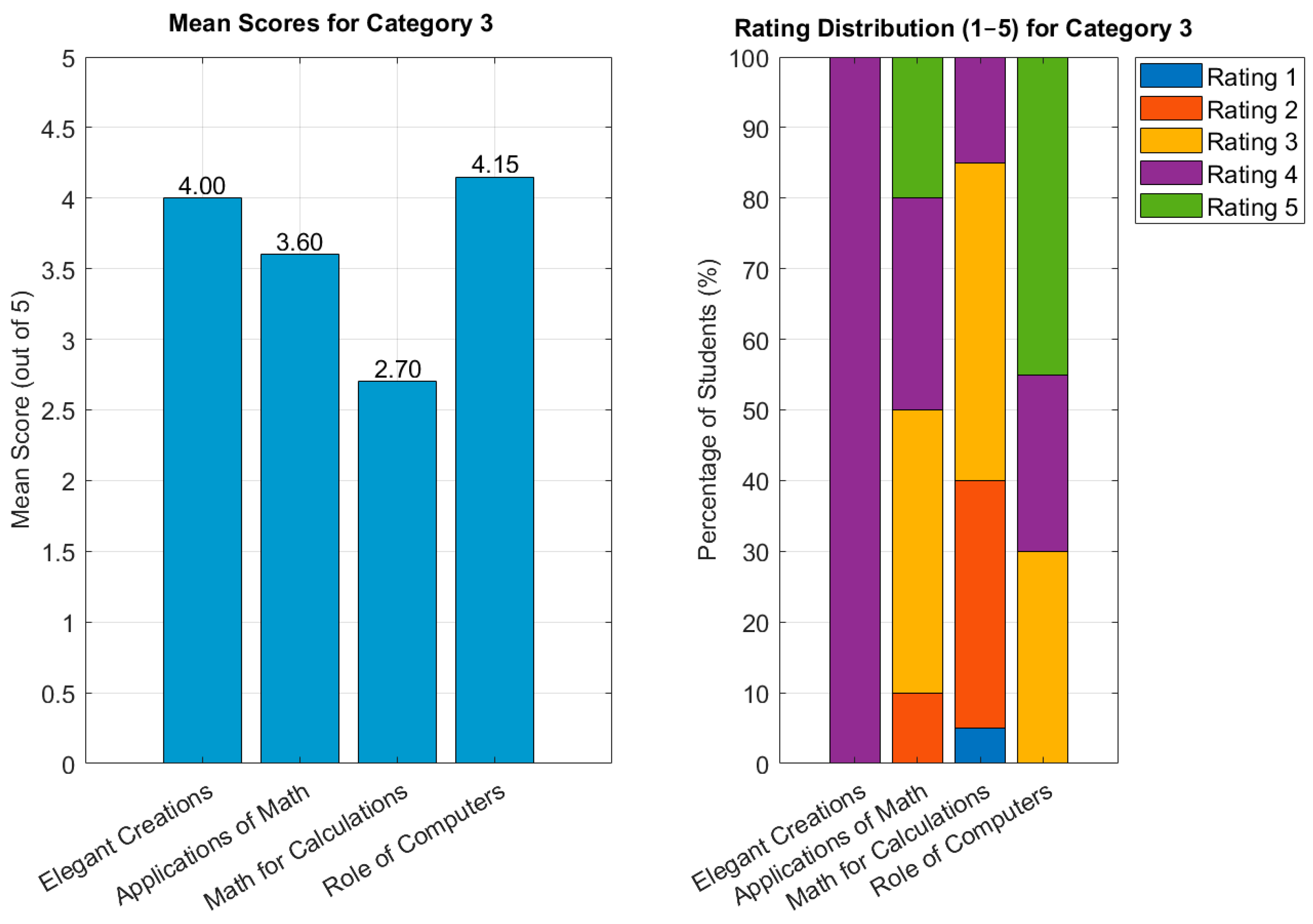
4.1. Belief Survey Results
4.2. Flipped-Classroom Survey Results
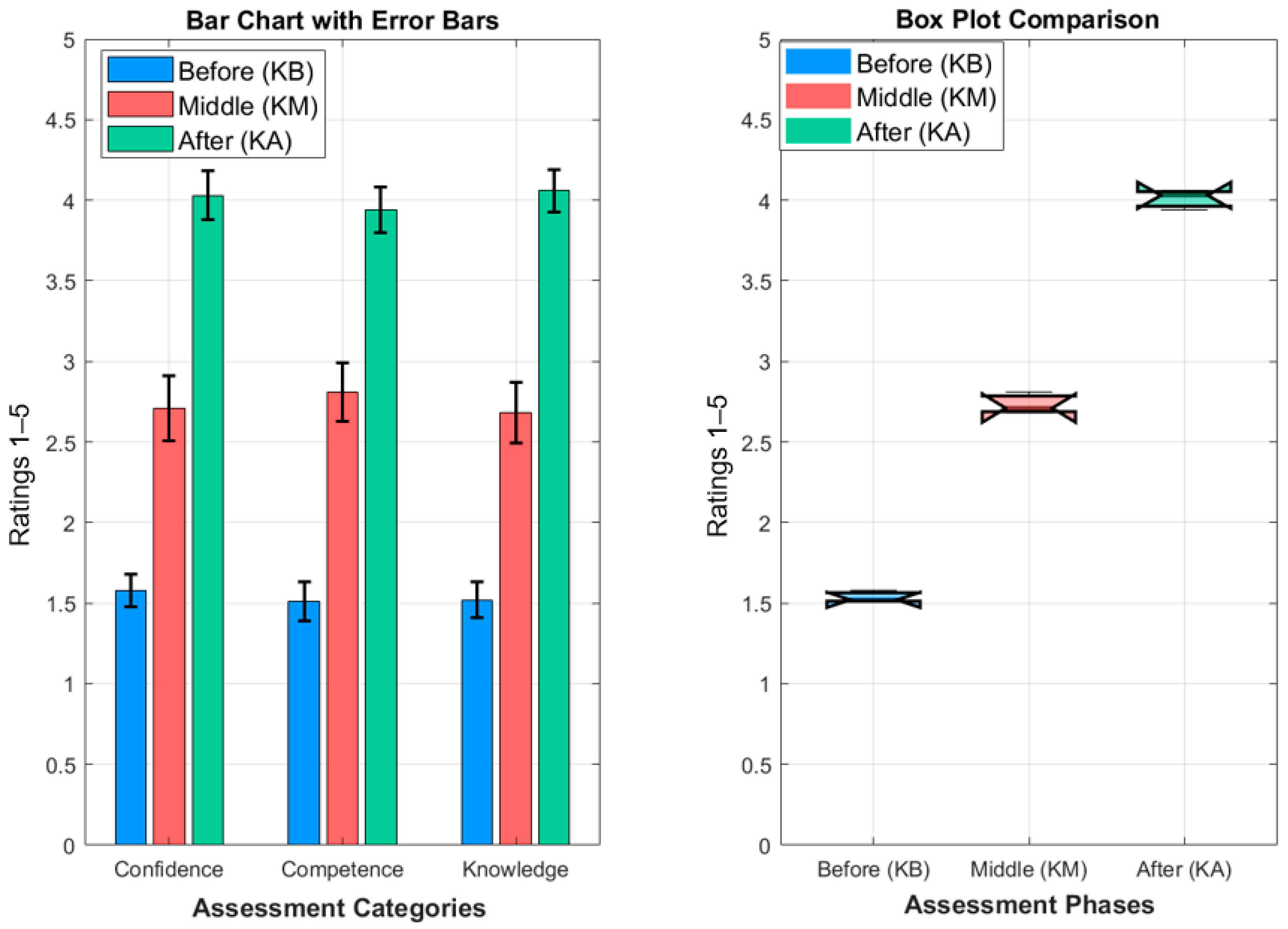
4.3. Statistical Analysis of Flipped-Classroom Survey Ratings
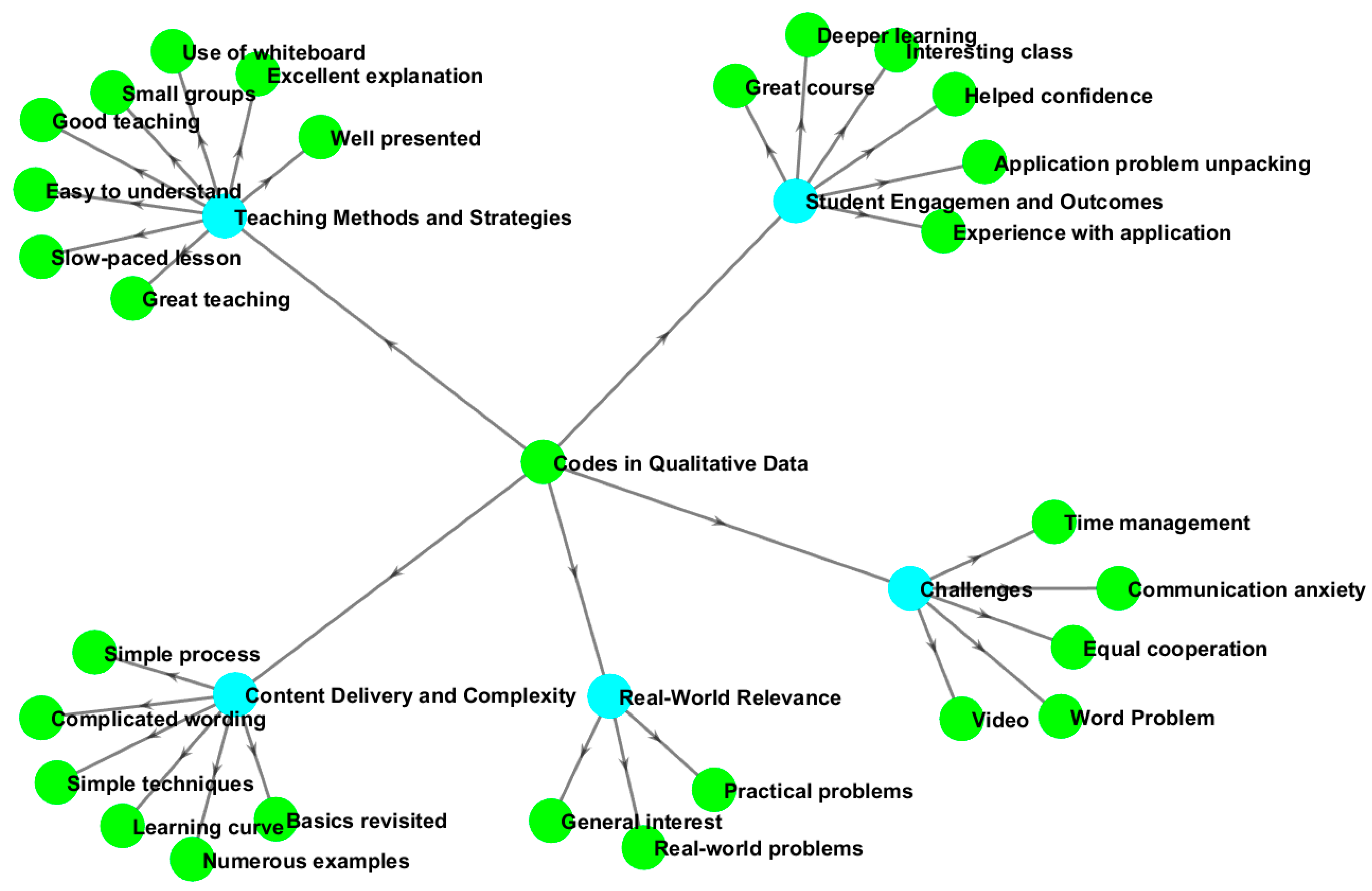
4.4. Qualitative Results
4.5. Contradictions (“Tensions”) Analysis
- Student Expectation–Curriculum Structure: The student sees a contradiction between engineering mathematics as a core or service course, whereby it is only for learning basic concepts, and advanced concepts with complex problem-solving are not of value in their program of study. The “tension” is in the exchange value of the core subject for the engineering program.“At first, I thought why do we need to these high-level problems when we will not use all of these in our engineering courses? I am doing surveying, I could understand it is interesting to see all the real-life examples, but I thought I might only use Trigonometry. Was wrong as teacher showed the connections with the topics and concepts”.
- Old and New Delivery System: The shift from passive learning to an active, interactive flipped classroom causes “tension” with students’ learning habits. Some students find it challenging with the transition in teaching delivery.“Given I have to cover the basics beforehand and then come to discuss concepts in class is new for me and I will need time to adjust to this. I am more use to taking in information in class and then work on my own. I must admit I did find myself lost sometimes being alone in the old style while I can share and talk more in this way”.
- Motivation and Anxiety: Students are motivated by application and real-life problem-solving but their communication and mathematics-related anxiety holds them from freely participating in the interactive sessions.“I like solving problems, but I always had an anxiety for mathematics and think I might ask silly questions or ask little things that everyone knows and embarrass myself. This however got a lot better after few sessions and now I do feel confident to share and discuss”.
- Self-Regulated Learning and Accountability: Prior completion of watching videos and other resources by students is a matter of self-regulation and accountability. It can be overwhelming for students with a high content load. Lack of immediate feedback and poor time management can lead to disengagement and frustration.“As a working student, finding time is an issue with me and when I cannot understand something, I need to ask to know which I cannot do while watching the video. I might or not watch the rest but not get the concepts. This is where I found supporting resources and links extremely helpful”.
- Learner Pace and Group Interactive Learning: The pace of learning in an interactive group setting is an important issue as some students can tend to lag if the other students are working at a faster pace than them when discussing and solving problems.“I sometimes feel that I am much slower in understanding to solve some problems and the group works faster, and I do not want to hold others back, but it becomes challenging for me as I take more time with some topics such as logarithms and exponentials for example which is very new to me, I may have forgotten the basics to be honest. I found talking to the tutor really helped in between to stitch the gaps”.
4.6. Recommendations
4.7. Limitations of This Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Category | Survey Questions |
|---|---|
| 2 | Solving a mathematics problem usually involves finding a rule or formula that applies. |
| 3 | The field of math contains many of the finest and most elegant creations of the human mind. |
| 2 | The main benefit of studying mathematics is developing the ability to follow directions. |
| 2 | The laws and rules of mathematics severely limit how problems can be solved. |
| 1 | Studying mathematics helps to develop the ability to think more creatively. |
| 1 | The basic ingredient for success in mathematics is an inquiring nature. |
| 1 | There are several different but appropriate ways to organise the basic ideas in mathematics. |
| 2 | In mathematics, there is usually just one proper way to do something. |
| 2 | In mathematics, perhaps more than in other fields, one can find set routines and procedures. |
| 3 | Mathematics has so many applications because its models can be interpreted in so many ways. |
| 3 | Mathematicians are hired mainly to make precise measurements and calculations for scientists. |
| 1 | In mathematics, perhaps more than in other areas, one can display originality and ingenuity. |
| 1 | There are several different but logically acceptable ways to define most terms in math. |
| 2 | Math is an organized body of knowledge that stresses the use of formulas to solve problems. |
| 1 | Trial-and-error and other seemingly haphazard methods are often necessary for mathematics. |
| 2 | Mathematics is a rigid discipline that functions strictly according to inescapable laws. |
| 3 | Many of the important functions of the mathematician are being taken over by the new computers. |
| 1 | Mathematics requires very much independent and original thinking. |
| 1 | There are often many ways to solve a mathematics problem. |
| 2 | The language of math is so exact that there is no room for a variety of expressions. |
| Questions |
|---|
| Subject: (First-Year Engineering Mathematics student) |
| What aspects of university transition is most challenging for Engineering Mathematics? |
| Will you be able to apply the knowledge to other problems on the same concept? |
| Do you have any background knowledge of the concepts? |
| Did your previous learning prepare you well for this course? |
| What obstacles do you see when solving the Maths problem(s)? |
| What are the “mental blocks” that hinder you to understand mathematical problems? |
| Objective (Learning Mathematics concepts for Engineering) |
| How important do you think learning mathematics concept are for your Engineering program? |
| Do you think this mathematics topics in this course will contribute to better understanding of other Engineering concepts? |
| Tools (Mediation) |
| Do you use any mathematical software or online tools or other online videos to understand mathematical concepts? How does it help you to learn the concepts? |
| Do you enjoy group work and interactive learning session in the flipped-classroom mode? Please explain why you do or do not? |
| What ENM1500 study desk resources do you rely on to help you with learning mathematical concepts? |
| Do you know how to use your scientific calculator to help in calculations? |
| Did you seek support from mathematics learning advisors, transition coordinators, and peer leaders at UniSQ? |
| Rules |
| Are you familiar with assessment policies and technical mathematical communication in ENM1500? |
| Community |
| Do you communicate with your peers in the course? |
| Do you feel a sense of belonging in the flipped-classroom class? Please explain. |
| Have you scheduled consultations with your lecturer or tutor when you needed help? |
| Division of Labor |
| Do you watch the recorded video on the study desk before coming to class? |
| Do you work on your assessment tasks every week as concepts is covered or do you do everything before the due date at once? |
| Have you made a timetable for your study for the semester? |
| Outcomes |
| What improvements can make to better cope with your study? |
| Are you using your same learning habit from your past learning before tertiary study or changed your approach? |
| Part 1: Please rate the following criteria. 1 means Low or Poor; 5 means High or Excellent | 1 | 2 | 3 | 4 | 5 |
| My knowledge of the concepts BEFORE this session. |  |  |  |  |  |
| My confidence level of the concepts BEFORE this session. |  |  |  |  |  |
| My competence level of the concepts BEFORE this session. |  |  |  |  |  |
| My knowledge of the course concepts MID session. |  |  |  |  |  |
| My confidence level of the course concepts MID session. |  |  |  |  |  |
| My competence level of the course concepts MID session. |  |  |  |  |  |
| My knowledge of the concepts AFTER this session. |  |  |  |  |  |
| My confidence level of the concepts AFTER this session. |  |  |  |  |  |
| My competence level of the concepts AFTER this session. |  |  |  |  |  |
| The knowledge and skills learned are relevant to my studies. |  |  |  |  |  |
Part 2: Comments
| |||||
References
- Alamri, W. A. (2019). Effectiveness of qualitative research methods: Interviews and diaries. International Journal of English and Cultural Studies, 2(1), 65–70. [Google Scholar] [CrossRef]
- Algarni, B., & Lortie-Forgues, H. (2023). An evaluation of the impact of flipped-classroom teaching on mathematics proficiency and self-efficacy in Saudi Arabia. British Journal of Educational Technology, 54(1), 414–435. [Google Scholar] [CrossRef]
- Anastasakis, M., Zakynthinaki, M., Trujillo-González, R., García-Alonso, I., & Petridis, K. (2022). An activity theory approach in explaining engineering students’ difficulties with university mathematics. International Journal of Mathematical Education in Science and Technology, 53(6), 1571–1587. [Google Scholar] [CrossRef]
- Ashwin, P. (2012). Analysing teaching-learning interactions in higher education: Accounting for structure and agency. Bloomsbury Publishing. [Google Scholar]
- Balwant, P. T., & Doon, R. (2021). Alternatives to the conventional ‘Oxford’ tutorial model: A scoping review. International Journal of Educational Technology in Higher Education, 18(1), 29. [Google Scholar] [CrossRef]
- Barab, S. A., Barnett, M., Yamagata-Lynch, L., Squire, K., & Keating, T. (2002). Using activity theory to understand the systemic tensions characterizing a technology-rich introductory astronomy course. Mind, Culture, and Activity, 9(2), 76–107. [Google Scholar] [CrossRef]
- Bergmann, J., & Sams, A. (2012). Flip your classroom: Reach every student in every class every day. International Society for Technology in Education. [Google Scholar]
- Chan, M. C. E., & Clarke, D. (2017). Structured affordances in the use of open-ended tasks to facilitate collaborative problem solving. ZDM, 49(6), 951–963. [Google Scholar] [CrossRef]
- Chen, Y., Zhao, T., Chen, L., Jiang, G., Geng, Y., Li, W., Yin, S., Tong, X., Tao, Y., Ni, J., Lu, Q., Ning, M., & Wu, C. (2024). SARS-CoV-2 Omicron infection augments the magnitude and durability of systemic and mucosal immunity in triple-dose CoronaVac recipients. mBio, 15(4), e02407-23. [Google Scholar] [CrossRef] [PubMed]
- Cooper, J., Gamlieli, H. L., Koichu, B., Karsenty, R., & Pinto, A. (2021, July 19–22). Instructional innovation in mathematics courses for engineering programs—A case study. 44th Conference of the International Group for the Psychology of Mathematics Education, Online. [Google Scholar]
- Durandt, R., Herbst, S., & Seloane, M. (2022). Teaching and learning first-year engineering mathematics at a distance: A critical view over two consecutive years. Perspectives in Education, 40(1), 143–163. [Google Scholar] [CrossRef]
- Engeström, Y. (2001). Expansive learning at work: Toward an activity theoretical reconceptualization. Journal of Education and Work, 14(1), 133–156. [Google Scholar] [CrossRef]
- Engeström, Y. (2014a). Activity theory and learning at work. Springer. [Google Scholar]
- Engeström, Y. (2014b). Learning by expanding: An activity-theoretical approach to developmental research. Cambridge University Press. [Google Scholar]
- Engeström, Y., & Sannino, A. (2011). Discursive manifestations of contradictions in organizational change efforts: A methodological framework. Journal of Organizational Change Management, 24(3), 368–387. [Google Scholar] [CrossRef]
- Entwistle, N. (2000, November 9–10). Promoting deep learning through teaching and assessment: Conceptual frameworks and educational contexts. TLRP Conference, Leicester, UK. [Google Scholar]
- Erickson, B. L., Peters, C. B., & Strommer, D. W. (2009). Teaching first-year college students. John Wiley & Sons. [Google Scholar]
- Faulkner, B., Earl, K., & Herman, G. (2019). Mathematical maturity for engineering students. International Journal of Research in Undergraduate Mathematics Education, 5, 97–128. [Google Scholar] [CrossRef]
- Flegg, J., Mallet, D., & Lupton, M. (2012). Students’ perceptions of the relevance of mathematics in engineering. International Journal of Mathematical Education in Science and Technology, 43(6), 717–732. [Google Scholar] [CrossRef]
- Foot, K., & Groleau, C. (2011). Contradictions, transitions, and materiality in organizing processes: An activity theory perspective. First Monday, 16(6). [Google Scholar] [CrossRef]
- Friedman, M. (1937). The use of ranks to avoid the assumption of normality implicit in the analysis of variance. Journal of the American Statistical Association, 32(200), 675–701. [Google Scholar] [CrossRef]
- Galligan, L., & Hobohm, C. (2015). Investigating students’ academic numeracy in 1st level university courses. Mathematics Education Research Journal, 27(2), 129–145. [Google Scholar] [CrossRef]
- Gamlath, S. (2022). Peer learning and the undergraduate journey: A framework for student success. Higher Education Research & Development, 41(3), 699–713. [Google Scholar]
- Gedera, D. S. (2016). The application of activity theory in identifying contradictions in a university blended learning course. In Activity theory in education: Research and practice (pp. 53–69). Springer. [Google Scholar]
- Godfrey, E., Aubrey, T., & King, R. (2010). Who leaves and who stays? Retention and attrition in engineering education. Engineering Education, 5(2), 26–40. [Google Scholar] [CrossRef]
- Gopalan, C., Bracey, G., Klann, M., & Schmidt, C. (2018). Embracing the flipped classroom: The planning and execution of a faculty workshop. Advances in Physiology Education, 42(4), 648–654. [Google Scholar] [CrossRef]
- Harris, D., Black, L., Hernandez-Martinez, P., Pepin, B., & Williams, J. (2015). Mathematics and its value for engineering students: What are the implications for teaching? International Journal of Mathematical Education in Science and Technology, 46(3), 321–336. [Google Scholar] [CrossRef]
- Harris, D., & Pampaka, M. (2016). They [the lecturers] have to get through a certain amount in an hour’: First year students’ problems with service mathematics lectures. Teaching Mathematics and Its Applications: International Journal of the IMA, 35(3), 144–158. [Google Scholar] [CrossRef][Green Version]
- Jablonka, E., Ashjari, H., & Bergsten, C. (2017). “Much palaver about greater than zero and such stuff”—First year engineering students’ recognition of university mathematics. International Journal of Research in Undergraduate Mathematics Education, 3(1), 69–107. [Google Scholar] [CrossRef]
- Jaworski, B., Robinson, C. L., Matthews, J., & Croft, T. (2012). An activity theory analysis of teaching goals versus student epistemological positions. International Journal for Technology in Mathematics Education, 19, 147–152. [Google Scholar]
- Jeong, J. S., González-Gómez, D., & Cañada-Cañada, F. (2021). How does a flipped classroom course affect the affective domain toward science course? Interactive Learning Environments, 29(5), 707–719. [Google Scholar] [CrossRef]
- Jooganah, K., & Williams, J. S. (2016). Contradictions between and within school and university activity systems helping to explain students’ difficulty with advanced mathematics. Teaching Mathematics and Its Applications: International Journal of the IMA, 35(3), 159–171. [Google Scholar]
- Jourdan, N., Cretchley, P., & Passmore, T. (2007, July 2–6). Secondary-tertiary transition: What mathematics skills can and should we expect this decade? 30th Annual Conference of the Mathematics Education Research Group of Australasia (MERGA 30), Hobart, Australia. [Google Scholar]
- Karanasios, S., Riisla, K., & Simeonova, B. (2017, July 6–8). Exploring the use of contradictions in activity theory studies: An interdisciplinary review. 33rd EGOS Colloquium: The Good Organization, Copenhagen, Denmark. [Google Scholar]
- Kay, R., MacDonald, T., & DiGiuseppe, M. (2019). A comparison of lecture-based, active, and flipped classroom teaching approaches in higher education. Journal of Computing in Higher Education, 31(3), 449–471. [Google Scholar] [CrossRef]
- Kift, S. (2015). A decade of transition pedagogy: A quantum leap in conceptualising the first year experience. HERDSA Review of Higher Education, 2(1), 51–86. [Google Scholar]
- King, D., & Cattlin, J. (2015). The impact of assumed knowledge entry standards on undergraduate mathematics teaching in Australia. International Journal of Mathematical Education in Science and Technology, 46(7), 1032–1045. [Google Scholar] [CrossRef]
- Kirschenman, M., & Brenner, B. (2010). Education for civil engineering: A profession of practice. Leadership and Management in Engineering, 10(1), 54–56. [Google Scholar] [CrossRef]
- Klein, K., Calabrese, J., Aguiar, A., Mathew, S., Ajani, K., Almajid, R., & Aarons, J. (2023). Evaluating active lecture and traditional lecture in higher education. Journal on Empowering Teaching Excellence, 7(2), 6. [Google Scholar]
- Kozulin, A. (2014). Dynamic assessment in search of its identity. In The Cambridge handbook of cultural-historical psychology (pp. 126–147). Cambridge University Press. [Google Scholar]
- Kuutti, K. (1996). Activity theory as a potential framework for human-computer interaction research. In Context and consciousness: Activity theory and human-computer interaction (pp. 17–44). MIT Press. [Google Scholar]
- Leong, E., Mercer, A., Danczak, S. M., Kyne, S. H., & Thompson, C. D. (2021). The transition to first year chemistry: Student, secondary and tertiary educator’s perceptions of student preparedness. Chemistry Education Research and Practice, 22(4), 923–947. [Google Scholar] [CrossRef]
- Leont’ev, A. A. (1981). Psychology and the language learning process. Pergamon. [Google Scholar]
- Liu, F., Wang, X., & Izadpanah, S. (2023). The comparison of the efficiency of the lecture method and flipped classroom instruction method on EFL students’ academic passion and responsibility. Sage Open, 13(2), 21582440231174355. [Google Scholar] [CrossRef]
- Lo, C. K., & Hew, K. F. (2017). A critical review of flipped classroom challenges in K-12 education: Possible solutions and recommendations for future research. Research and Practice in Technology Enhanced Learning, 12, 4. [Google Scholar] [CrossRef]
- Luria, A. K. (1971). Towards the problem of the historical nature of psychological processes. International Journal of Psychology, 6(4), 259–272. [Google Scholar] [CrossRef]
- Mason, M. J., & Gayton, A. M. (2022). Active learning in flipped classroom and tutorials: Complementary or redundant? International Journal for the Scholarship of Teaching and Learning, 16(2), 6. [Google Scholar] [CrossRef]
- Mazana, Y. M., Suero Montero, C., & Olifage, C. R. (2019). Investigating students’ attitude towards learning mathematics. International Electronic Journal of Mathematics Education, 14, 207–231. [Google Scholar] [CrossRef] [PubMed]
- McLean, S., Attardi, S. M., Faden, L., & Goldszmidt, M. (2016). Flipped classrooms and student learning: Not just surface gains. Advances in Physiology Education, 40(1), 47–55. [Google Scholar] [CrossRef]
- Morán-Soto, G., González-García, N. I., López-Torres, R. M., Cabrera-Martínez, R., Medina-Núñez, A., & Cardoza-Martínez, M. G. (2023, October 23–27). The importance of differential calculus in the performance of enginnering students. 2023 World Engineering Education Forum-Global Engineering Deans Council (WEEF-GEDC), Monterrey, Mexico. [Google Scholar]
- Murphy, E., & Rodriguez-Manzanares, M. A. (2008). Using activity theory and its principle of contradictions to guide research in educational technology. Australasian Journal of Educational Technology, 24(4), 442–457. [Google Scholar] [CrossRef]
- Nelson, C. P., & Kim, M.-K. (2001). Contradictions, appropriation, and transformation: An activity theory approach to L2 writing and classroom practices. Texas Papers in Foreign Language Education, 6(1), 37–62. [Google Scholar]
- Norman, G. (2010). Likert scales, levels of measurement and the “laws” of statistics. Advances in Health Sciences Education, 15, 625–632. [Google Scholar] [CrossRef]
- Pepin, B., Biehler, R., & Gueudet, G. (2021). Mathematics in engineering education: A review of the recent literature with a view towards innovative practices. International Journal of Research in Undergraduate Mathematics Education, 7(2), 163–188. [Google Scholar] [CrossRef]
- Piaget, J. (1967). On the development of memory and identity. Clark University Press. [Google Scholar]
- Piaget, J. (1976). Piaget’s theory. In Piaget and his school (pp. 11–23). Springer. [Google Scholar]
- Sijtsma, K., & Emons, W. (2010). Nonparametric statistical methods. In International encyclopedia of education (pp. 347–353). Elsevier. [Google Scholar]
- Silverstein, D., & Baker, J. (2003, June 22–25). Improving retention of calculus by engineering students in small programs. 2003 Annual Conference, Nashville, TN, USA. [Google Scholar]
- Skinner, B. F. (1985). Cognitive science and behaviourism. British Journal of Psychology, 76(3), 291–301. [Google Scholar] [CrossRef] [PubMed]
- Smallhorn, M. (2017). The flipped classroom: A learning model to increase student engagement not academic achievement. Student Success, 8(2), 43–53. [Google Scholar] [CrossRef]
- Steen-Utheim, A. T., & Foldnes, N. (2018). A qualitative investigation of student engagement in a flipped classroom. Teaching in Higher Education, 23(3), 307–324. [Google Scholar] [CrossRef]
- Street, S. E., Gilliland, K. O., McNeil, C., & Royal, K. (2015). The flipped classroom improved medical student performance and satisfaction in a pre-clinical physiology course. Medical Science Educator, 25, 35–43. [Google Scholar] [CrossRef]
- Tesfamicael, S. A. (2022). Prospective teachers’ cognitive engagement during virtual teaching using GeoGebra and Desmos. Pythagoras, 43(1), a691. [Google Scholar] [CrossRef]
- Vrbin, C. M. (2022). Parametric or nonparametric statistical tests: Considerations when choosing the most appropriate option for your data. Cytopathology, 33(6), 663–667. [Google Scholar] [CrossRef]
- Vygotsky, L. (1978). Social development theory. In Instructional design. Stipes Publishing Company. [Google Scholar]
- Vygotsky, L. S., & Cole, M. (1978). Mind in society: Development of higher psychological processes. Harvard University Press. [Google Scholar]
- Woolcott, G., Chamberlain, D., Whannell, R., & Galligan, L. (2019). Examining undergraduate student retention in mathematics using network analysis and relative risk. International Journal of Mathematical Education in Science and Technology, 50(3), 447–463. [Google Scholar] [CrossRef]
- Zhou, Q., & Zhang, H. (2025). Flipped classroom teaching and ARCS motivation model: Impact on college students’ deep learning. Education Sciences, 15(4), 517. [Google Scholar] [CrossRef]

| Primary Contradictions | Occur within the activity that brings about the conflict, where more than one value is associated with an element. The learner sees a contradiction between use value and exchange value. |
| Secondary Contradictions | Occur when the learner finds conflict in assimilating or integrating a new element. |
| Tertiary Contradictions | Occur when an advanced form of method emerges for achieving the objective. |
| Quaternary Contradictions | Occur between activities when the learner finds changes in an activity as conflicts with adjacent activities. |
| Student Background | Number of Participants | Age Range |
|---|---|---|
| Domestic Mature (Years left school > 5 years) | 8 | 30–60 |
| Domestic Secondary (Years left School < 2) | 6 | 20–29 |
| International (Years left School < 2) | 6 | 20–29 |
| Overall Average Before (KB) | Overall Average Middle (KM) | Overall Average After (KA) | |
|---|---|---|---|
| Confidence | 1.58 | 2.71 | 4.03 |
| Competence | 1.51 | 2.81 | 3.94 |
| Knowledge | 1.52 | 2.68 | 4.06 |
| Confidence Analysis Results | Competence Analysis Results | Knowledge Analysis Results |
|---|---|---|
| Friedman’s test statistic: 59.0, p-value: 0 | Friedman’s test statistic: 60.5, p-value: 0 | Friedman’s test statistic: 60.6, p-value: 0 |
| Significant difference (CFA, CFM, CFA) | Significant difference (CPA, CPM, CPA) | Significant difference (KB, KM, KA) |
| Wilcoxon’s Signed-Rank Test | Wilcoxon’s Signed-Rank Test | Wilcoxon’s Signed-Rank Test |
| Before vs. Mid: p = 0.0000005319 | Before vs. Mid: p = 0.0000005682 | Before vs. Mid: p = 0.0000000009 |
| Before vs. After: p = 0.0000010371 | Before vs. After: p = 0.0000000009 | Before vs. After: p = 0.0000000009 |
| Mid vs. After: p = 0.0000011325 | Mid vs. After: p = 0.0000005319 | Mid vs. After: p = 0.0000020929 |
| Significant difference between Before and Mid. | Significant difference between Before and Mid. | Significant difference between Before and Mid. |
| Significant difference between Before and After. | Significant difference between Before and After. | Significant difference between Before and After. |
| Significant difference between Mid and After. | Significant difference between Mid and After. | Significant difference between Mid and After. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raj, N.; Sharma, E.; Singh, N.; Downs, N.; Salmeron, R.; Galligan, L. Reforming First-Year Engineering Mathematics Courses: A Study of Flipped-Classroom Pedagogy and Student Learning Outcomes. Educ. Sci. 2025, 15, 1124. https://doi.org/10.3390/educsci15091124
Raj N, Sharma E, Singh N, Downs N, Salmeron R, Galligan L. Reforming First-Year Engineering Mathematics Courses: A Study of Flipped-Classroom Pedagogy and Student Learning Outcomes. Education Sciences. 2025; 15(9):1124. https://doi.org/10.3390/educsci15091124
Chicago/Turabian StyleRaj, Nawin, Ekta Sharma, Niharika Singh, Nathan Downs, Raquel Salmeron, and Linda Galligan. 2025. "Reforming First-Year Engineering Mathematics Courses: A Study of Flipped-Classroom Pedagogy and Student Learning Outcomes" Education Sciences 15, no. 9: 1124. https://doi.org/10.3390/educsci15091124
APA StyleRaj, N., Sharma, E., Singh, N., Downs, N., Salmeron, R., & Galligan, L. (2025). Reforming First-Year Engineering Mathematics Courses: A Study of Flipped-Classroom Pedagogy and Student Learning Outcomes. Education Sciences, 15(9), 1124. https://doi.org/10.3390/educsci15091124










