Enhancing Mathematics Instruction Through Laboratory Exercises

Abstract

This paper describes creating a new course for engineering technology students at Southeast Missouri State University that focuses on application-based mathematics instruction through laboratory experiments. The course structure comprises beginning the semester with pre-calculus and trigonometry and progressing to calculus and differential equations. The topics are covered from the engineering and engineering technology applications standpoint, with examples from electrical and mechanical systems. A hands-on, problem-based learning approach is selected for teaching the application of mathematics to engineering technology students. This entails students being presented with real-world problems, solving them using mathematical concepts, and then verifying results by using software tools. Specifically, twelve laboratory exercises using Scilab have been incorporated into the course. For engineering students, using engineering examples improves both their ability to understand the material’s relevance and their understanding of mathematical techniques that may be applied to real-world problems that they will likely encounter in their future jobs.

1. Introduction

Engineering students globally face significant hurdles in mathematics courses and studies generally categorize these challenges into three main areas. First, cognitive barriers arise from weak foundational skills (Song, 2019) and abstract teaching methods that do not incorporate engineering applications (Christensen et al., 2023). The second category includes math anxiety (Hopko et al., 2003; Lucietto et al., 2020; Sexton et al., 2022 ) and low self-efficacy resulting from previous negative experiences (Tossavainen et al., 2019). Third, environmental challenges involving poor time management (Susilawati et al., 2022), excessive use of social media (Susilawati et al., 2022), and ineffective teaching schedules form the final category (Athavale et al., 2021).

The literature survey reveals a critical disconnect between mathematical theory and engineering practice (Wilkinson, 2023). Students struggle with understanding decontextualized content (Harris et al., 2015) and lack understanding of mathematical applications (Christensen et al., 2023). This contributes to the 65–73% pass rates in foundation courses (Susilawati et al., 2022) and high attrition rates within undergraduate engineering programs (Zakariya, 2021). Effective interventions include contextualized learning that integrates field-specific examples (Christensen et al., 2023), tiered instructional approaches that address foundational gaps (Dlugosz, 2004), anxiety reduction strategies through experiential problem solving (Buchler, 2013), and technology-enhanced feedback systems (Athavale et al., 2021). In particular, cellphone usage shows a significant negative correlation with performance (r = −0.32) (Athavale et al., 2021), while structured peer learning improves results (Gopalan et al., 2017; Hossain & Rezal, 2018; Muitange, 2024). In addition, successful programs emphasize the implementation of continuous assessment loops.

Mathematics is often taught in a way that focuses only on theory. Many students find this method difficult to follow and uninteresting. Studies have shown that students understand math better when they learn by doing (Geraldi, 2024; Veillon, 2019). Studies suggest that Realistic Mathematics Education (RME) approaches successfully improve the problem-solving skills of students and are better than the traditional method in this aspect. In the RME approach, teachers check the answers of students by writing down detailed answers and providing reasons or explanations as to how the answer was obtained (Juandi et al., 2022; Yuanita et al., 2018). Laboratory exercises allow students to explore math in a hands-on way. These exercises make learning more active and practical. Effective implementation requires structured workflows, iterative feedback, teaching assistance programs (Mohammad et al., 2023), and a collaborative environment (Editorial, 2024).

The importance of an application-based mathematics teaching technique is immense. When it comes to teaching engineering technology students, the need for designing a course to introduce difficult mathematical concepts is very important, since these programs focus less on theoretical approaches to solving engineering problems in favor of hands-on approaches. An application-based mathematics course for engineering technology students helps prepare them for critical thinking, analytical reasoning, and problem solving (Mehrubeoglu et al., 2024). This approach allows students to apply math to typical engineering technology problems in a variety of fields. This means designing lessons and assignments that require students to apply mathematical concepts to real-world engineering problems rather than just solving abstract math problems. In addition to discussing theories and solving mathematical problems, a hands-on approach benefits students by having them using computers to solve complex calculus problems using numerical techniques and visualize the results for analysis. A hands-on approach can be particularly effective for students who may struggle with more traditional lecture-based methods of teaching mathematics (Benedict, 2021). It can help to make the material more concrete and meaningful and increase the motivation and engagement of students within the subject.

This paper looks at how laboratory exercises can improve math instruction within engineering technology programs. Different ways of designing and using labs in teaching are examined. The goal is to show how labs can help students understand and apply mathematics concepts more effectively. The main research questions are the following:

• How do application-based laboratory exercises in a mathematics course for engineering technology students impact student satisfaction and perceived learning?
• Which types of laboratory activities (e.g., integration, differential equations, plotting, and software basics) contribute most significantly to student satisfaction and engagement?
• What are the patterns in student performance across different laboratory topics, and how do these relate to course design and instructional interventions?

These questions were formulated based on gaps identified in the literature regarding the practical application of mathematics in engineering technology education and the need to assess the effectiveness of hands-on, contextualized learning approaches.

2. Course Design/Pedagogy

Prior to the course being introduced, which is the subject of this research study, students within this program were required to take a mathematics class that primarily focused on techniques and procedural fluency. Students would solve problems in integration, multi-variable integrals, and derivatives and perform separation of variables within a differential equations problem. However, there was little, if anything, tying these equations and solutions to real engineering problems. Similarly, in the prerequisite math classes students would focus on solving equations, performing integrations, and manipulating algebraic expressions without direct application to engineering contexts. The new course design aims to bridge this gap by embedding these internal mathematical practices within applied, context-rich engineering problems, thus extending students’ skills from abstract computation to practical application.

Before developing the course for engineering technology students, several options were considered for incorporating hands-on learning into the typically theory-based mathematics instruction:

• Use of real-world examples: In this method, the instructor shows students how math is used in practical, everyday situations in the engineering field, for example, through an in-class demonstration of how to calculate the strength of a beam using beam bending equations or how to design a circuit using Ohm’s law. Studies emphasize that applying mathematical concepts to practical scenarios, such as structural design, data analysis, and optimization, improves deeper comprehension and retention (Abramovich et al., 2019; Wardana et al., 2024). Integrating real-world applications into math instruction helps students connect abstract concepts to tangible outcomes, improving critical thinking and problem-solving abilities (Leatham et al., 2015).
• Hands-on activities and experiments: The instructor will have the students perform hands-on exercises to better understand math concepts. An example would include allowing students to create and test their circuits or to use computer-aided design (CAD) software to develop a small mechanical device. Although this approach has the advantage of introducing real-world experiments to both electrical and mechanical fields, it appeared to be a bit time-consuming given that a variety of mathematical concepts needed to be covered in the given three-credit hour course, which has two hours allotted for lecture and the remaining two hours for lab.
• Group work and collaboration: The objective is to encourage students to work in small groups and discuss concepts of math and their applications (Editorial, 2024). This approach helps students develop their problem-solving skills and improve their understanding of the material (Boaler et al., 2022). Studies show that group work improves exam performance in technical topics such as integration, with students in collaborative settings outperforming peers in individual work by 10% (Sofroniou & Poutos, 2016). Furthermore, structured teamwork in math classes promotes critical STEM (Science, Technology, Engineering, and Mathematics) career skills such as communication and collective problem solving, mirroring real-world engineering practices (Soares et al., 2025).
• Incorporate technology: The idea is to use technology such as online simulations and interactive software to help students visualize math concepts and see how they are applied in the real world (Hudson et al., 2010). The course design would include data analysis, simulation, and/or projects using software tools. Interactive simulations and dynamic software tools, such as MATLAB^® (version R2024a), Scilab (version 2024.1.0), GeoGebra, and Desmos, allow students to visualize abstract concepts and explore mathematical relationships in real-world contexts (Hidayat et al., 2024; Sacristán, 2017). These tools help provide a deeper understanding of the concepts by enabling hands-on exploration, data analysis, and plotting (Santos-Trigo, 2024). Additionally, these technologies prepare students for STEM careers by equipping them with practical skills in problem solving and computational tools.
• Offer additional resources: In this case, the instructor will provide students with additional resources, such as math learning/tutorial centers, assistance from graduate students, online tutorials, videos (Rasheduzzaman et al., 2021), and worksheets, to help them practice and reinforce their understanding of math concepts.

From these various approaches, it was found that the key to efficiently teaching mathematics to engineering technology students is to provide a mix of lectures, laboratory exercises using simulation software packages, and the use of real-world examples.

2.1. Instructional Methods

The course created within this research study is called “Computational Analysis in Engineering and Technology.” Students typically enroll as sophomores or juniors. It is a three-credit hour, 300-level course in an engineering technology program. The course is composed of two hours of lecture and two hours of lab each week. Prior to taking this course, students must complete courses in college algebra, trigonometry, and calculus I. While the course is taught in person, lab work is designed for flexibility. Students can complete lab assignments outside of class by following the instructor’s notes. The course includes twelve homework assignments and twelve lab assignments. There are also two exams and a final. These are used to measure student progress, performance, and whether learning outcomes were achieved.

2.2. Course-Specific Materials

Required materials for the course include instructor-provided notes, laboratory handouts, a reference textbook, and the Scilab software tool. Scilab and Matlab have many similar features, including tools for data analysis, visualization, and numerical computation. However, Scilab is a free and open-source software platform for engineers and scientists to perform numerical computations. It is often seen as an alternative to MATLAB. The main reason for choosing Scilab over MATLAB is that the former can be installed on students’ personal computers at no cost. This means that Scilab is a more appealing option for individuals or organizations with limited budgets. Scilab allows students to work on material off campus and more easily complete assignments at their own pace and in their own time. In addition to that, students are expected to use a calculator for assignments and in-class practice.

2.3. The Goals and Objectives of the Course

The primary goal of the course is to teach students how to solve mathematical problems for physical systems that are commonly found in engineering technology, both by hand and through the development of algorithms and numerical methods using software tools. The course is intended for students majoring in Engineering Technology with an emphasis on either electrical and automation systems or mechanical and manufacturing systems. The course focuses on solving technical problems using algebra, analytical geometry, derivatives, integrals, and differential calculus.

2.4. Student Learning Outcomes

As a 300-level course in the engineering technology program, students are expected to have completed foundational mathematics and introductory engineering courses prior to enrollment. Typically, this includes coursework in algebra, trigonometry, and introductory calculus covering basic differentiation and integration techniques. For reference, these students complete only one calculus course in the university’s three-course calculus sequence. Despite having some experience with calculus, many students have not engaged deeply with applied engineering problems involving full mathematization, modeling, or validation cycles prior to this course. While some may have encountered elementary engineering applications in earlier courses, the systematic use of mathematical modeling (e.g., translating real-world systems into differential equations and validating solutions) is new for most students. The course introduces advanced applications such as solving engineering problems with integrals and differential equations, using computational tools, and validating results, which go beyond the scope of previous coursework and are central to the new learning outcomes.

The following student learning outcomes are measured for the course:

(a)

Students will be able to model a physical system using integral and differential equations.

(b)

Students will be able to solve a mathematical model of an engineering system using computational methods.

(c)

Students will be able to use software to perform computational analysis.

Student learning outcomes are measured using exams, homework, and laboratory assignments.

2.5. Course Outline

The discussed topics include matrices, transcendental functions, complex numbers, vectors, systems of equations, sinusoidal motion, differentiation, solution of dynamical systems, and first- and second-order systems. The lectures contain discussions and in-class problem solving related to these topics. The course outline used in the most recent year is presented in

Table 1. Sample course outline from fall 2024.

Week	Lecture	Lab
1	Basic algebra	Intro to Scilab
2	Trigonometry	Built-in functions
3	Vectors	Labor day—No class
4	Complex numbers	Matrices
5	Sinusoids	Plotting
6	Systems of equations	Functions p1
7	Review	Exam 1
8	Derivatives p1	Functions p2
9	Derivatives p2	Control flow statements
10	Derivatives p3	Numeric DiffEQ p1
11	Integrals p1	Numeric DiffEQ p2
12	Integrals p2	Interpolation, curve fitting
13	Review	Exam 2
14	DiffEQ	Integrals
15	Fall break	Graphical programming
16	Review	Review
17	Final

.

The laboratory experiments are made up of simulations and analysis of systems using software tools. The topics covered in the laboratory sessions and the skills developed in those sessions are as follows:

• Introduction to programming with Scilab (Lab 1): In this topic, students get familiarized with the Scilab tool. The first lab teaches students how to setup Scilab on their computer, use Scilab as a simple calculator, use variables, learn the basics of scalar values and matrices, use SciNotes, and finally, use the help menu to search for commands.
• Scilab built-in functions (Lab 2): In the second lab, students solve mathematical problems utilizing some Scilab built-in functions, such as trigonometric functions, data analysis functions, random numbers, complex numbers, etc. These functions are essential to performing engineering calculations in some of the later labs.
• Use of matrices in engineering (Lab 3): In this topic, students learn how to use matrices to analyze complex systems such as stress networks and circuits with multiple sources. The lab handout starts with examples of matrices and vectors and then moves on to learning about transposing, finding max and min, indexing, use of colon operators, and some special matrix commands, such as zeros, ones, and diag. Students learn when to apply vector multiplication and when to apply scalar multiplication. Finally, students solve systems of linear equations using matrices consisting of engineering problems.
• Two- and three-dimensional-plotting techniques using Scilab (Lab 4): In this topic, students learn how to create 2D and 3D plots using Scilab. This involves learning how to import and manipulate data, as well as how to customize plots to display the data in various ways. Additionally, students learn about, e.g., logarithmic plots, bar and pie charts, subplots, histograms, plots with two y-axes, surface plots, mesh plots, and adding grids, legends, and texts in plots. A sample assignment from this lab is provided in the next section.
• Functions in Scilab (Labs 5 and 6): In this lab, students learn how to create their own functions (commonly known as user-defined functions) and handle functions with multiple inputs and outputs. Students also learn about the anonymous function structures and some common uses of well-known functions such as fsolve and fminsearch in solving engineering problems, such as finding height and zero crossing points for a projectile, etc. Additionally, students learn about the use of local and global variables in this lab session. Since students often struggle with user-defined functions, these topics are spread over two laboratory sessions to enhance the learning experience.
• Control flow statements (Lab 7): In this lab, students learn about relational and logical operators, pseudo-code and flow charts, and the find functions. Students then move on to learning conditional statements and looping structures. The examples include the use of if, if-else, switch-case, for loop, while loop, break-continue, etc.
• Applications of differential equations (Labs 8 and 9): Students spend two laboratory sessions learning the techniques of using Scilab to solve differential equations. Students first learn how to use the derivate function to find the derivative of a polynomial. After that, they move on to numderivative and diff functions. After mastering the concepts, students move on to use Scilab’s ordinary differential equation solver functions to perform numerical differentiation. The examples include solving a leaking bucket problem (first order), LC tank problem solution (second order), and solving the problem of an incompressible flow field in a laminar boundary layer on a flat plate (third order).
• Interpolation and curve fitting (Lab 10): In this topic, students learn how to use interpolation and extrapolation techniques to estimate values between or beyond known data points. These techniques are often used in engineering to make predictions or estimates based on limited data. Learning involves the use of linear, spline, and similar commands. The knowledge is then used to practice on some examples of curve fitting in engineering applications.
• Integration (Lab 11): In this topic, students learn how to use built-in functions in Scilab to perform numerical integration using the trapezoidal rule and spline. Examples also include the use of the integrate command and techniques to solve improper integrals.
• Modeling of systems using graphical approach (Xcos) (Lab 12): This topic involves using Scilab’s Xcos toolbox to model and simulate physical systems in mechanical and electrical engineering. The Xcos environment is first introduced. Students then learn how to set up and solve differential equations found in engineering problems. Examples include the modeling and simulation of a falling object and solving currents and voltages of a second-order RLC circuit.

To link the course learning outcomes with specific competencies and map them to the relevant laboratory exercises, modeling physical systems with differential equations is developed in Labs 8, 9, and 12; computational problem-solving skills in Labs 1–7; and proficiency with software tools in Labs 1–6 and 12. The goal of the course design is to create a clear and coherent plan for delivering the content of the course and helping students achieve the learning outcomes that have been identified earlier.

3. Student Score Analysis

In general, this course uses a focused, hands-on approach to teach engineering technology students how to solve real-world math problems. When students see how the techniques they are learning are used in their field of study, it makes the material more meaningful and relevant to them. It also helps them to see the value and importance of the material and to understand how it can be used in their future careers. Using examples from the same discipline also helps to make the material more concrete and to give students a better understanding of the context in which the techniques are used. To help determine the efficacy of the course design, student assessments from the course were analyzed. To ensure the consistent scoring of laboratory assignments across years, a detailed marking scheme was used for all labs, and the same instructor (and closely supervised teaching assistants) graded assignments each year. The assignments included hands-on problem solving, data analysis, simulation tasks, and Scilab codes, all designed to assess the conceptual understanding and application of mathematical methods in engineering contexts. In previous mathematics courses, students learn to solve first-order differential equations of the form $3{\displaystyle \frac{dy}{dx}}+y=0,y\left(0\right)=1$ using standard techniques but without connecting the mathematics to physical systems. In electrical engineering courses, students may analyze circuit behavior using formulas but may not construct or solve the underlying differential equations themselves. In this course, students are guided through the full modeling cycle: they derive the differential equation from a physical circuit, solve it analytically and numerically (using Scilab), interpret the solution in terms of circuit behavior, and validate the model by comparing simulated and expected results. This approach integrates and extends the content of both prior mathematics and engineering courses, emphasizing the process of mathematization, computational work, and validation. Figure 1 is a sample assignment that is used to evaluate student performance in Lab 9.. Another assignment is shown in Figure 2, which includes concepts from Scilab coding and plotting. The scores from the laboratory assignments are averaged by year. A comparison is then made between average scores obtained in a particular year. The comparison is shown in Figure 3.

The student score dataset consists of average scores for 12 lab assignments evaluated over three consecutive years. The three-year period shows interesting patterns in overall performance. In 2022, the baseline year showed consistent performance (average of 89.58%) with relatively moderate variation across labs (standard deviation of 6.36%). The highest score was 99% (Lab 8), and the lowest was 80% (Lab 5). In 2023, a noticeable decline occurred, with average performance dropping to 86.83%, accompanied by the highest variability (standard deviation of 10.07%). This year contained both a perfect score (Lab 1 at 100%) and the lowest score in the entire dataset (Lab 4 at 64%). Finally, 2024 was a strong recovery and improvement year, with the highest overall average (92.58%), featuring three perfect scores (Labs 1, 3, and 7), though Lab 11 showed concerning decline to 70%.

As far as the lab-specific performance goes, analyzing individual labs across years reveals several noteworthy patterns.

• Consistently Strong Performers: Lab 8 maintained excellent performance throughout (averaging 97.33%), while Lab 7 showed similar strength (96% average).
• Most Improved: Lab 5 showed consistent improvement each year (80% → 85% → 95%), demonstrating effective instructional adjustments.
• Most Volatile: Lab 4 experienced dramatic fluctuation, dropping from 91% in 2022 to 64% in 2023, then rebounding strongly to 98% in 2024.
• Concerning Decline: Lab 11 showed consistent deterioration (98% → 80% → 70%), suggesting a need for immediate instructional intervention. Considering that this is one of the difficult problems to grasp at this level, this trend is somewhat troubling. After careful observations, it was identified that a few more example problems related to the real-world scenario need to be included.

The score data also reveal several distinct patterns that merit deeper investigation. The number of labs achieving perfect scores increased from none in 2022 to one in 2023 (Lab 1) and then to three in 2024 (Labs 1, 3, and 7). This suggests overall improvement in instruction methods and student comprehension in specific areas. The noticeable decline in 2023’s overall performance can be attributed to the curriculum change, where students were required to take one less physics course that covered more of the physical system. The strong recovery in 2024 indicates that remedial actions were implemented to address the previous year’s challenges by spending more time in discussing the physical system during the lecture, resulting in the highest overall performance of the three years.

When student-by-student scores are analyzed, it is found that most scores fall between 75% and 100%. There are a few students who scored zeros on one or more labs, mainly because they were absent for that assignment. There are also a few students who scored 50% or lower on one or more labs. Such low scores are obtained when a student completes the in-class practice sessions but fails to complete the end of the lab assignment or does not turn in their work on Canvas for an assignment. A wide variation was observed for the last lab, which included the design and simulation of a second-order system. It was interesting to notice that students found the laboratory experiments to be effective in helping them understand difficult math concepts. Using hands-on, experiential learning can be a very effective way for students to engage with and learn new material, especially when it comes to subjects like math that may require more abstract thinking. These types of activities can also help to make the material more concrete and meaningful for students, which can increase their motivation and engagement with the subject. The course enhances the understanding of mathematical concepts by requiring engineering technology students to model, solve, and interpret results in real engineering contexts. For example, students not only solve differential equations but also analyze their solutions in terms of physical system behavior, deepening conceptual understanding beyond rote application. While there is a risk that understanding could be limited to specific applications, the course deliberately includes diverse examples to promote broader mathematical understanding for engineering technology students. The primary goal is to develop more effective engineering technologists rather than to train mathematicians.

4. Survey Data Analysis

Data were collected over three years (2022–2024, fall semesters). The course is offered once a year. A total of 40 samples were analyzed. The survey had 22 questions that focus on student demographics and background, lab structure and effectiveness, instructor/teaching environment, and overall course feedback. Among those, 14 key questions were selected as variables to fit the machine learning models to determine which lab activities contribute the most to student satisfaction and which aspects may need improvement. The original survey responses were in descriptive terms, and necessary data preprocessing was performed to transform these responses into ordinal variables, as depicted in

Table 2. Description of selected variables.

Variable Name	Type	Scale/Range
Academic status	Ordinal	Likert Scale (1–4)
Prior knowledge	Ordinal	Likert Scale (1–4)
Scilab labs	Ordinal	Likert Scale (1–3)
Plotting labs	Ordinal	Likert Scale (1–3)
Matrices labs	Ordinal	Likert Scale (1–3)
Differential equations labs	Ordinal	Likert Scale (1–3)
Interpolation and curve fitting labs	Ordinal	Likert Scale (1–3)
Integration labs	Ordinal	Likert Scale (1–3)
Graphical approach labs	Ordinal	Likert Scale (1–3)
Instructor role	Ordinal	Likert Scale (1–4)
Lab materials clarity and understandability	Ordinal	Likert Scale (1–4)
Adequate instructor interaction	Ordinal	Likert Scale (1–4)
Active collaboration in groups	Ordinal	Likert Scale (1–4)
Level of satisfaction	Ordinal	Likert Scale (1–4)

. Please note that labs 1, 2, 5, 6, and 7 were combined under the Scilab labs variable because these labs are used to familiarize students with the basic Scilab commands. This information was communicated to the students prior to completing the survey.

Because of the ordinal nature of the variables, the following three classification models were selected as the most appropriate algorithms for the dataset: (1) Ordered Logistic Regression as a traditional parametric model for ordinal classification, (2) the CatBoost classifier as a gradient boosting model for categorical data, and (3) the Random Forest classifier for nonparametric tree-based ensemble learning. Five-fold stratified cross-validation was used to ensure a reliable estimate of model performance, since class imbalance was identified during the EDA process. Model evaluation metrics include MAE (Mean Absolute Error; it captures prediction distance in ordinal outcomes), QWK (Quadratic Weighted Kappa; it assesses agreement between predicted and true satisfaction levels while accounting for ordinality), F1-score (reflects classification performance, particularly for underrepresented categories), and accuracy (reported only for completeness).

The following hyperparameters were used:

• Ordered Logistic Regression: alpha = 0 (no regularization to maintain interpretability).
• CatBoost Classifier: iterations = 500, learning rate = 0.1, and depth = 3.
• Random Forest Classifier: n estimators = 200.

All analyses were conducted using Python 3.11.5 in a macOS environment. The following library versions were used to ensure reproducibility and consistency across modeling tasks: scikit-learn 1.7.1; pandas 2.0.3; numpy 1.24.3; matplotlib: 3.7.2; seaborn: 0.12.2; mord 0.7; catboost 1.2.7.

5. Results and Discussion

5.1. Results

Table 3. Model performance metrics.

Model	MAE	QWK	Accuracy	F1	F1	F1
				(Class 2)	(Class 3)	(Class 4)
Ordered Logistic	0.475 ± 0.184	0.341 ± 0.343	57%	0.56	0.67	0.35
CatBoost	0.450 ± 0.187	0.419 ± 0.259	55%	0.71	0.63	0.13
Random Forest	0.425 ± 0.187	0.397 ± 0.398	60%	0.78	0.68	0.13

summarizes the results of the performance metrics for the three selected models. The Random Forest classifier achieves the lowest MAE (0.425 ± 0.187) and the highest accuracy (60%), while the CatBoost classifier ranks second in MAE (0.450 ± 0.187), and Ordered Logistic Regression ranks second in accuracy (57%). These results demonstrate that Random Forest produces the best predictive accuracy in estimating student satisfaction levels. In terms of QWK, which measures the ordinal agreement, the CatBoost classifier has the highest value (0.419 ± 0.259), followed by Random Forest and Ordered Logistic Regression, indicating that CatBoost captures ordinal relationships more effectively. The dataset shows a clear imbalance in satisfaction levels, with no observations in Class 1 (“Poor”), 25% in Class 2, 60% in Class 3, and only 15% in Class 4 (“Great”). This distribution poses challenges for machine learning models, which tend to be biased toward majority classes. As a result, all models in this study showed notably low F1-scores for Class 4, despite overall performance metrics such as accuracy and MAE appearing acceptable. Resampling strategies such as Synthetic Minority Oversampling Technique (SMOTE) or applying class weights during training are common solutions to address imbalance; however, they were not used here due to the small sample size, which increases the risk of overfitting. Instead, this study prioritized metrics like F1-score and Quadratic Weighted Kappa (QWK), which better capture performance across all classes in imbalanced settings.

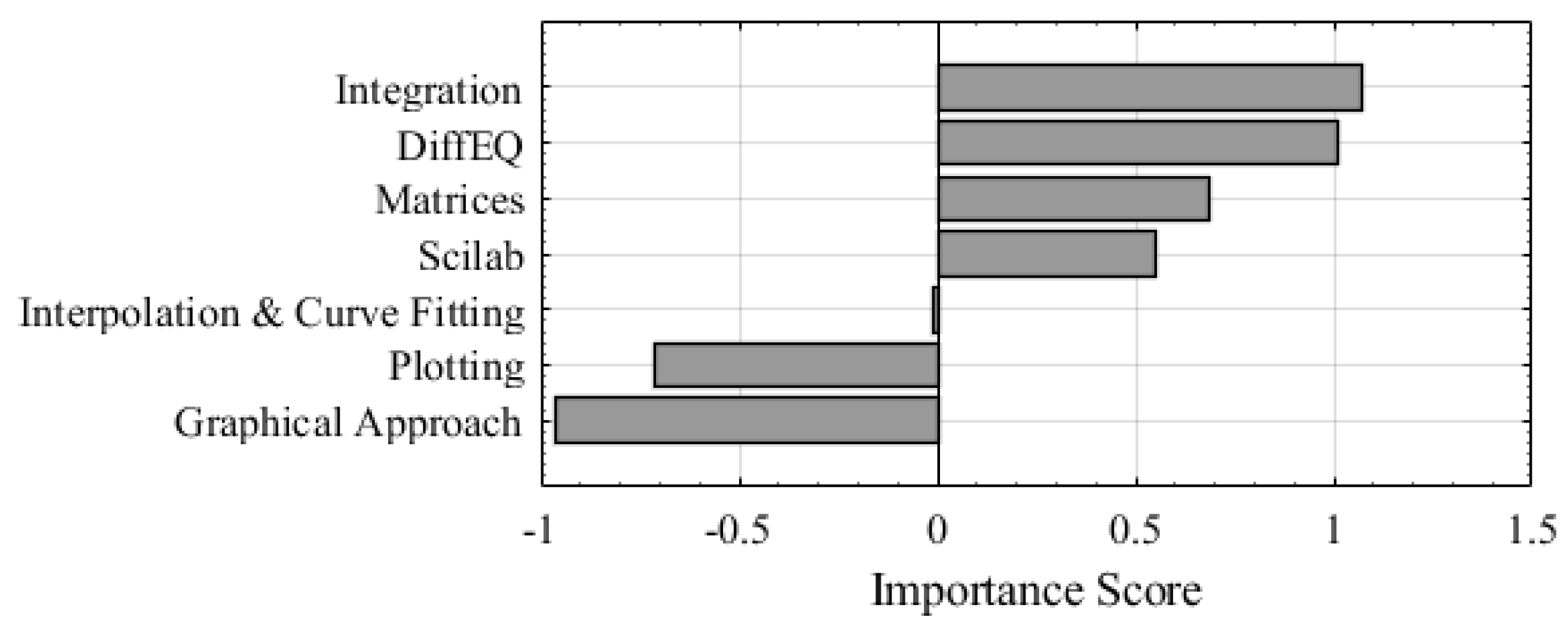
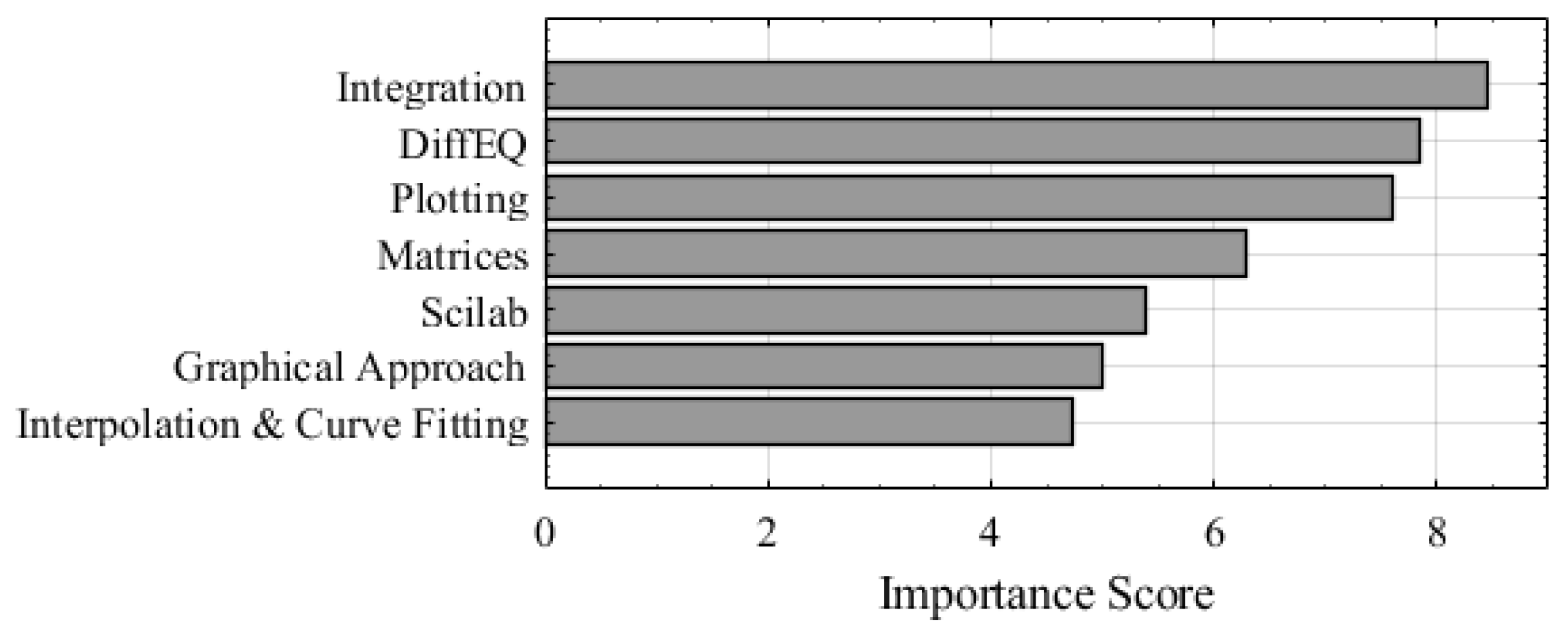
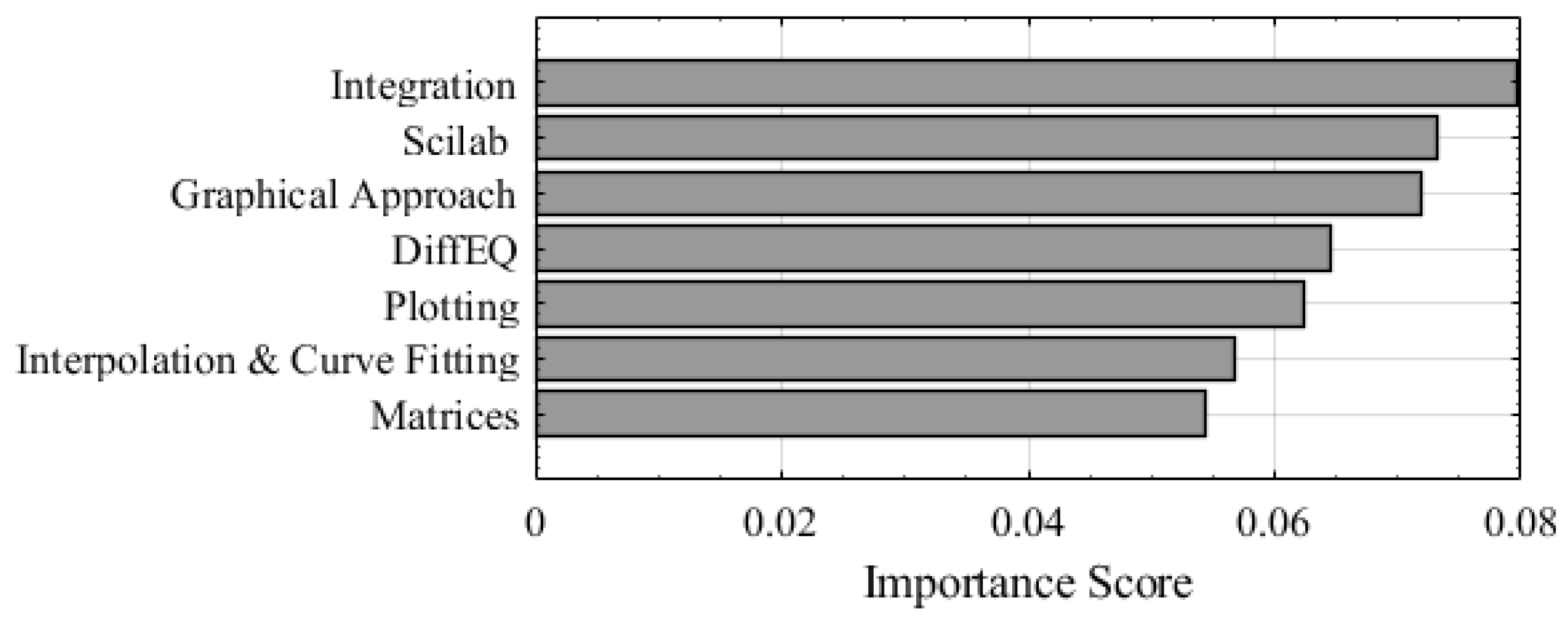
Figure 4, Figure 5 and Figure 6 illustrate the lab variable importance according to the selected models. For the Ordered Logistic Regression model (Figure 4), integration labs and differential equations labs are identified as having the highest positive coefficients, suggesting their strong contribution to overall student satisfaction.

Plotting labs and graphical approach labs are related to negative coefficients, indicating their negative impact on satisfaction. Based on Figure 5, the variable importance scores for integration labs and differential equation labs remain dominant in the CatBoost classifier, which is consistent with the results of the Ordered Logistic Regression model.

However, the plotting labs have now become more influential, ranking the third place among all labs. Matrices labs and Scilab labs are again in the middle of the ranking for CatBoost, and graphical approach labs have little or negative influence on student satisfaction, similar to the conclusion from the Ordered Logistic Regression model. Figure 6 shows the Random Forest feature importance rankings.

Integration labs remain the most significant factor, while Scilab labs as a whole concept gain increased importance compared with the previous models, ranked second. Graphical approach labs also perform a lot better in the Random Forest classifier, suggesting it may be more influential than previously expected. Differential equations labs still have recognizable importance in the Random Forest classifier.

5.2. Discussions

Among the three models, Random Forest is the best-performing model for general classification since it produces the lowest MAE and the highest accuracy. The CatBoost classifier captures the ordinal relationship better than other models with its highest QWK. Ordered Logistic Regression is more interpretable, but its performance is moderate compared with the other two models. Considering the variable importance results from all three models, we can generate the following insights for course improvement:

• Integration labs and differential equations labs are the most important labs that affect student satisfaction. These two labs are consistently ranked as the top features among all three models. Although the student score trends show a downward tendency in the integration lab, students still thought that these labs were the most important ones in the course. Since improving their design and delivery could significantly increase student satisfaction, sufficient efforts and resources should be allocated to ensure they are well-structured and engaging.
• Plotting labs and graphical approach labs show negative associations with satisfaction according to the Ordered Logistic Regression model and moderate-to-low importance on the other two models, which requires special attention from the course instructors. These two problematic labs indicate potential issues with clarity, difficulty, or relevance, requiring a radical lab revision such as simplifying course materials, adding interactive visual aids, improving explanations, etc.
• Interpolation and curve fitting labs demonstrate low importance across all three models, suggesting that students may not perceive them as highly valuable. There may be a lack of connection between the labs and the course objectives. To enhance their relevance, more real-world problems will be incorporated in future labs. Similarly, matrices labs display moderate importance in the Ordered Logistic Regression model and CatBoost classifier and very low importance in the Random Forest classifier, indicating that the matrices labs need to be improved, although they contribute to student learning. In the future, a few more example problems, including circuit analysis, structural dynamics, calculation of stress, etc., will be added.
• The variable “Scilab labs” encompasses all other labs that have been discussed, and the performance varied across different models. The best-performing Random Forest classifier shows that Scilab labs are indeed influential on course satisfaction. Their middle-ranked position in the other two models suggest that some labs within Scilab are valuable, while others may need improvement.

In terms of the limitation of the data analysis, one key aspect that needs to be pointed out is the small sample size of only 40 students, which may restrict the development of a robust machine learning model as well as generalizability to a larger population. The small dataset size constrained the degree to which hyperparameters could be extensively tuned. For Random Forest, we limited the number of trees to reduce complexity but did not manually prune tree depth or adjust node splitting thresholds, which may affect generalization. In CatBoost, although we used 500 iterations, the shallow tree depth and stable cross-validation metrics suggested that the model did not overfit. We acknowledge that more extensive tuning, including early stopping and regularization adjustments, should be considered in future studies with larger datasets. Another limitation is the class imbalance in the dataset, which causes all models to struggle to accurately classify students who reported the highest satisfaction level. While the results offer useful insights into lab effectiveness, they are constrained by the limited sample size and class imbalance. These factors may reduce the stability of model performance and restrict the generalizability of the findings, particularly for underrepresented satisfaction levels. The findings should be interpreted as exploratory and indicative rather than definitive.

6. Difficulties Faced

The mathematical concepts included in the course are selected for their relevance and applicability to engineering and engineering technology. This alignment ensures that students recognize the practical value of the material. Achieving an effective balance between theoretical content and applied practice was a significant challenge. Both elements are essential to establishing a strong conceptual and analytical foundation.

The course is rigorous and demands a high level of problem solving and critical thinking. Designing a curriculum that delivers comprehensive content without overwhelming students requires careful planning. One of the most notable challenges was the integration of Scilab as a computational tool. Students frequently reported difficulty in learning Scilab, largely due to the limited availability of online documentation and instructional examples.

To address this issue, collaborative learning was encouraged. Students were supported through guided instruction from both the course instructor and a graduate assistant. Assistance included detailed problem discussions, strategic hints, and contextual explanations that helped students relate abstract problems to real-world scenarios.

Successful implementation of software tools like Scilab requires alignment with curriculum objectives and adequate instructor preparation. As noted in the literature, meaningful integration of educational technology depends heavily on instructional design and faculty development (Jacobsen et al., 2002; Reiser et al., 2024; Roschelle et al., 2016). In some cases, instructors may experience difficulty adapting to multiple simulation platforms, particularly when professional development opportunities are limited.

A major challenge in teaching problem solving with software tools was found to be students’ misuse of generative AI. Students often rely too much on GenAI. This can reduce critical thinking and creativity. It also raises concerns about academic integrity (Alshamy et al., 2025). Instead of discouraging the use of AI, an interactive approach needs to be developed, which involves a flipped classroom setup (Kwan et al., 2025). To address this issue the course policies are updated to include how GenAI tools may be used, that students are required to disclose any AI assistance in their work, and that critical evaluation of AI-generated outputs is encouraged. These additions aim to help students develop both digital literacy and strong independent problem-solving skills.

7. Conclusions

The course is intended to give students hands-on experience in mathematics, which is essential to an engineering technology program. This course includes laboratory sessions created specifically to acquire insights into engineering technology-related challenges often discussed in upper-level classes. Students learn how to use matrices, integration and differentiation techniques, and graphing tools and interpret data from the solution while doing so. The course design involves the identification of realistic problems that engineering technology students might encounter in their future careers. The course design method encourages students to work in small groups to solve problems, allowing them to collaborate and discuss different approaches to solving the problem. As the students work on the problem, guidance and support are provided as needed. Three different machine learning models were used to study the performance metrics based on the student survey data. The models indicate that integration and differential equations labs are associated with higher student satisfaction. In addition to affects brought on by this research study, this correlation may also be influenced by factors such as repetition of challenging content, improved instructional support, or differences in teaching style compared with previous courses. It is important to continue finding ways to incorporate these types of activities into the engineering technology curriculum to help students better understand and retain the material. A course such as this one often has a diverse student body with varying levels of math aptitude and prior knowledge. It can be challenging to design a course that meets the needs of all students, regardless of their starting point. As a future work, students can be asked to present their solutions to the class, explaining how they used math to solve the problem. This will give them the opportunity to practice their communication skills and deepen their understanding of the math concepts they used. The outcome of the proposed course shows that the key is to make the math relevant and meaningful to the students by showing them how it can be used to solve real-world problems.