Compensatory Relation Between Executive Function and Fluid Intelligence in Predicting Math Learning
Abstract
1. Introduction
1.1. Fluid Intelligence and Executive Functions in Relation to Math Skills
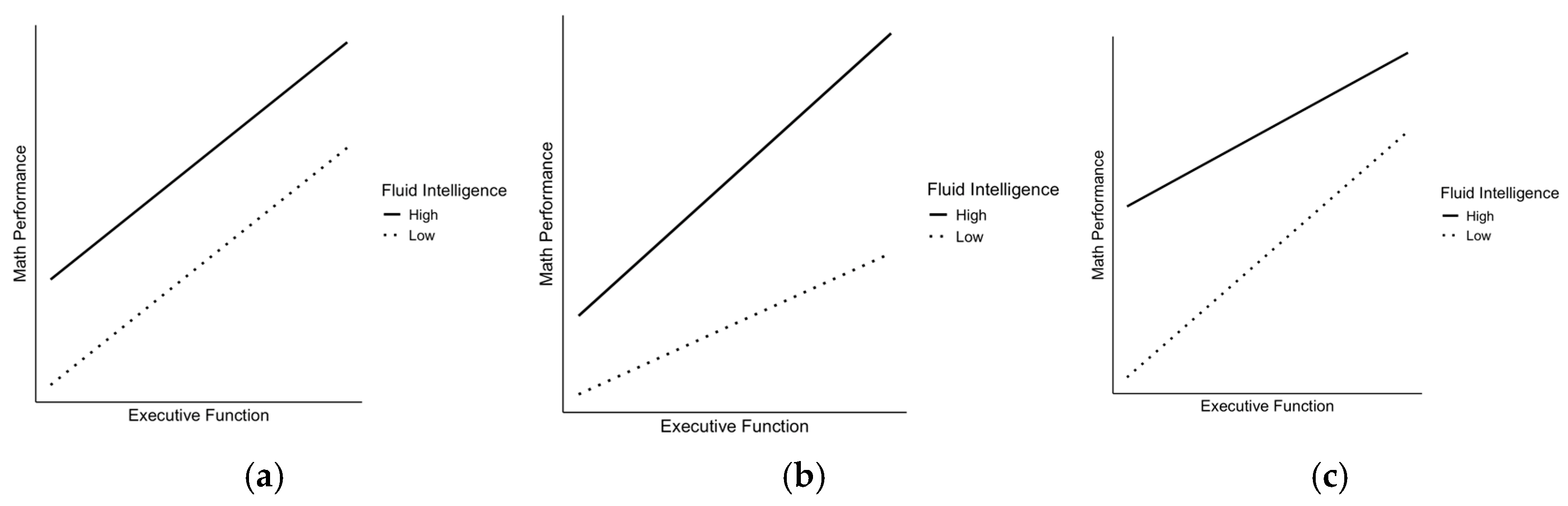
1.2. Considering an Interaction Between Fluid Intelligence and Executive Functions
1.3. Present Study
2. Materials and Methods
2.1. Participants
2.2. Materials
2.2.1. Math Assessment
2.2.2. Executive Functions
2.2.3. Fluid Intelligence
2.3. Procedure
2.4. Analysis
3. Results
3.1. Correlation Analyses
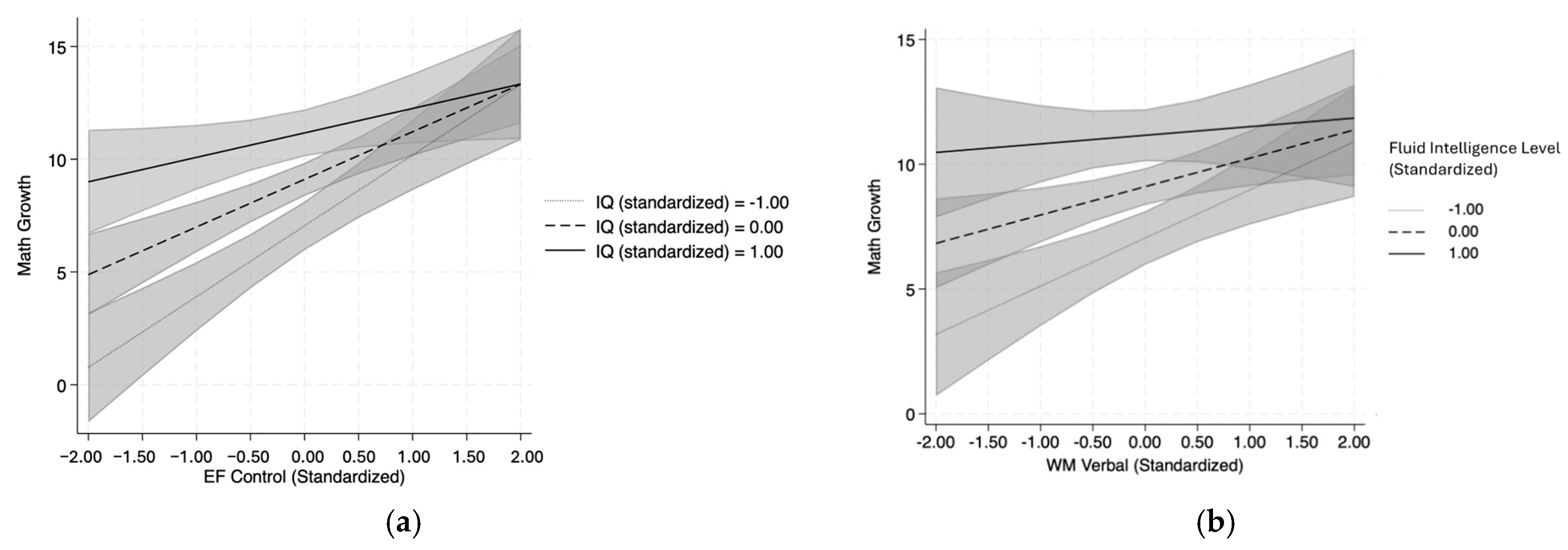
3.2. Regression Analysis
4. Discussion
4.1. Replicating Prior Findings: EF and Fluid Intelligence as Predictors of Math Learning
4.2. Extending Prior Findings: Interaction Between EF and Fluid Intelligence
4.3. Implications
4.4. Limitations and Future Directions
4.5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EF | Executive function |
| WM | Working memory |
| RT | Reaction time |
| SES | Socioeconomic status |
References
- Alloway, T. P., & Alloway, R. G. (2010). Investigating the predictive roles of working memory and IQ in academic attainment. Journal of Experimental Child Psychology, 106(1), 20–29. [Google Scholar] [CrossRef] [PubMed]
- Alloway, T. P., Gathercole, S. E., Adams, A. M., Willis, C., Eaglen, R., & Lamont, E. (2005). Working memory and phonological awareness as predictors of progress towards early learning goals at school entry. British Journal of Developmental Psychology, 23(3), 417–426. [Google Scholar] [CrossRef]
- Alloway, T. P., Gathercole, S. E., & Pickering, S. J. (2006). Verbal and visuospatial short-term and working memory in children: Are they separable? Child Development, 77(6), 1698–1716. [Google Scholar] [CrossRef] [PubMed]
- Andersson, U., & Östergren, R. (2012). Number magnitude processing and basic cognitive functions in children with mathematical learning disabilities. Learning and Individual Differences, 22(6), 181–203. [Google Scholar] [CrossRef]
- Arán Filippetti, V., & Richaud, M. C. (2017). A structural equation modeling of executive functions, IQ and mathematical skills in primary students: Differential effects on number production, mental calculus and arithmetical problems. Child Neuropsychology, 23(7), 864–888. [Google Scholar] [CrossRef]
- Aubrey, C., Godfrey, R., & Dahl, S. (2006). Early mathematics development and later achievement: Further evidence. Mathematics Education Research Journal, 18, 27–46. [Google Scholar] [CrossRef]
- Bayliss, D. M., Jarrold, C., Gunn, D. M., & Baddeley, A. D. (2003). The complexities of complex span: Explaining individual differences in working memory in children and adults. Journal of Experimental Psychology: General, 132(1), 71–92. [Google Scholar] [CrossRef]
- Bäckman, L., & Dixon, R. A. (1992). Psychological compensation: A theoretical framework. Psychological Bulletin, 112(2), 259. [Google Scholar] [CrossRef]
- Blair, C., & Razza, R. P. (2007). Relating effortful control, executive function, and false belief understanding to emerging math and literacy ability in kindergarten. Child Development, 78(2), 647–663. [Google Scholar] [CrossRef]
- Brock, L. L., Rimm-Kaufman, S. E., Nathanson, L., & Grimm, K. J. (2009). The contributions of ‘hot’ and ‘cool’ executive function to children’s academic achievement, learning-related behaviors, and engagement in kindergarten. Early Childhood Research Quarterly, 24(3), 337–349. [Google Scholar] [CrossRef]
- Carriedo, N., Rodríguez-Villagra, O. A., Pérez, L., & Iglesias-Sarmiento, V. (2024). Executive functioning profiles and mathematical and reading achievement in Grades 2, 6, and 10. Journal of School Psychology, 106, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Clark, C. A., Sheffield, T. D., Wiebe, S. A., & Espy, K. A. (2013). Longitudinal associations between executive control and developing mathematical competence in preschool boys and girls. Child Development, 84(2), 662–677. [Google Scholar] [CrossRef]
- Cragg, L., Keeble, S., Richardson, S., Roome, H. E., & Gilmore, C. (2017). Direct and indirect influences of executive functions on mathematics achievement. Cognition, 162, 12–26. [Google Scholar] [CrossRef]
- Davidson, M. C., Amso, D., Anderson, L. C., & Diamond, A. (2006). Development of cognitive control and executive functions from 4 to 13 years: Evidence from manipulations of memory, inhibition, and task switching. Neuropsychological, 44(11), 2037–2078. [Google Scholar] [CrossRef]
- Deary, I. J., Strand, S., Smith, P., & Fernandes, C. (2007). Intelligence and educational achievement. Intelligence, 35(1), 13–21. [Google Scholar] [CrossRef]
- Demetriou, A., Spanoudis, G., Christou, C., Greiff, S., Makris, N., Vainikainen, M. P., & Gonida, E. (2023). Cognitive and personality predictors of school performance from preschool to secondary school: An overarching model. Psychological Review, 130(2), 480–512. [Google Scholar] [CrossRef] [PubMed]
- Diamond, A. (2013). Executive functions. Annual Review of Psychology, 64(1), 135–168. [Google Scholar] [CrossRef]
- Diamond, A., Lee, C., Senften, P., Lam, A., & Abbott, D. (2019). Randomized control trial of Tools of the Mind: Marked benefits to kindergarten children and their teachers. PLoS ONE, 14(9), e0222447. [Google Scholar] [CrossRef]
- Dowker, A. (2019). Individual differences in arithmetic: Implications for psychology, neuroscience and education. Routledge. [Google Scholar]
- Engle, R. W., Tuholski, S. W., Laughlin, J. E., & Conway, A. R. (1999). Working memory, short-term memory, and general fluid intelligence: A latent-variable approach. Journal of Experimental Psychology: General, 128(3), 309. [Google Scholar] [CrossRef]
- Espy, K. A., Sheffield, T. D., Wiebe, S. A., Clark, C. A., & Moehr, M. J. (2011). Executive control and dimensions of problem behaviors in preschool children. Journal of Child Psychology and Psychiatry, 52(1), 33–46. [Google Scholar] [CrossRef]
- Finders, J. K., McClelland, M. M., Geldhof, G. J., Rothwell, D. W., & Hatfield, B. E. (2021). Explaining achievement gaps in kindergarten and third grade: The role of self-regulation and executive function skills. Early Childhood Research Quarterly, 54, 72–85. [Google Scholar] [CrossRef]
- Floyd, R. G., Shaver, R. B., & McGrew, K. S. (2003). Interpretation of the Woodcock-Johnson III tests of cognitive abilities: Acting on evidence. In WJ III clinical use and interpretation (pp. 1–46). Academic Press. [Google Scholar]
- Foley, A. E., Vasilyeva, M., & Laski, E. V. (2017). Children’s use of decomposition strategies mediates the visuospatial memory and arithmetic accuracy relation. British Journal of Developmental Psychology, 35(2), 303–309. [Google Scholar] [CrossRef] [PubMed]
- Friso-van den Bos, I., Van der Ven, S. H., Kroesbergen, E. H., & Van Luit, J. E. (2013). Working memory and mathematics in primary school children: A meta-analysis. Educational Research Review, 10, 29–44. [Google Scholar] [CrossRef]
- Fuchs, D., Kearns, D. M., Fuchs, L. S., Elleman, A. M., Gilbert, J. K., Patton, S., Peng, P., & Compton, D. L. (2019). Using moderator analysis to identify the first-grade children who benefit more and less from a reading comprehension program: A step toward aptitude-by-treatment interaction. Exceptional Children, 85(2), 229–247. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, L. S., Geary, D. C., Compton, D. L., Fuchs, D., Hamlett, C. L., & Bryant, J. D. (2010). The contributions of numerosity and domain-general abilities to school readiness. Child Development, 81(5), 1520–1533. [Google Scholar] [CrossRef]
- Fuchs, M. W., Nesbitt, K. T., Farran, D. C., & Dong, N. (2014). Longitudinal associations between executive functioning and academic skills across content areas. Developmental Psychology, 50(6), 1698. [Google Scholar]
- Fung, W. K., Chung, K. K. H., & Lam, C. B. (2020). Mathematics, executive functioning, and visual–spatial skills in Chinese kindergarten children: Examining the bidirectionality. Journal of Experimental Child Psychology, 199, 104923. [Google Scholar] [CrossRef]
- Geary, D. C. (2011). Cognitive predictors of achievement growth in mathematics: A 5-year longitudinal study. Developmental Psychology, 47(6), 1539–1552. [Google Scholar] [CrossRef]
- Gunzenhauser, C., & Nückles, M. (2021). Training executive functions to improve academic achievement: Tackling avenues to far transfer. Frontiers in Psychology, 12, 624008. [Google Scholar] [CrossRef]
- Henik, A., Rubinsten, O., & Ashkenazi, S. (2015). Developmental dyscalculia as a heterogeneous disability. In R. Kadosh, & A. Dowker (Eds.), The Oxford handbook of numerical cognition (pp. 662–677). Oxford University Press. [Google Scholar]
- Hughes, C., Ensor, R., Wilson, A., & Graham, A. (2009). Tracking executive function across the transition to school: A latent variable approach. Developmental Neuropsychology, 35(1), 20–36. [Google Scholar] [CrossRef]
- Huntsinger, C. S., Jose, P. E., & Luo, Z. (2016). Parental facilitation of early mathematics and reading skills and knowledge through encouragement of home-based activities. Early Childhood Research Quarterly, 37, 1–15. [Google Scholar] [CrossRef]
- Iglesias-Sarmiento, V., Carriedo, N., Rodríguez-Villagra, O. A., & Pérez, L. (2023). Executive functioning skills and (low) math achievement in primary and secondary school. Journal of Experimental Child Psychology, 235, 105715. [Google Scholar] [CrossRef]
- Ivanova, A., Kardanova, E., Merrell, C., Tymms, P., & Hawker, D. (2018). Checking the possibility of equating a mathematics assessment between Russia, Scotland and England for children starting school. Assessment in Education: Principles, Policy & Practice, 25(2), 141–159. [Google Scholar]
- Jordan, N. C., Kaplan, D., Ramineni, C., & Locuniak, M. N. (2009). Early math matters: Kindergarten number competence and later mathematics outcomes. Developmental Psychology, 45(3), 850. [Google Scholar] [CrossRef] [PubMed]
- Kyttälä, M., & Lehto, J. E. (2008). Some factors underlying mathematical performance: The role of visuospatial working memory and non-verbal intelligence. European Journal of Psychology of Education, 23, 77–94. [Google Scholar] [CrossRef]
- Lan, X., Legare, C. H., Ponitz, C. C., Li, S., & Morrison, F. J. (2011). Investigating the links between the subcomponents of executive function and academic achievement: A cross-cultural analysis of Chinese and American preschoolers. Journal of Experimental Child Psychology, 108(3), 677–692. [Google Scholar] [CrossRef]
- Laski, E. V., & Dulaney, A. (2015). When prior knowledge interferes, inhibitory control matters for learning: The case of numerical magnitude representations. Journal of Educational Psychology, 107(4), 1035. [Google Scholar] [CrossRef]
- Lee, K., Bull, R., & Ho, R. M. (2013). Developmental changes in executive functioning. Child Development, 84(6), 1933–1953. [Google Scholar] [CrossRef]
- Lee, K., Ng, S. F., Pe, M. L., Ang, S. Y., Hasshim, M. N. A. M., & Bull, R. (2012). The cognitive underpinnings of emerging mathematical skills: Executive functioning, patterns, numeracy, and arithmetic. British Journal of Educational Psychology, 82(1), 82–99. [Google Scholar] [CrossRef]
- LeFevre, J. A., Fast, L., Skwarchuk, S. L., Smith-Chant, B. L., Bisanz, J., Kamawar, D., & Penner-Wilger, M. (2010). Pathways to mathematics: Longitudinal predictors of performance. Child Development, 81(6), 1753–1767. [Google Scholar] [CrossRef]
- Lehto, J. E., Juujärvi, P., Kooistra, L., & Pulkkinen, L. (2003). Dimensions of executive functioning: Evidence from children. British Journal of Developmental Psychology, 21(1), 59–80. [Google Scholar] [CrossRef]
- Lin, X., & Powell, S. R. (2021). Examining the relation between whole numbers and fractions: A meta-analytic structural equation modeling approach. Contemporary Educational Psychology, 67, 102017. [Google Scholar] [CrossRef]
- McAuley, T., & White, D. A. (2011). A latent variables examination of processing speed, response inhibition, and working memory during typical development. Journal of Experimental Child Psychology, 108(3), 453–468. [Google Scholar] [CrossRef]
- McGrew, K. S., & Hessler, G. L. (1995). The relationship between the WJ-R Gf-Gc cognitive clusters and mathematics achievement across the life-span. Journal of Psychoeducational Assessment, 13(1), 21–38. [Google Scholar] [CrossRef]
- Miyake, A., Friedman, N. P., Emerson, M. J., Witzki, A. H., Howerter, A., & Wager, T. D. (2000). The unity and diversity of executive functions and their contributions to complex “frontal lobe” tasks: A latent variable analysis. Cognitive Psychology, 41(1), 49–100. [Google Scholar] [CrossRef]
- Nadler, R. T., & Archibald, L. M. D. (2014). The assessment of verbal and visuospatial working memory with school age Canadian children. Canadian Journal of Speech-Language Pathology and Audiology, 38(3), 262–279. [Google Scholar]
- Nesbitt, K. T., Farran, D. C., & Fuchs, M. W. (2015). Executive function skills and academic achievement gains in prekindergarten: Contributions of learning-related behaviors. Developmental Psychology, 51(7), 865. [Google Scholar] [CrossRef]
- Peng, P., Namkung, J., Barnes, M., & Sun, C. (2016). A meta-analysis of mathematics and working memory: Moderating effects of working memory domain, type of mathematics skill, and sample characteristics. Journal of Educational Psychology, 108(4), 455. [Google Scholar] [CrossRef]
- Peng, P., Wang, T., Wang, C., & Lin, X. (2019). A meta-analysis on the relation between fluid intelligence and reading/mathematics: Effects of tasks, age, and social economics status. Psychological Bulletin, 145(2), 189. [Google Scholar] [CrossRef]
- Pickering, S. J., & Gathercole, S. E. (2001). Working memory test battery for children. Pearson. [Google Scholar]
- Primi, R., Ferrão, M. E., & Almeida, L. S. (2010). Fluid intelligence as a predictor of learning: A longitudinal multilevel approach applied to math. Learning and Individual Differences, 20(5), 446–451. [Google Scholar] [CrossRef]
- Ramani, G. B., Daubert, E. N., Lin, G. C., Kamarsu, S., Wodzinski, A., & Jaeggi, S. M. (2020). Racing dragons and remembering aliens: Benefits of playing number and working memory games on kindergartners’ numerical knowledge. Developmental Science, 23(4), e12908. [Google Scholar] [CrossRef]
- Ramani, G. B., Rowe, M. L., Eason, S. H., & Leech, K. A. (2015). Math talk during informal learning activities in Head Start families. Cognitive Development, 35, 15–33. [Google Scholar] [CrossRef]
- Raven, J. C., Court, J. H., & Raven, J. C. (1990). Manual for Raven’s progressive matrices and vocabulary scales—Section 2: Coloured progressive matrices. Oxford Psychology Press. [Google Scholar]
- Ribner, A. D., Willoughby, M. T., & Blair, C. (2017). Executive function buffers the association between early Math and later academic skills. Frontiers in Psychology, 8, 12. [Google Scholar] [CrossRef] [PubMed]
- Rose, S. A., Feldman, J. F., & Jankowski, J. J. (2012). Implications of infant cognition for executive functions at age 11. Psychological Science, 23(11), 1345–1355. [Google Scholar] [CrossRef] [PubMed]
- Salthouse, T. A., Rogan, J. D., & Prill, K. A. (1984). Division of attention: Age differences on a visually presented memory task. Memory and Cognition, 12, 613–620. [Google Scholar]
- Scammacca, N., Fall, A. M., Capin, P., Roberts, G., & Swanson, E. (2020). Examining factors affecting reading and math growth and achievement gaps in grades 1–5: A cohort-sequential longitudinal approach. Journal of Educational Psychology, 112(4), 718–734. [Google Scholar] [CrossRef] [PubMed]
- Schneider, W., Niklas, F., & Schmiedeler, S. (2014). Intellectual development from early childhood to early adulthood: The impact of early IQ differences on stability and change over time. Learning and Individual Differences 32, 156–162. [Google Scholar] [CrossRef]
- Stevenson, H. W., Parker, T., Wilkinson, A., Hegion, A., & Fish, E. (1976). Longitudinal study of individual differences in cognitive development and scholastic achievement. Journal of Educational Psychology, 68(4), 377–400. [Google Scholar] [CrossRef]
- Szűcs, D., Devine, A., Soltesz, F., Nobes, A., & Gabriel, F. (2014). Cognitive components of a mathematical processing network in 9-year-old children. Developmental Science, 17(4), 506–524. [Google Scholar] [CrossRef]
- Ten Braak, D., Lenes, R., Purpura, D. J., Schmitt, S. A., & Størksen, I. (2022). Why do early mathematics skills predict later mathematics and reading achievement? The role of executive function. Journal of Experimental Child Psychology, 214, 105306. [Google Scholar] [CrossRef]
- Torgesen, J. K. (2004). Preventing early reading failure–and its devastating downward spiral. American Educator, 28(3), 6–19. [Google Scholar]
- Tymms, P., Merrell, C., & Wildy, H. (2015). The progress of pupils in their first school year across classes and educational systems. British Educational Research Journal, 41(3), 365–380. [Google Scholar] [CrossRef]
- Van der Ven, S. H., Kroesbergen, E. H., Boom, J., & Leseman, P. P. (2012). The development of executive functions and early mathematics: A dynamic relationship. British Journal of Educational Psychology, 82(1), 100–119. [Google Scholar] [CrossRef] [PubMed]
- Watts, T. W., Duncan, G. J., Siegler, R. S., & Davis-Kean, P. E. (2014). What’s past is prologue: Relations between early mathematics knowledge and high school achievement. Educational Researcher, 43(7), 352–360. [Google Scholar] [CrossRef]
- Wei, W., Li, Y., & Su, H. Y. (2020). Predicting the growth patterns in early mathematics achievement from cognitive and environmental factors among Chinese kindergarten children. Learning and Individual Differences, 79, 101841. [Google Scholar] [CrossRef]
- Wiebe, S. A., Sheffield, T., Nelson, J. M., Clark, C. A., Chevalier, N., & Espy, K. A. (2011). The structure of executive function in 3-year-olds. Journal of Experimental Child Psychology, 108(3), 436–452. [Google Scholar] [CrossRef]
- Willoughby, M. T., Kupersmidt, J. B., & Voegler-Lee, M. E. (2012). Is preschool executive function causally related to academic achievement? Child Neuropsychology, 18(1), 79–91. [Google Scholar] [CrossRef]
| Variable | Mean (SD) | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 1. Raven’s score | 25.0 (5.6) | -- | |||||
| 2. WM verbal | 8.8 (3.3) | −0.05 | -- | ||||
| 3. WM spatial | 9.8 (3.0) | 0.17 * | 0.35 ** | -- | |||
| 4. Inhibition | 31.2 (12.1) | 0.44 ** | 0.31 * | 0.28 * | -- | ||
| 5. Cognitive flexibility | 54.4 (13.7) | 0.48 ** | 0.35 * | 0.24 * | 0.76 ** | -- | |
| 6. Math, Time 1 | 50.5 (9.5) | 0.42 ** | 0.18 * | 0.24 * | 0.45 ** | 0.43 ** | -- |
| 7. Math, Time 2 | 60.1 (10.9) | 0.63 ** | 0.17 * | 0.30 * | 0.48 ** | 0.50 ** | 0.80 ** |
| Variable | Model 1 | Model 2 | ||||
|---|---|---|---|---|---|---|
| t | t | |||||
| Age | 0.05 | 0.43 | 0.67 | 0.05 | 0.45 | 0.65 |
| Sex | 0.04 | 0.98 | 0.33 | 0.03 | 0.74 | 0.46 |
| SES | 0.06 | 1.79 | 0.07 | 0.07 | 1.85 | 0.06 |
| Math, Time 1 | 0.69 | 17.47 | <0.001 | 0.74 | 17.81 | <0.001 |
| Raven’s | 0.32 | 8.15 | <0.001 | 0.29 | 7.33 | <0.001 |
| WM verbal | 0.19 | 2.83 | 0.005 | 0.18 | 2.72 | 0.007 |
| WM spatial | 0.07 | 1.72 | 0.08 | 0.05 | 1.18 | 0.20 |
| EF control | 0.17 | 4.31 | <0.001 | 0.19 | 4.76 | <0.001 |
| Ravens × WM verbal | −0.08 | −2.05 | 0.04 | |||
| Ravens × WM spatial | −0.003 | −0.06 | 0.90 | |||
| Ravens × EF control | −0.09 | −2.34 | 0.02 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasilyeva, M.; Lu, L.; Damoah, K.; Laski, E.V. Compensatory Relation Between Executive Function and Fluid Intelligence in Predicting Math Learning. Educ. Sci. 2025, 15, 790. https://doi.org/10.3390/educsci15070790
Vasilyeva M, Lu L, Damoah K, Laski EV. Compensatory Relation Between Executive Function and Fluid Intelligence in Predicting Math Learning. Education Sciences. 2025; 15(7):790. https://doi.org/10.3390/educsci15070790
Chicago/Turabian StyleVasilyeva, Marina, Linxi Lu, Kennedy Damoah, and Elida V. Laski. 2025. "Compensatory Relation Between Executive Function and Fluid Intelligence in Predicting Math Learning" Education Sciences 15, no. 7: 790. https://doi.org/10.3390/educsci15070790
APA StyleVasilyeva, M., Lu, L., Damoah, K., & Laski, E. V. (2025). Compensatory Relation Between Executive Function and Fluid Intelligence in Predicting Math Learning. Education Sciences, 15(7), 790. https://doi.org/10.3390/educsci15070790








