The Impact of Integrated Project-Based Learning and Flipped Classroom on Students’ Computational Thinking Skills: Embedded Mixed Methods
Abstract
1. Introduction
2. Literature Review
2.1. Project-Based Learning in Mathematics Instruction
2.2. Flipped Classroom with Active Learning
2.3. Computational Thinking Skills and Their Impact on Mathematics Instruction
3. Methods
3.1. Research Design
3.2. Population and Sample
3.2.1. Quantitative
3.2.2. Qualitative
3.3. Techniques and Instruments for Data Collection
- Example Question:
- A rectangular billiard table has four corner points: and . A ball is located at point and is hit towards another ball positioned at point . However, before reaching the ball at point F, the ball must first bounce off side CD of the billiard table. Determine the coordinates of the reflection point of the ball on side CD before reaching point F.
- Solution:
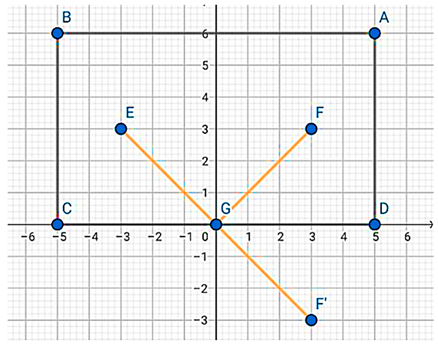
- The billiard table is a rectangle ABCD, with the ball at and aimed at hitting ball after bouncing on side CD. To determine the target point on CD, we first find the reflection of point with respect to , which is . Next, we determine the intersection of the line connecting and with the line . The equation of line EF’ is . Substituting gives , so the intersection point is . Therefore, the target point where the ball will bounce off side CD before reaching is .
3.4. Validity and Reliability of the Instruments
3.5. Data Analysis Techniques
3.6. Hypothesis Testing
3.7. Ethics in Mixed Methods Research
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdullah, A. H., Othman, M. A., Ismail, N., Rahman, S. N. S. A., Mokhtar, M., & Zaid, N. M. (2019, December 10–13). Development of mobile application for the concept of pattern recognition in computational thinking for mathematics subject. TALE 2019—2019 IEEE International Conference on Engineering, Technology and Education, Yogyakarta, Indonesia. [Google Scholar] [CrossRef]
- AlAli, R. (2024). Enhancing 21st century skills through integrated STEM education using project-oriented problem-based learning. Geo Journal of Tourism and Geosites, 53(2), 421–430. [Google Scholar] [CrossRef]
- Alonso-García, S., Fuentes, A.-V. R., Navas-Parejo, M. R., & Victoria-Maldonado, J.-J. (2024). Enhancing computational thinking in early childhood education with educational robotics: A meta-analysis. Heliyon, 10(13), e33249. [Google Scholar] [CrossRef] [PubMed]
- Awi, A., Naufal, M. A., Sutamrin, S., & Huda, M. (2024). Enhancing geometry achievement in pre-service mathematics teachers: The Impact of a scaffolded flipped classroom using a learning management system. Journal of Ecohumanism, 3(6), 637–645. [Google Scholar] [CrossRef]
- Bergmann, J., & Sams, A. (2012). Before you flip, consider this. Phi Delta Kappan, 94(2), 25. [Google Scholar] [CrossRef]
- Blumenfeld, P. C., Soloway, E., Marx, R. W., Krajcik, J. S., Guzdial, M., & Palincsar, A. (1991). Motivating project-based learning: Sustaining the doing, supporting the learning. Educational Psychologist, 26(3–4), 369–398. [Google Scholar] [CrossRef]
- Bolivar, R., Triviño Jaimes, N. R., & Gonzalez, E. A. (2023). Implementation and benefits of hybrid methodology: Flipped classroom and project-based learning in mechanical engineering courses. International Journal of Mechanical Engineering Education, 53(1), 102–124. [Google Scholar] [CrossRef]
- Buitrago-Florez, F., Danies, G., Restrepo, S., & Hernandez, C. (2019). Boosting 21st century competences through computational thinking and student centered strategies. In R. M. Lima, V. Villas-Boas, L. Bettaieb, & K. Akrout (Eds.), International symposium on project approaches in engineering education (Vol. 9, pp. 48–55). University of Minho. Available online: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85074940602&partnerID=40&md5=a4b4579100d67026f1f9a85e993fc03b (accessed on 14 September 2024).
- Çakiroğlu, Ü., & Erdemir, T. (2018). Online project based learning via cloud computing: Exploring roles of instructor and students. Interactive Learning Environments, 27(4), 547–566. [Google Scholar] [CrossRef]
- Chan, S.-W., Looi, C.-K., Ho, W. K., Huang, W., Seow, P., & Wu, L. (2021). Learning number patterns through computational thinking activities: A Rasch model analysis. Heliyon, 7(9), e07922. [Google Scholar] [CrossRef]
- Charbonneau-Gowdy, P., Cubric, M., Pechenkina, K., Dyer, R., Pyper, A., Söbke, H., & Spangenberger, P. (2023). EJEL editorial 2023: Trends and research gaps in e-learning. Electronic Journal of E-Learning, 21(3), 248–257. Available online: http://www.ejel.org/ (accessed on 15 September 2024).
- Clark, K. R. (2015). The effects of the flipped model of instruction on student engagement and performance in the secondary mathematics classroom. Journal of Educators Online, 12(1), 91–115. Available online: https://files.eric.ed.gov/fulltext/EJ1051042.pdf (accessed on 7 March 2025).
- Craig, T. T., & Marshall, J. (2019). Effect of project-based learning on high school students’ state-mandated, standardized math and science exam performance. Journal of Research in Science Teaching, 56(10), 1461–1488. [Google Scholar] [CrossRef]
- Creswell, J. W. (2014). Research design: Qualitative, quantitative, and mixed methods aapproaches. Sage Publications, Inc. [Google Scholar]
- Cubric, M., & Tripathi, V. (2009). A semantic web framework for generating collaborative e-learning environments. International Journal of Emerging Technologies in Learning, 4(3), 4–7. [Google Scholar] [CrossRef]
- del Olmo-Muñoz, J., Bueno-Baquero, A., Cózar-Gutiérrez, R., & González-Calero, J. A. (2023). Exploring gamification approaches for enhancing computational thinking in young learners. Education Sciences, 13(5), 487. [Google Scholar] [CrossRef]
- Deng, R., Feng, S., & Shen, S. (2023). Improving the effectiveness of video-based flipped classrooms with question-embedding. Education and Information Technologies, 29(10), 12677–12702. [Google Scholar] [CrossRef]
- Dinh, C. T., & Phuong, H. (2025). Teaching self-regulated learning strategies on efl students in moocs: A case study in Vietnam. Turkish Online Journal of Distance Education, 26(1), 101–121. [Google Scholar] [CrossRef]
- Dong, X., Zhang, X., & Li, X. (2024, July 29–August 1). Project-based flipped classroom model focusing on outcome communication and evaluation. 2024 International Symposium on Educational Technology (ISET) (pp. 305–309), Macau, Macao. [Google Scholar] [CrossRef]
- Durak, H. Y., & Saritepeci, M. (2018). Analysis of the relation between computational thinking skills and various variables with the structural equation model. Computers & Education, 116, 191–202. [Google Scholar] [CrossRef]
- Egara, F. O., & Mosimege, M. (2023). Effect of flipped classroom learning approach on mathematics achievement and interest among secondary school students. Education and Information Technologies, 29(7), 8131–8150. [Google Scholar] [CrossRef]
- Ergin, H., & Arıkan, Y. D. (2023). The effect of project based learning approach on computational thinking skills and programming self-efficacy beliefs. AJIT-e: Academic Journal of Information Technology, 14(55), 320–334. [Google Scholar] [CrossRef]
- Ersozlu, Z., Swartz, M., & Skourdoumbis, A. (2023). Developing computational thinking through mathematics: An evaluative scientific mapping. Education Sciences, 13(4), 422. [Google Scholar] [CrossRef]
- Erstad, O. (2002). Norwegian students using digital artifacts in project-based learning. Journal of Computer Assisted Learning, 18(4), 427–437. [Google Scholar] [CrossRef]
- Fernández-Martín, F.-D., Romero-Rodríguez, J.-M., Gómez-García, G., & Ramos Navas-Parejo, M. (2020). Impact of the flipped classroom method in the mathematical area: A systematic review. Mathematics, 8(12), 2162. [Google Scholar] [CrossRef]
- Fredriksen, H., Rebenda, J., Rensaa, R. J., & Pettersen, P. (2024). Inquiry-based linear algebra teaching and learning in a flipped classroom framework: A case study. PRIMUS, 1–21. [Google Scholar] [CrossRef]
- Gibson, I. S., O’Reilly, C., & Hughes, M. (2002). Integration of ICT within a project-based learning environment. European Journal of Engineering Education, 27(1), 21–30. [Google Scholar] [CrossRef]
- Gondal, S. A., Khan, A. Q., Cheema, E. U., & Dehele, I. S. (2024). Impact of the flipped classroom on students’ academic performance and satisfaction in Pharmacy education: A quasi-experimental study. Cogent Education, 11(1), 2378246. [Google Scholar] [CrossRef]
- Gong, J., Cai, S., & Cheng, M. (2023). Exploring the effectiveness of flipped classroom on STEM student achievement: A meta-analysis. Technology, Knowledge and Learning, 29(2), 1129–1150. [Google Scholar] [CrossRef]
- Holmes, V.-L., & Hwang, Y. (2016). Exploring the effects of project-based learning in secondary mathematics education. The Journal of Educational Research, 109(5), 449–463. [Google Scholar] [CrossRef]
- Hossein-Mohand, H., Trujillo-Torres, J.-M., Gómez-García, M., Hossein-Mohand, H., & Campos-Soto, A. (2021). Analysis of the use and integration of the flipped learning model, project-based learning, and gamification methodologies by secondary school mathematics teachers. Sustainability, 13(5), 2606. [Google Scholar] [CrossRef]
- Indriati, L., Mai, N., & Tan, H. Y.-J. (2024). Enhancing authentic assessment in large-class design education through authentic project-based learning. International Journal of Learning, Teaching and Educational Research, 23(9), 432–452. [Google Scholar] [CrossRef]
- Isabel Santos, A., & Serpa, S. (2020). Flipped classroom for an active learning. Journal of Education and E-Learning Research, 7(2), 167–173. [Google Scholar] [CrossRef]
- Kalemkuş, F., & Bulut-Özek, M. (2022). The effect of online project-based learning on metacognitive awareness of middle school students. Interactive Learning Environments, 32(4), 1533–1551. [Google Scholar] [CrossRef]
- Kim, D., & Lee, S. (2002). Designing collaborative reflection supporting tools in e-project-based learning environments. Journal of Interactive Learning Research, 13(4), 375–392. Available online: https://www.learntechlib.org/primary/p/9530/ (accessed on 7 March 2025).
- Kong, S. C. (2014). Developing information literacy and critical thinking skills through domain knowledge learning in digital classrooms: An experience of practicing flipped classroom strategy. Computers & Education, 78, 160–173. [Google Scholar] [CrossRef]
- Krajcik, J. S., Blumenfeld, P. C., Marx, R. W., & Soloway, E. (1994). A collaborative model for helping middle grade science teachers learn project-based instruction. The Elementary School Journal, 94(5), 483–497. [Google Scholar] [CrossRef]
- Kramer, B. S., Walker, A. E., & Brill, J. M. (2007). The underutilization of information and communication technology-assisted collaborative project-based learning among international educators: A Delphi study. Educational Technology Research and Development, 55(5), 527–543. [Google Scholar] [CrossRef]
- Li, M.-M., & Tu, C.-C. (2024). Developing a project-based learning course model combined with the think–pair–share strategy to enhance creative thinking skills in education students. Education Sciences, 14(3), 233. [Google Scholar] [CrossRef]
- Liu, L., Hew, K. F., & Du, J. (2024). Design principles for supporting self-regulated learning in flipped classrooms: A systematic review. International Journal of Educational Research, 124, 102319. [Google Scholar] [CrossRef]
- Maros, M., Korenkova, M., Fila, M., Levicky, M., & Schoberova, M. (2021). Project-based learning and its effectiveness: Evidence from Slovakia. Interactive Learning Environments, 31(7), 4147–4155. [Google Scholar] [CrossRef]
- Meyer, D. K., Turner, J. C., & Spencer, C. A. (1997). Challenge in a mathematics classroom: Students’ motivation and strategies in project-based learning. The Elementary School Journal, 97(5), 501–521. [Google Scholar] [CrossRef]
- Mohamed, H., Saidalvi, A., & Tashiron, N. A. (2019). Project based learning in flipped classroom based on student’s cognitive style. International Journal of Recent Technology and Engineering, 7(6S3), 696–700. [Google Scholar]
- Moss, D. M. (2000). Bringing together technology and students: Examining the use of technology in a project-based class. Journal of Educational Computing Research, 22(2), 155–169. [Google Scholar] [CrossRef]
- My Nguyen, H. T., Chau Nguyen, G. T., Hong Thai, L. T., Truong, D. T., & Nguyen, B. N. (2024). Teaching Mathematics through project-based learning in K-12 Schools: A systematic review of current practices, barriers, and future developments. TEM Journal, 13, 2054–2065. [Google Scholar] [CrossRef]
- Nayak, A., Satpathy, I., & Jain, V. (2024). The project-based learning approach (PBL): Enthralling students through Project-Based Learning approach (PBL) in Education 5.0. In Preconceptions of Policies, Strategies, and Challenges in Education 5.0 (pp. 158–174). IGI Global. [Google Scholar] [CrossRef]
- Ndiung, S., & Menggo, S. (2024). Project-based learning in fostering creative thinking and mathematical problem-solving skills: Evidence from primary education in Indonesia. International Journal of Learning, Teaching and Educational Research, 23(8), 289–308. [Google Scholar] [CrossRef]
- Nurbekova, Z., Grinshkun, V., Aimicheva, G., Nurbekov, B., & Tuenbaeva, K. (2020). Project-based learning approach for teaching mobile application development using visualization technology. International Journal of Emerging Technologies in Learning (IJET), 15(08), 130. [Google Scholar] [CrossRef]
- Patterson, B., McBride, C. R., & Gieger, J. L. (2018). Flipped active learning in your mathematics classroom without videos. PRIMUS, 28(8), 742–753. [Google Scholar] [CrossRef]
- Pokhrel, M., Sharma, L., Sharma, T., Prasad, M., & Poudel, L. G. C. (2024). Enhancing mathematics learning through self-directed pedagogy: Strategies and evaluation techniques for effective student engagement. Journal of Computational Analysis and Applications, 33(8), 841–854. Available online: https://eudoxuspress.com/index.php/pub/article/view/1471 (accessed on 22 October 2024).
- Rehman, N., Huang, X., Mahmood, A., AlGerafi, M. A. M., & Javed, S. (2024). Project-based learning as a catalyst for 21st-Century skills and student engagement in the math classroom. Heliyon, 10(23), e39988. [Google Scholar] [CrossRef]
- Remijan, K. W. (2017). Project-based learning and design-focused projects to motivate secondary mathematics students. Interdisciplinary Journal of Problem-Based Learning, 11(1), 1–15. [Google Scholar] [CrossRef]
- Rijken, P. E., & Fraser, B. J. (2023). Effectiveness of project-based mathematics in first-year high school in terms of learning environment and student outcomes. Learning Environments Research, 27(2), 241–263. [Google Scholar] [CrossRef]
- Rodríguez-Martínez, J. A., González-Calero, J. A., & Sáez-López, J. M. (2019). Computational thinking and mathematics using Scratch: An experiment with sixth-grade students. Interactive Learning Environments, 28(3), 316–327. [Google Scholar] [CrossRef]
- Saad, A., & Zainudin, S. (2024). A review of teaching and learning approach in implementing Project-Based Learning (PBL) with Computational Thinking (CT). Interactive Learning Environments, 32(10), 7622–7646. [Google Scholar] [CrossRef]
- Saheb, T., & Saheb, T. (2024). Mapping ethical artificial intelligence policy landscape: A mixed method analysis. Science and Engineering Ethics, 30(2), 9. [Google Scholar] [CrossRef]
- See, S., & Conry, J. M. (2014). Flip My Class! A faculty development demonstration of a flipped-classroom. Currents in Pharmacy Teaching and Learning, 6(4), 585–588. [Google Scholar] [CrossRef]
- Shekh-Abed, A. (2024). Metacognitive self-knowledge and cognitive skills in project-based learning of high school electronics students. European Journal of Engineering Education, 50(1), 214–229. [Google Scholar] [CrossRef]
- Shen, Y. (2024). Examining the efficacies of instructor-designed instructional videos in flipped classrooms on student engagement and learning outcomes: An empirical study. Journal of Computer Assisted Learning, 40(4), 1791–1805. [Google Scholar] [CrossRef]
- Shin, N., Bowers, J., Krajcik, J., & Damelin, D. (2021). Promoting computational thinking through project-based learning. Disciplinary and Interdisciplinary Science Education Research, 3(1), 7. [Google Scholar] [CrossRef] [PubMed]
- Singha, R., & Singha, S. (2024). Application of experiential, inquiry-based, problem-based, and project-based learning in sustainable education. In Teaching and learning for a sustainable future: Innovative strategies and best practices (pp. 109–128). IGI Global. [Google Scholar] [CrossRef]
- Soboleva, E. V., Kirillova, E. P., Lomakin, D. E., & Gribkov, D. N. (2021). Formation of computational thinking skills in the development of computer games for educational purposes. Perspektivy Nauki i Obrazovania, 49(1), 464–477. [Google Scholar] [CrossRef]
- Stadnick, N. A., Poth, C. N., Guetterman, T. C., & Gallo, J. J. (2021). Advancing discussion of ethics in mixed methods health services research. BMC Health Services Research, 21(1), 577. [Google Scholar] [CrossRef]
- Sung, W., Ahn, J., & Black, J. B. (2017). Introducing computational thinking to young learners: Practicing computational perspectives through embodiment in mathematics education. Technology, Knowledge and Learning, 22(3), 443–463. [Google Scholar] [CrossRef]
- Sung, W., & Black, J. B. (2020). Factors to consider when designing effective learning: Infusing computational thinking in mathematics to support thinking-doing. Journal of Research on Technology in Education, 53(4), 404–426. [Google Scholar] [CrossRef]
- Tekin, O., & Sarıkaya, E. E. (2020). Flipped classroom model in high school mathematics. Bartın University Journal of Faculty of Education, 9(2), 301–314. [Google Scholar]
- Tu, F., Wu, L., Kinshuk, Ding, J., & Chen, H. (2025). Exploring the influence of regulated learning processes on learners’ prestige in project-based learning. Education and Information Technologies, 30, 2299–2329. [Google Scholar] [CrossRef]
- Tucker, B. (2012). The flipped classroom. Education Next, 12(1), 82–83. Available online: https://www.educationnext.org/wp-content/uploads/2023/04/ednext_XII_1_what_next.pdf (accessed on 7 March 2025).
- Voon, X. P., Wong, S. L., Wong, L.-H., Khambari, M. N. M., & Syed-Abdullah, S. I. S. (2022). Developing computational thinking competencies through constructivist argumentation learning: A problem-solving perspective. International Journal of Information and Education Technology, 12(6), 529–539. [Google Scholar] [CrossRef]
- Wang, J. (2024). Research on the flipped classroom + learning community approach and its effectiveness evaluation—Taking college german teaching as a case study. Sustainability, 16(17), 7719. [Google Scholar] [CrossRef]
- Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L., & Wilensky, U. (2015). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology, 25(1), 127–147. [Google Scholar] [CrossRef]
- Xing, D., & Zeng, Y. (2024). Exploring the effects of secondary school student’s information and communication technology literacy on computational thinking skills in the smart classroom environment. Education and Information Technologies. [Google Scholar] [CrossRef]
- Yasin, M., & Nusantara, T. (2023). Characteristics of pattern recognition to solve mathematics problems in computational thinking. In AIP conference proceedings (vol. 2569, p. 40009). AIP Publishing. [Google Scholar] [CrossRef]
- Zarouk, M. Y., Olivera, E., Peres, P., & Khaldi, M. (2020). The impact of flipped project-based learning on self-regulation in higher education. International Journal of Emerging Technologies in Learning (IJET), 15(17), 127. [Google Scholar] [CrossRef]
- Zhang, W., Guan, Y., & Hu, Z. (2024). The efficacy of project-based learning in enhancing computational thinking among students: A meta-analysis of 31 experiments and quasi-experiments. Education and Information Technologies, 29(11), 14513–14545. [Google Scholar] [CrossRef]

| Initial | Gender | Age | Activity Level | Score |
|---|---|---|---|---|
| Creswel | Male | 18 Years | Active | 80.00 |
| Albert | Male | 18 Years | Active | 80.00 |
| Donald | Male | 17 Years | Active | 80.00 |
| Joseph | Male | 18 Years | Active | 85.00 |
| Charmaz | Female | 18 Years | Active | 85.00 |
| Collins | Female | 17 Years | Less Active | 80.00 |
| Cohen | Female | 16 Years | Less Active | 75.00 |
| Donna | Female | 18 Years | Less Active | 80.00 |
| Patricia | Female | 16 Years | Active | 85.00 |
| Katy | Female | 17 Years | Active | 85.00 |
| Basic Competency | Competency Achievement Indicator | Test Indicator | CT Level | Number of Questions |
|---|---|---|---|---|
| Analyzing and comparing transformations and compositions of transformations using matrices | Identifying transformation matrices (reflection) at point | Given point , students determine the reflection transformation matrix at point O(0,0) and the shadow coordinates. | Decomposition | 2 (1 multiple choice, 1 Essay) |
| Identifying transformation matrices (reflection) on the x-axis | , students determine the reflection matrix on the x-axis and explain the changes in coordinates. | Pattern Recognition | 2 (1 multiple choice, 1 Essay) | |
| Identifying transformation matrices (reflection) on the y-axis | , students determine the reflection matrix on the y-axis and identify the pattern differences compared to the reflection on the x-axis. | Pattern Recognition | 3 (2 multiple choice, 1 Essay) | |
| Determining the shadow of a transformation composition (reflection) using matrices | Given a point and two consecutive reflection transformations, students determine the final shadow using the composition transformation matrix. | Abstraction | 4 (2 multiple choice, 1 Short Answer, 1 Essay) | |
| Solving problems related to geometric transformation matrices (translation, reflection, dilation, and rotation) | Solving problems involving transformation (reflection) | Students are given a real-world problem requiring the application of the reflection concept in problem-solving. | Algorithmic Thinking | 4 (2 multiple choice, 1 Short Answer, 1 Essay) |
| Question Type | CT Dimension Assessed | Scoring Criteria | Max Score |
|---|---|---|---|
| Multiple-Choice | All CT dimensions | 1 = Correct. 0 = Incorrect. | 1 |
| Short-Answer | Abstraction, Algorithmic Thinking | 3 = Correct and structured problem-solving steps. 2 = Minor inaccuracies in problem-solving steps. 1 = Most steps are incorrect. 0 = No problem-solving steps written. | 3 |
| Essay | All CT dimensions | 90–100 = Deep analysis, logical solution, systematic approach. 70–89 = Mostly logical, minor errors in reasoning or structure. 50–69 = Partial understanding, significant logical or procedural errors. <50 = Lacks conceptual understanding, unsystematic response. | 100 |
| Skill | Cronbach’s Alpha |
|---|---|
| Decomposition | 0.94 |
| Pattern recognition | 0.86 |
| Abstraction | 0.83 |
| Algorithmic thinking | 0.91 |
| Category | Control | Experiment | ||||||
|---|---|---|---|---|---|---|---|---|
| V1 | V2 | V3 | V4 | V1 | V2 | V3 | V4 | |
| N | 45 | 46 | ||||||
| Exact Sig. (2-tailed) | 0.22 | 0.53 | 0.251 | 0.17 | 0.25 | 0.51 | 0.28 | 0.35 |
| Skill | Class | N | Mean | Standard Deviation |
|---|---|---|---|---|
| Decomposition | Control | 45 | 49.64 | 8.49 |
| Experiment | 46 | 60.01 | 9.91 | |
| Pattern recognition | Control | 45 | 36.22 | 6.17 |
| Experiment | 46 | 40.74 | 6.52 | |
| Abstraction | Control | 45 | 30.51 | 5.87 |
| Experiment | 46 | 35.78 | 5.95 | |
| Algorithmic thinking | Control | 45 | 34.30 | 6.44 |
| Experiment | 46 | 38.78 | 5.66 |
| Skill | Levene Statistic | Significance |
|---|---|---|
| Decomposition | 0.31 | 0.59 |
| Pattern recognition | 0.08 | 0.79 |
| Abstraction | 1.30 | 0.26 |
| Algorithmic thinking | 2.60 | 0.12 |
| Model | Sum of Squares | Mean Square | F | Significance |
|---|---|---|---|---|
| Regression | 2184.437 | 546.109 | 10.88 | 0.000 |
| Residual | 1053.425 | 50.163 | ||
| Total | 3237.862 |
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Significance |
|---|---|---|---|---|
| (Constant) | 55.92 | 5.50 | 0.000 | |
| Decomposition | 1.92 | 1.67 | 5.58 | 0.000 |
| Pattern recognition | −1.99 | −1.16 | −3.76 | 0.001 |
| Abstraction | 1.03 | 0.54 | 2.15 | 0.044 |
| Algorithmic thinking | −1.45 | −0.72 | −3.59 | 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fitrah, M.; Sofroniou, A.; Setiawan, C.; Widihastuti, W.; Yarmanetti, N.; Jaya, M.P.S.; Panuntun, J.G.; Arfaton, A.; Beteno, S.; Susianti, I. The Impact of Integrated Project-Based Learning and Flipped Classroom on Students’ Computational Thinking Skills: Embedded Mixed Methods. Educ. Sci. 2025, 15, 448. https://doi.org/10.3390/educsci15040448
Fitrah M, Sofroniou A, Setiawan C, Widihastuti W, Yarmanetti N, Jaya MPS, Panuntun JG, Arfaton A, Beteno S, Susianti I. The Impact of Integrated Project-Based Learning and Flipped Classroom on Students’ Computational Thinking Skills: Embedded Mixed Methods. Education Sciences. 2025; 15(4):448. https://doi.org/10.3390/educsci15040448
Chicago/Turabian StyleFitrah, Muh, Anastasia Sofroniou, Caly Setiawan, Widihastuti Widihastuti, Novi Yarmanetti, Melinda Puspita Sari Jaya, Jontas Gayuh Panuntun, Arfaton Arfaton, Septrisno Beteno, and Ika Susianti. 2025. "The Impact of Integrated Project-Based Learning and Flipped Classroom on Students’ Computational Thinking Skills: Embedded Mixed Methods" Education Sciences 15, no. 4: 448. https://doi.org/10.3390/educsci15040448
APA StyleFitrah, M., Sofroniou, A., Setiawan, C., Widihastuti, W., Yarmanetti, N., Jaya, M. P. S., Panuntun, J. G., Arfaton, A., Beteno, S., & Susianti, I. (2025). The Impact of Integrated Project-Based Learning and Flipped Classroom on Students’ Computational Thinking Skills: Embedded Mixed Methods. Education Sciences, 15(4), 448. https://doi.org/10.3390/educsci15040448









