The Impact of the COVID-19 Pandemic upon Mathematics Assessment in Higher Education

Abstract

Historically, the assessment of mathematics in higher education comprised closed-book, summative, proctored examinations. Related disciplines and subjects like statistics, mathematics education, and the history of mathematics lend themselves to a broader range of assessment techniques that have been reported to provide a more balanced picture of students’ abilities. In 2020, an online environment for the teaching and learning of mathematics was imposed on the academic world globally as a result of the COVID-19 pandemic. In an effort to teach and assess remotely while maintaining institutional academic standards, the majority of lecturers were in a situation where closed-book, proctored assessments were not an option. As a result, other methods were adopted. This paper reports on an investigation into how mathematics lecturers worldwide assessed mathematics before the pandemic, during the initial lockdown restrictions, and in the immediate aftermath, while some restrictions were still in place, to see if any changes were sustained. There was a statistically significant difference in the proportion of respondents who used many of the assessment types investigated across the three time periods, including open-book timed, open-book untimed, closed-book, multiple-choice questions, online proctored, in-person proctored, presentations, projects, and assignments. The majority of those who favoured closed-book proctored examinations prior to the pandemic moved to timed open-book assessments. Differences between the weightings of final examinations versus continuous assessments were also statistically significant, with greater weight given to continuous assessment once the pandemic began. Respondents’ satisfaction levels with their assessments were significantly different also, with the highest satisfaction levels prior to the pandemic and the lowest during the initial lockdown restrictions. Academic integrity was a key concern of the majority of respondents when assessing the learning outcomes of their modules and played a role in the vehicle of assessment they chose.

1. Introduction

The assessment of mathematics in higher education has long depended on closed-book, summative, proctored examinations (Iannone & Simpson, 2011; Davies et al., 2024). Arguments have been made to support the assertion that mathematics is in some way “different” as a discipline, in that it lends itself more to traditional forms of teaching and assessment, more so than might be the case in other subjects—but equally, more recently, such arguments have been refuted (Becher, 1994; Ní Fhloinn & Carr, 2017). Particularly since the early years of this millennium, research has been conducted into the possible modes of assessment into which mathematics could naturally expand, citing the fact that the traditional timed, closed-book assessment does not effectively assess skills such as problem-solving or the use of IT (Challis et al., 2003). It seems clear at least that mathematics assessment of this kind may fall short of the mark, as it may not give a fully comprehensive picture of a student’s learning achievement (Burton & Haines, 1997). Although assessment of a broader range of skills can be achieved through approaches such as report writing, projects, and oral examinations (Niss, 1998), it appears that alternative modes of assessment are only more prevalent in modules of statistics, history of mathematics, mathematics education, and final-year projects (Iannone & Simpson, 2011).

During the initial university closures due to COVID-19 in 2020, mainly out of necessity, a broader range of formative and summative assessment methods were embraced by the mathematics teaching community (Fitzmaurice & Ní Fhloinn, 2021). This was a positive outcome of the move to remote teaching, as alternative assessment strategies assess a broader range of learning outcomes (Pegg, 2003). However, while this change happened during the first months of the pandemic, when lecturers had to pivot to online assessment with little or no time to plan, it is of interest to determine what happened the following year, when lecturers still often had to assess mathematics online but had significantly more notice of the fact.

Two decades ago, online assessment in mathematics started becoming more prevalent as the internet became more conducive to mathematics (Engelbrecht & Harding, 2004). The use of technology in education is seen as an inherent component of a teaching and learning environment that seeks to fulfil the diverse needs of students in the 21st century (Valdez & Maderal, 2021). Digital technologies offer compelling tools to conduct formative assessments effectively in mathematics (Barana et al., 2021). Online assessment, or E-assessment, comprises an extensive range of assessment types, including but not limited to online essays and computer-marked online examinations (James, 2016). Online examinations are an efficient means of conducting diagnostic, formative, and summative assessments and providing students with the opportunity to perform to the best of their ability (Valdez & Maderal, 2021).

Recent years have seen exponential growth in the different modes of online assessment that are available. Research by Davies et al. (2024), conducted in 2024, however, indicates that Computer-Aided Assessment (CAA) in tertiary mathematics remains underutilised despite these reported advancements in assessment methods. The continued over-reliance by university-level mathematics lecturers on closed-book written exams referred to above prompts questions about whether CAA can provide a more effective alternative, particularly in formative assessment. Some studies have documented that CAA has been shown to improve examination performance (Greenhow, 2015), although Greenhow (Greenhow, 2015, 2019) recommends that it should complement rather than replace traditional mathematics assessments. When used effectively, online formative assessment has the potential to nurture a learner- and assessment-centred focus using formative feedback and enhanced learner engagement with worthwhile learning experiences (Gikandi et al., 2011). However, it should be noted that distance assessment is not always experienced as a positive for students, as they can struggle with access to technology and resources or simply with feelings of isolation (Kerka & Wonacott, 2000). Multiple-choice questions have also been shown to have the potential for bias in relation to students with varying learning styles or in relation to confidence levels (Sangwin, 2013). Specific training or knowledge of question creation is also needed, as questions assessed via computer-aided assessment are different from those graded by hand (Greenhow, 2015).

Iannone and Simpson’s more recent investigation into summative assessments in the UK (Iannone & Simpson, 2022) found that closed-book examinations are still tremendously popular; however, E-assessment has increased significantly in the decade since their last study on mathematics assessment. Systems like STACK and NUMBAS are widespread in many universities, mainly as part of some coursework components of first-year modules. These systems are attractive because of the time-saving aspects of electronic marking and the provision of rapid feedback (Iannone & Simpson, 2022). STACK is an open-source tool that can seamlessly integrate with learning management systems like Moodle, enabling the generation of randomised, automatically graded mathematics questions. Davies et al.’s (2024) work ratifies STACK as an assessment vehicle that delivers instant feedback, with adaptability in assessing complex mathematical concepts. NUMBAS is another open-source, web-based assessment tool designed specifically for mathematics. Similar to STACK, it provides interactive, automatically graded assignments and instantaneous feedback to participating students, which they tend to put great value on (Lishchynska et al., 2021). While the questions are customised and randomised, this can be quite a time-consuming process for lecturers who choose it (Lishchynska et al., 2021).

Valdez and Maderal (2021) state that online assessments in mathematics are increasing in use and popularity over the traditional paper-and-pen type as they evaluate student learning without the need for everyone to be physically present in the same room. The decrease in cost and increase in the availability of powerful technology have altered how many mathematics lecturers assess their modules (Stacey & Wiliam, 2012). Yet Iannone and Simpson (2022) found that there remains a relatively low level of variety in what they call ‘the assessment diet’ in mathematics in HE in the UK. There is a question over whether reasoning can be assessed online as efficiently as in a traditional examination setting; however, Sangwin (2019) demonstrated that typical closed-book exam questions in linear algebra could be replicated in an e-assessment system.

Academic integrity is a primary concern when selecting modes of assessment. Universities must uphold the academic veracity and exit standards of their degrees to preserve their reputation, and a move to online assessment can coincide with grade inflation if students are given increased time to complete assessments (Henley et al., 2022). Instances of academic misconduct have been shown to increase when assessment is fully in online format. Contract cheating refers to instances where students hire someone else to complete their work or provide answers on their behalf (Liyanagamage et al., 2025). Lancaster and Cotarlan (2021) found a 196% increase in contract cheating requests across five STEM subjects when comparing the periods from April to August 2019 and April to August 2020. This rise coincided with the shift to online assessments due to the COVID-19 pandemic. Trenholm (2007) contends that proctoring truly is the only method to eliminate cheating in online exams. However, Eaton and Turner’s (2020) research on E-proctoring, the systematic remote visual monitoring of students as they complete assessments, may have a detrimental impact on students’ mental health and well-being. Sarmiento and Prudente (2019) demonstrated that ways around this are achievable. Their work illustrates that it is possible to assess online and limit opportunities for copying. They used MyOpenMath to generate individualised homework assignments for students. They found it not only limited copying but also had a significant positive impact on students’ homework that was submitted and on their summative assessment performance (Sarmiento et al., 2018).

While there is an abundance of studies that examine student perceptions about online learning, there is a dearth in the literature on online assessment of mathematics (Valdez & Maderal, 2021), specifically which areas of mathematics lend themselves more to being assessed online. The university closures due to the COVID-19 pandemic forced lecturers worldwide out of their comfort zones and normal practices when it came to assessing their students. This research investigates the extent to which lecturers migrated from their conventional assessments when pressurised to do so, the lessons learnt during this time, the assessment changes that were preserved when they had a little more time to think and plan, and those that were discarded on their second attempt at online assessment. The research questions we explore in this paper are as follows:

• What assessment types were used by mathematics lecturers before the pandemic, during the initial university closures, and during the academic year 2020/2021?
• Were there changes to the weightings given to final examinations versus continuous assessment during these time periods?
• Did mathematics lecturers observe any changes in grade distribution within their modules during these time periods?
• Were mathematics lecturers satisfied with their assessment approaches during these time periods?
• What do mathematics lecturers believe are the easiest and most difficult aspects of mathematics to assess online?

2. Materials and Methods

2.1. Sample

The profile of the respondents in the survey can be seen in detail in

Table 1. Profile statistics of survey respondents (n= 190), showing their gender, age, years of experience teaching mathematics in higher education, and current employment status.

	Number	%
Gender
Male	87	46%
Female	99	52%
(Blank)	4	2%
Age
20–29 years	8	4%
30–39 years	52	27%
40–49 years	60	32%
50–59 years	50	26%
60+ years	19	10%
(Blank)	1	1%
Experience teaching maths in higher education
0–1 year	2	1%
2–3 years	11	6%
3–5 years	18	10%
5–10 years	28	15%
10–15 years	39	21%
15–20 years	17	9%
20+ years	75	40%
Employment status
Ph.D./Postdoc	2	1%
Short-term contract (≤1 yr)	4	2%
Long-term contract (>1 yr)	22	12%
Permanent	162	85%

, with gender, age, years of experience in teaching mathematics in higher education, and employment status given. There was a total of 190 respondents to the survey. The gender breakdown of the respondents was 52% female, which does not reflect the population of mathematics lecturers in higher education, as this is predominantly male. The survey was sent to a mailing list of female mathematicians in Europe, which likely accounts for the high response rate from female mathematicians. The age profile was fairly evenly spread, with 85% of respondents between 30 and 59 years of age and a similar percentage in permanent employment. Their teaching experience in higher education reflected the age profile, with 40% of respondents having more than 20 years of experience.

The respondents were based primarily in Europe, with only 12% based outside of the continent, most of these in the United States. The highest proportion by far was based in Ireland, as are the two researchers in this study. In total, respondents from 27 different countries answered the survey. Further details can be found in (Ní Fhloinn & Fitzmaurice, 2022).

Respondents were also asked about their mathematics teaching in the academic year 2020/2021 to provide context for their responses. Half of the respondents lectured students taking non-specialist (service) mathematics, while 60% taught students undertaking a mathematics major. We defined “small” classes as those having less than 30 students, “medium” as being those between 30 and 100 students, and “large” as more than 100 students. From our sample, 58% had small classes, 57% had medium classes, and 37% had large classes. Almost three-quarters of respondents did all their teaching online that year, with a further 17% doing it almost all online. Prior to the pandemic, 75% of respondents had done no online teaching of any kind, with a further 13% having done only a little.

2.2. Survey Instrument

This study falls under the umbrella of a larger investigation into the remote lecturing of tertiary-level students of mathematics during the COVID-19 pandemic. Our research design comprised the creation and dissemination of a purposely designed survey to investigate how lecturers and students were coping with remote mathematics education during the initial stages of the COVID-19 pandemic around the world. In 2020, we created an initial survey that would shed light on how mathematics lecturers were responding to the challenge of a spontaneous and forced move to remote teaching. The survey questions were original questions devised by the authors. The outcome of this research is reported in (Ní Fhloinn & Fitzmaurice, 2022).

To get a comprehensive insight into this experience and period of time where there were varying levels of restrictions enforced in 2021, we disseminated a follow-up survey in order to make comparisons between remote teaching in 2020 with that 12 months later. It is this follow-up survey on which this study focuses. It was largely based on the previous survey, with questions adapted to account for the fact that lecturers now had a year of remote teaching and assessment experience. It was an anonymous survey created in Google Forms, with a consent to participate checkbox on the landing page. We piloted the survey with a panel of experts within two university mathematics departments to increase the reliability and validity of the instrument. The lecturers were asked to review the questions to check for clarity of phrasing and if the questions were unbiased and aligned with the intended constructs. Suggestions for items we had not included were also welcomed. We asked the panel of experts to identify ambiguities, inconsistencies, or potential misinterpretations in a bid to improve content validity. Their feedback helped us refine question wording and format, thus increasing reliability. This process was conducted so that the survey would accurately address our research questions and produce consistent results across different respondents. The relevant survey questions are shown in Appendix A.

The survey began with a number of profiling questions, the results of which are shown in Table 1. There were then sections on their mathematics teaching allocation, the types of technology they used and the purpose of this, student experience, remote teaching experience, and personal circumstances, as well as the section which is the focus of this paper—online assessment in mathematics. Within this section, there were nine questions, four of which were open-ended.

2.3. Data Collection

The survey was made available exclusively online, using Google Forms, and was advertised via mailing lists for mathematics lecturers, as well as at mathematics education conferences relevant to those working in higher education.

2.4. Data Analyses

Respondents were asked in many places to give their approach at three specific time points: prior to the pandemic, during the initial university closures from March–June 2020, and during the academic year 2020/2021. Throughout the paper, we will refer to these as Period 1, Period 2, and Period 3 for simplicity.

Quantitative analysis was done using SPSS (version 29). For investigating binary changes over the three time periods, we used Cochran’s Q test, as this is a non-parametric test for comparing binary outcomes across three or more time periods for the same group of subjects. In our results reported below, a statistically significant result is one for which the p-value is less than 0.05. Where the results of Cochran’s Q tests were significant, we conducted post-hoc McNemar tests to ascertain where the significant differences lay. In this case, we needed to utilise a Bonferroni adjustment on the results because of making multiple comparisons, and so a statistically significant result is one for which the p-value is less than 0.017. To investigate changes in Likert-scale data over the three time periods, a Friedman test was used, as this is a non-parametric test for comparing ordinal data across three or more time periods for the same group of subjects. Where the results of the Friedman test were significant, we conducted post-hoc Wilcoxon signed-rank tests as above for the McNemar tests, with a similar Bonferroni adjustment.

For the qualitative responses, grounded theory was utilised, specifically general inductive analysis. Both researchers independently coded the responses initially to provide greater reliability in the results. Inter-coder reliability was 91%. We used the open discussion to categorise the disputed data points. This revealed minor differences in the interpretation of some data that, when clarified, led to almost perfect agreement.

3. Results

3.1. Assessment Types

Respondents were asked about the types of assessments that they conducted at three specific time points: Period 1, Period 2, and Period 3. The results are shown in Figure 1.

A Cochran’s Q test was conducted on each assessment type, and the outcomes are shown in

Table 2. Results of Cochran’s Q tests conducted on each assessment type, where a p-value of p < 0.05 represents a statistically significant difference in the proportion of respondents using each assessment type.

Assessment Type	Cochran’s Q Value	p-Value	Outcome
Open-book timed	138.078	<0.001	Significant
Open-book untimed	19.818	<0.001	Significant
Closed-book	163.538	<0.001	Significant
MCQ	27.167	<0.001	Significant
Online proctored	44.4	<0.001	Significant
In-person proctored	107.079	<0.001	Significant
Presentations	15.826	<0.001	Significant
Oral Assessments	2.583	0.275	Not significant
Essays	4.545	0.103	Not significant
Screencasts	4.750	0.093	Not significant
Projects	22.067	<0.001	Significant
Assignments	8.615	0.013	Significant

below. From this, we found that there was a statistically significant difference in the proportion of respondents using most of these assessment types over time: namely, open-book timed, open-book untimed, closed-book, MCQ, online proctored, in-person proctored, presentations, projects and assignments.

Further post-hoc McNemar tests were conducted for the assessment types that were statistically significant, and the results are shown in

Table 3. Results of McNemar tests conducted on the assessment types that showed as statistically significant in Table Y. A Bonferroni adjustment was applied so that p-values below 0.017 were considered significant. P1 = Period 1, P2 = Period 2 and P3 = Period 3.

Assessment Type	Periods Compared	p-Value	Outcome
Open-book timed	P1vP2	<0.001	Significant
	P1vP3	<0.001	Significant
	P2vP3	<0.001	Significant
Open-book untimed	P1vP2	<0.001	Significant
	P1vP3	<0.001	Significant
	P2vP3	0.832	Not significant
Closed-book	P1vP2	<0.001	Significant
	P1vP3	<0.001	Significant
	P2vP3	0.064	Not significant
MCQ	P1vP2	<0.001	Significant
	P1vP3	<0.001	Significant
	P2vP3	0.307	Not significant
Online proctored	P1vP2	<0.001	Significant
	P1vP3	<0.001	Significant
	P2vP3	<0.001	Significant
In-person proctored	P1vP2	<0.001	Significant
	P1vP3	<0.001	Significant
	P2vP3	0.092	Not significant
Presentations	P1vP2	0.002	Significant
	P1vP3	0.864	Not significant
	P2vP3	<0.001	Significant
Projects	P1vP2	0.027	Not significant
	P1vP3	0.021	Not significant
	P2vP3	<0.001	Significant
Assignments	P1vP2	0.481	Not significant
	P1vP3	0.096	Not significant
	P2vP3	0.004	Significant

below. From this, it can be seen that for open-book timed and online proctored assessments, there was a statistically significant difference between each of the three time periods when considered in pairs—so there was a significant difference between Periods 1 and 2, Periods 1 and 3, and Periods 2 and 3. For open-book untimed, closed-book, MCQ and in-person proctored assessments, there was a statistically significant difference between Periods 1 and 2 and Periods 1 and 3, but not between Periods 2 and 3. For presentations, there was no significant difference between Periods 1 and 3, although the other two pairings were significant. For projects and assignments, the only significant difference was between Periods 2 and 3.

3.2. Assessment Weightings

To measure the difference in weightings between different assessment types, respondents were asked how much their final examination was worth in comparison with continuous assessment in their modules. They had to select a percentage band, which was 20% wide (e.g., 100% final exam, 80–99% final exam, etc.). The results are shown in Figure 2. As can be seen in the chart, for Period 1, the most common approach was to have between 60–79% of the marks for the module assigned to the final examination (n = 68), which dropped during Periods 2 and 3 (n = 46) but remained the most common weighting throughout, although 40–59% became a very close second (n = 42) in Period 3. When a Friedman test was conducted on this data, there was a statistically significant difference between the weightings of final examinations and continuous assessments, measured across the three time periods (χ²(2) = 27.752, p < 0.001). Post-hoc analysis was conducted using Wilcoxon signed-rank tests with a Bonferroni correction applied, and this found statistically significant results between Period 1 and Period 2 (Z = −4.112, p < 0.001) and Period 1 and Period 3 (Z = −3.879, p < 0.001), but not between Period 2 and Period 3 (Z = −0.866, p = 0.387).

In fact, if we consider the changes for any individual respondent, shown in Figure 3, we find that 112 respondents did not alter how much their final exam was worth in relation to the continuous assessment at any point during the three time periods under investigation. Very few put more weight on final examinations between Periods 1 and 2, with most who made changes moving towards a greater weighting on continuous assessment (either a 1–19% increase or 60–79% increase, suggesting they either made minor weighting adjustments or substantial ones). Between Periods 2 and 3, the biggest adjustments were plus or minus 1–19% change in weightings, with respondents almost equally adjusting towards more final examination weighting or more continuous assessment weighting. Overall, looking at the change between Periods 1 and 3, there was a noticeable shift back towards increased weighting for continuous assessment, although again the most common response was a 1–19% increase in weighting.

There were 73 additional comments on this question, many describing specifics about their approach, but some elaborating on reasons for the choices made in terms of assessment at the various stages. The most common themes are highlighted in

Table 4. Responses given to the question “Any comments on changes to your approach to assessment this academic year?” (n = 73).

Themes	Number of Responses	Sample Comment
Cheating	10	Open book online assessments led to lots of cheating (e.g., Chegg)
No choice	5	The university rules did not allow changing the balance of exam vs. continuous assessment
Previous experience	4	Multiple choice exam last June in Linear Algebra was awful to create and very bad at assessing students—average mark was 90%. This year’s Stack based questions for quizzes and exams on Moodle was much more discriminating
Time-consuming	4	Assessment became much more difficult. In particular, the process of creating an exam and finding appropriate problems (which could not be solved trivially using online software or Math Stack Exchange) was extremely time-consuming

below, along with a sample comment made under each theme.

3.3. Grade Distribution

Respondents were then asked if they observed any differences in the distribution of grades within their modules during Period 3. Only just over 3% felt that there was a big difference in grade distribution that year, with 22% stating that there was no difference at all and the remaining responses falling somewhere between these poles, as shown in

Table 5. Responses given to the question “Was there a difference in the distribution of grades within your modules this academic year?”, where 1 = no difference and 5 = a big difference (n = 181).

Ranking	Number of Responses
1	40
2	52
3	54
4	29
5	6

.

When asked for their interpretation of any differences they observed, there were 89 further comments made. The most common themes to emerge are shown in

Table 6. The five most common themes mentioned by respondents when asked, “If you saw a difference (in grades), why do you think this was?”.

Theme	Number of Occurrences	Sample Comments
Exam type	40	Grades are possibly higher due to the large amount of coursework/continuous assessment. I don’t think I would have the same number of A’s if it was the usual proctored exam.
Copying	19	Students adapt to online exams and are more likely to cheat. It doesn’t appear that there was more cheating than there usually is.
Student divide	19	More bimodal—perhaps reflecting the difficulties a subgroup of students had with online learning. Struggling students withdrew but focused students had more time to study.
Engagement	9	Engagement in sessions was not as high during online learning as students were not as accountable as they would be in-person. Some students didn’t/couldn’t engage with the online environment.
Lecturer experience	9	It was hard to pitch the level of difficulty on Webwork…I think that was too generous and the resultant marks were slightly higher. Students scored higher in some classes because my questions were a bit too ‘traditional’.

.

3.4. Satisfaction with Assessments

Respondents then rated their satisfaction levels with their assessments during the three time periods in question. The results are shown in Figure 4. It can be seen that three-quarters of respondents to this question were either satisfied or very satisfied with their assessments during Period 1. This dropped as low as two-fifths of respondents for Period 2 and recovered to 55% for Period 3. When a Friedman test was conducted, there was a statistically significant difference between satisfaction levels with assessments over time (χ²(2) = 84.874, p < 0.001). Post-hoc analysis was conducted using Wilcoxon signed-rank tests with a Bonferroni correction applied, and this found statistically significant results between each of the three time periods when compared with each other in terms of respondent satisfaction with their assessments (Period 1 vs. Period 2: Z = −7.333, p < 0.001; Period 2 vs. Period 3: Z = −4.564, p < 0.001; Period 1 vs. Period 3: Z = −5.286, p < 0.001).

3.5. Easiest/Hardest Aspects of Mathematics to Assess Online

Finally, respondents were asked two more general questions about assessment in mathematics: namely, what aspects of mathematics they considered to be most difficult and easiest to assess online. The most common themes to emerge from the 123 responses to each question are shown in

Table 7. The most common themes that emerged when respondents were asked “What aspects of maths do you think are most difficult to assess online?” and “What aspects of maths do you think are easiest to assess online?” (n = 123).

Themes: Hardest to Assess	Frequency	Themes: Easiest to Assess	Frequency
Proof	29	Computation	38
Computation	26	None	13
Cheating	24	Understanding	11
Understanding	16	MCQs	8
Online solving	13	Cheating	5
Theory	12	Proof	5
Skills	9	Programming	4
Reasoning	7	Statistics	4

.

Table 8. The most common themes emerged when respondents were asked, “What aspects of maths do you think are most difficult to assess online?” along with sample comments under each theme (n = 123).

Theme	Number of Occurrences	Sample Comments
Proof	29	I believe there is much merit in asking students to learn to state theorems and to prove them. But this is tricky to assess online.
Computation	26	I think any procedural questions for service maths modules…are difficult to assess online—the fact that there are so many websites where fully worked solutions to questions can be easily generated makes it very difficult to stand over the integrity of online assessments.
Cheating	24	The fact that there are so many websites where fully worked solutions to questions can be easily generated makes it very difficult to stand over the integrity of online assessments.
Understanding	16	As ‘bookwork’ questions (e.g., proofs of theorems) are not possible…it can be difficult to assess a student’s understanding of the theory of any particular topic.
Online solving	13	The availability of online computational software and problem-solving sites makes it very difficult to assess students online. I don’t see any way around this without radically altering what we assess for. To some extent, this might be worth discussing even in the absence of online education.
Theory	12	Theoretical content
Skills	9	Basic skills
Reasoning	7	The problem I had was assessing their ability to think with insight into unfamiliar problems.

and

Table 9. Most common themes that emerged when respondents were asked “What aspects of maths do you think are easiest to assess online?” along with sample comments under each theme (n = 123).

Theme	Number of Occurrences	Sample Comments
Computation	38	Questions that have parameters are relatively easy to vary without changing the difficulty of the question.
None	13	There is really no aspect of Maths that is easy to assess online.
Understanding	11	More abstract concepts are possibly a little easier to assess online as the understanding of the students can be tested in different ways.
MCQs	8	Multiple choice questions and quizzes can be easily developed and completed which does help with assessment between sessions.
Cheating	5	However, there is no way to control or prevent students to contact each other during a timed exam they sit at home. Therefore, it is not clear if the exams assess if a particular student has understood the material.
Proof	5	Standard questions that are not (easily) solved on webpages or computer software like Mathematica. Such as ‘show this function is continuous’, ‘show this subgroup is normal’.
Programming	4	Programming…, by design, has been assessed online for a very long time—anything else wouldn’t really make sense.
Statistics	4	Giving students real data to work with and setting them online questions based on their individual data and/or project work. Students are very engaged too as they feel it is useful.

show the most common themes under “hardest to assess” and “easiest to assess”, respectively, along with the frequency of the theme and some sample comments made by respondents.

4. Discussion

In this study, we explored the assessment approaches taken by mathematics lecturers at three distinct periods to determine whether the forced inclusion of online assessment as a result of the COVID-19 campus closures might alter their opinions towards diversifying their assessment longer-term. Assessment in mathematics typically over-emphasises replication of content (facts) and skills (techniques) (Pegg, 2003). Assessment design should be heavily influenced by the mathematics that is considered most important for students to learn (Stacey & Wiliam, 2012). The respondents in this sample conducted almost no online teaching in Period 1, exclusively online teaching in Period 2, and almost all online teaching in Period 3. As such, the latter two periods did not reflect the “normal” situation for many of them but instead acted as a unique snapshot of time whereby they had to use online assessment.

4.1. What Assessment Types Were Used by Mathematics Lecturers Before the Pandemic, During the Initial University Closures, and During the Academic Year 2020/2021?

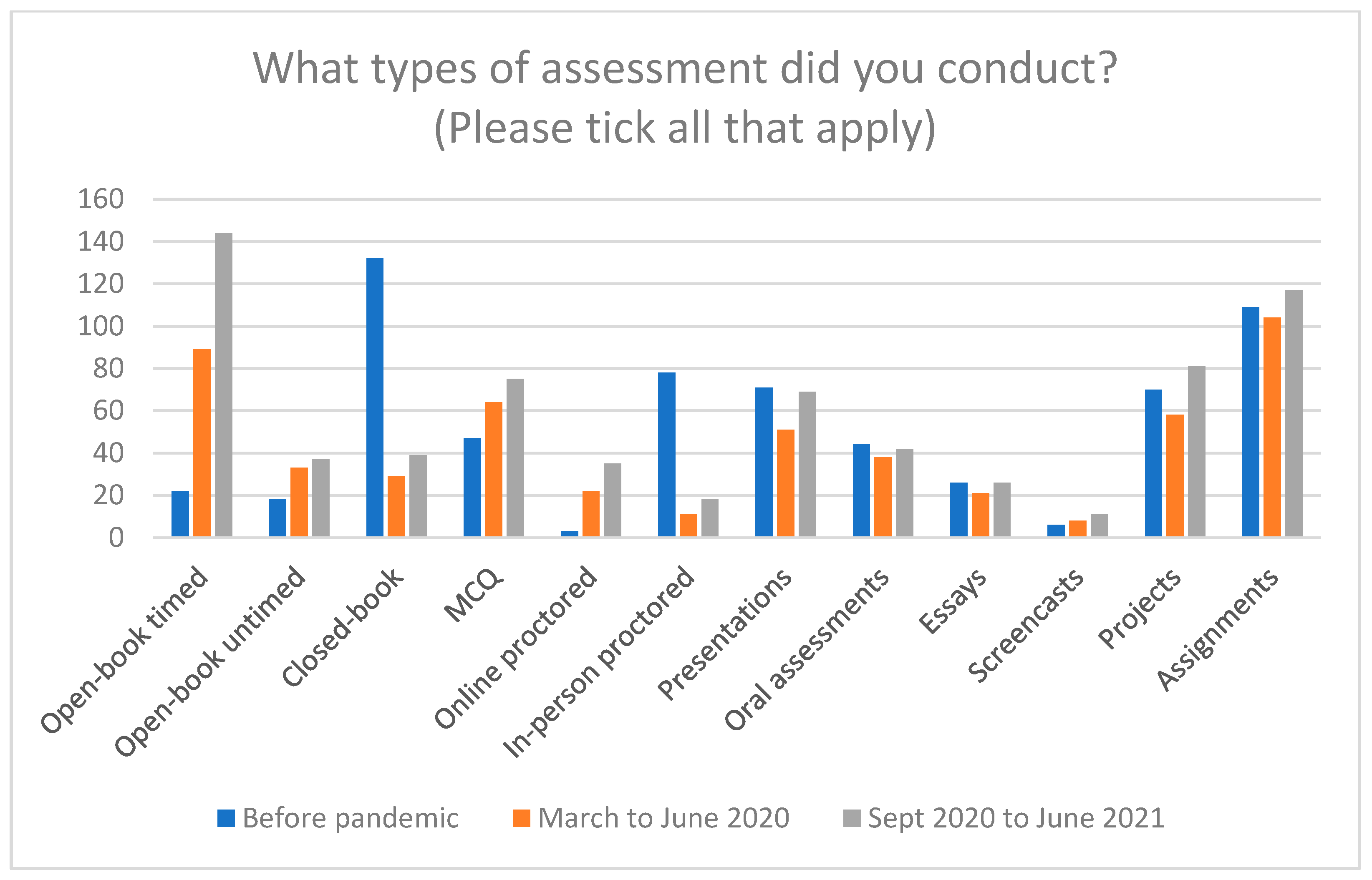
Our first research question explored the assessment types used by mathematics lecturers during the three periods under investigation. We found statistically significant changes in assessment types used by our sample in relation to 9 of the 12 assessment types investigated. We established that our sample was typical of the mathematics lecturer population during Period 1, in that 70% of respondents used closed-book examinations and 57% used assignments, both of which would be commonly used mathematics assessment approaches (Iannone & Simpson, 2022). By Period 3, open-book timed examinations had replaced the more popular closed-book examinations, even more so than in Period 2, when many respondents did not have sufficient time to implement such changes in their assessment. The findings clearly show a broader range of assessment modes in use in Period 3. After open-book timed assessments, projects, assignments and MCQs are the most popular modes of assessment. This is of interest as, according to Niss (1998), relaxing timing restrictions for students allows one to assess a broader range of concepts and skills. Suurtamm et al. (2016) say that implementing a range of assessment approaches allows students multiple opportunities to utilise feedback and demonstrate their learning. When a lecturer relies on one type of assessment, students often become experts at predicting likely assessment areas and choose their areas of revision accordingly (Burton & Haines, 1997). Seeley (2005) recommends designing assessments by “incorporating problem-solving, open-ended items, and problems that assess understanding as well as skills”, making assessment an integral part of teaching and learning. Of the three assessment types where no significant difference was observed, oral assessments were the most commonly used (by just over 20% of respondents). Although this was an under-utilised assessment type, it does appear to have been one that was able to be used across all three time periods, regardless of whether the assessment was in-person or online. This makes it an assessment type worthy of further consideration in relation to mathematics (Iannone et al., 2020).

4.2. Were There Changes to the Weightings Given to Final Examinations Versus Continuous Assessment During These Time Periods?

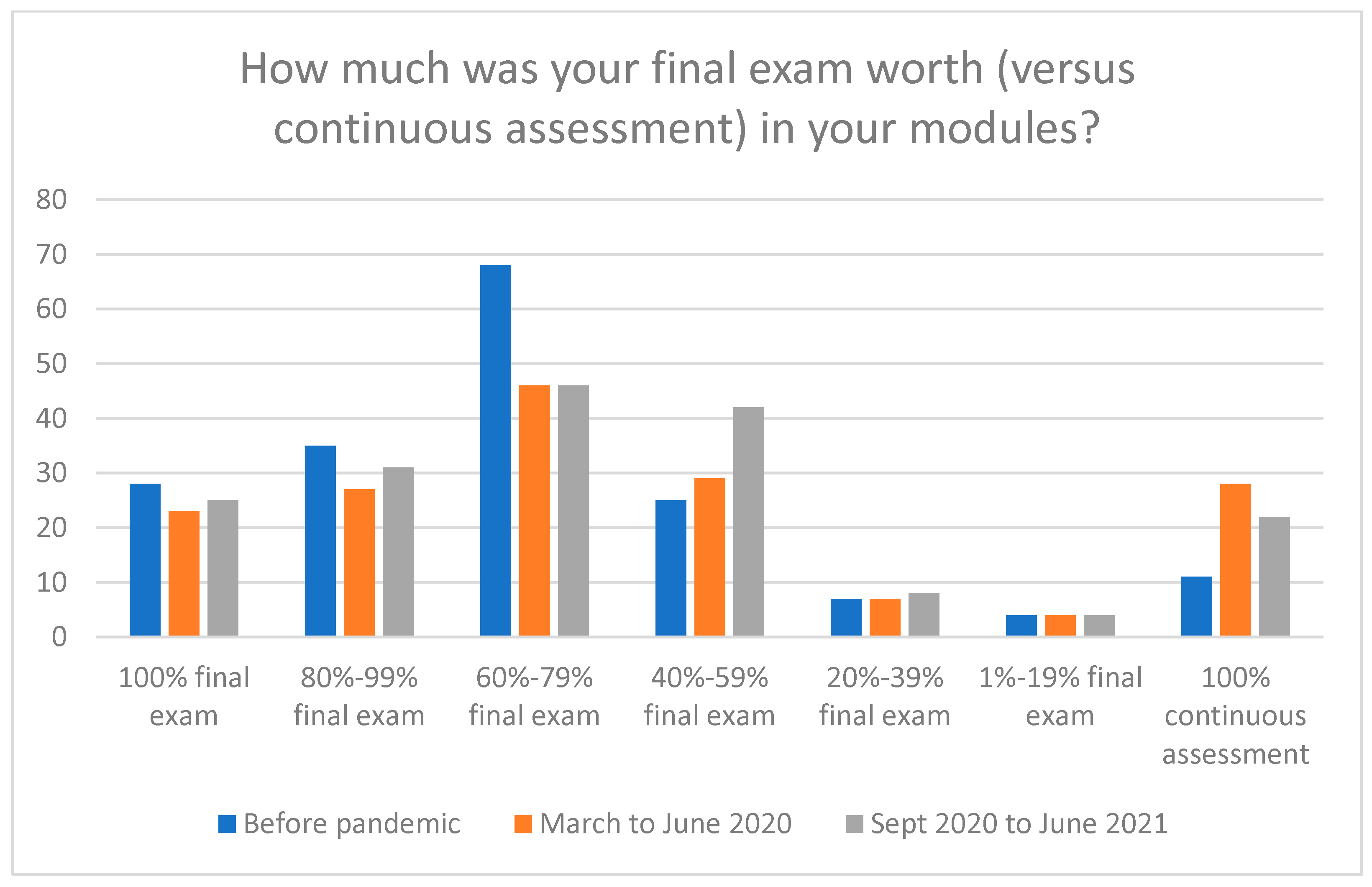
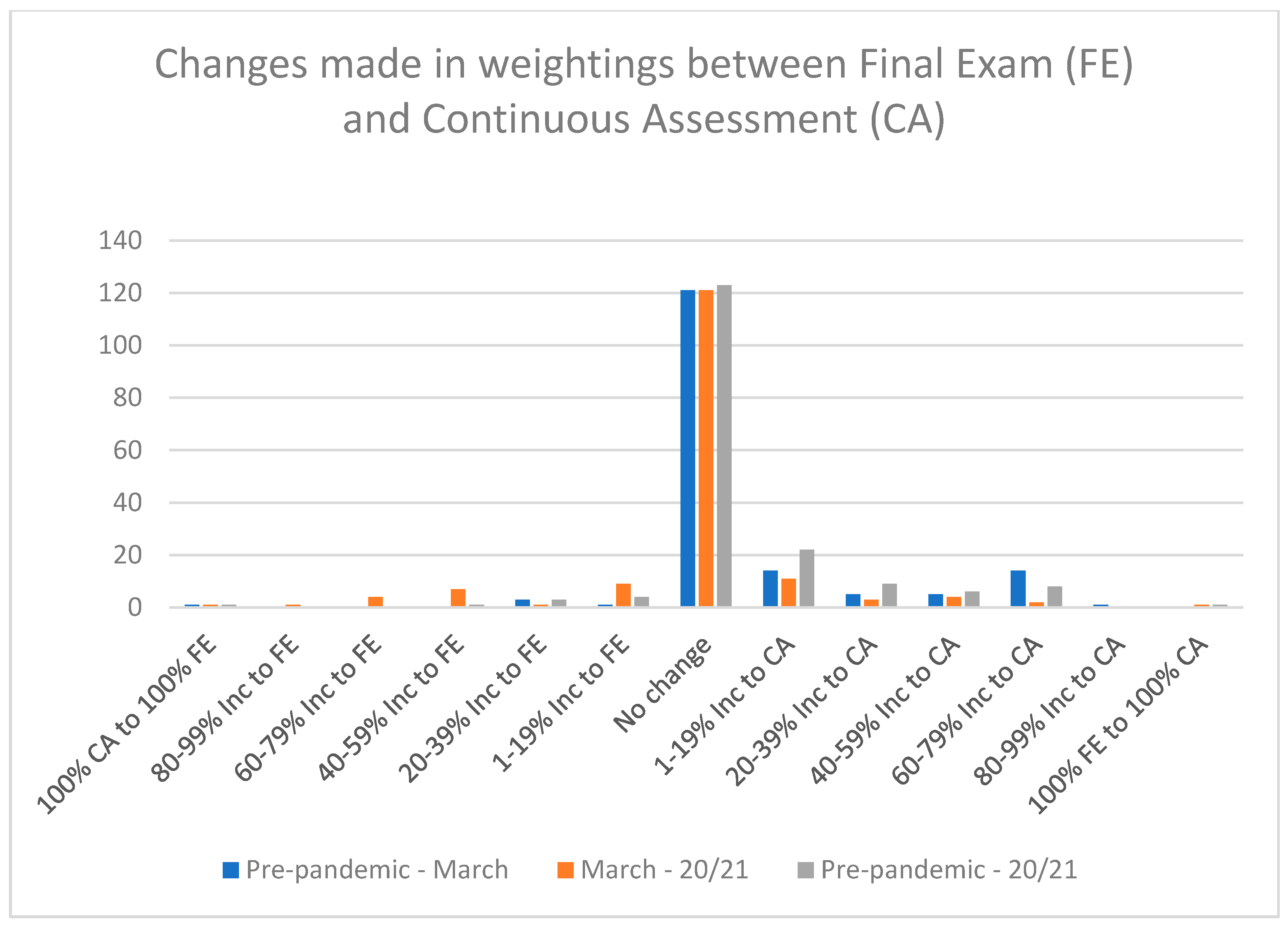
The proportion of lecturers who gave 80–100% final exams remained steady between Periods 1 and 3. There was a shift from the proportion who offered a 60–79% final exam towards a 40–59% exam. We do observe a statistically significant increase in lecturers favouring 100% continuous assessment in Period 3 when compared with Period 1. The number of those in favour of a 100% continuous assessment is in line with those in favour of a 100% final exam.

4.3. Did Mathematics Lecturers Observe Any Changes in Grade Distribution Within Their Modules During These Time Periods?

Overall, lecturers did not observe a vast difference in grade distribution between the three periods in question, although they gave varying reasons for this. The most prevalent theme was that of the type of examination that the students undertook. Some comments related this to a higher weighting on continuous assessment (“Grades are possibly higher due to the large amount of coursework/continuous assessment”), while others referenced the “binary right/wrong marking” of some online assessment tools, particularly in relation to multiple-choice questions. A number of respondents spoke of the impact of using open-book examinations where previously they would have had closed-book (“I don’t think I would have the same number of A’s if it was the usual proctored exam”). However, opinions were mixed on whether this was more or less difficult for the students, with one respondent stating, “open book exams plus timed online format skewed harder than in previous years as no book answers” while another felt that “open book made it easy for students to look at worked examples”. The next most common theme was that of copying—either another student’s work or using an online tool to cheat. Respondents observed that “cheating online is very easy” and that “students adapt to online exams and are more likely to cheat”. Conversely, one respondent felt that “it doesn’t appear that there was more cheating than there usually is”; however, this respondent stated that their module was fully assessed by continuous assessment both before the pandemic and during the academic year 2020/2021. Additionally, several respondents remarked on how, although they suspected there were students cheating, there was not as big a difference in the grade distribution as might have been expected because “there was probably cheating, but at the same time some students were less motivated”, and others echoed approaches similar to that in (Sarmiento & Prudente, 2019). Another strong theme to emerge was that of an increased divide in student performance, with many respondents pointing out how difficult it was for some of their students (“More bimodal—perhaps reflecting the difficulties a subgroup of students had with online learning”). Several respondents felt that, although it was more difficult for some students, others coped well (“I feel that some students were not able to concentrate online. The high achievers were able to perform well in both situations”), or in fact that some students excelled in this situation (“Struggling students withdrew but focused students had more time to study”). Several respondents also mentioned student engagement as a reason for greater disparity in grades, stating that “some students didn’t/couldn’t engage with the online environment” and “engagement in sessions was not as high during online learning as students were not as accountable as they would be in-person”. This could partly be attributed to the pandemic conditions, in which students from lower socio-economic backgrounds, or those with caring responsibilities, were impacted more in terms of engaging with online learning (Ní Fhloinn & Fitzmaurice, 2021). Finally, a number of respondents also alluded to their own lack of experience in setting different types of assessments as a reason for a differing grade profile, with some stating that they felt they made the assessment too easy as a result (“it was hard to pitch the level of difficulty on Webwork…I think that was too generous and the resultant marks were slightly higher”), while others felt the opposite had occurred (“Students scored higher in some classes because my questions were a bit too ‘traditional’”). Others simply observed that “there is a learning curve in terms of making a good online multiple-choice exam when all study aids are allowed. It is possible but requires some clever thinking”. This echoes the warning of Greenhow (2015) in relation to the creation of online assessments.

4.4. Were Mathematics Lecturers Satisfied with Their Assessment Approaches During These Time Periods?

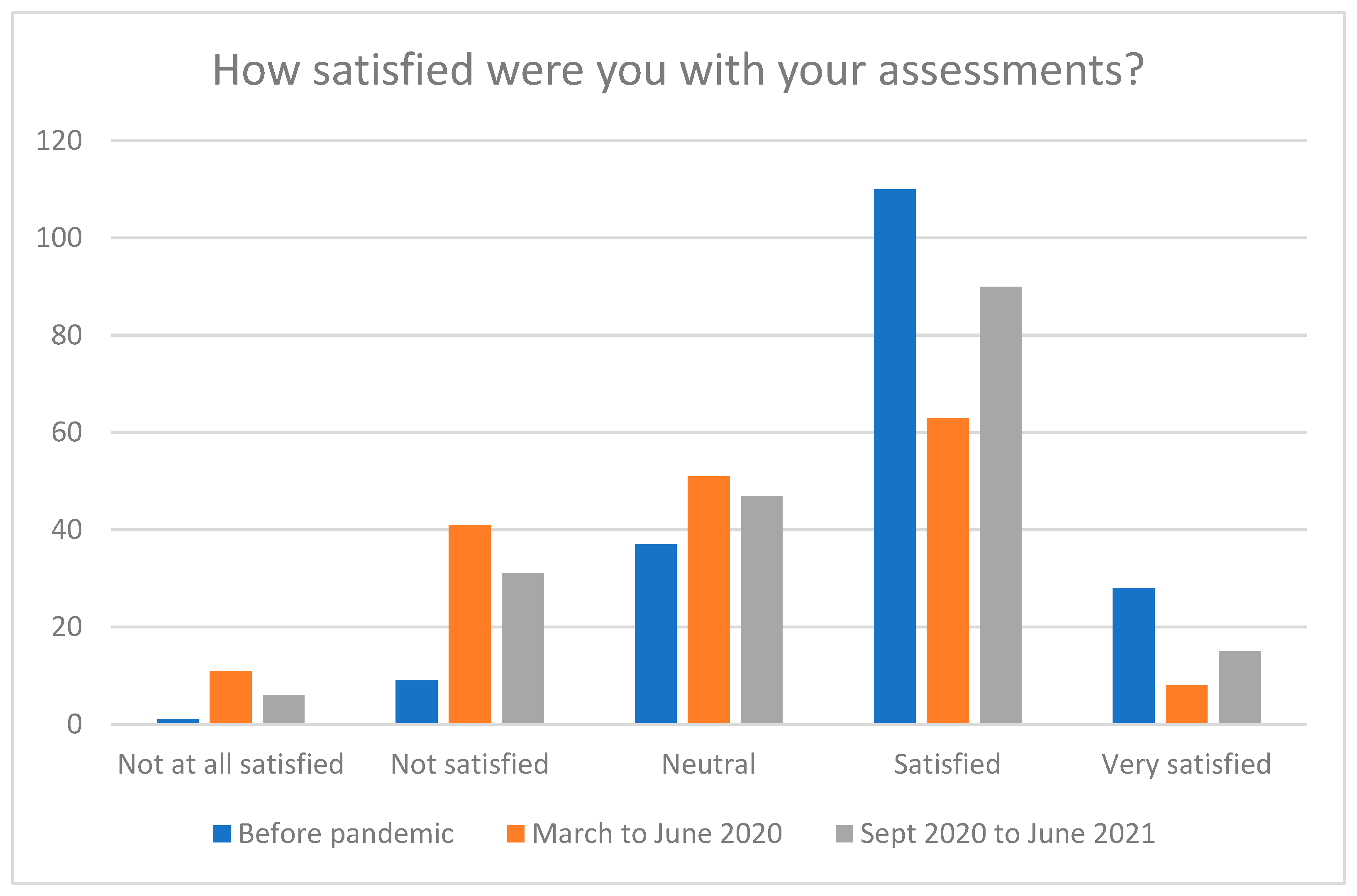
Although the academics had increased the number of assessment methods in use, fewer respondents were satisfied with their assessments in Period 3 than before the pandemic in Period 1. The differences in satisfaction levels between all three time periods were significant, with the highest satisfaction ratings given pre-pandemic, and the next highest in Period 3. Overall satisfaction was significantly lower in Period 2, which was to be expected, as this was when lecturers had to pivot to new assessment types with very little time or resources to implement or plan these new assessments.

4.5. What Do Mathematics Lecturers Believe Are the Easiest and Most Difficult Aspects of Mathematics to Assess Online?

Our final research question was in relation to what aspects of mathematics lecturers believed were easiest or most difficult to assess online. The end of Period 3 represented a unique snapshot in time to obtain this information, whereby the majority of lecturing staff had been obliged to conduct online assessments in mathematics, regardless of their previous experience with online teaching (Ní Fhloinn & Fitzmaurice, 2021). We particularly wanted to investigate if mathematics lecturers perceive an online environment to be more conducive to the assessment of some mathematical areas than others. Respondents mostly spoke about the topic being assessed. The most common theme among “hardest to assess” was that of “proof”. Many respondents pointed out the difficulty of assessing theorems online in the same manner as they would have in a closed, proctored examination (“I believe there is much merit in asking students to learn to state theorems and to prove them. But this is tricky to assess online”). Other respondents noted that it was difficult to assess students’ ability to “reproduce a long technical proof”, although some respondents did question whether there was evidence of understanding previously in this approach (“Understanding (or, perhaps, if we are very honest, memory of) proofs.”), and observed that “it does make you think about key aspects of a proof not just memory and regurgitation”. The small number of instances of “proof” being mentioned in terms of being easiest to assess online leaned towards “standard questions that are not (easily) solved on webpages or computer software like Mathematica. Such as ‘show this function is continuous’, ‘show this subgroup is normal’” or “applications of theorems”.

Notably, “computation” appeared as the second-most common theme in terms of “most difficult to assess” and as the most common theme in terms of “easiest to assess”. Those who found it easiest to assess tended to make comments around the ease of using software to develop “questions that have parameters are relatively easy to vary without changing the difficulty of the question”. In contrast, many of those who found it hardest to assess linked this difficulty to the issue of students cheating, either by getting the solution from their classmates or online software (“I think any procedural questions for service maths modules…are difficult to assess online—the fact that there are so many websites where fully worked solutions to questions can be easily generated makes it very difficult to stand over the integrity of online assessments”). Similarly, some mentioned the difficulty of assessing basic computational techniques in open-book examinations (“As we only used open-book methods when assessments were online, it is hard to gauge if students have gained mathematical skills or if they are very dependent on copying procedures from worked examples”).

Yet more mentioned the drawbacks of “MCQs [multiple-choice questions] that involve lots of arithmetic/algebraic manipulation—it is difficult to give half marks/quarter marks to students who have done it partly correct but reached an incorrect result”.

Plagiarism, copying or “cheating” was the third most common theme in the aspects that are hardest to assess. This was frequently linked to either the “proof” or “computation” themes, but also often cited on its own, with one respondent stating that the hardest thing to assess was “anything where you want to ensure the work is the student’s own” and another that it was “anything you can find the answer to online”. The difficulty of detecting such activity was summed up by one respondent who said that “catching collusion can be tricky, as sometimes there is basically one obvious way to get to the right answer”. Another observed that “the fact that there are so many websites where fully worked solutions to questions can be easily generated makes it very difficult to stand over the integrity of online assessments”. This theme emerged a few times also among the comments in relation to the easiest aspects to assess; usually as an addendum to other comments, such as “However, there is no way to control or prevent students to contact each other during a timed exam they sit at home. Therefore, it is not clear if the exams assess if a particular student has understood the material”.

The theme of “understanding” occurred almost equally frequently in both the hardest and easiest aspects to assess online. Among those who deemed it hardest to assess online, many simply mentioned “conceptual understanding” without elaboration; however, a few mentioned that it was difficult to know “whether students understand definitions (because open book)” and “as ‘bookwork’ questions (e.g., proofs of theorems) are not possible…it can be difficult to assess a student’s understanding of the theory of any particular topic”. For the respondents who deemed “understanding” easiest to assess, again several simply mentioned “conceptual understanding”. However, a couple explained that “more abstract concepts are possibly a little easier to assess online as the understanding of the students can be tested in different ways” and that misconceptions could be exposed “using basic mcqs or true false. It doesn’t require any written mathematics and can expose key misunderstanding. Although why those exist might require alternative approaches”.

The theme “online solving” made specific reference to students using apps, websites or software to solve the questions they were asked in their assessments and only appeared in relation to the hardest aspects to assess. One respondent linked this to a need to consider what it is that is assessed and the purpose of such assessment, even outside the need to assess online (“The availability of online computational software and problem-solving sites makes it very difficult to assess students online. I don’t see any way around this without radically altering what we assess for. To some extent, this might be worth discussing even in the absence of online education”).

The three other most common themes of “theory”, “skills” and “reasoning” again appeared only in the hardest aspects to assess online. Respondents did not elaborate much on any of these themes, mostly just mentioning “theoretical content”, “basic skills” or “mathematical reasoning”. However, one respondent did elaborate in terms of reasoning to explain that “the problem I had was assessing their ability to think with insight into unfamiliar problems”.

In terms of the easiest aspects to assess online, the second-most common was “none” with no further comments made on this. A number of respondents mentioned “multiple-choice questions (MCQs)”, stating “multiple choice questions and quizzes can be easily developed and completed which does help with assessment between sessions”. However, another respondent cautioned that “aspects that can be validly assessed by multichoice questions lend themselves to being tested in hands-on mode … but the design of good MCQs is very challenging, and not all knowledge and skills can be covered”.

Finally, both “programming” and “statistics” were mentioned a number of times as being the easiest to assess online. In relation to the former, one respondent observed that “programming…, by design, has been assessed online for a very long time—anything else wouldn’t really make sense”. For statistics, another respondent suggested “giving students real data to work with and setting them online questions based on their individual data and/or project work. Students are very engaged too as they feel it is useful”.

5. Conclusions

To conclude, only one significant change in assessment approach was observed across the three periods of study; a move from closed- to open-book timed examinations. Academic integrity was clearly a strong consideration of the lecturers who participated in this study. For them, this refers to cheating and significantly influences the assessment strategy they adopt. This echoes the findings of Henley et al. (2022), whose large-scale survey of mathematics departments across the UK and Ireland found academic misconduct on the part of students to be of significant concern over the same time period as this study. The authors state that a community-wide approach will be necessary moving forward if open-book online assessments are to be continued. They found that increasing the time available for students to complete the assessments remotely led to increases in instances of plagiarism and cheating (Henley et al., 2022). Assigning randomised and personalised assessments is one method suggested in recent studies for reducing this misconduct (Eaton & Turner, 2020; Sarmiento & Prudente, 2019). While this may sound very laborious and time-consuming, Henley et al. (2022) state that this is not necessarily true. Respondents to their survey listed several methods of achieving this, including, for example, LaTeX Macros, which can be used to create personalised mathematical problems and generate random values for assessments. Online proctoring may reduce incidents of cheating (Lancaster & Cotarlan, 2021) but then result in negative mental health outcomes for others (Eaton & Turner, 2020).

Moving away from closed-book, proctored assessments in any capacity is likely to lead to grade inflation for a variety of reasons. Our findings echo those of Iannone and Simpson (2022), who in 2021 found that there is little variety in the assessment strategies of mathematics departments in Higher Education institutions in the UK. They too found that the weighting of final assessments was shifting towards the inclusion of other methods, but progress is slow. Despite the unprecedented visit of a pandemic and a drastic sudden move to remote teaching and assessment, assessment in mathematics remained largely unchanged. Research conducted since the pandemic provides evidence that remote assessment of mathematics posed a momentous challenge for many lecturers during this unprecedented period (Cusi et al., 2023). More worryingly, a study conducted with almost 470 university mathematics lecturers in Kuwait and the UK during the same time period as reported in this study found that the lecturers were very much unconvinced of the merits of online assessment in mathematics and would likely revert to their tried and trusted methods when restrictions were lifted (Hammad et al., 2025). Continued professional development programmes that support the effective implementation of practical and fair assessment practices and provide practical strategies and hands-on training are necessary if progress forward instead of backwards is to be sustained (Cusi et al., 2023).

The future of mathematics education holds great promise for technological innovations and the integration of Generative Artificial Intelligence (GenAI). Personalised learning is expected to become more widespread, with adaptive learning platforms and intelligent tutoring systems analysing students’ needs and providing tailored instruction and assessment. This study was undertaken when the capacities of GenAI were considerably weaker than they are at the time of writing, and given the concerns expressed by lecturing staff in relation to academic integrity at this earlier time, we feel that this is likely to be at the forefront of any decisions taken in relation to new assessment approaches to mathematics in the future. A follow-up mixed-methods study is planned to investigate the current status of assessment in mathematics globally, with the emergence of GenAI and its availability to both lecturers and students.

There are a number of limitations which should be taken into account in relation to this study. Firstly, 36% of respondents were based in Ireland, with a total of 88% of respondents based in Europe, meaning that the results can only be considered reflective of practice in European countries and may not be generalisable further afield. In addition, the survey was only available in English; it was distributed and conducted online via mailing lists and advertisements at relevant mathematics education conferences. As a result, it is unknown how representative it is of the general population of mathematics lecturers in higher education.