Juggling Balls and Mathematics: An Ethnomathematical Exploration
Abstract
1. Introduction
1.1. Ethnomathematics
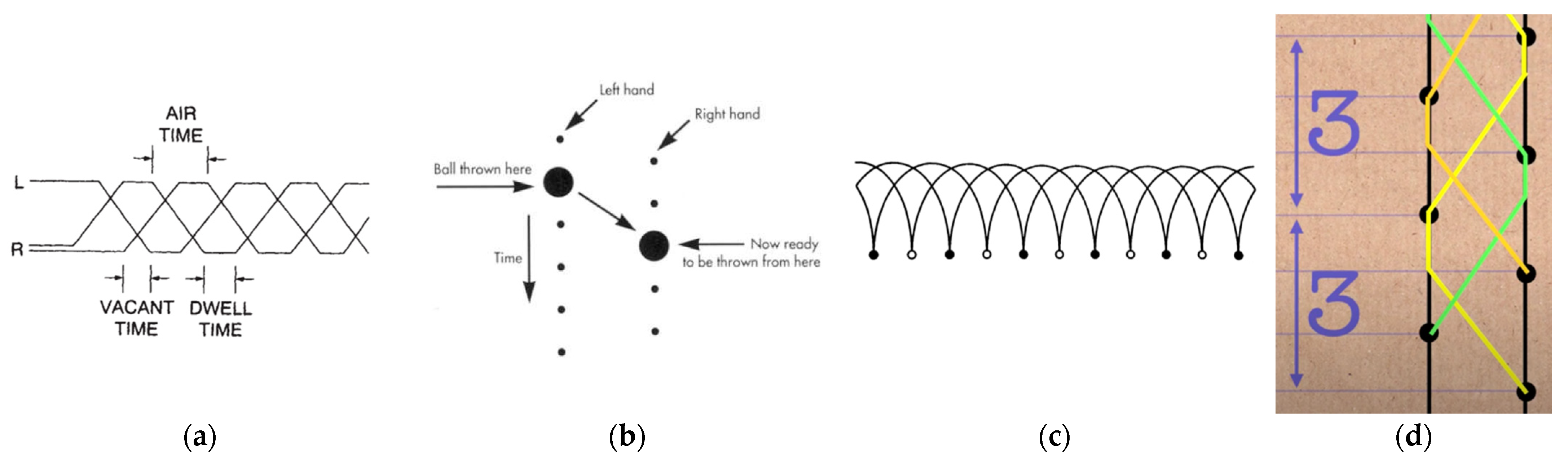
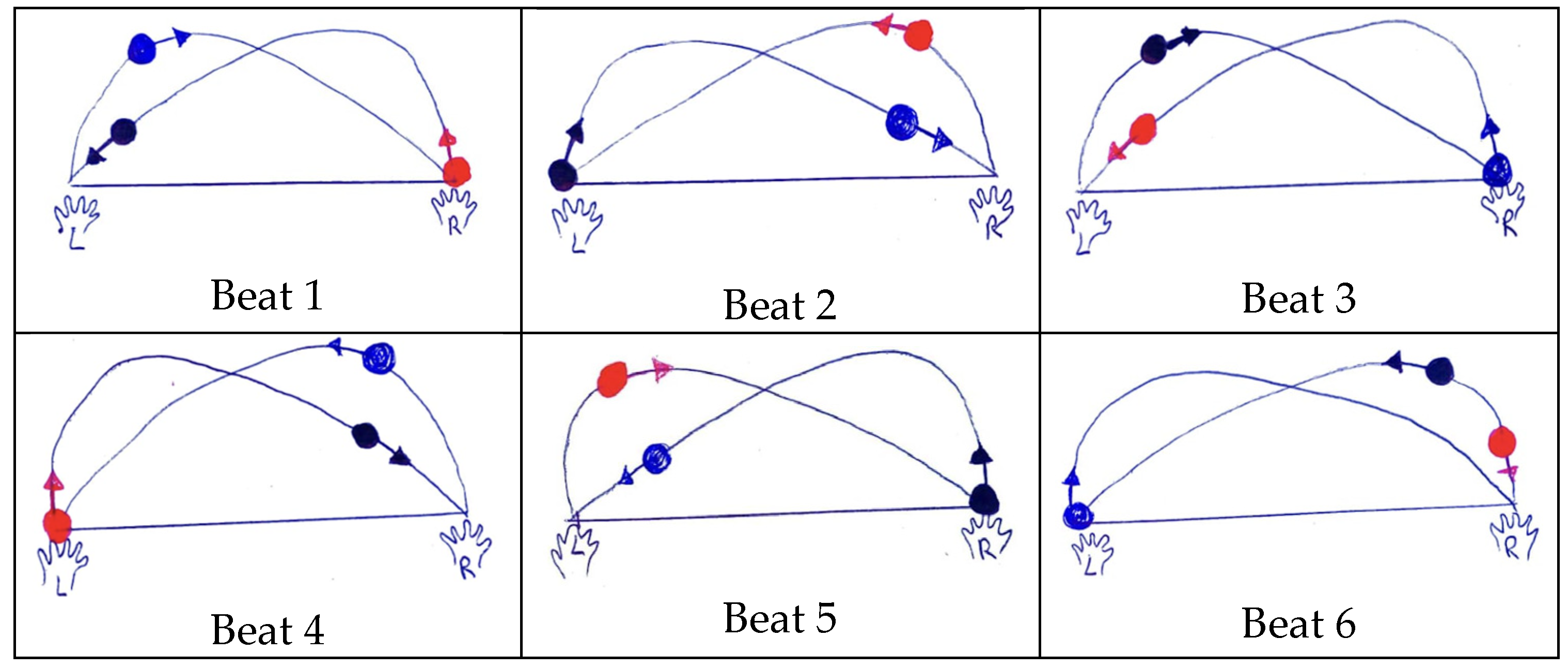
1.2. Juggling and Its (Mathematical) Representation
- The vertical axis symbolizes time, with the “rungs” of the ladder delineating evenly spaced beats within the pattern.
- Lines in the diagram represent the paths that props take through time and space.
- The number of paths that intersect any horizontal line on the diagram represents the number of props in the pattern.
- The sides of the diagram indicate whether throws and catches are made with the right or left hand.
- Quantity: A ladder diagram represents quantity through the number of props involved in the pattern, which can be seen by counting the number of lines that intersect any horizontal line on the diagram. The number of rungs crossed by each path also relates to the quantity of time that a prop spends in the air.
- Relationships: The diagram shows relationships through the connections between throws and catches and the order in which these occur in time. The paths of the props show how throws relate to each other, in terms of both timing and which hand is used. The ladder diagram’s structure shows the sequential relationships between throws and catches.
- Space: The spatial aspect is shown by the paths of the props, which represent movement through time and space (although the vertical dimension of physical patterns is ignored). The alternation of the throws between the hands and how paths intersect also imply spatial relationships.
2. Materials and Methods
2.1. Context and Participants
2.2. Techniques and Data Collection
2.3. Data Analysis
3. Findings
3.1. First Cycle: Ladder Diagram
3.1.1. The Ladder Diagram and Siteswap Notation
- Both hands throw alternate throws at equally spaced time intervals.
- Both hands throw at the same rhythm.
- One prop can be thrown from one hand at a time, or caught by one hand at a time.
3.1.2. Idea and Interaction in First Cycle
3.1.3. Critical Points and Potentialities in First Cycle
J1: It was natural to me to help them showing the three-ball cascade while they were solving the task.
R1: Actually, the juggling exercise and task 1 resolution should be performed simultaneously to be effective.(From field note, March 2024)
J1: The detected problem indicates a misunderstanding of the task.
R1: I think that the transition from reality to an adequate model did not occur in this specific instance.(From field note, March 2024)
R1: Just P1 and P2 worked on their own.
J1: They usually work together as a group during their workshop.
J1: Besides, I guess that the proposed tasks were too “artificial” compared to the juggling practice during the workshops.
R1: This could be the reason why the initial enthusiasm was followed by tiredness and someone gave up.(From field note, March 2024)
3.1.4. Variation in First Cycle
R1: I guess it could be quite tricky.
J1: And even dangerous for the guys.
R1: We could easily build a horizontal ladder, a paper model to be laid out on the floor.(From field note, April 2024)
3.2. Second Cycle: Floor Ladder
3.2.1. Idea and Interaction in Second Cycle
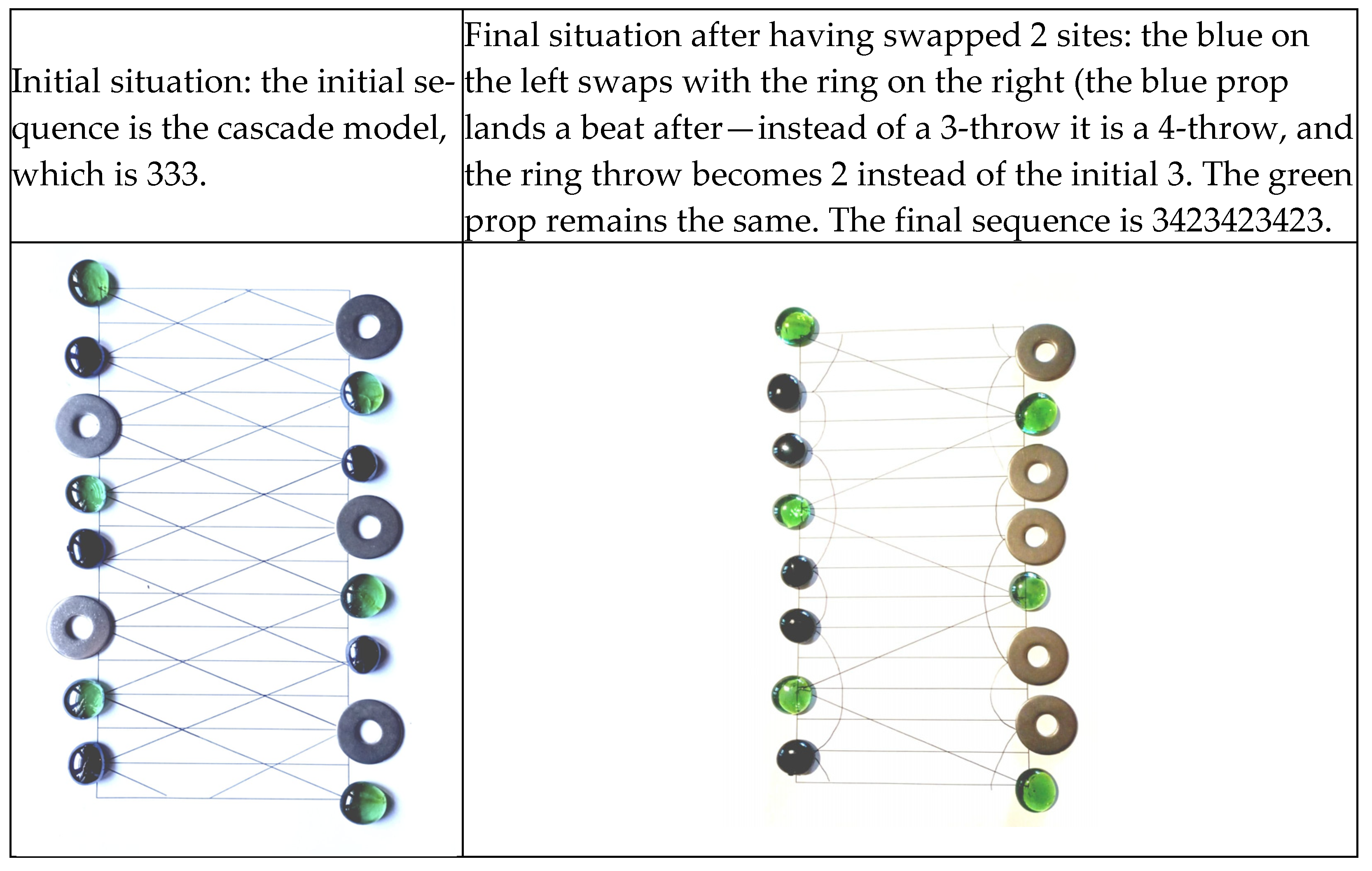
J1: I want to add some dynamism to the model…we usually use our body during our workshops! They [the participants] could throw the balls into the corresponding rings while walking!(From field note, April 2024)
R1: This new model could be used to generate new patterns from existing ones by swapping the landing times of any two “sites” (hence the name Siteswap). Actually, this is where the word Siteswap comes from!(From field note, April 2024)
3.2.2. Critical Points and Potentialities in Second Cycle
3.2.3. Variation in Second Cycle
R1: While the initial model was interactive and effective, it lacked dynamism.
J1: One possible solution could be to adjust the distance between the rungs of the ladder to match my step length.
J2: I guess we have to modify the metronome rhythm while he juggles the cascade.(From field note, April 2024)
3.3. Loop: Small-Scale Model
3.3.1. Idea and Interaction in the Loop Cycle
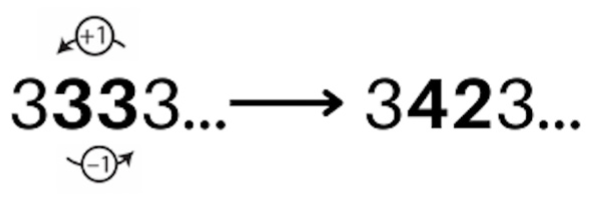
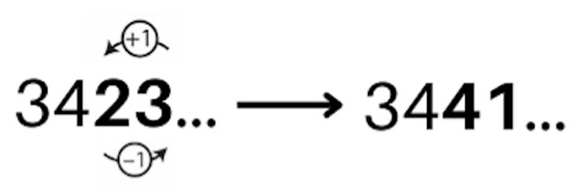
3.3.2. Critical Points and Potentialities in the Loop Cycle
3.3.3. Variation in the Loop Cycle
3.4. Third Cycle: Improved Floor Ladder
3.4.1. Idea and Interaction in the Third Cycle
3.4.2. Critical Points and Potentialities in the Third Cycle
3.4.3. Variation in the Third Cycle
J2: Why don’t we try with the hats? In this way we can decrease the level of difficulty of the exercise by using hats instead of taking out the throwing of the balls, eliminating the need to throw objects without.(From field note, May 2024)
3.5. Fourth Cycle: Hat Ladder
3.5.1. Idea and Interaction in the Fourth Cycle
J2: We could even use hair extensions to be tied to a girl’s head.
R1: Mathematically speaking, this exercise is very suitable for representing the movement of objects on a plane parallel to the direction of motion!(From field note, June 2024).
3.5.2. Critical Points and Potentialities in the Fourth Cycle
R1: Could you repeat the exercise by removing the time constraint played by the metronome and tightening the braid one at a time?(From field note, August 2024).
J1: I can try attaching the balls with a heavy rope I normally use to open the curtain of the chapiteau.(From field note, August 2024).
3.5.3. Variation in the Fourth Cycle
4. Discussion
5. Conclusions
- For the mathematician, juggling provided a tangible and engaging context to explore abstract mathematical concepts, which is a valuable resource to develop interdisciplinary mathematical tasks for formal education.
- For the juggler, the mathematical analysis of juggling sequences offered a deeper understanding of the underlying structures and patterns, empowering them to create and innovate new sequences with greater precision and intentionality.
6. Recommendations for Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Juggling by Numbers (Numberphile): https://www.youtube.com/watch?v=7dwgusHjA0Y (accessed on 1 February 2024) |
| 2 | Juggling simulator: https://jugglinglab.org/ (accessed on 2 February 2024) |
| 3 | 441 trick Video: https://youtu.be/oCm9TQQmy7E (accessed on 2 February 2025) |
| 4 | Juggling rings Video: https://youtube.com/shorts/3izO1EE7Ujs?feature=shared (accessed on 15 January 2025) |
| 5 | Braid Video: https://www.youtube.com/shorts/2rBYIYSnltc (accessed on 20 January 2025) |
References
- Adam, A., Alangui, W. V., & Barton, B. (2014). Lights and questions: Using mutual interrogation. For the Learning of Mathematics, 30(3), 10–16. [Google Scholar] [CrossRef]
- Adam, N. A. (2010). Mutual interrogation: A methodological process in ethnomathematical research. Procedia-Social and Behavioral Sciences, 8, 700–707. [Google Scholar] [CrossRef]
- Albanese, V. (2021). Bundles of ethnomathematical expertise residing with handicrafts, occupations, and other activities across cultures. In M. Danesi (Ed.), Handbook of cognitive mathematics (pp. 1–34). Springer. [Google Scholar] [CrossRef]
- Albanese, V., Adamuz-Povedano, N., & Bracho-López, R. (2017). The evolution of ethnomathematics: Two theoretical views and two approaches to education. In M. Rosa, L. Shirley, M. E. Gavarrete, & W. V. Alangui (Eds.), Ethnomathematics and its diverse approaches for mathematics education (pp. 307–328). Springer. [Google Scholar] [CrossRef]
- Albanese, V., & Herrera-Janques, M. E. (2024). Dancing symmetries: Unveiling patterns in couple dances. Symmetry: Culture and Science, 35(4), 503–517. [Google Scholar] [CrossRef]
- Barton, B. (1999). Ethnomathematics and philosophy. ZDM, 31(2), 54–58. [Google Scholar]
- Buhler, J., & Graham, R. (2004). Juggling patterns, passing and posets. In D. Hayes, & T. Shubin (Eds.), Mathematical adventures for students and amateurs (pp. 99–116). The Mathematical Association of America. [Google Scholar]
- Butler, S. (2010). The art of juggling with two balls or A proof for a modular condition of Lucas numbers. arXiv, arXiv:1004.4293. [Google Scholar]
- Chavarría-Arroyo, G., & Albanese, V. (2023). Problemas matemáticos elaborados por docentes: Un análisis desde la contextualización culturalmente significativa. Bolema-Boletim de Educação Matemática, 37(76), 731–753. [Google Scholar] [CrossRef]
- Coppe, C., & Mesquita, M. (2015). Fronteiras urbanas: Perspectivas para as investigações em etnomatemática. Bolema-Boletim de Educação Matemática, 29(53), 828–844. [Google Scholar] [CrossRef]
- D’Ambrosio, U. (1985). Ethnomathematics and its place in the history and pedagogy of mathematics. For the Learning of Mathematics, 5(1), 44–48. [Google Scholar]
- François, K., Mafra, J. R., Fantinato, M. C., & Vandendriessche, E. (2018). Local mathematics education: The implementation of local mathematical practices into the mathematics curriculum. Philosophy of Mathematics Education Journal, 33, 1–18. [Google Scholar]
- Lewbel, A. (1994). A free offer, a call to teachers, and the invention of juggling notations. Juggler’s World, 45(4), 34–35. [Google Scholar]
- Lundmark, H. (2004). Siteswap state diagrams. Available online: http://ultramatos.online.fr/paper/Hans-Lundmark_siteswap-state-diagrams.pdf (accessed on 12 March 2025).
- Mafra, J. R. (2020). Challenging the traditional curriculum by traditional knowledges: From ethnomathematical fieldwork to classroom practices. Revemop, 2, e202006. [Google Scholar] [CrossRef]
- Magnusson, B., & Tieman, B. (1989). The Physics of Juggling. Physics Teacher, 27(8), 584–589. [Google Scholar] [CrossRef]
- Meaney, T., Trinick, T., & Allen, P. (2021). Ethnomathematics in education: The need for cultural symmetry. In M. Danesi (Ed.), Handbook of cognitive mathematics (pp. 1–29). Springer. [Google Scholar] [CrossRef]
- Monahan, C., Munakata, M., Vaidya, A., & Gandini, S. (2020). Inspiring mathematical creativity through juggling. Journal of Humanistic Mathematics, 10(2), 291–314. [Google Scholar] [CrossRef]
- Moral, C. (2006). Criterios de validez en la investigación cualitativa actual. Revista de Investigación Educativa, 24(1), 147–164. [Google Scholar]
- Naylor, M. (2012). The mathematical art of juggling: Using mathematics to predict, describe and create. Bridges 2012: Mathematics, music, art, architecture, culture, 33–40. Available online: https://archive.bridgesmathart.org/2012/bridges2012-33.html#gsc.tab=0 (accessed on 12 March 2025).
- OECD. (2024). An evolution of mathematics curriculum. OECD Publishing. [Google Scholar] [CrossRef]
- Orey, D. C., & Rosa, M. (2021). Ethnomodelling as a glocalization process of mathematical practices through cultural dynamism. Mathematics Enthusiast, 18(3), 439–468. [Google Scholar] [CrossRef]
- Parra, A. (2017). Ethnomathematical barters. In H. Straehler-Pohl, N. Bohlmaer, & A. Pais (Eds.), The disorder of mathematics education (pp. 89–106). Springer. [Google Scholar]
- Parra, A. (2024). A performative and relational ethnomathematics. In B. Greer, D. Kollosche, & O. Skovsmose (Eds.), Breaking images: Iconoclastica analysis of matehmatics and its education (pp. 213–233). Open Book Publishers. [Google Scholar]
- Parra, A., & Caicedo, N. (2012). Matemáticas en el mundo nasa. El fuego azul. [Google Scholar]
- Polster, B. (2002). The Mathematics of juggling. Springer. [Google Scholar]
- Rosa, M., & Orey, D. C. (2011). Ethnomathematics: The cultural aspects of mathematics Etnomatemática: Os aspectos culturais da matemática. Revista Latinoamericana de Etnomatemática, 4(2), 32–54. Available online: http://www.redalyc.org/articulo.oa?id=274019437002 (accessed on 12 March 2025).
- Shannon, C. (1980). Scientific aspects of juggling. In N. Sloane, & A. Wyner (Eds.), Claude elwood shannon. collected papers (pp. 850–864). IEEE Press. [Google Scholar]
- Shimizu, Y., & Vithal, R. (2023). Mathematics curriculum reforms around the world. Springer. [Google Scholar]
- Tiemann, B., & Magnusson, B. (1991). A notation for juggling tricks. A lot of juggling tricks. Juggler’s World, 43(2), 31–33. Available online: http://www.juggling.org/jw/91/2/notation.html (accessed on 12 March 2025).
- Walker, J., & Francisco, S. (1982). Variations for numbers jugglers. Juggler’s World, 34(1), 11. [Google Scholar]
- Wright, C. (2017). Juggling by numbers-numberphile. Available online: https://youtu.be/7dwgusHjA0Y?feature=shared (accessed on 12 March 2025).
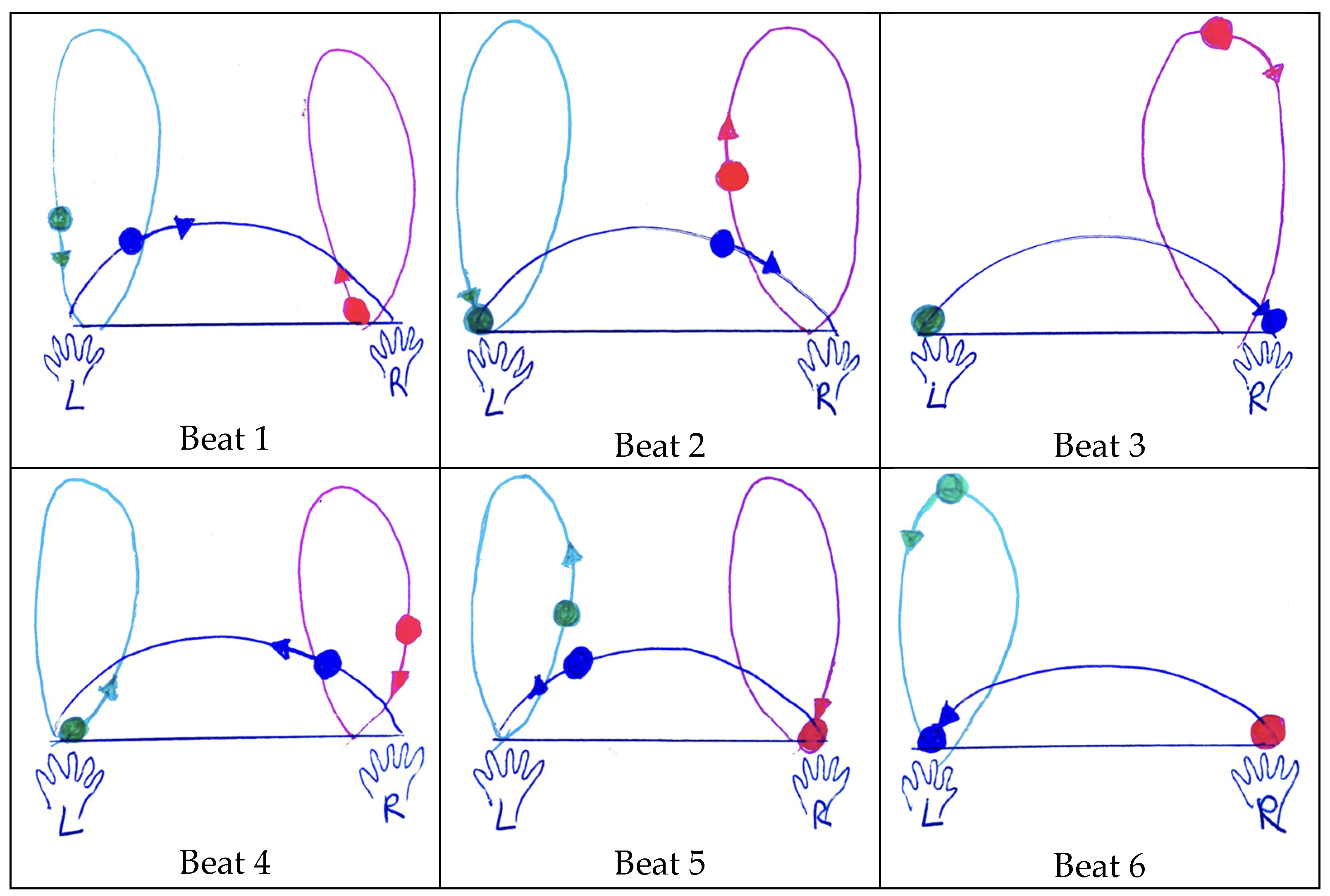




| Task 1 Formulation | Task 1 Solution | |
|---|---|---|
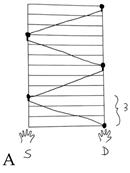
| A juggling pattern or juggling trick is a specific manipulation of props during the practice of toss juggling. Each juggling trick involving the throwing of objects (in our case, 3 balls of different colors) can be described graphically by a mathematical model called a ladder (see the picture below).  The model looks like a ladder and each rung represents a beat, counting from the bottom to the top. The right ladder rail represents the right hand and the left ladder rail the left hand. Each ball is represented by a circle of the same color as the ball used during the trick. The path that each ball makes is represented by an arc of the same color as the thrown ball:
|  | |
 | 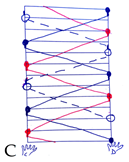 | |
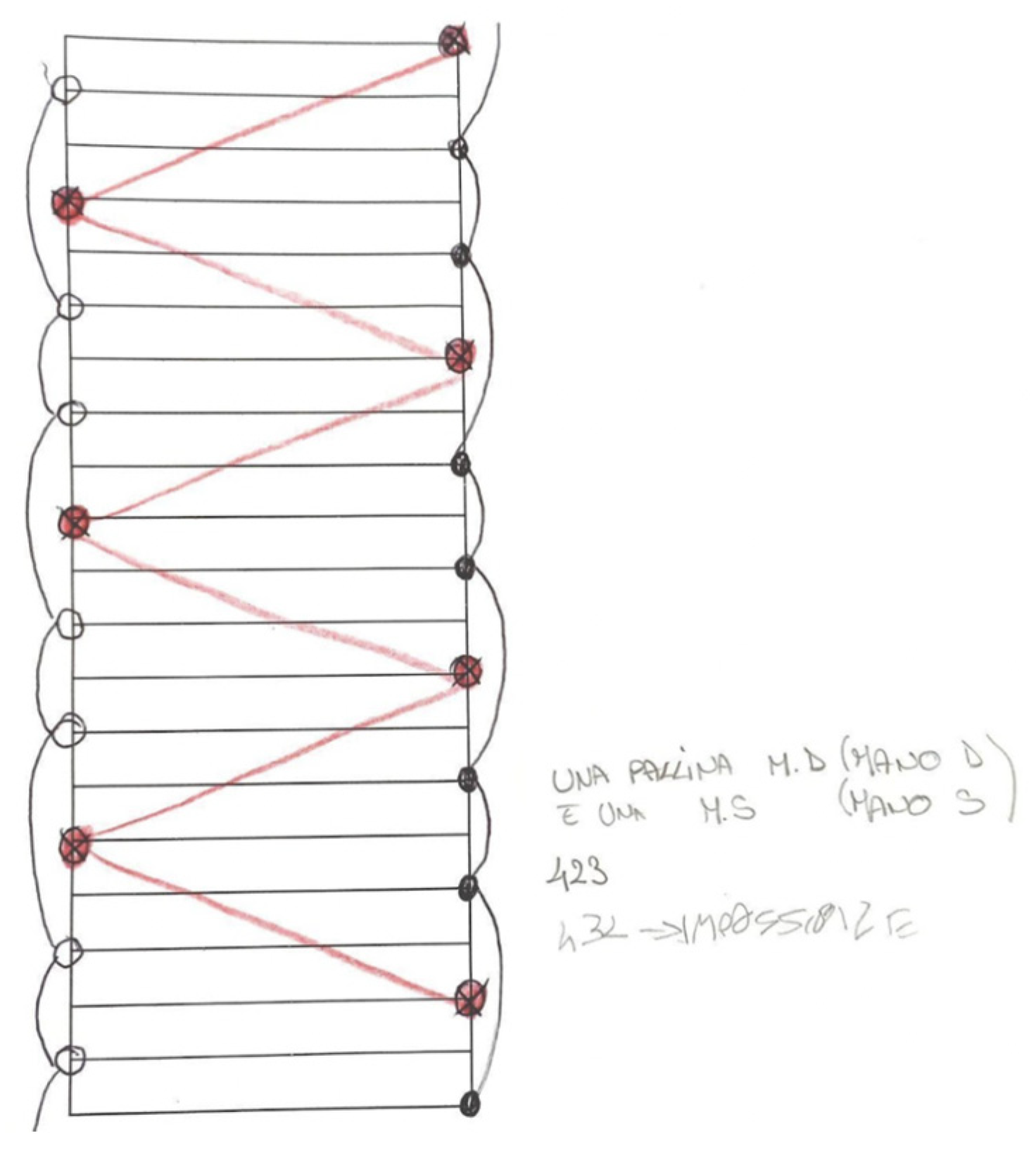
| Task 2 Formulation | Task 2 Solution |
|---|---|
| This is the model of the trick that jugglers call “423” with the ladder model. What can you state about the even-number throws and the odd-number throws? 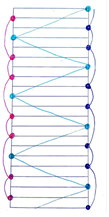 | Throws represented by even numbers are caught by the same hand, while the ones represented by odd numbers are caught by the other hand. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zito, G.; Albanese, V. Juggling Balls and Mathematics: An Ethnomathematical Exploration. Educ. Sci. 2025, 15, 387. https://doi.org/10.3390/educsci15030387
Zito G, Albanese V. Juggling Balls and Mathematics: An Ethnomathematical Exploration. Education Sciences. 2025; 15(3):387. https://doi.org/10.3390/educsci15030387
Chicago/Turabian StyleZito, Giovanna, and Veronica Albanese. 2025. "Juggling Balls and Mathematics: An Ethnomathematical Exploration" Education Sciences 15, no. 3: 387. https://doi.org/10.3390/educsci15030387
APA StyleZito, G., & Albanese, V. (2025). Juggling Balls and Mathematics: An Ethnomathematical Exploration. Education Sciences, 15(3), 387. https://doi.org/10.3390/educsci15030387





