Abstract
We present the continuation of a study on an international MOOC for the training of mathematics teachers who were introduced to the methodology of outdoor mathematics through MathCityMap. Previously, we presented the immediate learning and professional development outcomes achieved by teachers who participated in the MOOC. Here, using the theoretical framework of Meta-Didactical Transposition and performing a mixed-type analysis, we investigate the long-term impact of the MOOC on these teachers to whom we administered a questionnaire one year after the end of the MOOC. We conclude that for these teachers, practising mathematics outdoors has become a consolidated teaching practice, but they still feel quite uncomfortable for structural reasons about using some pedagogical instruments they have learned in the MOOC.
1. Introduction and Literature Review
The social and political relevance of teachers’ professional training and development is topical. For instance, it is the subject of a specific chapter (Chapter III: The Professional Development of Teachers) of the OECD report (OECD, 2009) of the TALIS survey (Teaching and Learning International Survey), one of the few reports of this kind that collect teachers’ opinions. On the other hand, it has been, for a long time, a relevant topic of research in mathematics education. In the past two decades, there has been a concentrated effort in the field of mathematics education research to emphasise the professional training of teachers. Specifically, the focus has been on creating both initial and continuous training initiatives or programs aimed at fostering professional development. These endeavours aim to assist teachers in discerning the significance of elements within the teaching and learning process, enabling them to make informed decisions and adeptly respond to various instructional situations (Ricart et al., 2022).
Regarding the modality by which training courses are offered, MOOCs (Massive Open Online Courses) are becoming widely popular among training programs, including for mathematics teacher education. MOOCs are courses offered openly to learners through the web, and appear as dynamic and diversified learning spaces with varying factors, such as flexible time frames, a massive number of students from different demographic areas, motivation to continue learning, and opportunities for designers to implement novel pedagogies including collaborative learning activities (Taranto et al., 2020). It has been observed that teachers often enter such online spaces to find professional learning opportunities (Anderson, 2020). They find communities where they can participate in critical reflection on their practices, learn about new contents or methods, access experts outside their personal network, and develop their teaching identity through discussion (Macià & García, 2016).
Regarding the contents to be covered in training programs, the literature recommends the use of technology for a more effective approach to teaching mathematics (Pimenta et al., 2023; Cai & Howson, 2013). The integration of technology in the mathematics classroom, however, is not just the use of ‘a software’: using a technology involves students seen as individuals and in the classroom context, teachers’ pedagogical strategies maths content. There are dynamics that go far beyond the mere transmission of knowledge, and then the technology that best suits the purpose must be chosen carefully. Thus, teaching requires the use of a variety of knowledge: mathematical knowledge, pedagogical knowledge, and technological knowledge. The relationship between the various areas of knowledge is well described by M. J. Koehler and Mishra (2005) when talking about “Technological pedagogical content knowledge” (TPACK). It is different from knowledge of all three concepts individually.
“[…] TPACK is the basis of effective teaching with technology, requiring an understanding of the representation of concepts using technologies; pedagogical techniques that use technologies in constructive ways to teach content; knowledge of what makes concepts difficult or easy to learn and how technology can help redress some of the problems that students face; knowledge of students’ prior knowledge and theories of epistemology; and knowledge of how technologies can be used to build on existing knowledge to develop new epistemologies or strengthen old ones”.(M. Koehler & Mishra, 2009, p. 66)
So, integrating technology in the maths classroom involves “what technology to use and how” in order to have effective teaching. Moreover, to integrate technology into pedagogical practices, it is necessary to implement sustainable professional development programs for in-service teachers (Pimenta et al., 2023). Professional development programs are sustainable if they produce effects on pedagogical practices in both the short and long term, which means that teachers continue to develop the proposed approach in the classroom after participating in the professional development program (Zehetmeier & Krainer, 2011).
In the case of this research report, we present the continuation of a study on teacher training through an international MOOC that intended to instruct teachers in integrating a technology that allows them to practise outdoor mathematics. While outdoor mathematics will be the subject of the next section, here we want to underline that the literature, at least to our knowledge, does not report studies investigating the long-term impact of MOOCs on mathematics teacher training. In this sense, the study proposed in this research report is pioneering. Furthermore, the MOOC we designed and conducted has a different profile from other MOOCs that have been present in the literature for the training of mathematics teachers. Generally, MOOCs for mathematics teacher training offer training on specific topics. For example, Taranto and Arzarello (2020) examine two MOOCs that shared resources and methodologies for teaching-learning geometry and algebra, respectively; Hollebrands and Lee (2020) examine a MOOC for teaching–learning statistics; Panero et al. (2017) examine a MOOC to support teachers in collaborative instructional design. Our MOOC presents a methodology (outdoor mathematics), a technology that helps the teacher to practise this methodology (MathCityMap) and training to be autonomous in the use of this technology and consciously integrate it into one’s own practices. At the end of the MOOC, the immediate impact recorded on teachers was positive and very engaging training (as documented in (Taranto et al., 2021)). In the present article, our goal is to investigate the impact that the MOOC had one year later. This involves investigating the following hypothesis: that massive training, if proposed in a certain way and on certain topics, goes beyond being effective and sustainable, and that the integration of technologies into teachers’ practice is possible in a conscious way.
Professional Development in Outdoor Mathematics
In recent years, outdoor mathematics has gained importance not only from a research perspective, but also from an educational point of view (Zender et al., 2020). The idea of outdoor mathematics is to leave the classroom, which is usually the “typical” location for education, and open up reality for learning mathematics. One approach is the mathematics trail (cf. Ludwig & Jesberg, 2015). During a mathematics trail (in the following math trail), students follow a route that guides them to several spots and real objects at which mathematical questions are posed. The students must transfer their mathematical knowledge to this situation, carry out simplifications and collect required data independently, which connects the approach to the idea of mathematical modelling (Jablonski, 2023). In addition, benefits of learning outdoors are seen in terms of motivation and performance (Zender et al., 2020).
Despite these advantages, teachers see obstacles that prevent them from teaching mathematics outdoors (Gurjanow et al., 2018). Among other things, leaving the classroom is associated with a feeling of insecurity and loss of control. Furthermore, it seems difficult to provide individual support during the math trail, as the students are usually in small groups and the teacher cannot supervise all groups together. This is why newer initiatives are taking the approach of using digital tools to alleviate teachers’ concerns and support them in preparation and implementation. One of these examples is the international MathCityMap system (Ludwig & Jesberg, 2015), which we present in more detail in this paper.
The use of new technologies in the field of outdoor mathematics at least helps to contain problems such as individual support. From the teacher’s perspective, however, new challenges arise: Studies in the field of professional development show that teachers perceive professional development initiatives as differently effective. For example, teachers name the aspects such as classroom application (easy transfer into their classroom), teacher as learner (hand-on-approach for teachers) and teacher networking (collaboration with colleagues) as contributions to effectiveness (Rogers et al., 2007). Furthermore, Clarke (2007) describes the duration of training courses as a decisive factor in providing sufficient time for reflection, experimentation and problem-solving. Especially when it comes to the use of digital tools in the classroom, it is important to close potential gaps between theory and practice (Ratnayake et al., 2020) and “assist them [the teachers] and their students to engage in technology-mediated mathematical thinking” (Thomas & Chinnappan, 2008, p. 184).
With these considerations, professional development initiatives for digitally supported outdoor mathematics seem to be meaningful. In the scope of this topic, the following challenges for professional development initiatives arise: First, teachers must be convinced of the potential benefits of learning mathematics outdoors; second, they must have ideas for developing outdoor mathematics activities; third, they must feel comfortable about leaving the classroom with their students for a mathematics activity; and, fourth, they must perceive the advantages of the use of a digital tool in this context. These issues can be related to the basic constituents of the TPACK model, as mentioned in the previous section.
Indeed, the outdoor mathematics idea in general, and its implementation in mathematics lessons, can be related to the area of content (CK) and pedagogical (PK) knowledge. The conjunction of these two items would therefore be connected to the teacher’s PCK, although when it comes to the creation of outdoor mathematics activities, specific mathematics knowledge of teaching (MKT; cf. Rakes et al., 2022) is additionally required. MKT refers to the teacher’s understanding of mathematics contents, and to the choice of appropriate pedagogical tools for effective teaching of mathematics. Moreover, the use of digital tools to implement outdoor mathematics in the classroom requires specific knowledge.
Thus, with the introduction of a digital tool to organise and facilitate outdoor mathematics, technological knowledge (TK) is triggered. According to Rakes et al. (2022), there are several levels connecting such kind of knowledge to the concurrence of PCK:
- Level 1 (Recognizing): Acknowledgement of the usefulness of technology, but no actual use in assessment.
- Level 2 (Accepting): Desire to integrate technology, but challenges exist when connecting it to the contents.
- Level 3 (Adapting): Noticeable adjustments in the pedagogy to test technology, also in assessment.
- Level 4 (Exploring): Seeking more ways to integrate technology throughout the curriculum.
- Level 5 (Advancing): Incorporation of technology as an essential and regular part of teaching and assessment tool.
Rakes et al. (2022) claim that only through reaching level 5, a definitive intersection of TK with PCK is possible. Thus, levels 1–4 represent a kind of technological knowledge that is not fully linked to the areas of pedagogical and content knowledge. So, with these five levels, it becomes clear—not only but also for the context of digitally enriched outdoor mathematics—that it requires effort for professional development initiatives to guide the teachers from recognition, acceptance, adaptation and exploration to an advanced implementation and, through this, create knowledge in the intersection of pedagogy, content and technology.
Regarding the implementation of outdoor mathematics through the specific use of the digital tool MathCityMap, a few teacher training activities have been reported and evaluated. For example, Milicic et al. (2020) describe a training plan in which teachers will experience both the educator and the learner perspective when following the recommended hands-on approach. Although the activities described in this training can be related to PCK and to TK, still, a complete intersection of these two sorts of knowledge, leading to a full TPACK output, could be questioned due to the brevity of the instruction period, and to the absence of experiments in the classroom during the training.
Let us remark that, besides contributing to fostering the intersection of TPACK knowledge, the system MathCityMap brings another relevant feature, namely, the importance of taking internationalisation into account. In fact, the tool—as it will be described in Section 3—develops an international, multilingual, database of math walks, allowing its use in many different countries all over the world. Therefore, it is potentially interesting for mathematics teachers—independent from their location.
In this direction, Jablonski and Ludwig (2020) present an international initiative to learn about digitally supported outdoor mathematics, which particularly highlights the relevance of the creation of an international teacher network. This perspective is also supported by the description of first attempts to implement, with the concourse of MathCityMap, hybrid (on and off-line, synchronous and asynchronous), outdoor mathematics, and professional development activities for teachers (Cahyono et al., 2023).
Finally, let us remark that in 2021, the first international and long-term MOOC in outdoor mathematics was conducted and—in contrast to the previous initiatives—systematically evaluated (Taranto et al., 2021).
In this research report, as mentioned, we present the continuation of a study on this international MOOC for mathematics teachers’ education. In particular, the topic outdoor mathematics supported by digital technology was taken up from a content, pedagogical and technological perspective. Teachers were introduced to the methodology of outdoor mathematics and its specifics and requirements from an organisational and educational point of view (related to PCK). In addition, teachers were introduced to MathCityMap as a technological system that helps in the design and conduction of outdoor mathematics trails (related to TK). Indeed, in Taranto et al. (2021), we have already presented the learning and professional development outcomes achieved by teachers who participated in this MOOC. In the current work, however, we want to investigate the long-term impact of the MOOC on these teachers, to whom we administered a questionnaire one year after the end of the MOOC. This long-term evaluation should be related to the TPACK framework, as it measures the actual use of the transmitted knowledge and, hypothetically, provides an idea of the achieved long-term knowledge.
In the following section, we introduce the theoretical framework underpinning our research. Section 3 presents the international MOOC we designed and conducted. Section 4 explains the research design. In particular, we briefly share what were the first learning outcomes at the conclusion of the MOOC (for detailed information, see (Taranto et al., 2021)) and set out the research question that guides this new study. Section 5 outlines the methodology we employed, describing the data collection tool we adopted, a questionnaire, and focusing on some of its constructs, both in qualitative and quantitative terms. In Section 6, we report the results and in Section 7, the discussions conclude the work.
2. Theoretical Framework
Meta-Didactical Transposition (MDT) is a theoretical model elaborated by Arzarello et al. (2014). It has been conceived to describe and analyse the relationship and reciprocal influence between two communities—the community of researchers and the community of teachers—involved in a course in mathematics education for professional development of their professional practices. In particular, the model aims to identify theoretical tools for analysing the dynamics that characterise the interactions between communities of teachers and communities of researchers, within the context of teacher training programmes, or research programmes, involving the active participation of teachers (Cusi et al., 2022). The notion of didactical transposition was introduced by Chevallard (1999) to characterise and investigate the transformation of knowledge, from scientific knowledge to taught knowledge, within a particular institution. By analogy, the notion of MDT was introduced (Arzarello et al., 2014) to characterise and investigate the transformation of didactical knowledge (theoretically based) into classroom teaching practices (Taranto et al., 2023). Indeed, the researchers have the objective of transposing a certain piece of knowledge, related to the teaching and learning of mathematics, to favour the professional development of the teachers, according to the reference institutions (national curricula, textbooks, …). In both cases, the didactical or meta-didactical transposition, the central concept that shapes the activities of the actors involved (teachers and researchers) to highlight the effects of these knowledge transformations, is the notion of praxeology (Chevallard, 1999). In the context of didactical transposition, the notion of praxeology relates to teachers instructing/tutoring in the classroom. On the other hand, referring to teachers as learners engaged in professional development activities, the MDT considers their praxeologies in a learning situation: for this reason, these praxeologies are called ‘meta-didactical’. The meta-level means that teachers are considered simultaneously as learners and as teachers reflecting on their teaching praxeologies (Robutti, 2018). Hence, the concept of meta-didactical praxeologies was introduced to describe activities involving task types that lead to reflections on teaching activities, developed through the interaction between a community of researchers (as teacher educators) and a community of teachers.
At both levels (didactical and meta-didactical), a praxeology consists, according to Chevallard (1999), of four components: task, technique, justification and theory. Inspired by Taranto et al. (2020), an example of the components of a didactical praxeology (of a teacher in a classroom) and an example of the components of a meta-didactical praxeology (of a teacher in professional development) is shown in Table 1. It should be noted that for the didactical praxeology, the solution of a second-degree equation is taken as an example; while for the meta-didactical praxeology, we could consider, as an example, what the MOOC instructors involved in this paper had the pleasure of conveying to teachers attending the MOOC.

Table 1.
Didactical and meta-didactical praxeology: components and examples.
In a praxeology, the assigned task and the technique used to solve it are the praxeology’s pragmatic components, while justification and theory are the theoretical components that validate the use of that technique. The components can be considered internal or external to a community (or an individual): they are internal if used by members of a community (or an individual), or external if not used. The internalisation process characterises the dynamics at play when external components, i.e., not initially part of the components of praxeologies within an institution, become internal and increase teachers’ and/or researchers’ knowledge at both pragmatic and theoretical levels (Taranto et al., 2023). If one or more components of a praxeology move from external to internal (i.e., internalisation process), then the community of teachers can evolve towards sharing this component among the community members, together with the researchers (considered in the role of teacher educators).
3. The MaSCE3 MOOC
The “Task design for math trails” MOOC was part of the Erasmus+ project “Math Trails in School, Curriculum and Educational Environments of Europe” (MaSCE3; www.masce.eu), designed and implemented to present the MathCityMap (in the following MCM) system for teaching mathematics outdoors.
The MCM system has two components, a web portal and an app available for smartphones and tablets (Figure 1). In the web portal, users can create tasks and trails that can be public after being reviewed. Moreover, all users can utilise, edit, or combine the tasks of the public trails to create new trails. In June 2024, there were more than 86.000 tasks and 18.000 trails authored by nearly 34.000 users in 16 idioms of more than 85 countries. With the MCM app, students can find and explore outdoor trails via codes. When students open a trail, the app guides them, presenting a map with their location, as well as the trail’s tasks. When the students select a task, they must look around for the involved object, obtain the required data and, optionally, ask for some hints. Then, they have to present a solution to the selected task, which the system validates by assigning points. Using the web portal interface or app, teachers can follow their students’ progress in real time, thanks to a feature of the system called Digital Classroom, which makes it possible to synchronously track both the progress of the students along the trail via GPS, and the performance of the students themselves during the trail, recording the response attempts introduced into the system.
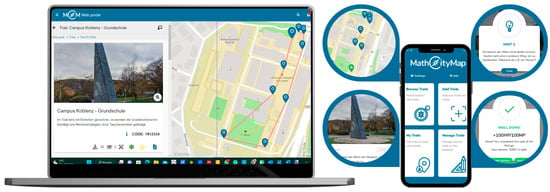
Figure 1.
Web portal (left) and MCM App (right).
In the MOOC, we wanted to educate teachers on the use of the system for outdoor mathematics so that they could use it consciously and consistently with their students. The structure of the MOOC followed the modules shown in Figure 2.
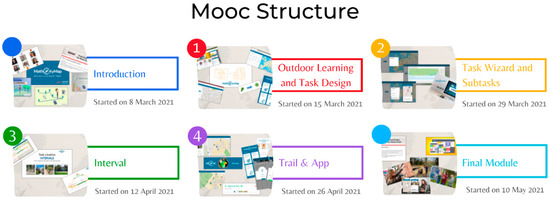
Figure 2.
MOOC structure.
The MOOC’s homepage, accessible just during the MOOC and to registered participants, had general information, and gave access to the modules, which were made available according to the schedule shown in Figure 2. In the introductory module, the context and goals of both the MaSCE3 project and MOOC were presented. In addition to the instructors’ presentation video, there was an overview of the MOOC setup and videos concerning outdoor learning and math trails. Module 1 “Outdoor Learning and Task Design” covered the MCM web portal presentation and detailed the elaboration of math tasks with different answering formats, the criteria for designing meaningful math tasks and the math task publication process. Module 2 “Task Wizard and Subtasks” presented the task wizard concept and examples through three videos and a tutorial on Sway (https://sway.office.com, accessed on 24 January 2025). The subtask content was introduced through a webinar. On Module 3 “Interval”, the design of interval tasks was explored through a video and a pdf that provide strategies to set the bounds of the interval. Module 4 “Trail & App” explained how to create a trail, modify it, and request its publication. It also gave an overview of the MCM App and the feature narrative. It explained how to setup the Digital Classroom (as previously mentioned, a tool to monitor, interact, and follow the students during the math trail). The “Final Module” outlined the trail’s implementation. The webinar “Closing Ceremony MOOC” was also part of this module.
4. Research Design
4.1. Initial Learning Outcomes Related to the MaSCE3 MOOC
In Taranto et al. (2021), we presented the learning outcomes that were directly linked to the MaSCE3 MOOC. In particular, we focused on the following:
- The changes in the attitude towards outdoor mathematics;
- The learning progress and usage concerning the digital features of MCM;
- The MOOC ratings.
For example, we asked the teachers to rate their awareness of their skills in “Designing math tasks to practice math outdoors”, “Designing math trails to practice math outdoors”, “Using the MCM web portal” and “Using the MCM app”—one time before the MOOC started and one time after the participants finished the MOOC. After completing the MOOC, the majority of teachers stated that their skills concerning the individual categories were at least good and on the technical level even very good. Before the MOOC started, many teachers stated that they only had poor skills in the named categories1.
In that previous work, 19 case studies were considered, selecting around 4 teachers from each MaSCE3 project partner country (France, Germany, Italy, Spain, Portugal). Through these, we were able to observe a positive evolution in terms of task and trail design and technical skills. In fact, of the 19 case studies, only 9 had previously gave outdoor mathematics lessons, only 5 had heard of math trails and only 4 had created and experienced outdoor math trails. Furthermore, all respondents, in general, and the 19 case studies, in particular, had stated their intention to use MCM in the future. As detailed in Taranto et al. (2021), these data support the success of the learning process assumed by the participants in this MOOC.
4.2. Research Question
Since the data concerning teachers’ awareness, and their intention to use MCM in the future were directly obtained after the MOOC’s end, here we want to investigate the long-term effect of the MOOC after a certain time. Indeed, our findings concerning teachers’ learning outcomes right after the MOOC led us to ask ourselves about their permanence and measure the actual teachers’ usage of MCM during the year after the MOOC’s end. We can recall that the MOOC shared the meta-didactical praxeology exemplified in Table 1. All teachers who completed the MOOC implemented the corresponding didactical praxeology (which will be further detailed in the next section). Now, after one year, after the teachers have reflected and practised, we are keen to investigate whether the teaching practice they implemented at the end of the MOOC has been internalised by them, i.e., whether it is part of their habitual teaching practices. Thus, to deepen and extend the results in Taranto et al. (2021), we would like to address now the following research question:
During the year following the end of the MOOC, to what extent did the internalisation process take place in the teachers’ community regarding the pragmatic and theoretical components of praxeology concerning the incorporation of the MathCityMap system into their teaching practices?
This question intends to analyse relevant information directly related to some of the inquiries addressed in Taranto et al. (2021), but now dealing with data obtained one year after the MOOC ended, concerning the use by teachers of outdoor mathematics and MCM, or teachers’ attitude towards outdoor learning and the use of digital components of MCM.
5. Methodology and Data Analysis
In order to answer the research question, we contacted all 503 registered MOOC participants one year after the MOOC’s end (May 2022). Both teachers who had finished the MOOC successfully and teachers who did not were contacted asking to answer an online questionnaire. Bearing in mind the focus of our research, we only consider in what follows those cases that had successfully finished the MOOC and answered the questionnaire one year after the MOOC’s end. In total, we collected 52 answers whereof 33 participants finished the MOOC successfully. In total, 24 of the 33 participants stated to be in-service teachers covering all educational levels from primary to upper secondary school. The remaining nine participants were either pre-service teachers or educators at the university level. Through the predominance of in-service teachers in the sample, we use the term “teachers” in the following referring to the sample of 33 participants. The teachers form an international sample (Table 2): 8 from France, 11 from Italy, 6 from Portugal and 3 from Spain, as well as 1 from Germany, Greece, Slovakia, United Kingdom, and Uruguay.

Table 2.
Country of respondents who finished the MOOC.
The questionnaire consists of different question blocks. The blocks that were relevant for those who had finished the MOOC are shown in Table 3. We remind the reader that the meta-didactical praxeology pursued during the MOOC training, i.e., formulated by the community of researchers to be shared with the community of teachers, is the one we exemplified in the theoretical framework (see Table 1). All those who completed the MOOCs certainly shared this praxeology, and as a result put the following didactical praxeology into practice:

Table 3.
Overview of the questionnaire.
- Task: propose an outdoor math trail to the students;
- Technique: designing the math trail with MCM; encouraging students to use the MCM App to enjoy the trail; monitoring students with the Digital Classroom during the use of the trail;
- Justification: using MCM simplifies the teacher’s design load and the Digital Classroom allows the class to be in control even in an external environment;
- Theory: practising mathematics outdoors with one’s students.
The questions in each block of the questionnaire were designed with the components of this didactical praxeology in mind. More specifically, apart from Section 1 and Section 2 of the questionnaire, which contain general questions, the other sections are distinguished as follows: 3, 4 and 5 fall under the pragmatic component of praxeology; 6 has questions that fall under both the pragmatic and theoretical components; 7 and 8 fall under the theoretical component (Table 3).
The questionnaire was reviewed by all MOOC instructors in order to assess whether the questions allowed the achievement of the objectives defined for the design of the questionnaire. Blocks 5 through 7 were predominantly formulated using Likert ascending scales, starting 0 or 1 up to 5 or 6, more specifically 33 items. In the remaining blocks of the questionnaire, multiple-choice, yes/no statements, and open questions were predominant.
As noted in Section 3.1 of Taranto et al. (2021), when collecting information about MOOC’s participants, we had considered 19 case studies. Among the 33 respondents we are considering here, of these 19 case studies, only 8 also answered the questionnaire administered one year after the end of the MOOC. They are balanced by country (there are 2 respondents from each partner country, with the exception of Portugal). These 8 respondents will also be considered as case studies to give a more general overview from an international point of view. In the following, to achieve our research objective, we will consider some of the questions in the blocks 3, 4, 5, 7 and 8 (Table 3).
The analyses are of a mixed nature (i.e., both qualitative and quantitative). In particular, for the qualitative part, we will refer to the lens of Meta-Didactical Transposition, trying to identify the phenomenon of internalisation. Moreover, as previously mentioned, we will consider case studies, also with a focus on the data of the previous study (Taranto et al., 2021), so as to outline an evolution between the situation that existed at the end of the MOOC and the one that emerges a year later. While, for the quantitative part, the data were analysed with IBM SPSS Statistics 29.0.1.0, R 4.4.1, RStudio 2024.04.2+764, and Excel 2016, and are also illustrated using diagrams. The questionnaire integrated constructs that focused on teachers’ perception of usability of the MCM web portal and awareness of one’s own skills. The analysis of these data is crucial for understanding whether and how the process of internalisation of the MCM system into teachers’ teaching practices took place. Details are presented in Section 5.1 and Section 5.2.
5.1. Perceptions About the Usability of MCM Web Portal and Skills’ Awareness
Although the questionnaire was designed to collect data from a qualitative analysis perspective, some of the questions of the blocks 5, 7 and 8 were part of instruments, namely scales, that, according to Taber (2017), are primarily used to assess perceptions, emotional or attitudinal constructs. The aim was to measure teachers’ perception of two characteristics: usability of the MCM web portal and awareness of one’s own skills.
For the first construct Teachers’ perceptions about the usability of the MCM web portal, 7 questions of block 5 were considered, which were organised into two dimensions (usage and learnability). Each question had a Likert scale of four levels (Table 4). The decision to use a 4-point scale was intended for teachers to position themselves on the positive or negative side.

Table 4.
Structure of the construct “Teachers’ perceptions about the usability of the MCM web portal”.
The construct was thoroughly reviewed and validated by educational and computing experts on MCM.
The confirmatory factor analysis (CFA) results indicate a statistically significant model fit with a chi-square value of 25.407, degrees of freedom of 13, and a p-value of 0.020 of a two-factor model (Table 5):

Table 5.
Latent variables.
- Factor Dimension 1 (factor_usage): Standardised loadings for u1, u2, u3, and u4 (the corresponding usage items, stated in Table 4) were 1.000, 0.819, 1.150, and 0.941, respectively (p < 0.001).
- Factor Dimension 2 (factor_learnability): Loadings of 1.000, 0.850, and 1.252 for items l1, l2, and l3 (the corresponding learnability items, stated in Table 4), respectively (p < 0.001).
Moreover, the covariance between factor_usage and factor_learnability is 0.190 (p < 0.001), meaning a positive interrelation, offering compelling evidence supporting the coherence and distinctiveness of the two-dimensional construct.
The structure of the second construct Teachers’ perceptions about the awareness of own skills a year ago, when finished the MOOC/One year after the MOOC had a set of four items (with a Likert scale from 0 to 6) to measure the level of the teachers’ awareness of their own skills (items of block 7, and four items of block 8). The questions compared two moments: when the teachers finished the MOOC; and one year after finishing the MOOC. This construct was also reviewed and validated by educational and computing experts on the MCM. The items are “r1—Designing math tasks to practice maths outdoors”; “r2—Designing math trails for outdoor maths practice”; “r3—Using the MathCityMap web portal” and “Using the MathCityMap app”. After conducting the Confirmatory Factor Analysis (CFA), despite the significant chi-square test result indicating a lack of fit between the proposed model and the observed data, the high factor loadings of items r2 (λ = 0.971, p < 0.001), r3 (λ = 0.949, p < 0.001), and r4 (λ = 0.867, p < 0.001) suggest a strong relationship between the observed variables and the latent construct.
5.2. Reliability
Cronbach’s alpha and McDonald’s omega are among the most widely used reliability coefficients to assess the internal consistency or reliability, allowing us to evaluate if a group of items reliably assesses the same characteristic. Selecting the appropriate coefficient is crucial to ensure the accuracy of the reliability estimates. According to Orçan (2023) and Dunn et al. (2014), when the tau-equivalence assumption is not met, Cronbach’s alpha tends to underestimate the true reliability of the scale. Considering Table 5, our analysis reveals significant variability in item factor loadings for the latent factors (u2 = 0.819, u3 = 1.150, u4 = 0.941 for factor_usage; l2 = 0.850, l3 = 1.252 for factor_learnability), indicating a violation of the tau-equivalence assumption. Several authors (Goodboy & Martin, 2020; Viladrich et al., 2017; Edwards et al., 2021; as cited in Orçan, 2023) advocate for omega’s robustness to such violations. These researchers argue that omega accurately estimates reliability without requiring equal factor loadings, making it a preferable choice when tau-equivalence is not met.
While discrepancies between alpha and omega become more pronounced with disparities in factor loadings, these differences are less impactful when average loadings are 0.7 or higher and the absolute difference is 0.2 or less (Edwards et al., 2021). In our case, this included the factor loadings for “factor_usage” (mean = 0.9775, max difference = 0.331) and “factor_learnability” (mean = 1.034, max difference = 0.402). Considering the potential impact of the sample size and unequal factor loadings on the estimation of omega, further analyses are warranted to ensure the validity and reliability of the results. By calculating both alpha and omega, we aim to provide a comprehensive evaluation of the scale’s internal consistency, taking into account potential biases.
The cut-off of acceptable values of alpha, most present in the literature, is 0.7 (Bujang et al., 2018), with a wide range of qualitative descriptors (Taber, 2017). Values above 0.7 are generally deemed acceptable also for omega. The results in Table 6 suggest a high degree of internal consistency for each scale, varying the values between 0.817 and 0.957 for omega and between 0.821 and 0.958 for alpha. However, in the literature, there are some concerns about too high alpha values because they may indicate item redundancy. Looking at the inter-item correlation values, we can see that, in the case of the first construct, the values are in the recommended range 0.15 and 0.8 (Paulsen & BrckaLorenz, 2017), despite the average inter-item correlation being a little higher than 0.5, while some authors recommended values between 0.15 and 0.5 (Paulsen & BrckaLorenz, 2017). Regarding the constructs on skill’s awareness, both the inter-item correlation and average inter-item correlation values are higher than the recommended values. In fact, skills’ awareness constructs have items that are particularly intercorrelated. The specific focus on scales of the narrowest constructs suggests closely related items, but not necessarily item redundancy.

Table 6.
Cronbach’s alpha and inter-item correlation results.
6. Results
In what follows, in order to answer the research question, we will focus, first, on the results of the constructs about teachers’ perception related to the usability of the MCM web portal and awareness of one’s own skills for dealing with outdoor mathematics one year before the MOOC and directly after the MOOC. Afterward, we are going to analyse the activities that the teachers carried out during the year after the MOOC’s end, considering questions from blocks 3, 4 and 8. Finally, we will have a more detailed view of the eight case studies we have referred to above.
6.1. Usability of the MCM Web Portal
The teachers’ perceptions about usability, concerning the usage and learnability dimensions, show that most consider the MCM web portal intuitive and easy to learn.
The usage dimension is related to the intuitive design of the architecture and navigation. By analysing Table 7, we perceive that teachers can orient themselves in the web portal (51.3% agree, 48.7% strongly agree) and find task creation intuitive (64.1% agree, 35.9% strongly agree). However, although most teachers consider trail creation intuitive (59% agree, 33.3% strongly agree), a small percentage disagreed (7.7%). Additionally, the majority also finds it easier to create outdoor tasks with MCM (41% agree, 53.8% strongly agree), while only two teachers disagreed (5.1%).

Table 7.
Teachers’ perceptions about usability of MCM web portal in the dimensions usage and learnability, using a Likert scale ranging from “Strongly Disagree” to “Strongly Agree”.
With respect to Learnability, that is the ease of learning, Table 7 highlights that it was easy to learn how the portal worked (59% agree, 35.9% strongly agree). The interaction between the web portal and the app is generally understood easily by teachers (61.5% agree, 30.8% strongly agree), but some disagreed (7.7%). Most teachers understand how Digital Classroom works (46.2% agree, 25.6% strongly agree), but 28.2% disagree or strongly disagree, suggesting these features could benefit from further improvements to enhance overall user satisfaction.
6.2. Teachers’ Awareness of Skills
In the question Rate your awareness of your skills in… (first in block 7 and then in block 8 of the questionnaire), we asked the teachers to give us an insight into the self-evaluation of their skills in the different components (technical and didactical) of MCM and outdoor mathematics.
Based on the Wilcoxon Signed Ranks Test (Table 8), the p-values for all four questions were greater than 0.05, indicating that we fail to reject the null hypothesis for each question. This suggests that there is no significant difference in teachers’ perceptions of their skills immediately after the MOOC and one year later. Thus, participants’ perceived that skill levels remained consistent over the year following the MOOC.

Table 8.
Wilcoxon Signed Ranks Test results.
In Figure 3 (top), we can see that the majority of the teachers rate their skills, for the time directly after the MOOC’s end, and in all branches, at least good. The mean value for all items is between good and very good. Please note that these data were collected retrospectively, meaning that the teachers had to evaluate their skills from one year ago. In Figure 3 (bottom), displaying the same information, but referring to the skills teachers think they have one year after the MOOC, we can observe a comparable result: the teachers still rate their awareness mostly between good and very good. The overall mean values have not changed significantly. It is obvious that the teachers already had high self-evaluated skills directly after the MOOC, which might explain why they do not obviously rate their skills to be better after one year. Still, they did not lose any of their skills, which leads the positive learning effect obtained through the MOOC into the direction of a long-term learning effect.
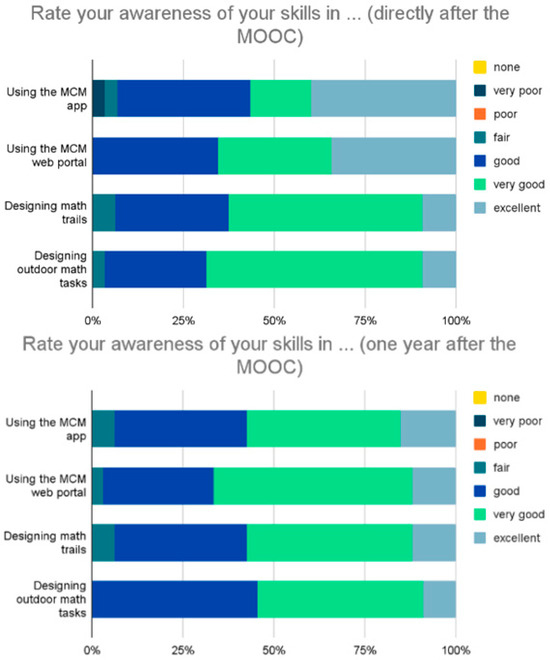
Figure 3.
Teachers’ current self-awareness directly after the MOOC (top) and one year after the MOOC (bottom).
In view of these positive results, it is perhaps worth remarking here that, among the eight case studies, and considering the questionnaire that was filled in by them during the first week of the MOOC, more than one year ago, only two teachers had given outdoor mathematics lessons (one from Italy and one from Spain) and only three had previously created and experienced an outdoor mathematics trail (the two from Italy and the teacher from Spain).
6.3. Activities During the Year After the MOOC
From the data related to block 3 of the questionnaire, as shown in Figure 4, we see that 16 out of 33 teachers created their own math trail tasks during the year (among them, 5 of the 8 case studies answered that they had achieved this: 2 from France, 1 from Germany, 1 from Italy and 1 from Spain). Most of these teachers teach at a secondary level in France, Italy, Portugal, or Spain. In total, 7 out of 16 created between 2 and 5 tasks (1 of the teachers from France and the one from Italy), 4 created between 6 and 10 (the other teacher from France, the teacher from Germany and the teacher from Spain) and another 4 created between 11 and 15. Overall, 12 teachers stated to have created trails: 6 claimed to have created 1 trail and the other 6 said they had created between 2 and 5 trails (the same 5 out of the 8 case studies mentioned before). In total, nine teachers ran one of their own maths trails with their students (only four of the eight case studies; of the five previously considered, it is the Italian who did not create their own maths trail). Overall, six teachers made use of the Digital Classroom (DC) during the year after the MOOC, most of them between 2 and 5 times (among the eight case studies, only one from France and one from Spain made use of the DC 1 time and between 2 and 5 times, respectively).
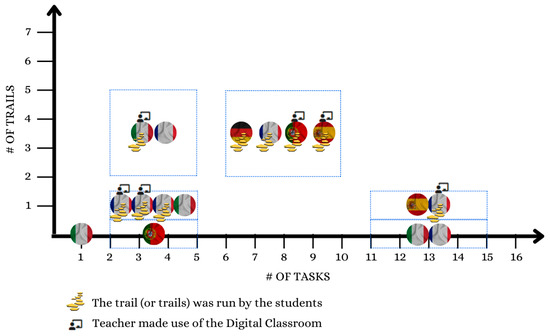
Figure 4.
Relation between the number of tasks and the number of trails created by each teacher.
Considering data from block 4 of the questionnaire, provided by the six teachers who used the DC, we made the following conclusions.
With respect to the use and management of the DC, the respondents expressed themselves as follows (Figure 5): four out of six (of which three agree and one strongly agree) found it easy to divide the students into groups and provide them with the necessary materials to run the trail; for all of them, it was easy to monitor the students via the DC; with respect to the usefulness of monitoring the students with the DC, we observe that one strongly disagreed, one disagreed, and the remaining split were between agreeing and strongly agreeing. Finally, for five respondents, the students enjoyed learning mathematics outdoors, while one strongly disagreed. For two case studies out of the eight under review, their answers were always between agree and strongly agree.
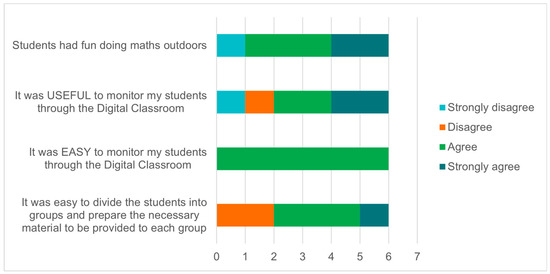
Figure 5.
Using and managing the Digital Classroom.
In an open question from block 8, the teachers named difficulties they faced during the preparation and conduction of a math trail with MCM (Figure 6). Whereas some teachers did not encounter any problems, 28 of the teachers answered the question. In total, 16 out of 28 teachers declared that their main problem was the task conception, e.g., finding suitable objects and locations, creating tasks for all grades and all topics (e.g., statistics), formulating tasks precisely and being creative. This issue is followed by time management, mentioned by five teachers, especially in the time that is needed to prepare a math trail, but also in the estimation of time that is needed to run a trail. Another issue that is raised by four teachers is the lack of technology and/or internet, stating that students do not have mobile devices or access to the internet is hindered. Finally, individual problems were faced, mainly in the general workflow, the pandemic restrictions, assessment and school permissions.
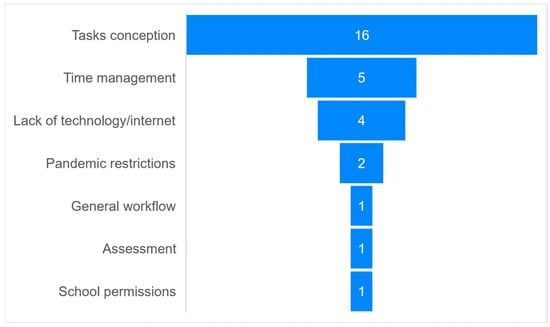
Figure 6.
Difficulties teachers faced during the preparation and conduction of a math trail with MCM.
Regarding the eight case studies, we observe that one of the teachers from France complains of problems with his mobile phone and the other French teacher states that he finds it difficult to find new tasks in new places. One Italian teacher states no difficulties, while the other states that he finds it hard to integrate MCM activities with curricular programming and time management. One teacher from Germany says he started with tasks that were too difficult for his students and that he had to lower the level of difficulty. On the other hand, the other teacher from Germany says that he has difficulties in devising tasks for grades 1 and 2. One teacher from Spain says that it is the pandemic that has generated difficulties and the other teacher from Spain that she finds it difficult to devise new tasks.
7. Discussion
In this paper, we addressed a research question regarding the impact of the MOOC (dealing with the educational use of math trails with the MCM) on the teachers that had followed it about one year ago. In particular, we posed the question of to what extent the process of internalisation took place in the teachers’ community with regard to the pragmatic and theoretical components of praxeology concerning the incorporation of the MCM system into their teaching practices. In line with the theoretical framework considered, the meta-didactical praxeology (cf. Robutti, 2018) of teachers in professional development within MOOCs can be described as follows2:
- Task: learning to design math trail tasks in order to create a math trail;
- Technique: solving the task using MCM;
- Justification: making use of MCM simplifies the teacher’s design load and the Digital Classroom allows the class to be in control even in an external environment;
- Theory: practicing mathematics outdoors with your own students.
Let us remark that, in Taranto et al. (2021), we mentioned that out of the 19 case studies, only 9 had experienced outdoor mathematics, only 5 had heard of maths trails, and only 4 had created and experienced an outdoor maths trail. Clearly, the results described in the previous section concerning teachers’ activities regarding outdoor mathematics during the year after the MOOC show a great increase in teachers’ knowledge of the potential of outdoor mathematics, as well as of teachers’ implementation of this didactical tool. And the figures are even more relevant if restricted to the eight case studies, taking into consideration the data in the Section 5.2. This, in terms of the Meta-Didactical Transposition, can be understood as an internalisation of the meta-didactical praxeology by the respondents at the end of the MOOC. Furthermore, as the data maintain a positive trend even one year after the end of the MOOC, particularly for the eight case studies, it can be assumed that internalisation implied a stabilisation of praxeology in some teachers and one can speak, for them, of didactical praxeology, i.e., that practising mathematics outdoors becomes a consolidated teaching practice of theirs.
Yet, it is evident that there is room for improvement. Indeed, it seems the internalisation process is not fully accomplished. For example, we see that only four teachers out of eight of the case studies ran one of their own math trails with their students during the past year. And, concerning more technical issues, such as the use of the Digital Classroom, just seven teachers (in the whole sample) did use it in that period, and only two of them are from the group of eight selected case studies. However, we must highlight the quite positive consideration by the majority of these 7 teachers of the Digital Classroom.
It is (indirectly) clear that teachers have changed their attitude towards outdoor mathematics and their feelings towards the use of MCM digital tools, since there are, now, substantially more teachers than one year before, involved in the development of such a methodological approach with MCM. But, on the other hand, they still feel quite uncomfortable about normalising the use of outdoor mathematics in the classroom as a pedagogical tool, and the reasons they present are quite structural (lack of time, lack of creativity to exploit mathematical opportunities in outdoor contexts –perhaps also related to the lack of time, lack of technological resources…). Thus, it seems that the validity of our MOOC learning experience is very much influenced by the generic difficulties for teachers to acquire, and develop in the classroom, new didactical approaches that could improve students’ mathematics learning.
These considerations can also be coupled with the considerations set out in the literature regarding the TPACK constructs and the five levels provided by Rakes et al. (2022). From a technical point of view, it seems that most teachers seem to belong to Level 2 (Accepting) or 3 (Adapting) after one year. We can see problems in task design that might refer to challenges in the way it connects to the contents of tasks, or in the way teachers tested the technology during the year after the MOOC. From the total amount of usage, a higher level in the sense of exploring or advancing cannot be assumed since the regularity might not be given. With this observation, it is not only possible to describe the teachers’ individual developments in terms of their TK. It is, in addition, to be seen as a point of reference to TPACK in general, and to the levels of Rakes et al. (2022) in particular. It can be seen that a MOOC allows teachers to recognize a digital tool and accept it and adapt to it. Still, we see that even after one year of bringing the technology into the classes, teachers do not seem to explore and use the technology in an advanced way. Potentially, it is linked to the specifics of outdoor mathematics education and the CK in this particular case. We can see that challenges in task design are mostly reported among our case studies. Therefore, it might not only be a case of TK, but of the intersection of CK and TK. Still, it can only be suspected and further research on the reasons for not reaching Levels 4 and 5 is needed. Therefore, implications for future professional development initiatives must be formulated and realised.
Finally, let us remark that our study has to be interpreted with several limitations in terms of the data collection and the data analysis. In fact, since we could only involve teachers that fulfilled both the initial questionnaire and the questionnaire one year after the end of the MOOC, we have to face a potential positive selection. It has to be assumed that the teachers being involved in the study used the system and outdoor mathematics more intensely than regular MOOC participants not willing to take part in the second questionnaire. Still, since we can see differences in the participants and in the selected case studies, it can be assumed that the study reveals different use cases describing what happened during the year after the MOOC’s end. In terms of the data collection via questionnaire, it can, in addition, be stated that the usability of the web portal is not as closely related to our research question than other categories. However, we decided to report it in terms of a detailed presentation of the participants’ experiences and developments throughout the year. In terms of data analysis, it can be stated that we reported a comparison of self-evaluation directly after the MOOC’s end and one year later. Due to the smaller number of respondents to the questionnaire, it happened only on a descriptive level, not during testing, and did not show any significant changes. Indeed, we are aware that, concerning the quantitative analysis of constructs, such as usability and perceptions concerning self-awareness of skills, a small sample size can impact the precision of both Cronbach’s alpha and omega coefficients, potentially leading to less accurate assessments of internal consistency. Thus, the potential trends we have identified should be rather considered in terms of a general overview, generating hypotheses whose precise confirmation demands future research.
Author Contributions
Conceptualization, E.T., S.J., T.R. and M.L.; methodology, E.T., S.J., T.R. and E.C.; formal analysis, E.T., S.J., T.R. and E.C.; investigation, E.T., T.R. and E.C.; resources, E.T., S.J., T.R., E.C., M.L. and M.F.M.; data curation, E.T., S.J., T.R. and E.C.; writing—original draft preparation, E.T., S.J., T.R. and E.C.; writing—review and editing, E.T., S.J., T.R., E.C. and M.F.M.; supervision, E.T., M.L. and T.R.; project administration, M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Institutional Review Board approval was not required since data did not include any personal identifying information. However, the study was conducted according to the guidelines of the Declaration of Helsinki.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available owing to privacy or ethical restrictions, as the MOOC participants come from different countries.
Acknowledgments
The creation of the MaSCE3 MOOC has been (partially) funded by the ERASMUS+ grant program of the European Union under grant no. 2019-1-DE03-KA201-060118. E. Taranto was partially supported by the “National Group for Algebraic and Geometric Structures, and their Applications” (GNSAGA - INdAM). M.F. Mammana was partially supported by the “PIACERI, EEEP&DLaD and SIA3” project of the University of Catania. These supports are gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1. | To allow the reader to have an understanding of the data, we report here the categories and the data analyzed (taken from Taranto et al., 2021) relating to the initial phases of the MOOC (pre) and after completing the MOOC (post). Designing math tasks for outdoor mathematics: Pre: 8/19 and Post: 17/19; Designing math trails for outdoor mathematics: Pre: 8/19 and Post: 16/19; Using MCM web portal: Pre: 8/19 and Post: 19/19; Using MCM app: Pre: 8/19 and Post: 18/19. |
| 2. | Note that this meta-didactical praxeology is similar to that in Table 1, but more detailed, in light of the clarifications on MCM made in the previous paragraphs. |
References
- Anderson, R. K. (2020). Social media facilitated collaboration: An analysis of in-the-moment support in a mathematics education Facebook group. In H. Borko, & D. Potari (Eds.), Proceedings of the twenty-fifth ICMI study (Lisbon, Portugal) (pp. 581–588). National and Kapodistrian University of Athens. [Google Scholar]
- Arzarello, F., Robutti, O., Sabena, C., Cusi, A., Garuti, R., Malara, N., & Martignone, F. (2014). Meta-didactical transposition: A theoretical model for teacher education programmes. In A. Clark-Wilson, O. Robutti, & N. Sinclair (Eds.), The mathematics teacher in the digital era: An international perspective on technology focused professional development, vol. 2 of the series: Mathematics education in the digital era (pp. 347–372). Springer. [Google Scholar] [CrossRef]
- Bujang, M. A., Omar, E. D., & Baharum, N. (2018). A review on sample size determination for Cronbach’s alpha test: A simple guide for researchers. The Malaysian Journal of Medical Sciences: MJMS, 25, 85–99. [Google Scholar] [CrossRef]
- Cahyono, A. N., Masrukan, Mulyono, Ludwig, M., Jablonski, S., & Oehler, D.-X. K. (2023). Indonesia-Germany MathCityMap training: Shifting mobile math trails teacher training to a hybrid environment. Journal on Mathematics Education, 14(1), 55–68. [Google Scholar] [CrossRef]
- Cai, J., & Howson, G. (2013). Toward an international mathematics curriculum. In M. A. (Ken) Clements, A. J. Bishop, C. Keitel, J. Kilpatrick, & F. K. S. Leung (Eds.), Third international handbook of mathematics education (pp. 949–974). Springer. [Google Scholar] [CrossRef]
- Chevallard, Y. (1999). L’analyse des pratiques enseignantes en théorie anthropologique du didactique. Recherches en Didactique des Mathématiques, 19(2), 221–265. [Google Scholar]
- Clarke, D. (2007). Ten key principles from research for the professional development of mathematics teachers. In G. C. Leder, & H. Forgasz (Eds.), Stepping stones for the 21st Century (pp. 27–39). Brill. [Google Scholar] [CrossRef]
- Cusi, A., Robutti, O., Panero, M., Taranto, E., & Aldon, G. (2022). Meta-Didactical Transposition. 2: The evolution of a framework to analyse teachers’ collaborative work with researchers in technological settings. In A. Clark-Wilson, N. Sinclair, & O. Robutti (Eds.), The mathematics teacher in the digital era. Mathematics education in the digital era (Vol. 16, pp. 365–389). Springer. [Google Scholar] [CrossRef]
- Dunn, T. J., Baguley, T., & Brunsden, V. (2014). From alpha to omega: A practical solution to the pervasive problem of internal consistency estimation. British Journal of Psychology (London, England: 1953), 105(3), 399–412. [Google Scholar] [CrossRef]
- Edwards, A. A., Joyner, K. J., & Schatschneider, C. (2021). A simulation study on the performance of different reliability estimation methods. Educational and Psychological Measurement, 81(6), 1089–1117. [Google Scholar] [CrossRef] [PubMed]
- Goodboy, A. K., & Martin, M. M. (2020). Omega over alpha for reliability estimation of unidimensional communication measures. Annals of the International Communication Association, 44(4), 422–439. [Google Scholar] [CrossRef]
- Gurjanow, I., Ludwig, M., & Zender, J. (2018). Aids and obstacles in the use of ICT-two surveys amongst MCM users. In F. J. Hsieh (Ed.), Proceedings of the 8th ICMI east Asia regional conference on mathematics education (Vol. 1, pp. 463–471). EARCOME. [Google Scholar]
- Hollebrands, K. F., & Lee, H. S. (2020). Effective design of massive open online courses for mathematics teachers to support their professional learning. ZDM Mathematics Education, 52(5), 859–875. [Google Scholar] [CrossRef]
- Jablonski, S. (2023). Is it all about the setting?—A comparison of mathematical modelling with real objects and their representation. Educational Studies in Mathematics, 113, 307–330. [Google Scholar] [CrossRef]
- Jablonski, S., & Ludwig, M. (2020). Development of an intensive study programme on outdoor mathematics teaching with digital tools. In M. Ludwig, S. Jablonski, A. Caldeira, & A. Moura (Eds.), Research on outdoor STEM education in the digiTal age. Proceedings of the ROSETA online conference in June 2020 (pp. 111–118). WTM. [Google Scholar] [CrossRef]
- Koehler, M. J., & Mishra, P. (2005). What happens when teachers design educational technology? The development of technological pedagogical content knowledge. Journal of Educational Computing Research, 32(2), 131–152. [Google Scholar] [CrossRef]
- Koehler, M. J., & Mishra, P. (2009). What is technological pedagogical content knowledge (TPACK)? Contemporary Issues in Technology and Teacher Education, 9(1), 60–70. [Google Scholar] [CrossRef]
- Ludwig, M., & Jesberg, J. (2015). Using mobile technology to provide outdoor modelling tasks—The MathCityMap-project. In Procedia proceedings of WCES (pp. 2776–2781). Elsevier. [Google Scholar]
- Macià, M., & García, I. (2016). Informal online communities and networks as a source of teacher professional development: A review. Teaching and Teacher Education, 55, 291–307. [Google Scholar] [CrossRef]
- Milicic, G., Jablonski, S., & Ludwig, M. (2020, November 9–10). Teacher training for outdoor education—Curricula development for the MathCityMap system. ICERI2020 Proceedings (pp. 3514–3522), Online. [Google Scholar]
- OECD. (2009). Creating effective teaching and learning environments: First results from TALIS. Available online: https://www.oecd.org/en/publications/creating-effective-teaching-and-learning-environments_9789264068780-en.html (accessed on 3 March 2025).
- Orçan, F. (2023). Comparison of Cronbach’s alpha and McDonald’s omega for ordinal data: Are they different? International Journal of Assessment Tools in Education, 10(4), 709–722. [Google Scholar] [CrossRef]
- Panero, M., Aldon, G., Trgalová, J., & Trouche, L. (2017, February 1–5). Analysing MOOCs in terms of teacher collaboration potential and issues: The French experience. Congress of European Research in Mathematics Education (pp. 2446–2453), Dublin, Ireland. [Google Scholar]
- Paulsen, J., & BrckaLorenz, A. (2017). Internal consistency. FSSE psychometric portfolio. Available online: https://nsse.indiana.edu/fsse/ (accessed on 3 March 2025).
- Pimenta, P., Domingo, A., & Costa, M. C. (2023, July 10–14). Sustainability of professional development programmes to teach mathematics using technology. 13th Congress of the European Society for Research in Mathematics Education (CERME), Budapest, Hungary. [Google Scholar]
- Rakes, C. R., Stites, M. L., Ronau, R. N., Bush, S. B., Fisher, M. H., Safi, F., Desai, S., Schmidt, A., Andreasen, J. B., Saderholm, J., Amick, L., Mohr-Schroeder, M. J., & Viera, J. (2022). Teaching mathematics with technology: TPACK and effective teaching practices. Education Sciences, 12(2), 133. [Google Scholar] [CrossRef]
- Ratnayake, I., Thomas, M., & Kensington-Miller, B. (2020). Professional development for digital technology task design by secondary mathematics teachers. ZDM Mathematics Education, 52, 1423–1437. [Google Scholar] [CrossRef]
- Ricart, M., Estrada, A., & Fortuny, J. M. (2022). Analysis of tutoring in the professional development of STEM teachers. Mathematics, 10(18), 3331. [Google Scholar] [CrossRef]
- Robutti, O. (2018). Meta-didactical transposition. In S. Lerman (Ed.), Encyclopedia of mathematics education. Springer. [Google Scholar] [CrossRef]
- Rogers, M. P., Abell, S., Lannin, J., Wang, C.-Y., Musikul, K., & Barker, D. (2007). Effective professional development in science and mathematics education: Teachers’ and facilitators’ views. International Journal of Science and Mathematics Education, 5, 507–532. [Google Scholar] [CrossRef]
- Taber, K. S. (2017). The use of Cronbach’s alpha when developing and reporting research instruments in science education. Research in Science Education, 48, 6. [Google Scholar] [CrossRef]
- Taranto, E., Aldon, G., Robutti, O., & Cusi, A. (2023). Design of resources for and by mathematics teachers: The process of internalization in MOOCs. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of digital resources in mathematics education. Springer international handbooks of education. Springer. [Google Scholar] [CrossRef]
- Taranto, E., & Arzarello, F. (2020). Math MOOC UniTo: An Italian project on MOOCs for mathematics teacher education, and the development of a new theoretical framework. ZDM—The International Journal on Mathematics Education, 52(5), 843–858. [Google Scholar] [CrossRef]
- Taranto, E., Jablonski, S., Recio, T., Mercat, C., Cunha, E., Lázaro, C., Ludwig, M., & Mammana, M. F. (2021). Professional development in mathematics education—Evaluation of a MOOC on outdoor mathematics. Mathematics, 9(22), 2975. [Google Scholar] [CrossRef]
- Taranto, E., Robutti, O., & Arzarello, F. (2020). Learning within MOOCs for mathematics teacher education. ZDM—The International Journal on Mathematics Education, 52(7), 1439–1453. [Google Scholar] [CrossRef]
- Thomas, M. O. J., & Chinnappan, M. (2008). Teaching and learning with technology: Realising the potential. In H. Forgasz, A. Barkatsas, A. Bishop, B. Clarke, S. Keast, W.-T. Seah, P. Sullivan, & S. Willis (Eds.), Research in mathematics education in Australasia 2004–2007 (pp. 167–194). Sense Publishers. [Google Scholar]
- Viladrich, C., Angulo-Brunet, A., & Doval, E. (2017). A journey around alpha and omega to estimate internal consistency reliability. Anales de Psicología/Annals of Psychology, 33(3), 755–782. [Google Scholar] [CrossRef]
- Zehetmeier, S., & Krainer, K. (2011). Ways of promoting the sustainability of mathematics teachers’ professional development. ZDM—International Journal on Mathematics Education, 43(6), 875–887. [Google Scholar] [CrossRef]
- Zender, J., Gurjanow, I., Cahyono, A. N., & Ludwig, M. (2020). New studies in mathematics trails. International Journal of Studies in Education and Science (IJSES), 1(1), 1–14. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).