Abstract
This study explored how bilingual Latine teacher candidates (TCs)—undergraduate students in a teacher preparation program working toward obtaining a teaching license and identifying as individuals from Latin America or of Latin American descent, using the gender-neutral term in Spanish, “Latine”, to encompass all genders—identified and addressed cultural assumptions in mathematics questions on the STAAR (State of Texas Assessments of Academic Readiness) test. Twenty Latine TCs who were enrolled at a major southern research university (pseudonym: Southland University) program reviewed fifth-grade STAAR mathematics questions to assess cultural assumptions and suggest revisions for cultural relevancy. The findings reveal that the TCs identified cultural assumptions in questions about probable unfamiliar currency, non-standard measurement units, and culturally specific terms that could impede students’ understanding. In their revisions, the TCs proposed simplifying language and provided contextual examples to enhance clarity, aligning with the first tenet of culturally relevant pedagogy (CRP). However, few revisions addressed CRP’s second and third tenets, which involve fostering cultural competence and critical consciousness. This study underscores the importance of integrating comprehensive CRP training in teacher preparation programs to better equip TCs to create culturally responsive teaching practices. The findings contribute to ongoing discussions about improving the cultural relevancy in standardized tests and supporting diverse student populations in achieving academic success.
1. Introduction
Research and practice continue to underscore the importance of recognizing identities, cultures, language, gender, sexuality, coloniality and community knowledge in addressing inequalities in mathematics (Ataide Pinheiro, 2021, 2022, 2023; Ataide Pinheiro et al., 2025a; Cox & Ataide Pinheiro, 2024; Dias & Ataide Pinheiro, 2024; Fúnez-Flores et al., 2024; Hong et al., 2023; Neto & Pinheiro, 2021; Goldberg et al., 2023). A leading body of work that has equipped educators with an understanding of ways to create a more just education system is Ladson-Billing’s (1995) work on culturally relevant pedagogy (CRP). CRP is a pedagogy that emphasizes (a) supporting students to develop academic success, (b) developing and maintaining cultural competency, and (c) developing critical consciousness about students’ social identities and contexts. This pedagogical framing provides educators with ways to make positive changes in the world regarding the development of their critical consciousness and understanding of injustices.
CRP’s conceptualization by Ladson-Billings (1995) was a long-awaited response to educators wanting educational practices to connect home culture and the content students learn in schools. In the context of the United States, where the population is constantly changing and becoming more diverse, making an explicit connection between students’ languages, cultures, community knowledge, and academic content is essential. In fact, while in 1995 the prekindergarten-through-twelfth-grade school population was 64.8% White and 13.5% Hispanic, The National Center for Educational Statistics estimates that by 2030, only 42.9% of students will be White compared to 29.7% Hispanic (U.S. Department of Education, National Center for Education Statistics, 2021). More specifically, emergent bilinguals (EBs—a student who is in the process of acquiring English and has another language as the primary language) comprise 10% of the public-school student population, with Spanish-speaking EBs representing 8% of this group (U.S. Department of Education, National Center for Education Statistics, 2021). Currently, 79% of public teachers in the United States are White (U.S. Department of Education, National Center for Education Statistics, 2018). This results in a cultural mismatch, as some teachers may struggle to effectively teach children of color (Khalifa et al., 2016). Therefore, in education preparation programs, we must start to understand how to prepare our TCs (teacher candidates—undergraduate students in a teacher preparation program working toward obtaining a teaching license) to become more culturally relevant educators, especially concerning the population of students that grows the most in schools in the U.S.—Hispanic students.
Most of the literature on bilingual teacher preparation has concentrated on the Spanish proficiency of bilingual TCs. This paper aims to contribute to the limited research on bilingual TCs, their preparation, and sense making of CRP. In this paper, we analyze the case of CRP regarding novice bilingual TCs from a state in the southwest region of the United States. We are specifically interested in understanding (a) how bilingual teacher candidates, who have been exposed to discussions and readings of CRP, assess cultural assumptions in fifth-grade mathematics tasks from a mandatory and significant standardized exam in Texas called the STAAR (State of Texas Assessments of Academic Readiness) and (b) the ways these same bilingual teacher candidates revised the math problems from the standardized exam for cultural relevance. In the next section, we provide a further discussion of the theorization of CRP and a revision of the literature on CRP and mathematics education.
2. Theoretical Framework and Cultural Relevant Pedagogy
As a critical pedagogical theory, CRP has many tenets and constructs that support how we envision bringing culture into education. Next, we discuss the theoretical underpinnings and some findings from the literature which inform our usage and understanding of this theoretical framework.
One the one hand, culturally relevant pedagogy (CRP) is a framework with a foundation in social justice, which aims to systematically address education gaps for historically oppressed groups (Allen et al., 2017). Gay (2002) defined it as “using the cultural characteristics, experiences, and perspectives of ethnically diverse students as conduits for teaching” (p. 106). CRP is a “pedagogy of opposition” meant to empower students to be critical of their place in society and propose change (Ladson-Billings, 2014; Tate, 1995). Ramsay-Jordan (2021) described CRP as a social construct that aims to respond to communities and classroom environments. Ladson-Billings (1995) defines the five constructs of CRP as follows: individual achievements, equity and excellence, developmental appropriateness, teaching the whole child, and student–teacher relationships.
On the other hand, mathematics teaching and learning have historically been exclusionary toward students from historically oppressed groups, including those from low-income socioeconomic backgrounds, urban communities, students of color, women, and queer individuals, among others (Ataide Pinheiro et al., 2025b; Martin, 2015; Spencer, 2015; Yeh & Rubel, 2020). Moreover, mathematical knowledge has often been assumed to be apolitical, acultural, and neutral, despite the fact that it is none of these (see Ferretti et al., 2024; Giberti et al., 2023; Kumashiro, 2004; Spagnolo & Nicchiotti, 2023). Therefore, CRP offers a means to promote critical and equitable mathematical learning opportunities by addressing the specific needs of historically oppressed students. In mathematics education, CRP has the potential to foster greater equity in mathematical learning (Willey & Ataide Pinheiro, 2019). In addition, math teachers who adhere to CRP constructs can sustain positive student–teacher relationships, leading to less conflict and increased academic learning (Ramsay-Jordan, 2021). However, there remains a limited practice of CRP in secondary mathematics education due to the belief that CRP does not align with rigorous content (Leonard et al., 2010; Mark & Id-Deen, 2022). A classroom environment that consistently values multiple approaches to solving a problem can allow learners to develop a critical consciousness about mathematics as a social practice, fostering discussions about why specific mathematical methods might be more valued by people than others (Rubel & Chu, 2012).
Teacher education programs play a critical role in considering how TCs are prepared to use CRP in a field such as mathematics that has traditionally thought itself unaffected by cultural diversity (Mark & Id-Deen, 2022). Including CRP practice in math classrooms would allow teachers to transform the curriculum academically, culturally, politically, and socially for their students and help address diverse needs (Sampson & Garrison-Wade, 2011). Aguirre et al. (2012) pointed out a lack of relevant opportunities for connecting theory to practice, which is a challenge throughout teacher education programs, causing many TCs to avoid these practices in the long term. Teacher preparation programs must educate their candidates to challenge injustice and racism within society and schooling, but this is only possible when the programs themselves are not maintaining these oppressive systems (Ledesma & Calderón, 2015) and challenge the idea that education is a great equalizer but continues to perpetuate oppression and forced assimilation (Lynn, 2024; Spring, 2021).
In this article, we use the three tenets written by Ladson-Billings (1995) to inquire how students see culture in state assessment questions and work to revise questions for cultural relevance. The three tenets have been defined as follows:
A pedagogy of oppression is not unlike critical pedagogy but is specifically committed to collective, not merely individual, empowerment. Culturally relevant pedagogy rests on three criteria or propositions: (a) students must experience academic success; (b) students must develop and/or maintain cultural competence; and (c) students must develop a critical consciousness through which they challenge the current status quo of the social order. (p. 160)
2.1. Review of the Literature
Through a review of the literature regarding CRP and teacher preparation programs in mathematics, we found three pertinent themes that the literature reinforces on CRP. Below, we present these themes and their nuances.
2.1.1. Benefits of CRP
There are many ways TCs grapple with enacting culturally responsive pedagogy through their teacher preparation programs. Research has shown that when TCs successfully implement CRP, students in the classroom increase their engagement with mathematics (Downing & McCoy, 2021; Hubert, 2014; Rubel & Chu, 2012), and the classroom has a better dynamic. Students respond positively to lessons that reflect their cultural backgrounds, showing promise for the effectiveness of CRP in improving mathematics teaching and learning (Ramsay-Jordan, 2021). In addition to enhancing students’ engagement, CRP also empowers students (especially emergent bilingual students) by making mathematics more relatable to their lives (Enyedy & Mukhopadhyay, 2007; Leonard et al., 2009). CRP has also shown promise in supporting students in seeing the value and applicability of mathematics in addressing real-world issues (Leonard et al., 2010). Research has shown that emergent bilingual students feel more motivated and confident in their mathematical abilities when they see their cultural identities reflected and valued in the curriculum (Leonard et al., 2009). Bringing CRP into mathematics has also shown promise in how mathematics is viewed as a discipline. Enyedy and Mukhopadhyay’s (2007) study demonstrated that CRP can reframe mathematics as a cultural activity, rather than a purely abstract and objective discipline. By highlighting cultural dimensions in mathematics, CRP bridges the gap between traditional mathematics pedagogy, which is often perceived as disconnected from the sociocultural and political aspects of society, and the learners’ cultural experiences. CRP has also shown benefits in terms of student achievement. Downing and McCoy (2021) found that implementing CRP in an undergraduate algebra mathematics course in a historically black college/university (HBCU) supported students to develop a stronger mathematical identity, as students saw their cultural backgrounds in mathematics and their experiences reflected in the curriculum. Their study also found that students performed better in the algebra course when they could relate the material to their own lives and sociopolitical contexts.
2.1.2. Challenges in Implementing CRP
While many benefits have been found regarding CRP and mathematics, there are also documented challenges, such as (a) the lack of concrete examples of what it means to implement CRP, (b) difficulties in integrating CRP with the existing curriculum, and (c) resistance from mentor teachers and school cultures that do not prioritize or support CRP (Ramsay-Jordan, 2021). Navarro et al. (2022) found the experiences of Teacher Candidates of Color (TCoCs) in Predominantly White Institutions (PWIs) with CRP to be inconsistent and superficial. Culture and language were misused, with the faculty relying on research instead of lived experiences, which limited their engagement with racial justice. The TCoCs also found themselves faced with microaggressions, tokenization, and exclusion from their classroom discussions, which could have been mediated by more faculty members of color, affirming spaces, and the embedding of CRP practice throughout their teacher education program. Gist (2017) examined how CRP supported TCoCs at a Hispanic-Serving Institution and found the integration of CRP into teacher education encouraged self-empowerment, sociopolitical awareness, and advocacy. This supports the need of teacher educators to embody CRP to ensure teacher education programs center racial and linguistic diversity beyond isolated courses. A critique on 134 studies on teacher candidate preparation for CRP in the U.S. found that that the studies focused on individual teacher deficiencies as opposed to institutional inequities; avoided direct discussion of race and racism, thus reducing CRP to merely cultural awareness without structural change; and did not center the experiences of teachers of color, which led to little to no challenges to White-dominated norms in teacher education (Chang & Viesca, 2022; Lynn, 2025).
There are also a lot of complexities involved in the practice of including CRP in the mathematics classroom. Leonard et al. (2010) noted that teachers struggled to balance traditional mathematical content with culturally relevant and socially just practices, often requiring significant adjustments to their instructional approaches. This struggle comes as standard curricula frequently lack the flexibility to incorporate cultural relevance and social justice; therefore, teachers must creatively adapt or supplement the curriculum to include these elements, which can be time-consuming and challenging without proper support and resources. In addition, teachers have pointed to the language barriers CRP practices pose for them. Language barriers from teachers have occasioned teachers needing to develop creative methods to bridge these gaps, such as using visual aids, gestures, and bilingual resources to facilitate understanding (Leonard et al., 2009). Another challenge that arises in research concerns the tensions CRP creates when brought into mathematics, mainly because of the conflicting goals between CRP and the perceived rigor and objectivity of mathematics instructions, as teachers struggle to balance maintaining high mathematical standards while making content culturally relevant (Enyedy & Mukhopadhyay, 2007).
2.1.3. Continued Need for Teachers’ Professional Development
Across multiple studies of CRP and mathematics, we found that these studies continue to emphasize the importance of professional development for teachers to be better equipped and prepared to bring CRP into their mathematics classrooms. Studies have pointed out that teachers need more robust professional development opportunities that are focused on CRP. These opportunities should include preservice and in-service training that provides teachers with practical strategies, resources, and ongoing support (Leonard et al., 2010; Ramsay-Jordan, 2021; Rubel & Chu, 2012). Teacher preparation programs are fundamental in preparing preservice teachers to implement CRP. Effective training programs are essential for equipping future teachers with the skills and confidence needed to apply CRP in diverse classroom settings (Mark & Id-Deen, 2022; Nolan & Xenofontos, 2023; Thomas et al., 2024). Preparation programs also must play a role in preparing teachers for culturally relevant and socially just teaching. These programs should emphasize the development of teachers’ cultural competence, critical consciousness, and pedagogical skills necessary for integrating these principles into their practice (Leonard et al., 2010).
3. Methods and Methodology
As discussed at the end of the Introduction Section, this paper aims to contribute to the limited research available on bilingual TCs and their experiences with CRP through their undergraduate programs. To achieve this goal, we seek to answer the following two research questions: (1) How do bilingual teacher candidates from a southwestern state in the U.S. who have been exposed to discussions and readings on culturally relevant pedagogy (CRP) assess cultural assumptions embedded in fifth-grade mathematics tasks from the STAAR exam? (2) In what ways do these TCs revise STAAR mathematics problems to enhance their cultural relevance?
3.1. Participants
The participants of this research included 20 Latine (gender-neutral term in Spanish used to describe individuals from Latin America or of Latin American descent) TCs. The purposive sampling strategy employed in this qualitative study was meticulously justified by the specific characteristics of the 20 TCs selected, as their profiles align closely with the research objectives and ensure representativeness within the study’s scope. The selection process prioritized relevance to the study’s aim by focusing on bilingual TCs who were grant recipients, a group uniquely positioned to provide insights into the intersection of bilingual education, financial support, and fast-track teacher preparation. All the participants were enrolled in the FastTeach program at a southwestern university, a distinctive accelerated model designed to expedite teacher training, making them particularly suitable for exploring the program’s challenges and effectiveness. These TCs were deliberately chosen as “information-rich” cases, offering detailed perspectives on their experiences with online coursework, in-person student teaching at partner schools, and grant-supported initiatives. The sample also reflected demographic diversity, comprising 20 Latine participants with a gender distribution of 19 women and 1 man, mirroring broader trends in teaching professions. Age diversity further enriched the sample, ranging from 19 to 55 years old, with notable clusters in younger (19–25 years old) and mid-career (36–40 years old) groups, enabling an analysis of how life stages influence participation in fast-track programs. In addition, 17 of the TCs identified as first-generation college students, a demographic that faces unique challenges and opportunities in higher education, and their inclusion ensured that the findings address barriers and support for this population. Contextual representation was also emphasized, as all the participants completed their practicum in FastTeach partner districts, grounding their experiences in real-world educational settings. While purposive sampling does not aim for statistical generalizability, it ensures conceptual representativeness by capturing diverse perspectives within this targeted population. This approach provides valuable insights into bilingual teacher preparation within fast-track programs but acknowledges limitations in representing all bilingual or Latine TCs across varying contexts or regions.
3.2. Context
The data for this study were elicited from bilingual TCs enrolled in a university-based, clinically intensive, competency-based Educator Preparation Program (EPP) in the southwestern United States. In addition to pursuing a generalist early childhood through sixth-grade certification, the TCs were also enrolled in a Special Populations course sequence, which includes six required courses focused on competency-based standards for supplemental certifications in English as a second language, special education, and bilingual education. This study defined bilingual TCs as those seeking Spanish-bilingual EC 6th-grade licensure. TCs enrolled in the EPP must complete (a) the required content area methods courses (mathematics, literacy, social studies, and science), (b) a Special Populations course (SPC) sequence (18 credit hours), (c) a year-long clinical teaching residency, (d) a Spanish content area bilingual course, and (e) required state content pedagogical and specialty certification exams. Before completing the assignment examined in this research, TCs engaged with coursework emphasizing equity literacy and academic achievement for all students. Foundational readings, such as Ladson-Billings’ (1995) seminal article on culturally relevant pedagogy (CRP), were integrated into their learning to prepare them with the knowledge and skills necessary to address educational inequities. While the study was closely tied to coursework, critical ethical considerations regarding informed consent, voluntary participation, grading practices, and power dynamics between researchers and participants were followed in accordance with the Institutional Review Board (IRB). To address the overlap between research activities and mandatory coursework and to ensure that participation was voluntary and free from coercion, the research analysis of the assignments occurred after the course was completed to rule out academic repercussions, uphold ethical research standards, and protect the participants’ autonomy.
In addition, the TCs studied the Sheltered Instruction Observation Protocol (SIOP), a research-based instructional framework designed to help emergent bilinguals acquire academic content while simultaneously developing their English language skills (Echevarria et al., 2017). The SIOP model incorporates various strategies and components that promote language acquisition and academic success, including (a) content objectives that align with academic standards; (b) language objectives that explicitly outline the language skills to be developed; (c) effective instructional strategies, such as explicit teaching, modeling, and guided practice; (d) meaningful learning activities that connect to students’ personal experiences; (e) opportunities for student interaction that promote language use and understanding; (f) strategies for building background knowledge to support comprehension; and (g) explicit vocabulary instruction that focuses on key terms. These content-related tasks allow students to apply their knowledge, while assessment strategies measure both language proficiency and content understanding, alongside ongoing monitoring and adjustments to instruction based on student needs (Echevarria et al., 2017).
The TCs also reviewed real-world case studies on diversity and social justice education, designed to challenge their thinking about equity and inclusion. These case studies encourage critical reflection on issues such as racism, sexism, and classism, prompting the TCs to examine their assumptions and biases, deepen their understanding of the challenges faced by marginalized students, develop empathy, and cultivate the skills necessary to create inclusive and equitable learning environments. This approach aligns with the principles of CRP, which emphasizes the importance of acknowledging and valuing student diversity, building on students’ cultural strengths, and creating a learning environment that is culturally relevant and affirming for all students (Gorski & Pothini, 2018).
3.3. Data Collection
The data comprising this study was part of a course assignment for 20 bilingual TCs from a major research institution in the southwestern region of the United States. Data were gathered in May 2024 as part of the TCs’ last course on the Special Populations course sequence and after the TCs completed two semesters of student teaching. As part of the assignment, the bilingual TCs were guided to review the fifth-grade STAAR mathematics test and identify one question they thought required cultural background knowledge that might be challenging linguistically for emergent bilingual students (E.B.s). In total, 20 students responded to two questions from the course assignment: (a) What cultural background does this question assume? (b) How would you revise the question to ensure cultural relevance? In this study, we analyzed the TCs’ answers to these two questions.
3.4. Data Analysis
To analyze the TCs’ responses to these questions, we employed inductive coding (Strauss & Corbin, 1990) of the responses provided by the TCs to the first question (What cultural background does this question assume?), followed by a thematic analysis (Braun & Clarke, 2006). For the inductive coding process, each author independently reviewed the data and applied in vivo coding, identifying verbatim fragments that reflected aspects of culture. This approach allowed us to examine how the TCs described the cultural elements embedded in the STAAR questions. After completing the in vivo coding, we identified overarching themes that emerged from the coded responses. These themes centered around specific terms within the STAAR questions that the TCs selected to highlight cultural assumptions (further explored in the findings section). Consequently, our findings related to the first research question were organized and reported based on common cultural assumption issues noted by groups of the TCs across different selected questions.
Following the inductive and thematic analyses, we conducted a deductive coding process (Strauss & Corbin, 1990) to analyze the TCs’ responses to the second question (How would you revise the question to ensure cultural relevance?). This deductive analysis was guided by the three tenets of CRP, as outlined in the Theoretical Framework Section. We examined whether the ways in which the TCs revised the STAAR questions addressed academic success, cultural competence, and/or the development of critical consciousness. Below, we present the findings for the two questions from the assignment.
4. Results
In this paper, our findings are presented in two main sections aligned with the objectives outlined in the introduction of the paper:
- The teacher candidates’ (TCs’) assessment of cultural assumptions in fifth-grade mathematics tasks;
- The TCs’ approaches to revising these math tasks for cultural relevance.
In responding to our question (What cultural background does this question assume? & How would you revise the question to ensure cultural relevance?), we found that the TCs chose similar questions from the STAAR mathematics test to discuss cultural assumptions. Out of 36 questions available in the STAAR math exam, the TCs chose only 6 of these, with some being discussed by multiple TCs. The responses of the TCs that are analyzed in this paper showcase how they saw cultural assumptions in their selected questions from the exam and how they revised the questions for cultural relevancy (Questions 5, 15, 21, 22, 27, and 32). For more information about these tasks, see Appendix A.
4.1. Cultural Assumptions in the Tasks of the STAAR Mathematics Test
The TCs who chose questions 27 (budget/allowance task), 22 (building a deck in the backyard task), 15 (carnival rides), 32 (money spent and “pair of pants” tasks), and 21 (selling jewelry task) saw the ways that some of the content of the tasks might present cultural assumptions specifically made in the context of students in the southwestern state where this study was conducted. The southwest state in question has a high percentage of emergent bilingual students in elementary classrooms, where students might not necessarily speak English as their first language. Also, many students in the classrooms are immigrants. Therefore, the TCs mostly pointed to cultural differences regarding national origins. See Appendix A for full examples of the STAAR mathematics questions.
The majority of the TCs (n = 8) chose to investigate cultural assumptions in question 27 about budgets and allowances. The TCs pointed out that this question assumes that all the students receive an allowance (or know what an allowance is), know what a budget is, and that the students know how to save. The TCs further explained that people do not believe in an allowance in some cultures. Therefore, this question would not be easy for one to solve without really knowing much about the concept of an allowance due to its inextensibility to their cultures. In explaining why there are some cultural assumptions to this question, the TCs went further to say that the concept of a “balanced budget” might be unfamiliar, especially for students who have not been exposed to budgeting practices at home. In addition, the question presents expenses such as cell phones, piano lessons, entertainment, and savings. TCs mentioned that these types of expenses vary according to cultural and socioeconomic backgrounds. Therefore, some students might not have the background to understand the idea of extracurricular activities. Another point brought up by the TCs was that “after-school jobs” might not be present in other cultures, while it is common in the U.S. for students to have part-time jobs while in school and be more familiar with this concept. Finally, the TCs recognized that budgeting might be something significantly emphasized in the U.S. culture through schooling, while this might not be true in other countries. At the same time, expense categories such as cell phones, piano lessons, and entertainment might not be prioritized in every culture, clarifying that these specific types of expense categories might not be relevant to other cultures.
The second most common task that the TCs chose (n = 4) was question 22 (building a deck in the backyard). The TCs mentioned that this question assumes that all students are familiar with measurement units, such as feet. The TCs recognized that most students might come from places where the metric system prevails; therefore, meters might be something that students understand better than units from the imperial system. Other TCs also recognized that building decks might not be relevant for fifth graders; therefore, the exam should ask questions that connect to fifth graders’ daily lives, which might not include building decks. Also, the TCs recognized that backyards might be connected to a high SES, since some students who live in apartments might not have a backyard themselves, which could lead to a disadvantage in understanding what backyards even mean. Finally, the TCs pointed out that decks might be commonly found in the U.S. but not in other countries. The TCs also pointed out that decks can mean many different things, such as a deck of cards; therefore, this word comes with ambiguity for its multiple meanings, which could be very challenging for EBs. Consequently, we see that the TCs not only recognized things that are specific to a higher SES in the context of the U.S., such as decks in backyards, but they also pointed to the ways that the language choice in the problem could be tricky and present difficulty for EBs.
The other three questions in which the TCs saw cultural assumptions were 15 (carnival rides) (n = 2), 32 (money spent and “pair of pants” tasks) (n = 2), and 21 (selling jewelry task) (n = 2). Regarding question 15, the TCs recognized that carnivals are a particular thing in the context of the U.S. but might not be a reality for other cultures. This question assumes that students may have been to a carnival or know what a carnival is. At the same time, in other cultures, this word might mean something very different and might end up confusing students and disadvantaging them from being able to understand the context of the question and answer it correctly. Regarding question 32, the TCs once again discussed the issues that language ambiguity could cause and the complications that could affect EB students. Specifically, the TCs mentioned that students might not know that the term “pair of pants” refers solely to one object and not two, as would be the case in other languages, like Spanish and Portuguese. Regarding question 21, the TCs recognized that the task assumes that students understand the dollar (USD) as currency. However, that might not be true as some immigrant students might come from countries where pesos or quetzals might be used as currency.
Two of the TCs’ responses were not assessed because they did not discuss any cultural assumptions related to their chosen task (question 5); instead, they only focused on the mathematical content of the task.
4.2. Revising Questions for Cultural Relevance
In addressing ways for revising cultural relevance in math tasks from the fifth-grade STAAR mathematics test, the TCs provided multiple ways the tasks they identified could be revised.
For question 27, about budgets and allowances, the TCs mainly mentioned revising this question for language clarity since EBs might not understand the terms originally used to write this question. The TCs suggested breaking down the question into more straightforward language (more universal terms), providing explanations of unfamiliar terms, using visual aids or examples to illustrate the problem, using the dictionary, providing extra time and other accommodations to solve the problem, and changing some of the expenses to easier ones that would more understandable for EBs. Some of the ways to change the terms used that were suggested by the TCs included changing “allowance” to “earnings” or “money from parents” and “after-school jobs” to “money from a job”. The TCs also suggested revising the problem to provide contextual examples using clear everyday terms for expenses, such as “fun activities” instead of “entertainment”. They also suggested addressing the goal of the question to be more precise by rephrasing it to “How does Spencer make his spending match his income?”. The TCs also provided further revisions for this problem by suggesting changes of terms such as “income” to “money coming in” and “expenses” to “money going out”. Finally, there was also a rewriting of some of the TCs’ work, replacing “piano lessons” with “music lessons”, which were judged by the TCs to be more accessible terms.
This first approach by the TCs regarding improving the language in the mathematics problems was the most common way they foresaw the revision of the problems for cultural relevance. In fact, modifying the wording in the math problems addresses more closely the first tenet of culturally relevant pedagogy (CRP), as the TCs were thinking about ways to improve the communication of the problem to facilitate students’ mathematical success.
In a more isolated case, two of the TCs suggested that we provide culturally relevant terms that align more with students and change the name in the problem from “Spencer” to “Jesus”, a more commonly used name for folks from Latine cultures. Not only did the TCs see changing the name as a clarification that “Spencer” refers to a person’s name, but also to support the students by presenting a name they are familiar with in the problem. This way of suggesting and revising the problem for cultural relevance aligned with the second tenet of CRP, which expresses the importance of maintaining or supporting the development of cultural competencies.
Finally, one TC discussed how they were aware that “Texas has linguistic accommodations for testing; however, they may only be provided when specifically asked by EBs” (Wright, 2019). Therefore, these TCs mentioned that they would familiarize themselves with the requirements for students to ask for accommodations and make their students aware that this is available to them so they can use it. This approach by this TC demonstrated the third tenet of CRP, in which the teacher envisions ways to support students in developing critical consciousness and fighting against the status quo.
The TCs who chose question 22 (building a deck in the backyard task), 15 (carnival rides), 32 (money spent and “pair of pants” tasks), and 21 (selling jewelry task) only suggested ways that aligned with the first tenet of CRP, emphasizing the importance of clarifying language for a possible better achievement.
In question 22, the TCs suggested analyzing the question in parts, using real-life examples, and using them constantly. The TCs suggested more accessible terms, such as ramps, house, and bridge, instead of deck. They also suggested choosing examples that students can relate to, such as using Roblox or Minecraft. Replacing deck with patio was also recommended, as the word patio is a Spanish cognate, making it easier for Spanish-speaking EBs. Finally, scaffolding was provided, words were broken down, visuals were used, and concepts were illustrated. The TCs also suggested the use of “$1” instead of “one dollar” and the usage of “made” instead of “earned”. Since these terms would most likely be more accessible to students, this approach of simplifying the language is backed up in the literature and discussed by Wright (2019): “The other accommodation that appears to have potential is to simplify the language so that EBs have a better chance of understanding the question. This accommodation is referred to as linguistic simplification”.
For question 15 (carnival rides), the TCs suggested the usage of a table chart, rather than a graph plot, because tables were covered in math across the K-5 math curriculum in their placements, plus they were easier to teach for understanding. The reorganization of data by columns, with one column containing the name of the ride and the other showing the ticket price, was visioned by the TCs as an uncomplicated way for students to solve this problem. The TCs even based this assumption on previous studies that stated that EBs are highly dependent on visuals and simplification (Wright, 2019). To revise the problem, a TC suggested the following wording: “How many rides require less than four tickets compared to those needing four or more tickets? What is the difference between these two groups?”. Through this rewording, the TCs saw the possibility of students focusing on comparing two groups and finding the numerical difference between them. They also foresaw the students being able to focus solely on the information needed to answer the problem and less on all the other information that might distract the students as they navigate solving this problem. All the solutions proposed for question 15 regard the first tenet of CRP, in which the TCs suggested ways to facilitate the possible comprehension of problems by students and, therefore, facilitate academic success.
Finally, in question 32 (money spent and “pair of pants” tasks), we noticed that the TCs only provided suggestions regarding improving the problem’s English. More specifically, the TCs saw using a “pair of pants” as very problematic for emerging bilingual students because a pair means two in other languages, like Spanish. Therefore, in revising this problem, the TCs suggested revising the question using another type of clothing (e.g., a jacket). Just as for question 15, in question 32, the suggestion by the TCs to use simpler language aligned with the first tenet of CRP, which suggests the TCs mostly want to provide students with more explicit tasks that potentially could facilitate academic success by enabling them to comprehend and possibly solve the question correctly. Table 1 presents the summarized findings.

Table 1.
Summary of the findings.
5. Discussion and Conclusions
The findings of this study add to the body of knowledge by providing valuable insights into how bilingual TCs identify and address cultural assumptions in standardized mathematics assessments, specifically the State of Texas Assessments of Academic Readiness (STAAR) test. The study’s findings establish connections and recommendations to advocate for and strengthen the practice of culturally responsive pedagogy (CRP) for preservice bilingual math teachers. The TCs in this study were able to promptly question what types of cultural assumptions might be present in the tasks of the STAAR mathematics test and provide possible modifications for the cultural relevance of these tasks. The significance of the findings speaks to what is visible to TCs being prepared to teach a more than ever evolving and changing classroom and U.S. society. Academic language is a currency in the classroom (Lynn, 2023), which makes it essential for TCs to gain insights into the fact that language matters.
In the context of mathematics, language can make mathematics problems trickier for those recently introduced to the U.S. context or for those who might not have access to certain benefits due to their socioeconomic statuses. The TCs were promptly able to notice that neutral language was not used in the problems, such as the choice of currency used, instead of treating it as money in general; the types of quantities used for measurement, such as feet, which is the quantity only used in very few countries, like the U.S.; and the highly linguistically marked terms, such as “carnival” or “pair of pants”. This attention to language encourages us to be able to critically provide exam writers with a reflection of what the TCs see as problematic cultural assumptions in exams, making us aware of the need for revisions to tasks to make them more culturally relevant to students and have less linguistic and context ambiguity, which might enable students who come from outside of the U.S. or from different SESs to successfully understand and respond to these questions (Leonard et al., 2009; Ramsay-Jordan, 2021).
Regarding the revision of questions for cultural relevance, the TCs were able to suggest revisions that touched the three tenets of CRP discussed in our Theoretical Framework Section (Ladson-Billings, 1995). However, we saw many limitations in how the TCs revised the problem for cultural relevance. Most of the TCs suggested revisions in the wording of the mathematics problems to make it easier for students to understand them. Only two TCs suggested revisions that addressed cultural relevance concerning the second tenet. Only one TC among 20 could suggest revisions that addressed the third tenet. These findings are relevant to researchers and teacher educators who are thinking of ways to support TCs in holistically seeing CRP. Mainly, the TCs demonstrated in this research project that they are concerned with making the content clear for students. Although this is a great start, the TCs must also learn ways to revise questions for cultural relevance that support students in developing and/or maintaining cultural competence and developing a critical consciousness through which they challenge the current status quo of the social order (Ladson-Billings, 1995). It is essential that teacher preparation programs support TCs to learn how to think through and be able to enact the three tenets of CRP. Programs can continue to offer comprehensive CRP training by providing practice-based learning opportunities in diverse classroom settings, modeling culturally responsive teaching, and fostering critical consciousness. Additionally, exposing TCs to critical studies, offering discussions on various historical perspectives, and exploring the intersections of gender, race, class, sexuality, and mathematics can deepen TCs’ conscientização (critical consciousness). Providing opportunities for TCs to engage in reflective practices, including analyzing their teaching through the CRP lens, can further help them integrate cultural relevancy into their teaching practices (see Spagnolo et al., 2021 for further recommendations on how TCs can be better supported in engaging with CRP beyond language clarification).
The findings of this study are significant and in alignment with multiple studies that found the role that teacher preparation programs play in supporting TCs in becoming effective implementers of CRP in the mathematics classroom (Leonard et al., 2010; Mark & Id-Deen, 2022; Ramsay-Jordan, 2021; Thomas et al., 2024). Based on the results of this study, teacher preparation programs should offer opportunities for TCs to create and revise math tasks that incorporate all aspects of CRP and provide explicit instruction and practice in addressing all three tenets of CRP (academic success, cultural competence, and critical consciousness). The results further highlight the complex interplay between language, culture, and mathematical understanding in the context of standardized testing. Additionally, teacher preparation programs could include opportunities through field experiences for TCs to interact with mathematics content in diverse classroom settings. This includes teacher preparation assignments that connect to the field and offer an opportunity to reflect and redesign the math curriculum so that it is aligned with CRP. For instance, TCs could interview leading mathematics CRP teachers in their local districts. Finally, we suggest role-playing scenarios where TCs identify and provide feedback on real mathematics classroom experiences. This could include scenarios where there is a lack of commitment from administrators in CRP or scenarios where the TCs practice embedding the three tenets for CRP into the mathematics curriculum.
The authors also encourage teacher educators to incorporate narrative inquiry as a research method and an inclusive lens to provide a deeper understanding of bilingual TCs’ experiences in teacher preparation programs. This approach aligns with Johnson Lachuk and Mosley’s (2012) recommendations, allowing researchers to access racial knowledge and perspectives of people of color more effectively. Teacher preparation programs must encourage TCs to engage in ongoing critical reflection on their own cultural assumptions and biases through the facilitation of peer discussion groups focused on cultural awareness and provide opportunities for TCs to analyze and revise standardized test questions for cultural relevance. By collecting and analyzing TCs’ personal stories, researchers can gain a better understanding of how TCs’ cultural backgrounds influence their approach to CRP and uncover nuanced cultural assumptions that may not be apparent through traditional research methods.
The findings of this CRP, math education, and bilingual TCs study are also presented to influence education policymakers. This study emphasizes how cultural assumptions particularly affect emergent bilingual and immigrant students in standardized assessments. We stress the point in showing how current math test questions unfairly disadvantage these students, potentially leading to inaccurate assessments of their mathematical abilities. The authors of this study similarly demonstrate how bilingual TCs were able to identify cultural assumptions that might not be apparent to AI software and test developers from a single cultural background reviewing math assessments. As professors and researchers, we argue for the inclusion of diverse perspectives in the test development process, showing how it can lead to more culturally relevant and fair assessments. Additionally, embedding a variety of scenarios that reflect a culturally diverse society may help EBs connect with the content and enhance their comprehension. Standardized assessment developers could also consider multiple ways to assess students’ mathematical content knowledge, for example, by providing different assessment formats and moving beyond multiple choice. Moreover, policy makers should be made aware that acquiring a language to a cognitive academic language proficiency (CALP) takes 5–7 years (Wright, 2019), thus impacting the standardized assessment results of EBs who have recently moved to the U.S.
Finally, the limitations of this study include limited participants (20 bilingual TCs) from a single teacher preparation program and the absence of observations or discussions with TCs regarding how CRP informs their pedagogical knowledge and teaching skills. Future studies should consider ways to engage TCs in developing a critical consciousness of the ways they can revise mathematics tasks to address the third tenet of CRP: “Students must develop a critical consciousness through which they challenge the current status quo of the social order” (Ladson-Billings, 1995, p. 160). Further research is needed to examine the phenomenon of TCs’ application of CRP in a qualitative context as it moves beyond surface-level changes, like language clarification, to foster more profound cultural competence and critical consciousness. By embedding real-world scenarios and culturally relevant examples into math problems, TCs can create more inclusive learning environments that affirm students’ identities and enhance engagement. Teacher preparation programs should provide explicit training on the tenets of CRP and offer practical opportunities for TCs to practice revising assessments and other curricula for cultural relevance.
Author Contributions
All authors contributed equally to the writing of all parts and revisions of this manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the US Department of Education under Grant number 21D026; Texas Tech University under Grant Devitt Jones Endowment Fund in Teacher Education.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of Texas Tech University Institutional Review Board for the project Competency-Based Teacher Preparation IRB2019-579 2021-05-01.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Figure A1.
Question 5 (published by the Texas Education Agency (2021)).
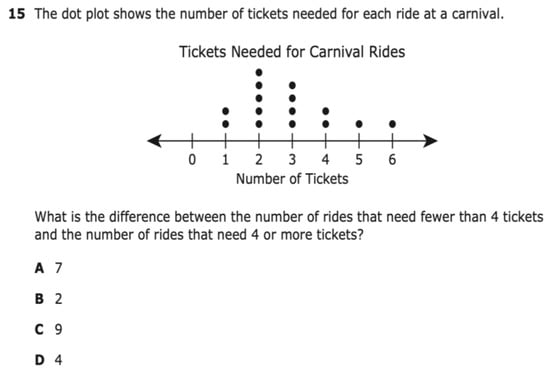
Figure A2.
Question 15 (published by the Texas Education Agency (2021)).

Figure A3.
Question 21 (published by the Texas Education Agency (2021)).
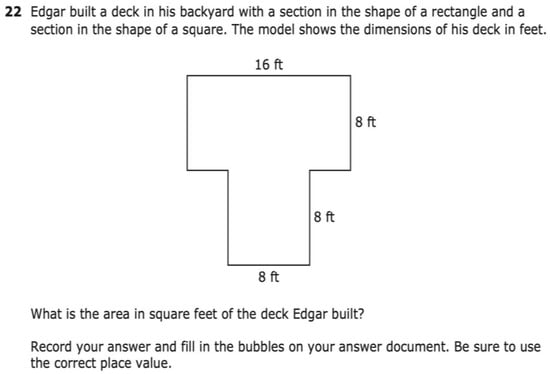
Figure A4.
Question 22 (published by the Texas Education Agency (2021)).

Figure A5.
Question 27 (published by the Texas Education Agency (2021)).

Figure A6.
Question 32 (published by the Texas Education Agency (2021)).
References
- Aguirre, J. M., Zavala, M. D. R., & Katanyoutanant, T. (2012). Developing robust forms of preservice teachers’ pedagogical content knowledge through culturally responsive mathematics teaching analysis. Mathematics Teacher Education and Development, 14(2), 113–136. [Google Scholar]
- Allen, A., Hancock, S. D., Starker-Glass, T., & Lewis, C. W. (2017). Mapping culturally relevant pedagogy into teacher education programs: A critical framework. Teachers College Record, 119(1), 1–26. [Google Scholar] [CrossRef]
- Ataide Pinheiro, W. (2021). Dismantling the ‘All-Boys Club’ A Narrative of Contradictions Women Experience in PhD Mathematics Programs: A Freirean Approach. International Electronic Journal of Mathematics Education, 16(3), 1–13. [Google Scholar] [CrossRef] [PubMed]
- Ataide Pinheiro, W. (2022). At the intersections: Queer high school students’ experiences with the teaching of mathematics for social justice(Publication No. 29320623). [Doctoral dissertation, Indiana University]. ProQuest Dissertations & Theses Global. [Google Scholar]
- Ataide Pinheiro, W. (2023). Gender and sexuality in mathematics education: Queer high school students’ experiences in the United States. Boletim do Grupo de Estudos e Pesquisa em Educação Matemática, (83), 78–121. [Google Scholar] [CrossRef]
- Ataide Pinheiro, W., Chávez, R., & Nguyen, U. (2025a). Exploring gendered experiences of high-achieving undergraduate women in mathematics. International Journal of Education in Mathematics, Science, and Technology (IJEMST), 13(1), 40–60. [Google Scholar] [CrossRef]
- Ataide Pinheiro, W., Kaur Bharaj, P., Cross Francis, D., Kirkpatrick Darwin, T., Esquibel, J., & Halder, S. (2025b). An Investigation of Gender Biases in Teacher-Student Interaction in Mathematics Lessons Within a Virtual Teaching Simulator. In C. Wilkerson Lee, L. Bondurant, B. Sapkota, & H. Howell (Eds.), Promoting Equity in Approximations of Practice for Mathematics Teachers (pp. 201–228). IGI Global. [Google Scholar] [CrossRef]
- Braun, V., & Clarke, V. (2006). Using thematic analysis in psychology. Qualitative Research in Psychology, 3(2), 77–101. [Google Scholar] [CrossRef]
- Chang, W.-C., & Viesca, K. M. (2022). Preparing teachers for culturally responsive/relevant pedagogy (CRP): A critical review of research. Teachers College Record, 124(2), 197–224. [Google Scholar] [CrossRef]
- Cox, J., & Ataide Pinheiro, W. (2024). Advancing equitable and responsible research involving gender and sexuality within mathematics education. The Educational Forum, 88(3), 283–308. [Google Scholar] [CrossRef]
- Dias, A., & Ataide Pinheiro, W. (2024). A scoping review of research methodologies used on studies of gender and sexuality within mathematics education. Perspectivas da Educação Matemática, 17(47), 1–27. [Google Scholar] [CrossRef]
- Downing, G. A., & McCoy, W. N. (2021). Exploring mathematics of the sociopolitical through culturally relevant pedagogy in a college algebra course at a historically Black college/university. Journal of Urban Mathematics Education, 14(1), 45–70. [Google Scholar]
- Echevarria, J., Vogt, M. E., & Short, D. J. (2017). Making content comprehensible for English learners (5th ed.). Pearson. [Google Scholar]
- Enyedy, N., & Mukhopadhyay, S. (2007). They don’t show nothing I didn’t know: Emergent tensions between culturally relevant pedagogy and mathematics pedagogy. The Journal of the Learning Sciences, 16(2), 139–174. [Google Scholar] [CrossRef]
- Ferretti, F., Gambini, A., & Spagnolo, C. (2024). Management of semiotic representations in mathematics: Quantifications and new characterizations. European Journal of Science and Mathematics Education, 12(1), 11–20. [Google Scholar] [CrossRef]
- Fúnez-Flores, J., Ataide Pinheiro, W., Mendoza Ávila, A., Phelps, R., & Shive, E. C. (2024). The sociopolitical turn in mathematics education and decolonial theory. London Review of Education, 22(1), 1–12. [Google Scholar] [CrossRef]
- Gay, G. (2002). Preparing for culturally responsive teaching. Journal of Teacher Education, 53(2), 106–116. [Google Scholar] [CrossRef]
- Giberti, C., Santi, G., & Spagnolo, C. (2023). The role of metaphors in interpreting students’ difficulties in operating with percentages: A mixed-method study based on large-scale assessment. European Journal of Science and Mathematics Education, 11(2), 297–321. [Google Scholar] [CrossRef] [PubMed]
- Gist, C. D. (2017). Culturally responsive pedagogy for teachers of color. The New Educator, 13(3), 288–303. [Google Scholar] [CrossRef]
- Goldberg, E. R., Darwin, T. K., Esquibel, J. S., Noble, S., Mullins, M., & Ataide Pinheiro, W. (2023). Contemporary debates on equity in STEM education: Takeaways from a doctoral seminar in Equity in STEM Education. Journal of Research in Science, Mathematics and Technology Education, 6(SI), 69–89. [Google Scholar] [CrossRef]
- Gorski, P. C., & Pothini, S. G. (2018). Case studies on diversity and social justice education (2nd ed.). Routledge. [Google Scholar]
- Hong, J., Cross Francis, D., Haskins, C., Chong, K., Aldrich, K., Ataide Pinheiro, W., Noon, S., & Dickinson, J. (2023). Wellbeing under threat: Multiply marginalized and underrepresented teachers’ intersecting identities. Teachers and Teaching: Theory and Practice, 30(6), 762–782. [Google Scholar] [CrossRef]
- Hubert, T. L. (2014). Learners of mathematics: High school students’ perspectives of culturally relevant mathematics pedagogy. Journal of African American Studies, 18, 324–336. [Google Scholar] [CrossRef]
- Johnson Lachuk, A. S., & Mosley, M. (2012). Us & them? Entering a three-dimensional narrative inquiry space with white pre-service teachers to explore race, racism, and anti-racism. Race Ethnicity and Education, 15(3), 311–330. [Google Scholar] [CrossRef]
- Khalifa, M. A., Gooden, M. A., & Davis, J. E. (2016). Culturally responsive school leadership: A synthesis of the literature. Review of Educational Research, 86(4), 1272–1311. [Google Scholar] [CrossRef]
- Kumashiro, K. (2004). Against common sense: Teaching and learning toward social justice. Routledge Falmer. [Google Scholar]
- Ladson-Billings, G. (1995). But that’s just good teaching! The case for culturally relevant pedagogy. Theory Into Practice, 34(3), 159–165. [Google Scholar] [CrossRef]
- Ladson-Billings, G. (2014). Culturally relevant pedagogy 2.0: A.k.a. the remix. Harvard Educational Review, 84(1), 74–84. [Google Scholar] [CrossRef]
- Ledesma, M. C., & Calderón, D. (2015). Critical race theory in education: A review of past literature and a look to the future. Qualitative Inquiry, 21(3), 206–222. [Google Scholar] [CrossRef]
- Leonard, J., Brooks, W., Barnes-Johnson, J., & Berry, R. Q., III. (2010). The nuances and complexities of teaching mathematics for cultural relevance and social justice. Journal of Teacher Education, 61(3), 261–270. [Google Scholar] [CrossRef]
- Leonard, J., Napp, C., & Adeleke, S. (2009). The complexities of culturally relevant pedagogy: A case study of two secondary mathematics teachers and their ESOL students. The High School Journal, 93(1), 3–22. [Google Scholar] [CrossRef]
- Lynn, R. (2023). Book review—Decolonising the Mind by Ngugi wa Thiong’o—Africa, a new perspective. International Journal of Academic Research in Business, Arts and Science, 5(9), 1–9. [Google Scholar] [CrossRef]
- Lynn, R. (2024). Extended book review: Unsettling the university, confronting the colonial foundations of US higher education: By Sharon Stein, Johns Hopkins University Press, 2022, 325 pp., ISBN 9781421445045 (hardcover), ISBN 9781421445052 (ebook). Globalisation, Societies and Education, 1–10. [Google Scholar] [CrossRef]
- Lynn, R. (2025). Academia: An image of imperialism. AJE Forum: The Forum of the American Journal of Education. Available online: https://sites.psu.edu/ajeforum/2025/01/29/academia-image_of_imperialism/ (accessed on 24 February 2025).
- Mark, S. L., & Id-Deen, L. (2022). Examining preservice mathematics and science teachers’ plans to implement culturally relevant pedagogy. Educational Action Research, 30(5), 725–746. [Google Scholar] [CrossRef]
- Martin, D. B. (2015). The collective Black and “principles to actions”. Journal of Urban Mathematics Education, 8(1), 17–23. [Google Scholar] [CrossRef]
- Navarro, O., Ronan, B., & Reyes Patron, I. (2022). Teacher candidates of Color experiences and perceptions of culturally responsive teaching within teacher education: “They hit the target, not the bullseye”. Journal for Multicultural Education, 16(4), 374–386. [Google Scholar] [CrossRef]
- Neto, V., & Pinheiro, W. A. (2021). The Problematic Issue of Gender in Mathematics Textbooks: A Comparative Analysis Between Brazil and the USA. Revista de Investigação e Divulgação em Educação Matemática, 5(1). [Google Scholar] [CrossRef]
- Nolan, K. T., & Xenofontos, C. (2023). The role of insights in becoming a culturally responsive mathematics teacher. Education Sciences, 13(10), 1028. [Google Scholar] [CrossRef]
- Ramsay-Jordan, N. N. (2021). How secondary mathematics preservice teachers grapple with enacting culturally responsive practices at placement sites. International Journal of Science and Mathematics Education, 19(5), 997–1013. [Google Scholar] [CrossRef]
- Rubel, L. H., & Chu, H. (2012). Reinscribing urban: Teaching high school mathematics in low income, urban communities of color. Journal of Mathematics Teacher Education, 15, 39–52. [Google Scholar] [CrossRef]
- Sampson, D., & Garrison-Wade, D. F. (2011). Cultural vibrancy: Exploring the preferences of African American children toward culturally relevant and non-culturally relevant lessons. The Urban Review, 43, 279–309. [Google Scholar] [CrossRef]
- Spagnolo, C., Capone, R., & Gambini, A. (2021, July 19–22). Where do students focus their attention on solving mathematical tasks? An eye tracker explorative study. 44th Conference of the International Group for the Psychology of Mathematics Education (Vol. 4, pp. 89–96), Khon Kaen, Thailand. [Google Scholar]
- Spagnolo, C., & Nicchiotti, B. (2023). Interpreting gender gap issues in standardized tests: Definition and application of a theoretical tool. Frontiers in Education, 8, 1303041. [Google Scholar] [CrossRef]
- Spencer, J. A. (2015). African American, minoritized student in school mathematics: New American or designated serf? In T. G. Bartell, K. N. Bieda, R. T. Putnam, K. Bradfield, & H. Dominguez (Eds.), Proceedings of the 37th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, East Lansing, MI, USA. Michigan State University. [Google Scholar]
- Spring, J. (2021). Deculturalization and the struggle for equality: A brief history of the education of dominated cultures in the United States (9th ed.). Routledge. [Google Scholar]
- Strauss, A. L., & Corbin, J. (1990). Basics of qualitative research. Sage. [Google Scholar]
- Tate, W. F. (1995). Returning to the root: A culturally relevant approach to mathematics pedagogy. Theory Into Practice, 34(3), 166–173. [Google Scholar] [CrossRef]
- Texas Education Agency. (2021). 2021 STAAR grade 5 mathematics test. Texas Education Agency. Available online: https://tea.texas.gov/student-assessment/staar/released-test-questions/2021-staar-5-math-test.pdf (accessed on 24 February 2025).
- Thomas, C. A., Berry, R. Q., III, & Sebastian, R. (2024). Examining the elements of culturally relevant pedagogy captured and missed in a measure of high-quality mathematics instruction. ZDM–Mathematics Education, 56, 953–964. [Google Scholar] [CrossRef]
- U.S. Department of Education, National Center for Education Statistics. (2018). Race and ethnicity of public school teachers and their students. Available online: https://nces.ed.gov/pubs2020/2020103/index.asp (accessed on 24 February 2025).
- U.S. Department of Education, National Center for Education Statistics. (2021). State nonfiscal survey of public elementary and secondary education, 1995–96 through 2019–20 and 2020–21 preliminary; and national elementary and secondary enrollment by race/ethnicity projection model, through 2030. Available online: https://nces.ed.gov/ (accessed on 24 February 2025).
- Willey, C., & Ataide Pinheiro, W. (2019). Supporting prospective urban teachers to mine and capitalize on children’s multiple mathematical knowledge bases: Community mathematical explorations. In T. G. Bartell, C. Drake, A. Roth McDuffie, J. M. Aguirre, E. E. Turner, & M. Q. Foote (Eds.), Transforming mathematics teacher education: An equity-based approach. Springer. [Google Scholar] [CrossRef]
- Wright, W. E. (2019). Foundations for teaching English language learners: Research, theory, policy, and practice (3rd ed.). Brookes Publishing. [Google Scholar]
- Yeh, C., & Rubel, L. (2020). Queering mathematics: Disrupting binary oppositions in mathematics pre-service teacher education. In N. Radakovic, & L. Jao (Eds.), Borders in mathematics pre-service teacher education (pp. 227–243). Springer. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).