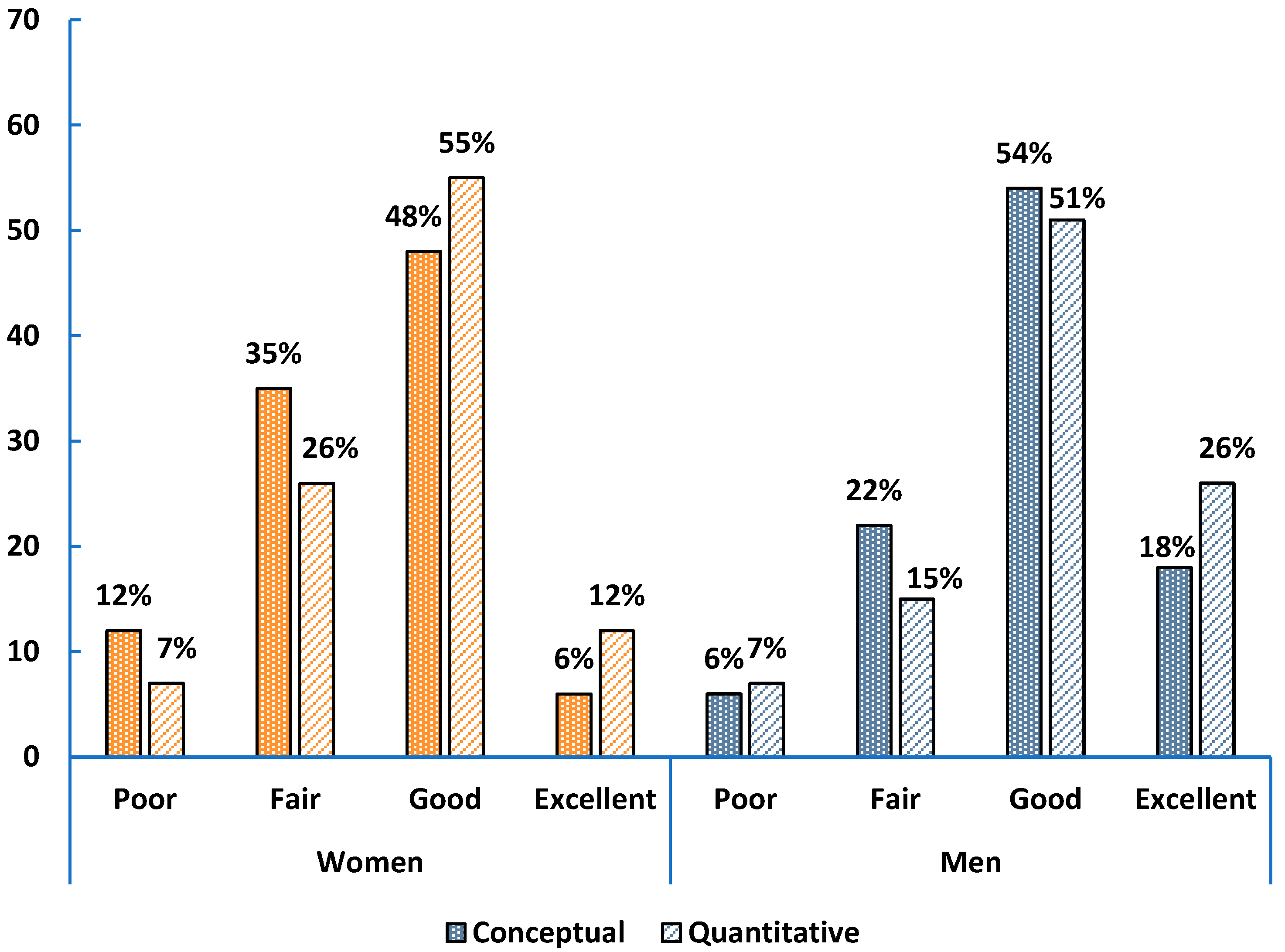4. Results
RQ1. How do introductory students define conceptual and quantitative problem-solving in physics, how do they recognize when someone is good at these, and what strategies do they recommend to peers for improving conceptual and quantitative problem-solving skills?
Introductory physics student responses were remarkably consistent across all courses and levels, indicating a shared understanding of conceptual and quantitative problem-solving in physics. Students described conceptual problem-solving skills in physics as the ability to understand and apply the underlying principles of physical phenomena without relying solely on numbers or equations. For many, it means being able to visualize what’s happening in a scenario, explain the reasoning behind formulas, and connect different concepts across contexts. Some noted that being able to teach or explain a concept to others, especially using visuals or real-world examples, was a strong indicator of conceptual mastery. One student wrote, “Conceptual problem-solving means having the capacity to describe to another person how to correctly solve a hypothetical problem and provide a real-life application. If I were able to explain how to find the volume of a sphere, without the use of values, for example, I would say I have a good conceptual understanding of that problem.” Rather than simply memorizing equations, many students at all levels emphasized the importance of understanding why those equations work and how to apply them thoughtfully in unfamiliar situations as conceptual problem-solving. For example, another student noted, “I believe that it is the ability to not just remember equations but being able to apply them to new concepts or completely different problems. I would know that I have good conceptual problem-solving skills in physics if I were able to sort of “connect-the-dots” between different concepts and be able to work through a problem that I have not seen before.”
To help peers improve their conceptual skills, students recommended a variety of strategies centered around active learning and consistent engagement with the course materials. Common tips included reading the textbook, attending office hours, watching explanatory videos, and drawing diagrams to visualize problems. Many emphasized practicing by explaining concepts aloud, redoing problems, and applying physics to real-life contexts. Many students stated that truly understanding what a question is asking and being able to break it down logically was key to success in conceptual problem-solving. Overall, they viewed conceptual problem-solving as essential not only for tackling physics problems but for building a deeper, lasting understanding of the subject.
Students defined quantitative problem-solving skills in physics as the ability to apply mathematical formulas and numerical reasoning to solve physics problems. For many, it involved identifying known and unknown values, selecting appropriate equations, and performing accurate calculations to arrive at a correct answer. One student explained, “Quantitative problem-solving skills in physics mean the ability to take what we conceptually know and apply it to numbers and equations that can help us reach an exact answer.” Several emphasized that success in this area depends not only on mathematical skills but also on understanding how equations relate to physical concepts. Some students highlighted the importance of unit analysis, equation manipulation, and deriving something or reasoning through problems even when the process was not entirely familiar while solving physics problems. Others described strong quantitative skills as being able to solve homework or test problems confidently and efficiently, even without full conceptual clarity.
To support peers struggling with quantitative skills, students at all levels overwhelmingly recommended consistent practice with the course materials in physics problem-solving. The most frequent advice included doing a variety of practice problems, reviewing mistakes, and making detailed equations or formula sheets. Many students also advised attending instructor and teaching assistant’s office hours, watching instructional videos (including YouTube channels), and studying with peers to gain different perspectives. Several stressed the importance of understanding units and variables, breaking problems into smaller steps, and staying organized with work. Overall, students viewed quantitative problem-solving as a trainable skill built through repetition, reflection, and focused use of resources.
From the responses given by students, it is quite clear that a majority of them possess a strong understanding of conceptual and quantitative problem-solving in the physics problem-solving context. Their definitions of conceptual and quantitative problem-solving, as well as the strategies they described using to improve on these, are often consistent with how many faculty typically described them (including in our interviews) in instructional and professional contexts.
RQ2. How do introductory women and men students’ self-assessed conceptual and quantitative problem-solving skills differ by gender across various levels of physics courses?
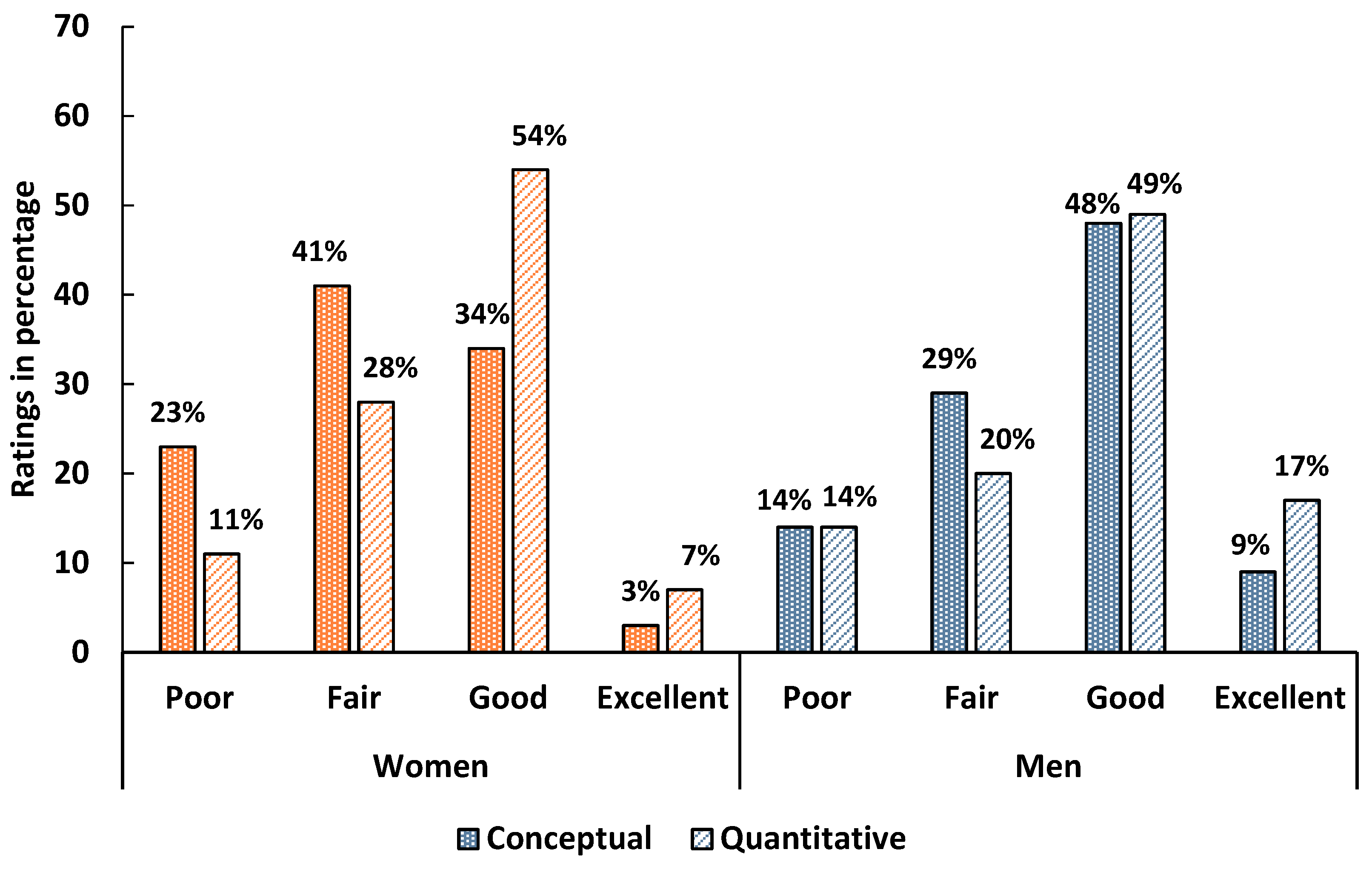
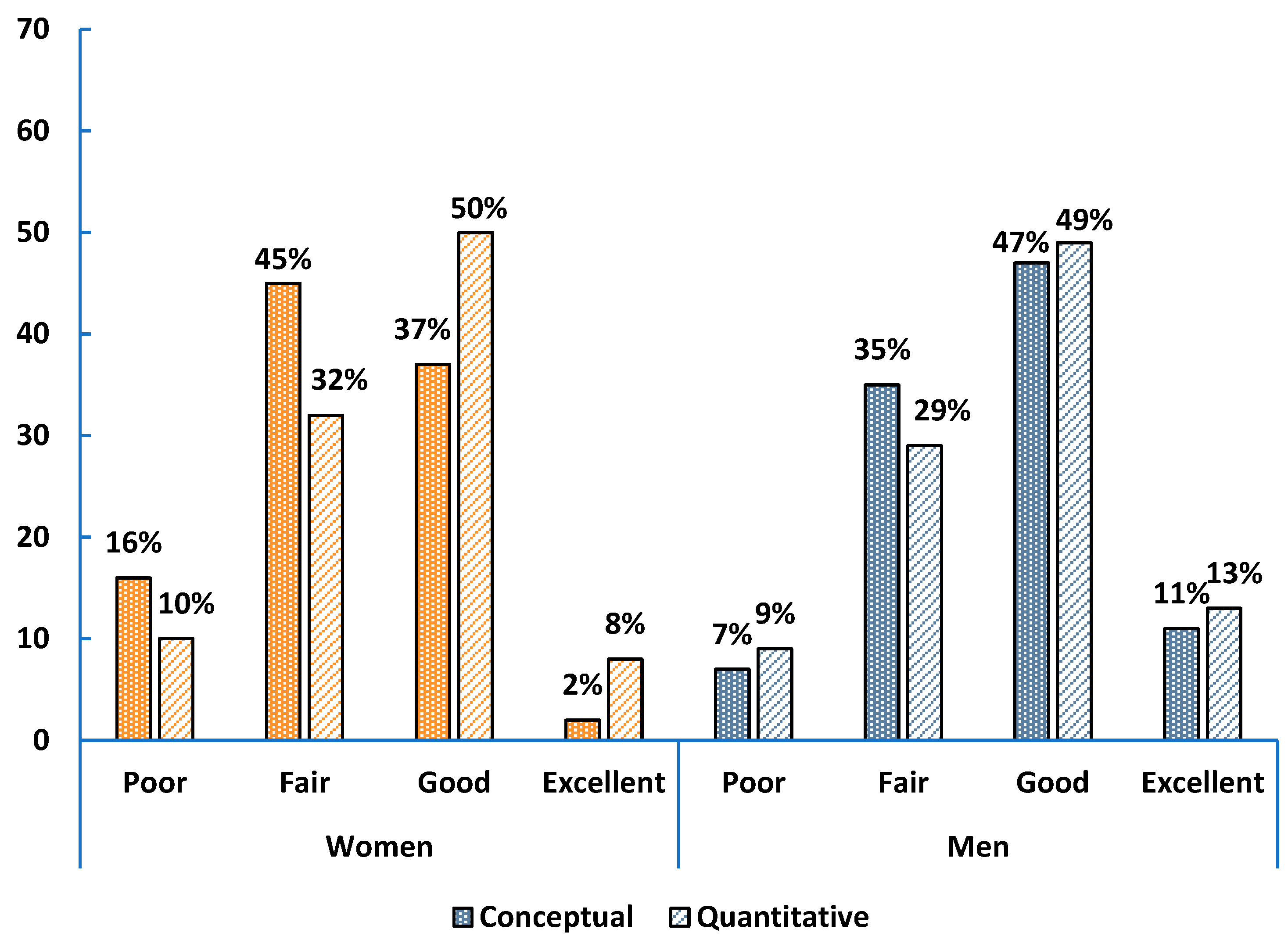
We examine how women and men self-assess their conceptual and quantitative problem-solving skills in introductory algebra-based and calculus-based physics courses, using four categories: poor, fair, good, and excellent. The graphs below show the percentage of respondents in each gender group within these categories for Physics 1 courses. The graphs for Physics 2 courses are included in
Appendix B. We present only the post-survey data here and the corresponding pre-survey data, are included in the
Appendix C. Women are represented by orange bars and men by blue bars.
As shown in
Figure 1, in algebra-based Physics 1, 43% of women and 58% of men rated their conceptual skills as good or excellent, while 60% of women and 69% of men rated their quantitative skills, similarly, showing women generally rate themselves lower. Both groups were more confident in quantitative than conceptual skills, with men increasing their quantitative self-ratings by course end compared to pre-survey (
Figure A5 in
Appendix C).
A similar pattern occurred in Physics 2 with 37% of women and 57% of men rating their conceptual skills as good or excellent, while quantitative ratings were 61% for women and 66% for men (
Figure A1 in
Appendix B), indicating a smaller gender gap in quantitative skills. Women more often chose “Good” and men “Excellent.” Both genders remained more confident in quantitative than conceptual skills, though conceptual self-ratings dropped 15–17% by the end of the course compared to pre-survey (
Figure A6 in
Appendix C), highlighting decreased confidence in this area.
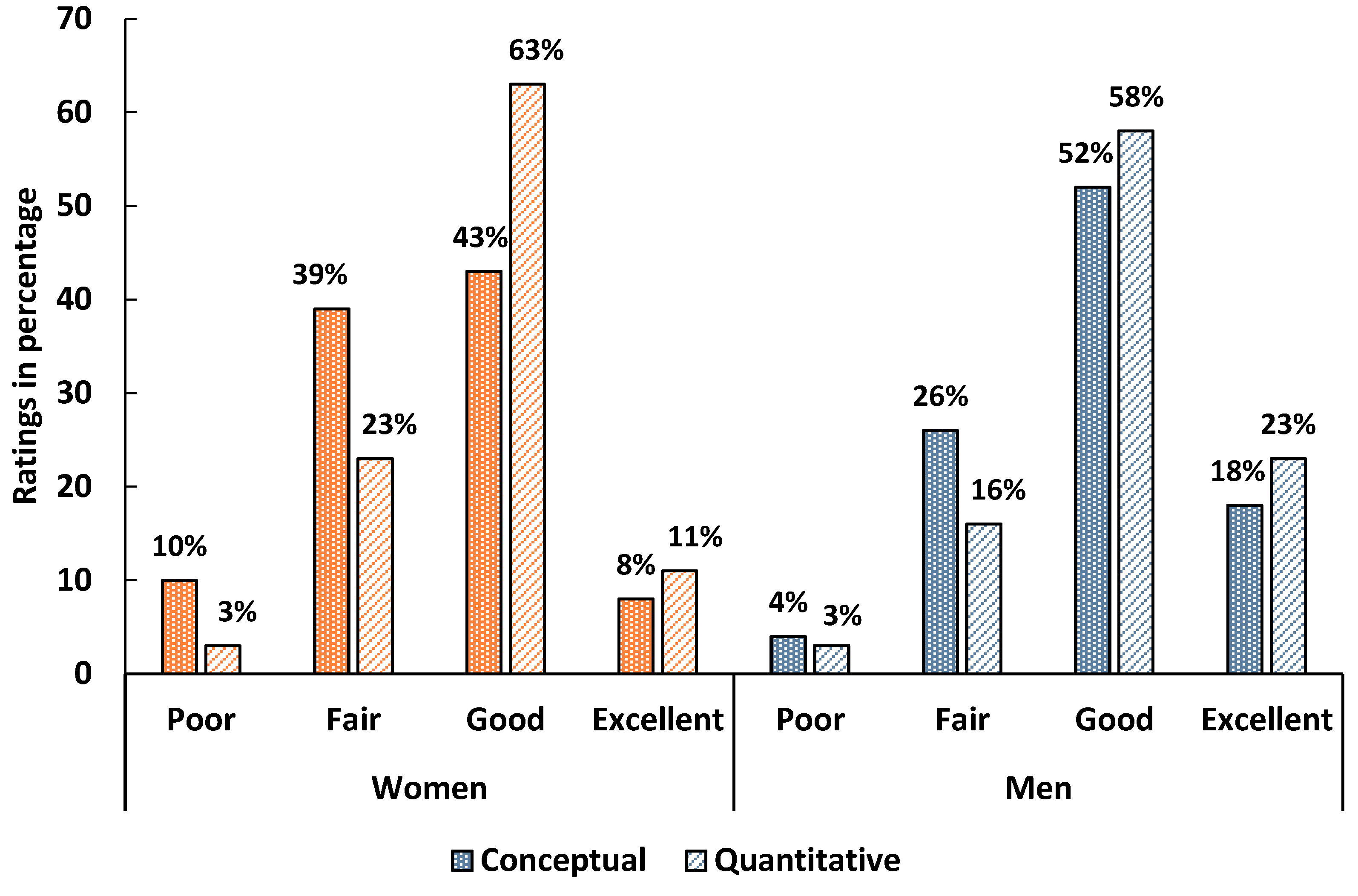
In calculus-based Physics 1, 49% of women and 68% of men rated their conceptual skills as good or excellent, while 61% of women and 74% of men did so for quantitative skills (
Figure 2). Men showed particularly high confidence in quantitative abilities, both relative to women and to men in algebra-based courses. Women’s quantitative self-ratings declined from 68% to 61% by course end, indicating a drop in confidence compared to the pre-survey (
Figure A7 in
Appendix C).
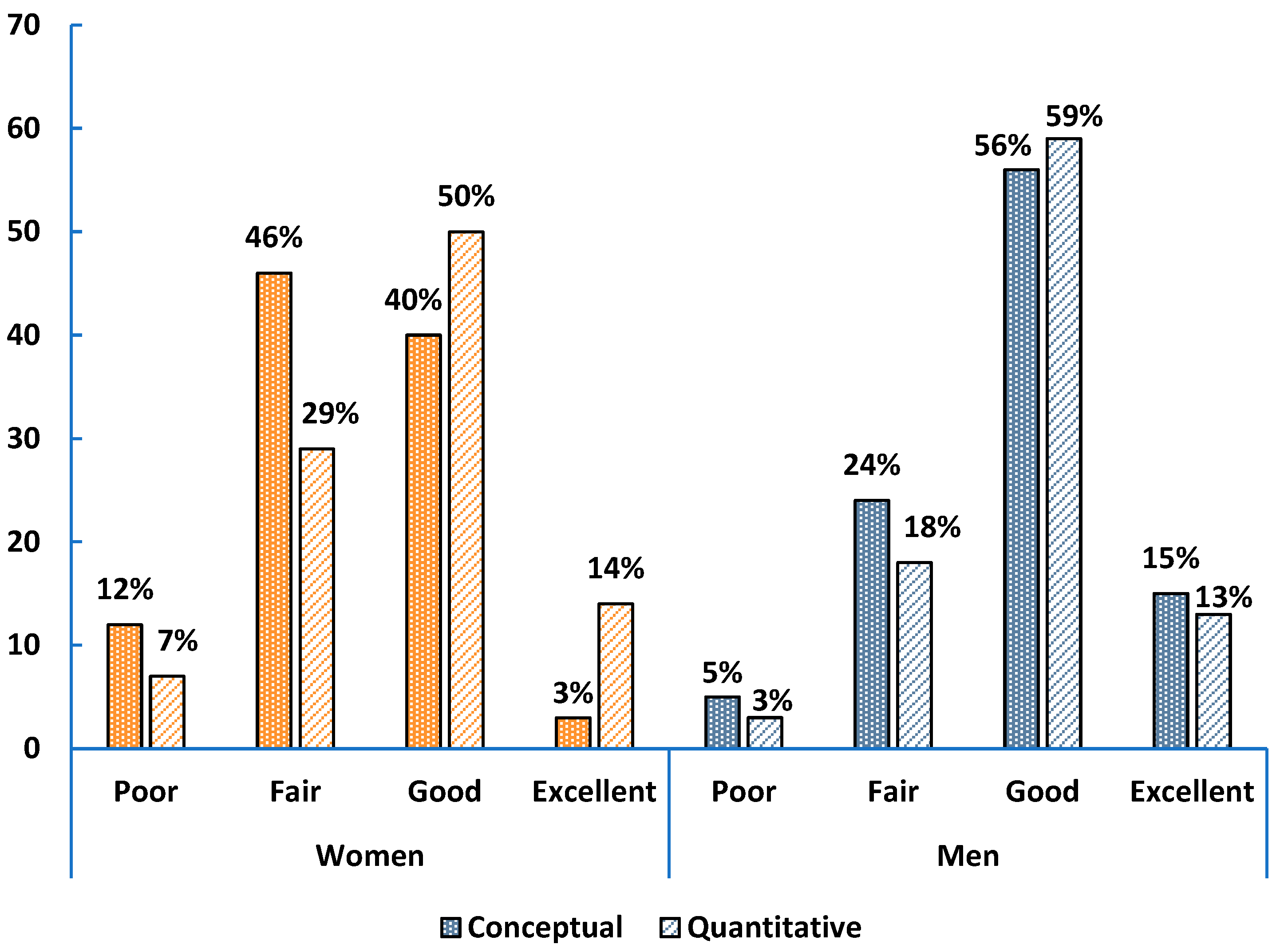
In calculus-based Physics 2, 51% of women and 70% of men rated their conceptual skills as good or excellent, while 74% of women and 81% of men did so for quantitative skills (
Figure A2 in
Appendix B). Women showed a clear gap between conceptual and quantitative self-ratings. Both genders reported higher confidence in quantitative skills than in other introductory courses, with nearly a 10% increase from the pre-survey (
Figure A8 in
Appendix C). Women’s conceptual ratings rose slightly, while men showed no notable change.
Overall trends across algebra and calculus-based courses show men consistently rated both skill types higher than women, with slightly higher conceptual ratings in calculus-based courses. Effect sizes along with 95% CI (shown as min and max value in
Table 6) indicate women rated their skills lower than men, with gender differences in conceptual skills statistically significant in both pre- and post-survey for all introductory courses. For quantitative skills, the gender gap was statistically significant in pre-survey for all courses. Similar results were observed for post-survey in all courses except algebra-based Physics 2. The emphasis on algorithmic problem solving over conceptual reasoning in graded work may contribute to lower self-efficacy in conceptual skills, especially in women.
RQ3. To what extent do upper-level undergraduates and graduate students’ self-assessments of conceptual and quantitative problem-solving skills change from the beginning to the end of the course, and how does this vary across course levels?
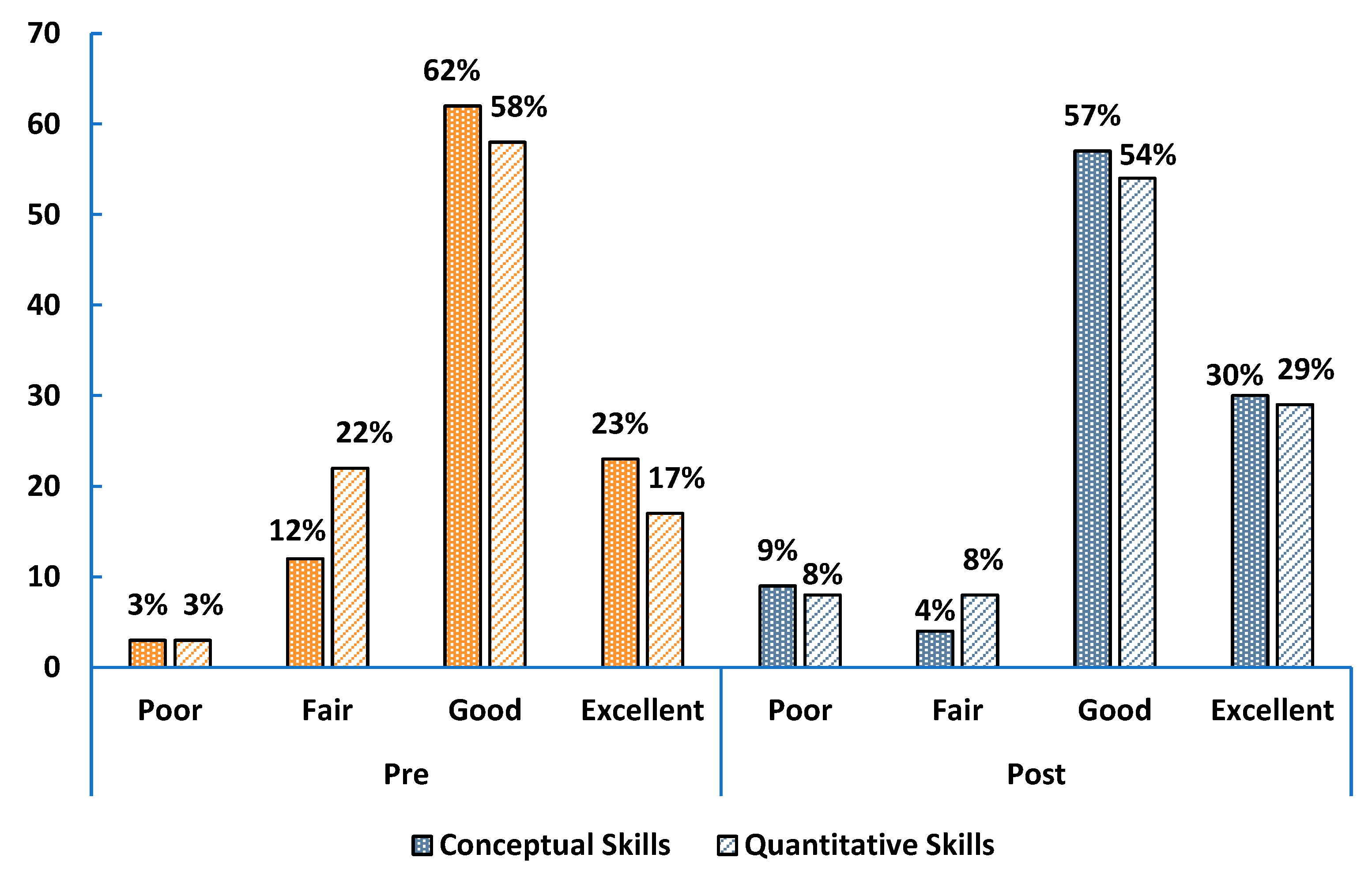
We examined student self-assessment ratings in upper-level undergraduate and graduate courses. The pre-survey is represented by orange bars and post survey by blue bars. Due to the small sample size, we did not separate responses by gender for these levels. In upper-level courses, 73% of students rated their conceptual skills as good or excellent in the pre-survey comparable to 71% in the post-survey (see
Figure 3). For quantitative skills, we see a similar trend as 71% of the students in the pre-survey and 70% in the post-survey rated their skills as good or excellent as observed in
Figure 3. Thus, no significant differences were observed in students’ ratings from the beginning to the end of the upper-level undergraduate courses. Notably, unlike in the introductory physics courses, we also did not find significant differences between the ratings of conceptual and quantitative skills.
For graduate students, 85% rated their conceptual skills as good or excellent in the pre-survey and 87% in the post-survey, while quantitative ratings rose from 75% to 83% (
Figure 4). Conceptual skills were consistently rated higher than quantitative skills. This may reflect graduate students’ independent, reflective approach, integrating physics and math beyond assignments or instructor guidance, which likely supports stronger conceptual self-assessments compared to introductory students.
Table 7 shows effect sizes with 95% CI results comparing pre- and post-survey self-ratings for upper-level undergraduates and graduate students. The smaller graduate sample should be noted. No statistically significant changes were observed in either conceptual or quantitative skills, suggesting that advanced students may have stable self-perceptions that are less influenced by short-term instructional experiences.
RQ4. How do women and men students’ preferences for instructional emphasis (conceptual vs. quantitative) compare with their perceptions of what their instructors emphasize and what the course actually emphasizes across different levels of physics courses at the beginning and end of the semester?
We surveyed students across introductory algebra-based and calculus-based physics courses, upper-level undergraduate courses, and graduate-level courses. Overall, the trends observed across these course levels were fairly consistent. Our focus was on understanding gender-based differences in how students, particularly women and men, hoped their courses would enhance their conceptual vs. quantitative problem-solving skills. In the pre-survey, students were asked what they wanted the course to improve, what they believed their instructors prioritized, and what they expected would actually happen. These questions were framed in the past tense for the post-survey to reflect their experience after completing the course.
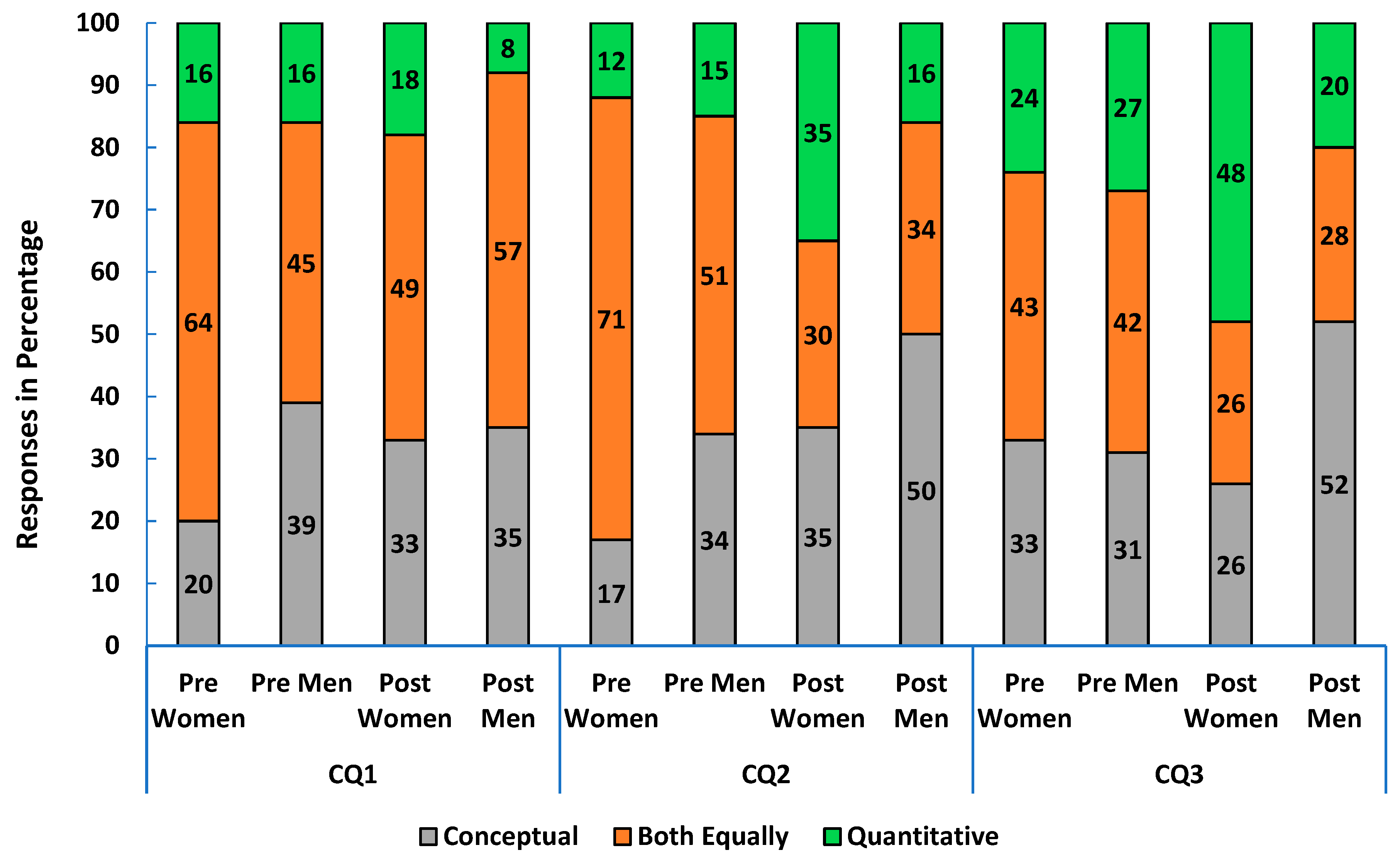
In algebra-based physics 1, most students wanted the course to balance conceptual and quantitative emphasis or strengthen conceptual skills. Over 70% of both women and men expected their instructor to favor this balance in the pre-survey. By course end, many students, especially women (38% vs. 30% of men) felt the course focused more on quantitative skills (CQ3 in
Figure 5).
In algebra-based physics 2, nearly half of students desired a balanced emphasis, with over 65% expecting the instructor to do the same in the pre-survey. By the end, 42% of women and 29% of men reported the course improved quantitative skills more (CQ3,
Figure A3 in
Appendix B).
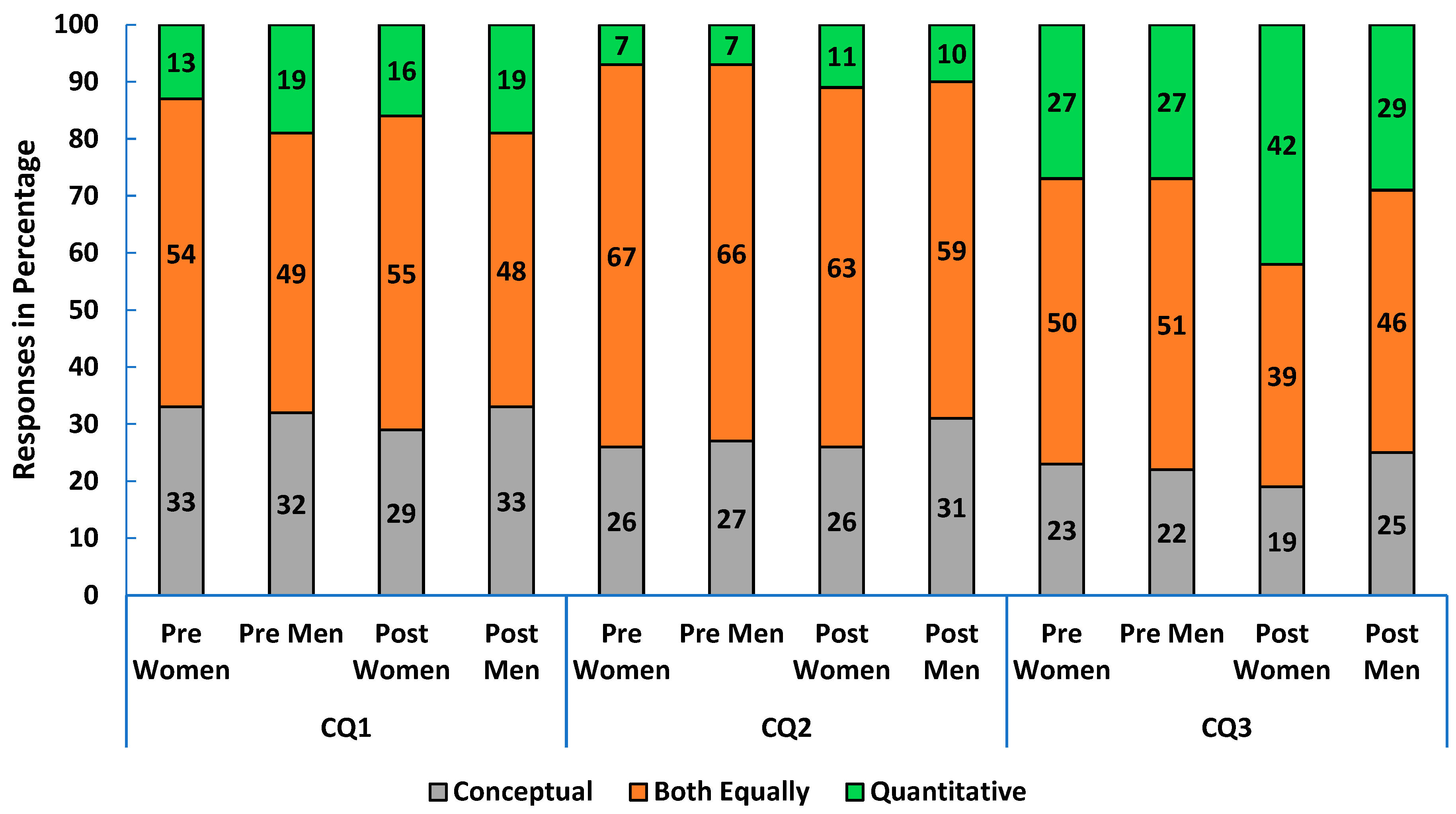
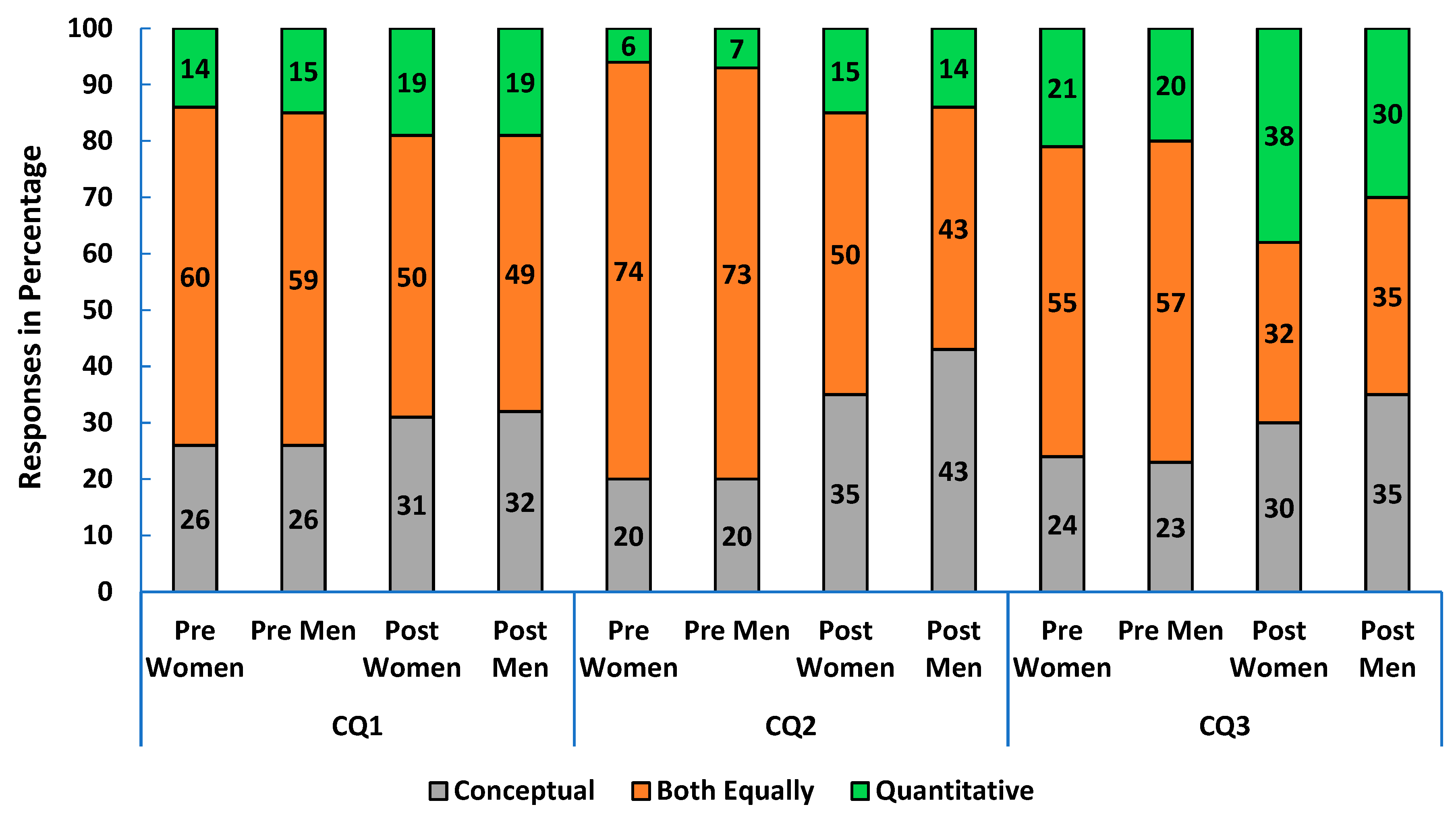
Similarly, in calculus-based physics 1, about 60% of the women and men expressed that they wanted the course to have a balance between conceptual and quantitative skills in the pre survey (CQ1 in
Figure 6). Over 70% of both women and men believed the instructor also would prefer a balance between conceptual and quantitative skills in the pre-survey (CQ2 in
Figure 6). By the end of the course, 39% of women and 28% of men reported that the course improved their quantitative skills more (CQ3 in
Figure 6).
In calculus-based physics 2, almost half of the women and men expressed that they wanted the course to have a balance between conceptual and quantitative skills (CQ1,
Figure A4 in
Appendix B). About 65% of both women and men believed the instructor also would prefer a balance between conceptual and quantitative skills in the pre-survey (CQ2,
Figure A4 in
Appendix B). By the end of the course, 39% of women and 33% of men reported that the course improved their quantitative skills more (CQ3,
Figure A4 in
Appendix B). These results suggest that regardless of whether students were enrolled in algebra-based or calculus-based courses, both women and men tended to feel that the course improved quantitative skills more than conceptual understanding.
We observed similar trends among upper-level undergraduates and graduate students. In upper-level undergraduate courses, 48% of women and 20% of men felt that the course improved their quantitative skills more in the post survey (CQ3 in
Figure 7), while in graduate courses, 22% of women and 15% of men reported the same (CQ3 in
Figure 8).
When asked about their instructors’ priorities, only 10–15% of students in introductory courses believed the focus was primarily on quantitative skills. In contrast, 35% of women in upper-level undergraduate courses perceived a quantitative emphasis in the post-survey by the instructor (CQ2 in
Figure 7). One might expect this percentage to align with what students felt actually happened in the course, but the responses suggest a disconnect. To better understand this discrepancy, we included open-ended follow-up prompts in the survey asking students to explain the reasoning behind each of their answers. This helped us capture nuanced insights into how students interpreted instructional emphasis relative to their expectations and experiences.
The reasonings reveal a noticeable gap between instructors’ intentions and students’ actual experiences in learning physics problem-solving skills. Many students believed that their instructors aimed to prioritize conceptual understanding, often using demonstrations, discussions, and conceptual questions. As one student noted, “Our teacher keeps emphasizing that we need to know the why behind things.” However, students’ reflections show that their quantitative skills often improved more than their conceptual skills. This was largely due to the structure of the assignments and exams, which leaned heavily on practice problems with a quantitative focus. For example, a student remarked, “I feel like I can get problems right with math and still not understand the concepts behind it.” Others noted that while conceptual ideas were discussed, they were either rushed or confusing, leading some to default on memorizing formulas for the kinds of problems they would be graded on. One student noted, “Demonstrations in class have helped with conceptual problem solving, but the homework and recitations are heavily based on math problems.” Another shared, “While I did gain a better understanding of the concepts, I think this course improved my quantitative problem-solving skills more. There were a lot of practice problems, worksheets, and homework sets that focused on applying formulas, solving for unknowns, and interpreting numerical results. Over time, I became more confident in working through multi-step problems and using math as a tool to support my understanding of physics. The repetition and feedback really helped me grow in that area.” These responses suggest that while instructors may have aimed to foster conceptual growth, students often gained more from the quantitatively driven aspects of the course. The difference lies in intent versus implementation: the teaching emphasized concepts, but assessment and practice prioritized equations and calculations. Thus, the students’ learning outcomes were often skewed toward quantitative proficiency due to the nature of homework, recitations, and personal study habits. This highlights a pedagogical tension between instructional goals and student learning experiences.
RQ5. How do faculty members perceive the alignment between students’ instructional preferences, their own teaching goals, actual course implementation, and assessment focus in physics courses pertaining to conceptual and quantitative problem-solving?
Faculty members who were interviewed in the study broadly agreed that conceptual and quantitative problem-solving in physics are inseparable, each enhancing the other. Conceptual reasoning allows students to interpret and frame physics problems, while quantitative aspects help carry those ideas through to a solution. As one faculty member put it, “You need skills doing both as you get harder and harder problems…if you only do conceptual, no quantitative, you’re kind of a bit restricted to certain qualitative aspects.” Another instructor emphasized that quantitative problem-solving without conceptual grounding is ineffective: “Quantitative can’t stand alone. I can’t imagine teaching a purely quantitative physics class with no concepts—it wouldn’t be successful.” Despite this agreement, faculty members acknowledged that the balance between the two depends heavily on the course level and student background.
At the introductory level, faculty often attempted to prioritize conceptual understanding because many students lack mathematical maturity for advanced quantitative reasoning. One instructor noted, “You can do a lot more with conceptual at the introductory level than you can with quantitative. Students don’t have the math background, so quantitative often turns into plug and chug.” Yet despite this intent, many courses still leaned heavily on quantitative assessments, which can lead students to focus on what earns points rather than what deepens understanding. As one instructor explained, “Students are driven by what is emphasized in exams…if a course emphasizes quantitative aspects, students will lean toward that, and vice versa.” Instructors also explained that student motivation varies by course type: “For students in the algebra-based classes, who are often pre-med, they are likely focused on quantitative problem solving to do well on the MCATs. For the calculus-based classes, which usually consist of engineering and other STEM majors, I think they might prioritize understanding concepts more, as they see physics as a class they need to get through.” Another instructor pointed out, “In algebra-based courses, the students don’t give a damn about physics. They just want to get an A. In the engineering courses, the students don’t give a damn about physics. They just want to get a C. But both of them [algebra-based and calculus-based introductory physics students] are more into plug and chug than the concepts. They want whatever is going to be the easiest way for them to satisfy this requirement.” However, our student survey data from these courses do not support this assumption. In fact, we find little difference between these two groups of students in how they perceived or valued conceptual and quantitative problem-solving skills. Regardless of course type, students overwhelmingly expressed a desire for a balanced approach, indicating a disconnect between faculty expectations and student perspectives.
Table 8 presents the number of faculty members who described what a typical student wants, what they themselves aim for, and what actually happens across all three levels, alongside the corresponding percentages of women and men who responded to the same items.
In upper-level physics courses, especially for majors, some faculty stated that they observe a shift in student motivation and maturity, and students begin to see the need for both skill sets and are more capable of integrating them. One instructor stated, “Physics majors are very interested in understanding the concepts behind the problem solving…they also want to achieve the problem solving because they know physics builds on itself.” Still, challenges remain. Another instructor observed that even at this level, “Students are usually better at the math…when they have trouble, it’s often because they don’t know where to start conceptually.” Faculty often stressed that upper-level courses should help students solidify conceptual foundations from earlier coursework and use them to tackle increasingly sophisticated quantitative challenges.
At the graduate level, the dynamic shifts again. Some interviewed faculty claimed that the graduate students tend to prioritize quantitative mastery, sometimes under the assumption that their conceptual understanding is already solid. For example, one instructor noted, “The students are more interested in the quantitative stuff at the graduate level because they think they already have the concepts down although it’s not clear what they really understand.” However, faculty often emphasized that advanced problem-solving requires embedded conceptual reasoning. For example, another instructor remarked, “I don’t think any students come away saying they’re better at quantitative problem-solving after a grad class…mostly conceptual or nothing at all.” Problems at this level demand understanding of approximations, modeling choices, and limits, all of which are deeply conceptual in nature, even if embedded within complex calculations. While some instructors stated that students shift focus from quantitative (introductory level) to conceptual (upper level) and back to quantitative (graduate), our cross-sectional student data does not support this trajectory. Instead, based upon our results discussed in the preceding sections, students across all levels consistently valued both skills and sought a balanced approach to learning and problem-solving in physics.
Some instructors also expressed skepticism about whether students understand what conceptual and quantitative problem-solving means. One instructor remarked, “What they call conceptual or quantitative may not be the same thing that I would call conceptual or quantitative.” Yet, our survey results contradict this assumption, and students consistently provided clear and accurate descriptions of these. As noted, they typically defined conceptual problem-solving as understanding and applying physical principles without relying on formulas, and quantitative problem-solving as using equations, calculations, and numerical reasoning to reach a solution. This type of consistent response from students suggests that the faculty’s doubts may reflect a misalignment between instructors’ perceptions and students’ actual understanding.
When discussing the focus of their assessments, instructors acknowledged that introductory physics assessments may often be seen by students as heavily quantitative, though they themselves aim for a more balanced approach. As one instructor noted, “My students would say it was quantitative, but I would say it’s a balance.” They explained that while most problems have numerical or symbolic answers, solving them still requires conceptual understanding. “To solve the quantitative questions, the students need to know the concepts…I don’t think you can strip those out and create a physics exam that’s just quantitative, unless it was like purely plug and chug.” In other words, even when assessments appeared to focus primarily on quantitative problem-solving to students, some interviewed instructors claimed that deep understanding of the underlying physics concepts is essential to solve them.
Another instructor mentioned that the complexity and structure of assessment tasks evolve significantly from introductory to graduate levels. At the introductory level, “most of the problems we give to students require basically one major problem-solving step,” which tends to fall neatly into either conceptual multiple-choice questions or straightforward quantitative problems. However, at the graduate level, assessments demand a more integrated and nuanced approach. “You’re not asking these simple multiple-choice questions…the conceptual understanding needs to be weaved into a more complex problem.” Some interviewed instructors stated that they expected students to evaluate methods, make valid approximations, and determine which terms to include, activities that reflect high-level conceptual thinking even when embedded in quantitative work. For example, one instructor noted, “I try to put those [conceptual] things into the problem…and not have a focus on solving integrals or differential equations. That’s not the main part.”
Despite these goals, interviewed instructors often felt restricted in how they design assessments, especially in large introductory courses since different instructors must be consistent across different sections of the same course. One instructor shared, “I don’t feel as though that’s necessarily representative of my preferences…there are conventions to assess our students in as uniform a manner as possible across different sections.” This pressure to align, e.g., with other colleagues’ exam styles, often emphasizing quantitative problem-solving, can limit their ability to incorporate conceptual problem-solving as freely as they’d like. “We end up being a little bit in lock…the prevailing point of view values more of quantitative problem-solving over conceptual understanding.” These institutional constraints highlight a tension between instructors’ pedagogical intentions and the standardized assessment practices that dominate many large introductory physics courses.
In conclusion, most faculty members who were interviewed recognized the importance of nurturing both conceptual and quantitative proficiency to develop expertise in physics problem-solving. However, the balance between them is often distorted by assessment norms and course structure. Some instructors acknowledged that students’ motivation to engage with conceptual or quantitative problem-solving in physics is heavily shaped by external factors, particularly what is emphasized in assignments and exams, and ultimately, what earns them points. As a result, it is not enough for instructors to state that conceptual understanding is important or to focus on it in lectures if this is not clearly reflected in the way assignments and assessments are designed to evaluate student learning. Our analysis further suggests that students often report greater improvement in their quantitative problem-solving skills by the end of a course, largely because these are the skills they repeatedly practice through homework and exams. This indicates that students understand the importance of conceptual problem-solving in physics, but they simply follow the cues that instructors and course structures provide. Therefore, faculty members must take greater responsibility for aligning their assessment practices with their instructional goals. The challenge for instructors is to design learning experiences and evaluations that reflect the true nature of physics as a discipline which demands integration of physics and math, and conceptual and quantitative problem-solving are two sides of the same coin. Thus, providing students with meaningful opportunities to develop expertise in physics problem-solving and demonstrate reasoning and learning that integrates physics and mathematics is critical.