When Support Hides Progress: Insights from a Physics Tutorial on Solving Laplace’s Equation Using Separation of Variables in Cartesian Coordinates
Abstract
1. Introduction
2. Literature Review and Framework
2.1. Integration of Mathematics and Physics in Physics Problem-Solving
2.2. Prior Investigations on Student Understanding in the Context of E&M
2.3. Student Understanding of Laplace’s Equation
2.4. Scaffolding While Problem-Solving and Zone of Proximal Development
2.5. Instructor Framing and Student Engagement
3. Methodology
3.1. Tutorial Development and Validation
3.2. Pre-/Posttests and Learning Objectives of the Tutorial
3.3. Interview Details
3.4. Course Implementation and Instructor Details
3.5. Data Analysis
4. Results and Discussion
4.1. Student Difficulties and How the Tutorial Addresses Them
4.1.1. Difficulty in Recognizing That Laplace’s Equation Applies for a Given Problem
Sarah: We can use Laplace’s equation for all three situations mentioned in Q1 (problem given in the tutorial). Although in option I (a point charge present near a grounded conducting plane), the method of images could be an effective method, solving Laplace’s equation to find the potential could also be an effective approach.
John: I disagree. Laplace’s equation is only applicable in situations where there is no charge density present within the region. Since for situations I and III (a thin disc with a uniform charge distributed on it) of Q1, there is non-zero charge density present in the region where we want to solve for the potential, we cannot use Laplace’s equation.
Checkpoints:
4.1.2. Difficulty in Using the Method of Separation of Variables and Finding Separation Constants
Emily: The equation can be broken down further into and (where and c are constants and ) using an argument similar to the one we used to separate the z variable. This way we would obtain three ordinary differential equations or ODEs for each variable x, y, and z.
Use separation of variables in the Cartesian coordinates to find the solutions of Laplace’s equation in the form . Obtain three different ODEs, one each for . Explain any pertinent steps. (Note that the separable solutions in this problem are different from the previous problem you solved).
4.1.3. Difficulties with Boundary Conditions
Let’s write down the boundary conditions for this problem mathematically.
- (a)
- (b)
- (c)
- (d)
- (e)
Answer the following questions:
- (a)
- (b)
John: I still don’t understand why a positive sign in front of the constant for the differential equation involving the function and a negative sign in front of the constant for the differential equation involving the function would not work.
Emily: In this problem, consistent with the boundary condition, involving the x coordinate must decay to zero far away from the plane, i.e., as . That means the solution involving the coordinate must involve the decaying exponential function. This means we must choose a positive sign in front of the constant for the differential equation involving the function
Sarah: I agree with Emily. Boundary conditions require to have at least two zeros, and only the oscillatory functions can satisfy these boundary conditions out of the given choices of solution. Therefore, we should choose a negative sign in front of the constant for the differential equation involving the function .
4.1.4. Difficulty in Finding General and Unique Solutions
Circle all the correct answers regarding the form of the general solution for Laplace’s equation obtained using linear superposition of separable solutions (which were found by imposing some of the boundary conditions to obtain the separation constants):
- I.
- II.
- III.
John: is the unique solution for the potential in the channel for the given problem, where .
Emily: I disagree. Since is dependent on n, , , or etc., can all be solutions of Laplace’s equation if takes the value , or , respectively. A linear combination of these solutions with n = 1, 2… is a general solution for Laplace’s equation with the boundary conditions used so far to obtain the separable solutions.
Sarah: I agree with Emily. The integer in can take any integer value from 1 to . Therefore, each of these separable solutions obtained can be written as . The general solution can be written as a linear combination of these separable solutions, . “General solution” means that this series solution applies to a family of boundary value problems which all satisfy the boundary conditions already applied but with one boundary condition yet to be applied.
Emily: I agree with Sarah! We can then obtain the unique solution of Laplace’s equation, which is the potential in the channel, when we find the coefficients in the linear superposition of separable solutions using the Fourier trick exploiting the remaining boundary condition.
4.1.5. Difficulty in Finding the Expansion Coefficients
John: We are completely done finding the unique solution for Laplace’s equation with the potential .
Emily: I disagree. We still must find the coefficients . We should use our remaining boundary condition (5a) at and Fourier’s trick to solve for the coefficients .
4.1.6. Student Engagement with Visual Representations Aids in Problem-Solving
“Draw a figure of this situation using the coordinate system you chose in the previous problem. Place the semi-infinite grounded conducting sides at and . Indicate the known potentials on the three sides of the channel (draw a 2D figure instead of a 3D figure).”
“Make a sketch of equipotential surfaces and electric field lines within the slot. You can do this using conceptual reasoning. Is the analytic solution for the potential expressed as an infinite series helpful in making the sketch?Hint: Electric field lines intersect at the boundaries of a conductor perpendicularly.Equipotential surfaces are perpendicular to the electric field lines.”
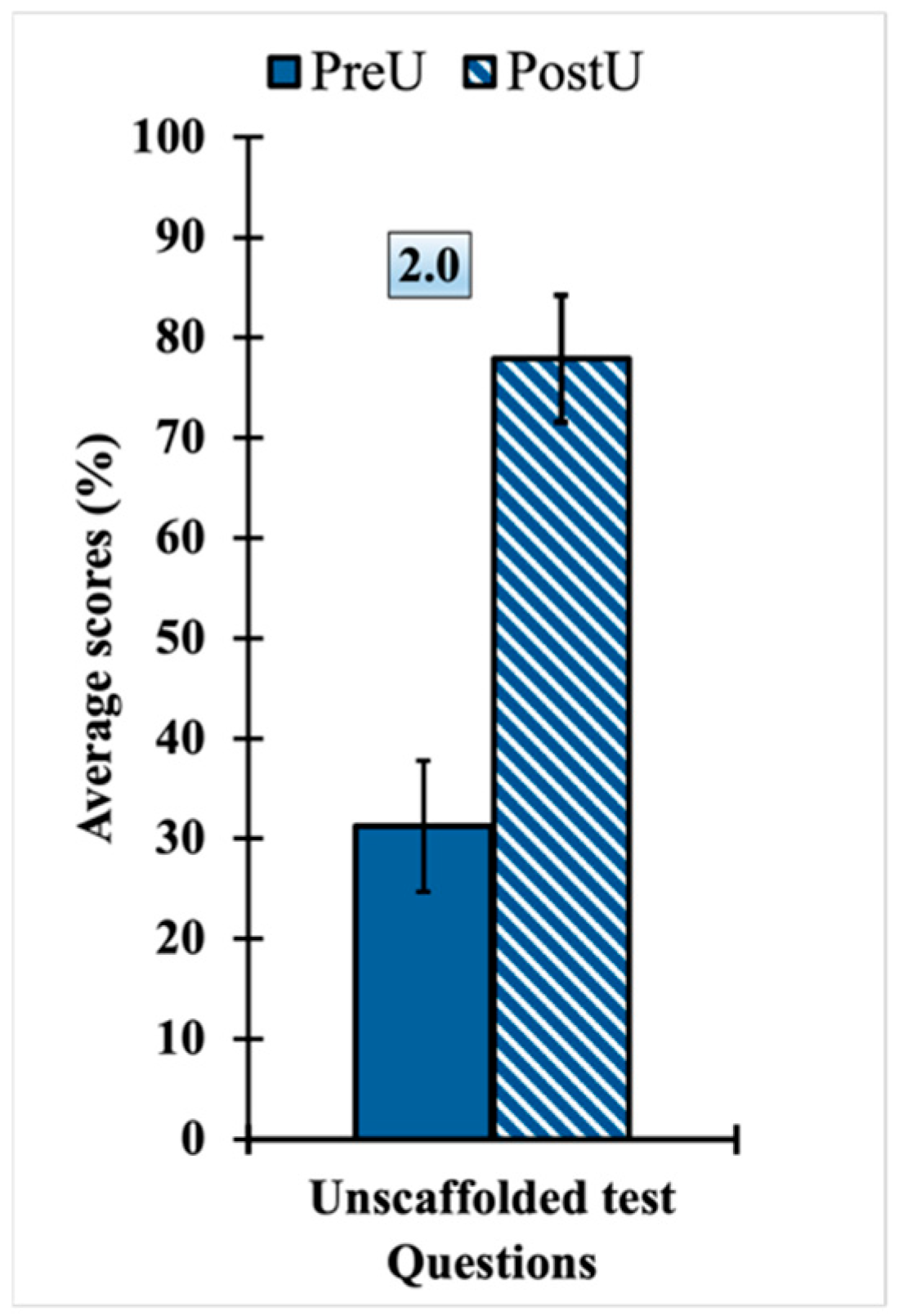
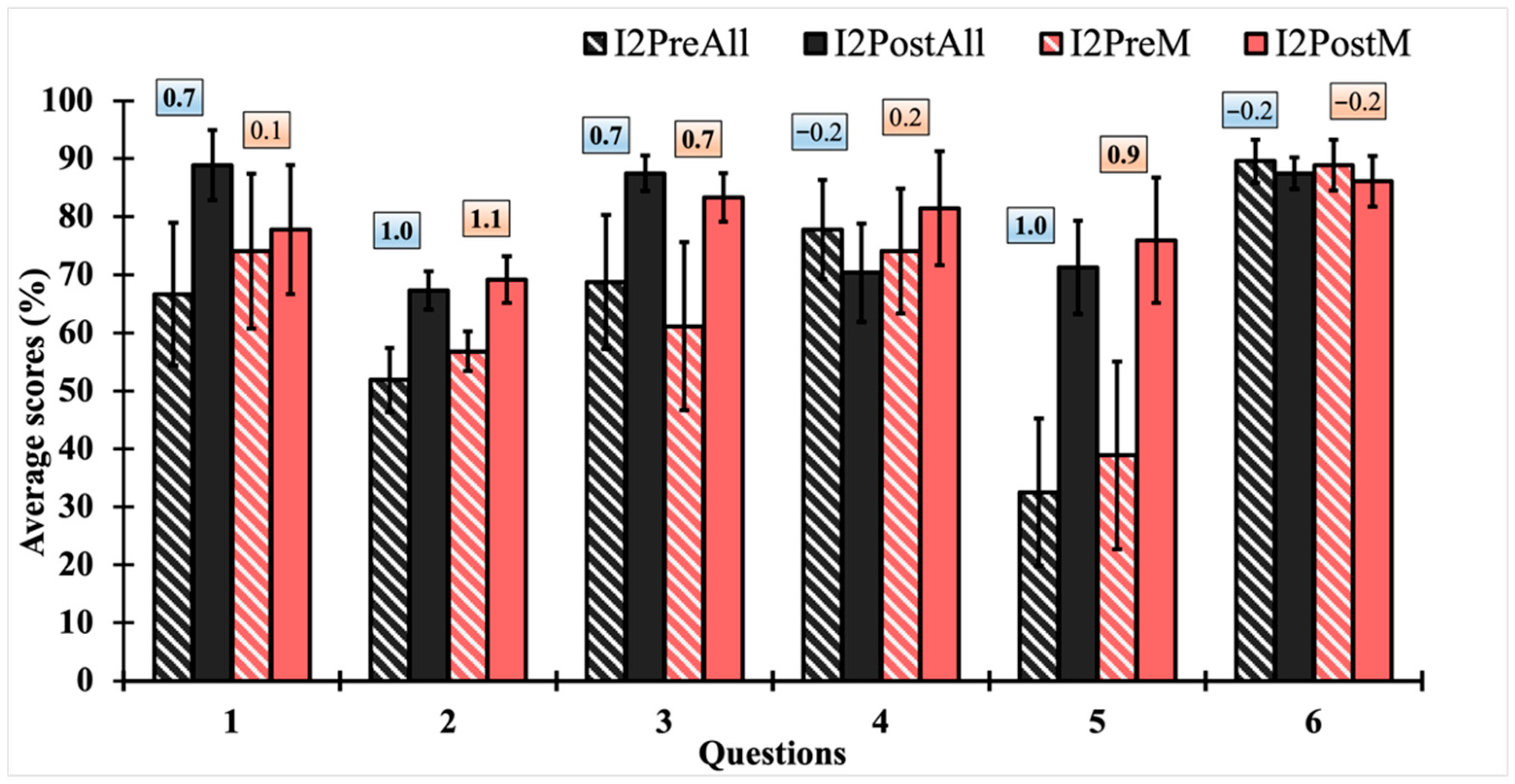
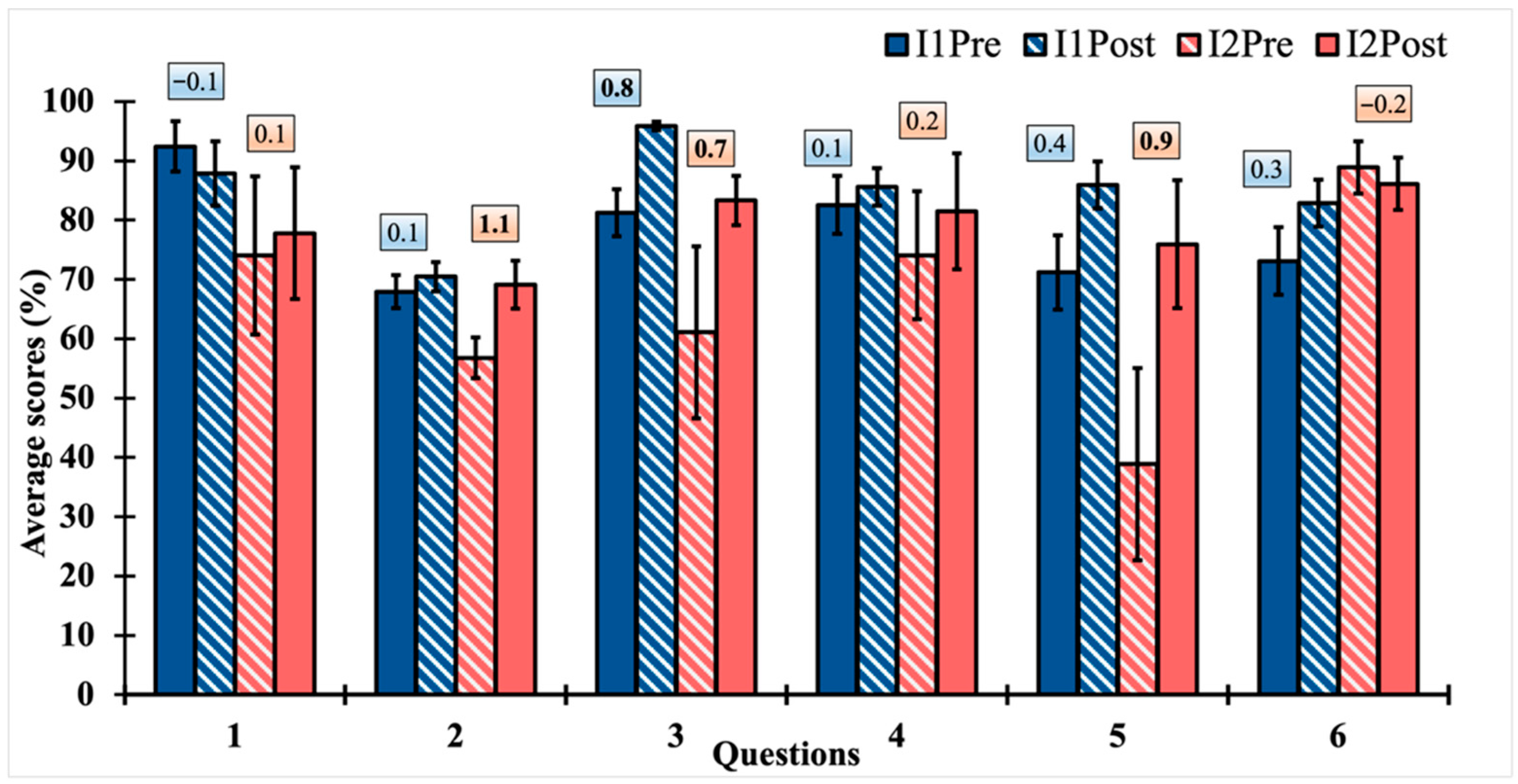
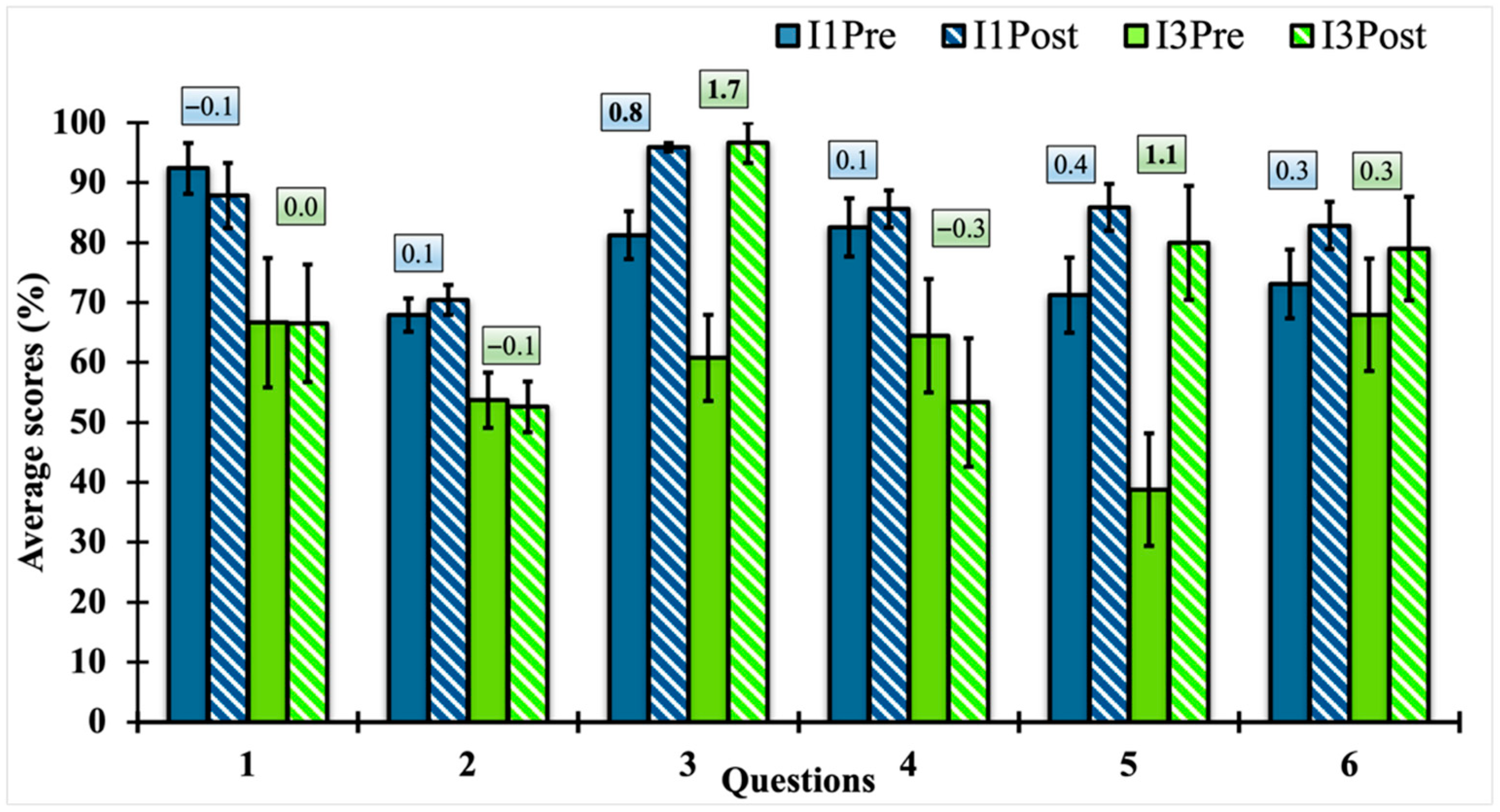
4.2. Results from Classroom Implementation
4.3. Reflection on the Scaffolding Paradox in Assessment
4.4. Reflection on the Impact of Instructor Framing on Student Engagement
5. Broader Discussion
6. Instructional Implications
7. Limitations and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Pretest
- For which of the following situations is solving Laplace’s equation, , an appropriate and effective method for finding the potential V? (Circle correct choice/choices) Explain your reasoning.
- A point charge q is located a distance d above a grounded conducting plane. We want to find the potential at any point in space.
- A uniformly charged spherical volume with radius a and total charge Q, enclosed within a concentric grounded conducting spherical shell, inner radius , carrying charge . We want to find the potential for .
- A channel with semi-infinite conducting sides. These two sides are grounded and coincide with the planes and . They are connected in the plane by a conducting sheet of width a held at potential (There is a thin insulating layer at each corner so that the conductors do not touch). We want to find the potential within the channel.
- Briefly explain the method of separation of variables applied to solve a partial differential equation such as Laplace’s equation.
- Consider the following boundary value problem: A channel consists of two parallel grounded conducting sides coinciding with the planes and . The channel is in the region and is bounded at with the surface set with the linear potential profile between the conducting sides, where is a constant. Find the potential within the slot.
- (a)
- Write down the boundary conditions for this problem.
- (b)
- This problem can be solved by the method of separation of variables. Which of the following choices are the orthogonal functions (in the variable ) which can be superposed to find the solution? In all cases, n is a positive integer.
- (c)
- Write down the general solution for the potential as a linear superposition of separable solutions.
- (d)
- According to the Fourier trick, applied to the boundary condition at on the general solution, the expansion coefficients for this problem are given byEvaluate the integral to obtain a simplified expression for the coefficients [Hint: Use integration by parts].Note: Substitution of the expression for the coefficients into the general solution gives the unique solution which represents the electric potential in the region of interest for the given boundary conditions.
Appendix A.2. Rubrics
| Pretest | ||
| Question | Deduction % | Explanation |
| Q1 | Correct. | |
| Incorrect choice or no attempt. | ||
| Circled both the correct choice and one incorrect choice. | ||
| Q2 | Correct. | |
| No mention of use of boundary conditions. | ||
| No mention of the use of the Fourier trick to obtain the coefficients in series expansion. | ||
| No mention of separation constants. | ||
| No mention of separation constants summing to zero. | ||
| No mention of attempt to solve by writing the solution as the product of functions in each of the variables. | ||
| No mention of converting the partial differential equation to a set of ordinary differential equations. | ||
| No attempt. | ||
| Q3 | Correct. | |
| Missing or incorrect boundary condition for . | ||
| All four boundary conditions are either incorrect or missing. | ||
| Three boundary conditions are either incorrect or missing. | ||
| Missing or incorrect boundary condition at . | ||
| Q4 | Correct. | |
| Correct choice plus two incorrect choices. | ||
| Correct choice plus one incorrect choice. | ||
| Incorrect choice. | ||
| Q5 | Correct. | |
| Incorrect or no answer. | ||
| Answer is not dimensionally correct. | ||
| Miscellaneous deduction. | ||
| Q6 | Correct. | |
| Did not write down the expression for integrand correctly. | ||
| Did not set up integration by parts. | ||
| Did not correctly perform the integrals. | ||
| Incorrect or no answer for the coefficients. | ||
| No attempt. | ||
| Minor error. | ||
| Various errors or lack of progress. | ||
| Posttest | ||
| Question | Point Value (Deduction) | Explanation |
| Q1 | Correct. | |
| Incorrect choice or no attempt. | ||
| Circled both the correct choice (II) and one incorrect choice. | ||
| Q2 | Correct. | |
| No mention of use of boundary conditions. | ||
| No mention of the use of the Fourier trick to obtain the coefficients in series expansion. | ||
| No mention of separation constants. | ||
| No mention of separation constants summing to zero. | ||
| No mention of attempt to solve by writing the solution as a product of functions in each of the variables. | ||
| No mention of converting the partial differential equation to a set of ordinary differential equations. | ||
| No attempt. | ||
| Q3 | Correct. | |
| Did not state: . | ||
| Did not state: . | ||
| Did not state: . | ||
| Did not state: . | ||
| Miscellaneous deduction. | ||
| Q4 | Correct. | |
| Correct choice plus two incorrect choices. | ||
| Correct choice plus one incorrect choice. | ||
| Incorrect choice. | ||
| Q5 | Correct. | |
| Incorrect or no answer. | ||
| Answer is not dimensionally correct. | ||
| Miscellaneous deduction. | ||
| Q6 | Correct. | |
| Did not write down the expression for integrand correctly. | ||
| Did not set up integration by parts. | ||
| Did not correctly perform the integrals. | ||
| Incorrect or no answer for the coefficients. | ||
| No attempt. | ||
| Minor error. | ||
| Various errors or lack of progress. | ||
- The purpose of the rubric is to compare student performance on scaffolded versus unscaffolded tests and to offer a standardized tool that can be used by other instructors and researchers.
- The rubric is designed to capture whether students demonstrate the problem-solving strategies that reflect their understanding before and after engaging with the tutorial.
- Students are not penalized for omitting a step explicitly, as long as there is evidence elsewhere in their solution that indicates understanding of that step (this statement may override some of the deductions listed below).
- Each row represents a step in the problem-solving process, with steps 1–7 weighted equally for 1 point each and steps 8–12 (calculation of ) weighted equally at 0.2 each. The first column indicates the step number, while the second column describes the conceptual focus. The third column provides a descriptive rubric based on a deduction scheme. The fourth column maps each step in the unscaffolded test to the corresponding step in the scaffolded version. For Q2, in the scaffolded version, students were only asked to describe the method of separation of variable rather than use it to solve the problem (as in the unscaffolded version).
| No. | Concept | Deduction Scheme (for Grading) |
| 1 | Diagram (optional) and boundary conditions. | −0% if diagram is missing but boundary conditions are written mathematically. −0% if one of the boundary conditions is missing. −50% if two of the boundary conditions are missing. −50% if the diagram is drawn correctly with grounding symbols, but mathematical boundary conditions are missing. −100% if three or all of the boundary conditions are missing. |
| 2 | Identify that Laplace’s equation (LE) should be used for the given problem, express mathematically. | −0% if identified correctly that LE should be used and stated it in some mathematical form. −50% if identified correctly that LE should be used but did not state it mathematically. −100% if could not identify that solving LE is an appropriate and effective method for the given problem. |
| 3 | Identify that separation of variables (SoV) can be used to find the solution and express SoV mathematically. | −0% if SoV applied correctly, mathematically. −50% if did not express SoV mathematically or did not apply correctly. −100% if could not identify that SoV can be used to find the solution. |
| 4 | Write ordinary differential equations (ODEs) with correct signs. | −0% if ODEs are stated correctly with correct signs. −50% if there are mistakes involving signs in ODEs. −50% for other miscellaneous errors. −100% if there is no attempt to write or use ODEs. Note: No point is lost if not stated that the separation constants add up to zero. |
| 5 | Apply boundary conditions correctly and identify correct form of the separable solutions. | −0% if boundary conditions applied correctly and found correct explicit form of separable solutions. −50% if there is error in applying one of the boundary conditions correctly. −100% if the separable solution is completely incorrect. |
| 6 | Apply boundary condition correctly to find constants ‘’ (obtained from ordinary differential equation). | −0% if the correct form of ‘’ is obtained, with ‘’ a positive integer. −50% if guessed the form of ‘’ but did not apply boundary condition correctly. −50% if ‘’ is defined incorrectly. −100% if did not find ‘’ at all. |
| 7 | Write general solution as a linear combination of separable solutions with coefficients. | −0% if the general solution is written correctly. −50% if expansion coefficients are missing. −100% if did not recognize that the general solution should be written. |
| 8 | Apply the remaining boundary condition correctly. | −0% if the correct remaining boundary condition applied correctly. −50% if boundary condition is not applied correctly. −100% if did not recognize that remaining boundary condition must be applied. |
| 9 | Apply the Fourier trick with correct integral and limits. | −0% if correct integral is set up. −50% if incorrect limits of integral are used. −100% if doesn’t know how to set up integral for the Fourier trick. |
| 10 | Apply the Fourier trick with correct multiplicative function. | −0% if the correct function with appropriate index is multiplied (i.e., the index must be different from the dummy index used for writing the general solution as a linear combination of separable solutions). −50% if incorrect function is multiplied (incorrect index or incorrect function). −100% if the step is missing. |
| 11 | Apply orthogonality (for e.g., ) condition correctly. | −0% if correct orthogonality relation is applied. −50% if orthogonality relation is not applied correctly. −100% if doesn’t know that orthogonality relation should be applied. |
| 12 | Solve the integral correctly after applying the Fourier trick. | −0% if solved completely correctly. −50% if there is any significant error. −100% if could not identify in integration by parts and did not proceed to solve. |
Appendix A.3. Previous Versions
- Previous version 1
- Pretest
- Posttest
- Rubric for Q5* Posttest
| Q5* | Correct. | |
| Did not write down the expression for the potential as an infinite series. | ||
| Did not apply the boundary condition at y = b to the infinite series. | ||
| Minor error. |
- Rubric for Q6* Posttest
| Q6* | Correct. | |
| Did not identify , for integration by parts. | ||
| Incorrect application of integration by parts. | ||
| Integral of equals zero. | ||
| Incorrect answer obtained by evaluating at the limits of integration. |
References
- Al Dehaybes, M., Deprez, J., van Kampen, P., & De Cock, M. (2025a). Students’ understanding of two-variable calculus concepts in mathematics and physics contexts. I. The partial derivative and the directional derivative. Physical Review Physics Education Research, 21(1), 010131. [Google Scholar] [CrossRef]
- Al Dehaybes, M., Deprez, J., van Kampen, P., & De Cock, M. (2025b). Students’ understanding of two-variable calculus concepts in mathematics and physics contexts. II. The gradient and the Laplacian. Physical Review Physics Education Research, 21(1), 010132. [Google Scholar] [CrossRef]
- Alexander John De, R. (2020, June 22). Examining knowledge transfer between thermodynamics and mathematics. 2020 ASEE Virtual Annual Conference, Virtual Online. Available online: https://peer.asee.org/34610 (accessed on 6 October 2025).
- Bassok, M., & Holyoak, K. J. (1989). Interdomain transfer between isomorphic topics in algebra and physics. Journal of Experimental Psychology: Learning, Memory, and Cognition, 15, 153–166. [Google Scholar] [CrossRef]
- Bilak, J., & Singh, C. (2007). Improving students’ conceptual understanding of conductors and insulators. AIP Conference Proceedings, 951(1), 49–52. [Google Scholar] [CrossRef]
- Bing, T. J., & Redish, E. F. (2007). The cognitive blending of mathematics and physics knowledge. AIP Conference Proceedings, 883, 26–29. [Google Scholar] [CrossRef]
- Bing, T. J., & Redish, E. F. (2009). Analyzing problem solving using math in physics: Epistemological framing via warrants. Physical Review Special Topics—Physics Education Research, 5(2), 020108. [Google Scholar] [CrossRef]
- Bing, T. J., & Redish, E. F. (2012). Epistemic complexity and the journeyman-expert transition. Physical Review Special Topics—Physics Education Research, 8(1), 010105. [Google Scholar] [CrossRef]
- Bollen, L., van Kampen, P., Baily, C., & De Cock, M. (2016). Qualitative investigation into students’ use of divergence and curl in electromagnetism. Physical Review Physics Education Research, 12(2), 020134. [Google Scholar] [CrossRef]
- Bollen, L., van Kampen, P., Baily, C., Kelly, M., & De Cock, M. (2017). Student difficulties regarding symbolic and graphical representations of vector fields. Physical Review Physics Education Research, 13(2), 020109. [Google Scholar] [CrossRef]
- Bollen, L., van Kampen, P., & De Cock, M. (2015). Students’ difficulties with vector calculus in electrodynamics. Physical Review Special Topics—Physics Education Research, 11(2), 020129. [Google Scholar] [CrossRef]
- Bollen, L., van Kampen, P., & De Cock, M. (2018). Development, implementation, and assessment of a guided-inquiry teaching-learning sequence on vector calculus in electrodynamics. Physical Review Physics Education Research, 14(2), 020115. [Google Scholar] [CrossRef]
- Bransford, J. D., & Schwartz, D. L. (1999). Rethinking transfer: A simple proposal with multiple implications. Review of Research in Education, 24, 61–100. [Google Scholar] [PubMed]
- Brown, B. R., Mason, A., & Singh, C. (2016). Improving performance in quantum mechanics with explicit incentives to correct mistakes. Physical Review Physics Education Research, 12(1), 010121. [Google Scholar] [CrossRef]
- Campos, E., Hernandez, E., Barniol, P., & Zavala, G. (2021). Phenomenographic analysis and comparison of students’ conceptual understanding of electric and magnetic fields and the principle of superposition. Physical Review Physics Education Research, 17(2), 020117. [Google Scholar] [CrossRef]
- Campos, E., Zavala, G., Zuza, K., & Guisasola, J. (2019). Electric field lines: The implications of students’ interpretation on their understanding of the concept of electric field and of the superposition principle. American Journal of Physics, 87(8), 660–667. [Google Scholar] [CrossRef]
- Campos, E., Zavala, G., Zuza, K., & Guisasola, J. (2020). Students’ understanding of the concept of the electric field through conversions of multiple representations. Physical Review Physics Education Research, 16(1), 010135. [Google Scholar] [CrossRef]
- Chaiklin, S. (2003). The zone of proximal development in Vygotsky’s analysis of learning and instruction. In Vygotsky’s educational theory in cultural context (Vol. 1, Issue 2, pp. 39–64). Cambridge University Press. [Google Scholar]
- Chasteen, S. V., Pepper, R. E., Caballero, M. D., Pollock, S. J., & Perkins, K. K. (2012a). Colorado upper-division electrostatics diagnostic: A conceptual assessment for the junior level. Physical Review Special Topics—Physics Education Research, 8(2), 020108. [Google Scholar] [CrossRef]
- Chasteen, S. V., Pollock, S. J., Pepper, R. E., & Perkins, K. K. (2012b). Transforming the junior level: Outcomes from instruction and research in E&M. Physical Review Special Topics—Physics Education Research, 8(2), 020107. [Google Scholar]
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences. L. Erlbaum Associates. [Google Scholar]
- Collins, A., Brown, J. S., & Newman, S. E. (1989). Cognitive apprenticeship: Teaching the crafts of reading, writing, and mathematics. In Knowing, learning, and instruction: Essays in honor of Robert Glaser (Vol. 18, pp. 32–42). Routledge. [Google Scholar]
- Crouch, C. H., Watkins, J., Fagen, A. P., & Mazur, E. (2007). Peer instruction: Engaging students one-on-one, all at once. In E. F. Redish, & P. J. Cooney (Eds.), Research-based reform of university physics (Vol. 1, pp. 40–95). American Association of Physics Teachers. [Google Scholar]
- Derman, A., Koçak, N., & Eilks, I. (2019). Insights into components of prospective science teachers’ mental models and their preferred visual representations of atoms. Education Sciences, 9(2), 154. Available online: https://www.mdpi.com/2227-7102/9/2/154 (accessed on 6 October 2025). [CrossRef]
- Ding, L., Jia, Z., & Zhang, P. (2021). From learning capacitance to making capacitors: The missing critical sensemaking. International Journal of Science and Mathematics Education, 19(7), 1357–1373. [Google Scholar] [CrossRef]
- Ding, L., Reay, N., Lee, A., & Bao, L. (2011). Exploring the role of conceptual scaffolding in solving synthesis problems. Physical Review Special Topics—Physics Education Research, 7(2), 020109. [Google Scholar] [CrossRef]
- DiSessa, A. A. (1993). Toward an epistemology of physics. Cognition and Instruction, 10(2–3), 105–225. [Google Scholar] [CrossRef]
- DiSessa, A. A. (2018, July 24–31). A friendly introduction to “knowledge in pieces”: Modeling types of knowledge and their roles in learning [Invited lectures]. 13th International Congress on Mathematical Education, Hamburg, Germany. [Google Scholar]
- Doughty, L., McLoughlin, E., & van Kampen, P. (2014). What integration cues, and what cues integration in intermediate electromagnetism. American Journal of Physics, 82(11), 1093–1103. [Google Scholar] [CrossRef]
- Dufresne, R., Mestre, J., Thaden-Koch, T., Gerace, W., & Leonard, W. (2005). Knowledge representation and coordination in the transfer process. In Transfer of learning from a modern multidisciplinary perspective (pp. 155–215). Information Age Publishing. [Google Scholar]
- Eylon, B. S., & Ganiel, U. (1990). Macro-micro relationships: The missing link between electrostatics and electrodynamics in students’ reasoning. International Journal of Science Education, 12(1), 79–94. [Google Scholar] [CrossRef]
- Galili, I. (2018). Physics and mathematics as interwoven disciplines in science education. Science & Education, 27(1), 7–37. [Google Scholar] [CrossRef]
- Garzón, I., De Cock, M., Zuza, K., van Kampen, P., & Guisasola, J. (2014). Probing university students’ understanding of electromotive force in electricity. American Journal of Physics, 82(1), 72–79. [Google Scholar] [CrossRef]
- Griffiths, D. J. (2013). Introduction to electrodynamics (4th ed.). Pearson. Available online: https://search.library.wisc.edu/catalog/9910134691602121 (accessed on 6 October 2025).
- Guisasola, J., Zubimendi, J., & Zuza, K. (2010). How much have students learned? Research-based teaching on electrical capacitance. Physical Review Special Topics. Physics Education Research, 6, 020102. [Google Scholar] [CrossRef]
- Guisasola, J., Zubimendi, J. L., Almudí, J. M., & Ceberio, M. (2002). The evolution of the concept of capacitance throughout the development of the electric theory and the understanding of its meaning by university students. Science & Education, 11(3), 247–261. [Google Scholar] [CrossRef]
- Hammer, D. (1994). Epistemological beliefs in introductory physics. Cognition and Instruction, 12(2), 151–183. [Google Scholar] [CrossRef]
- Hu, D., & Rebello, N. S. (2013). Using conceptual blending to describe how students use mathematical integrals in physics. Physical Review Special Topics—Physics Education Research, 9(2), 020118. [Google Scholar] [CrossRef]
- Justice, P. D., Marshman, E., & Singh, C. (2025). A Framework for understanding the impact of integrating conceptual and quantitative reasoning in a quantum optics tutorial on students’ conceptual understanding. Education Sciences, 15(10), 1314. Available online: https://www.mdpi.com/2227-7102/15/10/1314 (accessed on 6 October 2025). [CrossRef]
- Karam, R. (2014). Framing the structural role of mathematics in physics lectures: A case study on electromagnetism. Physical Review Special Topics—Physics Education Research, 10(1), 010119. [Google Scholar] [CrossRef]
- Karam, R. (2015). Introduction of the thematic issue on the interplay of physics and mathematics. Science & Education, 24(5), 487–494. [Google Scholar] [CrossRef]
- Karam, R., Uhden, O., & Höttecke, D. (2019). The “Math as Prerequisite” illusion: Historical considerations and implications for physics teaching. In G. Pospiech, M. Michelini, & B.-S. Eylon (Eds.), Mathematics in physics education (pp. 37–52). Springer International Publishing. [Google Scholar] [CrossRef]
- Kashyap, J. S., & Singh, C. (2024, July 10–11). Students’ sensemaking using pictorial analysis game in upper-level electrostatics. Proceedings of the Physics Education Research Conference, Boston, MA, USA. [Google Scholar]
- Kashyap, J. S., & Singh, C. (2025). Case study examining graduate student sensemaking using the epistemic game framework for Laplace’s equation in upper-level electrostatics. Physical Review Physics Education Research, 21(2), 020125. [Google Scholar] [CrossRef]
- Li, J., Maries, A., & Singh, C. (2023). Helping students apply superposition principle in problems involving spherical, cylindrical, and planar charge distributions. American Journal of Physics, 91(8), 613–616. [Google Scholar] [CrossRef]
- Li, J., & Singh, C. (2017). Investigating and improving introductory physics students’ understanding of the electric field and superposition principle. European Journal of Physics, 38(5), 055702. [Google Scholar] [CrossRef]
- Li, J., & Singh, C. (2018a). Investigating and improving introductory physics students’ understanding of electric flux. European Journal of Physics, 39(4), 045711. [Google Scholar] [CrossRef]
- Li, J., & Singh, C. (2018b). Investigating and improving student understanding of symmetry and Gauss’s law. European Journal of Physics, 39, 015702. [Google Scholar] [CrossRef]
- Li, J., & Singh, C. (2019). Investigating and improving introductory physics students’ understanding of electric field and the superposition principle: The case of a continuous charge distribution. Physical Review Physics Education Research, 15(1), 010116. [Google Scholar] [CrossRef]
- Lin, S.-Y., & Singh, C. (2015). Effect of scaffolding on helping introductory physics students solve quantitative problems involving strong alternative conceptions. Physical Review Special Topics-Physics Education Research, 11(2), 020105. [Google Scholar] [CrossRef]
- Lorenzo, M., Crouch, C. H., & Mazur, E. (2006). Reducing the gender gap in the physics classroom. American Journal of Physics, 74(2), 118–122. [Google Scholar] [CrossRef]
- Maries, A., Lin, S.-Y., & Singh, C. (2017). Challenges in designing appropriate scaffolding to improve students’ representational consistency: The case of a Gauss’s law problem. Physical Review Physics Education Research, 13(2), 020103. [Google Scholar] [CrossRef]
- Maries, A., & Singh, C. (2023). Helping students become proficient problem solvers Part I: A brief review. Education Sciences, 13(2), 156. [Google Scholar] [CrossRef]
- Mason, A. J., McCardell, J. M., White, P. A., & Colton, J. S. (2023). Improving performance in upper-division electricity and magnetism with explicit incentives to correct mistakes. Physical Review Physics Education Research, 19(2), 020104. [Google Scholar] [CrossRef]
- Mazur, E. (2009). Farewell, lecture. Science, 323(5910), 50–51. [Google Scholar] [CrossRef]
- McDermott, L. C. (1984). Research on conceptual understanding in mechanics. Physics Today, 37(7), 24–32. [Google Scholar] [CrossRef]
- McDermott, L. C. (2001). Oersted medal lecture 2001: “Physics education research—The key to student learning”. American Journal of Physics, 69(11), 1127–1137. [Google Scholar] [CrossRef]
- McDermott, L. C. (2021). Developing and learning from tutorials in introductory physics. In A view from physics: Discipline-based education research (Vol. 7). AIP Publishing LLC. [Google Scholar] [CrossRef]
- McDermott, L. C., & Redish, E. F. (1999). Resource letter: PER-1: Physics education research. American Journal of Physics, 67(9), 755–767. [Google Scholar] [CrossRef]
- McDermott, L. C., & Shaffer, P. (1992). Research as a guide for curriculum development: An example from introductory electricity. Part I: Investigation of student understanding. American Journal of Physics, 60, 994–1003. [Google Scholar] [CrossRef]
- McDermott, L. C., & Shaffer, P. S. (2002). Tutorials in introductory physics. Prentice Hall. [Google Scholar]
- McLeod, S. (2019). The zone of proximal development and scaffolding. Simply Psychology, 1(2), 15–28. [Google Scholar]
- Michelini, M., Stefanel, A., & Tóth, K. (2022). Implementing dirac approach to quantum mechanics in a Hungarian secondary school. Education Sciences, 12(9), 606. [Google Scholar] [CrossRef]
- Miller, K., Schell, J., Ho, A., Lukoff, B., & Mazur, E. (2015). Response switching and self-efficacy in peer instruction classrooms. Physical Review Special Topics—Physics Education Research, 11(1), 010104. [Google Scholar] [CrossRef]
- Nguyen, D.-H., & Rebello, N. S. (2011). Students’ difficulties with integration in electricity. Physical Review Special Topics—Physics Education Research, 7(1), 010113. [Google Scholar] [CrossRef]
- Nokes-Malach, T. J., & Mestre, J. P. (2013). Toward a model of transfer as sense-making. Educational Psychologist, 48(3), 184–207. [Google Scholar] [CrossRef]
- Olschewski, P., Herzmann, P., & Schlüter, K. (2023). Group work during inquiry-based learning in biology teacher education: A praxeological perspective on the task of (collaborative) protocol generation. Education Sciences, 13(4), 401. Available online: https://www.mdpi.com/2227-7102/13/4/401 (accessed on 6 October 2025). [CrossRef]
- Pepper, R. E., Chasteen, S. V., Pollock, S. J., & Perkins, K. K. (2012). Observations on student difficulties with mathematics in upper-division electricity and magnetism. Physical Review Special Topics—Physics Education Research, 8(1), 010111. [Google Scholar] [CrossRef]
- Pietrocola, M. (2008). Mathematics as structural language of physical thought. In Connecting research in physics education with teacher education (Vol. 2). IOP Publishing Ltd. [Google Scholar]
- Pospiech, G., Michelini, M., & Eylon, B.-S. (2019). Mathematics in physics education. Springer. [Google Scholar]
- Pozzi, F., Manganello, F., & Persico, D. (2023). Collaborative learning: A design challenge for teachers. Education Sciences, 13(4), 331. Available online: https://www.mdpi.com/2227-7102/13/4/331 (accessed on 6 October 2025). [CrossRef]
- Pride, T. O. B., Vokos, S., & McDermott, L. C. (1998). The challenge of matching learning assessments to teaching goals: An example from the work-energy and impulse-momentum theorems. American Journal of Physics, 66(2), 147–157. [Google Scholar] [CrossRef]
- Rebello, N. S., Cui, L., Bennett, A., Zollman, D., & Ozimek, D. (2017). Transfer of learning in problem solving in the context of mathematics and physics. In D. H. Jonassen (Ed.), Learning to solve complex scientific problems (pp. 223–246). Routledge. [Google Scholar] [CrossRef]
- Redish, E. F. (2004). Varenna summer school. In E. F. Redish, & M. Vicentini (Eds.), Research on physics education: Proceedings of the international school of physics “Enrico Fermi” course CLVI (Vol. 156, pp. 341–350). IOS Press. [Google Scholar]
- Reif, F. (2008). Scientific approaches to science education. Physics Today, 39(11), 48–54. [Google Scholar] [CrossRef]
- Ryan, Q. X., Wilcox, B. R., & Pollock, S. J. (2018). Student difficulties with boundary conditions in the context of electromagnetic waves. Physical Review Physics Education Research, 14(2), 020126. [Google Scholar] [CrossRef]
- Santana, L. M., Hickman, C., Bilak, J., & Singh, C. (2023). Investigating and improving student understanding of conductors and insulators. Education Sciences, 13(3), 242. [Google Scholar] [CrossRef]
- Schwartz, D., Bransford, J., & Sears, D. (2005). Efficiency and innovation in transfer. In J. Mestre (Ed.), Transfer of learning from a modern multidisciplinary perspective (Vol. 3, pp. 1–51). Information Age Publishing. [Google Scholar]
- Shaffer, P. S., & McDermott, L. C. (1992). Research as a guide for curriculum development: An example from introductory electricity. Part II: Design of instructional strategies. American Journal of Physics, 60(11), 1003–1013. [Google Scholar] [CrossRef]
- Sikorski, T. R., & Hammer, D. (2017). Looking for coherence in science curriculum. Science Education, 101(6), 929–943. [Google Scholar] [CrossRef]
- Singh, C. (2006). Student understanding of symmetry and Gauss’s law of electricity. American Journal of Physics, 74(10), 923–936. [Google Scholar] [CrossRef]
- Singh, C., & Maries, A. (2013). Core graduate courses: A missed learning opportunity? AIP Conference Proceedings, 1513(1), 382–385. [Google Scholar] [CrossRef]
- Singh, C., Maries, A., Heller, K., & Heller, P. (2023). Instructional strategies that foster effective problem-solving. In The international handbook of physics education research: Learning physics. Melville. [Google Scholar]
- Suárez, Á., Marti, A. C., Zuza, K., & Guisasola, J. (2024). Learning difficulties among students when applying Ampére-Maxwell’s law and its implications for teaching. Physical Review Physics Education Research, 20(1), 010143. [Google Scholar] [CrossRef]
- Thacker, B. A., Ganiel, U., & Boys, D. (1999). Macroscopic phenomena and microscopic processes: Student understanding of transients in direct current electric circuits. American Journal of Physics, 67(S1), S25–S31. [Google Scholar] [CrossRef]
- Tuminaro, J., & Redish, E. F. (2007). Elements of a cognitive model of physics problem solving: Epistemic games. Physical Review Special Topics—Physics Education Research, 3(2), 020101. [Google Scholar] [CrossRef]
- Tzanakis, C. (2016). Mathematics & Physics: An innermost relationship. In Didactical implications for their teaching & learning. Montpellier. [Google Scholar]
- Uhden, O., Karam, R., Pietrocola, M., & Pospiech, G. (2012). Modelling mathematical reasoning in physics education. Science & Education, 21(4), 485–506. [Google Scholar] [CrossRef]
- van Kampen, P. (2023). Students’ understanding of electricity and magnetism. AIP Publishing LLC. [Google Scholar] [CrossRef]
- Vygotsky, L. (1978). Mind in society: The development of higher psychological processes. Harvard University Press. [Google Scholar]
- Watkins, J., & Mazur, E. (2013). Retaining students in science, technology, engineering, and mathematics (STEM) majors. Journal of College Science Teaching, 42(5), 36–41. Available online: http://www.jstor.org/stable/43631580 (accessed on 6 October 2025).
- Wawro, M., Watson, K., & Christensen, W. (2020). Students’ metarepresentational competence with matrix notation and Dirac notation in quantum mechanics. Physical Review Physics Education Research, 16(2), 020112. [Google Scholar] [CrossRef]
- Wilcox, B. R., & Corsiglia, G. (2019). Cross-context look at upper-division student difficulties with integration. Physical Review Physics Education Research, 15(2), 020136. [Google Scholar] [CrossRef]
- Wilcox, B. R., & Pollock, S. J. (2015). Upper-division student difficulties with separation of variables. Physical Review Special Topics—Physics Education Research, 11(2), 020131. [Google Scholar] [CrossRef]
- Zuza, K., Almudí, J.-M., Leniz, A., & Guisasola, J. (2014). Addressing students’ difficulties with Faraday’s law: A guided problem solving approach. Physical Review Special Topics—Physics Education Research, 10(1), 010122. [Google Scholar] [CrossRef]
- Zuza, K., De Cock, M., van Kampen, P., Bollen, L., & Guisasola, J. (2016). University students’ understanding of the electromotive force concept in the context of electromagnetic induction. European Journal of Physics, 37(6), 065709. [Google Scholar] [CrossRef]
- Zuza, K., Guisasola, J., Michelini, M., & Santi, L. (2012). Rethinking Faraday’s law for teaching motional electromotive force. European Journal of Physics, 33(2), 397. [Google Scholar] [CrossRef]
- Zwolak, J. P., & Manogue, C. A. (2015). Assessing student reasoning in upper-division electricity and magnetism at Oregon State University. Physical Review Special Topics—Physics Education Research, 11(2), 020125. [Google Scholar]
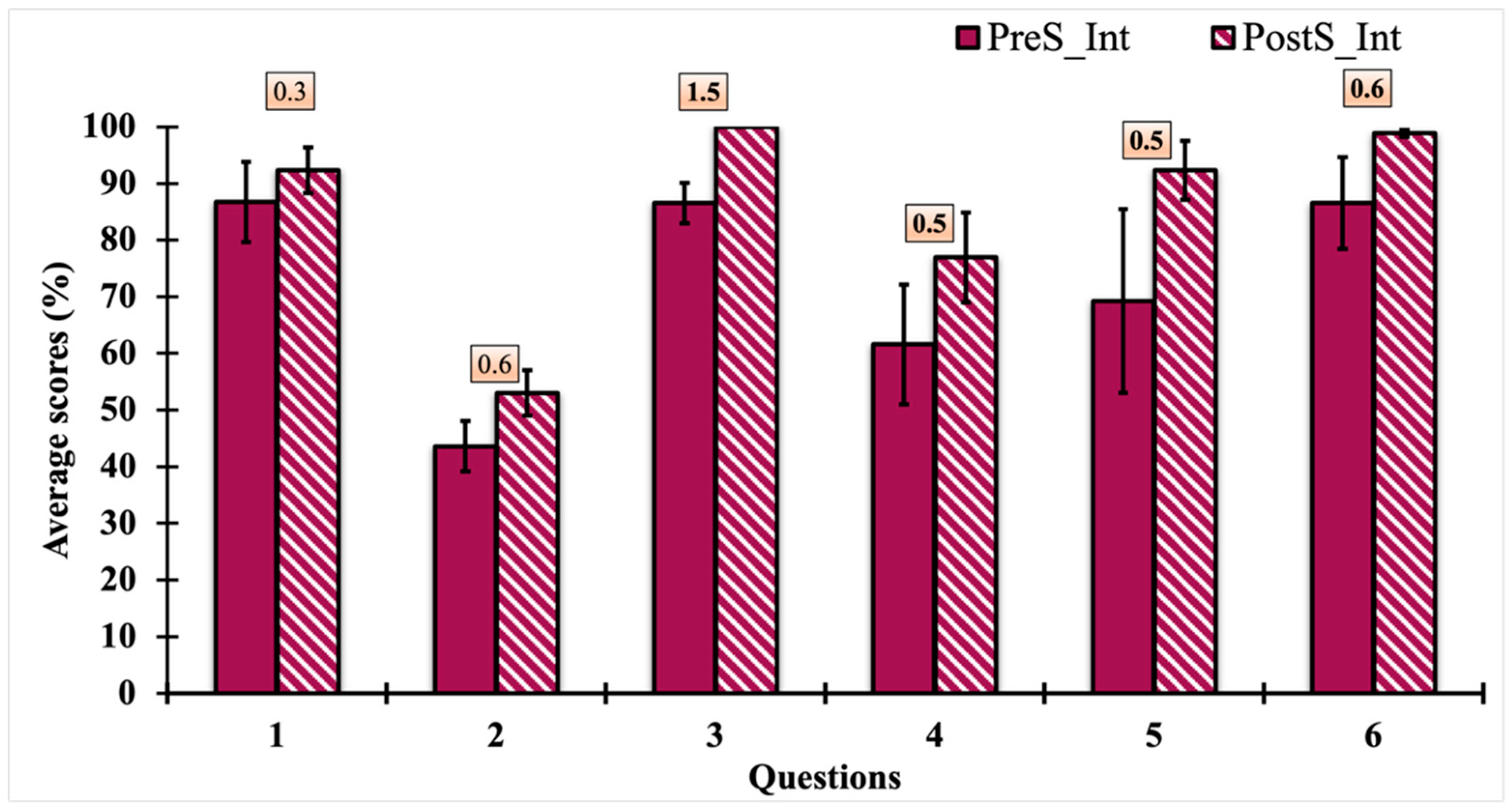
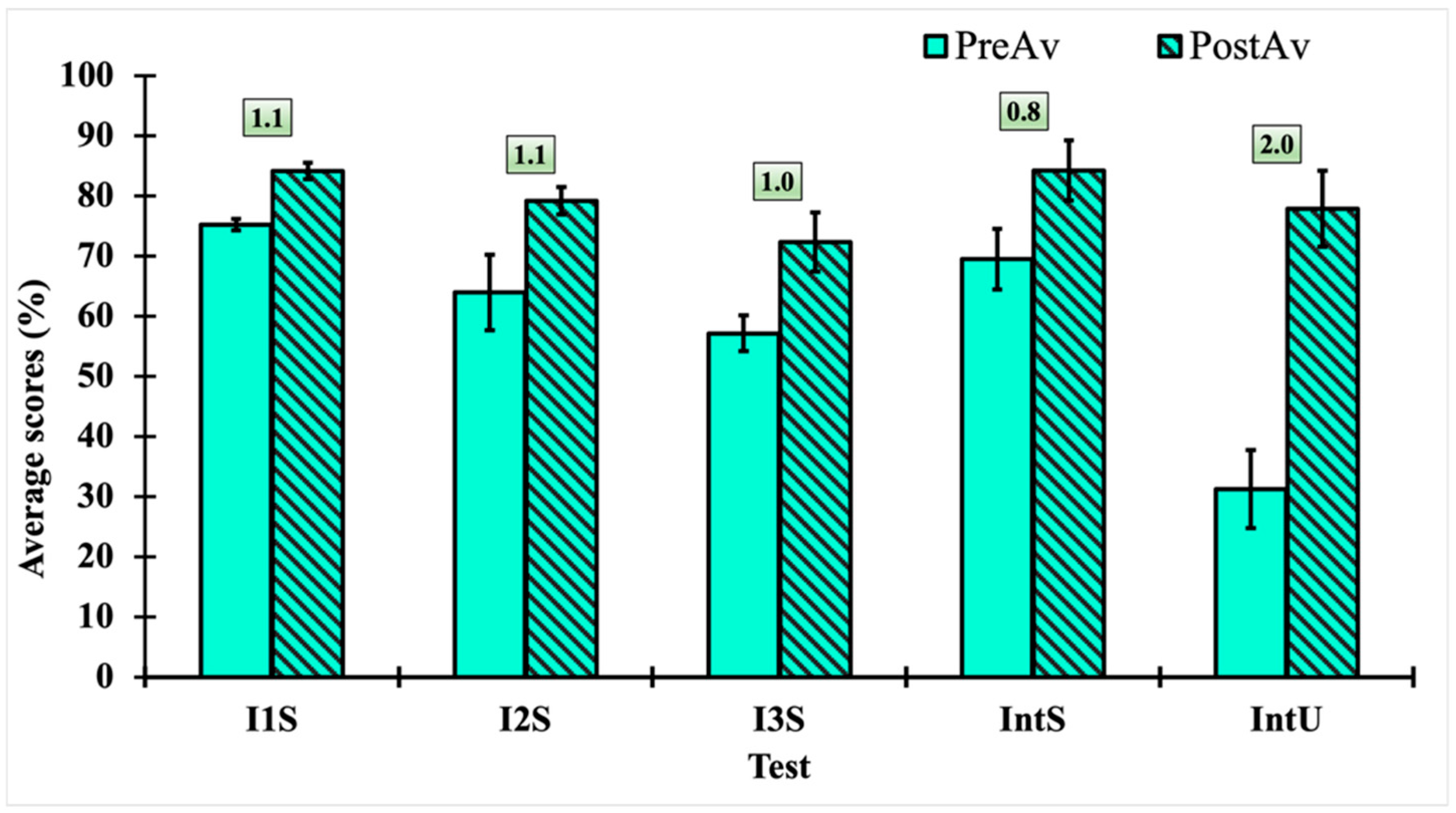
| Learning Objectives | Pretest or Posttest Question (Latest Version) | Corresponding Tutorial Question |
|---|---|---|
| identify the situation(s) in which Laplace’s equation can be used to find the potential | 1 | 1, 2 |
| identify a relevant coordinate system and coordinates | 3, 11, 28 (d) | |
| draw a diagram of the situation | 4, 28 (a) | |
| write and/or label or interpret boundary conditions for the given situation | 3 | 5, 10, 28 (b) |
| write Laplace’s equation for the relevant coordinate system | 6, 12 | |
| apply/explain the method of separation of variables | 2 | 7, 8, 9, 28 (c) |
| apply the boundary conditions to find different constants | 14, 15, 16, 18, 28 (e), 28 (f) | |
| write the separable solution | 4 | 13, 17 |
| write the general solution as a linear combination of separable solutions | 5 | 19, 20, 28 (g) |
| evaluate the expansion coefficients by applying the remaining boundary condition and using the Fourier trick | 6 | 21, 22, 23, 24, 27 |
| write the unique solution using the expansion coefficients | 25, 28 (h), 28 (i), 28 (j) | |
| draw the behaviors of electric field lines and equipotential surfaces for the given problem | 26 |
| Number of Students | |||
|---|---|---|---|
| Instructor | Pretest (All) | Posttest (All) | Pretest and Posttest (Matched) |
| I1 | 52 | 44 | 44 |
| I2 | 12 | 18 | 9 |
| I3 | 15 | 17 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kashyap, J.S.; Devaty, R.; Singh, C. When Support Hides Progress: Insights from a Physics Tutorial on Solving Laplace’s Equation Using Separation of Variables in Cartesian Coordinates. Educ. Sci. 2025, 15, 1345. https://doi.org/10.3390/educsci15101345
Kashyap JS, Devaty R, Singh C. When Support Hides Progress: Insights from a Physics Tutorial on Solving Laplace’s Equation Using Separation of Variables in Cartesian Coordinates. Education Sciences. 2025; 15(10):1345. https://doi.org/10.3390/educsci15101345
Chicago/Turabian StyleKashyap, Jaya Shivangani, Robert Devaty, and Chandralekha Singh. 2025. "When Support Hides Progress: Insights from a Physics Tutorial on Solving Laplace’s Equation Using Separation of Variables in Cartesian Coordinates" Education Sciences 15, no. 10: 1345. https://doi.org/10.3390/educsci15101345
APA StyleKashyap, J. S., Devaty, R., & Singh, C. (2025). When Support Hides Progress: Insights from a Physics Tutorial on Solving Laplace’s Equation Using Separation of Variables in Cartesian Coordinates. Education Sciences, 15(10), 1345. https://doi.org/10.3390/educsci15101345






