Next Article in Journal
Aligning the Operationalization of Digital Competences with Perceived AI Literacy: The Case of HE Students in IT Engineering and Teacher Education
Previous Article in Journal
Application for Admission: The Poetics of Erasure in Doctoral Education
Previous Article in Special Issue
Latent Profile Analysis of Computational Thinking Skills: Associations with Creative STEM Project Production
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 15
Issue 12
10.3390/educsci15121581
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Developing Mathematical Creativity in High-Potential Kindergarten English Learners Through Enrichment and Tangram Activities

by
Gülnur Özbek
1,*,
Rachel U. Mun
2,
Yuyang Shen
2,
Weini Lin
2,
Melissa Spence
3 and
Seokhee Cho
4
1
Center for Creativity and Gifted Education, St. John’s University, Jamaica, NY 11439, USA
2
Department of Educational Psychology, University of North Texas, Denton, TX 76201, USA
3
Department of Learning and Teaching, School of Education, California Lutheran University, Thousand Oaks, CA 91360, USA
4
Administrative and Instructional Leadership, The School of Education, St. John’s University, Jamaica, NY 11439, USA
*
Author to whom correspondence should be addressed.
Educ. Sci. 2025, 15(12), 1581; https://doi.org/10.3390/educsci15121581
Submission received: 14 October 2025 / Revised: 17 November 2025 / Accepted: 19 November 2025 / Published: 24 November 2025
(This article belongs to the Special Issue Creativity and Education)
Browse Figure
Versions Notes

Abstract

Early mathematical learning predicts later academic achievement, and creativity within mathematics plays a central role in higher-order thinking. This study examined the effects of linguistically responsive mathematics enrichment programs for nurturing mathematical creativity. Participants were 250 high-potential kindergarten English Learners across six urban schools in New York, Texas, and California. A linguistically responsive enrichment intervention adapted from the Mentoring Young Mathematicians (M2) math curriculum was implemented for 80 h across seven months. Using the Tangram Creativity Assessment, fluency, flexibility, and originality were measured in students’ tangram problem solving. Additional predictors included Tangram Problem Solving Speed (TPSS), general reasoning (CogAT), and mathematical achievement (NWEA MAP Math). ANCOVA showed significant post-test differences favoring the intervention group across all creativity components. Two-group structural equation modeling analysis supported measurement invariance and explained 55–60% of posttest creativity variance. TPSS emerged as the strongest predictor, with greater effects for the intervention group. These findings highlight the potential of enrichment programs and language-accessible geometry tasks to cultivate creativity in young gifted ELs by strengthening their mathematical foundation while supporting flexible and original problem solving.

1. Introduction

Children are capable of learning and mastering mathematical concepts from an early age, and longitudinal studies show that early mathematics learning is a strong predictor of later achievement (Li & Disney, 2023). Within mathematics, creativity plays an important role. Mathematical creativity is a key aspect of higher-order thinking (Stolte et al., 2020), and early engagement with tasks that promote flexibility, abstraction, and originality can indicate young children’s future mathematical achievement. Mathematical creativity is complex and difficult to define, and scholars note that creativity itself carries multiple meanings across disciplines (Dickman, 2018; Puryear & Lamb, 2020). Mathematical creativity generally is understood to build on foundations such as intelligence, motivation, and curiosity, applying them specifically within mathematics (Meier et al., 2024; Schoevers et al., 2020; Starko, 2022; Stolte et al., 2020). It involves both the discovery of new mathematical ideas and the construction of proofs, emphasizing exploration, problem-solving, and original solutions beyond rote exercises (Schoevers et al., 2020; Starko, 2022; Stolte et al., 2020).
Cultivating mathematical creativity has many benefits and should be an essential goal in educating elementary-aged children, including young, gifted English Learners (ELs). Experts recommend that teachers design authentic learning experiences that allow students to draw on varied mathematical knowledge, approach problems from multiple perspectives, and represent ideas in different ways, particularly when applying learning to real-world contexts (Yang et al., 2023b). Research shows the value of open-ended tasks and multiple solution tasks (MSTs) in math to promote creativity (Kozlowski & Chamberlin, 2022; Schoevers et al., 2020). Open-ended tasks allow multiple correct answers, whereas MSTs allow a single correct answer attainable through multiple strategies. In a qualitative study, graduate students identified MSTs as especially effective in fostering mathematical creativity in elementary classrooms because they encouraged children’s divergent thinking (Levenson, 2013).
In early mathematics, spatial reasoning and shape composition play an especially important role. Early proficiency in geometry and visual-spatial reasoning has been shown to strongly predict success in other areas of mathematics as well as long-term academic achievement (Yang & Cho, 2024). These skills help children manipulate and transform figures while laying the groundwork for geometric concepts such as symmetry, equivalence, and area. For young, gifted ELs, open-ended geometry activities like tangram puzzles provide opportunities to showcase both spatial reasoning and creative flexibility. Such tasks encourage children to explore multiple strategies and extend their critical thinking beyond rote learning (Starko, 2022; Yang et al., 2023b). Beyond the quality and originality of solutions, task-specific problem-solving speed (i.e., how quickly students generate and implement ideas) may also be informative, as prior research suggests that efficient cognitive processing supports creative performance (Beaty et al., 2016; Benedek & Neubauer, 2013; Guilford, 1968) and that fluent problem solving is associated with mathematical creativity (R. Leikin, 2009; Silver, 1997).
Despite the importance of these skills, limited empirical research has examined domain-specific mathematical creativity in young children (Kozlowski & Chamberlin, 2022), and even less is known about effective ways to support young, gifted ELs in this area (Yang et al., 2023b; Yang & Cho, 2024; Mun et al., 2020). Further investigation is needed to better understand the K–3 population and to identify the structures, task designs, and instructional supports most effective in fostering creativity at this developmental stage. Building on these gaps, the present study explores how EL kindergarteners with gifted potential use composition of shapes and spatial reasoning to solve geometry problems as early indicators of mathematical creativity. Specifically, it examines the types of puzzle solutions produced, the challenges students encounter, and the extent to which geometry instruction influences early creative markers such as cognitive flexibility and figure apprehension.
We begin by reviewing the literature that examines mathematical creativity, its relationship to achievement, and its role in early childhood learning. Particular attention is given to how instructional support and enrichment programs foster mathematical creativity, especially for gifted ELs. We then present our theoretical framework for understanding mathematical creativity in early childhood and outline the methods used to address our research questions. Finally, we present the study’s findings and discuss their implications for teachers, researchers, and practitioners in gifted education.

1.1. Mathematical Creativity in Young English Learners with High Potential

1.1.1. Definition and Characteristics of Mathematical Creativity

Mathematical creativity plays a critical role in the advancement of mathematics as both a discipline and a mode of thinking (Sriraman, 2009). Scholars describe creativity as a multifaceted construct, and mathematical creativity specifically involves generating novel and appropriate ideas, applying concepts flexibly, and approaching problems from multiple perspectives (Abbott, 2010; Sak & Maker, 2006; Schoevers et al., 2020; Sriraman et al., 2013; Stolte et al., 2020). Hadamard (2020), in The Mathematician’s Mind, showed that eminent mathematicians often achieve breakthroughs through unconscious incubation followed by sudden insight. He emphasized that mathematical creativity rarely follows a purely linear path; instead, it arises from the interplay of deliberate effort, intuition, and imagination. Balka (1974) identified several indicators of mathematical creativity, including the ability to formulate hypotheses about mathematical relationships, decompose problems into meaningful subproblems, identify patterns, and break away from established mental sets. Similarly, Starko (1994) emphasized shifting among representations, comparing solution strategies, and integrating multiple concepts to view mathematical ideas from diverse perspectives. Sak and Maker (2006) found that increased domain knowledge enhances students’ creative processes by strengthening divergent thinking, while Price and Yates (2015) observed that highly creative students tend to show greater persistence and maturity in mathematical problem solving.
Broader creativity literature provides a useful foundation for understanding mathematical creativity. Guilford (1968) identified fluency, flexibility, elaboration, and originality as core dimensions of creative thinking, and these have been widely applied in mathematics education (Beghetto, 2017; Siswono, 2011; Imai, 2000; R. Leikin & Lev, 2007; Kim et al., 2004). Fluency refers to producing multiple solutions or approaches; flexibility involves shifting strategies or perspectives; elaboration denotes the ability to justify and explain solutions in depth; and originality captures the generation of uncommon or unique ideas. More general definitions emphasize that creativity emerges through the interaction of individual ability, processes, and environmental factors to produce ideas that are both novel and appropriate within a social context (Plucker et al., 2004; Runco & Jaeger, 2012).
Amabile’s (1996) Componential Model of Creativity emphasizes that foundational knowledge serves as the raw material for generating and evaluating creative ideas. Within mathematics specifically, creativity has been defined as the capacity to generate numerous, different, and applicable solutions to a mathematical situation (Jensen, 1973), to apply principles in multiple ways to produce correct outcomes (Sak & Maker, 2006), or to formulate novel solutions and new questions (Sriraman et al., 2013). Poincaré (1948) described mathematical creative thinking as a process of discernment and choice, highlighting its inherently generative and exploratory nature. Taken together, these perspectives show that mathematical creativity involves both divergent and convergent thinking—the ability to produce multiple possibilities and to ensure their mathematical soundness—anchored in strong domain knowledge and flexible cognitive strategies.

1.1.2. Mathematical Creativity in Young Children

For young children, creativity is not typically expressed as a fixed or obvious talent but rather as a developing skill that emerges through intentional learning experiences and supportive teaching environments. These experiences aim to build foundational capacities such as fluency, flexibility, and problem-solving, which are essential for later mathematical development (Bai et al., 2024). Early mathematical experiences—especially those involving play and exploratory activities—play a crucial role in shaping long-term academic achievement (Yildirim & Yilmaz, 2023). Instead of offering only a limited set of math-related materials, it is beneficial to expose children to a wide variety of resources, such as puzzles, building blocks, cards, board games, and other mathematical toys. These materials stimulate children’s curiosity, creativity, and problem-solving abilities (Clements & Sarama, 2004/2011; Novita et al., 2018). Mathematical creativity, which is closely intertwined with cognitive growth, develops progressively across different stages of learning, as discussed in the following sections on early childhood through the elementary years and their pedagogical implications. Mathematical creativity, closely tied to cognitive growth, develops across stages of learning, as discussed in the following sections on early childhood through the elementary years and their pedagogical implications.

1.1.3. Open-Ended Tasks (Tangrams, Block Play, Puzzles)

During early childhood, mathematical creativity is often expressed through role play, mathematical exploration, and open-ended problem solving (National Association for the Education of Young Children & National Council of Teachers of Mathematics, 2010). At this stage, children’s curiosity and creative thinking can be nurtured by engaging them with building blocks, tangrams, puzzles, and similar hands-on materials, which encourage them to explore and experiment with different mathematical ideas. As children engage repeatedly with these exploratory activities, they strengthen their memory retrieval and mental operations, which support deeper mathematical understanding over time (Bai et al., 2024). During this stage, creativity is closely linked with spatial reasoning, shape synthesis, and number sense. Given young children’s limited attention spans, instructional tasks should be concise and teacher-guided to sustain engagement and support learning (National Center for Education Evaluation and Regional Assistance, 2013).
Elementary School Stage. Upon entering elementary school, children’s cognitive flexibility gradually increases, allowing them to apply mathematical concepts more effectively. At this stage, they begin to connect their earlier spatial and geometric experience with more systematic mathematics ideas such as number operations and fractions (National Center for Education Evaluation and Regional Assistance, 2013). Open-ended tasks play a particularly important role during this period. Thiel and Perry (2018) emphasized that such tasks can motivate students’ creativity, enhance problem-solving abilities, and encourage the use of diverse strategies, while also requiring students to provide logically sound and mathematically correct solutions, such as through multiple solution approaches to word problems (Thiel & Perry, 2018; Yildirim & Yilmaz, 2023).

1.1.4. Mathematics-Specific Knowledge and Skills and Mathematical Creativity

The relationship between mathematical knowledge and creativity has been examined from multiple perspectives. Some scholars argue that engaging with mathematics creatively deepens students’ conceptual understanding, thereby strengthening their mathematical ability (Starko, 1994). Others contend that creativity in mathematics depends fundamentally on a solid knowledge base. Mann (2005), for example, found that students without sufficient mathematical content knowledge were unlikely to demonstrate creative mathematical thinking, identifying mathematical achievement as a strong predictor of creative performance. More recently, a meta-analysis of 30 studies involving over 11,000 participants (Bicer et al., 2021) provided evidence of this association, reporting a moderate positive correlation between mathematical creativity and achievement among children and adolescents. Despite these differing emphases, researchers widely agree that creativity and mathematical knowledge are closely intertwined and mutually reinforcing.
A substantial body of work supports the view that domain-specific knowledge provides the foundation for creativity within the same domain. Amabile’s (1996) Componential Model of Creativity identifies domain-relevant skills—factual knowledge, technical proficiency, and specialized talents—as essential for producing novel and appropriate solutions. Applied to mathematics, this means that students’ ability to generate original or flexible solutions depends on their understanding of mathematical concepts and procedures. Building on this foundation, Sriraman (2009) and R. Leikin and Lev (2007) propose a mathematics-specific framework in which fluency, flexibility, and originality are core indicators of mathematical creativity. Tasks such as MSTs effectively reveal creativity when students apply domain-specific strategies in flexible and meaningful ways, situating mathematical creativity at the intersection of general reasoning and mathematical content knowledge.
Empirical evidence reinforces this domain-specific perspective. Lin and Cho (2011) examined Korean students’ performance on open-ended problem-solving tasks and found that mathematical knowledge significantly predicted fluency, flexibility, and originality. Students with stronger mathematical foundations were more capable of producing diverse and original solutions, illustrating that domain knowledge enables rather than constrains creative expression. Their work highlights that mathematical creativity is best understood as a knowledge-embedded process, emerging through the integration of mathematical understanding and flexible strategic thinking.
Complementary findings come from the development of the Mathematical Creative Problem Solving Ability Test (MCPSAT) by Kim et al. (2004), which distinguishes mathematical creativity from mathematical thinking ability while recognizing their interdependence. Their model supports the claim that creativity flourishes when students possess the knowledge base needed to generate and evaluate novel approaches.
Finally, while domain-general frameworks such as Guilford’s (1968) Structure of Intellect model and Torrance’s (1974) Tests of Creative Thinking identify broad cognitive dimensions of creativity (e.g., fluency, flexibility, originality, elaboration), they offer limited explanatory power for understanding how creativity manifests in mathematics. In contrast, Amabile’s componential model, mathematics-specific frameworks, and empirical studies such as Lin and Cho (2011) converge to show that mathematical creativity is best conceptualized as a domain-embedded construct. It emerges most powerfully when learners apply solid mathematical knowledge in flexible and original ways to produce meaningful solutions.

1.2. Instructional Support to Develop Mathematical Creativity

Mathematical creativity is a mental process that can be developed and enhanced through teacher-led interventions and enrichment programs by well-trained teachers (Kozlowski et al., 2019). Research emphasizes the central role of teachers in shaping students’ creative mathematical thinking by designing challenging tasks, fostering flexible strategies, and encouraging original problem solving (Nadjafikhah et al., 2012; Yang et al., 2023b). At the same time, enrichment programs offer extended opportunities beyond the standard curriculum, providing gifted learners with more opportunities to engage in content of interest and the chance to develop their talents in supportive environments (Miller & Gentry, 2010; Mun & Hertzog, 2018; Yang et al., 2023b). Together, these approaches illustrate how formal instruction and supplemental enrichment can work to cultivate creativity in mathematics.

1.2.1. Teacher-Led Interventions

Nadjafikhah et al. (2012) emphasized the critical role of teachers in fostering students’ mathematical creative thinking. Yang et al. (2023a) also emphasized that teachers are key for “the development of talent in young gifted ELs”, stressing the need for a challenging curriculum, specialized teacher preparation, and the use of effective classroom teaching. Several teacher-led interventions have been shown to be effective in promoting mathematical creativity (Kozlowski et al., 2019). Below, we describe these interventions.
Problem-Solving and Problem-Posing Tasks. Problem-Solving and Problem-Posing Tasks (Silver, 1997) involve formulating, attempting to implement, and reformulating a strategy, and ultimately solving the problem. A typical problem-solving task might be “Given the set of numbers {3, 21, 2, 10} and the symbols for addition, subtraction, multiplication, and division, create as many combinations as possible that equal 17.” (Maxwell, 1974). An example of a problem-posing task could involve presenting participants with a complete cross-number puzzle and asking them to generate the questions, encouraging diverse and creative thinking (Haylock, 1985). Throughout the intervention, students engage in generating multiple solutions, shifting strategies when encountering obstacles, and producing original problem-solving approaches (Silver, 1997). By posing their own problems, students also practice creating diverse problem sets, designing tasks that encourage divergent thinking, and analyzing and constructing novel problems (Silver, 1997).
Multiple Solution Tasks. MSTs are a practical intervention for assessing students’ creative thinking in mathematics. According to a systematic review by Kozlowski and Chamberlin (2022), MSTs are easy to administer and score. They are straightforward to use because they do not require complex responses and are commonly employed to evaluate students’ mathematical learning outcomes at the end of each semester. However, one limitation of MSTs is that they may not effectively promote higher-order cognitive processes (Yonker, 2011), and the feedback provided is typically limited (Chattopadhyay, 2016).
Model-Eliciting Activities. Model-eliciting activities (MEAs) (Chamberlin, 2013, 2016) foster students’ conceptual understanding by engaging them in model creation and complex problem-solving. As Gilat and Amit (2013) describe in their case study, MEAs supported several cognitive characteristics such as flexibility, combination, and analogy, while also promoting affective dimensions of motivation and interest, self-efficacy and persistence, and metacognition and self-reflection. In MEAs, students also have opportunities to develop multiple solutions that satisfy the problem’s requirements, and this open-ended structure fosters fluency, innovation, and idea generation (Stohlmann, 2013).
Open-Ended Questions. Open-ended questions provide students with opportunities to apply fluency, flexibility, and originality in their thinking (Silver, 1997). The problem-solving carried out with a group of students also allow students to observe and reflect on their peers’ mathematical reasoning and justifications (Hiebert et al., 1997). Exposure to multiple solutions stimulates students’ desire to be creative, encouraging them to internalize and apply creative strategies in future learning. In such environments, creativity is made visible and nurtured, rather than being constrained or isolated (Kozlowski et al., 2019).

1.2.2. Math Enrichment Programs

Although mathematics is a required subject taught in all schools, enrichment math is commonly offered outside of regular school hours, especially in elementary and middle schools, with the goal of providing challenging, in-depth exploration of topics to further develop students’ talents and abilities that are not typically covered in the standard curriculum (Mun & Hertzog, 2018). The National Association for Gifted Children (2025) defines enrichment as “enrichment activities that add or go beyond the existing curriculum. They may occur in the classroom or in a separate setting such as a pull-out program.” Enrichment programs (e.g., after-school classes, Saturday programs) can offer both academic and social benefits for gifted students from diverse backgrounds. These programs have been shown to improve their school performance, increase enrollment in advanced courses, and eventually influence their decisions to pursue higher education (Miller & Gentry, 2010). Math enrichment classes provide students with opportunities to explore topics in greater depth than is typically possible in regular classrooms. They allow students to pursue existing interests, develop new ones, and engage in challenging and stimulating instructional practices and learning environments (Mun & Hertzog, 2018).
For gifted ELs, enrichment programs play a critical role in nurturing mathematical creativity by combining cognitively demanding content with strategic language support. Evidence from Project HOPE’s implementation of the M3 curriculum illustrates this effect. In a study of mathematically promising third-grade ELs, students who participated in the after-school M3 enrichment program for one year made significantly greater gains in mathematics achievement than peers in comparison classrooms (effect size = 0.63), reflecting the curriculum’s emphasis on advanced mathematical reasoning and embedded language scaffolds (Cho et al., 2015).
Building on this foundation, Project BRIDGE integrates the RED model (Recognition, Expectation, Differentiation) with structured language scaffolding to support young gifted ELs. Observational studies found that students were more motivated and engaged in BRIDGE after-school classes than in their regular math classes across all levels of English proficiency and mathematical ability. The use of enriched tasks, culturally responsive teaching, and “Talk Moves” facilitated students’ mathematical reasoning and communication, with teacher use of Talk Moves significantly predicting students’ outcomes (Yang et al., 2023b).
Collectively, these studies demonstrate that well-designed enrichment programs can cultivate ELs’ mathematical creativity by deepening conceptual understanding, encouraging flexible problem solving, and supporting the development of mathematical language. This dual focus on content and language provides gifted ELs with meaningful opportunities to express creative mathematical thinking.

1.3. Mathematical Creativity and Gifted English Learners

An EL is federally defined as a student aged 3–21, enrolled in elementary or secondary school, who was either not born in the U.S. or has a non-English native language—including Native American or Alaska Native students whose home language limits English proficiency (United States Department of Education, 2016). ELs are the fastest-growing student population in America over the previous two decades (Doan et al., 2024) and make up almost 11% of all public school students (National Center for Education Statistics, 2024). Many gifted ELs are immigrants or children of immigrants, reflecting broader U.S. immigration patterns (Mun et al., 2020). Most ELs are Hispanic (77.9%), followed by Asian (9.7%), White (6.1%), Black (4.2%), and smaller percentages from other racial or ethnic groups (National Center for Education Statistics, 2024). Nearly one-quarter of ELs under 18 live with at least one immigrant parent, with the majority born in the U.S. (Migration Policy Institute, 2019). Growing linguistic diversity is evident, as the number of people who speak a non-English language at home rose from 23.1 million in 1980 to 67.8 million in 2019, with Spanish, Chinese, Tagalog, Vietnamese, and Arabic among the most common (United States Census Bureau, 2022).
While ELs face challenges, they also bring important strengths, including funds of knowledge—cultural and experiential knowledge developed over time (Moll et al., 1992; Mun et al., 2016; Castellano & Francis, 2022). Gifted ELs, in particular, could demonstrate high potential across academics, creativity, leadership, and the arts (Harris et al., 2007). They often contribute unique cultural and linguistic assets by showing pride in their heritage, translating for peers, and navigating between languages and cultures with advanced skills such as code-switching (Valdés Fallis, 1978; Castellano, 2002). Many also display global awareness, strong mathematical and creative abilities, and superior intellectual or academic talent even while learning English.
Although a growing body of work has examined mathematical creativity and its relationship to achievement (Starko, 1994; Mann, 2005; Akgul & Kahveci, 2016), there is limited research focusing specifically on young, gifted ELs (Cho et al., 2015; Yang et al., 2023b; Yang & Cho, 2024; Mun et al., 2020). Most studies address mathematical creativity within general populations or gifted education more broadly (Sriraman et al., 2013; Kozlowski & Chamberlin, 2022), with relatively little attention to the intersection of creativity, enrichment programming, and linguistic diversity. Given evidence that teacher-led interventions and enrichment programs can play a critical role in fostering mathematical creativity (Nadjafikhah et al., 2012; Yang et al., 2023b; Mun & Hertzog, 2018), additional research is needed to understand how such approaches may support both talent development and language acquisition among young, gifted ELs.
  • (RQ1) To what extent do creativity outcomes differ between intervention and comparison groups?
  • (RQ2) Which factors significantly predict creativity outcomes?

2. Materials and Methods

This study employed a quasi-experimental pretest–posttest comparison group design to examine Tangram Creativity Assessment outcomes, and a correlational predictive design to identify the predictors of creativity performance.

2.1. Participants

This study consists of 250 kindergarten ELs with high potential. Participants were nominated by their teachers using the Scales for Rating the Behavioral Characteristics of Superior Students (Renzulli et al., 2009). Teachers rated students on traits commonly associated with mathematical talent (e.g., preference for challenging tasks and using creative or unusual problem-solving strategies; Gavin, 2005). Students were then randomly assigned to intervention and comparison groups. The study occurred across six schools in large urban districts in New York, Texas, and California. Demographic information for participants is presented in Table 1.

2.2. Instruments

2.2.1. Tangram Creativity Assessment (TCA)

In the tangram creativity assessment, kindergarten ELs with high potential were asked to complete a large triangle using small tangram pieces of triangles, squares, and parallelograms (See Table 2). Although there are only five possible correct configurations, the three Torrance creativity dimensions—fluency, originality, and flexibility—remain distinct and meaningful for assessment.
Fluency
Fluency measures the total number of unique correct solutions generated by a student. Fluency answers the question: How many correct solutions did the student find? While fluency captures productivity, it does not differentiate between common and uncommon responses.
Flexibility
Flexibility measures the variety of conceptual or strategic approaches used to solve the problem. The five solutions can be categorized by structural or procedural attributes (e.g., triangle, square, or parallelogram configurations). Flexibility scores are calculated by counting the number of distinct categories represented in a student’s set of solutions. This ensures recognition of students who shift between different approaches, rather than relying on a single strategy.
Flexibility is the ability to shift between different categories of ideas.
In this tangram case, the three categories were decided based on conceptual meaning and solution strategy or structure (see Table 2)
Category A: Triangle configurations (Responses 1 and 2)
Category B: Square configurations (Response 3)
Category C: Parallelogram configurations (Responses 4 and 5)
The number of different categories that a student’s responses fall into was counted. For example:
Student finds responses 1, 2, 3 → if 1 & 2 are both in Category A and 3 is in Category B, flexibility score = 2.
Student finds Responses 1, 3, 5 → if they span three distinct categories, flexibility score = 3.
Originality
Originality answers a question: How unusual or rare were those solutions compared to peers? It is operationally defined as statistical rarity relative to a reference sample. Following TTCT-style frequency norming and subsequent uses in a mathematics context, higher values were assigned to statistically less frequent solutions in the sample. Because the tangram task affords a finite solution space (five valid configurations), rarity can be estimated precisely and stably. The following cut-points were adopted: rare <10% = 3 points; infrequent 10–19% = 2 points; occasional 20–40% = 1 point; common >40% = 0 points (See Table 3).
For the tangram task, originality captures a qualitative difference in thinking, not just quantity. For example, if two students might both have a fluency score of 3, but if Student A’s solutions are Responses 1, 2, and 3, and Student B’s are Responses 1, 2, and 5, Student B has shown more original thinking. This aligns with Torrance’s intent: originality is about deviation from the norm, even if fluency already counts the total responses.
Including originality and flexibility scores alongside fluency provides a more comprehensive assessment of creative thinking, even within a constrained problem space (See Table 4). It captures not only productivity but also the novelty and versatility of students’ problem-solving processes.

2.2.2. Tangram-Specific Problem-Solving Speed (TPSS)

Task-specific problem-solving speed was measured to examine how cognitive efficiency supports creative performance (Beaty et al., 2016; Benedek & Neubauer, 2013; Guilford, 1968) and how problem-solving fluency relates to mathematical creativity (R. Leikin, 2009; Silver, 1997). Tangram-specific Problem-Solving Speed (TPSS) was assessed to capture how quickly high-potential kindergarten ELs could compose shapes using given tangram pieces (see Table 5). This measure focused on the time taken to achieve the first correct solution type, with higher scores reflecting faster completion. Children were instructed to cover part of a triangle using the tangram pieces, and their responses were timed and scored on a 0–3 scale. The scoring rubric emphasized both efficiency and accuracy in covering the target space without extending beyond the shape’s perimeter.

2.2.3. Cognitive Abilities Test

CogAT was administered to measure general reasoning ability across verbal, quantitative, and nonverbal domains, providing an index of the cognitive flexibility and problem-solving capacity that may support creative mathematical thinking (Krutetskii, 1976; Sriraman, 2009).

2.2.4. Mathematics Achievement

NWEA MAP Growth math was administered to measure mathematical achievement, reflecting mastery of grade-level concepts and skills through a computer-adaptive format (NWEA, 2025). It provides national norms for instructional planning. The grade percentile rank on the NWEA MAP Growth Math assessment indicates a student’s performance relative to grade-level peers nationwide.
Using these measures allowed us to examine whether mathematical creativity among high-potential ELs is more strongly linked to general cognitive reasoning or to domain-specific achievement or to Tangram problem-specific skills, thereby providing a nuanced understanding of creativity’s predictors in early mathematics learning.

2.3. Implementation

Intervention students participated in after-school math classes, which used a modified version of the Mentoring Young Mathematicians (M2) math curriculum. The M2 is a curriculum designed around the focus of teaching advanced mathematics using research-based practices and standards in mathematics education and early childhood education (Casa et al., 2017; Gavin et al., 2013a, 2013b). The modifications included routine and adaptive scaffolding (de Oliveira & Athanases, 2017) tailored to make advanced subject content comprehensible for linguistically diverse students (Yang & Cho, 2024; Yang et al., 2021, 2023a, 2023b). The intervention group teachers attended a five-day professional development workshop during which they learned about strategies in teaching math to ELs. Two units (geometry and measurement) were implemented in kindergarten for 80 h of instructional time over four months. The comparison group students were also enrolled in an after-school program for the same number of hours, where the same grade-level school curriculum was implemented.

2.4. Data Analysis

Analyses focused on the Tangram Creativity Assessment across fluency, flexibility, originality scores, CogAT, TPSS, and NWEA MAP Growth Math. Data were analyzed using Mplus Version 8.5 (Muthén & Muthén, 1998–2017).
MANOVA was conducted to examine group (intervention vs. comparison) differences in pre-test scores. ANCOVAs were performed on post-test scores, using pre-test as a covariate to estimate intervention effects.
The two-group structural equation modeling (intervention vs. comparison) analysis was conducted. The two latent factors (Pre-TCA and Post-TCA) were indicated by three observed variables (fluency, flexibility, originality). We evaluated configural invariance (same pattern of loadings) and then metric invariance by constraining factor loadings to equality across groups. Model adequacy was evaluated using fit indices. The structural paths predicting Post-TCA from Pre-TCA, TPSS, CogAT, and NWEA were compared across groups.

3. Results

3.1. Comparison of Tangram Creativity Assessment Scores

The intervention group demonstrated higher post-TCA mean scores for fluency, flexibility, and originality than the comparison group. A MANOVA was conducted to examine the effect of group (intervention vs. comparison) on pre-test TCA scores across fluency, flexibility, and originality (see Table 6). Results indicated no significant main effect of the group on the combined TCA scores, and there were no significant group differences on fluency, flexibility, or originality (all ps > 0.05).
The ANCOVA results examining post-TCA scores on fluency, flexibility, and originality between groups after adjusting for pre-test scores were presented (See Table 7). For total TCA, results indicated a significant group effect. The intervention group achieved higher adjusted post-test scores (M = 3.02, SE = 0.22) than those in the comparison group (M = 2.16, SE = 0.28). For fluency, the group effect was significant; the intervention group scored significantly higher (M = 1.02, SE = 0.07) than the comparison group (M = 0.72, SE = 0.09). For flexibility, the group effect was significant. Adjusted post-test scores were higher for the intervention group (M = 0.93, SE = 0.06) than for the comparison group (M = 0.71, SE = 0.08). Finally, for originality, results showed a significant effect of group effect, and the intervention group again outperformed those in the comparison group (M = 1.09, SE = 0.11 vs. M = 0.72, SE = 0.14). Taken together, these findings indicated that, after controlling for pre-test performance, the intervention group scored significantly higher than those in the comparison group across all outcomes (total TCA, fluency, flexibility, and originality).

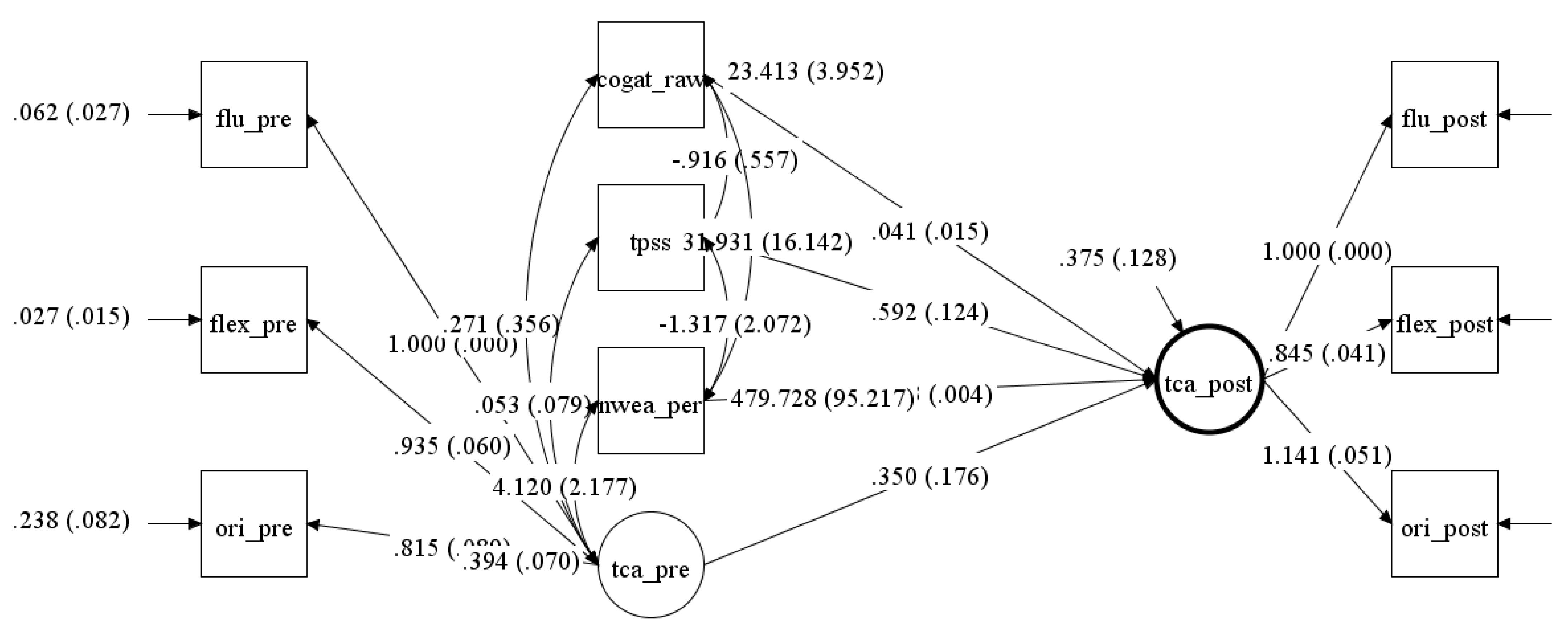
3.2. Path Analysis of Tangram Creativity Assessment Across Fluency, Flexibility, and Originality Scores

A path analysis was conducted to examine predictors of TCA scores across fluency, flexibility, and originality as well as CogAT, TPSS, and NWEA MAP Growth Mathematics (See Figure 1). The configural/metric measurement model was significant (See Table 8). Factor loadings were constrained to equality across groups (metric invariance), and model fit did not degrade relative to the unconstrained model (ΔCFI < 0.010, ΔRMSEA < 0.015). This indicates that metric invariance was supported, allowing comparisons of structural paths across groups.
The latent TCA factors (Pre and Post) were well defined by fluency, flexibility, and originality indicators, with moderate-to-strong loadings (≈0.80–1.15). These loadings provide evidence of internal consistency and convergent validity of the construct in this study’s sample. The autoregressive path from Pre-TCA to Post-TCA was small to moderate, indicating that prior performance explained part, but not all, of the variance. Across all participants, predictors accounted for approximately 55–60% of the variance in Post-TCA, providing strong evidence of predictive validity. TPSS emerged as the most robust predictor, while CogAT and NWEA Math showed only modest and non-robust effects when pooling groups. Collectively, these results support the reliability and validity of the TCA as a measure of creative performance in this sample.
TPSS positively predicted TCA in both groups (INT: β = 0.74, p < 0.001; COM: β = 0.60, p < 0.001). COGAT predicted TCA in INT (β = 0.24, p = 0.005) but not in COM (β = 0.02, p = 0.80), likewise NWEA Math. The autoregressive path from Pre-TCA to Post-TCA was modest. Explained variance was R2 = 0.69 for INT and R2 = 0.46 for COM, indicating substantively stronger prediction in the intervention group. In the INT group, the predictors (TPSS, COGAT, NWEA Math, and Pre-TCA) together account for 69% of the variance, versus 46% in COMP. It was indicated that the model is more informative and linked to outcomes for INT, consistent with a more coherent effect pattern in the intervention group driven by TPSS.
Results indicated that general cognitive ability, mathematics achievement, and tangram problem-solving speed contributed to TCA performance, with TPSS emerging as the most consistent and robust predictor. CogAT and TPSS significantly predicted higher post-TCA scores, suggesting that both higher cognitive ability and faster Tangram-specific problem-solving speed were associated with more original and flexible solutions. Overall, these findings demonstrate that TCA performance is shaped by a combination of cognitive and achievement factors, with problem-solving speed playing a particularly influential role.

4. Discussion

This study investigated the intervention effects, predictors, and outcomes of mathematical creativity among high-potential kindergarten ELs using MANOVA and structural equation modeling (SEM) conducted in Mplus. Grounded in Amabile’s (1996) Componential Model of Creativity and Sriraman’s (2009) framework of mathematical creativity, the study examined how general reasoning ability, mathematical achievement, and task-specific problem-solving skills contribute to creativity outcomes on the Tangram Creativity Assessment (TCA), and whether a targeted enrichment intervention can foster creativity in early mathematics learning. The use of SEM allowed for simultaneous examination of the unique contributions of each predictor variable, offering a more comprehensive understanding of the relationships among ability, achievement, and creativity than would be possible with simple regression or correlational analyses. The discussion below interprets these findings in light of the theoretical framework and prior research, focusing first on the predictors of mathematical creativity, followed by the effects of the intervention, the relationship between creativity and achievement, and implications for early gifted education.

4.1. Predictors of Mathematical Creativity

Structural equation modeling (SEM) using Mplus clarified how cognitive and achievement-related factors contribute to mathematical creativity. General reasoning ability (CogAT), domain-specific achievement (NWEA Map Growth Math), and task-specific problem-solving efficiency (TPSS) had significant direct effects on fluency, flexibility, and originality. The results supported arguments that general cognitive abilities—such as flexible reasoning and pattern recognition—underpin creative mathematical performance (Krutetskii, 1976; Sriraman, 2009). Domain-specific knowledge also emerged as a significant predictor, consistent with theories emphasizing content knowledge as a foundation for creativity (Amabile, 1996; R. Leikin & Lev, 2007; Sriraman, 2009) and theories that higher mathematical achievement supports higher math creativity (Mann, 2005; Plucker et al., 2004; Runco & Jaeger, 2012; Starko, 1994); the negative path coefficient in the SEM model was due to reversed percentile rankings. TPSS scores were the strongest predictors of creativity, reflecting their closer alignment with the cognitive and spatial demands of the creativity task. This underscores the value of domain-proximal performance measures and of fostering both conceptual understanding and automatization to support flexible, creative thinking (Sweller, 1988; Sweller et al., 1998; Beaty et al., 2016).
Taken together, these results suggest that the intervention’s impact on ELs’ conceptual understanding and skill mastery contributed to improved performance on the key cognitive and domain-specific predictors of mathematical creativity. By improving conceptual comprehension and procedural mastery, the intervention appears to have strengthened the foundational knowledge and skills necessary for creative mathematical performance. This underscores the importance of both enrichment opportunities and domain-proximal performance measures in fostering creative mathematical thinking (Sweller, 1988; Sweller et al., 1998; Beaty et al., 2016).

4.2. Effects of Enrichment Intervention

The ANCOVA results showed that, after controlling for pretest differences, the intervention group significantly outperformed the comparison group on posttest mathematical creativity scores. These consistent effects indicate that the modified Mentoring Young Mathematicians (M2) curriculum, adapted for linguistically diverse learners, effectively fostered mathematical talent development—including creativity (Cho et al., 2015; Mun & Hertzog, 2018; Yang et al., 2023b). The enrichment-based approach provided gifted ELs with structured opportunities to engage deeply with advanced mathematical concepts, develop a strong conceptual understanding, and master key mathematical skills, while simultaneously strengthening their language and reasoning abilities (Doan et al., 2024).
This solid foundation in mathematical knowledge and problem-solving processes appears to have laid the groundwork for students to generate flexible and original solutions, leading to significant growth in mathematical creativity. Supporting this interpretation, Tangram Problem Solving Speed (TPSS) emerged as the strongest predictor of creativity outcomes on the Tangram Creativity Assessment (TCA), with a larger effect in the intervention group than in the comparison group. Students who quickly and accurately solved the tangram tasks were likely drawing on well-developed conceptual schemas and efficient strategies, which freed cognitive resources for creative exploration of alternative solutions.
These findings are highly consistent with Lin and Cho’s (2011) empirical work, which demonstrated that students with stronger mathematical foundations were better able to produce diverse and original solutions to novel problems. Similar to their results, the present study shows that conceptual mastery and efficient strategy use serve as critical enablers of mathematical creativity, particularly among students who receive targeted enrichment. Together, these findings highlight how strengthening foundational knowledge through enrichment can directly support the development of creative mathematical thinking in gifted ELs.

4.3. Language Proficiency and Creativity Performance

Language proficiency influenced how students demonstrated creativity. For ELs, limited proficiency may have constrained performance on language-dependent assessments by diverting cognitive resources away from flexible thinking (Cummins, 1979; Swain & Lapkin, 1995). However, in tangram-based mathematical creativity tasks with low linguistic demands, EL students were able to better demonstrate their creative potential by relying on visual–spatial reasoning. This aligns with research linking bilingualism to enhanced cognitive flexibility and associative thinking (Kharkhurin, 2010; M. Leikin, 2013), highlighting that language proficiency can act as both a barrier and a resource depending on task characteristics.

4.4. Limitations and Future Directions

Several limitations should be acknowledged. First, although students were randomly assigned to groups, teacher nominations may have introduced selection bias (Renzulli et al., 2009). Second, originality scoring was based on sample-wide frequency, which may vary across contexts; replication in different settings would strengthen validity (Torrance, 1974; Suherman & Vidákovich, 2022). Third, while this study examined creativity within a constrained tangram problem space, future work should extend to broader mathematical domains (Tabach & Friedlander, 2013).
Future research should examine longitudinal trajectories: Do early creativity gains persist into the elementary grades, and how do these gains influence later achievement? In addition, future work should investigate whether students who are more mathematically creative at a given time point also achieve higher in mathematics, highlighting the concurrent relationship between creativity and achievement. Qualitative analyses of student strategies could further illuminate the processes underlying creative problem solving among ELs (Levenson, 2013; Beghetto, 2017).

5. Conclusions

This study provides evidence that high-potential kindergarten ELs demonstrate meaningful levels of mathematical creativity when engaged in open-ended, geometry-based tasks. Creativity outcomes were predicted by both general cognitive ability and domain-specific mathematical reasoning, underscoring the multidimensional nature of mathematical talent (Krutetskii, 1976; Sriraman, 2009). Importantly, the intervention using a linguistically responsive version of the M2 curriculum significantly enhanced students’ creativity compared to business-as-usual instruction (Mun & Hertzog, 2018; Yang et al., 2023b).
The findings carry the following three key messages. Creativity is measurable and observable in early childhood, even within structured problem spaces like tangrams (Torrance, 1974; Kozlowski et al., 2019). Instructional support matters—targeted enrichment programs can meaningfully foster creativity in young ELs with high potential (Miller & Gentry, 2010; Nadjafikhah et al., 2012). Equity in gifted education requires new approaches that recognize and nurture the creative potential of linguistically diverse learners (Mun et al., 2020; Yang & Cho, 2024).
By embedding creativity-focused tasks within both classroom instruction and enrichment programs, educators can ensure that ELs’ talents are recognized and cultivated early. This work reinforces the argument that creativity is not ancillary to mathematics learning but central to developing the flexible, original thinkers needed for future innovation (Plucker et al., 2004; Starko, 2022).

Author Contributions

Conceptualization, G.Ö. and S.C.; methodology, G.Ö. and S.C.; software, G.Ö.; validation, G.Ö. and S.C.; formal analysis, G.Ö.; investigation, G.Ö., R.U.M., Y.S., W.L., M.S. and S.C.; resources, G.Ö., R.U.M., Y.S., W.L., M.S. and S.C.; data curation, G.Ö.; writing—original draft preparation, G.Ö., R.U.M., Y.S., W.L., M.S. and S.C.; writing—review and editing, G.Ö., R.U.M., Y.S., W.L., M.S. and S.C.; visualization, G.Ö. and S.C.; supervision, S.C.; project administration, S.C.; funding acquisition, S.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Jacob K. Javits Gifted and Talented Students Education Program: S206A170028.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of St. John’s University (protocol code 0118-143) on 5 February 2018.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Data is unavailable due to privacy or ethical restrictions.

Acknowledgments

During the preparation of this manuscript/study, the author(s) used ChatGPT-4 to assist with APA formatting and to improve clarity through manuscript review. The authors have reviewed and edited all AI-generated content and take full responsibility for the content of this publication.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ELsEnglish Learners
TCATangram Creativity Assessment
CogAT_RAWCognitive Abilities Test (CogAT) total raw score
CogAT_GPRCognitive Abilities Test (CogAT) grade percentile rank
TPSSTangram Problem Solving Speed
NWEANWEA MAP Growth Mathematics
NWEA PER NWEA MAP Growth Mathematics Achievement Percentiles
INTIntervention Group
COMComparison Group

References

  1. Abbott, D. H. (2010). Constructing a creative self-efficacy inventory: A mixed methods inquiry (Publication No. 3402936) [Doctoral dissertation, University of Nebraska–Lincoln]. ProQuest Dissertations Publishing. [Google Scholar]
  2. Akgul, S., & Kahveci, N. G. (2016). A study on the development of a mathematics creativity scale. Eurasian Journal of Educational Research, 62(1), 57–76. [Google Scholar] [CrossRef]
  3. Amabile, T. M. (1996). Creativity in context: Update to the social psychology of creativity. Westview Press. [Google Scholar]
  4. Bai, H., Mulder, H., Moerbeek, M., Leseman, P. P. M., & Kroesbergen, E. H. (2024). The development of divergent thinking in 4- to 6-year-old children. Creativity Research Journal, 36(4), 656–674. [Google Scholar] [CrossRef]
  5. Balka, D. S. (1974). Using research in teaching: Creative ability in mathematics. The Arithmetic Teacher, 21(7), 633–636. [Google Scholar] [CrossRef]
  6. Beaty, R. E., Benedek, M., Silvia, P. J., & Schacter, D. L. (2016). Creative cognition and brain network dynamics. Trends in Cognitive Sciences, 20(2), 87–95. [Google Scholar] [CrossRef]
  7. Beghetto, R. A. (2017). Lesson unplanning: Toward transforming routine tasks into non-routine problems. ZDM Mathematics Education, 49(7), 987–993. [Google Scholar] [CrossRef]
  8. Benedek, M., & Neubauer, A. C. (2013). Revisiting Mednick’s model on creativity-related differences in associative hierarchies: Evidence for a common path to uncommon thought. The Journal of Creative Behavior, 47(4), 273–289. [Google Scholar] [CrossRef]
  9. Bicer, A., Chamberlin, S., & Perihan, C. (2021). A meta-analysis of the relationship between mathematics achievement and creativity. The Journal of Creative Behavior, 55(3), 569–590. [Google Scholar] [CrossRef]
  10. Casa, T. M., Firmender, J. M., Gavin, M. K., & Carroll, S. R. (2017). Kindergarteners’ achievement on geometry and measurement units that incorporate a gifted-education approach. Gifted Child Quarterly, 61(1), 52–72. [Google Scholar] [CrossRef]
  11. Castellano, J. A. (2002). Renavigating the waters: The identification and assessment of culturally and linguistically diverse students for gifted and talented education. In J. A. Castellano, & E. Diaz (Eds.), Reaching new horizons: Gifted and talented education for culturally and linguistically diverse students (pp. 94–116). Allyn & Bacon. [Google Scholar]
  12. Castellano, J. A., & Francis, E. M. (2022). Identifying and educating gifted English language learners. In J. A. Castellano, & K. L. Chandler (Eds.), Identifying and serving diverse gifted learners: Meeting the needs of special populations in gifted education (pp. 217–239). Routledge. [Google Scholar]
  13. Chamberlin, S. A. (2013). Statistics for kids: Using model-eliciting activities to investigate concepts in statistics. Prufrock Press. [Google Scholar]
  14. Chamberlin, S. A. (2016). Probability for kids: Using model-eliciting activities to investigate probability concepts. Prufrock Press. [Google Scholar]
  15. Chattopadhyay, O. (2016). Multiple choice question tests for educational assessment. Indian Journal of Hygiene and Public Health, 2(1), 92–100. [Google Scholar]
  16. Cho, S., Yang, J., & Mandracchia, M. (2015). Effects of M3 curriculum on mathematics and English proficiency achievement of mathematically promising English language learners. Journal of Advanced Academics, 26(2), 112–142. [Google Scholar] [CrossRef]
  17. Clements, D. H., & Sarama, J. (2011). Learning trajectories in early mathematics: Sequences of acquisition and teaching. Lawrence Erlbaum Associates. (Original work published 2004). [Google Scholar]
  18. Cummins, J. (1979). Cognitive/academic language proficiency, linguistic interdependence, the optimum age question and some other matters. Working Papers on Bilingualism, 19, 121–129. [Google Scholar]
  19. de Oliveira, L. C., & Athanases, S. Z. (2017). A framework to reenvision instructional scaffolding for linguistically diverse learners. Journal of Adolescent & Adult Literacy, 61(2), 123–129. [Google Scholar] [CrossRef]
  20. Dickman, B. (2018). Creativity in question and answer digital spaces for mathematics education: A case study of the water triangle for proportional reasoning. In V. Freiman, & y. J. L. Tassell (Eds.), Creativity and technology in mathematics education (pp. 233–248). Springer. [Google Scholar]
  21. Doan, S., Morales, S., Özek, U., & Schwartz, H. (2024). Educational spillover effects of new English Learners in a new destination state. Educational Evaluation and Policy Analysis. advance online publication. [Google Scholar] [CrossRef]
  22. Gavin, M. K. (2005). Are we missing anyone? Identifying mathematically promising students. Gifted Education Communicator, Fall/Winter, 24–29. [Google Scholar]
  23. Gavin, M. K., Casa, T. M., Adelson, J. L., & Firmender, J. M. (2013a). The impact of advanced curriculum on the achievement of mathematically promising elementary students. Gifted Child Quarterly, 57(4), 271–282. [Google Scholar] [CrossRef]
  24. Gavin, M. K., Casa, T. M., Firmender, J. M., & Carroll, S. R. (2013b). The impact of advanced geometry and measurement curriculum units on the mathematics achievement of first-grade students. Gifted Child Quarterly, 57(2), 71–84. [Google Scholar] [CrossRef]
  25. Gilat, T., & Amit, M. (2013). Exploring young students creativity: The effect of model eliciting activities. PNA, 8(2), 51–59. [Google Scholar] [CrossRef]
  26. Guilford, J. P. (1968). Intelligence, creativity, and their educational implications. R.R. Knapp. [Google Scholar]
  27. Hadamard, J. (2020). The mathematician’s mind: The psychology of invention in the mathematical field. Princeton University Press. [Google Scholar]
  28. Harris, B., Rapp, K. E., Martinez, R. S., & Plucker, J. A. (2007). Identifying English language learners for gifted and talented programs: Current practices and recommendations for improvement. Roeper Review, 29(5), 26–29. [Google Scholar] [CrossRef]
  29. Haylock, D. W. (1985). Conflicts in the assessment and encouragement of mathematical creativity in schoolchildren. International Journal of Mathematical Education in Science and Technology, 16(4), 547–553. [Google Scholar] [CrossRef]
  30. Hiebert, J., Carpenter, T. P., Fennema, E., Fuson, K., Wearne, D., Murray, H., Oliver, A., & Human, P. (1997). Making sense: Teaching and learning mathematics with understanding. Heinemann Publishers. [Google Scholar]
  31. Imai, T. (2000). The influence of overcoming fixation in mathematics towards divergent thinking in open-ended mathematics problems on Japanese junior high school students. International Journal of Mathematical Education in Science and Technology, 31(2), 187–193. [Google Scholar] [CrossRef]
  32. Jensen, L. R. (1973). The relationships among mathematical creativity, numerical aptitude and mathematical achievement [Doctoral dissertation, The University of Texas at Austin]. [Google Scholar]
  33. Kharkhurin, A. V. (2010). Bilingual verbal and nonverbal creative behavior. International Journal of Bilingualism, 14(2), 211–226. [Google Scholar] [CrossRef]
  34. Kim, H., Cho, S., & Ahn, D. (2004). Development of mathematical creative problem solving ability test for identification of the gifted in math. Gifted Education International, 18(2), 164–174. [Google Scholar] [CrossRef]
  35. Kozlowski, J. S., & Chamberlin, S. A. (2022). Mathematical creativity research in the elementary grades. In S. A. Chamberlin, P. Liljedahl, & M. Savić (Eds.), Mathematical creativity. Research in mathematics education (pp. 65–80). Springer. [Google Scholar] [CrossRef]
  36. Kozlowski, J. S., Chamberlin, S. A., & Mann, E. (2019). Factors that influence mathematical creativity. The Mathematics Enthusiast, 16(1), 505–540. [Google Scholar] [CrossRef]
  37. Krutetskii, V. A. (1976). The psychology of mathematical abilities in school children. University of Chicago Press. [Google Scholar]
  38. Leikin, M. (2013). The effect of bilingualism on creativity: Developmental and educational perspectives. International Journal of Bilingualism, 17(4), 431–447. [Google Scholar] [CrossRef]
  39. Leikin, R. (2009). Exploring mathematical creativity using multiple solution tasks. In R. Leikin, A. Berman, & B. Koichu (Eds.), Creativity in mathematics and the education of gifted students (pp. 129–145). Sense Publishers. [Google Scholar]
  40. Leikin, R., & Lev, M. (2007). Multiple solution tasks as a magnifying glass for observation of mathematical creativity. In J.-H. Woo, H.-C. Lew, K.-S. Park, & D.-Y. Seo (Eds.), Proceedings of the 31st conference of the international group for the psychology of mathematics education (Vol. 3, pp. 161–168). The Korea Society of Educational Studies in Mathematics. [Google Scholar]
  41. Levenson, E. (2013). Tasks that may occasion mathematical creativity: Teachers’ choice. Journal of Mathematics Teachers Education, 16, 269–291. [Google Scholar] [CrossRef]
  42. Li, L., & Disney, L. (2023). Young children’s mathematical problem solving and thinking in a playworld. Mathematics Education Research Journal, 35(1), 23–44. [Google Scholar] [CrossRef]
  43. Lin, C. Y., & Cho, S. (2011). Predicting creative problem-solving in math from a dynamic system model of creative problem solving ability. Creativity Research Journal, 23(3), 255–261. [Google Scholar] [CrossRef]
  44. Mann, E. L. (2005). Mathematical creativity and school mathematics: Indicators of mathematical creativity in middle school students (Publication No. 3205573) [Doctoral dissertation, University of Connecticut]. ProQuest Dissertations Publishing. [Google Scholar]
  45. Maxwell, A. A. (1974). An exploratory study of secondary school geometry students: Problem solving related to convergent-divergent productivity [Doctoral dissertation, The University of Tennessee]. [Google Scholar]
  46. Meier, M. A., Ehrengruber, A., Spitzley, L., Eller, N., Reiterer, C., Rieger, M., Skerbinz, H., Teuschel, F., Wiemer, M., Vogel, S. E., & Grabner, R. H. (2024). The prediction of mathematical creativity scores: Mathematical abilities, personality, and creative self-beliefs. Learning and Individual Differences, 113, 102473. [Google Scholar] [CrossRef]
  47. Migration Policy Institute. (2019). Legal protections for K-12 English learners and immigrant-background students. Available online: https://www.migrationpolicy.org/sites/default/files/publications/EL-Insight_Legal-Framwork_Final.pdf (accessed on 18 November 2025).
  48. Miller, R., & Gentry, M. (2010). Developing talents among high-potential students from low-income families in an out-of-school enrichment program. Journal of Advanced Academics, 21(4), 594–627. [Google Scholar] [CrossRef]
  49. Moll, L. C., Amanti, C., Neff, D., & Gonzalez, N. (1992). Funds of knowledge for teaching: Using a qualitative approach to connect homes and classrooms. Theory Into Practice, 31(2), 133–141. [Google Scholar] [CrossRef]
  50. Mun, R. U., Hemmler, V., Langley, S. D., Ware, S., Gubbins, E. J., Callahan, C. M., McCoach, D. B., & Siegle, D. (2020). Identifying and serving English Learners in gifted education: Looking back and moving forward. Journal for the Education of the Gifted, 43(4), 297–335. [Google Scholar] [CrossRef]
  51. Mun, R. U., & Hertzog, N. B. (2018). Teaching and learning in STEM enrichment spaces: From doing math to thinking mathematically. Roeper Review, 40(2), 121–129. [Google Scholar] [CrossRef]
  52. Mun, R. U., Langley, S. D., Ware, S., Gubbins, E. J., Siegle, D., Callahan, C. M., McCoach, D. B., & Hamilton, R. (2016, December). Effective practices for identifying and serving English learners in gifted education: A systematic review of the literature. National Center for Research on Gifted Education. [Google Scholar]
  53. Muthén, L. K., & Muthén, B. O. (1998–2017). Mplus user’s guide (8th ed.). Muthén & Muthén. [Google Scholar]
  54. Nadjafikhah, M., Yaftian, N., & Bakhshalizadeh, S. (2012). Mathematical creativity: Some definitions and characteristics. Procedia—Social and Behavioral Sciences, 31, 285–291. [Google Scholar] [CrossRef]
  55. National Association for Gifted Children. (2025). Glossary of terms. Available online: https://www.nagc.org/glossary-of-terms (accessed on 18 November 2025).
  56. National Association for the Education of Young Children & National Council of Teachers of Mathematics. (2010). Early childhood mathematics: Promoting good beginnings. National Association for the Education of Young Children. [Google Scholar]
  57. National Center for Education Evaluation and Regional Assistance. (2013). Teaching math to young children: A practice guide (NCEE 2014-4005). Institute of Education Sciences, U.S. Department of Education.
  58. National Center for Education Statistics. (2024). English learners in public schools. Condition of education. U.S. Department of Education, Institute of Education Sciences. Retrieved [Date]. Available online: https://nces.ed.gov/programs/coe/indicator/cgf (accessed on 18 November 2025).
  59. Novita, R., Putra, M., & Herman, T. (2018). Design learning in mathematics education: Engaging early childhood students in geometrical activities. Journal of Physics: Conference Series, 1097(1), 012137. [Google Scholar]
  60. NWEA. (2025). MAP growth. Available online: https://www.nwea.org/map-growth/ (accessed on 18 November 2025).
  61. Plucker, J. A., Beghetto, R. A., & Dow, G. T. (2004). Why isn’t creativity more important to educational psychologists? Potentials, pitfalls, and future directions in creativity research. Educational Psychologist, 39(2), 83–96. [Google Scholar] [CrossRef]
  62. Poincaré, H. (1948). Science and method. Dover. [Google Scholar]
  63. Price, D. A., & Yates, G. C. R. (2015). Impact of a brief ego depletion procedure on creative behaviour in the upper primary classroom. Educational Psychology, 35(3), 328–340. [Google Scholar] [CrossRef]
  64. Puryear, J. S., & Lamb, K. N. (2020). Defining creativity: How far have we come since Plucker, Beghetto, and Dow? Creativity Research Journal, 32(3), 206–214. [Google Scholar] [CrossRef]
  65. Renzulli, J. S., Siegle, D., Reis, S. M., Gavin, M. K., & Reed, R. E. S. (2009). An investigation of the reliability and factor structure of four new scales for rating the behavioral characteristics of superior students. Journal of Advanced Academics, 21(1), 84–108. [Google Scholar] [CrossRef]
  66. Runco, M. A., & Jaeger, G. J. (2012). The standard definition of creativity. Creativity Research Journal, 24(1), 92–96. [Google Scholar] [CrossRef]
  67. Sak, U., & Maker, C. J. (2006). Developmental variation in children’s creative mathematical thinking as a function of schooling, age, and knowledge. Creativity Research Journal, 18(3), 279–291. [Google Scholar] [CrossRef]
  68. Schoevers, E. M., Kroesbergen, E. H., & Kattou, M. (2020). Mathematical creativity: A combination of domain-general creative and domain-specific mathematical skills. The Journal of Creative Behavior, 54(2), 242–252. [Google Scholar] [CrossRef]
  69. Silver, E. A. (1997). Fostering creativity through instruction rich in mathematical problem solving and problem posing. ZDM—Mathematics Education, 29(3), 75–80. [Google Scholar] [CrossRef]
  70. Siswono, T. Y. E. (2011). Level of student’s creative thinking in classroom mathematics. Educational Research and Reviews, 6(7), 548–553. [Google Scholar]
  71. Sriraman, B. (2009). The characteristics of mathematical creativity. ZDM Mathematics Education, 41(1), 13–27. [Google Scholar] [CrossRef]
  72. Sriraman, B., Haavold, P., & Lee, K. (2013). Mathematical creativity and giftedness: A commentary on and review of theory, new operational views, and ways forward. ZDM Mathematics Education, 45(1), 215–225. [Google Scholar] [CrossRef]
  73. Starko, J. A. (1994). Creativity in the classroom. Longman. [Google Scholar]
  74. Starko, J. A. (2022). Creativity and mathematics: A beginning look. In S. A. Chamberlin, P. Liljedahl, & M. Savić (Eds.), Mathematical creativity. Research in mathematics education (pp. 3–13). Springer. [Google Scholar] [CrossRef]
  75. Stohlmann, M. (2013). Model eliciting activities: Fostering 21st century learners. Journal of Mathematics Education at Teachers College, 4(2). [Google Scholar] [CrossRef]
  76. Stolte, M., García, T., Van Luit, J. E., Oranje, B., & Kroesbergen, E. H. (2020). The contribution of executive functions in predicting mathematical creativity in typical elementary school classes: A twofold role for updating. Journal of Intelligence, 8(2), 26. [Google Scholar] [CrossRef]
  77. Suherman, S., & Vidákovich, T. (2022). Assessment of mathematical creative thinking: A systematic review. Thinking Skills and Creativity, 44(1), 101019. [Google Scholar] [CrossRef]
  78. Swain, M., & Lapkin, S. (1995). Problems in output and the cognitive processes they generate: A step towards second language learning. Applied Linguistics, 16(3), 371–391. [Google Scholar] [CrossRef]
  79. Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12(2), 257–285. [Google Scholar] [CrossRef]
  80. Sweller, J., van Merriënboer, J. J. G., & Paas, F. G. W. C. (1998). Cognitive architecture and instructional design. Educational Psychology Review, 10(3), 251–296. [Google Scholar] [CrossRef]
  81. Tabach, M., & Friedlander, A. (2013). School mathematics and creativity at the elementary and middle-grade levels: How are they related? ZDM Mathematics Education, 45(1), 227–238. [Google Scholar] [CrossRef]
  82. Thiel, O., & Perry, B. (2018). Innovative approaches in early childhood mathematics. European Early Childhood Education Research Journal, 26(4), 463–468. [Google Scholar] [CrossRef]
  83. Torrance, E. P. (1974). The Torrance tests of creative thinking: Technical-norms manual. Scholastic Testing Services. [Google Scholar]
  84. United States Census Bureau. (2022). Nearly 68 million people spoke a language other than English at home in 2019. Available online: https://www.census.gov/library/stories/2022/12/languages-we-speak-in-united-states.html (accessed on 18 November 2025).
  85. United States Department of Education. (2016). Elementary and Secondary Education Act (ESEA) as amended by the every student succeeds act of 2015. Available online: https://www.ed.gov/laws-and-policy/laws-preschool-grade-12-education/esea/esea-guidance (accessed on 18 November 2025).
  86. Valdés Fallis, G. (1978). A Comprehensive approach to the teaching of spanish to bilingual Spanish-speaking students. The Modern Language Journal, 62(3), 102–110. [Google Scholar] [CrossRef]
  87. Yang, J., & Cho, S. (2024). Developing hidden talent: An exploratory study of advanced math curriculum implementation and its effects on young mathematically promising English Learners. Journal for the Education of the Gifted, 47(4), 410–434. [Google Scholar] [CrossRef]
  88. Yang, J., Jo, S., Campbell, J., & Cho, S. (2021). Recognition, expectation, and differentiation for mathematical talent development of young gifted English learners. In E. Kuusisto, M. Ubani, P. Nokelainen, & A. Toom (Eds.), Good teachers for tomorrow’s schools (pp. 217–239). Brill Sense. [Google Scholar]
  89. Yang, J., Özbek, G., & Cho, S. (2023a). Teachers’ beliefs and their influence on math instructions for gifted English learners. Education Sciences, 13(7), 728. [Google Scholar] [CrossRef]
  90. Yang, J., Özbek, G., Liang, S., & Cho, S. (2023b). Effective teaching strategies for teaching mathematics to young gifted English learners. Gifted Education International, 39(2), 226–246. [Google Scholar] [CrossRef]
  91. Yildirim, Y., & Yilmaz, Y. (2023). Promoting creativity in early childhood education. PLoS ONE, 18(12), e0294915. [Google Scholar] [CrossRef]
  92. Yonker, J. E. (2011). The relationship of deep and surface study approaches on factual and applied test-bank multiple-choice question performance. Assessment & Evaluation in Higher Education, 36(6), 673–686. [Google Scholar] [CrossRef]
Education 15 01581 g001
Figure 1. Multi-group (COM vs. INT) Path Diagram of Tangram Creativity Assessment. Note. TCA = Tangram Creativity Assessment. CogAT_RAW = Cognitive Abilities Test (CogAT) total raw score. TPSS = Tangram Problem Solving Speed. NWEA = NWEA MAP Growth Mathematics. NWEA PER = NWEA MAP Growth Mathematics Achievement Percentiles.
Figure 1. Multi-group (COM vs. INT) Path Diagram of Tangram Creativity Assessment. Note. TCA = Tangram Creativity Assessment. CogAT_RAW = Cognitive Abilities Test (CogAT) total raw score. TPSS = Tangram Problem Solving Speed. NWEA = NWEA MAP Growth Mathematics. NWEA PER = NWEA MAP Growth Mathematics Achievement Percentiles.
Education 15 01581 g001
Table 1. Demographic information of participants.
Table 1. Demographic information of participants.
Category InterventionComparisonTotal
(n = 155, 62%)(n = 95, 38%)(n = 250, 100%)
n%n%n%
GenderFemale8353.54547.412851.2
Male7246.55052.612248.8
EthnicityHispanic9460.65962.115361.2
Asian2314.877.43012.0
African American53.222.172.8
Not specified3321.32728.46024.0
Number of classes 1661.51038.536100
Table 2. Tangram creativity assessment.
Table 2. Tangram creativity assessment.
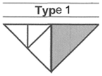
The White Space Inside the Shape Must Be Completely Covered and Does Not Go Outside the Shape’s Perimeter.Small Tangram Pieces to Design Composition of Shapes
Education 15 01581 i001Education 15 01581 i002Education 15 01581 i003
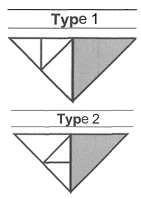Composition of triangles
Education 15 01581 i004
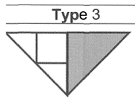Composition of square
Education 15 01581 i005
Composition of parallelogram
Table 3. Originality Score Justification.
Table 3. Originality Score Justification.
Response%ff CutoffsOriginality PointsOriginality
Education 15 01581 i0062012Occasional (20–40%)1Moderate
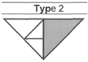Education 15 01581 i0072314Occasional (20–40%)1Moderate
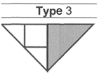Education 15 01581 i0084326Common (>40% occurrence)0Common
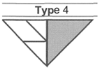Education 15 01581 i009138Infrequent (10–19%)2Elevated
Education 15 01581 i01011Rare (<10%)3Exceptional
Table 4. Example fluency, originality, flexibility, and TCA total scoring of high-potential ELs.
Table 4. Example fluency, originality, flexibility, and TCA total scoring of high-potential ELs.
Child Image
Response		FluencyFlexibilityOriginalityTCA Total
Number of
Solutions		ScoreNumber of
Categories		ScoreNumber of
Unusual or Rare Solutions		ScoreAdding Fluency, Flexibility, and Originality
A
(1, 2)		B
(3)		C
(4, 5)		 3
(0 pt)		1, 2
(1 pt)		4
(2 pt)		5
(3 pt)
Education 15 01581 i011111--1-1--13
Education 15 01581 i012111--1-1--13
Education 15 01581 i01311-1-11---02
Education 15 01581 i01411--11--1-24
Education 15 01581 i01511--11---135
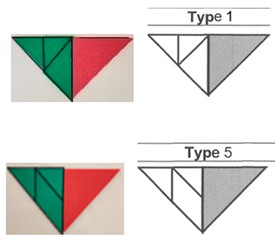Education 15 01581 i016221-12-1-148
Education 15 01581 i01733111311-1410
Table 5. Grade K tangram problem-solving speed.
Table 5. Grade K tangram problem-solving speed.
Item PromptMath
Focus/Skill		Scoring CriteriaChild Image ResponseScore Explanation
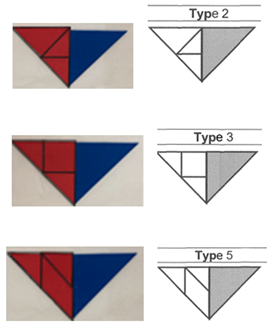
The triangle covers this part. Please cover this part using the other shapes [point to the white part and the tangram]. Spatial reasoning and composition of shapesA. Time Needed to Solve 1st Way
≤30 s (3 pt)
≤1 min (2 pt)
≤3 min (1 pt)
≥3 min (0 pt)
 
Total: 3 pt max		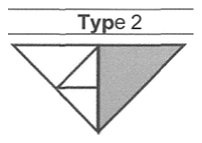Education 15 01581 i018Education 15 01581 i019Solved at 20 s
Score: 3
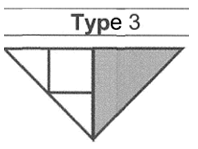Education 15 01581 i020Education 15 01581 i021Solved at 46 s
Score: 2
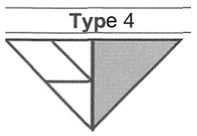Education 15 01581 i022Education 15 01581 i023Solved at 2 min
Score: 1
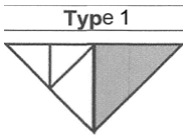Education 15 01581 i024Education 15 01581 i025Solved at 20 s
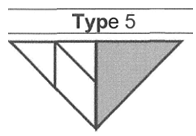Education 15 01581 i026Education 15 01581 i027+ extra at 2:30
Score: 3
Note. Accept any design that completely covers the white space inside the shape and does not go outside the shape’s perimeter. All solutions shown (Type 1–5) are possible solutions that are considered “different” on the scoring rubric. Note that some use the exact same shapes but are positioned differently.
Table 6. Descriptive statistics for pre-TCA and post-TCA scores across fluency, flexibility, and originality, and MANOVA.
Table 6. Descriptive statistics for pre-TCA and post-TCA scores across fluency, flexibility, and originality, and MANOVA.
AssessmentGroup MANOVA
Intervention
(n = 155, 62%)		Comparison
(n = 95, 38%)
EffectM(SD)M(SD)Wilks’ LambdaF (df1, df2)pη2p
Intercept 0.63046.374 (3, 246)<0.0010.370
Group 0.9871.006 (3, 246)0.3910.013
Pre-TCA1.55(2.02)1.37(1.80)
Pre-Fluency0.57(0.73)0.52(0.64) 0.398 (1, 248)0.5290.002
Pre-Flexibility0.55(0.66)0.45(0.60) 1.341 (1, 248)0.2480.006
Pre-Originality0.43(0.85)0.40(0.72) 0.082 (1, 248)0.7750.000
Post-TCA3.05(3.07)2.22(2.67)
Post-Fluency1.03(0.99)0.74(0.84)
Post-Flexibility0.94(0.86)0.70(0.77)
Post-Originality1.09(1.45)0.77(1.18)
Table 7. Post-TCA across fluency, flexibility, and originality differences between groups.
Table 7. Post-TCA across fluency, flexibility, and originality differences between groups.
MeasureSourceF(1, 246)pη2p
Total TCAPre-test45.26<0.0010.169
Group5.720.0180.025
FluencyPre-test49.03<0.0010.180
Group7.060.0080.031
FlexibilityPre-test36.68<0.0010.141
Group4.620.0330.020
OriginalityPre-test28.32<0.0010.113
Group4.380.0380.019
Table 8. Model Fit and Measurement Invariance.
Table 8. Model Fit and Measurement Invariance.
Mplus Stepχ2(df)pCFITLIRMSEA [90% CI]SRMRΔCFIΔRMSEA
Configural (multi-group)68.53 (48)0.0270.9770.9690.059 [0.021, 0.089]0.077——
Metric (loadings equal across groups)68.53 (48)0.0270.9770.9690.059 [0.021, 0.089]0.0770.0000.000
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Özbek, G.; Mun, R.U.; Shen, Y.; Lin, W.; Spence, M.; Cho, S. Developing Mathematical Creativity in High-Potential Kindergarten English Learners Through Enrichment and Tangram Activities. Educ. Sci. 2025, 15, 1581. https://doi.org/10.3390/educsci15121581

AMA Style

Özbek G, Mun RU, Shen Y, Lin W, Spence M, Cho S. Developing Mathematical Creativity in High-Potential Kindergarten English Learners Through Enrichment and Tangram Activities. Education Sciences. 2025; 15(12):1581. https://doi.org/10.3390/educsci15121581

Chicago/Turabian Style

Özbek, Gülnur, Rachel U. Mun, Yuyang Shen, Weini Lin, Melissa Spence, and Seokhee Cho. 2025. "Developing Mathematical Creativity in High-Potential Kindergarten English Learners Through Enrichment and Tangram Activities" Education Sciences 15, no. 12: 1581. https://doi.org/10.3390/educsci15121581

APA Style

Özbek, G., Mun, R. U., Shen, Y., Lin, W., Spence, M., & Cho, S. (2025). Developing Mathematical Creativity in High-Potential Kindergarten English Learners Through Enrichment and Tangram Activities. Education Sciences, 15(12), 1581. https://doi.org/10.3390/educsci15121581

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop