The Role of Automated Diagnostics in the Identification of Learning Disabilities: Bayesian Probability Models in the Diagnostic Assessment

Abstract

This study investigates the application of Bayesian probability models in the diagnostic assessment of learning disabilities. The objective of this study was to determine whether specific conditions identified in expert reports could predict subsequent diagnoses. The sample consisted of 201 expert reports on children diagnosed with learning disabilities, which were analysed using qualitative content analysis, fuzzy set qualitative comparative analysis (fsQCA), and Bayesian conditional probability models. Variables such as vocabulary, working memory index, processing speed, and visuomotor coordination were examined as potential predictors. The analysis demonstrated that Bayesian networks captured conditional links, such as the strong association between working memory and perceptual inference, as well as an unexpected negative link between vocabulary and verbal comprehension. The study concludes that Bayesian networks provide a transparent and data-driven framework for pre-screening and risk assessment in special education settings. The limitations of this study include the absence of a control group and exclusive reliance on SNI cases. Future research should explore the integration of abductive reasoning into automated diagnostic software to enhance inclusivity and support decision-making.

1. Introduction

The diagnosis of learning disabilities (LDs) has long been debated because of the risk of stigmatisation and deficit-oriented framing in international classification systems. The Diagnostic and Statistical Manual of Mental Disorders, Fifth Edition (DSM-5; American Psychiatric Association, 2013) and the International Classification of Diseases, 11th Revision (ICD-11; World Health Organization, 2019) describe LDs primarily in terms of deviations from normative development, often highlighting deficits rather than strengths. This diagnostic framing can have unintended consequences, including reduced self-esteem and limited educational opportunities (Haft et al., 2023; Wilmot et al., 2023; Woodcock & Moore, 2018).

To address these challenges, recent scholarship has turned to decision-theoretic models that combine abductive reasoning, fuzzy set qualitative comparative analysis (fsQCA), and Bayesian probability theory. Abduction provides a framework for generating plausible diagnostic hypotheses, fsQCA identifies the necessary and sufficient conditions for classification, and Bayesian networks quantify the likelihood of diagnostic outcomes. In combination, these methods make it possible to map diagnostic pathways step by step, allowing researchers to replicate how specific conditions contribute to a diagnosis.

Previous studies have applied abduction to conceptualize diagnostic reasoning in special education (Vida & Sántha, 2024) and explored the potential of fsQCA for identifying complex condition patterns (Ragin & Rihoux, 2004). Bayesian networks have also been shown to effectively represent probabilistic dependencies in educational and medical contexts (Koopman & Renooij, 2021; M. P. K. Webb & Sidebotham, 2020). However, few studies have combined these methods to explore the diagnostic practices for LDs.

The present study aimed to

(1)

Identify frequent diagnostic variables in expert reports on students with LDs.

(2)

Identify the probabilistic relationships between these variables were modelled using Bayesian networks.

(3)

Evaluate the potential of abductive and probabilistic reasoning to enhance transparency, inclusivity, and efficiency in LD diagnosis.

Based on these aims, we hypothesised that Bayesian modelling can capture both expected and unexpected diagnostic pathways, thereby providing an evidence-based tool to support early identification and inclusive educational decision-making.

1.1. Abductive Reasoning in the Diagnosis of Learning Disabilities

The rigid boundaries of diagnostic categories have hindered learning disability identification, necessitating qualitative comparative analysis (QCA) (Horvath, 1988; Manghirmalani et al., 2012; David & Kannan, 2010). Learning disorders are diagnosed based on test results and expert opinion. However, the diagnostic groups were not linked to diagnostic clusters (ICD11 and DSM5-TR) based on the measurement results. The conceptualisation of learning disabilities is fluid and neither quantitative nor qualitative. The decision-theoretic process for diagnosing learning disabilities has been minimally studied. The pedagogical stages of learning disabilities can be identified as steps of abduction (Vida & Sántha, 2024), conceptualised as oscillation between induction and deduction (Sántha & Gyeszli, 2022). The reflection of inductive and deductive directional changes can be effectively traced (Mingers, 2012; Sántha, 2011), which is fundamental for fulfilling the abduction criteria. Exploring the therapeutic pedagogical aspects of abduction is more associated with diagnosticians’ perspectives and reflections based on previous research (Vida & Ambrus, 2022) than the theoretical constructs of diagnostic systems. Qualitative content analysis and fsQCA have indicated (Vida & Ambrus, 2022, 2023) that educational diagnosis can be implemented as abduction, mitigating overemphasis on deficit-oriented test results and rendering the process traceable and transparent, supporting intuitive views with a transparent inference path (Sántha et al., 2024).

Abduction can facilitate the creativity and flexibility of diagnosticians, as learning problems in special education diagnostics form a complex relationship. Its description is challenging, as “deduction proves that something must be; induction shows that something really is and works; abduction merely suggests that something may be” (Peirce, 1998, p. 171; Strand, 2005, p. 273). Abduction may prove beneficial in diagnosing learning disorders as a creative process (Strand, 2005). The application of abduction in identifying a learning disorder is a means of ascertaining the child’s actual state, aligning with the “ah-ha experience” that characterises abduction and can be interpreted as a sudden moment of insight (Reichertz, 2009).

1.2. The Place and Role of fsQCA in the Construction of Bayes Nets

The use of fsQCA was justified by the specificity of the research problem. Learning disability categories lack clear boundaries, enabling the identification of necessary and sufficient conditions. Assessing the validity of learning disability symptoms in test results is essential. Learning disabilities cannot be reduced to single-outcome measures because of the variability in learning and children’s abilities.

This raises the question of how effectively a child’s performance aligns with learning disability theory in educational diagnosis. The diagnostic process can be modelled, traced, and rendered transparent using the appropriate tools.

Using fsQCA, we elucidated the conditions underlying learning disability diagnosis. We extracted regularities and described typable diagnostic pathways to understand inferential pathways. This was presented as a connection diagram (Vida & Sántha, 2024), which is a significant step toward rendering the decision-theoretic approach accessible.

Previous research indicates indistinct stages of the diagnostic process, corroborated in language disorders (Short et al., 2020, Learning disability as a blurred system is not new) (Horvath, 1988), and emerging as a tool for predicting dyslexia (Vanitha & Kasthuri, 2021) or for educational specialists (Hernandez et al., 2009). Attempts have been made to enhance the efficiency of the diagnostic category system (Manghirmalani et al., 2012), albeit with increasing redundancy and conceptual polymorphism. It has been used for data mining in diagnostic tests and textual materials (David & Kannan, 2010). The application of fuzzy set logic in special education is not unprecedented in the international discourse.

Adapted to this research, fuzzy systems logic is pertinent because a measurement result’s significance does not necessarily predispose to learning disorder identification and cannot be approximated by direct induction or deduction.

The necessity and sufficiency of a given condition, such as an IQ test score, can be established. By constructing a Bayesian network, the probability of identifying a learning disability can be determined using other conditions based on the investigators’ decision-theoretic approach. Calibrating fsQCA thresholds is a potential concern regarding model validity, as setting thresholds remains the researchers’ prerogative (Pappas & Woodside, 2021). Our observations indicate that altering the thresholds or breakpoints can modify the output results.

1.3. Bayesian Network as an Acyclic Graph of the Diagnostic Process

As mentioned in the introduction, Bayesian networks facilitate the mapping of complex causal relationships and likelihoods, and it is hypothesised that they can validate and potentially complement the connectivity diagram obtained in fsQCA. Based on our insights and research findings, learning disabilities align with this concept. A Bayesian network is a directed acyclic graph (DAG) in which nodes represent variables and edges represent cause-and-effect relationships. Each node represents a probability distribution with a specified degree of dependence. This corresponds to the emergence of a learning disorder in which numerous variables in complex relationships determine outcomes.

It has been demonstrated to be applicable to similar complex phenomena, such as the social components of school dropout (Barnard-Brak et al., 2023), and has been utilised to predict the mathematical performance of children with special educational needs.

Bayes’ conditional probability theorem can effectively identify learning disabilities and determine developmental directions, addressing seemingly chaotic datasets with flexibility. It revises previous probabilities based on existing data and prior probabilities, thereby allowing the calculation of new ones. When a new condition is introduced, the probability of an expected event can be modified. This is particularly useful in medical pedagogy, where numerous factors must be considered for diagnosis, and new data may be incorporated.

In practice, the Bayesian network structure represents possible decision-theoretic pathways that describe the sequence of events leading to a diagnosis. In this study, it was adapted to the system’s specificities, but it can be flexibly adapted to any educational system for diagnosing learning disabilities. This can also be considered a validation or quantification of the fsQCA.

1.4. Beliefs, Beliefs in Diagnostics

In assessing learning disabilities, we identified the present and absent elements of abductions using Peirce’s logic. Research suggests that professionals’ beliefs influence diagnosis more than learning disability theories (Vida & Ambrus, 2022). This perspective is recognised in educational science (McCarthy, 2005; Smith et al., 2005; Strand, 2005) and is relevant to learning disability diagnosis. The conceptual framework of abduction can explore perspectives on special education (Sántha et al., 2024).

Peirce defined beliefs as ideas, elucidating phenomena and interconnected signs that represent reality. Correct beliefs delineate genuine relationships between events and objects, but fully comprehending the complexity of reality is unfeasible (McCarthy, 2005; Sántha et al., 2024).

This approach analyzes expert opinions as reflective texts encoding learning disabilities and interpreting abductions in diagnoses involving theory generation, development and evaluation (Haig, 2005; Sántha et al., 2024).

An educational information set often comprises subjective, situational, and uncertainty-based elements. Babbie (2003) noted the subjectivity of social science information. Analysts can make subjective information precise or use a methodology to handle it (Molnár et al., 2014). This study considers the latter to expand methodological pathfinding. Special education diagnosis requires consideration of numerous factors, with variable diversity potentially leading to new data. Uncertainty recurs when exploring this topic, stemming from incomplete data, imprecise knowledge, linguistic uncertainties, measurements and complex conceptual structures.

Models that address uncertainty include symbolic models, heuristic methods, and numerical probability models, such as Bayesian models. The fuzzy model is relevant for vague, imprecisely defined sets that deal with the degree of occurrence of ill-defined events (Brassai, 2019; Kóczy & Tikk, 2000).

Ragin illustrated the difference between probability and fuzzy theory using the role of beer in human life. The truth value of “beer is a deadly poison” is approximately 0.05, suggesting that it is not entirely false, yet millions consume beer while avoiding beverages with a 0.05 death probability (Ragin, 1987).

2. Materials and Methods

2.1. Participants

This study was based on 201 expert reports issued by a county-level special education committee in Hungary during the 2019/2020 academic year. All participating children were officially diagnosed with a specific learning disability (DLD). The reports included demographic information (age and sex), results of standardised cognitive tests, and qualitative observations. Due to anonymisation requirements, detailed socioeconomic and family background data were not available, which represents a limitation. The sample was stratified to reflect the diversity of cases handled by the committee (cf. Horvath, 1988; Manghirmalani et al., 2012). It is important to note that international classification systems, such as the Diagnostic and Statistical Manual of Mental Disorders, Fifth Edition (DSM-5; American Psychiatric Association, 2013) and the International Classification of Diseases, 11th Revision (ICD-11; World Health Organization, 2019), cannot serve as direct diagnostic criteria in this context. In fact, both systems often list broader neurodevelopmental or sensory impairments as exclusionary conditions for learning disabilities, which means that relying on them for identification may obscure the educationally relevant manifestations of DLD in practice.

2.2. Variables and Measures

The variables were extracted from diagnostic reports and included both cognitive indices (e.g., vocabulary, working memory index, processing speed index, perceptual inference index, reading comprehension) and behavioural/functional indicators (e.g., visuomotor coordination, pencil grip, and text comprehension). Variables were coded following prior qualitative content analyses (Vida & Ambrus, 2022; Sántha & Gyeszli, 2022; Vida & Sántha, 2024), ensuring consistency across cases. Similar approaches have been reported in international research on fuzzy and Bayesian modelling in special education (David & Balakrishnan, 2013).

2.3. Procedure

The reports were digitised and pre-processed. A word frequency analysis was conducted using Voyant Tools web application to generate an initial list of terms (n = 5376). Personal data and legal references were removed to comply with the data protection regulations. Each case was coded separately, and the categories were refined using qualitative content analysis and fuzzy-set qualitative comparative analysis (fsQCA). These codes were subsequently transformed into variables for Bayesian modelling (Pappas & Woodside, 2021; Ragin & Rihoux, 2004).

2.4. Design and Data Analysis

The study applied a mixed-method design combining qualitative content analysis, fsQCA, and Bayesian network modeling. First, fsQCA was used to identify the necessary and sufficient conditions for diagnosis. Second, Bayesian conditional probability models were constructed to estimate the likelihood of diagnosis based on specific conditions. Correlation matrices and heatmaps were generated using SPSS 25 and Python 3.12 (cf. Dufraisse et al., 2020). Conditional probability distributions (CPDs) were calculated to define the structure of the Bayesian networks, which were visualised in a directed acyclic graph (DAG) format (Koponen, 2020; Koopman & Renooij, 2021).

2.5. Ethical Considerations

This study was conducted in accordance with the ethical guidelines of the University of Sopron and Hungarian regulations on educational research. Permission to access anonymised archival reports was obtained from the relevant authorities. All data were anonymised before analysis, and no personally identifiable information was used. As the data were archival expert reports rather than newly collected assessments, informed consent was not required from the legal guardians. Similar approaches have been reported in related educational diagnostic research using archival materials (Haft et al., 2023; Woodcock & Moore, 2018).

3. Results

The results are presented in three subsections according to the study objectives: (1) descriptive probabilities of diagnostic variables, (2) correlation analysis, and (3) Bayesian network modelling.

(1)

P(A): A priori probability that the child has been diagnosed with DLD.

(2)

P(B∣A): The probability that a given word occurs when a child has a DLD diagnosis.

(3)

P(B∣¬A): The probability that a given word occurs when the child is not diagnosed with DLD.

(4)

P(B): The probability that a given word occurs in the full text.

Because only DLD cases were included in the data, it was possible to calculate P(B|A), but P(B|¬A) was not available because we did not have data on non-DLD cases. However, we can examine how often each word occurs in texts that identify DLD.

In this case, the Bayes theorem is as follows.

P(A∣B) = (P(B∣A)·P(A))/P(B)

(1)

Because P(A) = 1, P(A∣B) = P(B∣A). This implies that the probability of the occurrence of each word is also a conditional probability.

The sampling and peer review processes ensured that all examined texts involved children identified as having a learning disability (DLD). Thus, a child was diagnosed for each instance of word occurrence.

The conditional probabilities of all identified variables were calculated. However, we lack information about the interrelationship of terms; therefore, we can generate a Bayesian network in which the central node is the DLD (event A) and each word (event B) is connected by edges pointing to it.

3.1. Descriptive Statistics of Diagnostic Variables

Table 1. Probability and frequency of conditions (Note: Relative frequency = occurrence in corpus; conditional probability = probability given DLD diagnosis).

Terms and Conditions	Relative Frequency	Conditional Probability
A. Vocabulary	0.130417	0.131086
B. Processing speed index	0.128711	0.129371
C. Working memory index	0.118126	0.118732
D. Perceptual inference index	0.115438	0.116030
E. Full IQ test	0.099724	0.100235
F. Pencil grip	0.094690	0.095175
G. Visual motor coordination	0.078272	0.078674
H. Reading comprehension	0.076761	0.077154
I. Thinking by analogy	0.043001	0.043222
J. Verbal comprehension index	0.029129	0.029279
K. Reading pace	0.026305	0.026440
L. Spatial analysis synthesis	0.017241	0.017330
M. Inverse number series	0.010207	0.010260
N. Rule recognition	0.008410	0.008453
O. Auditory differentiation	0.006955	0.006991
P. Spatial orientation	0.006100	0.006131
Q. Timely orientation	0.003373	0.003390
R. Auditory short-term memory	0.001399	0.001406
S. Mathematical operations	0.000638	0.000641
T. Attention control	0.000264	0.000531
U. Dictation for writing	0.000000	0.000000
V. Text comprehension	0.000000	0.000000

presents the relative frequencies and conditional probabilities of the most frequently occurring diagnostic variables in expert reports. Variables such as vocabulary (13.0%), processing speed index (12.8%), and working memory index (11.8%) were the most frequently cited predictors.

The conditions in Table 1 represent those deemed most pertinent based on the Voyant Tools analysis, corresponding to previous qualitative content analysis codes, while constituting a more comprehensive framework for the analysis. New terms were partially included based on distribution and frequency data. This approach was not considered risky, as subsequent analyses would elucidate any absence of correlation between the included terms and learning disability diagnosis.

The key aspects of the model are the nature and interrelationships between these conditions. Currently, software alone cannot detect learning disabilities, as available procedures lack the automatic abduction capability to delineate the decision-theoretic model that informs diagnosis in special education.

3.2. Correlation Analysis

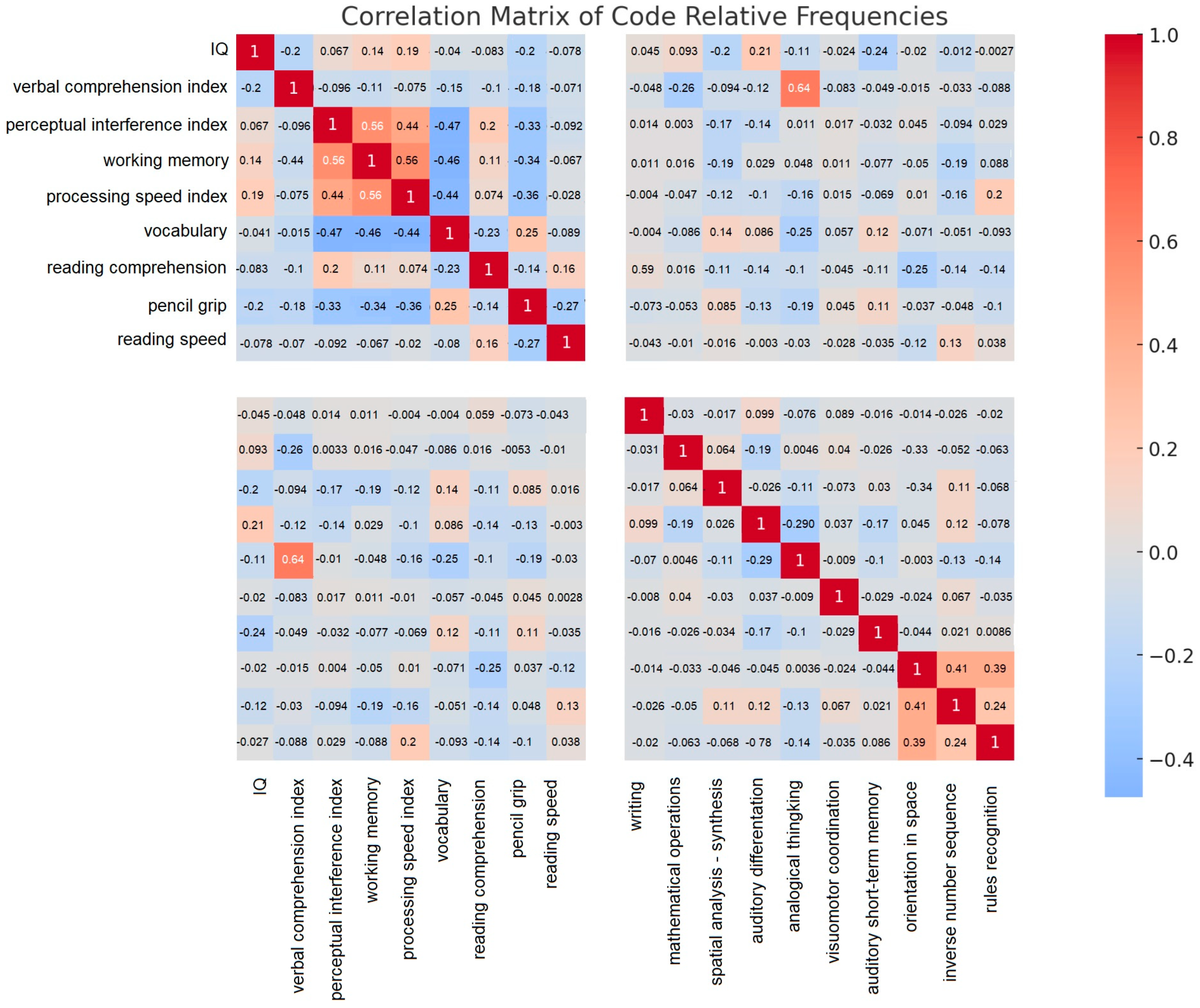
Correlation coefficients can be used to explore relationships, and once the conditional probabilities are obtained, the Bayesian network structure is defined. This can be visualised by arranging the correlation coefficients between the conditions in a matrix and identifying strongly related and independent variables. Correlation coefficients were validated using SPSS 25 and Python 3.12 outputs, ensuring consistency across analytic tools. SPSS 25 software was used to create the correlation matrix, a heatmap was generated using the ChatGPT 4o subscription module, and a code sequence obtained by redesigning the command line in several steps was inserted into the Python 3.12 software. Correlation coefficients were computed to examine the relationships between the variables. Figure 1 shows the correlation matrix, where darker shades indicate stronger relationships.

Scheme 3. 12 (Note: Strong correlations > 0.50, moderate correlations between 0.30 and 0.49). Negative correlations are indicated in red. Source: self-made Python 3.12, (Van Ginkel et al., 2018; Kramer et al., 2020). The matrix colours indicate strong or weak correlations. A strong correlation indicates a robust positive or negative correlation between conditions, indicating a direct relationship in the Bayesian network. In cases of weak or no correlation, it can be hypothesised that there is a weak or non-existent relationship between the conditions, suggesting relative independence.

A correlation matrix was used to elucidate the relationship directions. A positive correlation coefficient indicates that if one condition is satisfied, the other is more likely to be satisfied. Bayesian networks represent causal relationships between statements, conceptualised as a directed acyclic graph, where nodes represent statements and edges represent causal relationships. When inferring with Bayesian networks, it is possible to deduce the effects of causes, infer causal effects, provide explanations, and substantiate the conclusions. Van Ginkel et al. (2018) emphasised that a successful mentoring process largely depends on the mentor’s diagnostic skills. This may apply to special education, as using a specific methodology such as abduction, the Bayesian model, and conceptualisation in special education diagnostics can lead to accurate causal relationships. We hypothesised that highly correlated variables could be linked to a Bayesian network. However, caution is needed because correlation alone does not inform causality, and cause and effect cannot be inferred. These relationships are linked to the investigator’s prior knowledge and experience, representing a potential limitation; however, we posit that this is a potential abductive inference.

A strong positive correlation (0.641) was observed between visuomotor coordination and the perceptual inference index, suggesting a robust relationship. However, this is not the case in special education.

Additionally, a strong positive correlation between the working memory index and perceptual inference index (0.561) was identified, which represents a novel observation. The underlying mechanisms cannot be fully elucidated by current research, necessitating further investigation.

A moderately strong negative correlation between the verbal comprehension index and vocabulary (−0.474) was also noted, suggesting further investigation and representing an unexpected finding. Vocabulary is related to pedagogical tests, whereas the verbal comprehension index is a cognitive test that incorporates vocabulary. Elucidating this relationship presents a new research question and raises concerns regarding the specificity of these assessments.

No strong correlation was observed between certain variables, such as the inverse number series and auditory short-term memory, suggesting independence in the network. This observation is discussed in the following sections.

3.3. Summary and Key Findings of Correlation Matrix Results

The absence of a correlation between the two variables may indicate a lack of relationship between the conditions under study. In such instances, it is unnecessary to establish an edge between the nodes in the Bayesian network.

Consequently, variables that are independent of each other can be treated as such in a network.

However, this does not preclude an indirect link between these two variables. In a given scenario, if the Vocabulary and Working Memory indices are not directly correlated but both are correlated with a third variable, such as the Perceptual Inference index, they may possess an indirect relationship in the network. However, exploring and substantiating this hypothesis is beyond the scope of our resources and capabilities.

This enhances the role of abduction, as correlation analysis is valuable, but it is not a substitute for flexible movement between induction and deduction, as it would be unfeasible to recognise correlations on a unidirectional logical path. Although progress has been made in establishing a decision-theoretic model, further investigation is warranted regarding the relevance and hidden relationships of independent and unrelated conditions, nodes, and even the revealed relationships.

(1)

A strong positive correlation was observed between visuomotor coordination and the perceptual inference index (r = 0.641).

(2)

A moderate positive correlation was found between the working memory index and perceptual inference index (r = 0.561).

(3)

An unexpected negative correlation was found between vocabulary and verbal comprehension index (r = –0.474). This counterintuitive result suggests that vocabulary scores in pedagogical tests may not align with standardized cognitive test scores (cf. Chen & Kalyuga, 2021; Winter, 2024).

(4)

Certain variables (e.g., inverse number series and auditory short-term memory) showed no correlation, indicating independence of the variables.

These results highlight that correlation analyses can reveal both intuitive and counterintuitive patterns. However, as noted in previous research, correlation does not establish causality (Hull & Pataki, 2018; M. P. K. Webb & Sidebotham, 2020).

4. Structure of Bayes Net

4.1. Creating Nodes

Each node represents a variable in the Bayesian network identified using a correlation matrix. These variables may be the states or measurements that we aim to model during the analysis. To construct a network of links for diagnosing learning disabilities, these relationships must be explored.

Conditional probability denotes the probability that an event (node) will occur, given that another event has occurred. We define the conditional probability as

P(B∣A)

This denotes the probability of event B occurring subsequent to event A. The conditional probabilities, CPDs (Conditional Probability Distributions), are represented by their probability values. CPDs are essential in a Bayesian network for determining the probability that a node assumes certain values. The values are listed in

Table 2. Case numbers to define CPDs.

Perceptual Inference Index	Working Memory Index	Number of Cases
Low (0)	Low (0)	30
Low (0)	High (1)	10
Medium (1)	Low (0)	20
Medium (1)	High (1)	20
High (2)	Low (0)	5
High (2)	High (1)	25

. The table indicates the number of cases out of 201 that exhibit a low “Perceptual Inference Index”, low “Working Memory Index”, and so forth. All conditions and states were examined.

The edges connecting the nodes represent the connections and indicate the directions of the conditional probabilities. When a hypothesised causal relationship exists between variables, such as between the “Perceptual Inference Index” and “Working Memory Index”, a directed edge can be drawn. This signifies that the change in the “Working Memory Index” measurement is dependent on the “Perceptual Inference Index”. Thus, CPD provides the probability value that the “Working Memory Index” assumes a certain value, given the known value of the “Perceptual Inference Index”. This also applies to the other edges. The table below illustrates the dependence of the “Working Memory Index” status on the “Perceptual Inference Index”.

CPDs represent a quantitative progression in conceptualising CPDs, enabling the assignment of additional “states” to a variable and enhancing the resolution of the Bayesian network. These can be categorised into three states for the perceptual inference index node: low, medium, and high. This approach is similar to fsQCA truth tables; however, the establishment of “thresholds” may be perceived as more transparent.

4.2. Calculation of Relative Frequencies

The basic step is that although we have already calculated conditional probabilities for the diagnosis of “learning disability (DLD), we cannot infer the relative probabilities of the conditions. This is essential for the identification of edges and the construction of the Bayesian network.

An example of the steps involved is as follows.

• Low “Perceptual inference index” (0):

$$P(Working Memory Index=low \mid \mathrm{ }Perceptual Inference Index=\mathrm{ }0)={\displaystyle \frac{30}{30+10}}=0.75$$

$$P(Working Memory Index=high \mid \mathrm{ }Perceptual Inference Index\mathrm{ }=\mathrm{ }0)={\displaystyle \frac{10}{30+10}}=0.25$$

• Medium “Perceptual inference index”, (1)

$$P(Working Memory Index=low\mid Perceptual Inference Index=1)={\displaystyle \frac{20}{20+20}}=0.5$$

$$P(Working Memory Index=high \mid Perceptual Inference Index=1)={\displaystyle \frac{20}{20+20}}=0.5$$

• High “Perceptual inference index”, (1)

$$P(Working Memory Index=low \mid \mathrm{ }Perceptual Inference Index=\mathrm{ }2)={\displaystyle \frac{5}{5+25}}=0.167$$

$$P(Working Memory Index =high \mid \mathrm{ }\mathrm{ }Perceptual Inference Index\mathrm{ }=\mathrm{ }2)={\displaystyle \frac{25}{5+25}}=0.833$$

Using the above conditional probabilities, we can generate the CPD (conditional probability distribution) for the “Working Memory Index”, which determines the probabilities of the working memory state in the different states of the “Perceptual Inference Index” (as can be seen in

Table 3. Conditional probability distributions.

Perceptual Inference Index	Working Memory Index = Low (0)	Working Memory Index = High (1)
0 (Low)	0.75	0.25
1 (Medium)	0.50	0.50
2 (High)	0.167	0.833

).

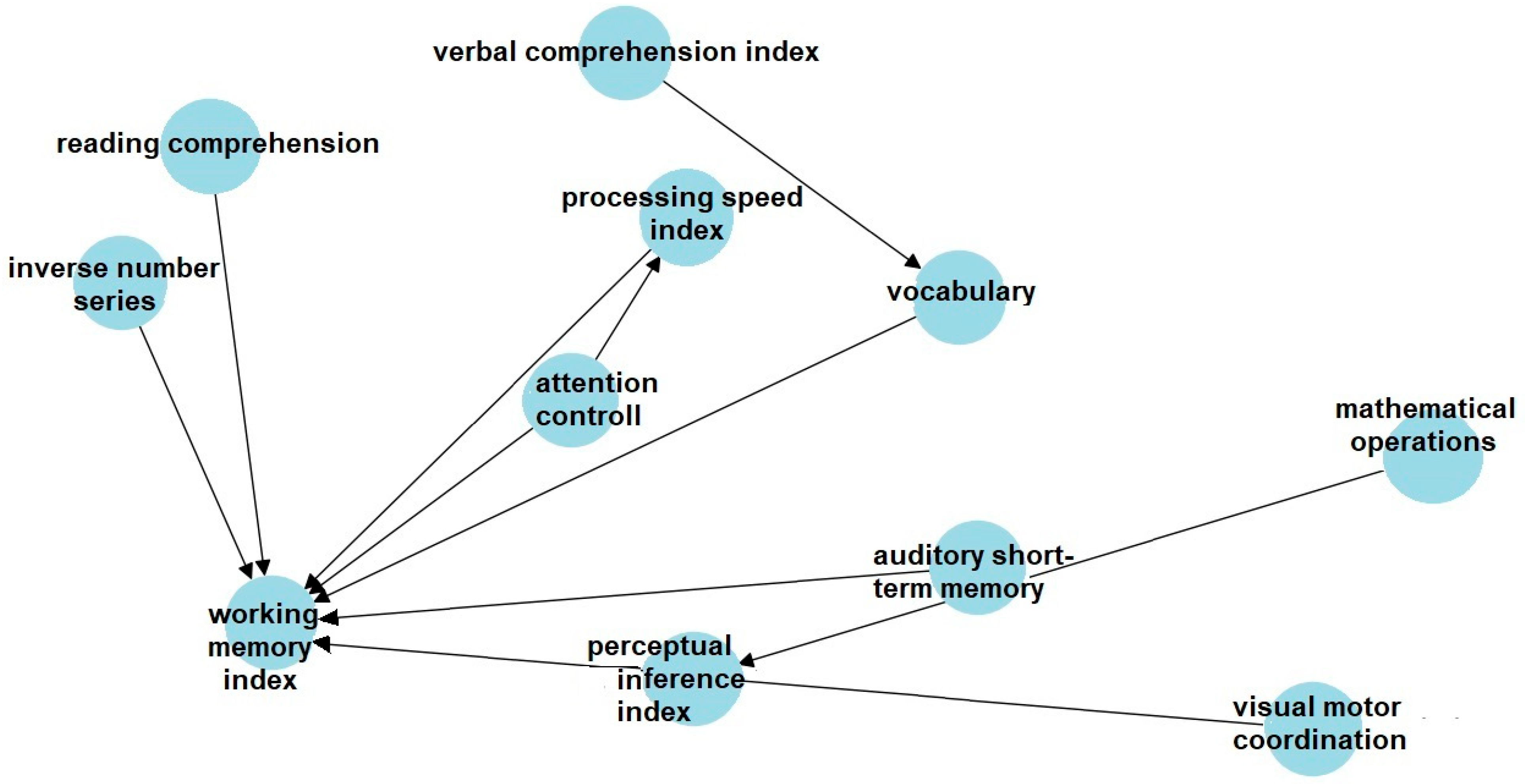
4.3. Graph—Bayes Nets—The Identified Connections

We then obtained all the values required to create the Bayesian network using Python 3.12. The model was checked, refined, and checked again using the software. These results indicate that the proposed model is valid and reliable, as presented in Figure 2.

The following results were obtained from the Bayes net construction and conditional probabilities.

The main relationships identified were as follows:

• Working Memory ↔ Perceptual Inference
  High perceptual inference was associated with high working memory in 83% of the cases.
• Processing Speed ↔ Attention Control
  High attention control predicted a high processing speed (70%).
• Vocabulary ↔ Parent Nodes
  Vocabulary was more likely to be high when both verbal comprehension and processing speed were elevated.
• Reading Comprehension ↔ Working Memory
  High working memory increased the likelihood of adequate reading comprehension, although the probability was modest (30%).
• Perceptual Reasoning ↔ Visuomotor Coordination and Mathematical Operations
  When visuomotor coordination and math operations were strong, perceptual reasoning was high in 30% of cases.

These findings indicate that Bayesian modelling can capture both expected and counterintuitive relationships among diagnostic variables, offering a transparent framework for exploring the diagnostic pathways as presented in Figure 2. Similar applications of Bayesian networks have been reported in school dropout (Barnard-Brak et al., 2023) and dyslexia (Vanitha & Kasthuri, 2021) predictions.

5. Limitations

The Bayesian network delineated in this study represents conditional independence/dependence relationships, potentially elucidating causal relationships. However, these interpretations should be approached with caution. The directionality of association relationships cannot necessarily be inferred, and the precise causal directionality may remain unclear. This limitation may account for the relationships not being directly deducible from the theory, warranting further investigation. Alternatively, a latent, unidentified variable could be responsible for association dependence, possibly overlooked because of data loss (Pribék, 2018), or other factors (Hull & Pataki, 2018).

Although an associative relationship between two variables may result from a causal relationship, the Bayesian network structure alone does not always permit such a conclusion; therefore, relationships may require further verification in all instances.

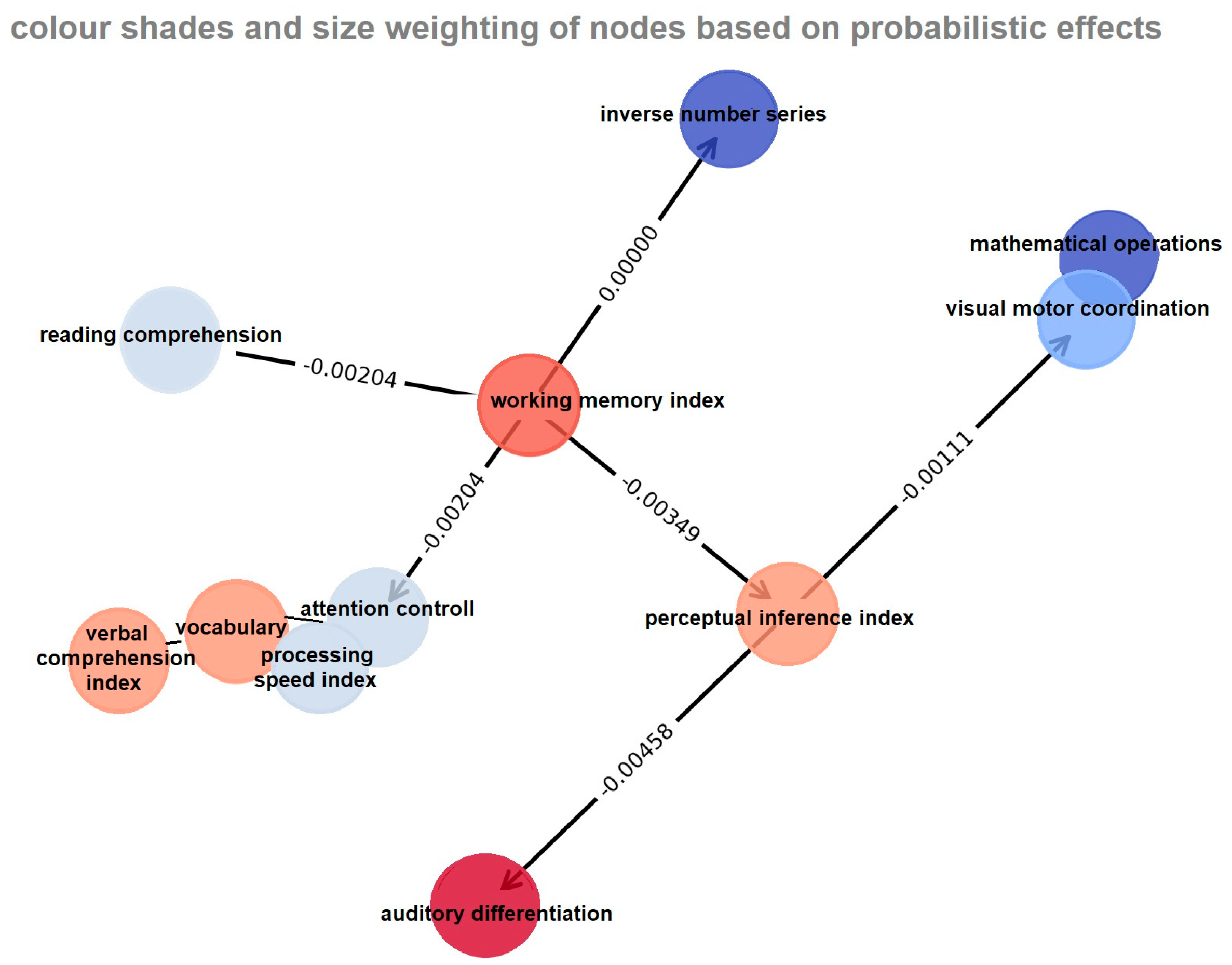
6. Addendum

To minimise bias from prior knowledge, we employed naïve Bayesian classification. This method estimates the conditional probability for a set of conditions based on whether the features are conditionally independent of a given feature (Tan et al., 2006/2011). Subsequently, we generated a naïve Bayesian network using the available data.

An example of conditional independence is the relationship between text comprehension and reading skills. Participants who exhibited superior recall also demonstrated better reading skills. This relationship can be elucidated by visuomotor coordination. Children with reading or learning disabilities may exhibit poor visuomotor coordination, which significantly affects their reading skills related to letter recognition.

If visuomotor coordination data are available, the observed relationship between working memory and reading skills may be attenuated, as incorrect letter recognition supersedes the significance of working memory, which is essential for reading (Molokopeeva, 2023; Kocaarslan, 2021). Thus, working memory and reading skills are conditionally independent when visuomotor coordination varies (Tan et al., 2006/2011). We constructed a naïve Bayes net to demonstrate what can be inferred from the data, which is relatively independent of the assumptions.

The shading in Figure 3 indicates the node weights. Red denotes a greater weight in determining learning disabilities, whereas blue indicates less relevance. Negative numbers demonstrate the strength and impact of the relationships between nodes in the naïve Bayesian network, indicating the direction of dependency. Negative values indicate a negative correlation between the variables. A negative relationship between nodes signifies an inverse directional relationship, and an increase in one variable is associated with a decrease in the other variable.

A negative value between the “working memory index” and “perceptual inference index” indicates that if working memory increases, the probability of perceptual inference decreases, or vice versa. This is addressed in the limitations section, as its explanation necessitates further research beyond theoretical knowledge. This interpretation depends on the network structure and probability distributions, which require further research. Negative values typically indicate an inverse relationship between nodes, a decrease in probability dependency, or hidden variables.

7. Discussion

This study aimed to (1) identify diagnostic variables in expert reports, (2) model probabilistic relationships using Bayesian networks, and (3) evaluate the integration of abductive and probabilistic reasoning into learning disability (LD) diagnostics. The results provide evidence that Bayesian networks can capture both expected relationships (e.g., between working memory and perceptual inference) and counterintuitive findings (e.g., the negative association between vocabulary and verbal comprehension). These outcomes align with previous studies that demonstrated the potential of Bayesian models to represent complex educational and medical phenomena (Barnard-Brak et al., 2023; Gelsema, 1996).

The finding of unexpected or counterintuitive correlations highlights the need for abductive reasoning in diagnostic modelling. Abduction allows practitioners to treat surprising results not as errors but as hypotheses to be explored further (Peirce, 1998; Reichertz, 2009). For instance, the negative relationship between vocabulary and verbal comprehension may reflect differences between pedagogical testing and standardized cognitive assessment, a distinction that has been previously emphasized in learning disability research (Chen & Kalyuga, 2021; Winter, 2024).

In practical terms, Bayesian networks support transparency and replicability in diagnostic processes by explicitly defining the conditional relationships among variables. However, correlation-based modelling alone cannot determine causality, and diagnostic reasoning must combine probabilistic inference with abductive judgment. This resonates with previous work on abduction in educational diagnostics (Vida & Sántha, 2024), suggesting that software-based tools can be developed to integrate both probabilistic calculations and abductive reasoning pathways. In educational practice, such tools could provide targeted support for diagnosticians, for example by pre-screening large volumes of expert reports in regions with limited professional capacity.

The limitations of this study must also be acknowledged. The dataset was restricted to children already diagnosed with LD (DLD classification), which meant that no control group was available. Furthermore, socio-economic and family background data were not included due to anonymisation, which limited the contextual interpretation of the results. These issues reduce the generalisability of the findings, although they are consistent with the limitations reported in other studies using archival diagnostic materials (Haft et al., 2023; Wilmot et al., 2023).

Despite these constraints, this study contributes to the growing literature on probabilistic and abductive modelling in inclusive education. Future research should include larger and more diverse samples, integrate control groups, and explore how abductive reasoning can be operationalised in software-based AI systems for special-education diagnostics. Such developments could help bridge the gap between human expertise and automated tools, ensuring that automation enhances, rather than replaces, professional judgment.

8. Conclusions

This study demonstrated that Bayesian networks can serve as a transparent and probabilistic framework for modelling diagnostic pathways in learning disability (LD) assessments. By integrating qualitative content analysis, fsQCA, and Bayesian conditional probability models, we identified both expected and counterintuitive relationships between diagnostic variables. These results highlight the potential of probabilistic modelling to complement traditional diagnostic reasoning and support pre-screening for inclusive education.

The practical implications of this study are twofold. First, Bayesian networks can improve the transparency and replicability of diagnostic decisions, providing professionals with data-driven support in complex cases. Second, abductive reasoning remains indispensable: while algorithms can model probabilities, the creative and interpretive dimensions of diagnostic practice require human expertise. Therefore, a realistic future direction is the development of hybrid decision-support systems that combine probabilistic modelling with abductive reasoning frameworks.

The limitations of this study must be acknowledged. The dataset was restricted to children already diagnosed with LD (DLD classification), and no control group was included in the study. Socioeconomic and family data were unavailable due to anonymisation, which reduced contextual interpretation. These constraints limit generalisability but are consistent with the challenges faced by archival studies in education (Haft et al., 2023; Wilmot et al., 2023).

Future research should address these limitations by incorporating control groups, integrating socioeconomic background data, and testing the model across multiple regions and educational systems. Further work is needed to explore how abductive reasoning can be operationalised in software-based tools to ensure that automation enhances, rather than replaces, professional judgment.

In summary, Bayesian networks offer a promising tool for enhancing the transparency, inclusivity, and efficiency of LD diagnostics. When combined with abductive reasoning, they may pave the way for innovative diagnostic practices that balance the strengths of automation with the irreplaceable role of professional expertise.