A Follow-Up on the Development of Problem-Solving Strategies in a Student with Autism

Abstract

Students with autism spectrum disorder (ASD) often face difficulties in solving arithmetic word problems, particularly in transitioning from informal counting strategies to more efficient methods based on number facts and formal operations. This study examined the development of problem-solving strategies in a single student with ASD and intellectual disability across two sequential single-case experiments using multiple baseline designs. Study 1 (age 13 years 9 months; 17 sessions) employed Modified Schema-Based Instruction (MSBI) to teach addition and subtraction change problems, while Study 2 (age 14 years 10 months; 18 sessions) utilized the Conceptual Model-based Problem Solving (COMPS) approach for multiplication and division equal-group problems. Success was defined as both correctness of the response and correctly identifying the required operation. Results indicated that the student’s performance improved in all problem types in both studies, with maintenance observed 8 weeks after Study 1 and 5 weeks after Study 2. Instruction effects generalized to two-step addition and subtraction problems in Study 1, and to two-step addition and multiplication problems in Study 2. The findings indicate that both MSBI and COMPS facilitated the student’s shift from informal strategies to efficient operation-based problem solving. Implications for practice include the need for individualized reinforcements, careful adaptation of instruction, and providing teachers with a variety of problems and knowledge of these teaching methods to support students with ASD in developing advanced problem-solving skills.

1. Introduction

Mathematical problem solving is a fundamental component of mathematics education, as it enables students to connect their knowledge to practical, real-world situations (Spooner et al., 2017). Furthermore, problem-solving engages a range of cognitive skills simultaneously, including interpreting the problem statement, constructing a mental representation of the key relationships involved, and developing and executing a solution strategy. This process can be particularly challenging for many students with autism spectrum disorder (ASD), who often face difficulties with verbal comprehension and executive functioning (Root et al., 2021). Previous studies have found that students with ASD tend to employ less efficient problem-solving strategies compared to their typically developing peers (Polo-Blanco et al., 2024b). Additionally, research has shown a frequent reliance on counting-based strategies on drawings or concrete representations among students with ASD (Bruno et al., 2024; Goñi-Cervera et al., 2023), which may be linked to visual strengths commonly observed in some individuals on the autism spectrum.

In this work, we focus on arithmetic word problems. They are verbal statements presented with the aim of finding an unknown quantity through the application of basic arithmetic operations. These problems are typically classified according to their underlying structure into additive and multiplicative problems (e.g., Carpenter & Moser, 1984; Nesher, 1992). In additive problems, the unknown is determined using addition or subtraction, whereas multiplicative problems involve multiplication or division. Additive problems can be further categorized into three main subtypes: combination, change, and comparison problems. Likewise, multiplicative problems are commonly divided into equal-groups, comparison, and Cartesian product problems.

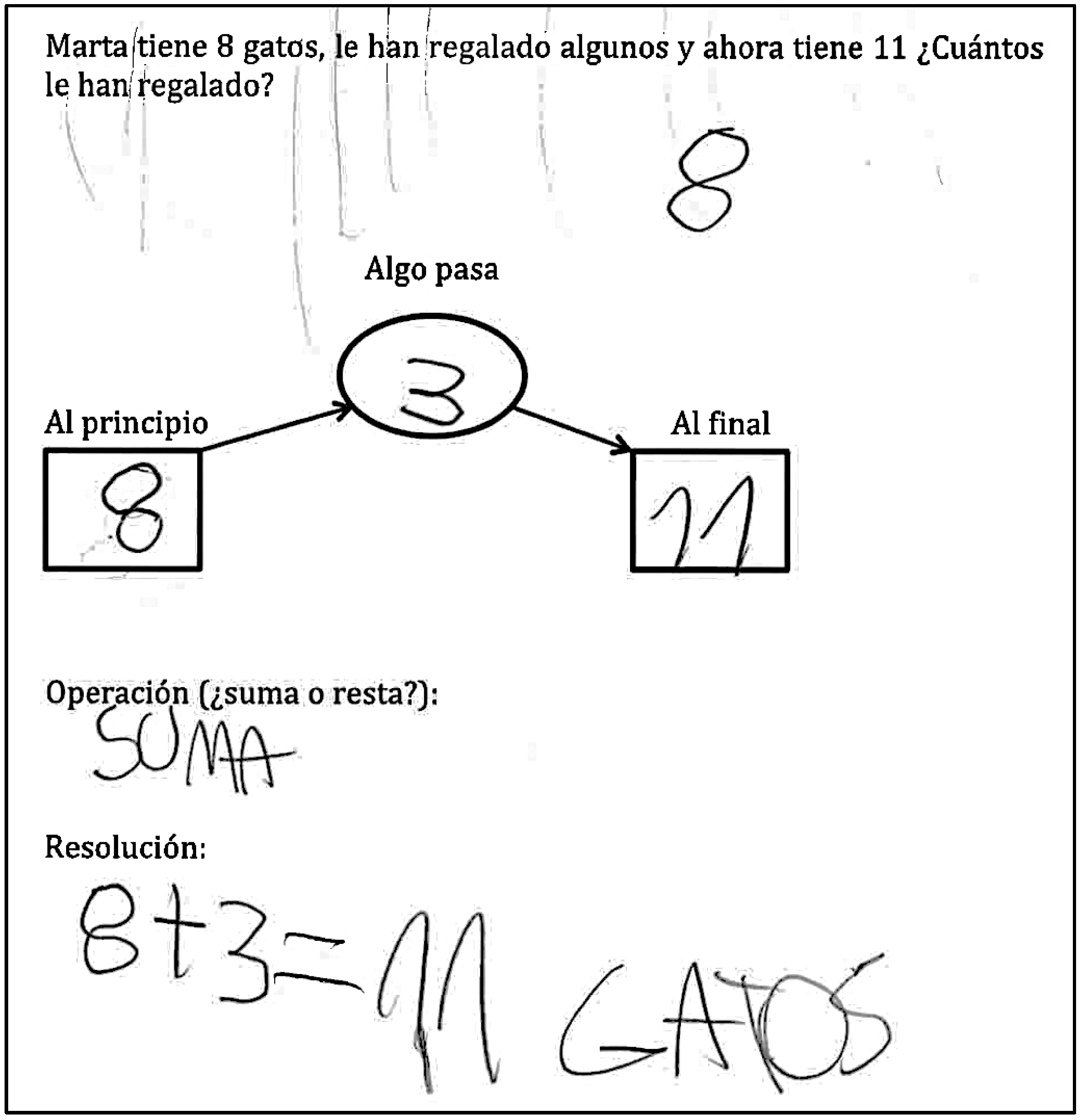
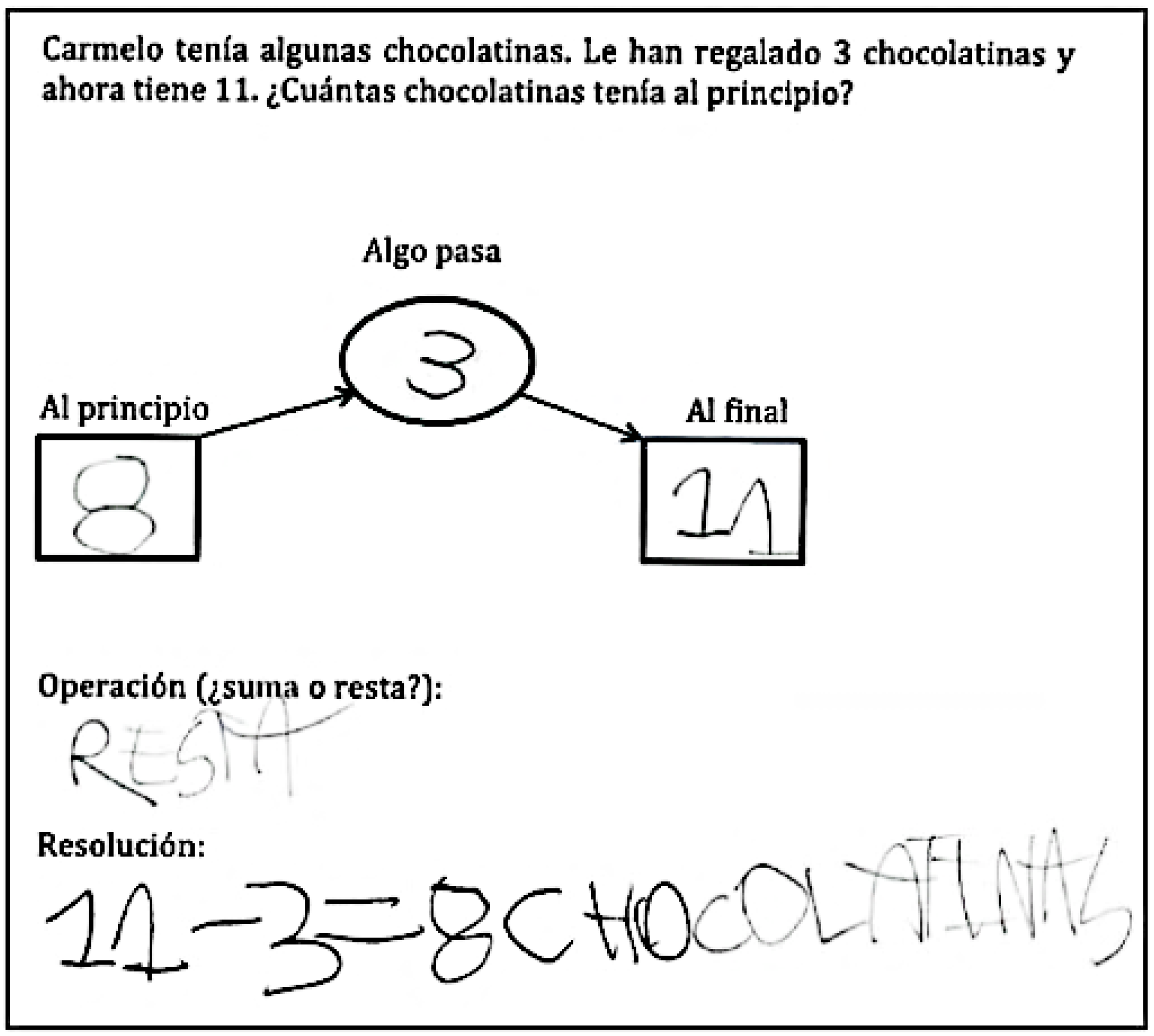
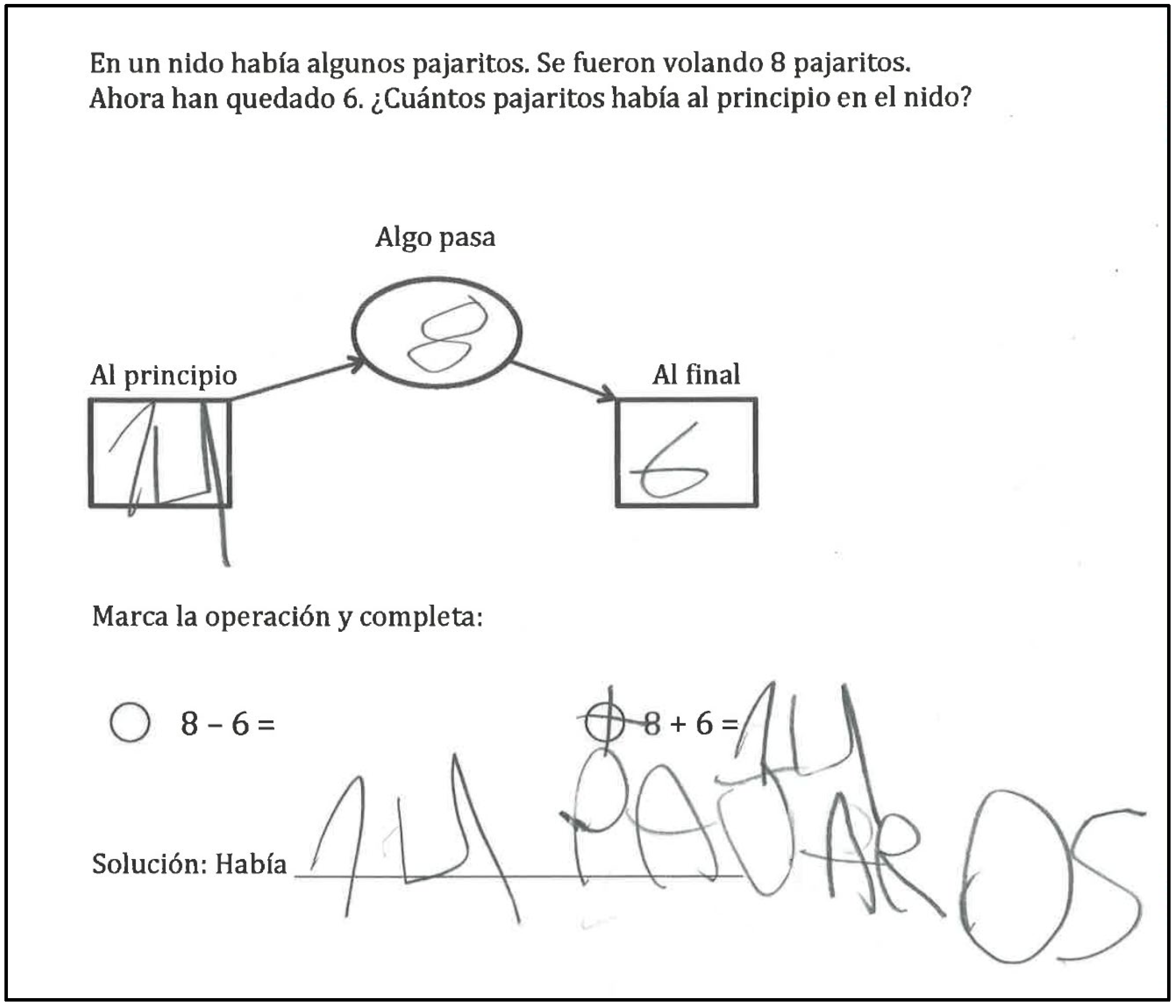
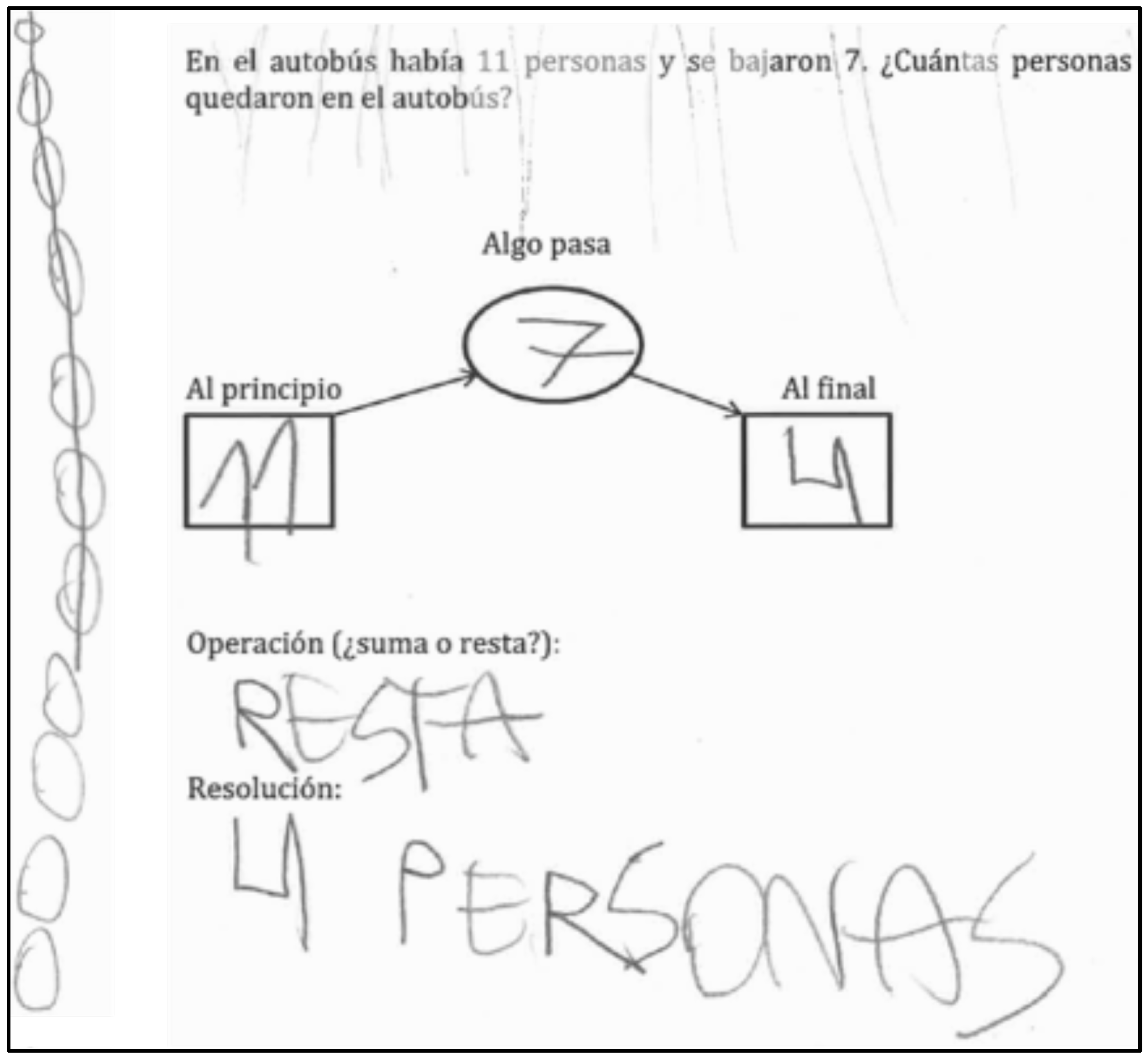
Additive change problems describe situations in which an initial quantity is either increased or decreased through an action, resulting in a different final quantity. Depending on the position of the unknown quantity, three types of change problems can be distinguished: final amount unknown (DDU), change amount unknown (DUD), and initial amount unknown (UDD). Each of these types can be further characterized as either “get more” or “get less” problems, depending on the action described by the verb. For instance, “John has 13 marbles. He lost 7 marbles. How many marbles does John have now?” is a “get less” problem of type DDU. Previous research has shown that DDU problems are generally the easiest for students to solve, followed by DUD problems, with UDD problems being the most difficult (Carpenter & Moser, 1984; Riley et al., 1983). Change problems can also be classified as consistent or inconsistent, based on whether the required arithmetic operation aligns with the relational term in the problem statement (Verschaffel et al., 2000). For example, in the following UDD problem, “Dan had some marbles. He found 9 more marbles. Now he has 15 marbles. How many marbles did he have to start with?”, the problem requires subtraction to determine the initial amount although a “get more” scenario is described. This makes it an inconsistent UDD “get more” problem (Lewis & Mayer, 1987). There are three types of inconsistent change problems, namely, those of type DUD “get more” and the UDD problems (both “get more,” and “get less”).

Due to the challenges that some students with ASD face in comprehending problem statements and mapping the relationships among the given quantities, problems involving inconsistent language may be particularly difficult for these learners. As Hardy et al. (2025) showed, keyword-based strategies are ineffective for solving such problems. Conversely, students with ASD may benefit from instructional approaches that explicitly support the understanding of problem statements (Bruno et al., 2021).

Schema-Based Instruction (SBI) is an evidence-based practice to teach problem-solving skills to students with ASD (Root et al., 2021). This approach integrates visual representations, heuristics, and explicit instruction (Clausen et al., 2021). By emphasizing the semantic structure of word problems, SBI associates each problem subtype—combine, change, and comparison—with a specific schema that illustrates the relationships among the given quantities. These schemas support students in understanding the problem situation and identifying the appropriate mathematical operation needed to solve for the unknown.

While SBI has demonstrated effectiveness for students with developmental disabilities, it may require further adaptation for learners with moderate to severe disabilities. In this regard, Spooner et al. (2017) proposed a conceptual model for Modified Schema-Based Instruction (MSBI), incorporating evidence-based practices across four components: access to the problem, conceptual understanding, procedural knowledge, and generalization of skills. The model also incorporates systematic instruction by dividing each session into three phases, following a model–lead-test sequence. In the model phase, the instructor provides the student with a demonstration for solving a problem. During the lead phase, the student is guided through solving problems while the instructor implements strategies such as error correction with time delay, model and retest, or a system of least prompts. In the test phase, the student solves problems independently, without the instructor’s assistance.

Building on this framework, Root et al. (2022) offered practical guidance on implementing MSBI to teach problem-solving strategies to students with ASD and intellectual disabilities (ID). Several studies have applied MSBI to enhance additive word problem-solving skills in students with ASD. In the case of combine problems, Root and Browder (2017) used a multiple probe across participants design to establish a functional relation between an MSBI-based intervention and the problem-solving performance of three students with ASD and ID, aged 12 to 14. Similarly, Root et al. (2018) demonstrated the effectiveness of MSBI in improving the problem-solving skills of three students, aged 10, 11, and 12, with ASD, two of whom had co-occurring ID. In the same line, Fernández-Cobos and Polo-Blanco (2024) reported positive outcomes from an MSBI intervention delivered to four students aged 11 to 16 with ASD and language impairments. For comparison problems, Root et al. (2017) found a functional relation between MSBI and improved problem-solving skills in three students with ASD and moderate ID, aged 7, 9, and 11.

With respect to change problems, Polo-Blanco et al. (2024a) demonstrated the effectiveness of an MSBI-based intervention in enhancing problem-solving abilities in three students aged 13, 14, and 17, with mild ID, two of whom had an ASD diagnosis. All the students showed difficulties with inconsistent language problems in baseline condition, but their performance improved during the intervention. The instruction focused on making the students understand that they could not rely only on the action of the verb, and the schema helped make the relationship between the given quantities explicit (Bruno et al., 2021).

Multiplicative problems are generally categorized into three types (e.g., Nesher, 1992): equal-group problems, where a certain quantity is repeated a given number of times (e.g., “There are 5 tables in a classroom. At each table, there are 4 chairs. How many chairs are there in the classroom?”); comparison problems, in which a quantity is compared to a reference based on a multiplicative factor (e.g., “Mario has 3 marbles. María has 4 times as many marbles as Mario. How many marbles does María have?”); percentage or proportion, where cross-multiplication and equivalence fractions are used to solve them (e.g., “George inflates 3 ballons in 2 min. How many ballons will he inflate in 6 min?”); and Cartesian product problems, where all possible combinations between two sets are considered (e.g., “In her closet, Claudia has 3 shirts and 2 pairs of pants. How many different outfits can she wear?”). Multiplicative problems may involve either multiplication or division, depending on the unknown quantity. Moreover, multiplicative comparison problems can also be classified as either consistent or inconsistent, based on whether the language used provides a clear indication of the required operation.

Several studies have examined the strategies employed by students with ASD when solving multiplicative problems. For example, Goñi-Cervera et al. (2023) examined the problem-solving strategies of 10 students with ASD, both with and without ID, aged between 8 and 13, when tackling equal-group problems. Most students relied on low-level strategies, such as counting, and made limited use of formal multiplication and division procedures. Later, Polo-Blanco et al. (2024b) conducted a comparative study involving 26 students with ASD without intellectual disabilities, and 26 typically developing peers. They found a higher proportion of students with problem-solving difficulties in the group with ASD compared to the comparison group. Among students with ASD, those who performed more poorly tended to rely on less abstract strategies than the other autistic children.

Although to a lesser extent, MSBI has also been applied to support the development of multiplicative problem-solving skills in students with ASD, including comparison problems (Gilley et al., 2021; Root et al., 2022) and proportion problems (Cox & Root, 2020). Another visual strategy used for teaching multiplicative problem-solving is the Conceptual Model-based Problem Solving approach (COMPS; Xin, 2012). Rather than focusing on the semantic structure of the problem, COMPS emphasizes the use of a conceptual model—represented by an algebraic equation—that captures the mathematical relationships within the problem (e.g., “Part1 + Part2 = Whole” for additive problems, or “Unit rate × Multiplier = Product” for multiplicative problems). The COMPS instructional sequence also aligns with a model–guide–independent framework (Xin, 2012). It involves explicit explanation of strategies and modeling, followed by dynamic teacher-student interaction during guided practice, continuous performance monitoring with corrective feedback, and independent practice (Xin, 2012). COMPS is more general than schemas, as it supports connections across different types of problems by highlighting the underlying mathematical structure. While Ma and Xin (2023) evaluated the effect of COMPS on PPW word problem solving involving three elementary students with ASD, Polo-Blanco et al. (2022) undertook a case study with a 14-year-old student with ASD and ID, employing a COMPS-based approach for teaching multiplicative structure problems.

Most research on students with ASD examines their mathematical performance during instructional experiences, such as those described above (e.g., Cox & Root, 2020; Fernández-Cobos & Polo-Blanco, 2024); however, studies that track the development of performance over several years are scarce and particularly valuable (e.g., Kim et al., 2018). To address this gap, the present paper describes the development of problem-solving strategies demonstrated by a student with ASD and ID across two instructional processes tailored to his individual needs for solving additive and multiplicative word problems. At age 13 years 9 months, the student engaged with additive problems through the MSBI approach (Study 1), while at 14 years 10 months, he addressed multiplicative problems using the COMPS approach (Study 2). Improvements were observed in both studies, as the student progressed from using informal strategies based on counting to employing more advanced strategies, such as identifying the appropriate arithmetic operation and either recalling memorized number facts or performing calculations to obtain the correct answer. Therefore, this study poses the following research question: How do problem-solving strategies develop over time in a student with ASD and ID when supported at two different points in time through two different approaches, namely MSBI for additive word problems and COMPS for multiplicative word problems?

2. Materials and Methods

Two single-case studies were conducted at different points in time using a multiple baseline design—across participants (Study 1) and across behaviors (Study 2)—to evaluate the effectiveness of MSBI and COMPS on the problem-solving performance of students with ASD and ID. The results presented in this article focus on Peter (pseudonym), the student who participated in both studies.

The multiple baseline design is a widely used approach for evaluating the effectiveness of interventions in educational and clinical contexts (Kratochwill et al., 2013). It provides evidence of a student’s progress throughout an intervention by means of repeated, practice-based data collection. This design involves assessing student performance at multiple time points, with each assessment informing decisions on how to further guide instruction. Before instruction begins, a baseline assessment is conducted to determine the student’s initial level of performance. This baseline is typically repeated across several sessions to ensure performance stability over time. Once instruction is underway, assessments are administered at the end of each session to evaluate whether the student has met predefined success criteria and to guide subsequent instructional decisions. After the instructional phase, post-intervention assessments are carried out to determine whether the student can generalize the acquired skills to novel situations—where no explicit instruction was provided—and whether those skills are maintained over time. Specific details on how this method was implemented in each study are provided below.

Study 1 involved three participants and focused on additive change problems using MSBI. A multiple baseline across participants design was used to establish a functional relationship between the MSBI intervention and students’ performance. Study 2 took place ten months later and included only Peter as a participant. This second study employed a multiple baseline across behaviors design to address three types of multiplicative word problems—equal groups, multiplicative comparison, and Cartesian product—using COMPS instruction adapted to Peter’s individual needs. In both studies, the instructor leading the sessions was the same, and had prior experience teaching mathematics to Peter. In this article, we report findings related to Peter’s participation in Study 1 (additive change problems) and Study 2, specifically focusing on the first behavior targeted—equal-group problems.

All sessions in both studies were video recorded to capture Peter’s reasoning processes and problem-solving steps in detail. All his written responses were also collected for analysis. One researcher in each study categorized the strategies, distinguishing whether the answer to the problem was correct or not.

Although this work focuses on describing the type of strategy used by the participant in both studies, as mentioned above success was defined as both identifying the required operation and providing the correct response. These data were analyzed through visual analysis. The percentage of nonoverlapping data (PND) was calculated across the sessions involving all types of problems. In Study 1, Peter showed a mean performance of 35.00% (SD = 8.37) during baseline. During the instructional sessions, the average performance increased to 72.22% (SD = 19.25), showing an upward trend and 66.67% of non-overlapping data compared to baseline. In the maintenance session, performance further improved, reaching 100%.

In Study 2, Peter showed a stable performance across four baseline sessions, consistently at 25%. An immediate effect was observed during the first instructional session, with an improvement of 50 percentage points compared to baseline. Performance further increased during the second session, stabilizing at 100% in the last three sessions. In this condition, the mean performance was 93.75% (SD = 12.50), with no overlap between baseline and training data. During the follow-up, the student responded correctly to all problems except in one session, in which a single error occurred. Consequently, the mean performance was 96.43% (SD = 9.45).

2.1. Participant

Peter was diagnosed with ASD at the age of six, following clinical evaluations based on DSM-IV diagnostic criteria. No additional comorbidities were identified during the assessment. According to the Childhood Autism Rating Scale (Schopler et al., 1988), Peter falls within the severe range of autism. He displays a wide array of stereotyped behaviors, a tendency toward repetitive actions, and strong, focused interests in specific areas.

Peter attended a mainstream school until the age of ten, where he received significant curricular adaptations in both language and mathematics. Since then, he has been enrolled in a special education center. According to his most recent evaluation by the center’s support team, Peter shows social interest in peers, though his participation in play and social interactions is limited. He responds positively to structured routines and feels more comfortable when events are anticipated. His emotional and cognitive development appears to be delayed, with impairments in symbolic processing. Peter has an intellectual disability, with a Full-Scale IQ of 54, as measured by the Wechsler Intelligence Scale for Children—Fifth Edition (WISC-V; Wechsler, 2014).

At the time of Study 1, Peter was 13 years and 9 months of age. In terms of mathematical skills, he scored 56 on the Test of Early Mathematical Ability (3rd edition; TEMA-3; Ginsburg et al., 2007), corresponding to a mathematical age of 7 years 8 months. His subtest scores were as follows: 96% in number skills, 78% in number facts, 71% in concepts, and 50% in number comparison and calculation skills. According to the most recent assessment by the center’s support team, his reading ability is comparable to that of an 8- to 9-year-old, which allows him to read and understand problem statements, although he has trouble understanding certain vocabulary. Prior to the intervention, Peter had limited experience with additive word problems involving addition and subtraction. In some cases, he was able to solve them—often relying on memorized number facts—but in an unstable pattern and only in consistent DDU change problems.

At the time of Study 2, Peter was 14 years and 10 months. He was following an adapted mathematics curriculum for approximately four hours per week. He demonstrated good reading comprehension, which allowed him to read and understand word problems, although he continued to experience difficulties with some specific vocabulary. Prior to the intervention, he had practiced solving additive word problems and was able to correctly identify the required operation (addition or subtraction), often relying on memorized number facts. Regarding multiplication, Peter had been introduced to the concept as repeated addition. However, he had not memorized the multiplication tables and had not received formal instruction in multiplication or division algorithms. In terms of multiplicative word problems, Peter demonstrated partial understanding of equal-group multiplication problems and could sometimes solve them using informal strategies, such as drawing or counting. As such, it was considered an appropriate time to introduce instruction on other types of multiplication and division word problems, specifically equal- group problems.

2.2. Strategy Categories for Study 1 and Study 2

Building on prior research on strategies for solving one-step word problems (Carpenter et al., 2015; Bermejo & Díaz, 2007; Mulligan, 1992), we have used the following categories to code the student responses to both additive and multiplicative problems.

• Direct Answer (DA). The student provides the answer without showing the steps or procedure used to obtain it.
• Direct Modeling (DM). The student uses manipulatives or drawings to represent the quantities and relationships described in the problem, then counts the objects or marks to find the answer.
• Counting (C). The student obtains the answer by reciting counting sequences to determine the answer, without using physical or pictorial representations of the problem.
• Operations (O). The student determines the arithmetic operation needed to solve the problem and either recalls memorized number facts or performs calculations to obtain the answer.

A mixed strategy may be employed, in which two or more of the above strategies are used when solving the problem.

2.3. Study 1 MSBI

2.3.1. Experimental Design and Data Collection

The study started at the beginning of the school year and spanned a period of six months. Weekly sessions lasting approximately 50 min were conducted, all of which took place at the student’s special education school.

The multiple baseline design used to assess the effectiveness of the MSBI intervention for teaching students to solve addition and subtraction change problems consisted of the following phases: baseline, instruction on each type of change problem introduced sequentially (first DDU, then DUD, and finally UDD), generalization (to an untrained setting and to two-step problems), and maintenance. Each session within these phases included probes to assess the student’s performance and monitor progress. These probes typically involved one-step change problems, except in one session in the baseline phase and in one session in the generalization phase, where two-step problem-solving probes were administered. The number sets considered in the problems included addends whose sums did not exceed 15.

A total of 17 sessions were conducted with Peter, distributed as follows: 7 baseline sessions; 7 instructional sessions (each followed by a performance probe); 2 generalization sessions (one in an untrained setting and one involving two-step problems); and 1 maintenance session, conducted eight weeks after the final instructional session. Details on the implementation of each phase and the corresponding probes are provided below.

2.3.2. Implementation of the Experimental Design

One teacher from Peter’s school, with over eight years of experience, delivered the instruction. Before the beginning of the study, the researchers explained the different phases to the teacher to ensure that the instructional procedures were implemented correctly. In particular, the teacher received guidance on how to use the schemas effectively. The researchers held weekly meetings with the teacher to review important aspects of the previous session and to provide a script with teaching instructions for the upcoming session. These scripts offered flexible guidance, allowing the teacher to adapt instruction based on the student’s specific difficulties (e.g., “If the student does not identify the larger amount in the problem, use the manipulatives to model the situation”).

Sessions were conducted early in the morning, during school hours, in a familiar room within the school, ensuring a distraction-free environment for the student.

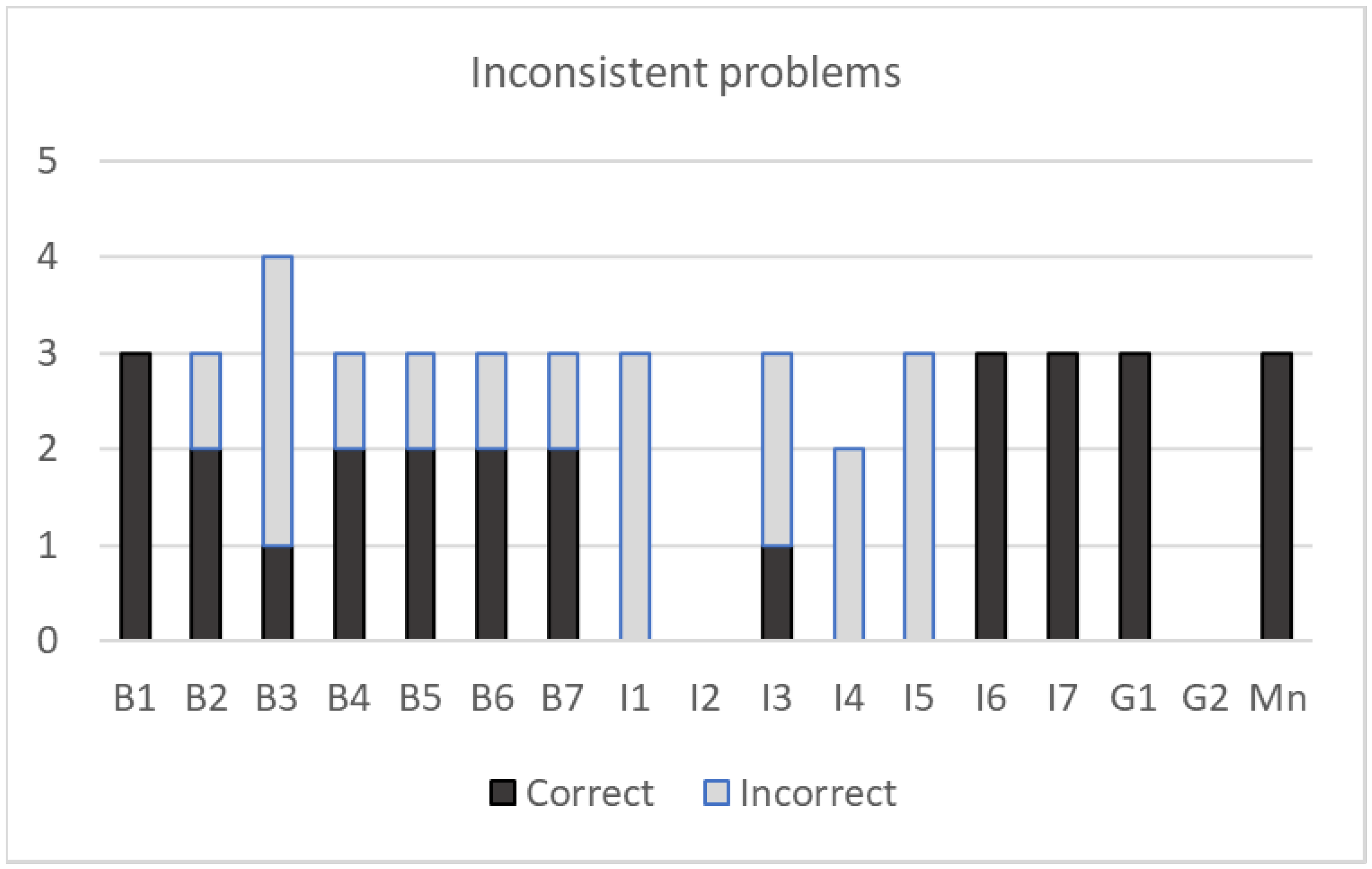
All baseline sessions—except for session 2—consisted of probes with six one-step change problems, including two of each type: DDU, DUD, and UDD. Among these six problems, three were inconsistent, representing all three possibilities: DUD “get more,” UDD “get more,” and UDD “get less”. The problems were randomly ordered in each probe. Baseline session 2 was dedicated to two-step change problems. An example of such problem is: “At the beginning of a birthday party, there were 10 children. Then, 4 more children arrived, and 3 left. How many children were at the party in the end?” Across all these sessions, the student was provided only with the written statement of each problem on a separate sheet of paper. He was asked to solve the problems independently, without teacher assistance, except in cases where clarification of unfamiliar vocabulary was needed. No feedback or guidance was provided during these sessions.

To determine whether behavior was stable during the baseline phase—or to decide when to introduce a new type of problem during instruction—we used the following scoring system: each problem was worth a maximum of two points—one point for correctly identifying the required arithmetic operation, and one point for providing the correct numerical answer.

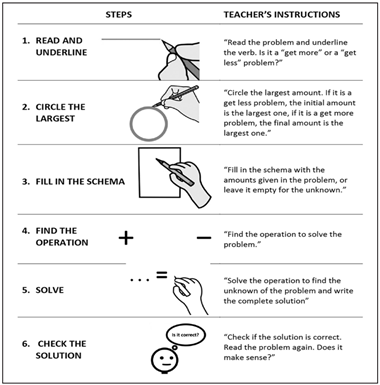
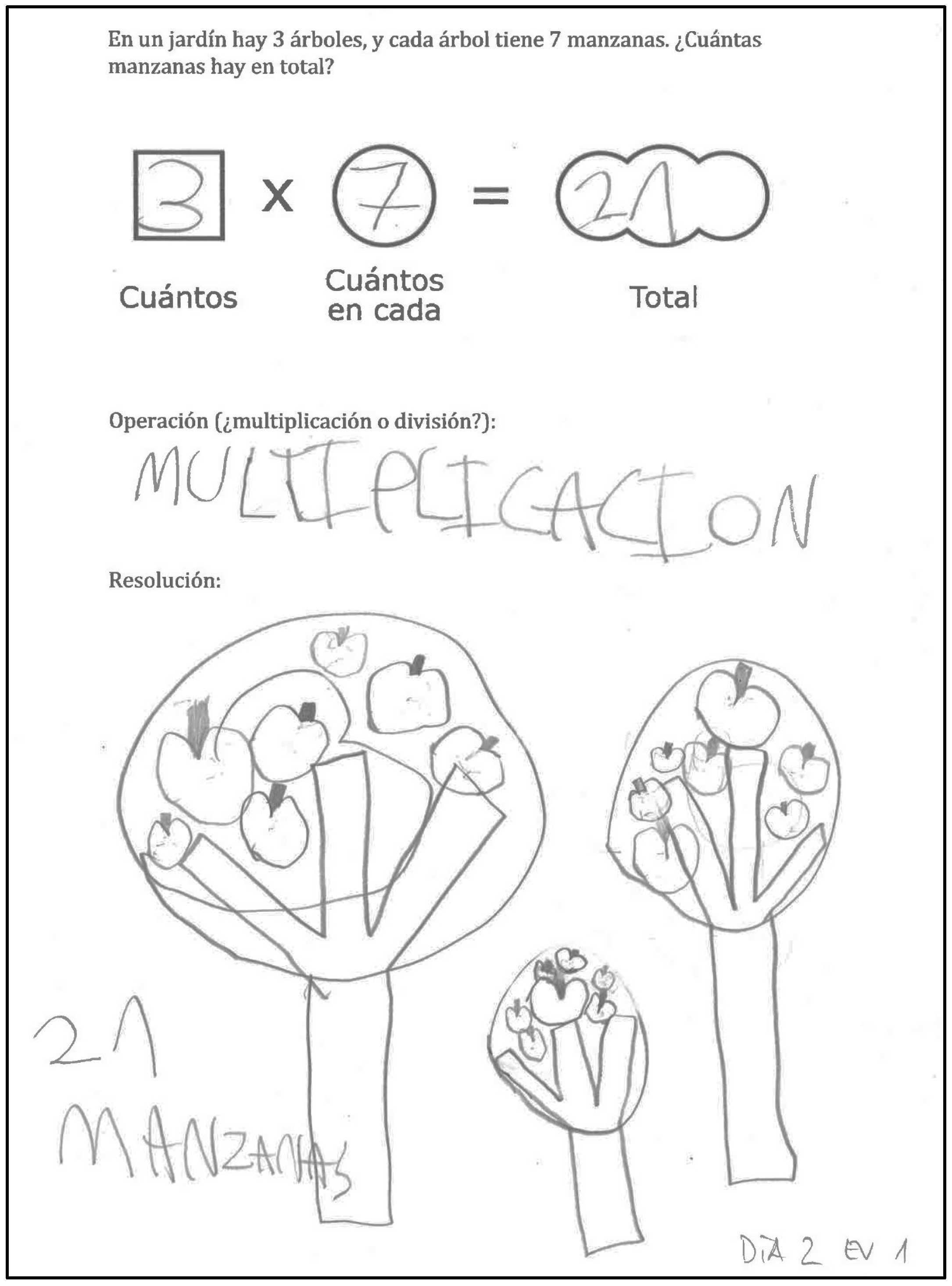
After achieving a stable baseline—defined as at least two baseline probes with no more than one-point difference between them—the instructional phase began. The MSBI approach, adapted from Cox and Root (2020) and Browder et al. (2018), included explicit instruction on using a guiding-questions sheet that incorporated visual representations—pictograms—for each step (Figure 1), the use of schematic diagrams, and systematic prompting and feedback.

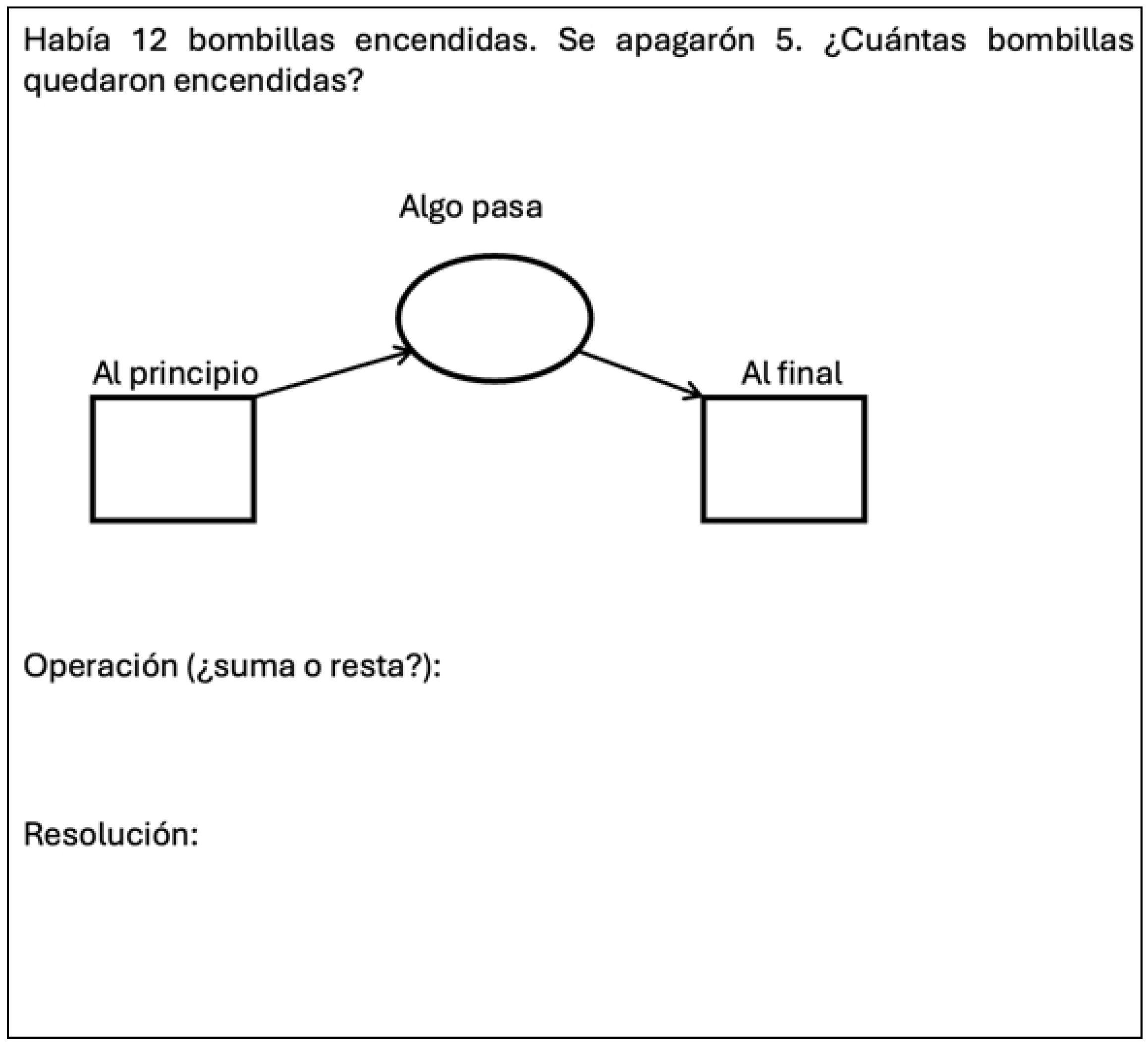
Additionally, the problems were presented using a structured worksheet that included a standard schema for change problems, as illustrated in Figure 2.

The instruction was delivered in two periods, following the recommendations of Xin (2008):

• Period I. The problem-schema instruction. During the first instructional session, the student was introduced to change stories, i.e., change situations without unknowns. The instructor demonstrated how to follow the first three steps of the guiding-questions sheet—underline the action, circle the largest amount, and fill the schema.
• Period II. The problem-solving instruction. The student was then introduced to change problems. Instruction emphasized using the schema to solve each type of change word problem, according to the position of the unknown (first DDU, then DUD, and finally UDD), based on prior research on difficulty levels (Riley et al., 1983).

In each instructional session, the instructor followed a model–lead–test sequence: first, they demonstrated how to solve a change problem by following the guiding-questions sheet. Then, the student was guided though solving up to eight problems. The instructor encouraged the student to follow the steps, clarified unfamiliar vocabulary, and provided error correction, using manipulatives to model the situations whenever the student had difficulty understanding the problem statement. Finally, the session was evaluated by means of a probe consisting of six change problems. The student independently completed these problems. If the student scored over 75% on the probe, the next problem type was introduced in the following instruction session.

The second instructional session was assessed through six DDU change problems. DUD problems were introduced in the third instructional session, which, along with the fourth session, was assessed using a combination of one DDU and five DUD change problems. UDD problems were introduced in the fifth instructional session. The fifth, sixth, and seventh instructional sessions were assessed using a balanced set of DDU, DUD, and UDD change problems, representing “get more” and “get less” scenarios.

Once instruction was completed, generalization to an untrained setting was assessed. The student completed a probe consisting of the six variants of change problems. This probe was administered in the student’s regular classroom, in the presence of other students and their regular teacher, who was not the same instructor who had provided the intervention.

In a separate session, generalization to two-step problems was evaluated using a probe consisting of eight problems, all with the unknown in the final quantity (DDDU). These problems included various combinations of “get more” and “get less” scenarios.

Finally, to assess whether the acquired skills were maintained over time, the student completed a maintenance probe eight weeks after the conclusion of the instructional sessions. This probe consisted of six change problems—two DDU, two DUD, and two UDD—covering both “get more” and “get less” varieties.

2.4. Study 2 COMPS

2.4.1. Experimental Design and Data Collection

The study was conducted during the first half of the academic year and spanned a period of six months. One 30 min session was held each week at the student’s special education school. The experimental phases consisted of baseline, instruction and instructional performance probes, follow-up, generalization tests involving two-step problems that combined addition and multiplication, and maintenance conducted five weeks after instruction. The probes were completed in written format. As in Study 1, they allowed for a distinction between two aspects of performance: accuracy in identifying the appropriate operations needed to solve the problems and the correct execution of those operations (i.e., performing the calculations).

The intervention followed a structured sequence, introducing three types of multiplicative word problems across successive phases: equal-group problems, multiplicative comparison problems, and Cartesian product problems. A total of 16 instructional sessions were conducted with Peter —five sessions focused on equal-group problems, six on comparison problems, and five on Cartesian product problems. This study focuses exclusively on the five sessions dedicated to solving equal-group problems.

2.4.2. Implementation of the Experimental Design

All the sessions were conducted outside regular school hours. If Peter appeared tired or had difficulty maintaining focus, the instructional session was split into two shorter sessions on consecutive days. Although the experimental design included multiplicative problems of all three types, in this article, we include only the information related to equal-group problems.

During each session in the baseline phase, the student was assessed using two one-step word equal-group problems, one involving multiplication and the other involving division. An additional session was conducted with two generalization problems that required solving with two operations. For instance, one of the problems read: “Ana bought 4 bags of gummy candies for her birthday party. Each bag contains 3 strawberry gummies and 2 lemon gummies. How many gummies did she buy in total?” After five baseline sessions, one of the target behaviors was introduced, provided that the baseline was stable. The problems were presented in written form on separate sheets. Peter was asked to complete the problems independently and was encouraged to do his best. No help was provided unless he encountered an unfamiliar word, in which case the instructor explained the meaning verbally.

After the baseline assessment, five instructional sessions (I0 to I4) were conducted, focusing on equal-group problems. As in Study 1, instruction began with stories without a question (I0), progressed to multiplication problems (I1), followed by division problems (I2 and I3), and concluded with mixed problems involving both operations (I4). The criteria for phase change were also determined based on the score, which took into account, for each problem, both the identification of the operation and the correct numerical answer.

Instruction was guided by the COMPS model, using a structured teaching sequence inspired by Engelmann (1980) direct instruction and Xin (2012) model–lead–test approach. Each session began with the modeling phase, where the instructor introduced the problem using a visual representation and demonstrated how to map the quantities onto a schematic diagram. This was followed by guided practice in which the instructor posed questions to help Peter work through similar problems. Throughout this process, the instructor provided continuous feedback and clarification as needed. Finally, Peter solved new problems independently in the test phase for evaluation of his understanding in each session.

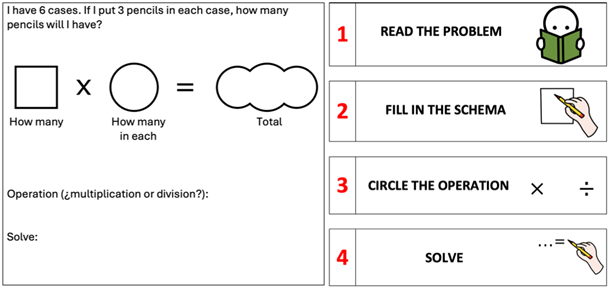
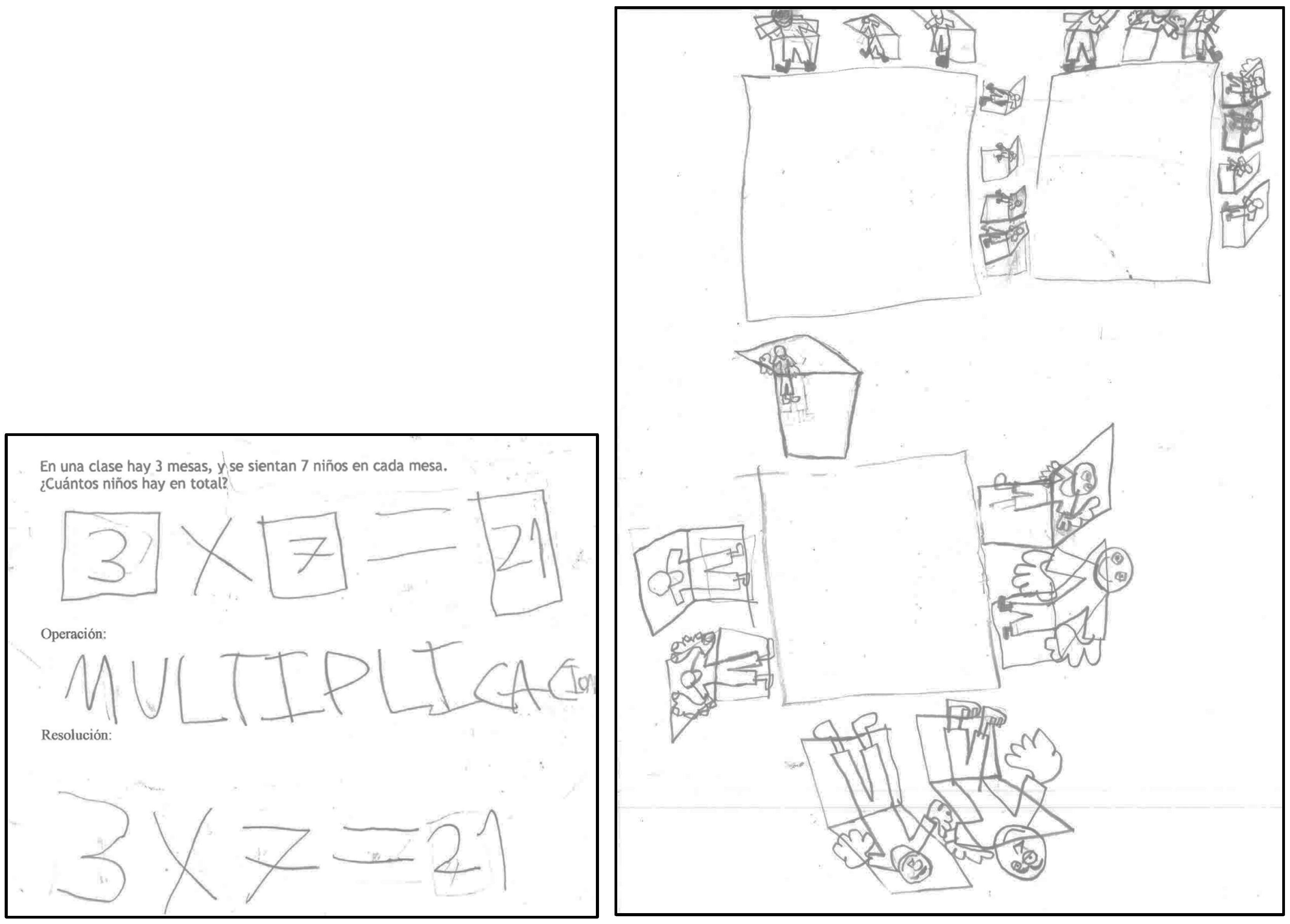
The first instructional session aimed to familiarize Peter with the schema associated with equal-group problems. Problem numbers were chosen so that totals did not exceed 30, allowing Peter to solve them using informal strategies rather than relying on multiplication facts he had not yet memorized. Care was taken to avoid problems with repeated numbers (e.g., 3 × 3), ensuring that Peter had to interpret the specific role of each quantity within the diagram (e.g., identifying whether a number represented “how many in each group,” “how many groups,” or “total”).

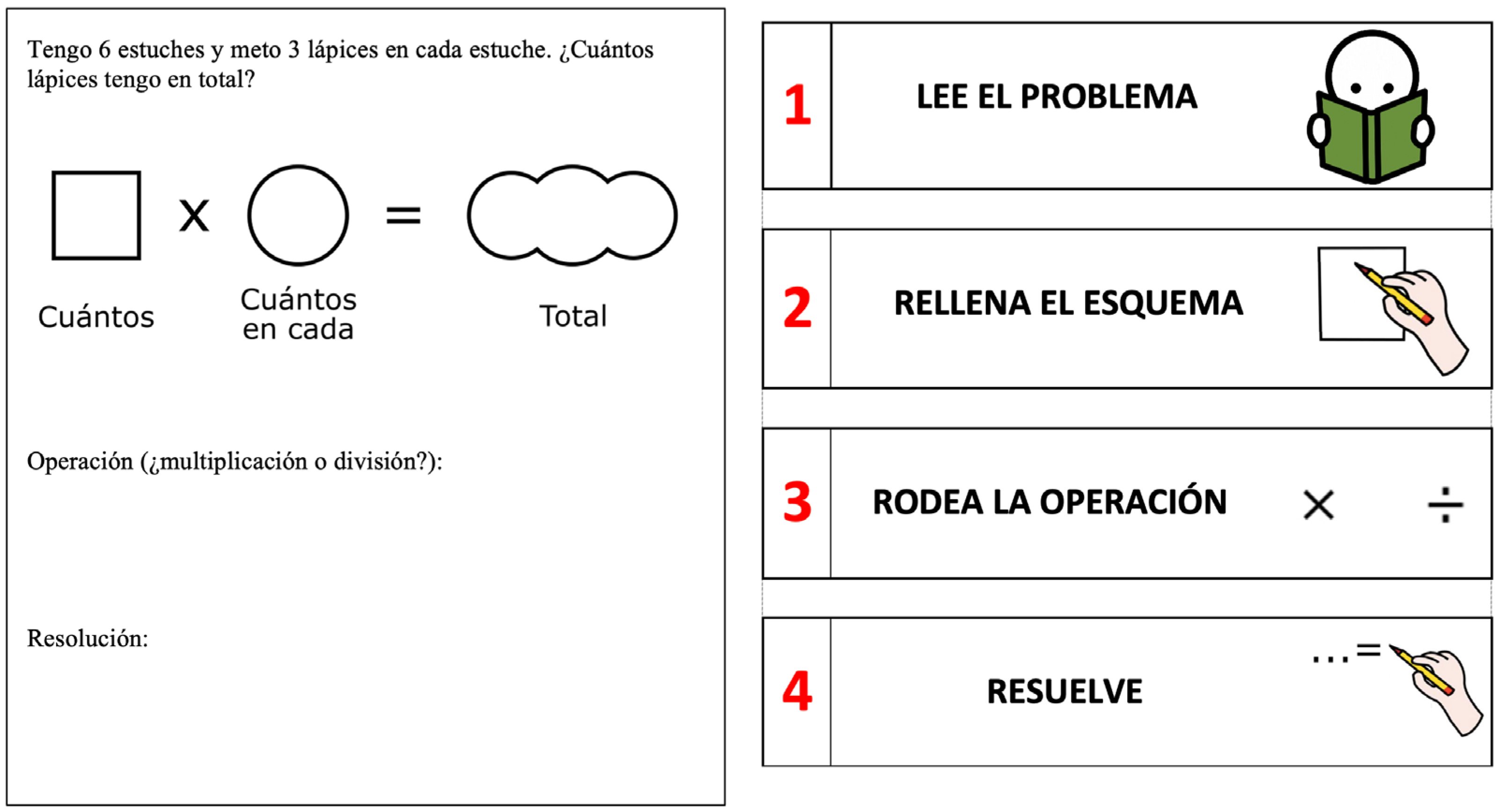
Each problem was presented on a structured worksheet (see Figure 3), which included the problem statement alongside a schematic diagram. Peter read the problem and, with the help of guiding questions, placed the relevant quantities in the appropriate places on the diagram. If he struggled with understanding the problem context, the instructor would supplement the task with a concrete visual, such as a drawing or tree diagram, to ease the transition toward abstract reasoning. Once the diagram was complete, Peter was asked to identify the correct operation, write it down, and then solve the problem by explicitly performing the calculation. A visual reference sheet outlining the steps served as a scaffold to support him throughout the task.

During multiplication instruction, the emphasis was on helping Peter connect the problem scenario with the diagram and identify multiplication as the operation needed. He often successfully completed the problems using the diagram and would sometimes add illustrative drawings, reflecting his comfort with visual supports even when not strictly necessary for the solution. When addressing division problems, the instructor placed particular focus on vocabulary such as “in each” and “distributed equally,” ensuring Peter understood the context. He was guided to match the numbers from the word problem to the correct positions in the diagram—typically identifying known totals and groupings to infer the unknown. This helped reinforce the concept of division as the inverse of multiplication. Peter was then instructed to write “division” in the operation section and write the operation as a fraction for simplicity. While this notation was used for clarity, formal symbolic representation was not emphasized to keep the focus on understanding the structure of the problems.

Once the instruction period was completed, the follow-up phase began, where Peter was evaluated seven times over four months (F1 to F7). In the problem statements, the COMPS diagram was not provided, as the goal was to assess his strategies over time without direct influence from the instruction sessions. After the end of the follow-up phase with one operation, a generalization test was given consisting of two two-step problems (adding and multiplying, and adding and dividing, respectively). Finally, a maintenance probe was conducted five weeks after the end of the instruction.

2.5. Inter-Rater Agreement

To ensure internal validity, an additional researcher independently recoded 100% of the strategies. Inter-rater agreement was calculated by dividing the number of agreements by the total number of coding decisions and multiplying the result by 100.

The inter-rater agreement in Study 1 was 98%, 97%, 100% and 100% for baseline, instruction, generalization, and maintenance, respectively. In Study 2, inter-rater agreement was 100%, 94%, 93%, 100% and 100% for baseline, instruction, follow up, post-test, and maintenance, respectively. Both results show strong inter-observer agreement.

3. Results

We present the results alongside illustrative examples showing how the strategies evolved. The English translation of each figure is provided in Appendix A.

3.1. Results Study 1

The results of Peter’s performance across the different phases of Study 1 are summarized in Figure 4. Additional details regarding the type of operation (addition or subtraction) are provided in

Table A1. Number of problems, success and types of strategies for additive change problems.

	B1	B2	B3	B4	B5	B6	B7	I1	I2	I3	I4	I5	I6	I7	G1	G2	Mn
No. problems	6	8	6	6	6	6	6	6	6	6	6	6	6	6	6	8	6
Correct	6	5	4	4	4	5	4	-	6	3	1	3	6	6	4	7	6
	Incorrect Strategies
DA	-	1	1S	-	1S	1S	1S	-	-	-	-	-	-	-	-	-	-
DM	-	1	1S	1S	-	-	1S	-	-	-	-	-	-	-	-	-	-
C	-	1	-	1A	1S	-	-	-	-	-	-	-	-	-	-	-	-
O	-	-	-	-	-	-	-	-	-	3S	5S	1A2S	-	-	2S	1	-
	Correct Strategies
DA	-	1	-	2S	-	2A2S	2A1S	-	-	-	-	-	-	-	-	-	-
DM	2A4S	3	3S	1A1S	2A	1S	1S	-	-	-	-	-	-	1S	-	-	1S
C	-	1	1A	-	2S	-	-	-	-	-	-	-	1A3S	2A3S	-	-	-
O	-	-	-	-	-	-	-	-	3A3S	3S	1S	1A2S	1A1S	-	2A2S	7	2A3S

of Appendix B. A clear progression can be observed toward the use of operation-based strategies, along with an increase in the number of correct answers. Although with some variability, the number of correct answers in inconsistent problems also increased (see Figure 5). The following sections provide a detailed description of the results in each phase.

3.1.1. Baseline Results

In the baseline phase, Peter did not explicitly identify the arithmetic operation in any of the problems and did not use correct operation (O) strategies. However, in most problems (27 out of 36), he employed strategies that led to the correct numerical answer—he solved correctly 15 out of 18 consistent problems, and 12 of 18 inconsistent ones. The most frequently used correct strategy was direct modeling (DM), used in 15 of the 27 cases, followed by direct answer (DA) in 9 cases, and counting (C) in 3 cases.

Figure 6 shows a DM strategy used by Peter to solve a DDU subtraction change problem. As the baseline sessions progressed, correct DA strategies became more frequent, particularly in sessions B6 and B7, where most of the correct strategies were DA.

Incorrect strategies (9 out of 36) were mostly associated with inconsistent problems (6 out of 9). In 4 of these 9 problems, Peter employed a DA strategy. Figure 7 illustrates an example.

Peter performed best on DDU problems, solving 11 of 12 correctly, mostly with a DM strategy. His performance was lower on DUD (9/12) and UDD problems (7/12), where he used DM, DA, and C strategies in roughly equal proportions.

Focusing on the arithmetic operations, Peter solved nearly all addition problems correctly, including the inconsistent ones, as illustrated in Figure 8. Most errors arose in subtraction—especially inconsistent problems—where incorrect answers were mainly linked to DA strategies.

In the second baseline session, Peter correctly solved 5 of 8 two-step problems, favoring the DM strategy, followed by DA and C. For DDDU-type problems (later assessed in a generalization session), he used DA twice (1 correct) and DM twice (1 correct).

3.1.2. Instruction Results

During the instructional sessions, the worksheet encouraged to use the operation strategy, which became dominant (28 out of 36). Interestingly, in the final instructional sessions (6 and 7), Peter occasionally returned to using C and DM strategies.

Peter correctly solved nearly all the DDU problems. However, when introducing DUD problems in the second instructional session, he had errors in identifying the appropriate arithmetic operation in inconsistent problems. An example is shown in Figure 9.

To reduce reliance on counting strategies, problems with larger numbers were introduced in the fourth instructional session. This support proved highly effective, as from that point onward, Peter identified the appropriate arithmetic operation in inconsistent problems (see Figure 10).

Finally, with the introduction of UDD problems in the fifth instructional session, Peter correctly used the operation strategy (see Figure 11) and maintained this skill in sessions 6 and 7.

3.1.3. Generalization to Untrained Setting Results

Peter correctly solved four out of the six problems in the probe. Notably, he successfully solved all three inconsistent problems in this session (see Figure 12). However, he failed to arrive at the correct answers in two subtraction problems (DDU and DUD).

3.1.4. Generalization to Two-Step Problems Results

Peter correctly solved 7 out of the 8 problems using the operation strategy. Figure 13 shows an example.

3.1.5. Maintenance Results

Peter correctly solved all six problems of the maintenance session, employing an operation strategy in five of them. In the remaining problem—a DDU subtraction problem—he reverted to a DM strategy (see Figure 14).

3.2. Results Study 2

Figure 15 summarizes the results of Peter’s evaluations across the different research phases of Study 2.

Table A2. Number of problems, success and types of strategies for equal-group problems.

	B1	B2	B3	B4	B5 (G)	I1	I2	I3	I4	F1	F2	F3	F4	F5	F6	F7	PT (G)	Mn
No. problems	2	2	2	2	2	4	4	4	4	2	2	2	2	2	2	2	2	2
Correct	1	1	1	1	0	3	4	4	4	2	2	1	2	2	2	2	2	2
	Incorrect Strategies
DA	-	-	-	-	1D	-	-	-	-	-	-	-	-	-	-	-	-	-
DM	1D	1D	1D	1D	1M	-	-	-	-	-	-	-	-	-	-	-	-	-
DM and O	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
C and O	-	-	-	-	-	-	-	-	-	-	-	1D	-	-	-	-	-	-
O	-	-	-	-	-	1M	-	-	-	-	-	-	-	-	-	-	-	-
	Correct Strategies
DA	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-	-
DM	1M	1M	1M	1M	-	-	-	-	-	-	-	-	-	-	-	-	1M1D	-
DM and O	-	-	-	-	-	2M	1D	-	-	1M	-	-	1M1D	1M1D	1M	1M	-	1M
C and O	-	-	-	-	-	1M	1D	1D	1M2D	1D	1M1D	1M	-	-	1D	1D	-	1D
O	-	-	-	-	-	-	2D	3D	1M	-	-	-	-	-	-	-	-	-

in Appendix B shows more details on the type of operation (multiplication or division). After a stable baseline relied on DM strategies, the instructional sessions broadened the range of strategies and increased the number of correct answers, eventually stabilizing in correct mixed strategies (DM and O, C and O). The following sections provide a detailed description of the results in each phase.

3.2.1. Baseline Results

In the baseline sessions B1 to B4 (non-generalization), Peter solved all the problems using a DM strategy. He correctly solved all the multiplication problems by drawing the groups indicated by the multiplicand and repeating them the number of times specified by the multiplier, as shown in Figure 16. The level of detail in the drawings is noteworthy.

Peter answered all division problems incorrectly, applying the same strategy used for multiplication. In each problem, he consistently drew the same number of objects in each group (see Figure 17).

During the generalization baseline B5, two problems involving two operations were presented, one combining addition and multiplication, the other addition and division. Peter answered both problems incorrectly, applying only the addition operation and failing to perform the subsequent operation (see Figure 18).

3.2.2. Instruction Results

Peter was successful in the evaluation of each instruction session, except for one multiplication problem in I1. The most notable change was in his strategies, with a marked shift away from modeling toward choosing the correct operation, with or without counting. Figure 19 and Figure 20 illustrate this progression from a DM strategy (Figure 19) to a counting and operation strategy, visible through his fingers (Figure 20).

3.2.3. Follow-Up Results

In each follow-up probe, Peter correctly solved one multiplication problem and one division problem. Figure 21 shows that, in addition to the drawings—which he continued to use—he also integrated the use of the diagram, setting up the operation and solving it correctly.

As shown in Figure 21, Peter maintained the use of the COMPS diagram in most of the follow-up problems, in the form of three squares created by himself, especially when he followed an operation strategy. On occasions when he solved the problem by modeling, he abandoned the diagram and instead made a drawing, leaving the operation in the resolution section, as shown in Figure 22.

During the follow-up phase, Peter only solved one division sharing problem incorrectly, applying an incorrect operation strategy (Figure 23). He made only one error on a division sharing problem, incorrectly applying an operation strategy. He attempted the subtraction 18 − 3, miscalculated, and recorded “14” as the quotient. He solved a similar problem correctly (see Figure 24).

3.2.4. Generalization to Two-Step Problems Results

Unlike those performed in the baseline phase, Peter now responded correctly using a modeling strategy and without setting up any operations. Figure 25 shows his response to a problem where he had to add two quantities and then performed a multiplication.

3.2.5. Maintenance Results

In the maintenance probe, Peter solved two problems correctly: one by modeling with an operation (Figure 26), and the other a sharing division problem using the counting operation strategy. He solved the problem by drawing for a long time and with a lot of detail. Then, he counted everything, went back to the problem statement, and wrote the scheme with the numbers 3, 7, and 21. Then he wrote “multiplication” and completed the operation.

4. Discussion

The results obtained in both studies show a positive evolution in the problem-solving strategies used by Peter.

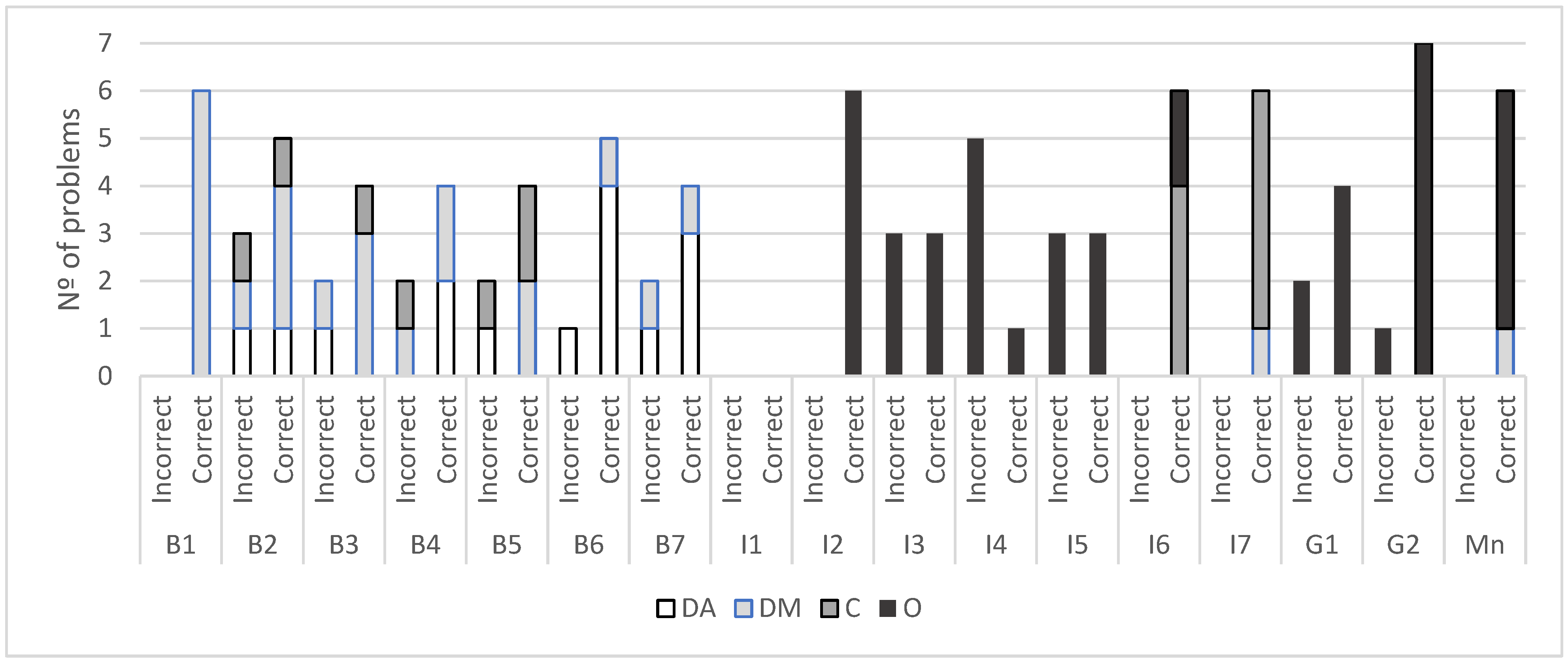
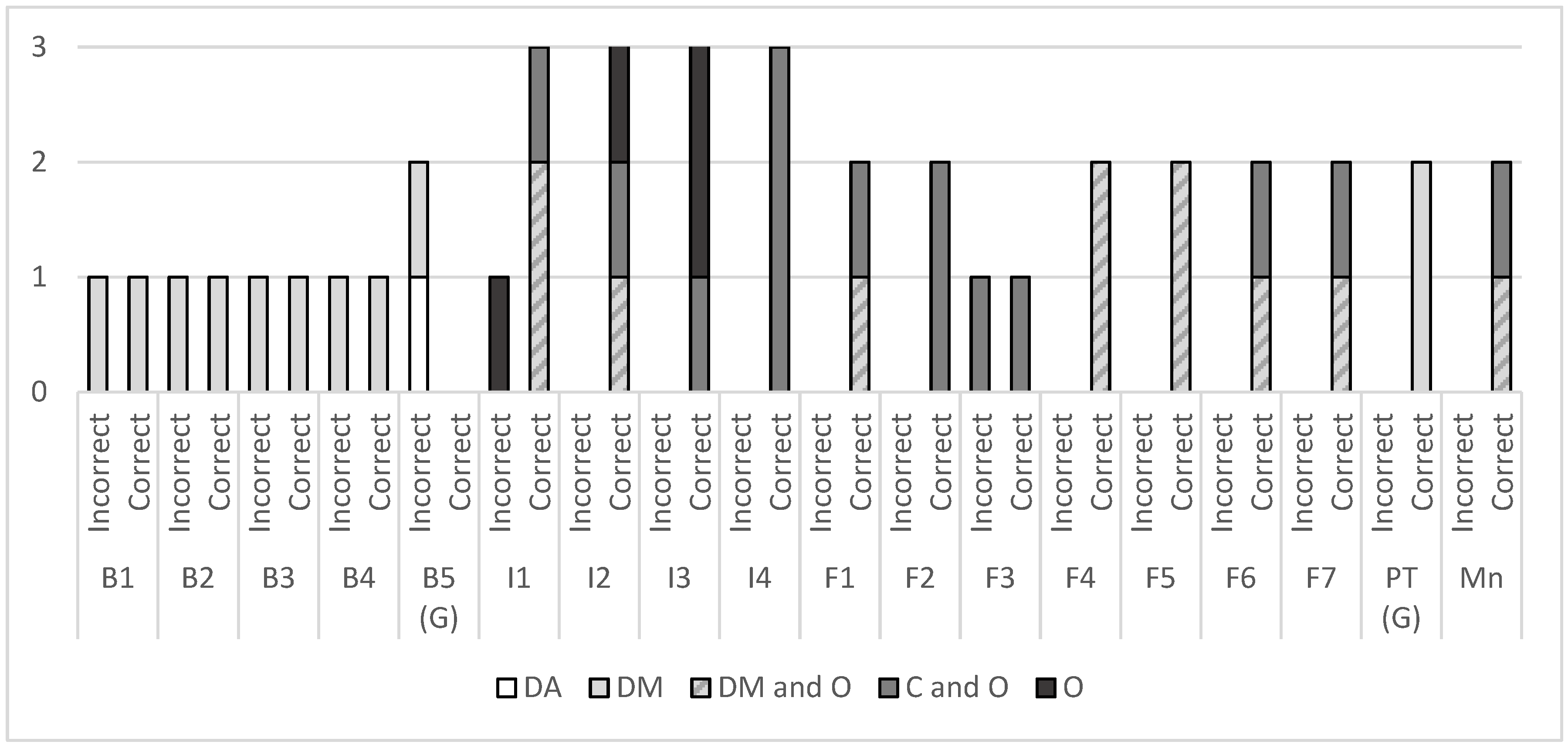
In Study 1, a transition was observed from DA and DM strategies to a consistent use of operation strategies, which represents a significant advance in solving change problems, including inconsistent problems. Although there were some initial fluctuations, Peter quickly learned to transfer the problem data to the schema and correctly solved the DDU problems. In problems DUD or UDD, he had difficulty identifying the arithmetic operation, especially in inconsistent subtraction problems. On some occasions, he even provided the correct numerical answer despite choosing the wrong operation. This behavior aligns with his prior knowledge, which allowed him to model the situation and find the numerical answer counting, but was not effective and did not help him advance his understanding of arithmetic operations. He overcame this difficulty from instructional session 4 onwards, when he successfully solved problems involving large numbers. At this moment, the initial steps of the guiding-questions sheet also proved particularly useful. Deciding whether the situation was about “getting more” or “getting less,” and circling the larger number, helped Peter better understand DUD and UDD problem statements. Additionally, the final step of the guiding-questions sheet—interpreting the obtained solution—was very relevant: since Peter had a good understanding of change stories, rereading the problem while incorporating the numerical solution allowed him to check the correctness of his response. Therefore, the objective of helping Peter connect addition and subtraction operations to the situations described in the problems (Xin, 2012) was achieved across all types of change problems. The correct resolution of inconsistent problems also indicates an improvement in understanding the problem statements. The errors he made in solving some problems in untrained settings suggest that contextual factors, such as a change of environment, affect performance. These results highlight the importance of considering situational variability when assessing learning and strategy transfer in students with ASD.

In Study 2, initial results showed mastery of equal-group multiplication problems using modeling strategies and a clear difficulty with division problems, which were approached using the same procedures as multiplication. Before the instruction, Peter relied heavily on informal modeling strategies and demonstrated a reasonable understanding of the problem statements without setting up formal mathematical operations. Following instruction, a notable change was observed towards the correct identification of multiplication, with or without counting support. Peter consistently paired modeling and multiplication identification. This finding highlights the effectiveness of the COMPS methodology in fostering more formal mathematical reasoning in multiplicative problem solving, even in the absence of memorization of multiplication tables. Peter’s trajectory with division problems differed. At baseline, he did not solve nor demonstrate comprehension of division problems, indicating a gap in both understanding and strategy use. After instruction, he made notable progress by adopting a broader range of strategies, including operational and counting techniques. While he demonstrated comprehension of division problems and the corresponding operations, he tended to rely less on modeling strategies compared to multiplication problems. The only context in which Peter did not employ formal operations was in two-step problems combining multiplication and division. In these more complex problems, he successfully relied solely on drawings to solve them, indicating that visual representation remained a valuable tool for managing problem complexity. The difficulty observed in solving two-step problems confirms the need for greater support in tasks that require the coordination of multiple operations.

In both studies, Peter occasionally reverted to DM or C strategies during some final sessions. This should not be interpreted as a setback; rather, it suggests that Peter returned to more basic forms that gave him security or even as a playful activity, given his love of drawing. This reinforces the idea that, in students with ASD, individual preferences can coexist with the use of more advanced strategies, without necessarily limiting their progress.

5. Conclusions

The results of two single-case studies conducted at different times with the same participant have been presented, evaluating the effectiveness of MSBI (additive problems, Study 1) and COMPS (multiplicative problems, Study 2) on the problem-solving performance of a student with ASD and intellectual disability. Improvements were observed in both studies in the acquisition of additive and multiplicative problem-solving skills, respectively.

The results of Study 1 show that the MSBI methodology has proven effective in helping Peter progress from informal strategies based on counting (DM and C) to formal strategies in which he identifies the arithmetic operation that solves the problem and either recalls memorized number facts or performs addition and subtraction calculations to obtain the answer. Consistent with the findings of Rockwell et al. (2011), the type of change problem, depending on the unknown, played a key role in the learning process. Adapting instruction in each session to reflect the student’s evolving progress was essential in supporting the learning process. Consistent with the MSBI framework, targeted adjustments were implemented in response to the specific challenges identified during each session. Given the wide variability in learning profiles among students, we agree with prior research emphasizing the need for personalized instructional strategies. While general guidelines—such as use of schematic diagrams, structured worksheets or guiding-question sheets—provide a solid foundation, individualized adaptations are also essential for effectively addressing the diverse needs of students with ASD (Polo-Blanco et al., 2024a). Teachers play a crucial role in these processes. Their professional development, along with the provision of appropriate school conditions—such as low student-to-teacher ratios—is fundamental to ensuring the success of these initiatives.

In Study 2, the COMPS approach proved to be well adapted to the participant’s profile, effectively addressing key characteristics associated with ASD, such as strong visual processing skills, language comprehension difficulties, and executive functioning challenges. By relying on conceptual model diagrams, specific drawings, story grammar questions, and a detailed checklist, the method provided a structured and visually supported framework that facilitated problem solving. The model equation proved useful as a tool to reflect on the problem statement and the given data, helping the participant decide which operation to perform. Notably, he used the model equation spontaneously in the posttests where it was not provided, indicating a clear understanding and internalization of the method. In this sense, the findings of this study align with previous research highlighting the effectiveness of the COMPS approach for students with mathematics learning disabilities (Xin, 2012; Xin et al., 2011, 2020) and for students with ASD (e.g., Polo-Blanco et al., 2022). Overall, this study adds further evidence supporting the efficacy of COMPS in helping a student with ASD improve multiplication problem-solving skills.

It has been shown how both MSBI and COMPS proved effective in supporting the student’s progress toward more advanced, operation-based problem-solving strategies. Although both approaches share similarities, such as providing visual support and aligning with a model–guide-independent framework that fosters autonomy in problem-solving, MSBI emphasizes the semantic structure of word problems, linking each subtype to a schema that visually illustrates the relationships among quantities. COMPS, on the other hand, shifts the focus from semantic structures to conceptual models represented by algebraic equations, highlighting the mathematical relationships underlying different problem types. By doing so, COMPS unifies different problem types and schema diagrams under one algebraic model equation, and advances student thinking to an algebraic level of operation while fostering meaningful connections between mathematical ideas (Xin, 2019).

In both studies, drawing emerged as a crucial strategy to make sense of the resolution of the mathematical problems. He frequently used modeling strategies, in particular visual representations to organize information and support his problem-solving process. This reliance on drawing aligns with a common tendency observed in many individuals with ASD, who often engage in visual thinking—a cognitive style characterized by reasoning through images and visual systems rather than purely verbal or symbolic forms. As described by Grandin (1995), this visual mode of thought can serve as an effective means of communication and understanding, particularly given the communication challenges frequently associated with ASD. Research supports this observation, showing that students with ASD often use drawing-based strategies when solving algebraic tasks and word problems (Goñi-Cervera et al., 2023; Polo-Blanco et al., 2025).

These findings illustrate the importance of incorporating visual and structured strategies into math instruction for students with ASD by tailoring interventions to their unique cognitive profiles, which can support the development of more advanced problem-solving strategies. Overall, the results provide evidence of the potential effectiveness of approaches like MSBI and COMPS in promoting improvements in problem-solving skills in students with ASD, in line with previous research (e.g., Polo-Blanco et al., 2022, 2024a; Root & Browder, 2017). Both approaches are well adapted to cognitive and learning characteristics commonly observed in students with ASD, including strengths in visual processing and the benefits of predictable routines. This study also allows for a comparison of outcomes under the two approaches, showing that both methods facilitated the student’s progression from informal counting strategies to operation-based problem-solving, with differences in the types of problems emphasized at each time point. From a practical perspective, these findings highlight the value of individualized reinforcement, carefully planned instructional sequences, and the use of varied problem types, offering educators concrete ideas for adapting instruction to different student profiles and individual learning needs.

Finally, a limitation of this work, stemming from the single-case design, is that results must be interpreted cautiously and cannot be generalized to all students with ASD. Moreover, this study focuses only on arithmetic word problems, which also limits its applicability. Despite these constraints, this research provides a novel contribution by documenting the longitudinal development of problem-solving strategies across two evidence-based instructional approaches. Future research should build on these findings by evaluating MSBI and COMPS with larger and more diverse samples, a broader range of problem types, and different instructional settings to further validate their effectiveness and provide additional guidance for educational practice.