Examining Fraction Performance and Learning Trajectories in Students with Learning Disabilities: Effects of Whole-Class Intervention
Abstract
1. Introduction and Review of Literature
- To what extent did students with LD who did and did not participate in a whole-class game-enhanced intervention improve their fraction performance and their fraction schemes?
- What operational development is evident in students’ learning strategies who did and did not participate in the whole-class game-enhanced intervention?
1.1. Learning Disabilities and Fractions
1.2. Traditional Fraction Instruction and Whole-Class Interventions
1.3. Games as Innovative, Whole-Class Interventions
1.4. Study Framing
Fraction LT and Schemes—Students with LD
1.5. The Current Study
2. Materials and Methods
2.1. Participants and Setting
2.2. Research Design
2.3. Data Sources and Measures
2.4. Procedures
2.4.1. Intervention Procedures
2.4.2. Data Collection Procedures
2.5. Data Analysis
2.5.1. Quantitative Analysis
2.5.2. Qualitative Analysis
2.6. Merging and Final Interpretation
3. Results
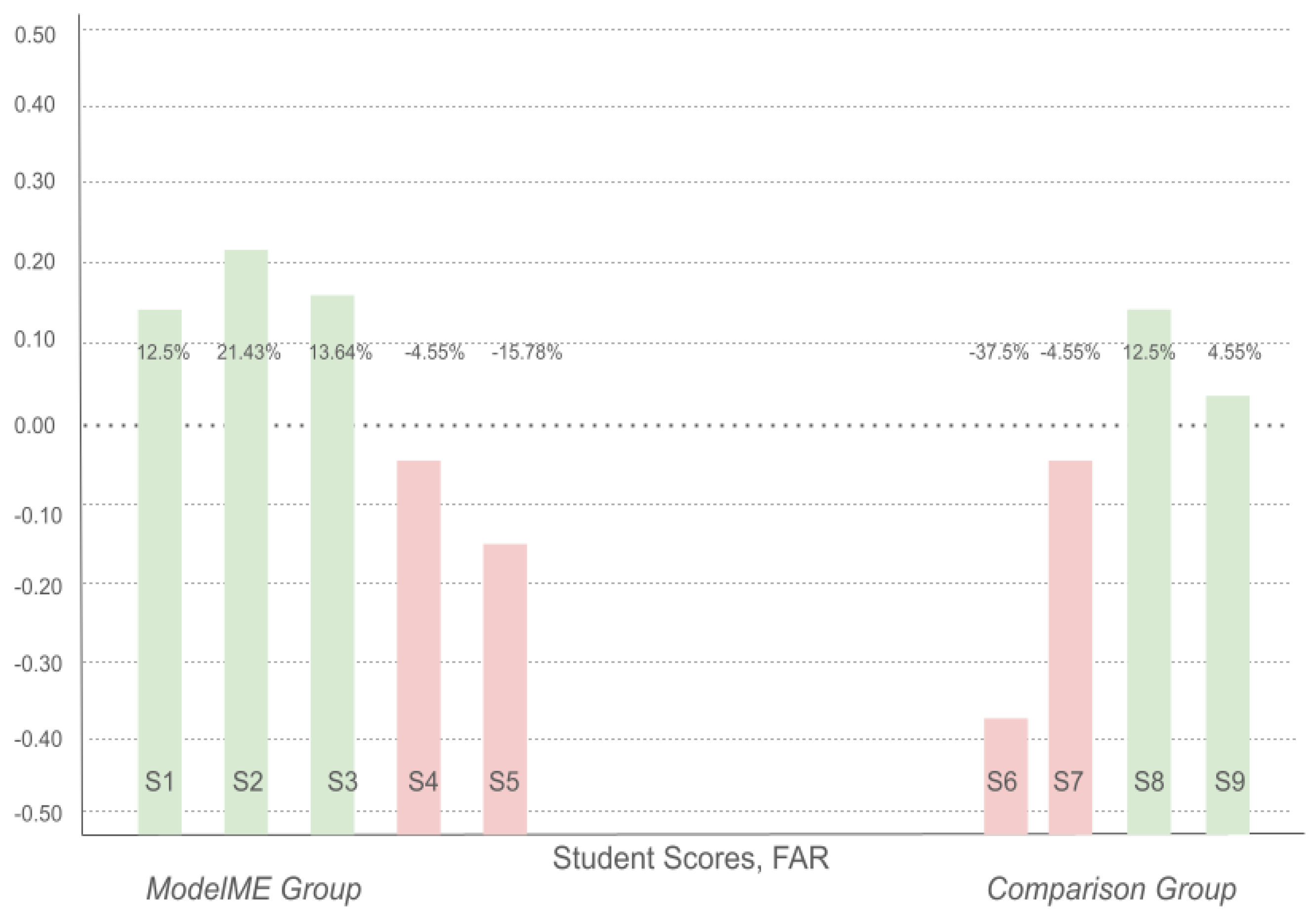
3.1. Student Performance and Scheme Change
3.2. Students’ Learning Trajectories
3.2.1. Partitioning
3.2.2. Iterating
3.3. Merging and Interpretation
Individual Trajectories
4. Discussion
Limitations and Future Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alghamdi, J., & Holland, C. (2017). Game-play: Effects of online gamified and game-based learning on dispositions, abilities and behaviours of primary learners. In Tomorrow’s learning: Involving everyone. Learning with and about technologies and computing: 11th IFIP TC 3 world conference on computers in education, WCCE 2017, Dublin, Ireland, July 3–6, 2017, revised selected papers 11 (pp. 55–63). Springer International Publishing. [Google Scholar]
- Brantlinger, E., Jimenez, R., Klingner, J., Pugach, M., & Richardson, V. (2005). Qualitative studies in special education. Exceptional Children, 71(2), 195–207. [Google Scholar] [CrossRef]
- CAST. (2024). Universal design for learning guidelines version 3.0. Available online: https://udlguidelines.cast.org (accessed on 14 June 2025).
- Cecotti, H., & Callaghan, M. (2021, December 5–8). Practical application of the learning mechanics-game mechanics framework for serious games design and analysis for the development of mental computation in virtual reality. 2021 IEEE International Conference on Engineering, Technology & Education (TALE) (pp. 1067–1072), Wuhan, China. [Google Scholar]
- Clark, D. B., Tanner-Smith, E. E., & Killingsworth, S. S. (2016). Digital games, design, and learning: A systematic review and meta-analysis. Review of Educational Research, 86(1), 79–122. [Google Scholar] [CrossRef]
- Confrey, J., & Maloney, A. (2010, June 29–July 2). The construction, refinement, and early validation of the equi-partitioning learning trajectory. International Conference of the Learning Sciences (pp. 968–975), Chicago, IL, USA. [Google Scholar]
- Crawford, A. R. (2022). Exploring a diverse learner’s equipartitioning learning trajectory. Investigations in Mathematics Learning, 14(4), 288–304. [Google Scholar] [CrossRef]
- Creswell, J. W. (1999). Mixed-method research: Introduction and application. In Handbook of educational policy (pp. 455–472). Academic Press. [Google Scholar]
- Daro, P., Mosher, F. A., & Corcoran, T. B. (2011). Learning trajectories in mathematics: A foundation for standards, curriculum, assessment, and instruction. Available online: https://eric.ed.gov/?id=ED519792 (accessed on 30 June 2025).
- Empson, S. (1999). Equal sharing and shared meaning: The development of fraction concepts in a first-grade classroom. Cognition and Instruction, 17(3), 283–342. [Google Scholar] [CrossRef]
- Empson, S. B., Junk, D., Dominguez, H., & Turner, E. (2005). Fractions as the coordination of multiplicatively related quantities: A cross-sectional study of student’s thinking. Educational Studies in Mathematics, 63, 1–18. [Google Scholar] [CrossRef]
- Flick, U. (2014). Qualitative data analysis. In An introduction to qualitative research (pp. 365–376). Sage Publications Ltd. [Google Scholar]
- Fuchs, L. S., Malone, A. S., Schumacher, R. F., Namkung, J., & Wang, A. (2017). Fraction intervention for students with mathematics difficulties: Lessons learned from five randomized controlled trials. Journal of Learning Disabilities, 50(6), 631–639. [Google Scholar] [CrossRef] [PubMed]
- Gersten, R., & Edyburn, D. (2007). Defining quality indicators for special education technology research. Journal of Special Education Technology, 22(3), 3–18. [Google Scholar] [CrossRef]
- Hackenberg, A. J. (2013). The fractional knowledge and algebraic reasoning of students with the first multiplicative concept. The Journal of Mathematical Behavior, 32(3), 538–563. [Google Scholar] [CrossRef]
- Hake, R. R. (1998). Interactive-engagement versus traditional methods: Six-thousand-student survey of mechanics test data for introductory physics courses. American Journal of Physics, 66(1), 64–74. [Google Scholar] [CrossRef]
- Hansen, N., Jordan, N. C., & Rodrigues, J. (2017). Identifying learning difficulties with fractions: A longitudinal study of student growth from third through sixth grade. Contemporary Educational Psychology, 50, 45–59. [Google Scholar] [CrossRef]
- Hunt, J. H., & Empson, S. B. (2015). Exploratory study of informal strategies for equal sharing problems of students with learning disabilities. Learning Disability Quarterly, 38(4), 208–220. [Google Scholar] [CrossRef]
- Hunt, J. H., MacDonald, B. L., & Silva, J. (2019a). Gina’s mathematics: Thinking, tricks, or “teaching”? The Journal of Mathematical Behavior, 56, 100707. [Google Scholar] [CrossRef]
- Hunt, J. H., Martin, K., Khounmeuang, A., Silva, J., Patterson, B., & Welch-Ptak, J. (2023a). Design, development, and initial testing of asset-based intervention grounded in trajectories of student fraction learning. Learning Disability Quarterly, 46(2), 63–76. [Google Scholar] [CrossRef]
- Hunt, J. H., & Silva, J. (2020). Emma’s negotiation of number: Implicit intensive intervention. Journal for Research in Mathematics Education, 51(3), 334–360. [Google Scholar] [CrossRef]
- Hunt, J. H., Silva, J., & Lambert, R. (2019b). Empowering students with specific learning disabilities: Jim’s concept of unit fraction. The Journal of Mathematical Behavior, 56, 100738. [Google Scholar] [CrossRef]
- Hunt, J. H., Taub, M., Duarte, A., Bentley, B., Womack-Adams, K., Marino, M., Holman, K., & Kuhlman, A. (2023b). Elementary teachers’ perceptions and enactment of supplemental, game-enhanced fraction intervention. Education Sciences, 13(11), 1071. [Google Scholar] [CrossRef]
- Hunt, J. H., Taub, M., Marino, M., Duarte, A., Bentley, B., Holman, K., & Banzon, A. (2022). Enhancing Engagement and Fraction Concept Knowledge with a Universally Designed Game Based Curriculum. Learning Disabilities: A Contemporary Journal, 20(1), 77–95. [Google Scholar]
- Hunt, J. H., Taub, M., Marino, M., Duarte, A., Bentley, B., Holman, K., & Kuhlman, A. (2023c). Effects of game-enhanced supplemental fraction curriculum on student engagement, fraction knowledge, and STEM interest. Education Sciences, 13(7), 646. [Google Scholar] [CrossRef]
- Hunt, J. H., Taub, M., Marino, M., Holman, K., & Womack-Adams, K. (2025). Increasing student engagement, fraction knowledge, and STEM interest through game-based intervention. Journal of Special Education Technology, 01626434251314014. [Google Scholar] [CrossRef]
- Hunt, J. H., Tzur, R., & Westenskow, A. (2016a). Evolution of unit fraction conceptions in two fifth-graders with a learning disability: An exploratory study. Mathematical Thinking and Learning, 18(3), 182–208. [Google Scholar] [CrossRef]
- Hunt, J. H., Welch-Ptak, J. J., & Silva, J. M. (2016b). Initial understandings of fraction concepts evidenced by students with mathematics learning disabilities and difficulties: A framework. Learning Disability Quarterly, 39(4), 213–225. [Google Scholar] [CrossRef]
- Hunt, J. H., Westenskow, A., Silva, J., & Welch-Ptak, J. (2016c). Levels of participatory conception of fractional quantity along a purposefully sequenced series of equal sharing tasks: Stu’s trajectory. The Journal of Mathematical Behavior, 41, 45–67. [Google Scholar] [CrossRef]
- Jensen, E. O., & Skott, C. K. (2022). How can the use of digital games in mathematics education promote students’ mathematical reasoning? a qualitative systematic review. Digital Experiences in Mathematics Education, 8(2), 183–212. [Google Scholar] [CrossRef]
- Jordan, N. C., Rodrigues, J., Hansen, N., & Resnick, I. (2017). Fraction development in children: Importance of building numerical magnitude understanding. In D. C. Geary, D. B. Berch, R. J. Ochsendorf, & K. M. Koepke (Eds.), Acquisition of complex arithmetic skills and higher-order mathematics concepts (pp. 125–140). Elsevier. [Google Scholar] [CrossRef]
- Kalra, P. B., Hubbard, E. M., & Matthews, P. G. (2020). Taking the relational structure of fractions seriously: Relational reasoning predicts fraction knowledge in elementary school children. Contemporary Educational Psychology, 62, 101896. [Google Scholar] [CrossRef]
- Kashikar, L., Soemers, L., Lüke, T., & Grosche, M. (2023). Does the ‘Learning Disability’ label lower teachers’ performance expectations? Social Psychology of Education, 26(4), 971–1000. [Google Scholar] [CrossRef]
- Kovaleski, J. F., VanDerHeyden, A. M., Runge, T. J., Zirkel, P. A., & Shapiro, E. S. (2022). The RTI approach to evaluating learning disabilities. Guilford Publications. [Google Scholar]
- Leech, N. L., & Onwuegbuzie, A. J. (2009). A typology of mixed methods research designs. Quality & Quantity, 43, 265–275. [Google Scholar]
- Makhubele, Y. E. (2021). The analysis of grade 8 fractions errors displayed by learners due to deficient mastery of prerequisite concepts. International Electronic Journal of Mathematics Education, 16(3), em0645. [Google Scholar] [CrossRef]
- Malaluan, J. S., & Andrade, R. R. (2023). Contextualized question-embedded video-based teaching and learning tool: A pathway in improving students’ interest and mathematical critical thinking skills. International Journal of Science, Technology, Engineering and Mathematics, 3(2), 39–64. [Google Scholar] [CrossRef]
- Namkung, J. M., Fuchs, L. S., & Koziol, N. (2018). Does initial learning about the meaning of fractions present similar challenges for students with and without adequate whole-number skill? Learning and Individual Differences, 61, 151–157. [Google Scholar] [CrossRef]
- National Mathematics Advisory Panel. (2008). Foundations for success: The final report of the National Mathematics Advisory Panel. US Department of Education.
- Norton, A., & Wilkins, J. L. (2009). A quantitative analysis of children’s splitting operations and fraction schemes. The Journal of Mathematical Behavior, 28(2–3), 150–161. [Google Scholar] [CrossRef]
- O’Connor, C., & Michaels, S. (2019). Supporting teachers in taking up productive talk moves: The long road to professional learning at scale. International Journal of Educational Research, 97, 166–175. [Google Scholar] [CrossRef]
- Olive, J., & Steffe, L. P. (2002). The construction of an iterative fractional scheme: The case of Joe. Journal of Mathematical Behavior, 20, 413–437. [Google Scholar] [CrossRef]
- Powell, S. R., & Nelson, G. (2021). University students’ misconceptions about rational numbers: Implications for developmental mathematics and instruction of younger students. Psychology in the Schools, 58(2), 307–331. [Google Scholar] [CrossRef]
- Shin, M., & Bryant, D. P. (2015). Fraction interventions for students struggling to learn mathematics: A research synthesis. Remedial and Special Education, 36(6), 374–387. [Google Scholar]
- Siegler, R. S., Fazio, L. K., Bailey, D. H., & Zhou, X. (2013). Fractions: The new frontier for theories of numerical development. Trends in Cognitive Sciences, 17(1), 13–19. [Google Scholar] [CrossRef] [PubMed]
- Silva, J. M., Hunt, J. H., & Welch-Ptak, J. (2023). From (and for) the invisible 10%: Including students with learning disabilities in problem-based instruction. Journal for Research in Mathematics Education, 54(4), 260–278. [Google Scholar] [CrossRef]
- Simon, M. (2020). Hypothetical learning trajectories in mathematics education. In Encyclopedia of mathematics education (pp. 354–357). Springer International Publishing. [Google Scholar]
- Simon, M., Saldanha, L., McClintock, E., Akar, G. K., Watanabe, T., & Zembat, I. O. (2010). A developing approach to studying students’ learning through their mathematical activity. Cognition and Instruction, 28(1), 70–112. [Google Scholar] [CrossRef]
- Simon, M. A. (2006). Key developmental understandings in mathematics: A direction for investigating and establishing learning goals. Mathematical Thinking and Learning, 8(4), 359–371. [Google Scholar] [CrossRef]
- Simon, M. A., Tzur, R., Heinz, K., & Kinzel, M. (2004). Explicating a mechanism for conceptual learning: Elaborating the construct of reflective abstraction. Journal for Research in Mathematics Education, 35, 305–329. [Google Scholar] [CrossRef]
- Steffe, L. P., & Olive, J. (2009). Children’s fractional knowledge. Springer Science & Business Media. [Google Scholar]
- Thomas, S. (2016). Future ready learning: Reimagining the role of technology in education. In 2016 national education technology plan. Office of Educational Technology, US Department of Education. [Google Scholar]
- Tzur, R. (2007). Fine grain assessment of students’ mathematical understanding: Participatory and anticipatory stages in learning a new mathematical conception. Educational Studies in Mathematics, 66, 273–291. [Google Scholar] [CrossRef]
- Tzur, R., & Hunt, J. H. (2022). Nurturing fractional reasoning. In Enabling mathematics learning of struggling students (pp. 315–335). Springer International Publishing. [Google Scholar]
- U.S. Department of Education (DOE). (2024). National assessment of educational progress (NAEP). Institute of Education Sciences, national Center for Education Statistics. Available online: https://nces.ed.gov/nationsreportcard/ (accessed on 30 June 2025).
- U.S. National Center for Education Statistics (NCES). (2024). Available online: https://nces.ed.gov/ (accessed on 30 June 2025).
- Von Glasersfeld, E. (2013). Radical constructivism. Routledge. [Google Scholar]
- Waber, D. P., Boiselle, E. C., Forbes, P. W., & Sideridis, G. D. (2022). Special education services and school-related quality of life in children with learning disorders and their families: A one-year follow-up study. Journal of Learning Disabilities, 55(5), 351–358. [Google Scholar]
- Wilkins, J. L., & Norton, A. (2018). Learning progression toward a measurement concept of fractions. International Journal of STEM Education, 5, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Wilkins, J. L., Norton, A., & Boyce, S. J. (2013). Validating a written instrument for assessing students’ fractions schemes and operations. The Mathematics Educator, 22(2), 31–44. [Google Scholar] [CrossRef]





| Concept/ Scheme | Definition |
|---|---|
| Unit fractions (1/n) | A measure of the whole that fits n times within the whole such that the whole is n times as much of 1/n. Operations: Partitioning, iterating |
| Partitive Fractions (m/n) | Iterating a given unit fraction (1/n) a few (m) times, not exceeding the n/n whole (i.e., m ≤ n), yields a composite fraction that is m times as much as 1/n. Operations: Iterating, partitioning |
| Iterative Fractions (m/n) | Iterating a given unit fraction (1/n) a few (m) times exceeding the n/n whole (i.e., m ≤ n), yields a composite fraction that is m times as much as 1/n. Operations: Iterating and partitioning together |
|
Reversible Fractions (m/n → 1/n → n/n) | Reversing the iteration supposedly used to create a composite fraction m/n by partitioning it into m parts to create 1/n and then “undo” the initial partitioning of the whole, which created 1/n, by iterating n times to make the n/n whole. Operations: Partitioning and iterating together |
| ModelME Group | Comparison Group | ||||
|---|---|---|---|---|---|
| Gender | Race | Disability | Gender | Race | Disability Status |
| Female (4) | Black (2) | LD (5) | Female (2) | Black (1) | LD (4) |
| Male (1) | White (2) | Male (2) | White (3) | ||
| Vietnamese (1) | Vietnamese (0) | ||||
| Student 1 | Student 2 | Student 3 | Student 4 | Student 5 | Student 6 | Student 7 | Student 8 | Student 9 | |
|---|---|---|---|---|---|---|---|---|---|
| Z score | 0.725 | 0.404 * | 0.404 * | 0.199 | −0.094 | 0.199 | −0.094 | −1.41 * | −1.79 * |
| Student 1 | Student 2 | Student 3 | Student 4 | Student 5 | Student 6 | Student 7 | Student 8 | Student 9 | |
|---|---|---|---|---|---|---|---|---|---|
| Z score | 0.726 * | 1.215 * | 0.789 * | −0.291 | −0.91 * | −2.09 * | −0.291 | 0.726 * | −0.291 |
| Partitioning | Iterating | |||||
|---|---|---|---|---|---|---|
| Halving | In Action | Before Action | Trial and Error | Planned Adjustment | Iterating to Partition | |
| Intervention Group, Pre | 2 | 3 | 0 | 5 | 0 | 0 |
| Intervention Group, Post | 0 | 4 | 1 | 0 | 1 | 4 |
| Comparison Group, Pre | 3 | 1 | 0 | 3 | 1 | 0 |
| Comparison Group, Post | 2 | 2 | 0 | 2 | 2 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hunt, J.H.; Taub, M.; Marino, M.; Holman, K. Examining Fraction Performance and Learning Trajectories in Students with Learning Disabilities: Effects of Whole-Class Intervention. Educ. Sci. 2025, 15, 1234. https://doi.org/10.3390/educsci15091234
Hunt JH, Taub M, Marino M, Holman K. Examining Fraction Performance and Learning Trajectories in Students with Learning Disabilities: Effects of Whole-Class Intervention. Education Sciences. 2025; 15(9):1234. https://doi.org/10.3390/educsci15091234
Chicago/Turabian StyleHunt, Jessica H., Michelle Taub, Matthew Marino, and Kenneth Holman. 2025. "Examining Fraction Performance and Learning Trajectories in Students with Learning Disabilities: Effects of Whole-Class Intervention" Education Sciences 15, no. 9: 1234. https://doi.org/10.3390/educsci15091234
APA StyleHunt, J. H., Taub, M., Marino, M., & Holman, K. (2025). Examining Fraction Performance and Learning Trajectories in Students with Learning Disabilities: Effects of Whole-Class Intervention. Education Sciences, 15(9), 1234. https://doi.org/10.3390/educsci15091234







