Abstract
Complex systems (CSs) have garnered increasing attention in science education due to their prevalence in the natural world and their importance in addressing pressing issues such as climate change, pandemics, and biodiversity loss. However, the instruments for assessing one’s CS knowledge are limited, and the knowledge of CSs among in-service teachers remains underreported. Guided by the complexity framework, we launched a study to develop and validate a survey instrument for measuring the knowledge of CSs among high school teachers and undergraduate students, as well as delineating the contours of their knowledge. In this article, we present the development and validation of a Complex Systems Knowledge Survey (CSKS), and we use the survey to compare the CS knowledge among 252 high school teachers and 418 undergraduate students in the United States. Our key findings include that (1) both high school teachers and undergraduates exhibit relatively low knowledge of decentralization and stochasticity, (2) undergraduates, especially those in non-STEM majors, demonstrate moderate to low knowledge of emergence, (3) few teachers and undergraduates differentiate between complicated and complex systems, and (4) teachers and undergraduates recognize CS examples across natural and social systems. The implications of our findings are discussed.
1. Introduction
Complex systems (CSs) refer to a type of system characterized by numerous interacting elements that collectively achieve a holistic outcome [1,2,3,4]. Many STEM practitioners and researchers deal with and study CSs due to the prevalence of CSs in our world and the fact that many imperative issues, such as climate change, pandemics, biodiversity loss, and energy consumption, emerge from this type of system [2,4]. Accordingly, developing learners’ CS knowledge and the ability to understand CSs has gained increasing attention in STEM education since the last century [5,6,7]. For example, the Benchmarks for the Science Literacy Field [8] include understanding systems and applying a systemic perspective to explain natural phenomena and solve real-life problems as a major science learning goal. The current U.S. K-12 science education standards, Next Generation Science Standards (NGSS), include systems and system models as one of the crosscutting concepts in science learning and stipulate that U.S. secondary students should be able to utilize mathematical and computational tools to understand CSs [9]. At the postsecondary level, CS knowledge and the ability to make sense of CSs have been defined as core competencies for undergraduates in various STEM disciplines [7,10]. Similar educational emphases can be identified from the science education documents in other countries, such as Germany and The Netherlands [11,12].
Education researchers contend that instruction must be deliberately designed and implemented to develop and broaden students’ CS knowledge because such knowledge does not come naturally for students and often is not developed through daily experience [5,13,14,15,16,17,18]. Unfortunately, educators face a range of obstacles to providing rigorous instruction on CS knowledge. First, the current U.S. science education standards have not clearly defined what a complex system is. The phrase “more complex systems” is used to vaguely refer to an array of mechanical, social, and biophysical systems. These systems may be classified into complicated systems and complex systems as they present some distinct features [3,19]. Second, the instruments to assess one’s CS knowledge are limited. Interviews and artifact analyses (e.g., analyses of concept maps or drawings) were primarily used before now to reveal people’s understanding of CSs [1,17,20]. We only identified a few relevant studies using or developing survey instruments for CSs. Dori et al. [21] distributed a survey to systems scientists to explore their worldviews and assumptions related to systems, and Dolansky et al. [22] reported the development of a systems thinking scale to measure systems thinking for healthcare professionals. Currently, there are no survey instruments available for science educators at the secondary and postsecondary levels to quickly assess their students’ CS knowledge. Third, secondary in-service teachers’ understanding of CSs largely remains underreported as the relevant studies disproportionately focused on students [6,23]. The existing studies suggest that many teachers possessed incomplete CS knowledge, which appeared to lower their self-efficacy and impede their abilities to teach these topics in classrooms [24,25,26,27,28]. Given that secondary science teachers play a crucial role in setting the foundation on which to formally develop students’ CS knowledge and ability to think of CSs, further studies on secondary science teachers’ CS knowledge are needed.
This article presents an exploratory study that aimed to develop and validate an instrument, the Complex Systems Knowledge Survey (CSKS), based on the existing systems theories and the literature, to examine the CS knowledge among high school teachers and undergraduates in the United States. This effort also aimed to answer the following research questions:
- What are the characteristics of CS knowledge among high school teachers and undergraduates?
- How do the views of complex systems vary between high school teachers and undergraduates? What kind of heterogeneity in views exists within the group of teachers and undergraduates?
- To what extent can high school teachers and undergraduates discern between complex systems and complicated systems?
- Which systems do high school teachers and undergraduates regard as examples of complex systems?
2. Theoretical Framework
2.1. What Is a System?
The notion of a system is vital in STEM disciplines as it provides a conceptual lens for asking productive questions, constructing explanations, and designing solutions [8,14,29]. At its simplest, a system is regarded as “an arrangement of parts or elements that together exhibit behavior or meaning that the individual constituents do not” [21] (p. 1). When taking a close look, it quickly becomes apparent that a system is viewed and defined differently in different disciplinary fields. After surveying 59 systems practitioners and scholars in the International Council on Systems Engineering (INCOSE), Dori et al. [21] identified five worldviews on systems. All five worldviews hold that a system consists of internal elements and structures that may give rise to collective system behaviors, but they vary in considering the nature and criteria of a system. The formal minimalist worldview defines a system as a strict conceptual and abstract entity, the moderate realist worldview considers a system to be a mental structure, a physical structure in the real world, or both, and the extreme realist worldview contends that systems must exist in the physical world. The constructive worldview contends that a system may consist of two or more related components, whereas the complexity- and life-focused worldview posits that an entity must be complex enough to qualify as a system. Furthermore, Dori et al. [21] summarized five domains of systems: (1) software systems and formal models of engineered technological systems, (2) traditional deterministic technological engineered systems, (3) enterprise and organizational systems, (4) naturally occurring systems, and (5) autonomous adaptive technological systems, and suggested that each domain is associated with one or several worldviews. For example, the moderate realist and complexity- and life-focused worldviews may contribute to studying enterprise and organizational systems, such as human activity systems, while the extreme realist and complexity- and life-focused worldviews are often found among scholars who study naturally occurring systems, such as living systems.
The U.S. K-12 science education documents define a system as “an organized group of related objects or components that form a whole. Systems can consist, for example, of organisms, machines, fundamental particles, galaxies, ideas, numbers, transportation, and education” [13] (p. 116). By acknowledging that systems may consist of physical elements (e.g., organisms, fundamental particles, galaxies), human-designed artifacts (e.g., machines), social organizations (e.g., transportation and education), and conceptual notions (e.g., ideas and numbers), the scope of this definition is so broad that it may encompass all five domains of systems mentioned in Dori et al. [21]. A close examination of the science education standards shows that students primarily learn about three types of systems: (1) the traditional deterministic technological engineered systems when conducting engineering design, (2) the naturally occurring systems when learning about physical and living systems, such as chemical reactions and ecosystems, and (3) the enterprise and organizational systems when exploring the impacts of human activities on natural systems. These systems vary in degrees and kinds of complexity, so some of them are relatively simple and others are more complex [17].
2.2. What Is a Complex System?
In complexity science, a complex system (CS) involves “interactions of numerous individual elements or agents (often relatively simple), which self-organize to show emergent and complex properties not exhibited by the individual elements” [1] (p. 42). The three aspects of a CS present in this definition—system element, interactions of elements, and system behavior—are parallel with the definition of a system from Dori et al. [21], but each of these aspects possesses specific characteristics that distinguish a CS from other types of systems. We will further articulate these characteristics and distinctions in the section of our survey constructs. Here, we take the position that not all systems with many constituents or more complicated internal processes are complex systems, because it is important to distinguish between complicated systems and complex systems [19].
A complicated system is comprised of many interconnected parts that perform a deterministic function [3,19]. The interactions among the parts in a complicated system are often highly ordered to fulfill the desired function. For example, an automobile car is made of hundreds of parts and designed to be a vehicle. In this case, most of the traditional deterministic technological engineered systems are complicated systems. Some natural systems, such as the human digestive system, are also complicated systems. For most complicated systems, the removal of one or several major parts may lead to malfunction. For instance, a car with an engine or battery failure becomes undrivable, and people with a stomach disease often suffer from indigestion.
In comparison, the elements in a complex system interact following a set of simple rules and give rise to emergent, non-deterministic behaviors as a whole [30]. Complex systems possess several unique features. First, the element interactions are often decentralized, meaning they are not controlled by one or several core individuals [31]. Second, disorder is a built-in component of complex systems, so complex systems are stochastic in nature. Thus, complex systems may generate different results with the same set of inputs [30,32]. Third, the system outcomes are emergent because they are collectively caused by all system elements through their continuous, simultaneous interactions. Such system outcomes cannot be predicted just by looking at the behavior of individual elements. The noticeable distinction between element behaviors and system behaviors reveals a key characteristic of complex systems—the hierarchical levels of the systems [30]. A good example is the individual bird and the flock it is in. Computer models have revealed that individual birds may only perform three simple behaviors—alignment, separation, and cohesion—to interact with their nearby birds, and they collectively generate complex, unpredictable flocking movements [33,34]. Complex systems can tolerate the removal of some elements, and some complex systems may adapt to changes [3]. Many naturally occurring systems and human organizational systems are complex systems, such as ecosystems and human communities. They both exhibit rich system-level behaviors that remain robust when some living organisms or humans move in or out of the systems.
Many key ideas of complex systems have been reflected in the following statements from the National Science Education Standards [13] (p. 117).
“Types and levels of organization provide useful ways of thinking about the world… Physical systems can be described at different levels of organization—such as fundamental particles, atoms, and molecules. Living systems also have different levels of organization—for example, cells, tissues, organs, organisms, populations, and communities. The complexity and number of fundamental units change in extended hierarchies of organization. Within these systems, interactions between components occur. Further, systems at different levels of organization can manifest different properties and functions”.
The statements above explicate the occurrence of interactions among individual elements and highlight the hierarchical levels of systems. However, complex systems have not been formally defined in U.S. science education documents. In A Framework for K-12 Science Education (the Framework, [14]), the phrase “more complex systems” is used to refer to the systems with many components and many interactions in general. Therefore, a very broad range of systems, such as mechanic systems, human body systems, ecosystems, earth systems, and galaxies, are all grouped under the category of “more complex systems”. This could cause problems for teachers and students in accurately understanding complex systems because the phrase appears to have merged complex and complicated systems into one large group. We believe that students need to develop adequate knowledge of complex systems so that they may distinguish them from other types of systems and, therefore, interpret relevant phenomena properly. To achieve this goal, teachers must understand students’ existing CS knowledge. Therefore, there is a need for an instrument to assess students’ CS knowledge, which will serve as the foundation for designing and implementing effective learning experiences about CSs. Additionally, this instrument can be used to assess pre-service and in-service teachers’ CS knowledge, helping to prepare future science teachers and develop effective professional development programs for in-service teachers.
3. Students’ and Teachers’ Understanding of CSs
Decades of studies have suggested that people often do not develop accurate CS knowledge from daily experiences. For example, prior to formal instruction, students at all ages were often found to primarily focus on the individual components of a CS [35], misconceived the simultaneous, continuous interactions within a CS [36], failed to identify the feedback processes [28], and failed to recognize the emergent, dynamic nature of system outcomes [1]. Studies also showed that adults still possessed misconceptions similar to those of youths. People with limited CS knowledge tended to possess a reductionist perspective, assumed centralized control and linear relationships, had difficulties in recognizing feedback, were confused by emergent levels, and failed to consider causal processes in time [37,38,39].
A vast number of studies have been conducted to investigate students’ views and understandings of CSs at the secondary level and higher education [6,23]. In addition to the studies mentioned above, Yoon et al. [40] examined secondary students’ learning progression for CSs. They found that students could easily comprehend the concepts of levels and the interconnected nature of systems but had difficulties understanding the concepts of decentralization and the unpredictability of CSs. After analyzing the explanations for behaviors of sand dunes from secondary students, undergraduates, and graduate students, Barth-Cohen [41] found that, regardless of academic levels, students often started with centralized thinking while combining centralized, transitional, and decentralized components in their explanations. Due to the built-in uncertainties and disorders, the CS outcomes cannot be precisely predicted. Unfortunately, students often have difficulties understanding this notion [1]. In a study on building a biology concept inventory, Garvin-Doxas and Klymkowsky [42] found that the majority of undergraduates failed to recognize that randomness exists in complex systems all the time and it can influence emergent system behaviors. In addition, Talanquer [43] surveyed and interviewed undergraduate students enrolled in an introductory chemistry course and reported that the undergraduates commonly used an additive, rather than an emergent, framework to predict the sensory properties of chemicals.
The studies on teachers’ understanding of complex systems are limited compared to those on secondary and postsecondary students. Only a few studies have reported on the trends in secondary teachers’ understandings. Sweeney and Sterman [28] interviewed 11 middle school teachers and found that only 32% of them could recognize feedback structures. Skaza et al. [27] surveyed 81 high school teachers who taught system models in their courses. They found only 34–35% of the teachers could correctly identify the causal relationships in the tested systems. Goh [25] investigated 90 high school science teachers’ CS knowledge and found teachers had the most difficulties in understanding the dynamic nature of CSs. Teachers’ CS knowledge influences their instruction. Studies have found that teachers with a better understanding of certain CS concepts are more likely to integrate those concepts into their instruction [24,25]. In summary, the existing literature justifies the need for more studies on teachers’ knowledge of CSs.
4. The Development of a Complex Systems Knowledge Survey (CSKS)
Guided by the complex systems theory [1,4,30] and the current literature [19,20], this study aimed to develop a survey instrument for examining the alignment between respondents’ views of CSs and those of experts in complexity science. Following a multi-stepped approach [44], we developed a Complex Systems Knowledge Survey (CSKS) organized around five constructs: element, micro-interaction, decentralization, stochasticity, and emergence. We focus on these five constructs above because they include the three fundamental aspects of a system—element, interaction, and system-level outcome (i.e., emergence)—and two essential features that discern complicated systems and complex systems, i.e., decentralization and stochasticity. Table 1 displays the characteristics we utilize to describe and differentiate complicated systems from complex systems. We acknowledge that some features of complex systems are not included in this work. Given the scope of complex systems in current systems science, it was impossible for this survey to cover all the features. Considering that the long-term goal of this study was to assess and enhance secondary students’ understanding, we chose to focus on the aspects of CSs that are necessary and suitable for this grade level. Below, we elaborate on the five constructs.

Table 1.
Comparisons of survey constructs in complicated systems and complex systems and examples.
4.1. Elements
Most systems researchers agree that a CS should contain an adequate number of individuals that interact with one another to exchange energy, matter, or information. These individuals may belong to the same or different kinds. Individuals of the same kind present similar properties and behaviors but are not identical. They exist in a context and are influenced by the factors in the context [2,4,30]. For example, an ecosystem may consist of producers, consumers, and decomposers. All the individual producers, consumers, or decomposers have similar features and interact with others following simple behavioral rules. Within the system, producers use sunlight and inorganic molecules to make organic matter, consumers obtain energy and matter from producers, and decomposers break down organic matter. However, no two producers, consumers, or decomposers are identical. The individual living organisms exist in a context, e.g., the abiotic environment of an ecosystem.
4.2. Micro-Interactions
Micro-level interactions are essential in all CSs, as no patterns or structures may form without interactions [30]. Chi et al. proposed five features of the interaction among individual elements in CSs: (1) individuals interact following a set of relatively simple rules, (2) all individuals may interact with any other random individuals, (3) all individuals interact simultaneously, (4) all individuals interact independently of one another at a time, and (5) all individuals interact continuously regardless of the status of system patterns [36]. Consider the diffusion of a drop of food color in water; food color and water molecules both perform simple kinetic movements, and they may collide with any other food color and water molecules that are on their moving trajectories. Such interactions occur simultaneously across the system. At any moment in time, the interaction between two molecules is independent of interactions among other molecules at the same time. The food color and water molecules continuously interact with one another regardless of the status of diffusion.
4.3. Decentralization
Decentralization in CSs refers to the idea that complex systems organize through spontaneous order, where outcomes are not controlled by one or a few central individuals but arise from continuous, simultaneous interactions among members [30,31,36]. Among all these interactions, no interactions are more controlling than others. The interactions often only achieve local goals or form small local substructures. Thus, control in a CS is distributed across all its individuals, and the system may produce outcomes without a “leader”. For example, the adaptation of a species is not controlled by one or a few individuals but results from the survival and reproduction of all individuals in the population.
4.4. Stochasticity
Stochasticity in CSs relates to the notion that CS outcomes cannot be precisely predicted due to uncertainties or disorders [2,32]. Given that disorder is a necessary condition of CSs [30], CSs are stochastic in nature. Compared to deterministic systems that always generate the exact same result based on the same input, stochastic systems may produce different results for the same inputs. Most naturally occurring systems and the enterprise and organizational systems are CSs as they are non-deterministic, due to uncertainty or disorder existing in the individuals’ behaviors or micro-level interactions [21]. Traffic flow in a major city is an excellent example illustrating stochasticity. As vehicles interact based on numerous unpredictable human decisions and external factors, the resulting traffic patterns can be quite unpredictable. To analyze CSs effectively, probability principles and statistics are employed.
4.5. Emergence
Emergence refers to the generation of robust system-level patterns or behaviors through self-organization in a CS [45]. The key to this characteristic lies in the fact that the robust patterns or behaviors are collectively, rather than additively, caused by the continuous interactions among all individuals in the system [30,36]. Therefore, the emergent system patterns or behaviors may look very different from the individuals’ behaviors and cannot be reduced to individuals’ behaviors. The multiple causal processes and feedback structures enable a CS to amplify a small action or recover from a considerable interruption. Furthermore, the changes in a CS are dynamic and often nonlinear. For example, in ant colonies, complex social structures and roles emerge from the simple behaviors of individual ants. Despite each ant following relatively simple rules, their collective actions lead to organized colony behavior such as foraging, nest building, and defending.
4.6. Instrument Development
In developing the survey, we were attentive to the fact that our target respondents are busy individuals with many demands on their time. We prioritized close-ended Likert-scale survey items to assess respondents’ CS knowledge. We adopted the formative measurement model framework [46] to design the Likert-scale items for two reasons. First, complex systems are multifaceted, meaning they contain various distinct but related aspects, such as constitution, micro-interaction, system behaviors, and other features of CSs. Second, as suggested in the literature, all these CS aspects are also multifaceted. For example, Chi et al. [17] proposed five attributes of micro-interactions. Therefore, formative indicators [47], i.e., the items that measure a construct together but are not interchangeable, better suit our assessment goals. Meanwhile, we also designed questions that assess respondents’ ability to identify complex systems. Therefore, in our measurement model, the Likert-scale questions measure the exogenous variables, and the complex system identification questions measure the endogenous variables [48].
The development of the CSKS followed a multi-stepped approach [44]. We first defined essential CS constructs and then designed indicators for each construct based on our research questions, complexity theory, and extensive literature review (Table A1). The first version of the questionnaire contained 35 Likert-scale questions and 4 multiple-choice questions. The survey items were first reviewed by two experts and then piloted with 78 undergraduate students to establish face validity and content validity. We interviewed a portion of respondents after they responded to the survey to examine the language use and clarity of the items.
Then, the questionnaire was revised based on the survey responses and respondent feedback in the first pilot. We consulted with the same experts again to improve the language in some survey items. The second version of the questionnaire consisted of 31 Likert-scale questions and 4 multiple-choice questions. A total of 618 undergraduate students and 168 teachers responded to this questionnaire via Qualtrics in the second round of the pilot. We conducted reliability and validity analyses on the responses and interviewed a small portion of respondents for feedback and clarifications.
The questionnaire was revised again based on the statistical analyses and respondent feedback with the aim of shortening the questionnaire and improving clarity. The third version of the CSKS questionnaire consisted of 30 Likert-scale items and 12 binary items. For each Likert-scale item, the scale ranged as follows: Very True, True, True for Some Systems but Untrue for Others, Untrue, and Very Untrue. An option “I am not sure” was included for all questions to avoid forcing respondents to guess an answer. We also revised the multiple-choice questions into 12 binary items, which asked respondents to decide whether the 12 provided system examples were complex systems. The system examples consisted of one simple system, four complicated systems, and seven complex systems. They were selected because they were from the existing literature or commonly mentioned by respondents in the first two pilot processes. In addition, we included one open-ended question to ask respondents to provide examples of complex systems before they saw the binary complex system identification question. A new set of teachers and undergraduates responded to this questionnaire via Qualtrics. In this article, we present the validation of this last version of the questionnaire and report the respondents’ CS knowledge that was measured.
5. Materials and Methods
5.1. Participants
Our target survey respondents were high school teachers and undergraduates in the United States. We chose these two populations for distinct reasons. First, we selected United States regions because we were interested in focusing on populations where the Next Generation Science Standards [9] guide the K-12 curriculum. Second, high school teachers were chosen because there is limited information in the existing literature about the CS knowledge this group possesses, even though they play a crucial role in introducing CSs to students. We included high school teachers in four major content disciplines (math, science, language, social studies) to examine these teachers’ CS knowledge as a whole group and in each of these disciplines. Third, surveying undergraduates allowed us to compare our results with the existing studies on undergraduates’ CS knowledge. We focused on recruiting undergraduates from lower-division courses because assessing freshman and sophomore undergraduates would potentially allow us to explore the CS knowledge students developed at the high school level. Finally, in this study, instead of focusing on one discipline area, we recruited undergraduates in STEM and non-STEM fields.
We used non-probability methods to distribute the survey to teachers, relying on known networks of high school teachers. Since we were limited by the timeframe and in our abilities to compensate participants, we chose to pursue this convenience sampling strategy. We acknowledged this as a limitation of the study and were careful not to generalize the findings beyond the (sub) population(s) sampled. This study was approved by our Institutional Review Board for Social Science research. Both teachers and undergraduates received a link to our survey and voluntarily completed this survey during their spare time. The undergraduate respondents received research credits or bonus points for their participation. As Table 2 shows, our analytic sample consisted of 252 high school in-service teachers and 418 undergraduate students, with both groups disproportionately including respondents who identified as female, white, teaching more than 10 years, and teaching in non-STEM disciplines. Up to 25% of teacher respondents were teaching in California, 60% in Kentucky, 10% in Massachusetts, and 5% in other states. The undergraduate students were recruited at our institution from lower-division courses.

Table 2.
Demographics of respondents.
5.2. Data Collection and Analysis
The third version of the CSKS questionnaire was distributed through Qualtrics [49]. A recruiting email containing the link to the consent form and survey was sent to the target teachers and undergraduate population. Two weeks later, a reminder email was sent to the same population. The survey was closed by the fourth week.
Our analysis process had two phases: validating the questionnaire and evaluating the respondent’s CS knowledge. All statistical analyses were completed in SPSS 29 and Smart-PLS 4.1 [50]. To evaluate the measurement model, the Likert-scale items were analyzed using the partial least squares (PLS) in Smart-PLS 4.1. Because these items were formative indicators, internal reliability analysis was not appropriate. Instead, we followed the guidelines suggested by Hair et al. [48] to examine convergent validity, indicator collinearity, and indicator weights and loadings. An item was removed only if (1) it had a low non-significant outer loading (<0.5) and (2) it was not essential for the related construct. Internal reliability analyses were only performed on the 12 binary system identification questions because they are reflective indicators. Then, the path coefficients and R2 were examined to gain insights into the relationships among the constructs [48,51]. When examining the path coefficients, we considered values of 0.5 and above as large effect sizes, values between 0.3 and 0.5 as medium effect sizes, and values below 0.3 as small effect sizes [52].
When evaluating respondents’ CS knowledge, we examined their answers to the validated items. Two points were given to each answer that aligned with the system expert’s CS view, one point was given when the respondents chose “true for some systems but untrue for the others”, and zero was given for an answer inconsistent with the system expert’s view or the option “I am not sure”. Then, we calculated the respondents’ total scores and the scores of each construct. All these scores were converted to percentages for the successive statistical analyses. We classified the CS examples provided by the respondents into natural systems, social systems, and mechanical systems based on the system categories from Dori et al. [21].
To answer research questions 1 and 2, we summarized the descriptive statistics of teachers’ and undergraduates’ scores and then ran t-tests or ANOVA to compare the scores (1) among five constructs, (2) between teachers and undergraduates, (3) among teachers in different subject areas, and (4) between the STEM major and non-STEM major undergraduates. A level of 0.05 was used as the cutoff for statistical significance. For all t-tests, effect sizes were calculated based on the standardized mean difference between two groups of independent observations for the samples, known as Cohen’s ds, and the values of 0.2, 0.5, and 0.8 were used as the thresholds for small, medium, and large effect sizes, respectively [53]. To answer research questions 3 and 4, we compared respondents’ classifications of the 12 system examples and summarized the complex system examples provided by the respondents.
6. Results
6.1. Instrument Validation
The PLS analyses resulted in the retention of 20 Likert-scale items (Appendix A). Ten Likert-scale items were removed due to low non-significant outer loadings and their vague language, which did not clearly reflect the essential aspects of the constructs. For example, we removed the item “it takes time for a complex system to exhibit a change” on the basis that it was vague, in particular, because the respondents had no reference for how to define the time duration in the statement. The outer weight and loading of the item were also low and insignificant. In contrast, 19 of the 20 retained items had a significant indicator weight or loading. We kept item 18 despite its low non-significant outer weight and outer loading because it captured the essential aspect of stochasticity. No collinearity issues were detected among these 20 items (Table 3). The response data were provided in the Supplementary Materials (Table S1).

Table 3.
PLS analysis results on 20 formative Likert-scale items.
The path coefficients and R2 of a structural model suggest the extent to which one variable affects another variable and, therefore, inform us of the variable relationships of the structural model [54]. When building the relationships among the five constructs, we chose the directionalities among the five constructs based on two considerations. The first is the complex system theoretical framework. For example, we directed the element construct to the other four constructs because system elements serve as the foundation of a system; we directed the other four constructs toward the emergence construct because emergence describes the system properties resulting from other aspects collectively. The second consideration was based on the relationships we aimed to investigate. In this study, we were interested in the effects of respondents’ knowledge of micro-interactions on their knowledge of decentralization and stochasticity. Therefore, we pointed the model arrows from the micro-interaction construct to decentralization and stochasticity.
The results based on 10,000 bootstrapped samples showed that all the path coefficients (P) among the five constructs were significant and greater than 0.1, but the R2 values were low, ranging from 0.128 to 0.488. The element construct exhibited a large effect on micro-interaction (P = 0.541), a medium effect on decentralization (P = 0.302), and a low effect on stochasticity (P = 0.230) and emergence (P = 0.189). Micro-interaction exhibited a weak effect on both decentralization (P = 0.276) and stochasticity (P = 0.176). Although emergence was significantly affected by the other four constructs, only the micro-interaction construct exhibited a medium effect (P = 0.414), whereas element, decentralization, and stochasticity only displayed weak effects (Figure 1). The internal reliability analysis of the 12 binary complex system identification items produced a result of 0.606, which is acceptable for an exploratory study like this one [51]. However, we failed to establish the convergent validity because the path coefficients between the five constructs and the system identification variable were insignificant (Figure 1) and the average variance extracted (AVE) was only 0.133.
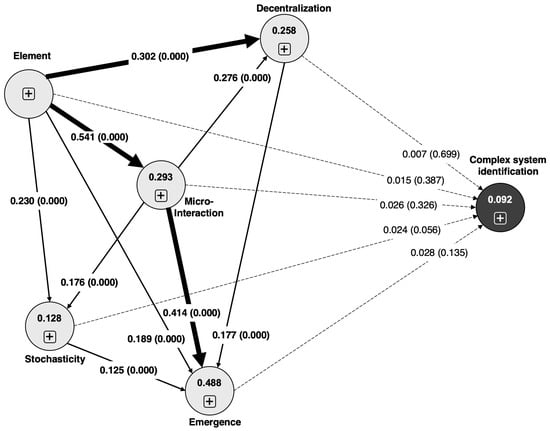
Figure 1.
Path coefficients and R2 of the CSKS measurement model. The path coefficients are displayed on the path connection, and the R2 values are shown in the variable circles. Solid lines are used for significant path coefficients, whereas the dashed lines are for insignificant path coefficients. The thick solid lines are used for significant path coefficients greater than 0.3.
Although convergent validity was not established between the exogenous variables (i.e., the five CS constructs) and the endogenous variable (i.e., the system identification ability), the significant indicator weights and loadings suggested that most of the survey items strongly contributed to these variables. Therefore, we proceeded to use these retained items to examine the high school teachers’ and undergraduates’ CS knowledge.
6.2. Characteristics and Differences of Teachers’ and Undergraduate Students’ Knowledge of CSs
As indicated by their total percentage scores, both teachers (M = 80.90%, SD = 9.14%) and undergraduates (M = 72.14%, SD = 12.24%) possessed a moderate level of CS knowledge. The teacher group’s scores were significantly higher than those of the undergraduate group, with a moderately high effect size (Cohen’s ds = 0.784). Both teachers and undergraduates received high scores on element, micro-interaction, and emergence, while scoring low in decentralization and stochasticity. Teachers outperformed undergraduates across all five constructs. However, the effect sizes showed that the knowledge differences between the two groups were weak in element and decentralization, while they were moderate in the other three constructs (Table 4).

Table 4.
T-test results of teachers’ and undergraduates’ percentage scores.
Within the teacher group, no significant differences were identified among the teachers in different subject areas, although science teachers received slightly higher total scores. Within the undergraduate group, undergraduates with a STEM or STEM-related major received significantly higher scores on total, element, micro-interaction, and emergence than the undergraduates with a non-STEM major. The effect sizes showed that the knowledge differences between the STEM and non-STEM groups were moderate to low. No significant differences in decentralization and stochasticity scores were found between the two groups (Table 5).

Table 5.
T-test results of STEM majors’ and non-STEM majors’ scores.
When comparing non-STEM and STEM undergraduates based on years, statistical differences were only identified in freshman and sophomore students (Figure 2). One-way ANOVA suggested significant differences in scores for total, element, decentralization, and micro-interaction for students in different years. Post hoc comparison using Tukey’s HSD test indicated that (1) the freshmen students received a significantly higher total score (M = 74.36%, SD = 10.82%) than the sophomores (M = 69.50%, SD = 13.61%) and juniors (M = 69.35%, SD = 13.02%); (2) the freshmen students received a significantly higher element score (M = 88.06%, SD = 14.87%) than the juniors (M = 80.36%, SD = 23.55%); (3) the freshmen received a significantly higher micro-interaction score (M = 81.93%, SD = 18.37%) than the sophomores (M = 75.50%, SD = 21.02%); and (4) there were no significant differences among undergraduates’ scores for decentralization and stochasticity. The effect sizes of the significant differences ranged from low to medium (Figure 2).
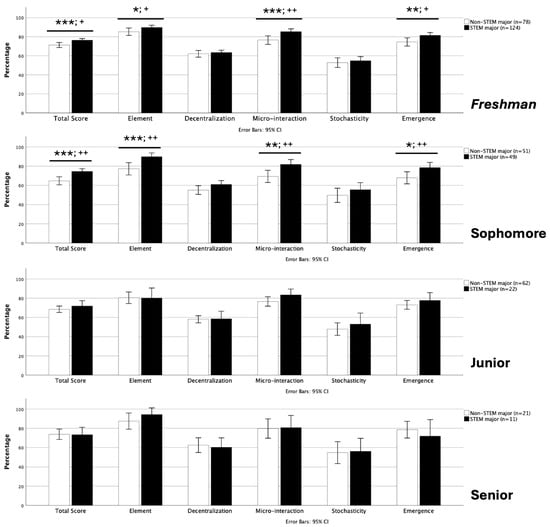
Figure 2.
Comparisons of STEM and non-STEM undergraduates’ CS knowledge based on years. The STEM freshmen and sophomores received higher total scores than their non-STEM counterparts (*: p < 0.05; **: p < 0.01; ***: p < 0.001; +: Cohen’s ds = 0.2~0.49 (low effect size); ++: Cohen’s ds = 0.5~0.79 (medium effect size)). No differences were found for juniors and seniors. All students received higher scores on element, micro-interaction, and emergence but lower scores on decentralization and stochasticity.
6.3. Teachers’ and Undergraduates’ Identification of CSs
Most teachers and undergraduates could discern between simple systems and non-simple systems, and 33% of undergraduates identified a pendulum as a complex system, as indicated by only 23% of teachers. However, most teachers and undergraduates did not distinguish between complicated systems and complex systems because, although most teachers (73–98%) and undergraduates (77~91%) could successfully identify the seven complex systems, a large portion of teachers (77–96%) and undergraduates (68~91%) also identified the four complicated systems as complex systems (Figure 3).
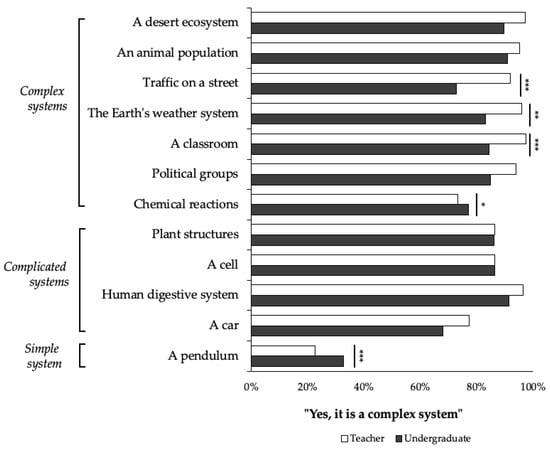
Figure 3.
Percentages of teachers and undergraduates who identified the provided system examples as complex systems. Significantly more teachers identified traffic on a street, the Earth’s weather system, and a classroom as complex systems than undergraduates, and significantly fewer teachers regarded chemical reactions and a pendulum as complex systems than undergraduates (*: p < 0.05; **: p < 0.01; ***: p < 0.001).
When ranking the 12 systems, the teachers appeared to have a better understanding of complex systems than the undergraduates. This trend was illustrated by significantly fewer teachers regarding a pendulum as a complex system than undergraduates (Χ2 (1, 518) = 22.370, p < 0.001) and significantly more teachers regarding traffic on a street (Χ2 (1, 599) = 10.332, p < 0.001), the Earth’s weather system (Χ2 (1, 617) = 7.394, p = 0.007), and a classroom (Χ2 (1, 633) = 16.716, p < 0.001) as complex systems than undergraduates. Nonetheless, significantly more undergraduates regarded chemical reactions as a complex system than teachers (Χ2 (1, 596) = 5.336, p = 0.021) (Figure 3).
6.4. Complex System Examples from Teachers and Undergraduates
A total of 405 undergraduates and 242 teachers provided examples of complex systems. We identified three patterns among these examples. First, the respondents significantly more often cited social systems, with 425 mentions (63.4%, n = 670), and natural systems, with 360 mentions (53.7%), than mechanical systems, with 16 mentions (2.4%). Second, only a small portion of respondents provided their CS examples from more than one system category. Up to 57.8% of respondents’ examples fell into one of the three system categories (i.e., natural, social, and mechanical), while 29.3% of respondents provided examples from two system categories, often the natural and social systems. Meanwhile, seven respondents, 1%, provided examples from all three categories. Third, both complicated and complex systems were mentioned as CS examples, often without differentiation, instantiated by the following responses, “Cells, ant hills, human economies”, “The human body, corporations, and a community”, and “I thought of a large group of people like a sports team. Also I thought of different parts in a car that all work together”.
Chi-squared tests suggested that teachers and undergraduates were equally likely to mention natural, social, or mechanical systems. However, more teachers mentioned examples from two system categories than undergraduates (Χ2 (1, 583) = 19.408, p < 0.001). Significantly more science/STEM teachers mentioned natural systems than teachers in other subject areas (Χ2 (3, 252) = 19.409, p < 0.001), and significantly fewer science/STEM teachers mentioned social systems (Χ2 (3, 252) = 22.979, p < 0.001). Only science/STEM teachers provided CS examples from mechanical systems, such as cars, trains, etc.
STEM undergraduates were also significantly more likely to cite a natural system as the CS example (STEM = 59.7%) than non-STEM undergraduates (non-STEM = 46.7%, Χ2 (1, 418) = 7.102, p = 0.008), but there was no significant difference among STEM and non-STEM undergraduates in mentioning social systems as CS examples (STEM = 60.7%, non-STEM = 61.8%). There was also no significant difference in mentioning natural or social systems as CS examples among undergraduates at different years.
7. Discussion and Implications
The present study was an exploratory effort that aimed to develop and validate a survey instrument for assessing the knowledge of complex systems (CSs) among high school teachers and undergraduates. Our current work generated a 20-item survey questionnaire that measures respondents’ CS knowledge through five constructs. Furthermore, this research unearthed the attributes of CS knowledge among high school teachers and undergraduate students and the knowledge disparities between and within these two groups. Below, we discuss the insights gained in this exploratory work and connect the findings to the existing literature.
Developing a CS knowledge survey is challenging because CSs must be defined through multiple aspects, and each of these aspects possesses multiple features. We addressed this challenge by including the essential aspects of CSs as the measurement constructs and designing formative measurement indicators for each construct. Combining the PLS analysis results with complexity science theory, we identified 20 items that could be used to measure high school teachers’ and undergraduates’ CS knowledge about system elements, decentralization, micro-interactions, stochasticity, and emergence. The low variance inflation factor (VIF) values suggest these items may measure respondents’ CS knowledge independently. Nineteen of twenty items displayed significant indicator weights, suggesting they possess sufficient measurement quality. Hair et al. [51] pointed out that an indicator with low non-significant loading can still be retained if there is strong theoretical support for its inclusion. Therefore, in this study, we retained item 18, “The outcome of a complex system can be predicted from individuals’ characteristics”, despite its low non-significant outer loading because it directly asks about the unpredictability of CSs, a key feature of stochasticity [30].
Our structural model’s path coefficients and R2 produced important insights into the respondents’ CS knowledge. First, there were significant interconnections among respondents’ considerations of the five constructs, with the magnitudes ranging from small to high. Second, the ways in which respondents considered system elements influenced their views of the other four constructs, with the strongest impact on the micro-interactions and the weakest on emergence. Third, the respondents’ considerations of emergence were mainly affected by their views of system micro-interactions. Fourth, decentralization and stochasticity appeared to play a limited role in affecting respondents’ current CS knowledge, with us finding that they were weakly influenced and exhibited a weak influence themselves. We believe these findings are important for CS education because they present the first model regarding high school teachers’ and undergraduates’ CS knowledge based on the five constructs. Future investigations could involve testing this model with more respondents, and additional data could be collected to explain the magnitudes of the interconnections among these constructs.
The second challenge we faced was the lack of an existing survey instrument for CS knowledge. The survey questions used by Dori et al. [21] do not differentiate among different types of systems. The other relevant scale [22] measures systems thinking rather than CS knowledge. Therefore, we used respondents’ ability to identify CSs as an alternative reflectively measured variable [51]. The limitation of this design is that the respondents may not identify CSs based on the formative constructs. The low convergent validity, low non-significant path coefficients between the five constructs and the CS identification variable, and low R2 value suggest this is likely to be the case, because none of the five constructs affect how they identify CSs. Therefore, the next step to further this study would be to investigate the criteria respondents utilized to identify CSs.
Although a formative measurement model was not fully established in this study, the construct validity of the retained 20 formative measurement items and 12 system identification items was ascertained based on the low collinearity, significant indicator weights and loadings, and acceptable internal reliability. Therefore, although we may not have made a direct connection between respondents’ CS knowledge and their ability to identify CSs, we can still use these items to measure respondents’ CS knowledge and their ability to identify CSs separately.
We identified two significant findings on the respondents’ CS knowledge. First, both teachers and undergraduates participating in this study demonstrated relatively high knowledge of system elements and low knowledge of decentralization and stochasticity, and these patterns remained the same within teacher and undergraduate groups. Within the teacher group, no significant differences for the five constructs were identified in teacher CS knowledge across four disciplinary areas (i.e., science, math, social studies, and language arts). Within the undergraduate group, although STEM majors outperformed the non-STEM majors on the constructs of element, micro-interaction, and emergence, they both received low scores on decentralization and stochasticity. In fact, all undergraduates received low scores on decentralization and stochasticity regardless of their majors and years. More detailed information can be found by looking into the individual measurement items of the two constructs. For decentralization, most teachers and undergraduates believe “organizers” or “leaders” are necessary for CSs (merely 12.0% of undergraduates and 18.7% of high school teachers disagreed with this statement). For stochasticity, only 19.9% of undergraduates and 24.6% of high school teachers recognized the unpredictability of CSs. The second major finding was that the undergraduates possessed moderate to low knowledge of emergence. This was particularly evident in the non-STEM majors. Looking into the individual items for emergence, we found that only 48.1% of the non-STEM majors and 57.4% of STEM majors agreed that a CS may maintain stability when individuals within it constantly interact with one another. These findings on undergraduates are consistent with the previous studies that showed undergraduates did not possess a sufficient understanding of decentralization, stochasticity, and emergence [40,41,42,55,56]. In regard to teachers’ knowledge of CSs, our findings add new knowledge to the existing literature by revealing the knowledge of decentralization and stochasticity that teachers in our study demonstrated.
There were additional nuances in the undergraduates’ understandings of the five constructs. Within the undergraduate group, STEM majors outperformed the non-STEM majors on the constructs of element, micro-interaction, and emergence, while both undergraduate groups received low scores on decentralization and stochasticity. It is interesting to see that freshmen students outperformed sophomores and juniors on the constructs of element and micro-interaction. This finding might indicate that freshman students received more instruction about systems at the high school level than the instruction sophomores and juniors received in their coursework. The results suggest that more concentrated instruction on CSs within high school and college courses is needed. Further investigations are necessary to reveal the underlying reasons for the differences in undergraduate students’ understandings of the five CS constructs.
Another salient contribution of this study is to reveal a common challenge among both teachers and undergraduates in distinguishing between complicated and complex systems, because most of the teachers and undergraduates identified all non-simple system examples as complex systems. This was also reflected by the fact that many teachers and undergraduates cited complicated systems when they were asked to provide examples of complex systems. We suspect this could be related to the lack of differentiation of complicated and complex systems in current science education standards and curricula.
Finally, we noted that, although teachers and undergraduates provided CS examples from both natural systems and social systems, the respondents who achieved a higher knowledge score, i.e., the science teachers and STEM majors, more frequently provided CS examples from natural systems. Further studies could be conducted on whether there is a correlation between exposure to complex natural systems and respondents’ proficiency in CS knowledge.
The current study has four main implications for science education in the United States. First, our findings suggest that there is a need for clear and precise definitions of complex systems within current science education frameworks. In the current U.S. K-12 science standards [9,14], the phrase “more complex systems” encompasses both complicated systems and complex systems. Based on teachers’ responses in our survey, the absence of a clear definition for complex systems, particularly the absence of the notions of decentralization and stochasticity, impedes teachers’ ability to effectively differentiate between the two types of systems. This may also prevent them from tailoring their instructional strategies. For example, human body systems (e.g., the digestive system, circulatory system, etc.) and ecosystems have distinct features, and teachers need to help their students understand these systems with different methods and learning objectives. At the secondary level, the definitions from Jacobson [1] and Mitchell [2] could be considered as they capture the essential features of CSs.
Second, educators must assess learners’ knowledge of CSs in terms of multiple aspects to reveal their existing knowledge. This study developed an assessment tool for educators to gauge learners’ CS knowledge in five aspects. We suggest that this tool be used before teaching CSs in science classes so that educators may gain a holistic understanding of their students’ CS knowledge and use it to inform their teaching.
Third, our findings suggest a pressing need for the deliberate design and implementation of enhanced learning experiences, including college courses and teacher professional development programs, to deepen their comprehension of CSs, especially the notions of decentralization, stochasticity, and emergence and their relationships. The survey scores directly show the low knowledge of decentralization and stochasticity among the teachers and undergraduates, while the weak path coefficients in the inner model suggest that these respondents did not closely connect decentralization and stochasticity to emergent system outcomes. The inner model and survey scores also show that, even though respondents appeared to possess an acceptable understanding of system elements and micro-interactions, such knowledge does not necessarily lead to a good grasp of decentralization and stochasticity. Therefore, explicit learning about these concepts is needed.
Fourth, on the bright side, our results show that teachers and undergraduates have a certain level of CS knowledge, including (1) viewing all five constructs as related, (2) possessing knowledge of the elements and micro-interactions of CSs, and (3) recognizing CS examples across natural and social systems. Curriculum developers and professional development facilitators may leverage this existing knowledge as a foundation upon which to build and expand undergraduates’ and teachers’ CS knowledge. Furthermore, the integration of appropriate technologies can effectively support learners’ comprehension. For instance, agent-based computer models have been successfully used to aid students in comprehending the concepts of decentralization and emergence in CSs [57].
This study has limitations. First, the responses to the current version of the survey were gathered online, potentially limiting our ability to address any uncertainties or questions that respondents may have had regarding survey items. To address this, we will conduct ongoing interviews with a portion of the respondents to ensure the clarity and accessibility of the survey items. Second, the system identification items are binary. However, individuals’ perceptions of whether a system qualifies as a CS may fall in a spectrum. To address this limitation, we will replace the binary option with a Likert scale for the system identification items in the next version. Third, the current survey does not establish convergent validity. In subsequent studies, we plan to design items that directly capture respondents’ complex systems knowledge as the endogenous variable to facilitate the examination of convergent validity. Fourth, we used non-probability methods to distribute the survey to teachers, so the teacher respondents might not be highly representative of the high school teacher population in the USA. For example, only 12% of the teachers were in social studies. Additionally, both the teacher and undergraduate groups disproportionately included respondents who identified as female and white. Our audience must consider these limitations of the participants when interpreting our results.
Complex systems have gained rapidly increasing attention in STEM education over the past two decades [23] due to their importance and prevalence in our lives. Our study aimed to devise an instrument for gauging CS knowledge, which will serve as the foundation for developing further cognitive procedures, such as systems thinking. We acknowledge that this effort marks merely the initial phase of our work. Through publishing this article, we intend to initiate dialogue and refine perspectives. We extend an invitation to STEM educators and systems educators to utilize this instrument now and engage in collaborative thought to advance this field of inquiry.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/educsci14080837/s1, Table S1: CS scale minimal dataset_1.
Author Contributions
Conceptualization, L.X.; methodology, L.X. and Z.M.; formal analysis: L.X. and Z.M.; validation, Z.M., A.P. and R.K.; investigation, L.X. and A.P.; writing—original draft preparation, L.X.; writing—review and editing, L.X., Z.M., A.P. and R.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study was conducted in accordance with the Declaration of Helsinki and approved by the Institutional Review Board of the University of Kentucky (IRB # 55150; Approval Date: 14 January 2022).
Informed Consent Statement
Informed consent was obtained from all subjects involved in this study.
Data Availability Statement
All data can be obtained from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Five CS constructs and 20 retained measurement items.
Table A1.
Five CS constructs and 20 retained measurement items.
| Element | Complexity Science View | |
|---|---|---|
| Item 01 | A complex system should contain a sufficient number of individuals. (Numerosity) | True |
| Item 02 | A complex system may contain different types of individuals. (Element type) | True |
| Item 05 | In a complex system, individuals are affected by certain environmental conditions. (System environment) | True |
| Item 07 | In a complex system, individuals of the same type still differ from one another. (Heterogeneity) | True |
| Decentralization | ||
| Item 09 | In a complex system, “organizers” or “leaders” are necessary for forming any internal sub-groups. (Central control) | Untrue |
| Item 10 | In a complex system, one individual may affect all other individuals. (Interdependence) | True |
| Item 11 | In a complex system, one individual only directly interacts with a portion of other individuals at a time. (Local interactions) | True |
| Item 12 | In a complex system, every individual may affect the system at different times. (Decentralized control) | True |
| Micro-interaction | ||
| Item 15 | In a complex system, every individual may be simultaneously affected by multiple factors. (Simultaneous) | True |
| Item 16 | In a complex system, when an individual takes an action on another individual, the action may yield an impact on the individual that takes the action. (Feedback) | True |
| Item 17 | A complex system contains more than one causal process. (Multiple causalities) | True |
| Item 22 | Individuals stop interacting when the complex system they are in reaches an equilibrium. (Continuous) | Untrue |
| Stochasticity | ||
| Item 18 | The outcome of a complex system can be predicted from individuals’ characteristics. (Unpredictability) | Untrue |
| Item 20 | Disorder needs to be eliminated from a complex system as much as possible to maintain the system stability. (Impact of disorder) | Untrue |
| Item 23 | All complex systems contain disorder. (Existence of disorder) | True |
| Emergence | ||
| Item 21 | A complex system cannot remain stable when individuals within it constantly interact with one another. (Dynamic stability) | Untrue |
| Item 24 | In a complex system, a small change to individuals may significantly affect the overall system outcome. (Nonlinearity) | True |
| Item 25 | The behavior of a complex system may look very different from the individuals’ behaviors. (Hierarchy of levels) | True |
| Item 27 | The outcome of a complex system evolves over time. (Adaptability) | True |
| Item 29 | In a complex system, some individuals’ behaviors may be inconsistent with the overall system outcome. (Collective emergence) | True |
References
- Jacobson, M.J. Problem solving, cognition, and complex systems: Differences between experts and novices. Complexity 2001, 6, 41–49. [Google Scholar] [CrossRef]
- Mitchell, M. Complexity: A guided Tour; Oxford University Press: New York, NY, USA, 2009. [Google Scholar]
- Rickles, D.; Hawe, P.; Shiell, A. A simple guide to chaos and complexity. J. Epidemiol. Community Health 2007, 61, 933–937. [Google Scholar] [CrossRef] [PubMed]
- Siegenfeld, A.F.; Bar-Yam, Y. An introduction to complex systems science and its applications. Complexity 2020, 2020, 6105872. [Google Scholar] [CrossRef]
- Jacobson, M.J.; Wilensky, U. Complex systems in education: Scientific and educational importance and implications for the learning sciences. J. Learn. Sci. 2006, 15, 11–34. [Google Scholar] [CrossRef]
- Yoon, S.A.; Goh, S.-E.; Park, M. Teaching and learning about complex systems in K–12 science education: A review of empirical studies 1995–2015. Rev. Educ. Res. 2018, 88, 285–325. [Google Scholar] [CrossRef]
- York, S.; Lavi, R.; Dori, Y.J.; Orgill, M. Applications of systems thinking in STEM education. J. Chem. Educ. 2019, 96, 2742–2751. [Google Scholar] [CrossRef]
- American Association for the Advancement of Science (AAAS). Benchmarks for Science Literacy; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- NGSS Lead States. Next Generation Science Standards: For States, By States; The National Academies Press: Washington, DC, USA, 2013. [Google Scholar]
- Boehm, B.; Mobasser, S.K. System thinking: Educating T-shaped software engineers. In Proceedings of the 2015 IEEE/ACM 37th IEEE International Conference on Software Engineering, Florence, Italy, 16–24 May 2015; pp. 333–342. [Google Scholar]
- Riess, W.; Mischo, C. Promoting systems thinking through biology lessons. Int. J. Sci. Educ. 2010, 32, 705–725. [Google Scholar] [CrossRef]
- Gilissen, M.G.; Knippels, M.-C.P.; van Joolingen, W.R. Bringing systems thinking into the classroom. Int. J. Sci. Educ. 2020, 42, 1253–1280. [Google Scholar] [CrossRef]
- National Research Council. National Science Education Standards; National Academies Press: Washington, DC, USA, 1996. [Google Scholar]
- National Research Council. A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas; National Academies Press: Washington, DC, USA, 2012. [Google Scholar]
- Fichter, L.S.; Pyle, E.; Whitmeyer, S. Strategies and rubrics for teaching chaos and complex systems theories as elaborating, self-organizing, and fractionating evolutionary systems. J. Geosci. Educ. 2010, 58, 65–85. [Google Scholar] [CrossRef]
- Hmelo-Silver, C.E.; Azevedo, R. Understanding complex systems: Some core challenges. J. Learn. Sci. 2006, 15, 53–61. [Google Scholar] [CrossRef]
- Taylor, S.; Calvo-Amodio, J.; Well, J. A method for measuring systems thinking learning. Systems 2020, 8, 11. [Google Scholar] [CrossRef]
- Yoon, S.A.; Anderson, E.; Klopfer, E.; Koehler-Yom, J.; Sheldon, J.; Schoenfeld, I.; Wendel, D.; Scheintaub, H.; Oztok, M.; Evans, C. Designing computer-supported complex systems curricula for the Next Generation Science Standards in high school science classrooms. Systems 2016, 4, 38. [Google Scholar] [CrossRef]
- Sammut-Bonnici, T. Complexity theory. In Wiley Encyclopedia of Management; Cooper, C.L., McGee, J., Sammut-Bonnici, T., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2015; Volume 12, pp. 1–2. [Google Scholar]
- Lavi, R.; Dori, Y.J. Systems thinking of pre-and in-service science and engineering teachers. Int. J. Sci. Educ. 2019, 41, 248–279. [Google Scholar] [CrossRef]
- Dori, D.; Sillitto, H.; Griego, R.M.; McKinney, D.; Arnold, E.P.; Godfrey, P.; Martin, J.; Jackson, S.; Krob, D. System definition, system worldviews, and systemness characteristics. IEEE Syst. J. 2019, 14, 1538–1548. [Google Scholar] [CrossRef]
- Dolansky, M.A.; Moore, S.M.; Palmieri, P.A.; Singh, M.K. Development and validation of the systems thinking scale. J. Gen. Intern. Med. 2020, 35, 2314–2320. [Google Scholar] [CrossRef]
- Bielik, T.; Delen, I.; Krell, M.; Assaraf, O.B.Z. Characterising the literature on the teaching and learning of system thinking and complexity in STEM education: A bibliometric analysis and research synthesis. J. STEM Educ. Res. 2023, 6, 199–231. [Google Scholar] [CrossRef]
- Gilissen, M.G.; Knippels, M.-C.P.; Verhoeff, R.P.; van Joolingen, W.R. Teachers’ and educators’ perspectives on systems thinking and its implementation in Dutch biology education. J. Biol. Educ. 2019, 54, 485–496. [Google Scholar] [CrossRef]
- Goh, S.-E. Investigating Science Teachers’ Understanding and Teaching of Complex Systems. Ph.D. Dissertation, University of Pennsylvania, Philadelphia, PA, USA, 2015. [Google Scholar]
- Lee, T.D.; Gail Jones, M.; Chesnutt, K. Teaching systems thinking in the context of the water cycle. Res. Sci. Educ. 2019, 49, 137–172. [Google Scholar] [CrossRef]
- Skaza, H.; Crippen, K.J.; Carroll, K.R. Teachers’ barriers to introducing system dynamics in K-12 STEM curriculum. Syst. Dyn. Rev. 2013, 29, 157–169. [Google Scholar] [CrossRef]
- Sweeney, L.B.; Sterman, J.D. Thinking about systems: Student and teacher conceptions of natural and social systems. Syst. Dyn. Rev. J. Syst. Dyn. Soc. 2007, 23, 285–311. [Google Scholar] [CrossRef]
- Nordine, J.; Lee, O. Crosscutting Concepts: Strengthening Science and Engineering Learning; NSTA Press: Richmond, VA, USA, 2021. [Google Scholar]
- Ladyman, J.; Lambert, J.; Wiesner, K. What is a complex system? Eur. J. Philos. Sci. 2013, 3, 33–67. [Google Scholar] [CrossRef]
- Zywicki, T.J. Epstein and Polanyi on simple rules, complex systems, and decentralization. Const. Pol. Econ. 1998, 9, 143. [Google Scholar] [CrossRef]
- Qian, H. Stochastic physics, complex systems and biology. Quant. Biol. 2013, 1, 50–53. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. In Proceedings of the 14th annual conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 27–31 July 1987; pp. 25–34. [Google Scholar]
- Wilensky, U. NetLogo Flocking Model; Center for Connected Learning and Computer-Based Modeling, Northwestern University: Evanston, IL, USA, 1998. [Google Scholar]
- Hmelo-Silver, C.E.; Pfeffer, M.G. Comparing expert and novice understanding of a complex system from the perspective of structures, behaviors, and functions. Cogn. Sci. 2004, 28, 127–138. [Google Scholar] [CrossRef]
- Chi, M.T.; Roscoe, R.D.; Slotta, J.D.; Roy, M.; Chase, C.C. Misconceived causal explanations for emergent processes. Cogn. Sci. 2012, 36, 1–61. [Google Scholar] [CrossRef]
- Jacobson, M.; Working Group 2 Collaborators. Complex Systems and Education: Cognitive, Learning, and Pedagogical Perspectives. In Planning Documents for a National Initiative on Complex Systems in K-16 Education. Available online: https://necsi.edu/complex-systems-and-education-cognitive-learning-and-pedagogical-perspectives (accessed on 10 May 2024).
- Doerner, D. On the difficulties people have in dealing with complexity. Simul. Games 1980, 11, 87–106. [Google Scholar] [CrossRef]
- Wilensky, U.; Resnick, M. Thinking in levels: A dynamic systems approach to making sense of the world. J. Sci. Educ. Technol. 1999, 8, 3–19. [Google Scholar] [CrossRef]
- Yoon, S.A.; Goh, S.-E.; Yang, Z. Toward a learning progression of complex systems understanding. Complicity Int. J. Complex. Educ. 2019, 16, 285–325. [Google Scholar] [CrossRef]
- Barth-Cohen, L. Threads of local continuity between centralized and decentralized causality: Transitional explanations for the behavior of a complex system. Instr. Sci. 2018, 46, 681–705. [Google Scholar] [CrossRef]
- Garvin-Doxas, K.; Klymkowsky, M.W. Understanding randomness and its impact on student learning: Lessons learned from building the Biology Concept Inventory (BCI). CBE—Life Sci. Educ. 2008, 7, 227–233. [Google Scholar] [CrossRef]
- Fick, S.J.; Barth-Cohen, L.; Rivet, A.; Cooper, M.; Buell, J.; Badrinarayan, A. Supporting students’ learning of science content and practices through the intentional incorporation and scaffolding of crosscutting concepts. In Proceedings of the Summit for Examining the Potential for Crosscutting Concepts to Support Three-Dimensional Learning, Arlington, TX, USA, 6–8 December 2018; pp. 15–26. [Google Scholar]
- Groves, R.M.; Fowler, F.J., Jr.; Couper, M.P.; Lepkowski, J.M.; Singer, E.; Tourangeau, R. Survey Methodology; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 561. [Google Scholar]
- Goldstein, J. Emergence as a construct: History and issues. Emergence 1999, 1, 49–72. [Google Scholar] [CrossRef]
- Coltman, T.; Devinney, T.M.; Midgley, D.F.; Venaik, S. Formative versus reflective measurement models: Two applications of formative measurement. J. Bus. Res. 2008, 61, 1250–1262. [Google Scholar] [CrossRef]
- Bollen, K.; Lennox, R. Conventional wisdom on measurement: A structural equation perspective. Psychol. Bull. 1991, 110, 305–314. [Google Scholar] [CrossRef]
- Hair, J.F.; Hult, G.T.M.; Ringle, C.M.; Sarstedt, M.; Danks, N.P.; Ray, S. Partial Least Squares Structural Equation Modeling (PLS-SEM) Using R: A Workbook; Springer Nature: New York, NY, USA, 2021. [Google Scholar]
- Qualtrics. Qualtrics. 2022. Available online: https://www.qualtrics.com/en-au/free-account/?rid=ip&prevsite=en&newsite=au&geo=TH&geomatch=au (accessed on 10 May 2024).
- Ringle, C.M.; Wende, S.; Becker, J.-M. SmartPLS 4. Available online: https://www.smartpls.com (accessed on 10 May 2024).
- Hair, J.F.; Risher, J.J.; Sarstedt, M.; Ringle, C.M. When to use and how to report the results of PLS-SEM. Eur. Bus. Rev. 2019, 31, 2–24. [Google Scholar] [CrossRef]
- Mohamed, Z.; Ubaidullah, N.; Yusof, S. An evaluation of structural model for independent learning through connectivism theory and web 2.0 towards students’ achievement. In Proceedings of the International Conference on Applied Science and Engineering (ICASE 2018), Sukoharjo, Indonesia, 6–7 October 2018; pp. 1–5. [Google Scholar]
- Lakens, D. Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Front. Psychol. 2013, 4, 863. [Google Scholar] [CrossRef] [PubMed]
- Wong, K. Mastering Partial Least Squares Structural Equation Modeling (PLS-SEM) with SmartPLS in 38 Hours; iUniverse: Bloomington, IN, USA, 2019. [Google Scholar]
- Goh, S.-E.; Yoon, S.A.; Wang, J.; Yang, Z.; Klopfer, E. Investigating the relative difficulty of complex systems ideas in biology. In Proceedings of the 10th International Conference of the Learning Sciences: The Future of Learning, ICLS 2012, Sydney, Australia, 2–6 July 2012. [Google Scholar]
- Talanquer, V. Students’ predictions about the sensory properties of chemical compounds: Additive versus emergent frameworks. Sci. Educ. 2008, 92, 96–114. [Google Scholar] [CrossRef]
- Rates, C.A.; Mulvey, B.K.; Chiu, J.L.; Stenger, K. Examining ontological and self-monitoring scaffolding to improve complex systems thinking with a participatory simulation. Instr. Sci. 2022, 50, 199–221. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).