Students’ Epistemological Framings When Solving an Area Problem of a Degenerate Triangle: The Influence of Presence and Absence of a Drawing
Abstract
1. Introduction
Which has the larger area? A triangle with sides of three, four, five, or a triangle with sides of 300, 400, and 700?
Wrong!… The second triangle is degenerate. It’s a straight line. Its area is zero.
2. A Brief Review of Problem Statements Involving Uncommon Triangles
And saying, it is the triangle A.B.C. with the base B.C. which is 20 “canna” and A.B. of 12 “canna”, and A.C. of 8 “canna”, it is asked how much is the surface [i.e., area]. You should know, that if the side A.B. is summed with the side A.C., and their sum is not longer than the base B.C., this question cannot be answered, however similar questions might be given to people with low knowledge.
In triangle ABC, AB = 12, AC = 7, and BC = 10. If sides AB and AC are doubled while BC remains the same, then: (A) the area is doubled, (B) the altitude is doubled, (C) the area is four time the original area, (D) the median is unchanged, (E) the area of the triangle is 0.
There are really two answers to this problem, but they come to pretty same thing. Sticklers in mathematics would say there is no such triangle because the sum of the lengths on any two side of a triangle must be greater than the length of the third side, and here 700 = 400 + 300. Less fussy people would say that the area of the triangle is zero because it has collapsed to a line segment. You can take your choice.
3. Method
3.1. Research Focus
3.2. Population and Sample
3.3. Instrument
- (a)
- Describe verbally, without using a formula, the procedure you will use;
- (b)
- Execute the plan mathematically and state the solution; and, once the problem is solved;
- (c)
- Rate the difficulty of the task, with one option to choose from: very difficult, difficult, normal, easy, and very easy.
3.4. Data Collection and Analysis Procedure
4. Results and Analysis
4.1. Quantitative Analysis
4.2. Qualitative Analysis
5. Discussion and Conclusions
- They reconsider their original epistemological framing, change it considering the new situation, and give the correct answer;
- They deny the stated result, do not change their epistemological framing, and force a non-zero result.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Acerbi, F.; Vitrac, B. Metrica Héron d’Alesandrie; Fabrizio Serra Editore: Pisa, Italia, 2014. [Google Scholar]
- Bruins, E.M. (Ed.) Codex Constantinopolitanus; Part Three. Translation and Commentary; E. J. Brill: Leiden, Holland, 1964. [Google Scholar]
- Sánchez, E. Test de Razonamiento Lógico y Test de Reflexión Cognitiva Como Posibles Predictores del Desempeño de los Estudiantes en la Resolución de Problemas Matemáticos. Master’s Thesis, Benemérita Universidad Autónoma de Puebla, Puebla, México, June 2022. [Google Scholar]
- Dugopolski, M. Precalculus with Limits: Functions and Graphs; Addison-Wesley: New York, NY, USA, 2002. [Google Scholar]
- Fisher, R.C.; Riner, J.; Silver, J.; Waits, B.K. Introductory Mathematic: A Prelude to Calculus; Charles E. Merrill Publishing Company: Columbus, OH, USA, 1975. [Google Scholar]
- Barton, D. Theta Mathematics: NCEA Level 2; Pearson Longman: Auckland, New Zealand, 2005. [Google Scholar]
- Foerster, P.A. Precalculus with Trigonometry: Concepts and Applications; Springer Science & Business Media: Emeryville, CA, USA, 2003. [Google Scholar]
- Carter, J.A. Glencoe Algebra 2; McGraw-Hill Education: Columbus, OH, USA, 2014. [Google Scholar]
- Gardner, M. Riddles of the Sphinx: And Other Mathematical Puzzle Tales; Mathematical Association of America: Washington, DC, USA, 1987. [Google Scholar]
- Gardner, M. Entertaining Mathematical Puzzles; Dover Publications: New York, NY, USA, 1986. [Google Scholar]
- Jaime, A.; Chapa, F.; Gutiérrez, A. Definiciones de triángulos y cuadriláteros: Errores e inconsistencias en libros de texto de E.G.B. Epsilon 1992, 23, 49–62. [Google Scholar]
- Nemrawi, Z.; Abu, M.; Jaradat, Y. The evaluation of mathematics textbooks from the perspective of mathematics teachers in Jordan. Inf. Sci. Lett. 2022, 5, 1427–1433. [Google Scholar] [CrossRef]
- Nurjanah, A.; Retnowati, E. Analyzing the extraneous cognitive load of a 7th grader mathematics textbook. J. Phys. Conf. Ser. 2018, 1097, 012131. [Google Scholar] [CrossRef]
- Ruiz-Estrada, H.; Slisko, J.; Nieto-Frausto, J. Detección de errores y contradicciones en un problema de un libro de texto de matemáticas: Una exploración inicial del pensamiento crítico de los maestros. Acta Latinoamérica Matemática Educ. 2018, 31, 106–114. [Google Scholar]
- Slisko, J.; Hernández, L.; Nabor, A.; Ramirez, S. Inadequate learning sequence and erroneous fact-like statement in a mathematic textbook: What can students take from them? In Proceedings of the Third International Conference on Mathematics Textbook Research and Development, Paderborn University, Paderborn, Germany, 16–19 September 2019; pp. 317–322. [Google Scholar]
- Juárez, J.; Hernández, L.; Slisko, J. Aceptando la existencia de un terreno inexistente en un problema matemático: El uso prevalente de argumentos pragmáticos por docentes de primaria. Av. Investig. Educ. Matemática 2014, 6, 45–61. [Google Scholar] [CrossRef]
- Goffman, E. Frame Analysis: An Essay on the Organization of Experience; Northeastern University Press: Boston, MA, USA, 1986. [Google Scholar]
- Minsky, M. The Society of Mind. Pers. Forum 1987, 3, 19–32. Available online: http://www.jstor.com/stable/20708493 (accessed on 20 December 2023). [CrossRef]
- Schank, R.C. Tell Me a Story: A New Look at Real and Artificial Memory; Charles Scribner’s Sons: New York, NY, USA, 1990. [Google Scholar]
- Bartell, R.; Hutchison, P. Off-task interaction as a mechanism to support on-task participation. In Proceedings of the 14th International Conference of the Learning Science (ICLS), Nashville, TN, USA, 19–23 July 2020; pp. 621–624. [Google Scholar]
- Redish, E.F.; Smith, K.A. Looking Beyond Content: Skill Development for Engineers. J. Eng. Educ. 2008, 97, 295–307. [Google Scholar] [CrossRef]
- Redish, E.F. A Theoretical Framework for Physics Education Research: Modeling Student Thinking. In Proceedings of the International School of Physics “Enrico Fermi”, Course CLVI, Varenna, Italy, 15–25 July 2003; Redish, E.F., Vicentini, M., Eds.; IOS Press: Amsterdam, The Netherlands, 2004; pp. 1–64. [Google Scholar]
- Bing, T.J.; Redish, E.F. Analyzing problem solving using math in physics: Epistemological framing via warrants. Phys. Rev. Spec. Top. Phys. Educ. Res. 2009, 5, 020108-1. [Google Scholar] [CrossRef]
- Bannister, N.A. Reframing Practice: Teacher Learning Through Interactions in a Collaborative Group. J. Learn. Sci. 2015, 24, 347–372. [Google Scholar] [CrossRef]
- Shekell, C.A. Framing for Sense Making in Whole-Class Mathematics Discussions. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PE, USA, 2019. Available online: https://www.proquest.com/openview/93ec32cc9d2da477a44b0ffcaa81910a/1?pq-origsite=gscholar&cbl=18750&diss=y (accessed on 20 December 2023).
- Scheiner, T. Exploring deficit-based and strengths-based framings in noticing student mathematical thinking. In Proceedings of the 45th Conference of the International Group for the Psychology of Mathematics Education (Vol. 3); Universidad de Alicante: Alicante, España, 2022; pp. 18–23. Available online: https://web.ua.es/pme45 (accessed on 18 February 2024).
- Hammer, D.; Elby, A.; Scherr, R.; Redish, E.F. Resources, framing, and transfer. In Transfer of Learning: Research and Perspectives; Mestre, J.P., Ed.; Information Age Publishing: Greenwich, CT, USA, 2005; Volume 89. [Google Scholar]
- MacLachlan, G.; Reid, I. Framing and Interpretation; Melbourne University Press: Melbourne, Australia, 1994. [Google Scholar]
- Forestani, L. Practica d’Arithmetica e Geometria Nuevamente Posta in Luce; Appresso Georgio Varisco: Venetia, Italia, 1603. [Google Scholar]
- Forestani, L. Practica d’Arithmetica e Geometria; Revised by Francesco Ferroni; Stamparia de Pubblico Siena: Siena, Italia, 1682. [Google Scholar]
- Salkind, C.T. The Contest Problem Book. Problems from the Annual High School Contests of the Mathematical Association of America; Random House: New York, NY, USA, 1961. [Google Scholar]
- Klymchuk, S. Provocative mathematics questions: Drawing attention to a lack of attention. Teach. Math. Appl. 2015, 34, 63–70. [Google Scholar] [CrossRef]
- Book, D.L. Problems for Puzzlebusters; Enigmatics Press: Washington, DC, USA, 1992. [Google Scholar]
- Yan, K.C. More Mathematical Quickies & Trickies; MATHPLUS Publishing: Singapore, 2018. [Google Scholar]
- Harshman, E.J.; MacHale, D.; Sloane, P. Classic Lateral Thinking Puzzles; Main Street: New York, NY, USA, 2004. [Google Scholar]
- Tanton, J.S. Geometry: An Interactive Journey to Mastery; Course Book; The Great Success: Chantily, VT, USA, 2014. [Google Scholar]
- Francis, R.L. Word problems: Abundant and deficient data. Math. Teach. 1978, 71, 6–11. [Google Scholar] [CrossRef]
- Nitsche, J.C.C. Introduction to Minimal Surfaces; Cambridge University Press: New York, NY, USA, 1989. [Google Scholar]
- Pogonowski, J. Essays on Mathematical Reasoning. Cognitive Aspect of Mathematical Research and Education; LIT Verlag: Münster, Germany, 2021. [Google Scholar]
- O’Rourke, J. How to Fold It. The Mathematics of Linkages, Origami, and Polyhedral; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- MacHale, D. Puzzleology: Tough Puzzles for Smart Kids; Mercier Press: Cork, Ireland, 2006. [Google Scholar]
- Sloan, P.; MacHale, D. Mathematical Lateral Thinking Puzzles; Puzzle Wright Press: New York, NY, USA, 2015. [Google Scholar]
- Krutetskii, V.A. The Psychology of Mathematical Abilities of Schoolchildren; The University of Chicago Press: Chicago, IL, USA, 1976. [Google Scholar]
- Fraenkel, J.R.; Wallen, N.E.; Hyun, H.H. How to Design and Evaluate Research in Education; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
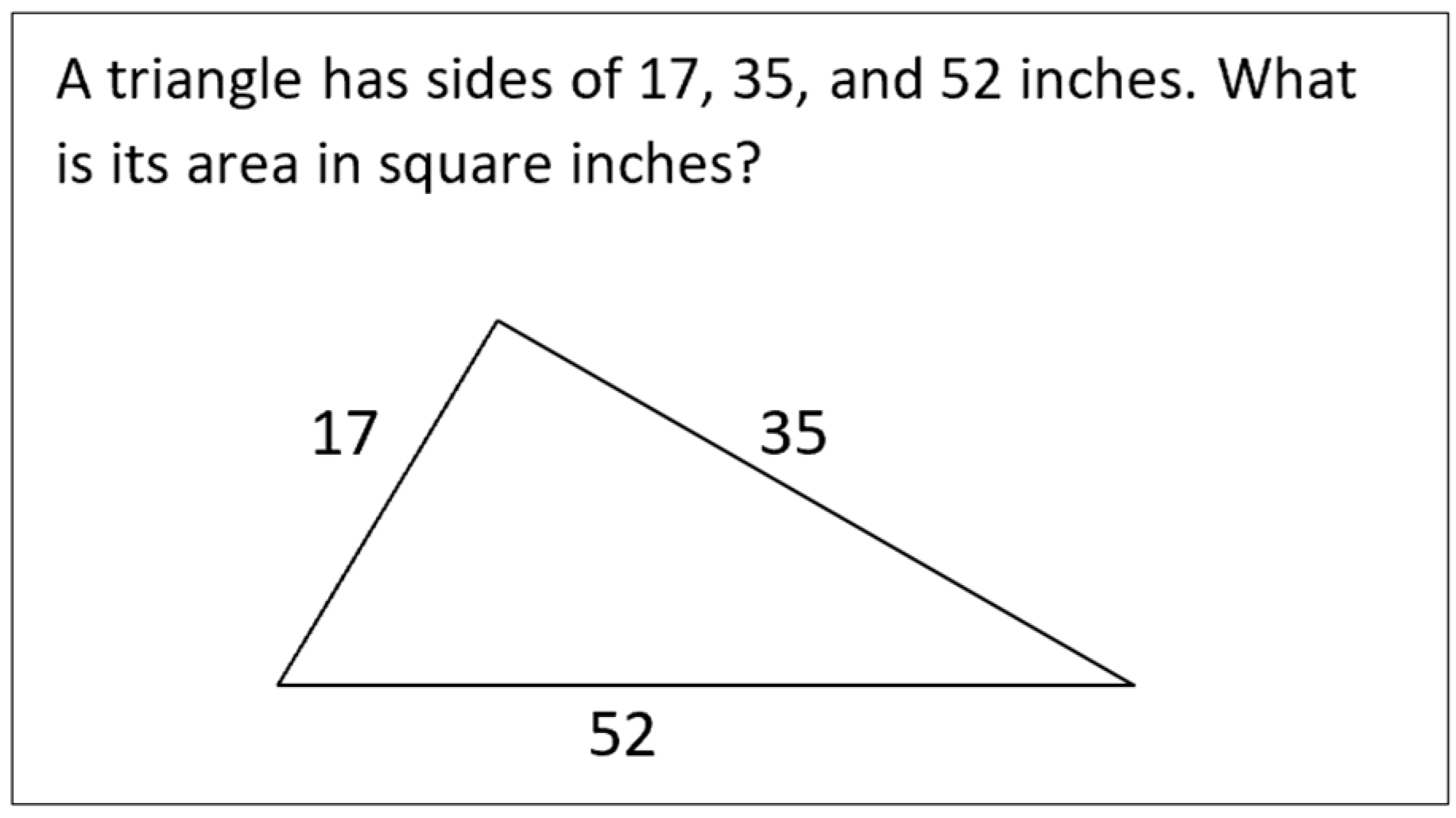
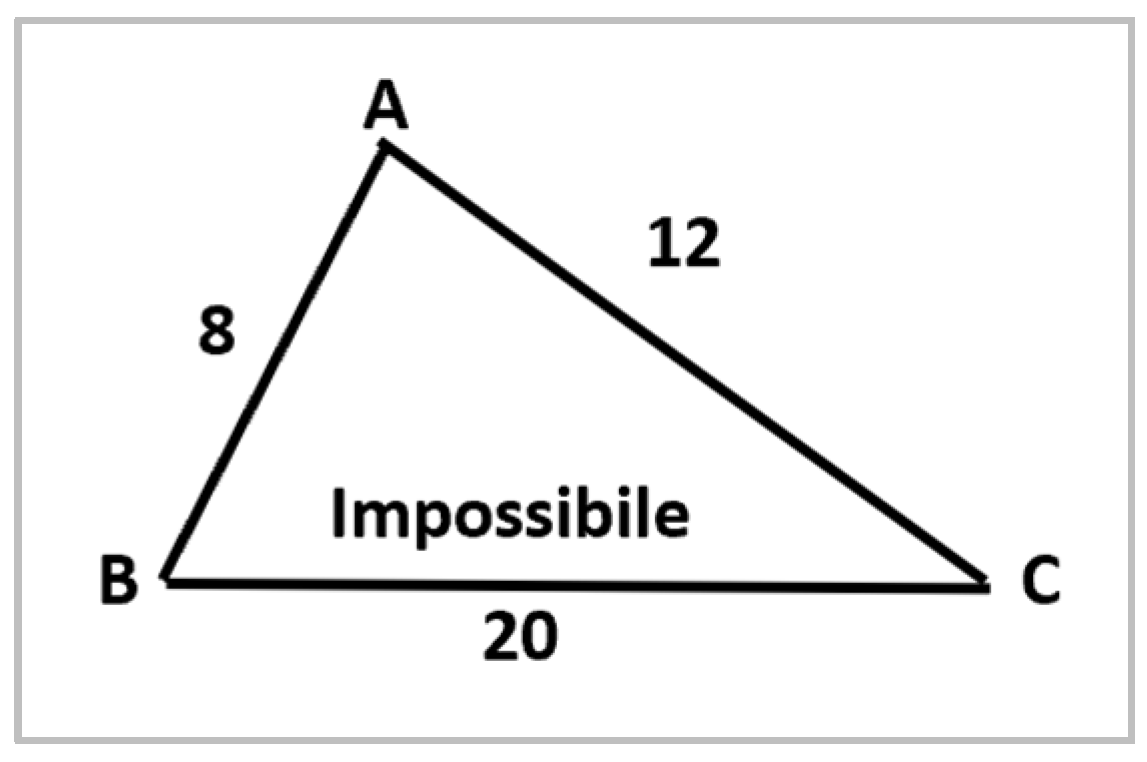







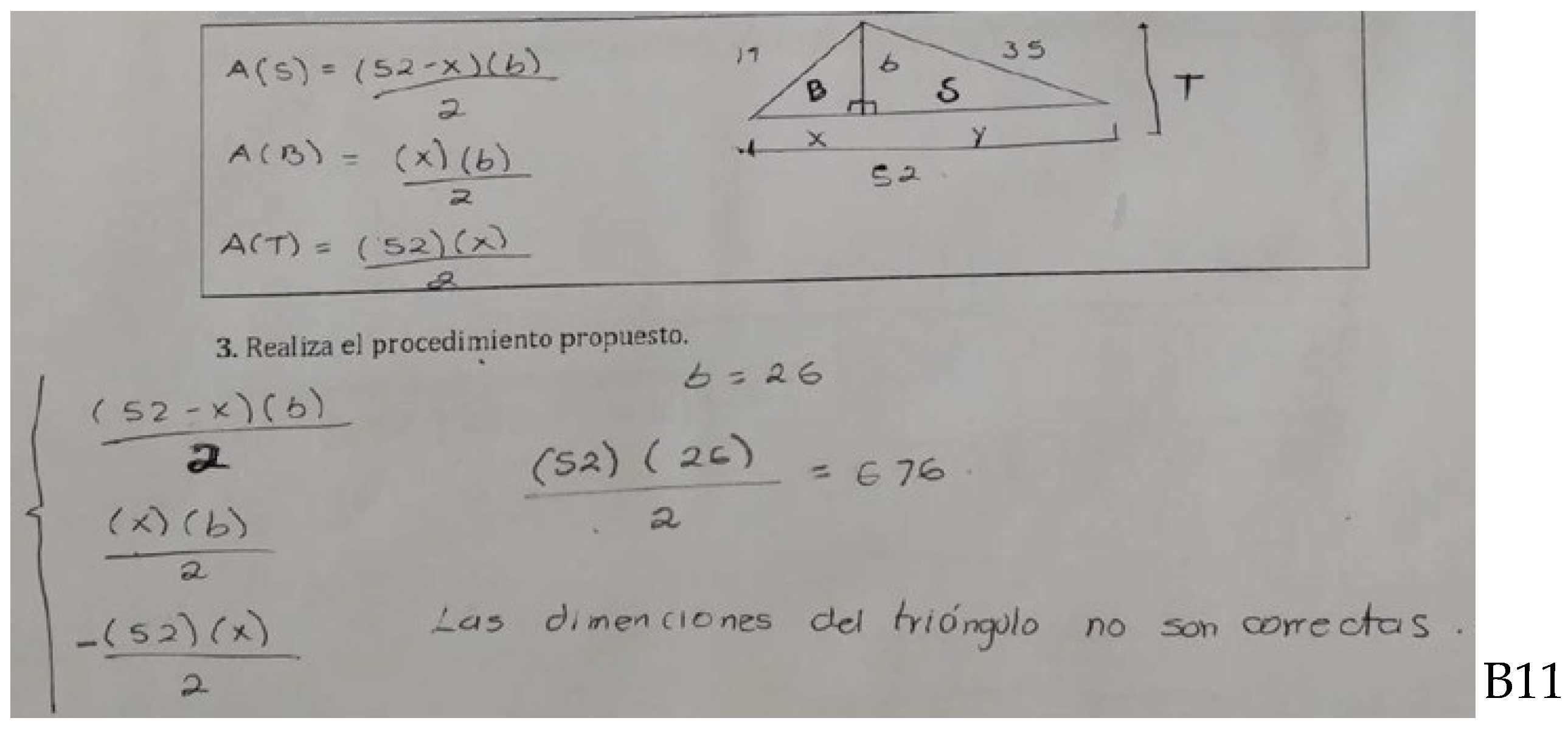



| Puzzle | Authors’ Answer |
|---|---|
| “A triangle has sides of 17, 42, and 59 inches. What is its area?” [33] (p. 66). | “Since 17 + 42 = 59, this is a very skinny triangle. Its area is zero” [33] (p. 187). |
| “A triangle has sides 17 cm, 42 cm, and 59 cm. Find its area” [34] (p. 26). | “Since 17 + 42 = 59, what results is a very skinny triangle. Its area is zero” [34] (p. 184). |
| “Which triangle is larger—one with sides measuring 200, 300, and 400 cm or one with sides measuring 300, 400, and 700 cm?” [35] (p. 171). | “The first triangle is larger-one with sides measuring 200, 300, and 400 cm. The triangle with sides measuring 300, 400, and 700 cm has an area of zero!” [35] (p. 273). |
| Group A (No Triangle) | Group B (With Triangle) | |
|---|---|---|
| Correct answers | 67.6% | 43.9% |
| Incorrect answers | 32.4% | 56.1% |
| Resolution Strategy | Group A (No Triangle) | Group B (With Triangle) |
|---|---|---|
| Heron’s formula | 43.2% | 39% |
| Triangle inequality | 32.4% | 22% |
| Pythagoras theorem | 8.1% | 22% |
| Trigonometric ratios | 0% | 7.3% |
| Area formula | 8.1% | 7.3% |
| Other | 8.1% | 2.4% |
| Group A (Without Triangle Drawing) | Group B (With Triangle Drawing) | |
|---|---|---|
| Very difficult | 2.7% | 4.9% |
| Difficult | 40.5% | 29.3% |
| Regular | 45.9% | 36.6% |
| Easy | 5.4% | 12.2% |
| Very easy | 5.4% | 0% |
| Unanswered | 0% | 17.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juárez-Ruiz, E.; Sliško, J. Students’ Epistemological Framings When Solving an Area Problem of a Degenerate Triangle: The Influence of Presence and Absence of a Drawing. Educ. Sci. 2024, 14, 224. https://doi.org/10.3390/educsci14030224
Juárez-Ruiz E, Sliško J. Students’ Epistemological Framings When Solving an Area Problem of a Degenerate Triangle: The Influence of Presence and Absence of a Drawing. Education Sciences. 2024; 14(3):224. https://doi.org/10.3390/educsci14030224
Chicago/Turabian StyleJuárez-Ruiz, Estela, and Josip Sliško. 2024. "Students’ Epistemological Framings When Solving an Area Problem of a Degenerate Triangle: The Influence of Presence and Absence of a Drawing" Education Sciences 14, no. 3: 224. https://doi.org/10.3390/educsci14030224
APA StyleJuárez-Ruiz, E., & Sliško, J. (2024). Students’ Epistemological Framings When Solving an Area Problem of a Degenerate Triangle: The Influence of Presence and Absence of a Drawing. Education Sciences, 14(3), 224. https://doi.org/10.3390/educsci14030224







