Teachers in the Loop: Integrating Computational Thinking and Mathematics to Build Early Place Value Understanding

Abstract

With increasing attention on the potential overlap between computational thinking (CT) and mathematical reasoning, STEM education researchers seek to understand how integrating CT and mathematics can deepen student learning across disciplines. Although there are various professional development programs that introduce teachers to CT concepts and strategies for curriculum integration, limited research exists on how teachers might apply this knowledge to create math + CT activities for use with their students. Additionally, the majority of research on CT integration through programming has focused on upper elementary grades, leaving the early grades (K-2) relatively unexplored. This qualitative exploratory study aims to examine how teachers in a graduate STEM education program collaborated with university STEM faculty to explore and critique a set of integrated math + CT block-based programming activities designed to build place value conceptual understanding. In-service elementary teachers enrolled in an online graduate CT course for educators (n = 13) explored these activities as learners and drew on their experiences as classroom teachers to offer feedback for program redesign. A sequence of deductive pattern coding and inductive holistic coding of course transcripts, collaborative problem-solving slides, and individual teacher reflections provided insights into how teachers were able to establish connections between their mathematical knowledge related to teaching place value and their emerging understanding of CT concepts, such as abstraction, algorithms, decomposition, and debugging. Implications for the design of professional development for elementary teachers on integrating CT and mathematics are offered.

1. Introduction

As school districts strive to make computing technologies available to more students in U.S. classrooms, they rely on organizations such as CSforAll and Code.org to provide coding resources for students. These organizations have emphasized the general value of the computational thinking (CT) curriculum in PK-12 education [1,2], but there is growing interest in integrating CT into existing school subjects [3]. While the educational research community has not adopted a singular definition of CT in PK-12 education, the conceptualization of CT as the practices of computer science that help us to explain and interpret the world [4] is especially appropriate for designing integrated CT curricula at the elementary level. CT is more than a computing skill; it is the capacity to think creatively and rationally about problems that can be solved with or without a computer. Integrating CT into educational settings should enable students to think abstractly, make conceptual connections, and express their ideas more effectively during problem-solving [5,6]. Yet the absence of a unified definition of CT and teachers’ limited experiences with computational concepts (e.g., algorithms and abstraction), practices (e.g., decomposition and debugging), and tools (e.g., Scratch, NetLogo, etc.) have contributed to the difficulty of translating CT knowledge into classroom practice. Furthermore, without specific alignment of CT with the school subject curriculum and standards, teachers may struggle to create meaningful opportunities for students to engage in CT learning related to school subjects such as mathematics.

The natural and historical connection between CT and mathematics [7] stems from a shared emphasis on pattern-seeking and the generalization of quantitative relationships. Math + CT integration can facilitate students’ reasoning using abstraction, decomposition, pattern recognition, and algorithms, thereby enhancing their understanding of mathematical concepts and skills. Much of the research on teacher professional development for math + CT integration has focused on developing teachers’ knowledge of programming and CT skills and providing methods to implement this knowledge in the classroom. Although teachers can build their understanding of CT concepts and practices through professional development, studies have indicated that teachers struggle to translate their CT knowledge in designing CT lessons that enhance mathematics curriculum and instruction [8,9,10,11].

Teachers need professional development opportunities to see how computer programming can enrich the mathematics experiences they are creating for their students. In the unique context of early elementary classrooms, the potential of CT as a tool for sense-making is still in the early stages of exploration and assessment in professional development programs [12,13]. We argue that facilitating math + CT activities with young children as early as kindergarten can both foster their CT skills and deepen their mathematical understandings. As Yadav and colleagues [14] recommended, the teacher education faculty should work closely with the computer science faculty to design productive professional development opportunities for teachers. To that end, we, as research faculty from the computer science and teacher education departments at one southeastern university, partnered with in-service teachers enrolled in a graduate CT education course (n = 13). We developed a set of Scratch place value programming activities aligned with grade-level mathematics standards, relying on teachers’ mathematical representations and reflections to iteratively revise the activities. We sought to better understand how teachers might use Scratch programs to build early number sense through student-driven representations of place value decomposition. Teachers experienced these activities as mathematical problem solvers and reflected on how they would adapt the Scratch programs for use with their own students. This exploratory qualitative study describes how this collaborative effort between researchers and teachers shed light on how teachers utilized their emergent CT knowledge to represent their place value reasoning in Scratch. It further describes how researchers can leverage teachers’ expertise to design math + CT activities that build on teachers’ unique knowledge of the learning needs of their students. The following research questions guided this study:

• How do early childhood teachers enrolled in a graduate STEM education program apply the facets of CT to represent their mathematical thinking about place value in a block-based programming activity?
• What insights do early childhood teachers offer about how a place value programming activity could be changed for use in their own mathematics classrooms?

2. Literature Review

While there is no scholarly consensus on the definition of computational thinking [15], we find that the Cuny et al. [16] definition of CT as “the thought processes involved in formulating problems and their solutions so that the solutions are represented in a form that can be carried out by an information-processing agent” (p. 1) captures the potential to connect mathematical thinking with computational artifacts as dynamic visual representations. CT is a problem-solving process with specific characteristics related to problem formulation, organization and analysis of data, use of models and simulations, and the efficiency and generalizability of solutions [17]. These contemporary definitions of CT support the performance of mathematics through computing, as originally conceptualized by Papert [18] and his constructionist approach to learning mathematics through computer programming. The natural connection between CT and mathematical practices has motivated investigations into the integration of CT into K–12 mathematics education and the impact on teachers’ approaches and students’ learning outcomes [19].

Shute and colleagues [20] synthesized the expansive research base on CT in primary, secondary, and post-secondary education to provide a general model for both assessing and supporting CT learning. This framework is composed of six facets: (1) decomposition, (2) abstraction, (3) algorithms, (4) debugging, (5) iteration, and (6) generalization. These components guided not only our structuring of the graduate CT education course but also our analysis of how early childhood teachers applied these facets of CT as they engaged in a mathematics activity. Ye et al.’s [21] recent systematic literature review on the integration of CT and mathematics further describes this disciplinary relationship as an interactive and cyclical process of reasoning mathematically and reasoning computationally to generate mathematical knowledge in parallel with the development of CT.

The integration of CT and mathematics has been applied to various elementary mathematical domains, including but not limited to geometry, algebra, and number theory [22]. Research on the integration of CT into elementary mathematics has often focused on evidence of process-oriented activities (such as engagement, communication, and creativity) [23]. There is a need for more research on how teachers apply the facets of CT in the context of the mathematics standards that they are responsible for teaching.

2.1. Computer Programming as a Tool for Teaching Mathematics

Calls to integrate computer programming in school subjects, particularly science and mathematics, are growing [3,24]. Teachers can leverage the structure of computer programming to design integrated activities that assist students in representing their mathematical thinking and deepening their understanding of mathematics. Rich et al. [25] identified several contexts within the mathematics curriculum where CT ideas related to repetition, sequence, and conditionals could be explored. Similarly, teachers can use CT content to teach mathematics in fully integrated lessons [26].

Programming can serve as an intermediary tool for understanding basic mathematics disciplines, such as number sense, algebra, and geometry [27]. Moreover, programming goes beyond aiding in understanding mathematics but also helps in developing algorithmic thinking and problem-solving skills in both disciplines together [28,29]. The use of programming platforms to engage students in problem-solving and mathematical reasoning has been shown to positively influence students’ learning of mathematics [30]. The synergy between programming and mathematics enhances students’ abilities to think logically, solve complex problems, and apply mathematical concepts to real-world situations.

Block-based programming platforms like Scratch have been utilized to facilitate students’ participation in mathematical reasoning activities [31]. Scratch provides a more accessible interface for elementary students than traditional text-based programming languages. Through the interaction with its customizable blocks and sprites, students have the opportunity to develop their mathematical thinking [32]. Scratch can be described as a mathematical action technology, as it engages students in programming a computer to perform mathematical tasks and represent mathematical concepts [33]. As students explore these new ways of representing mathematical ideas and relationships, they acquire not only mathematical knowledge but also knowledge of basic programming concepts, such as loops, sequences, and events [21]. They also apply computational concepts such as abstraction, decomposition, and debugging [34,35,36].

2.2. Using Block-Based Programming as a Mathematical Representation of Place Value

Understanding place value is essential in developing early childhood number sense and fluency with arithmetic operations [37]. Place value refers to the numerical value of a digit based on its position in the number (e.g., ones, tens, hundreds, etc.). It serves as the foundation for students’ construction of flexible methods of numerical grouping and multi-digit arithmetic operations [38]. Reasoning about place value can be challenging as students try to integrate abstract ideas of quantity, place names, and written numerals [39]. Benton and colleagues [40] have used Scratch programming to support elementary students in making sense of the concept of trading or exchanging equal quantities (e.g., ten ones for one ten) by using ones and tens sprites to represent place value digits. Their Scratch program models the action of incrementing a number in the tens place to represent an exchange of 10 ones for 1 ten.

In early childhood mathematics, students use physical manipulatives (base 10 blocks) to begin to make sense of place value. The physical action of interacting with multiple representations builds students understanding of the correspondence between numerical symbols and concrete or pictorial representations of numbers. Mathematics education researchers (e.g., [41]) have further described how computer-based, or virtual, manipulatives can be used instead of concrete blocks to develop integrated concrete knowledge, particularly in relation to place value. Sarama and Clements [42] highlighted the unique affordances of digital environments in linking concrete representations and symbolic representations. They used place value as an illustration of this affordance.

Physical base-ten blocks can be so clumsy, and the manipulations so disconnected from one another, that students see only the trees—manipulations of many pieces—and miss the forest—place-value ideas. In addition, students can break computer base-ten blocks into ones, or “glue” ones together, to form tens.

Incorporating programming into place value teaching approaches may offer further opportunities for making sense of place value because of the computational affordances of automation and efficiency in how students use mathematical manipulatives. Students are not limited by the available quantity of physical blocks or space for modeling. The computer program can also display symbolic equivalents of the virtual model, thereby telling the student how many tens and ones they have modeled along with the base 10 numerical representations.

2.3. Supporting Elementary Teachers in Teaching Mathematics Using Block-Based Programming

The integration of block-based programming into mathematical teaching can facilitate students’ development of both mathematical and CT knowledge [6,43,44]. Teachers play a pivotal role in guiding students to develop mathematical knowledge through programming. When teachers integrate programming and mathematics, students are less focused on memorizing mathematical information and instead develop a deeper conceptual understanding of mathematical concepts through decomposition and debugging [45]. To facilitate the incorporation of CT into the mathematics curriculum, it is essential for teachers to build not only CT knowledge and pedagogical skills but also methods for relating CT to reasoning about and representing mathematical concepts. Therefore, teachers need educational experiences that equip them with the necessary skills in order to achieve this objective [23,46]. CT can be introduced to teachers in a variety of ways, including professional development, technology integration programs, computing education, and teacher educational programs [47].

Traditional professional development programs are primarily focused on equipping teachers with content knowledge of programming rather than providing them with the pedagogical content knowledge needed for integrating programming into their subjects [48,49]. The majority of the programming experiences for teachers have focused on the higher grades, with less emphasis on early elementary teachers [50,51]. Prior research has shown that teachers who experience CT-focused professional development may feel unprepared to integrate programming into their core curriculum [52]. They may also have difficulty in establishing a connection between programming and mathematics, developing integrated activities without clear guidance on how to use block-based programming, or recognizing the value of integrating programming into their subjects [53,54,55,56].

Teachers have described multiple barriers to CT integration, including a lack of programming experience, limited time for integration, and limited access to professional development and continuous support [57,58]. Additionally, they may feel challenged in assessing and supporting students in their different approaches to programming and addressing individual needs [59,60]. Teachers have identified additional challenges specific to mathematics integrated activities, including students’ difficulties with decomposing word problems, creating and recognizing loop sequences in word problems, as well as gaining a clear understanding of variables and control flow [61].

To effectively prepare teachers to embed programming into their teaching, professional development should emphasize building teachers’ capacity in terms of content knowledge, pedagogical knowledge, and technology knowledge [62]. Teachers need engaging experiences that encourage them to explore multiple ways for learning and integrating programming into their teaching practices [63]. Furthermore, there should be ongoing mentorship-based professional development programs rather than relying solely on one-time events [64]. Each of these design expectations for integrated CT professional development motivated the design of the math + CT experience in our graduate CT course for practicing teachers.

3. Method

In this qualitative study, we analyzed course artifacts in the form of discussion transcripts, in-class programming activities, and out-of-class teacher reflections to describe how teachers applied the facets of CT [20] in their representations of place value in Scratch programming activities. We also synthesized evidence of teachers’ feedback during the activities to explore the redesign of the Scratch programming activities to reflect teachers’ ideas about how to best support student learning.

3.1. Participants

The study was conducted in an online graduate-level STEM education course designed to build elementary teacher capacity to integrate CT concepts in their disciplinary instruction. The second author (education faculty) was the course instructor. The participants taught pre-kindergarten (n = 4), first grade (n = 4), second grade (n = 4), and third grade (n = 4) in schools in one large urban district. We used convenience sampling for this study as all teachers were participants in Project InTERSECT, a United States Department of Education grant to support early childhood STEM professional development in high-needs schools. The goal of this project was to deepen pedagogical content knowledge in mathematics, CT, and STEM integration through teacher inquiry into classroom implementation. The CT course was the second in a series of three courses required to earn a certificate in elementary STEM teacher leadership. The courses were designed to build experienced teachers’ capacity to integrate STEM in their classroom teaching.

3.2. Research Context

We selected place value as a critical and challenging mathematics concept at the early elementary level with potential for modeling decomposition with virtual manipulatives with an accessible block-based computer program. Students usually engage with these concepts using physical manipulatives, ten frames, and place value mats in accordance with the state-level mathematics standards and curriculum (

Table 1. Adaptation of state-level mathematics standards document.

Relevant Mathematics Standards	Sample Mathematics Questions Aligned with  Standards
Kindergarten  Represent whole numbers from 10 to 20, using a unit of ten and a group of ones, with objects, drawings and expressions or equations.	Sample Task  Have students provide a different way to fill in the blanks. Students should give more than one answer when possible. 16 is the same as ____ tens and ____ ones
First Grade  Compose and decompose two-digit numbers in multiple ways using tens and ones. Demonstrate each composition or decomposition with objects, drawings, and expressions or equations.	Sample Task  Part A. Look at each equation in the table below. Circle true or false for each expression.  2 tens + 4 ones = 1 tens + 14 ones   4 tens + 0 ones = 40 tens   6 tens + 13 ones = 83  8 tens + 16 ones = 96
Second Grade  Compose and decompose three-digit numbers in multiple ways using hundreds, tens, and ones. Demonstrate each composition or decomposition with objects, drawings, and expressions or equations.	Sample Task  The number 317 can be expressed as 3 hundreds + 1 tens + 7 ones or as 31 tens + 7 ones.  Explain using objects or drawings how both expressions equal 317.  Sample Task  Use a place value model to show how the number 134 can be represented as 13 tens and 4 ones.  Express the number 783 using only hundreds and ones.  Express the number 783 in multiple ways using only tens and ones.

).

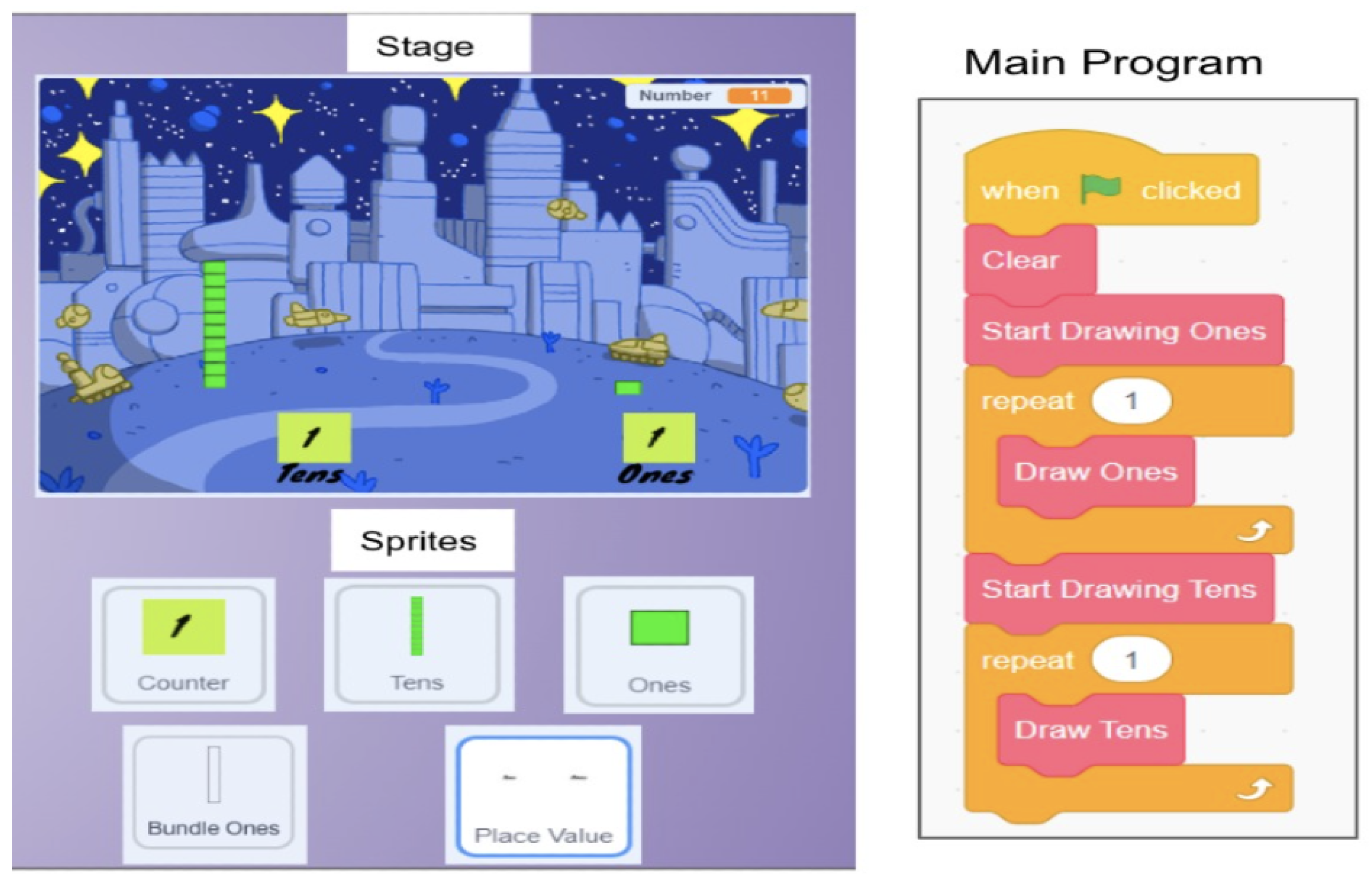
3.2.1. Designing the Scratch Place Value Programs

A series of Scratch programs were developed to align with the Grade K, 1, and 2 place value standards. The programs differed from one grade level to the next with respect to the maximum number that students would be modeling with base ten blocks. Our design goal was to integrate opportunities to apply the facets of CT in a Scratch programming context (e.g., abstraction, decomposition, and algorithmic thinking) with opportunities to reason deeply and flexibly about place value and numerical decomposition [65]. The program used multiple sprites and custom blocks to represent the physical base 10 blocks that students typically access in the classroom when they are making sense of place value. The programs were designed so that students could modify parameters to designate the number of ones, tens, and hundreds to create visual representations of “unit” sprites (each with a value of 1), “rod” sprites (each with a value of 10), and “flat” sprites (each with a value of 100). These sprites are virtual “units” and “rods” analogous to physical place value manipulatives. This program supports teachers and students in building a flexible concept of place value. They can use code to efficiently generate multiple decompositions of decimal numbers. For example, they can represent the number 27 with 2 tens and 7 ones or 1 ten and 17 ones.

The main program (Figure 1) uses two repeat Scratch blocks to iterate the creation of “unit” sprites and “rod” sprites (each with a value of 10). The first repeat block takes the number of ones as an input from the student, while the second repeat block takes the number of tens as an input from the student. As the first repeat block executes, “unit” sprites appear on the screen one at a time until the user-entered number of ones is reached. Simultaneously, the program updates both the ones counter and the counter displayed at the top of the stage to reflect the current value of the number represented by the sprites. If the number of ones entered by the student exceeds ten, the set of ten individual “units” changes color to show equivalence to a “rod”. Following the completion of the first repeat block, the program executes the second repeat block, iterating a number of times equivalent to the user-entered count of tens. With each iteration, a “rod” sprite appears on the stage, and the “tens” counter is incremented. The total value of the number represented by the sprites is displayed in the top right-hand corner. The remaining blocks in the main program are custom Scratch blocks with the functionality needed to create and position each individual sprite and to group sets of 10 “units”. This design decision hides the complexity of generating these representations from the students. By applying the CT concept of abstraction in the algorithmic design, students only need to understand the functionality of the main program.

3.2.2. Piloting the Place Value Programs with a Kindergarten Teacher

Prior to exploring the place value programming activity with the teachers in the CT course, we shared the pilot version of the Grade K program with one elementary teacher who had experience facilitating CT professional development courses. We asked her to provide feedback on whether the activities provided opportunities for students to apply CT concepts while reasoning about mathematics in the context of Scratch programming. Her feedback about balancing the complexity of the visual representations and the complexity of the code supported our first cycle of revisions. She emphasized the mathematical importance of representing ones, bundles of 10 ones, and tens at scale for young learners. She recommended color and orientation revisions to replicate the physical base 10 blocks students were accustomed to using in the classroom.

She also observed that the program exhibited unusual behavior when the number of ones exceeded twenty. We had originally designed the Scratch program to align with kindergarten standards for representing numbers up to 20 using tens and ones. The program would only bundle two groups of ten ones. When she tried to decompose a number using more than 20 ones, there was a discrepancy between the value displayed on the counter in the bottom right part of the stage and the actual number of one blocks shown on the stage. Additionally, she observed that only the first two sets of ten “units” were bundled as one “rod”.

Our rationale for setting the maximum value for the ones counter to twenty was based on the program’s alignment with kindergarten standards. In this context, students are expected to compose and decompose numbers from 11 to 19 into tens and ones. Although the program would execute for numbers greater than 20, there would be a mismatch between the symbolic display and the counter sprite. We chose to leave this logic error in place so that we could assess teachers’ debugging skills.

3.2.3. Facilitating the Place Value Program with Participants

Prior to the lesson on integrating mathematics and CT in Week 7 of the 11–week online graduate STEM education course, teachers engaged in CT in both unplugged (without a computer) and plugged (with a computer) activities. The Week 2–5 modules introduced teachers to the CT facets of algorithmic thinking, decomposition, abstraction, debugging, iteration, and generalization. As part of these modules, the teachers collaboratively modified two Scratch programs: (1) creating a short story with dialogue between sprites; and (2) drawing a a brick wall using mathematical patterns.

3.3. Data Collection

We collected data across four phases of the place value programming activity in Week 7 of the CT course. In the first phase, teachers examined the main program to share their predictions about the functionality of the program. We captured these predictions in a Zoom recording of the whole group discussion. In the second phase, teachers worked in small groups in Zoom breakout rooms to explore and make sense of the Scratch program. Teachers were positioned as learners as they modified the code to represent the number 34 using “units” and “rods” in at least two different ways. They recorded their representations by using screenshots of the coding blocks and the Scratch stage in Google Slides. In the third phase, teachers collaboratively responded to prompts in Google Slides about opportunities for students to learn CT and mathematics from their perspective as educators. They discussed what adjustments they would make to the Scratch program if they were to use this activity in their classroom instruction. The fourth phase of the place value programming activity was completed outside of class as teachers responded to written instructor feedback about their coding decisions and suggested program adjustments. This feedback was documented in teachers’ digital interactive notebooks (DINbs) [66] as a formative assessment of math + CT content knowledge and pedagogical content knowledge. The DINbs included copies of the teachers’ problem-solving slides from the class meeting. The instructor and the teacher used Google comments to provide feedback to one another about the integration of CT and mathematics [67].

The sources of qualitative data collected from the four phases of this study were artifacts of teachers’ interactions with the Scratch program in their group Google Slides, teachers’ reflections on the activity in their individual DINbs, transcripts of in-class discussions, and researcher observations of teachers’ interactions with the Scratch program.

3.4. Data Analysis

We engaged in iterative, collaborative coding of the qualitative data, using both categorizing and connecting strategies [68] to reason deductively about teachers’ application of CT knowledge (RQ1) and to reason inductively about teachers’ ideas for modifying the Scratch programming activity for classroom use (RQ2). For our first cycle of coding [69] of transcripts of in-class discussion, we used the six facets of CT [20] as a priori codes (decomposition, abstraction, algorithms, debugging, iteration, and generalization).

Based on this first cycle of coding, we narrowed the six a priori codes to four anchor codes of abstraction, decomposition, algorithms, and debugging because these codes were most prevalent in teachers’ interpretations and usage of the Scratch place value program as a tool for mathematical reasoning and representation.

To answer our first research question, we analyzed the small group slides and individual reflections using the four anchor codes. We assigned the abstraction code when teachers recognized layering to hide complexity in the computer program and identified relationships between functions. We coded for decomposition when teachers dissected the program into manageable parts. We assigned the algorithms code when teachers interpreted the program as a series of logical, ordered instructions. We coded for debugging when teachers identified errors and discussed how the computer program was not functioning as they expected. For example, we interpreted the following teacher statement as debugging: “When the program was running, we noticed that when it went to the third set of tens the numbers counted oddly”. We then conducted a second cycle of pattern coding [69] to look for differences across groups in how they were engaging in these four facets of CT. We further collapsed the anchor codes into three themes related to teachers’ application of CT knowledge.

To answer our second research question, we collaboratively used holistic coding [69] to describe teachers’ ideas for redesigning the Scratch place value program for use with their students. We analyzed each of the teachers’ DINbs and the instructor’s feedback to describe these ideas. This inductive approach allowed us to look for broad topics describing the additional opportunities that teachers wanted to create for students to learn mathematics. Our analysis of these broad topics yielded two themes related to teaching addition and subtraction and managing errors or exceptional situations that might occur during the execution of the program.

4. Results

In this section, we present the findings from our analysis of the qualitative data. The results are structured in accordance with the research questions.

4.1. RQ1: Teachers’ Use of CT in the Place Value Programming Activity

Teachers varied in their application of CT knowledge in both their initial predictions about what the program would do and in representations of the number 34 using “unit” and “rod” Sprites in Scratch. We identified three themes related to teachers’ understanding of decomposition and abstraction in the context of Scratch, teachers’ abilities to generate place value representations using the main program in Scratch, and teachers’ debugging skills.

4.1.1. Theme 1—Applying Decomposition and Abstraction in Block-Based Programming

During the initial prediction phase of the place value programming activity, teachers offered different interpretations of how the Scratch program functioned and what mathematical representations it created by examining the main program and the output. A pre-kindergarten teacher (Denise) described the program from a higher-level perspective as a black box that accepted input, processed it, and generated output by stating, “It looks like the program takes a number and then gives you units and flats that make that number”. Denise did not illustrate her understanding of decomposition as a CT skill when she predicted that the computer would create the visual representation by interpreting the digits in the ones place and the tens place. Her response suggests that she may only have been looking at the stage in Scratch and not the coding blocks as she predicted the functionality of the code. She connected the “11” as the value of the variable “Number” to the visual representation of one “rod” and one “unit” on the screen.

A Grade 3 teacher (Maria) interpreted the program to be a sequential counter that bundled ten ones. She suggested, “The program composes the ones until it goes until a 10 and then makes a ten rod and then it leaves the one in the ones place to make one”. Maria relied on her own mathematical knowledge for teaching place value to make her prediction. She understood the code could simulate the action of grouping ten ones and replacing the group with one ten. However, she was not applying her CT knowledge of algorithms as a sequence of steps to explain the functionality of the code. She did not communicate that the main program was creating one “unit” to represent 1 one and one “rod” to represent 1 ten.

A Grade 3 teacher (Paula) was able to interpret the repeat blocks in the main program to recognize the decomposition of place value representations.

“You’ve only told it to draw one and draw one, so it’s only going to draw a one and a ten. It’s going to make 11. So as you change the numbers on the repeat you’re changing the numbers that it’s going to create.”

Paula applied her understanding of algorithms, decomposition, and abstraction in computer programming to predict the functionality of the code. She understood that the student could change the parameters for the number of ones and the number of tens to represent place value in multiple ways. Her explanation of changing the number of ones followed by the changing number of tens suggests that she was interpreting the coding blocks in the sequence in which they were written.

During the second phase of the place value programming activity, each group adopted a different approach to interact with the code to create two visual representations of the number 34 using “units” and “rods”. Three groups were able to use the Scratch program to decompose 34 into three “rods” and four “units” and two “rods” and fourteen “units” (Figure 2). They represented this mathematical decomposition by adding screenshots of the Scratch programming stage with the correct numbers of “units” and “rods” blocks. Only two of the four groups placed screenshots of the main program with modified parameters alongside the screenshots of the sprites on the Scratch programming stage. Their decision to connect coding blocks to mathematical representations using Sprites provides evidence of their use of CT decomposition and abstraction to represent their place value understanding.

We saw variations in each of the four groups’ abilities to communicate their understanding of CT decomposition and abstraction in the context of mathematics. One group decomposed the number 34 in two distinct ways (3 tens + 4 ones, 2 tens + 14 ones). Two other groups attempted to express the number 34 in three different ways (3 tens + 4 ones, 2 tens + 14 ones, and 34 ones). Moreover, they demonstrated an advanced application of CT by determining that the code would not display the sprites correctly if the number of ones exceeded 20. The fourth group struggled to represent the number 34. They did not translate their knowledge of decomposition to identify that the ones and tens were encoded with two distinct custom blocks. Renee, a Grade 3 teacher, offered an outside-of-class reflection explaining the challenges that her group had faced with abstraction along with the affordances of exploring existing code to understand decomposition.

“We spent so much time missing huge chunks that I now understand the need to ensure all relevant parts of the code are showing. But the struggle did get us to play with a lot of blocks we wouldn’t have otherwise.”

Renee’s reflection provided additional evidence of the challenge that her group faced in differentiating the main program from the custom blocks that created and positioned sprites. They were not able to translate their understanding of abstraction as a CT skill to interpret which parameters they should manipulate in the code. She further described her challenge in making sense of abstraction.

“I have a better understanding of the pink blocks. I understood the concept, but in tinkering, I can now apply it and manipulate it. I will be honest, this code is still escaping me. I still do not fully understand what it is doing and how it works. For me, there is so much going on, it is hard to follow. I think there are several separate things going on with the visual numbers and the counting. I think what would have helped me to understand it better is to have practice with a program that did one of those things, then practice with a code that did the other. Then, practice with code that does both.”

During this second phase of the place value programming activity, three of the four groups effectively applied their CT decomposition skills, leading to the understanding that the program is broken down into multiple blocks. Each of these blocks implements a specific functionality within the program. Furthermore, by employing their CT abstraction skills, they understood that each custom block abstracts a specific functionality and they were not required to delve into the details of its implementation. On the other hand, one group struggled to apply abstraction CT skills. This group focused more on understanding the details of each custom block. With the challenges they had in finding the main program and changing parameters to represent the number 34, one of the teachers in this group expressed hesitancy about adopting integrated activities in her classroom.

4.1.2. Theme 2—Applying Algorithms in Concrete Representations of Place Value

Three groups were able to understand the algorithm employed in the main program to represent 34. They understood that the algorithm requires two inputs, representing the number of ones and the number of tens, and that the visual representation on the stage serves as the output. Furthermore, their understanding extended to recognizing the three main steps of the algorithm: clearing the screen, representing the ones as “unit” sprites based on the number given to the first repeat block, and subsequently representing the tens as “rod” sprites using the number provided to the second repeat block. The fourth group did not apply their knowledge of algorithms to modify the Draw Tens custom block and Draw Ones custom blocks in the main program. Rather than initially understanding the algorithm in the main program to represent the number 34 in multiple ways, they started by modifying the custom blocks in a way to visually represent 34. They were able to correctly display the number 34 in the upper right corner, but the “unit” sprites and “rod” sprites and tens blocks displayed a different value.

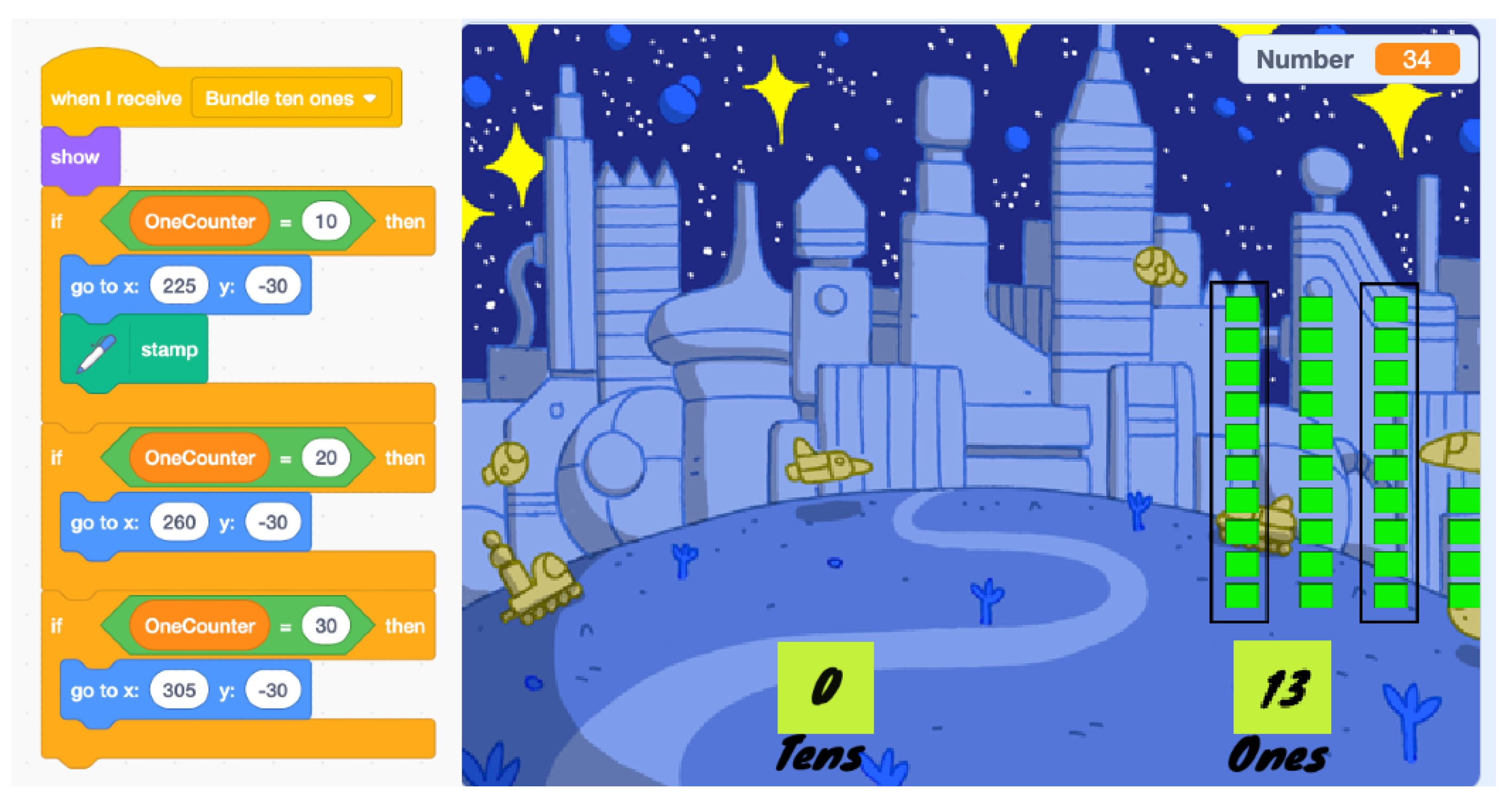
4.1.3. Theme 3—Applying Debugging to Identifying Logic Errors in Symbolic and Concrete Representations of Place Value

Three groups debugged the logic error in the program that we had identified during the pilot implementation with a kindergarten teacher. The symbolic display and the counter sprite did not match when attempting to represent the number 34 using either 1 ten and 24 ones or 34 ones (Figure 3). One group observed that the counter sprite was reset to zero when the number of ones exceeded 20. The other two groups observed that when 34 ones were used to represent the number, the number was displayed correctly as a symbol in the upper right corner of the stage. However, they noticed an error in the ones counter sprite in the lower right corner of the stage as they wrote, “The numbers counted oddly so it actually went up to 20 and then it started over at the numbers zero and so and it counted up 13”.

Two groups used their knowledge of elementary mathematics, CT debugging, variables, and conditions to attempt to fix the error. They modified the code to bundle three groups of ten ones. However, after running the modified program, they observed that it only bundled the first and third groups of ten ones (Figure 4). Because of the limited class time for this activity, the groups did not debug the program further. They wrote, “We did not have time to troubleshoot and figure out why. I think our big realization was watching it count up and seeing that it did not play by the rules that we thought it would play with”.

4.2. RQ2: Teachers’ Ideas for Revising the Place Value Programming Activity

Teachers were able to apply their pedagogical content knowledge for teaching mathematics and their emerging CT skills to recommend changes to the Scratch place value program. They suggested modifications to the program to better support the learning trajectory of elementary students. They appreciated that the program allowed for flexible representation of place value with virtual base 10 blocks and gave students the opportunity to use code to represent the same number in multiple ways. They recognized the power of a computer program as a digital manipulative to create concrete representations of place value more quickly and efficiently than with physical manipulatives.

Based on our analysis of teachers’ recommendations and reflections in their group problem solving slides and in their individual DINbs, we found that teachers saw the potential to enhance the Scratch representations of place value to teach regrouping for addition and subtraction operations. They also extended conversations with the instructor about the maximum number of ones and tens that students should be able to specify to avoid errors in the number of “ones” and “tens” sprites on the stage.

4.2.1. Teaching Addition and Subtraction using CT

One of the groups suggested automating regrouping in to model addition and subtraction in code. They saw the potential for a Scratch programming activity to help early elementary students to see exchanging 1 ten for ten ones supports subtraction and how exchanging 10 one for one ten supports addition. The course instructor challenged these teachers to think about the distinction between the original place value programming activity, where the students were making the mathematical decisions about representations, and the functionality they were proposing. An automated regrouping program would demonstrate mathematics instead of supporting students in reasoning mathematically.

Instructor: “We would love to write a program for these operations. Tell us more about what you would like the stage to look like (in terms of sprites or code blocks).”

Alyssa (Grade 2 Teacher): “I am not really sure? I have been thinking about it for a few weeks. I like how in this place value program it shows the blocks for the number. I think it would be helpful for students to see the blocks for the numbers they are adding and then see how they are bundled to make a 10 or 100. My second graders struggle with the concept of making a bigger unit when adding. I keep thinking about a lasso grabbing 10 ones and trading it for 1 ten.”

Instructor: “I am still thinking about your ideas. Let’s continue to think about how much the computer should do and how much the student should do. In our other program, the computer is automating students’ ideas about decomposing numbers.”

The teachers’ recommendations for developing computer programs for mathematical concepts were often focused on designing a program that demonstrates mathematical operations rather than developing a tool that allows students to make sense of the mathematical concept and consequently deepen their understanding of the concept.

4.2.2. Theme 2: Managing Errors or Exceptional Situations

Teachers drew upon both their CT knowledge and their mathematics knowledge as they described how to modify the program to accept larger numbers as inputs without creating errors. Alyssa suggested a closer alignment of the program with the Grade 1 standard of representing place value for numbers with up to 99 ones. The original program allowed for a maximum of 20 ones. She acknowledged that representing the number 86 with 86 ones was less efficient than using 8 tens and 6 ones, but she believed it was valuable for students to create inefficient representations as part of their sense-making. She also related the space limitations of the Scratch stage to her own classroom experiences with a limited number of physical manipulatives. She proposed writing code to say that the Scratch cat is unable to draw this number of ones and to prompt the student to represent the number in a different way. Her suggestion provided evidence that she was ready to understand exception handling as a programming concept, even though neither the course nor the study addressed this topic. The teacher and the instructor were engaging in programming design together.

Instructor: “What number of ones would you like the program to be able to count up to in this program? What would be your rationale?”

Alyssa: “I think to meet the first grade standard, the program would need to be able to count up to 99 ones. First grade students need to be able to compose and decompose two-digit numbers in multiple ways using tens and ones. Second grade students need to be able to compose and decompose three-digit numbers in multiple ways using hundreds, tens, and ones. The number 241 can be expressed as 2 hundreds + 4 ten + 1 one or as 24 ten + 1 one or as 241 ones. 241 ones would be too many ones for the program to draw. Maybe have the sprite say, “That is a lot of ones to draw, can you think of another way to represent the number?”

Instructor: “You are echoing the same conversations we as researchers had around the program design! May we have the sprite say your exact words? We also think we will set a limit at 9 tens for the same reason.”

Alyssa: “That is what I tell my students when they are drawing quick tens and ones to solve a problem. It will take them a long time to draw so many ones. I always tell them that the drawing would be correct with that many ones but it would not be efficient.”

Helen, another second grade teacher, offered another perspective on the value of being able to specify up to 99 ones for numbers up to 100 in the program, even though it was not efficient. “We have students that truly need that experience of counting it out by ones. Conceptually, they need to be able to manipulate by ones before they can swap out to tens”. She recognized the potential for students to make sense of these ideas with virtual “units” and “rods” in a computer program.

5. Discussion and Implications

Our goal in this study was to describe how researcher–teacher collaborations support teachers in applying the facets of CT as they both experience a math + CT activity as learners and critically consider its potential for use with early elementary students. In our analysis, we found differential evidence of teachers’ application of knowledge of abstraction, decomposition, and debugging as they thought creatively about mathematics in the context of a Scratch program designed to align with Grades K-2 mathematics standards. We also reported on how teachers would want to modify a block-based place value programming activity to better support student mathematics learning.

Although all teachers had prior experiences in applying and identifying the facets of CT in both standalone unplugged and plugged CT activities, there were variations in how they applied their knowledge of abstraction, algorithms, and debugging in the integrated Scratch math + CT activity. Some teachers struggled to apply their understanding of CT to represent place value, while others demonstrated a strong understanding of abstraction, algorithms, and debugging to create multiple representations. These understandings were made more explicit because teachers were engaging with Scratch as a mathematics action technology [33] and making sense of program functionality in the context of mathematics. Teachers’ experiences as learners with Scratch were consistent with Benton et al.’s [40] findings about how students can learn to program for the purpose of moving beyond procedural knowledge about place value. Scratch programs can foster learners’ deeper conceptual understanding of the meaning of the tens digit and the ones digit with visual representations of quantity.

The teachers’ experiences as learners also serve as evidence that the place value programming activity aligned with state-level mathematics standards offers promising opportunities for students to enhance their computational thinking skills in decomposition and debugging while learning mathematics. The open-ended nature of the activity promoted teachers’ ability to make sense of mathematical concepts through code and to diagnose errors when the program did not create the mathematical representations they expected. These findings are consistent with prior research about the interactive and cyclical nature of reasoning both mathematically and computationally in integrated activities [21].

Evidence from this study raises new questions for us about how to deepen teachers’ understanding of CT in an integrated mathematics context. These questions are important to consider in the design of teacher professional development. As we facilitated this place value programming activity with teachers, we debated how much to explain to them about the functionality and organization of the code. We understand that teachers learn to apply CT knowledge when they have opportunities to collaboratively tinker and explore unfamiliar activities [67]. However, they also need support to explicitly connect CT ideas to mathematics teaching and learning. For elementary teachers, prior experiences with mathematics and technology often involve activities where students mainly provide answers to questions. However, as teachers learn to use and modify computer programs from a learner’s standpoint, they start recognizing the creative possibilities of coding in relation to mathematical reasoning.

Professional development for teachers in CT integration should provide opportunities for tinkering, exploration, and modification of existing code followed by reflection on the use of code to teach mathematics. This sequence of experiencing programming as learners followed by reflection on how the program might fit into their mathematics curriculum equips them with the expertise needed to design similar open and creative learning experiences for their students. When teachers have the opportunity to experiment with code as learners in professional development contexts, they think more deeply about how coding can become a representation of mathematical sense-making. As they engage in program design with university faculty, they can be challenged to reflect on how much demonstration is required versus how much they want students to tinker and explore independently.

We also have new questions about how to better encourage teachers to see the conceptual distinction between a program that requires students to use and modify code to represent mathematical thinking instead of executing code that does the mathematics for them. The teachers’ ideas about modifying the program to model regrouping in addition and subtraction are more consistent with a demonstration of a concept. Professional development for teachers should emphasize that integrating CT should support students in making sense of mathematics concepts through programming. Another challenge that should be explored is how to prepare teachers to formulate questions about what students see in order to enhance their sensemaking process. Teachers need to anticipate the mistakes students might make while interacting with the program. They should view both their own mistakes and their students’ mistakes as learning opportunities that will aid in the expansion of their understanding of CT concepts. University faculty who facilitate professional development for teachers should model both productive questioning and positive responses to mistakes.

Each of these implications for the design of professional development (opportunities for exploration, distinguishing between using code to represent student thinking and using code to demonstrate concepts, and modeling productive questioning strategies) has the potential to change how students experience both CT and mathematics. Using block-based programming could help students reinforce their understanding of mathematical concepts by making abstract ideas more tangible. It also motivates students to dynamically and interactively explore mathematical concepts, allowing them to navigate activities at their own pace and gain a more comprehensive understanding of concepts.

As program designers, we learned that feedback from in-service teachers is critical in the design of integrated math + CT activities. Our initial design of the Scratch program aligned with the kindergarten grade level standard and allowed students to correctly represent a maximum of 20 ones because that was the upper limit of the standard. We were aware that this design decision would result in incorrect representations if the teachers tried to represent a number of ones in excess of 20, but we decided to share this version with teachers to increase their opportunities for CT learning. While this design decision was valuable for us as professional development facilitators because it deepened the quality of debugging and CT learning during the class session, the mixed reactions of the teachers to this design decision were informative. Some of the teachers appreciated the opportunity to learn more about the underlying functionality of the various sprites within the Scratch program as they tried to understand why it was not possible to represent 37 ones. Melissa applied this debugging knowledge in her recommendation to build in an exception handler. Other teachers were frustrated that they were not able to correctly create all possible place value representations of the number 34. While we hesitate to conclude from this experience that we should include this type of debugging challenge in integrated activities for elementary students, we also do not discount the instructional value of this experience.

We acknowledge several limitations in this research. The study was conducted as part of one online graduate STEM course, and all 13 participants were practicing teachers with at least three years of experience in one urban school district. The homogeneity of this sample limits the transferability of the findings to other elementary mathematics teaching contexts. Because these teachers volunteered to be part of a study with full tuition and a participation stipend, they may have been more motivated to explore CT integration. Moreover, the study specifically focused on a single programming activity within the number sense mathematical domain. Further research should explore faculty–teacher collaboration in math + CT integration in other mathematics domains, including patterns and geometry.

Our future research on professional learning for teachers would also benefit from a more robust data set. The transcript data collected in this study from discussions among teachers was limited to whole group conversations. Recordings of the four Zoom breakout room conversations among small groups of teachers as they engaged in abstraction, decomposition, algorithmic thinking, and debugging would offer deeper insight into how they were drawing on their CT knowledge as they explored the place value programming activity. Our data collection was limited to artifacts generated in the graduate course in which teachers experienced the place value programming activity as learners. Research on professional development for CT + math integration should include both interviews with participating teachers about their professional development experiences and classroom observations as teachers facilitate these integrated CT + math activities with their own students.

6. Conclusions

The evolution of computing involves incorporating computational skills into elementary education to prepare children for a technologically driven world. Scratch programming activities that automate mathematical representations that are typically constructed with physical manipulatives have the rich potential to change the ways in which students experience mathematics in the classroom. Teachers must be partners in this activity development so that they are prepared to facilitate CT and problem solving. We facilitated the place value programming activity with teachers to model how they could use programming in mathematical problem solving with their own students. The teachers were not passive recipients of our curriculum; instead, they actively engaged as learners and collaborators in both our design and research on integrating CT in elementary mathematics. Teachers made the mistakes that we might expect students to make related to abstraction and algorithms. They identified errors in our programming designs. They proposed redesigns to the place value programming activity, extending its applicability across multiple grade levels, incorporating additional mathematical functionality, and handling errors for user input that exceeded the possible values in the program.

This exploratory research study was conducted in the context of an online graduate STEM education course for practicing teachers. Future research should focus on lesson planning and classroom implementation to better understand how teachers facilitate learning and how to enhance their understanding of place value in a programming context while fostering their creativity and problem-solving skills. The integration of mathematics and CT can also be further explored by introducing programming in mathematics content and pedagogy courses for prospective teachers. By expanding this work in both pre-service and practicing teacher education, the education research community will create more equitable opportunities for students to deepen their learning in both mathematics and in CT in the classroom.