Investigating Students’ Conceptual Knowledge of Quantum Physics to Improve the Teaching and Learning Process
Abstract
1. Introduction
2. How to Investigate Conceptual Knowledge—Tests in Quantum Mechanics
QPCS Test in Accordance with the Learning Outcomes of the Croatian Physics Curriculum
3. Methodology of the Study
- How valid and reliable is the QPCS in the context of Croatian secondary education?
- How do the results of Croatian students compare to existing studies using the same test?
- What prior knowledge of quantum physics do Croatian students have before quantum physics lessons in their final year of secondary school?
- Did Croatian students’ understanding of quantum physics concepts improve after quantum physics education?
4. Results and Discussion
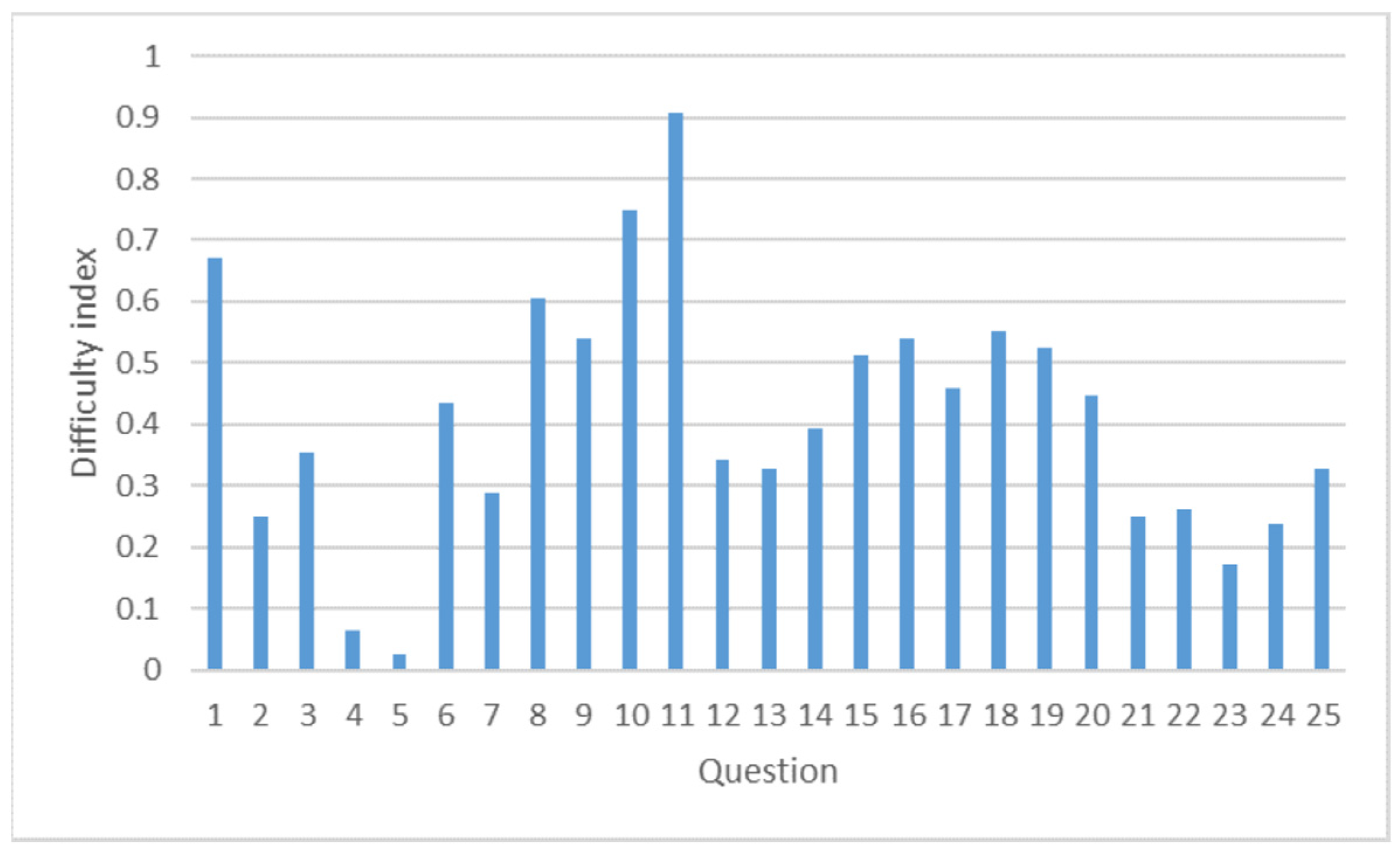
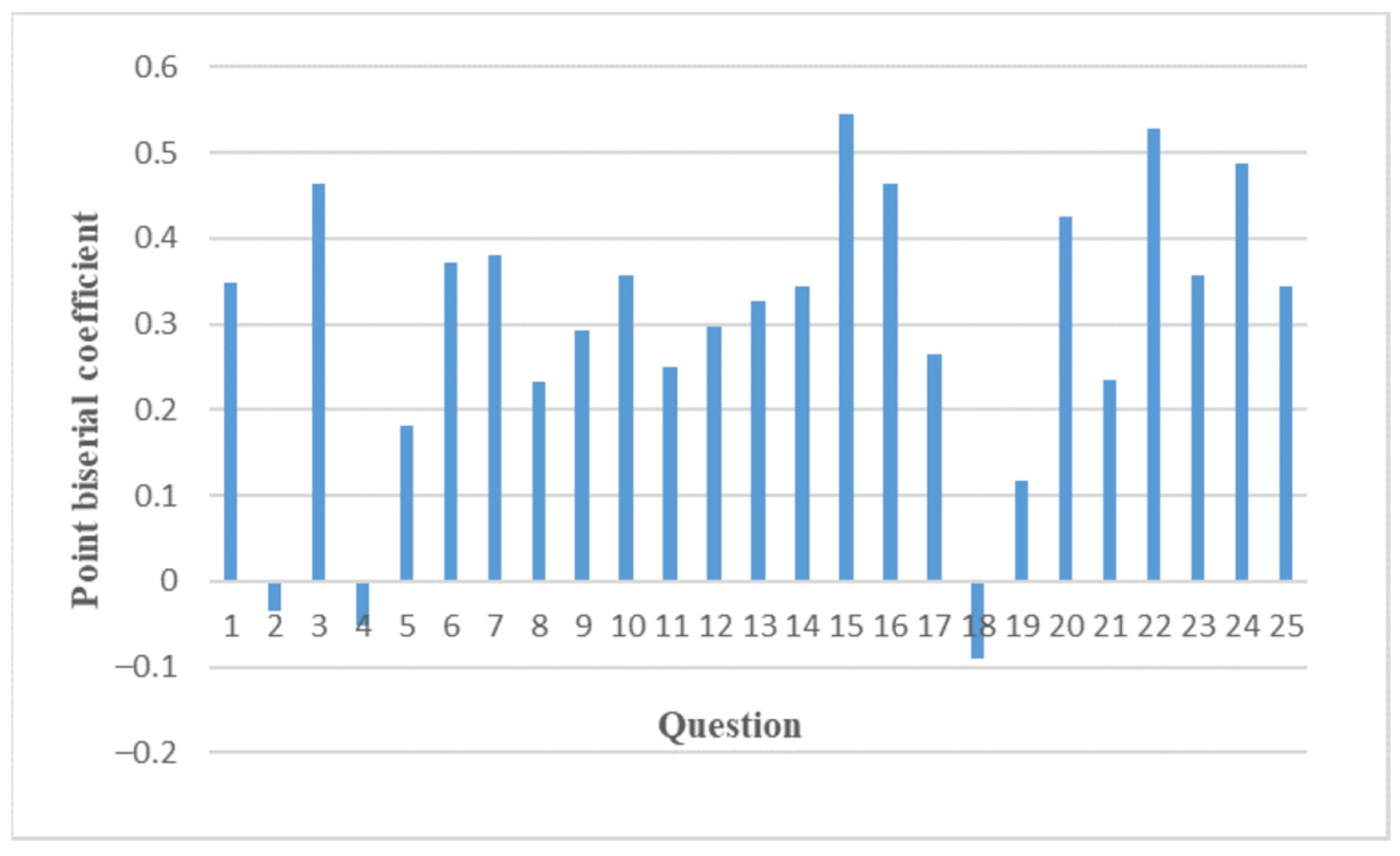
4.1. Reliability of the QPCS Test
4.1.1. Reliability of the Test within the Croatian Education System
4.1.2. Reliability of the Test in Three Different Educational Systems
4.2. Analysis of the Results by Topic
4.2.1. Croatian Sample
4.2.2. Comparison with Previously Published Results
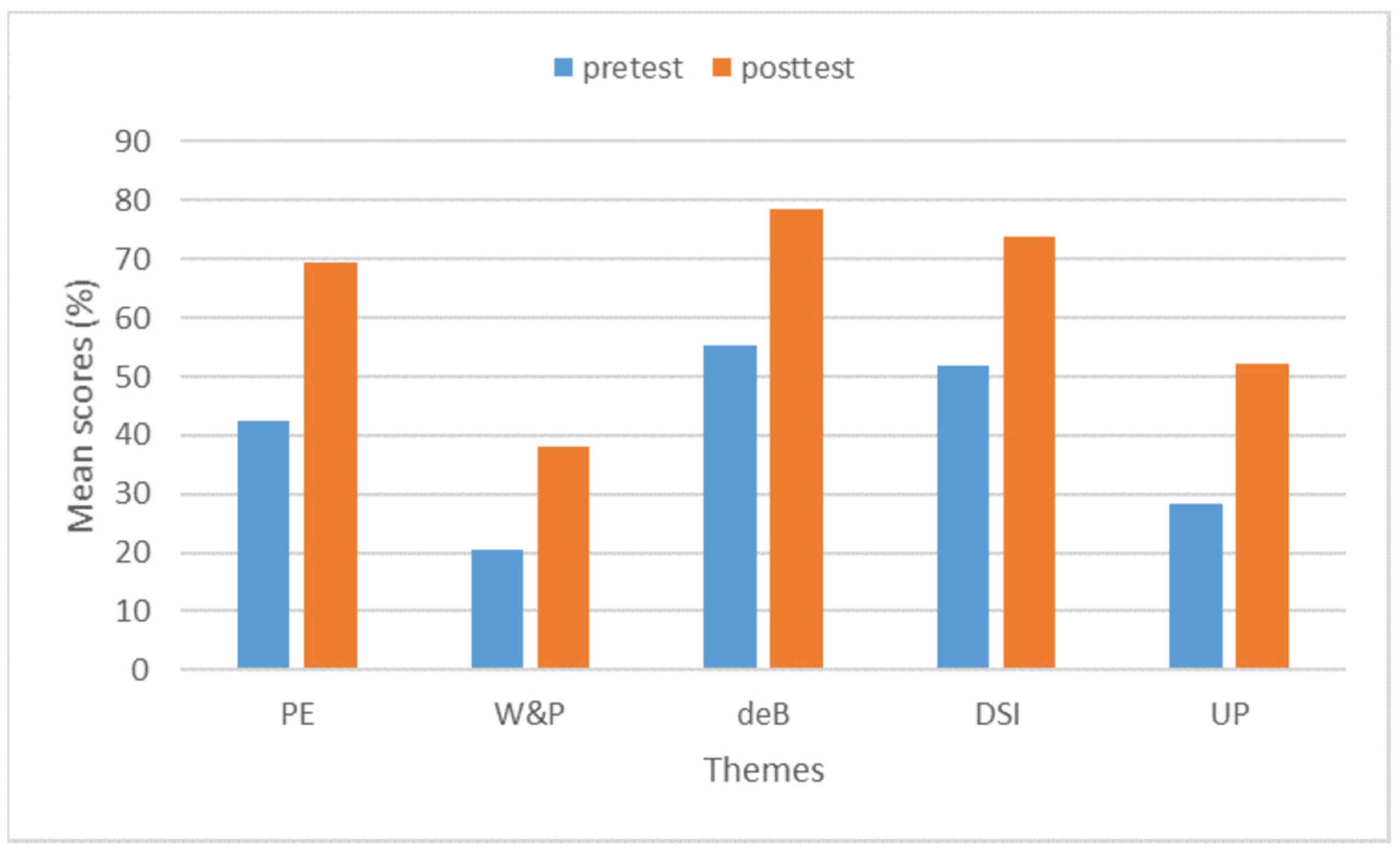
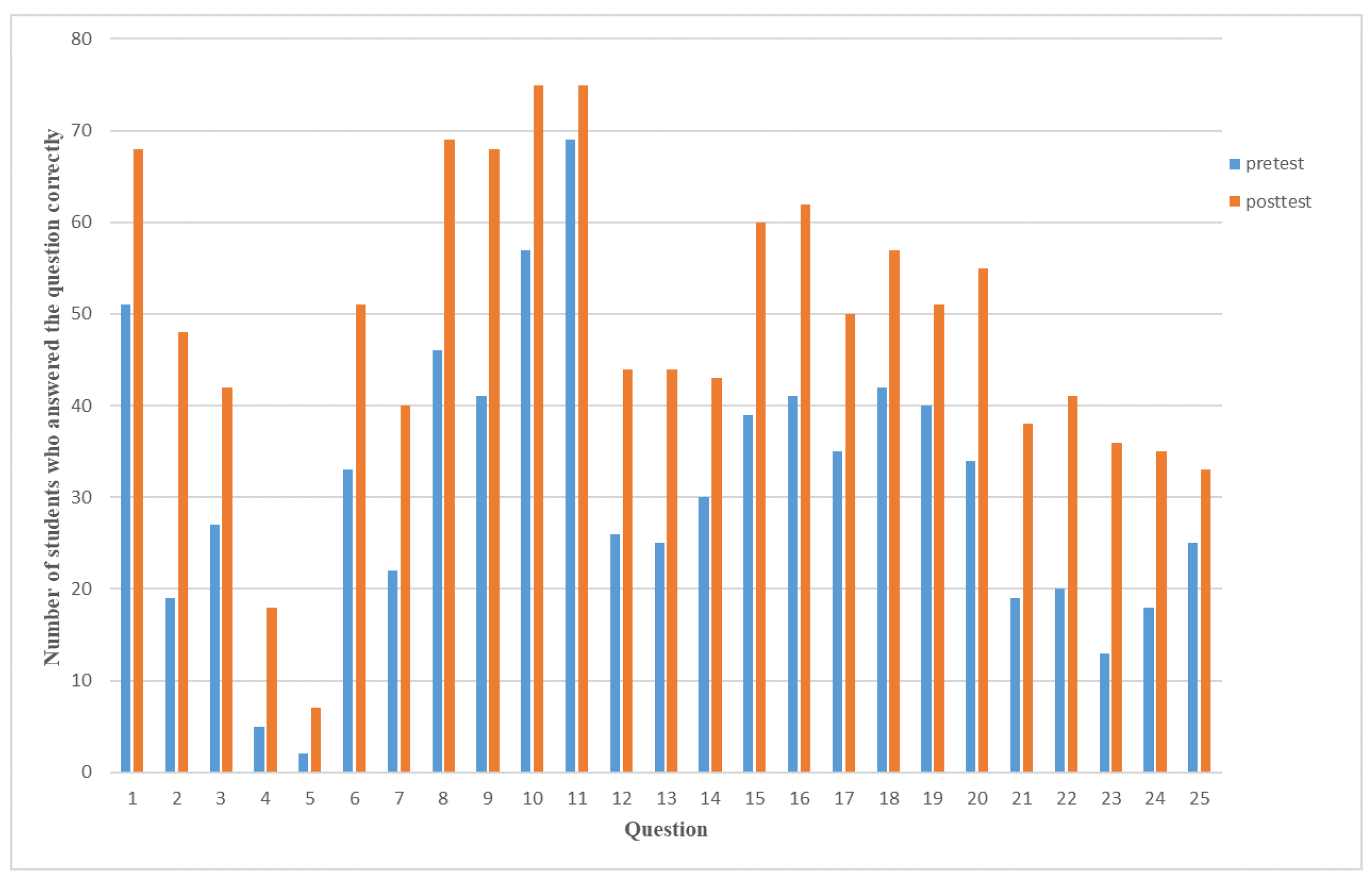
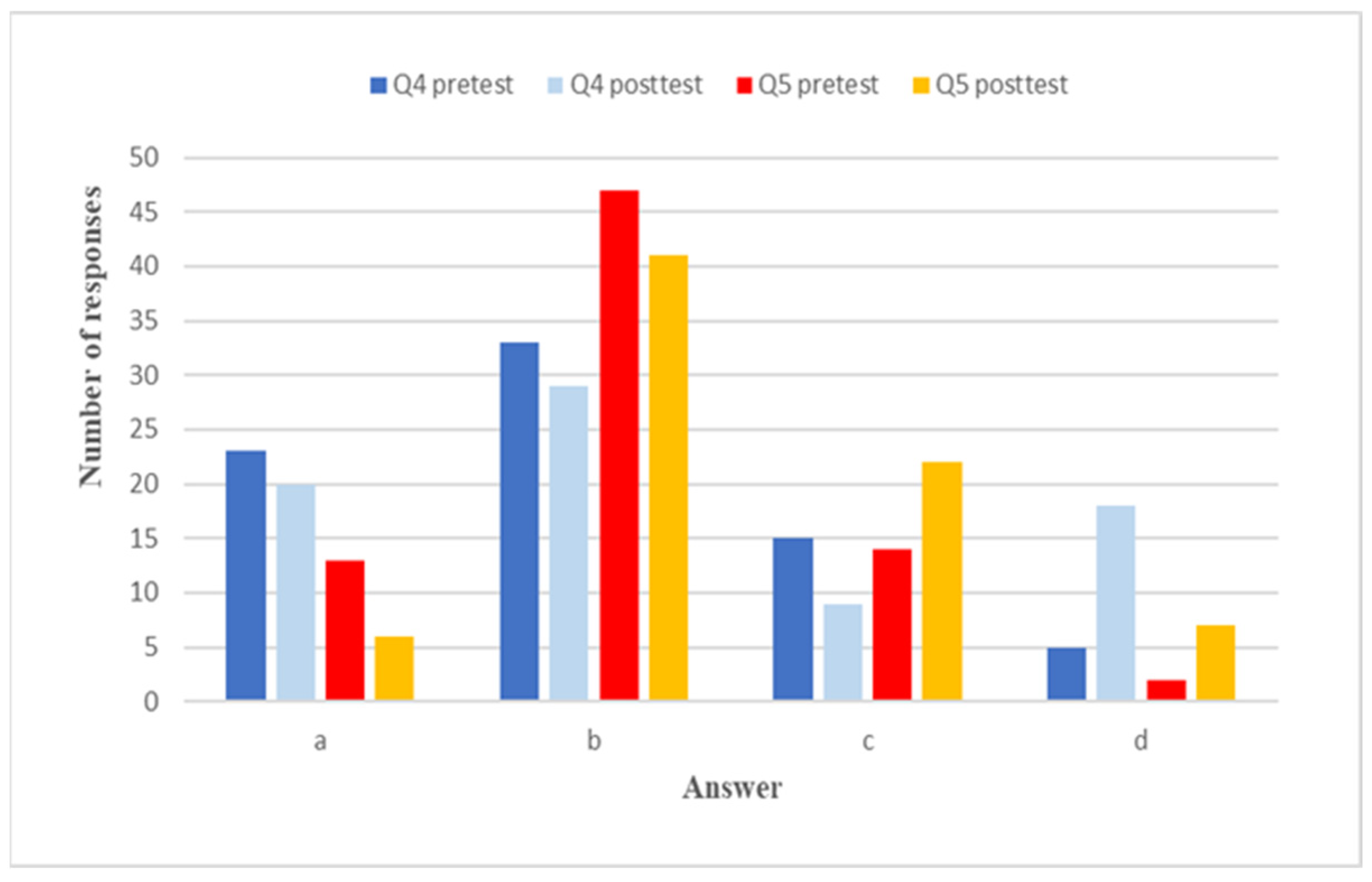
4.3. Comparison of Pretest and Posttest Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- Quantum Physics Conceptual Survey (QPCS)

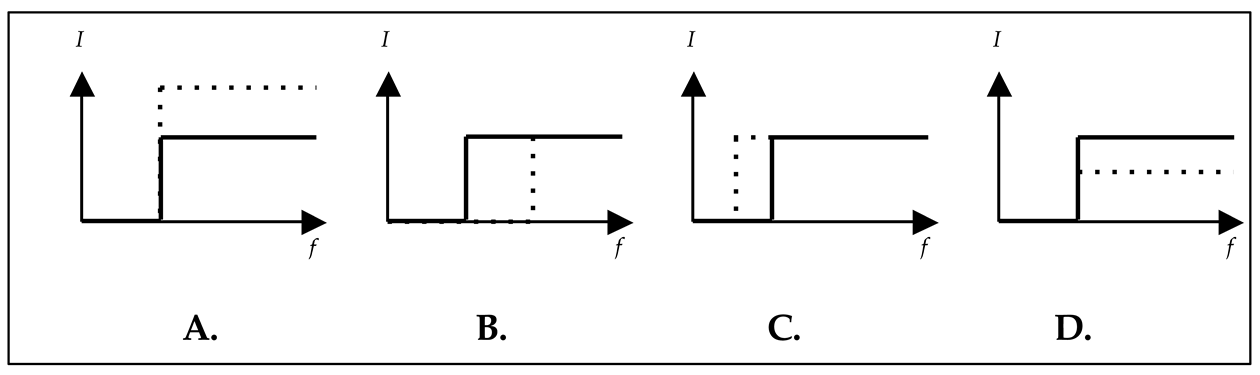
- 3.
- In an experiment to demonstrate the photoelectric effect the following observations are made:
- light of high frequency shone onto some materials causes electrons to be ejected; and
- if the frequency of light is decreased (with any amplitude) there is a cut-off frequency below which electrons are no longer ejected. These observations are believed to support a particle theory of light, rather than a wave theory. Which one of the statements is inconsistent with the observations?
- In particle theory, ejection of electrons is explained by collisions with photons. Each collision can give a single electron enough energy to escape.
- In a wave theory, ejection of electrons is explained by the electromagnetic wave causing the electrons to vibrate, which gives some electrons enough energy to escape.
- In a particle theory, the cut-off is explained because at very low frequencies the photons have very low energies and no individual photon has enough energy to eject an electron.
- In a wave theory, the cut-off is explained because a very low-frequency wave could not make the electrons vibrate energetically enough, even at very high amplitudes.
- In one experiment electrons are traveling from a source to a detecting screen.
- In a second experiment light is traveling from a source to a photographic plate.
- It is behaving like a particle.
- It is behaving like a wave.
- It is behaving like both a particle and a wave.
- You cannot tell if it is behaving like a particle or a wave.
- The de Broglie wavelength of the particle will increase.
- The de Broglie wavelength of the particle will decrease.
- The de Broglie wavelength of the particle will remain the same.

- The de Broglie wavelength of the particle will increase.
- The de Broglie wavelength of the particle will decrease.
- The de Broglie wavelength of the particle will remain the same.
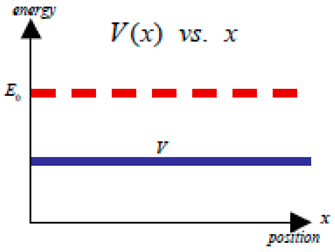

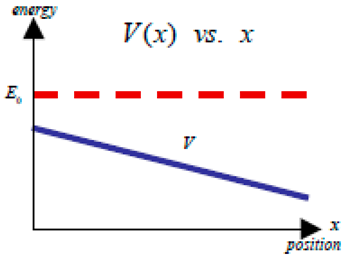
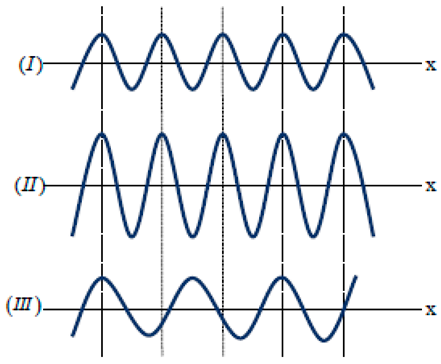
- vII > vI > vIII
- vII > vIII > vI
- vI = vII > vIII
- vII > vI = vIII


- 20.
- According to the uncertainty principle, the more we know about an electron’s position, the less we know about its,
- speed.
- momentum.
- kinetic energy.
- all of these.
- 21.
- Choose the answer A through D which is most appropriate answer according to the standard (Copenhagen) interpretation of quantum mechanics?The Heisenberg Uncertainty Principle is mostly applied to very small objects such as electrons and protons. Why don’t we use the uncertainty relation on larger objects such as cars and tennis balls?
- The errors of measurement can always, in principle, be made smaller by using more sensitive equipment.
- Large objects at any instant of time have an exact position and exact momentum and with sufficient care we can measure both precisely.
- Large objects obey Newton’s laws of motion, to which the uncertainty principle does not apply.
- Because it does apply to large objects, but the uncertainties are so small that we don’t notice them.
- Poorly defined position, well defined wavelength
- Well defined position, poorly defined wavelength
- Well defined position, well defined wavelength
- Poorly defined position, poorly defined wavelength



- It is, in principle, possible to measure which slit an electron went through and still see a multiple fringe pattern, if the technology is sophisticated enough.
- Each electron must have gone through one slit or the other, but it is impossible to measure which slit any one particular electron went through.
- It is possible to measure which slit an electron went through, but if you make this measurement, the beam of electrons will no longer form the multiple fringe pattern on the screen.
References
- Michelini, M.; Santi, L.; Stefanel, A. Research Based Proposals to Build Modern Physics Way of Thinking in Secondary Students. In New Learning Environments and Methods in Physics Education; Király, A., Tél, T., Eds.; Eötvös Loránd University: Budapest, Hungary, 2017; pp. 331–349. [Google Scholar]
- Michelini, M. Approaching the theory of quantum mechanics: The first steps towards a coherent synthesized interpretation with a supporting formalism. In Frontiers of Physics Education; Jurdana-Sepic, R., Labinac, V., Zuvic-Butorac, M., Susac, A., Eds.; Zlatni: Rijeka, Croatia, 2008; pp. 93–101. [Google Scholar]
- Bondani, M.; Chiofalo, M.L.; Ercolessi, E.; Macchiavello, C.; Malgieri, M.; Michelini, M.; Mishina, O.; Onorato, P.; Pallotta, F.; Satanassi, S.; et al. Introducing Quantum Technologies at Secondary School Level: Challenges and Potential Impact of an Online Extracurricular Course. Physics 2022, 4, 1150–1167. [Google Scholar] [CrossRef]
- Stadermann, H.K.E.; Van Den Berg, E.; Goedhart, M.J. Analysis of secondary school quantum physics curricula of 15 different countries: Different perspectives on a challenging topic. Phys. Rev. Phys. Educ. Res. 2019, 15, 010130. [Google Scholar] [CrossRef]
- Singh, C.; Marshman, E. Review of Student Difficulties in Upper-Level Quantum Mechanics. Phys. Rev. Spec. Top.-Phys. Educ. Res. 2015, 11, 020117. [Google Scholar] [CrossRef]
- Bouchée, T.; de Putter-Smits, L.; Thurlings, M.; Pepin, B. Towards a Better Understanding of Conceptual Difficulties in Introductory Quantum Physics Courses. Stud. Sci. Educ. 2022, 58, 183–202. [Google Scholar] [CrossRef]
- Bao, L.; Redish, E.F. Understanding Probabilistic Interpretations of Physical Systems: A Prerequisite to Learning Quantum Physics. Am. J. Phys. 2002, 70, 210–217. [Google Scholar] [CrossRef]
- Bøe, M.V.; Viefers, S. Secondary and University Students’ Descriptions of Quantum Uncertainty and the Wave Nature of Quantum Particles. Sci. Educ. 2023, 32, 297–326. [Google Scholar] [CrossRef]
- Tarng, W.; Pei, M.-C. Application of Virtual Reality in Learning Quantum Mechanics. Appl. Sci. 2023, 13, 10618. [Google Scholar] [CrossRef]
- Didiş, N. The analysis of analogy use in the teaching of introductory quantum theory. Chem. Educ. Res. Pract. 2015, 16, 355–376. [Google Scholar] [CrossRef]
- Erol, M.; Özdemir, E. Teaching uncertainty principle by hybrid approach: Single slit diffraction experiment. Lat. Am. J. Phys. 2010, 4, 473–480. [Google Scholar]
- Greca, I.M.; Freire, O. Teaching introductory quantum physics and chemistry: Caveats from the history of science and science teaching to the training of modern chemists. Chem. Educ. Res. Pract. 2014, 15, 286–296. [Google Scholar] [CrossRef]
- Michelini, M.; Santi, L.; Stefanel, A. Teaching Modern Physics in Secondary School. In Proceedings of the Frontiers of Fundamental Physics 14—PoS(FFP14); Sissa Medialab: Trieste, Italy, 2016. [Google Scholar]
- Michelini, M.; Pospiech, G.; Faletič, S.; Stefanel, A. GIREP Community on Teaching/Learning Quantum Physics in Secondary School. J. Phys. Conf. Ser. 2021, 1929, 012044. [Google Scholar] [CrossRef]
- Michelini, M.; Faletic, S.; Pospiech, G. Work Group 3 Position Paper: Teacher Education and Teaching/Learning Quantum Physics. J. Phys. Conf. Ser. 2022, 2297, 012015. [Google Scholar] [CrossRef]
- Cataloglu, E.; Robinett, R.W. Testing the development of student conceptual and visualization understanding in quantum mechanics through the undergraduate career. Am. J. Phys. 2002, 70, 238–251. [Google Scholar] [CrossRef]
- Kohnle, A.; Baily, C.; Hooley, C.; Torrance, B. Optimization of Simulations and Activities for a New Introductory Quantum Mechanics Curriculum. In Proceedings of the Physics Education Research Conference, Portland, ON, USA, 17–18 July 2013; pp. 209–212. [Google Scholar] [CrossRef]
- Henriksen, E.K.; Bungum, B.; Angell, C.; Tellefsen, C.W.; Frågåt, T.; Bøe, M.V. Relativity, quantum physics and philosophy in the upper secondary curriculum: Challenges, opportunities and proposed approaches. Phys. Educ. 2014, 49, 678–684. [Google Scholar] [CrossRef]
- Mashhadi, A.; Woolnough, B. Insights into students’ understanding of quantum physics: Visualizing quantum entities. Eur. J. Phys. 1999, 20, 511–516. [Google Scholar] [CrossRef]
- Müller, R.; Wiesner, H. Teaching quantum mechanics on an introductory level. Am. J. Phys. 2002, 70, 200–209. [Google Scholar] [CrossRef]
- Michelini, M.; Ragazzon, R.; Santi, L.; Stefanel, A. Proposal for quantum physics in secondary school. Phys. Educ. 2000, 35, 406–410. [Google Scholar] [CrossRef]
- Escalada, L.T.; Rebello, N.S.; Zollman, D.A. Student explorations of quantum effects in LEDs and luminescent devices. Phys. Teach. 2004, 42, 173–179. [Google Scholar] [CrossRef]
- Hoekzema, D.; Van Den Berg, E.; Schooten, G.; Van Dijk, L. The particle/wave-in-a-box model in Dutch secondary schools. Phys. Educ. 2007, 42, 391–398. [Google Scholar] [CrossRef]
- Lautesse, P.; Valls, A.V.; Ferlin, F.; Héraud, J.-L.; Chabot, H. Teaching Quantum Physics in Upper Secondary School in France. Sci. Educ. 2015, 24, 937–955. [Google Scholar] [CrossRef]
- Swarnkar, S.; Roy, R.; Kaur, T.; Blair, D. On the effectiveness of the early introduction of modern physics in school curriculum: The case of the structure of atom versus wave-particle duality. arXiv 2023, arXiv:2311.16525. [Google Scholar] [CrossRef]
- Bungum, B.; Henriksen, E.K.; Angell, C.; Tellefsen, C.W.; Bøe, M.V. ReleQuant—Improving teaching and learning in quantum physics through educational design research. Nord. Stud. Sci. Educ. 2015, 11, 153–168. [Google Scholar] [CrossRef]
- Ministry of Science and Education Croatia. Kurikulum Nastavnog Predmeta Fizika za Osnovne Škole i Gimnazije. Official Gazette Croatia, 2019, NN 10/2019. Available online: https://narodne-novine.nn.hr/clanci/sluzbeni/2019_01_10_210.html (accessed on 15 June 2024).
- Velentzas, A.; Halkia, K. The Use of Thought Experiments in Teaching Physics to Upper Secondary-Level Students: Two examples from the theory of relativity. Int. J. Sci. Educ. 2013, 35, 3026–3049. [Google Scholar] [CrossRef]
- Krijtenburg-Lewerissa, K.; Pol, H.J.; Brinkman, A.; Van Joolingen, W.R. Insights into teaching quantum mechanics in secondary and lower undergraduate education. Phys. Rev. Phys. Educ. Res. 2017, 13, 010109. [Google Scholar] [CrossRef]
- Asikainen, M.A.; Hirvonen, P.E. Probing pre- and in-service physics teachers’ knowledge using the Double-Slit Thought Experiment. Sci. Educ. 2014, 23, 1811–1833. [Google Scholar] [CrossRef]
- Reiner, M.; Burko, L.M. On the limitations of thought experiments in physics and the consequences for physics education. Sci. Educ. 2003, 12, 365–385. [Google Scholar] [CrossRef]
- Hestenes, D.; Wells, M.; Swackhamer, G. Force concept inventory. Phys. Teach. 1992, 30, 141–158. [Google Scholar] [CrossRef]
- Goldhaber, S.; Pollock, S.; Dubson, M.; Beale, P.; Perkins, K.; Sabella, M.; Henderson, C.; Singh, C. Transforming Upper-Division Quantum Mechanics: Learning goals and assessment. AIP Conf. Proc. 2009, 1179, 145–148. [Google Scholar] [CrossRef]
- McKagan, S.B. Exploring Student Understanding of Energy through the Quantum Mechanics Conceptual Survey. AIP Conf. Proc. 2006, 818, 65–68. [Google Scholar] [CrossRef]
- Baily, C.; Finkelstein, N.D. Teaching and understanding of quantum interpretations in modern physics courses. Phys. Rev. Spec. Top.-Phys. Educ. Res. 2010, 6, 010101. [Google Scholar] [CrossRef]
- Singh, C.; Belloni, M.; Christian, W. Improving students’ understanding of quantum mechanics. Phys. Today 2006, 59, 43–49. [Google Scholar] [CrossRef]
- Johnston, I.D.; Crawford, K.; Fletcher, P.R. Student difficulties in learning quantum mechanics. Int. J. Sci. Educ. 1998, 20, 427–446. [Google Scholar] [CrossRef]
- Olsen, R.V. Introducing quantum mechanics in the upper secondary school: A study in Norway. Int. J. Sci. Educ. 2002, 24, 565–574. [Google Scholar] [CrossRef]
- Cheong, Y.W.; Song, J. Different levels of the meaning of Wave-Particle duality and a suspensive perspective on the interpretation of quantum theory. Sci. Educ. 2013, 23, 1011–1030. [Google Scholar] [CrossRef]
- Singh, C. Interactive learning tutorials on quantum mechanics. Am. J. Phys. 2008, 76, 400–405. [Google Scholar] [CrossRef]
- Larkin, T.L.; Meade, P.; Uscinski, J. Probing a deeper understanding of modern physics concepts. In Proceedings of the 2011 Frontiers in Education Conference (FIE), Rapid City, SD, USA, 12–15 October 2011. [Google Scholar] [CrossRef]
- Nikolaus, P.; Dželalija, M. Understanding of Modern physics concepts at Croatian State matura. In Proceedings of the ICERI Proceedings, Online, 8–9 November 2021. [Google Scholar] [CrossRef]
- PhysPort. Assessments-Quantum Physics Conceptual Survey. Available online: https://www.physport.org/assessments/assessment.cfm?A=QPCS (accessed on 15 June 2024).
- Wuttiprom, S.; Sharma, M.D.; Johnston, I.D.; Chitaree, R.; Soankwan, C. Development and use of a conceptual survey in introductory quantum physics. Int. J. Sci. Educ. 2009, 31, 631–654. [Google Scholar] [CrossRef]
- Engelhardt, P. An introduction to classical test theory as applied to conceptual multiple-choice tests. In Getting Started in PER; Henderson, C.R., Harper, K.A., Eds.; American Association of Physics Teachers: College Park, MD, USA, 2009; Volume 2, Available online: https://www.per-central.org/items/detail.cfm?ID=8807 (accessed on 15 June 2024).
- Asikainen, M.A. Probing University Students’ Pre-Knowledge in Quantum Physics with QPCS Survey. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 1615–1632. [Google Scholar] [CrossRef][Green Version]
- Hake, R.R. Interactive-engagement versus traditional methods: A six-thousand-student survey of mechanics test data for introductory physics courses. Am. J. Phys. 1998, 66, 64–74. [Google Scholar] [CrossRef]
- Quantum Composer. Available online: https://www.quatomic.com/composer/ (accessed on 15 June 2024).
- Quantum Technology Education (Qtedu). Available online: https://qtedu.eu/ (accessed on 15 June 2024).
- Singh, C. Student Understanding of Quantum Mechanics at the Beginning of Graduate Instruction. Am. J. Phys. 2008, 76, 277–287. [Google Scholar] [CrossRef]
- McDermott, L.C.; Redish, E.F. Resource Letter PER-1: Physics Education Research. Am. J. Phys. 1999, 67, 755–767. [Google Scholar] [CrossRef]
- Wuttiprom, S.; Chitaree, R.; Soankwan, C.; Sharma, M.D.; Johnston, I.D. Developing a Prototype Conceptual Survey in Fundamental Quantum Physics; UniServe Science: Sydney, Australia, 2006; pp. 133–138. [Google Scholar]




| Test | Modern/Quantum Content Knowledge |
|---|---|
| Quantum Mechanics Concept Assessment (QMCA) (https://www.physport.org/assessments/assessment.cfm?A=QMCA, accessed on 13 June 2024) | wave functions, measurement, time dependence, probability, infinite square well, 1D tunnelling, energy levels, spins |
| Quantum Mechanics Conceptual Survey (QMCS) (https://www.physport.org/assessments/assessment.cfm?A=QMCS, accessed on 13 June 2024) | wave functions, probability, wave-particle duality, uncertainty principle, infinite square well, one-dimensional tunnelling, energy levels |
| Quantum Mechanics Formalism and Postulates Survey (QMFPS) (https://www.physport.org/assessments/assessment.cfm?A=QMFPS, accessed on 13 June 2024) | quantum mechanics formalism, quantum mechanics postulates |
| Quantum Mechanics Survey (QMS) (https://www.physport.org/assessments/assessment.cfm?A=QMS, accessed on 13 June 2024) | wave functions, measurement, expectation values, Hamiltonian, time dependence, probability, infinite square well, finite square well, harmonic oscillator, 1D tunnelling |
| Quantum Physics Conceptual Survey (QPCS) (https://www.physport.org/assessments/assessment.cfm?A=QPCS, accessed on 13 June 2024) | de Broglie wavelength, double-slit interference, uncertainty principle, photoelectric effect, wave-particle duality |
| Quantum Mechanics Visualization Instrument (QMVI) (https://www.physport.org/assessments/assessment.cfm?A=QMVI, accessed on 13 June 2024) | wave functions, probability, infinite square well, 1D tunnelling, time dependence, momentum space, 2D potentials, visualization of the relationship between potentials and wave functions |
| Quantum Mechanics Assessment Tool (QMAT) (https://www.physport.org/assessments/assessment.cfm?A=QMAT, accessed on 13 June 2024) | wave functions, measurement, time dependence, probability, infinite square well, 1D tunnelling, energy levels |
| Quantum Mechanics Concept Inventory (QMCI) (https://www.physport.org/assessments/assessment.cfm?A=QMCI, accessed on 13 June 2024) | wave functions, probability, 1D tunnelling |
| Learning Outcomes | Elaboration of Learning Outcomes |
|---|---|
| Analyses the wave-particle model of light and matter |
|
| Analyses atom models and energy spectra |
|
| Explains the model of the atomic nucleus and nuclear reactions |
|
| Analyses radioactive decay and describes the effects of ionizing radiation on living organisms |
|
| Describes and applies the basic ideas of STR |
|
| Theme | Question |
|---|---|
| Photoelectric effect | 1–3 |
| Waves and particles | 4–7 |
| de Broglie wavelength | 8–14 |
| Double-slit interference | 15–19 |
| Uncertainty principle | 20–25 |
| Question | Item Difficulty Index | Item Discrimination Index | Item Point Biserial Coefficient |
|---|---|---|---|
| 1 | |||
| 2 | X | X | X |
| 3 | |||
| 4 | X | X | X |
| 5 | X | X | X |
| 6 | |||
| 7 | X | ||
| 8 | X | ||
| 9 | X | ||
| 10 | |||
| 11 | X | X | |
| 12 | X | ||
| 13 | X | ||
| 14 | |||
| 15 | |||
| 16 | |||
| 17 | X | ||
| 18 | X | X | |
| 19 | X | X | |
| 20 | |||
| 21 | X | X | |
| 22 | X | ||
| 23 | X | ||
| 24 | X | ||
| 25 |
| Test Statistic | Possible Value | Desired Value | Croatian Sample | Original Sample (First Year Student) | Finnish Sample | ||
|---|---|---|---|---|---|---|---|
| Pretest (n = 76) | Posttest (n = 76) | Pretest (n = 95) | Posttest (n = 56) | Pretest (n = 103) | |||
| Item difficulty index | 0 to 1 | ≥0.3 | 0.41 1 | 0.64 1 | 0.46 1 | 0.61 1 | 0.46 1 |
| Item discrimination index | −1 to 1 | ≥0.3 | 0.33 1 | 0.30 1 | 0.33 1 | 0.32 1 | 0.34 1 |
| Point biserial coefficient | −1 to 1 | ≥0.2 | 0.30 1 | 0.27 1 | 0.16 1 | 0.17 1 | 0.19 1 |
| KR-21 reliability test | 0 to 1 | ≥0.7 | 0.50 | 0.53 | 0.74 | 0.79 | 0.49 |
| Ferguson’s delta | 0 to 1 | ≥0.9 | 0.94 | 0.93 | 0.94 | 0.93 | / |
| Theme | Photoelectric Effect | Waves and Particles | de Broglie Wavelength | Double-Slit Interference | Uncertainty Principle | Overall |
|---|---|---|---|---|---|---|
| Croatian student’s | 0.39 | 0.20 | 0.44 | 0.43 | 0.32 | 0.39 |
| Australian first year student’s | 0.27 | 0.02 | 0.17 | 0.33 | 0.42 | 0.23 |
| Mean Score and Standard Deviation (%) | |||
|---|---|---|---|
| Theme | Croatian Sample | Finnish Sample | Original Sample |
| Overall | 41.0 ± 13.7 | 45.9 ± 13.6 | 45.9 ± 12.8 |
| Photoelectric effect | 43 | 40 | 50 |
| Waves and particles | 20 | 20 | 23 |
| de Broglie wavelength | 55 | 43 | 54 |
| Double-slit interference | 52 | 63 | 56 |
| Uncertainty principle | 28 | 42 | 38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikolaus, P.; Dželalija, M.; Weber, I. Investigating Students’ Conceptual Knowledge of Quantum Physics to Improve the Teaching and Learning Process. Educ. Sci. 2024, 14, 1113. https://doi.org/10.3390/educsci14101113
Nikolaus P, Dželalija M, Weber I. Investigating Students’ Conceptual Knowledge of Quantum Physics to Improve the Teaching and Learning Process. Education Sciences. 2024; 14(10):1113. https://doi.org/10.3390/educsci14101113
Chicago/Turabian StyleNikolaus, Patricija, Mile Dželalija, and Ivana Weber. 2024. "Investigating Students’ Conceptual Knowledge of Quantum Physics to Improve the Teaching and Learning Process" Education Sciences 14, no. 10: 1113. https://doi.org/10.3390/educsci14101113
APA StyleNikolaus, P., Dželalija, M., & Weber, I. (2024). Investigating Students’ Conceptual Knowledge of Quantum Physics to Improve the Teaching and Learning Process. Education Sciences, 14(10), 1113. https://doi.org/10.3390/educsci14101113






