Abstract
The science education literature is littered with “new”, “correct”, “novel”, “explanations”, “theories”, and “approaches” to aerodynamic lift. One might infer from reading the growing number of these articles that there is a fundamental gap in classical physics, where our scientific prowess has failed us. In fact, if you read popular sources, you would believe “no one can explain why planes stay in the air”. This is a disconcerting thought to have while sitting inside a modern engineering marvel provided by Boeing or Airbus. However, rationally, since you are sat in that fuel-efficient and safe aeronautical wonder, the logical conclusion is that some are obviously aware of why planes stay in the air. In this paper, a century of educational literature on the topic of aerodynamic lift and flight is presented. The body of literature encompasses 140 articles, commencing in 1920. It is obvious from the content contained within them that there is more of a misunderstanding rather than an understanding of flight in the education context. There are two paradigms treated as mutually exclusive: those using Bernoulli and those using Newton. Throughout the literature, there are gems lost in the rubble; if the reader does not have an understanding, how will they know what is worth reading? This review attempts to clarify what is worth reading, by presenting a qualitative overview of aerodynamics education in undergraduate engineering, to understand why these opposing camps exist in the literature.
Keywords:
aerodynamics; aeronautics; engineering education; flight; flight mechanics; physics education; STEM 1. Introduction
On the topic of aerodynamics, there are what should be described as classic texts that form the foundation of our collective knowledge [1,2,3,4]. Bloor [5] reviews some early aerodynamics from 1909 to 1930, with the first half of the 20th century reviewed in more detail by Goldstein [6]. For an even larger historical overview of aerodynamics, see Anderson [7]. These previous reviews establish that the fundamental knowledge of lift was well developed in the early 1900s. This followed a period of confusion from D’Alembert and Euler in the mid-18th century to the late-19th century, an aerodynamic dark age [8]. However, in this work, the review is limited to the education literature on lift and flight.
The aim of this work is to review the educational literature on aerodynamic lift and flight. The intent is to present all of the arguments used, such that if there are flaws, they can be understood, and any shortcomings can be explained. The term aerodynamic lift, the force generated by an airfoil or a wing, will be referred to as lift. A detailed search of the literature was conducted, through Google Scholar, Scopus, JSTOR, and publishers’ databases (Science Direct, Taylor and Francis, etc.). In Google Scholar, the “Cited by” link for every collected reference was searched, as was their reference list. This provided confidence that the population of education literature on lift and flight mechanics is limited to the 140 articles found, up to and including 2022. The structure of this article is as follows; first, the background section will give a qualitative introduction to the topic of fluids and lift in the context of aerodynamics education for undergraduate engineering. After that, some common features from the literature are introduced. This is followed by the literature review presented in chronological order, with some grouping used to reduce repetition. Finally, summaries of the theories are provided, noting that the key underpinning knowledge about how wings work is given in the background, and the criticism of erroneous points and misconceptions is provided along with the review.
2. Background
2.1. Fundamentals
2.1.1. Fluids
Fluids include both gases and liquids. What differentiates a fluid from a solid is its response to a shearing force. If you take a thick book and you shear it by applying a force to the front cover, you obtain a shear strain. That is, the book’s cross-section deforms from a rectangle to a parallelogram (shown in Figure 1a). However, if you shear a fluid, the amount of deformation continues at a constant rate dictated by the viscosity of the fluid (shown in Figure 1b). That is, a fluid flows in response to a shearing force, unlike a solid.

Figure 1.
The difference between a solid (a) and a fluid (b) is what happens in response to an applied shear stress, τ. (a) For a solid, the result is a shear strain corresponding to a displacement as a function of height, d. (b) For a fluid, the result is a shear rate, which is a velocity that is a function of height, u.
Viscosity is a complex property that is not fully understood [9]. It can basically be thought of as the attractive force that exists between fluid elements, and it is a manifestation of intermolecular attraction [10]. As noted in the definition of a fluid, viscosity is a fundamental property that encapsulates friction in fluids, such as drag. The more viscous a fluid, the slower the shearing rate for a given applied force, and, hence, the harder it is to move through the fluid or for the fluid to flow. Honey is used as a typical example, which has a high viscosity, relative to something like a mineral oil, commonly used as a lubricant. If we ignore viscosity, we call the resultant flow inviscid.
The mathematical study of fluids is called continuum mechanics. Here, the fluid is described as a single continuous substance. We know that fluids are made up of molecules. For example, water is made up of H2O molecules, and air is made up of N2, O2, and other molecules. However, the size of the molecules, and the distances between them, is insignificant relative to the dimensions of the fluid we are interested in. Hence, we accept the continuum hypothesis, and we do not consider free-molecule flow. In fluid mechanics, the relevant parameter is the Knudsen number, which is the ratio of two properties. The first is the mean free path, which is the average distance a molecule travels between collisions with neighboring molecules. The second is the representative length scale of the flow, which, for a wing, could be the cord length, wingspan, or thickness. If the object scale is much greater than the mean free path, then it is continuum flow. If the object is on the same scale as the mean free path, then it is free-molecule flow. In between the two is low-density flow, where one transitions into the other, and, hence, properties of both exist.
Another property of fluids to consider is if they are compressible or incompressible. For incompressible flow, the density of the fluid is constant. If, however, the density is not constant, then the flow is considered compressible. For relatively small slow aircraft, with airspeeds less than 100 m/s, we can assume air is incompressible. For large commercial jets, flying at faster speeds, the assumption that the density does not change is no longer valid; the air begins to compress as the aircraft flies through it. The important parameter here is the Mach number, which is the ratio of the speed of the flow to the speed of sound in the fluid. For an aircraft flying at around 100 m/s, this is approximately Mach 0.3, given that the speed of sound in air is 340 m/s.
Finally, we can consider fluids as being either laminar or turbulent. When people use the adjective streamlined, they are referring to smooth motion through a fluid. This is associated with laminar flow, where there are smooth continuous streamlines. In contrast, turbulent flow does not have nice, neat streamlines; they are chaotic on the smaller scale, while still having structure on the larger scale, for example, flowing in the same direction on average. A common example to illustrate laminar and turbulent flow is from a faucet. If you have a single transparent stream flowing from the tap, this is laminar flow; if you have a fuzzy, bubbly jet of water, it is turbulent flow. The parameter here is the Reynolds number, which is the ratio of the fluid’s inertial forces relative to the viscous forces. Very high Reynolds numbers (high inertial forces) correspond to turbulent flow, while very low Reynolds numbers (high viscous forces) correspond to laminar flow.
2.1.2. Bernoulli
There is a wealth of educational literature on Bernoulli. In fact, about half a dozen of the articles reviewed in Section 4 are just on Bernoulli, but they are linked to the lift literature as key references. There is a correct derivation of Bernoulli’s equation from Euler’s equation [11], while most, including physics textbooks, use a simplified version. Regardless, we are only interested in the resultant equation and only the version that links static and dynamic pressure. That is, we are not interested in head pressure, which is Pascal’s principle.
Bernoulli’s equation states that the work done on a fluid (or by a fluid) due to pressure forces is equal to the change in kinetic energy of the flow.
P1 + ½ρ u12 = P2 + ½ρ u22 = constant = PT,
Bernoulli’s equation then relates the pressure and velocity along a streamline; that is, P1 and u1 are related to P2 and u2 along the same streamline. The sum of these two components, the static pressure (P) and the dynamic pressure (q), is said to be constant along a streamline. In aeronautics, we call this constant the total pressure (PT). While this quantity is technically only conserved along a streamline, if we have irrotational flow, this is constant across all streamlines, and hence, constant throughout the flow, assuming the flow is inviscid, which is the case when using Euler’s equation.
Bernoulli’s principle is demonstrated perfectly by the venturi tube, shown in Figure 2. Inside the venturi tube, the air flows through both a converging and diverging section, where the cross-sectional area reduces and increases, respectively. For incompressible air flow, with speeds less than 100 m/s, the result is a decrease in static pressure and an increase in dynamic pressure (flow speed) through the converging section. This is followed by a reduction in dynamic pressure and an increase in static pressure through the diverging section. The typical textbook derivation of Bernoulli’s equation makes use of another important fluid mechanics concept, the continuity equation—specifically, the conservation of mass. Consider dropping 1 kg through a venturi; 1 kg must pass through both A1 and A2. If 1 kg per second is dropped through A1, 1 kg per second must also pass through A2. This is simply the mass per unit time, or the mass flow rate. Importantly, what was “dropped” was not stated, and many would imagine a rock, etc. However, since this is aeronautics, we care about the flow of air. So, the mass flow rate of air through each area needs to be constant. The mass can be converted to volume using density, giving a volume flow rate. Similarly, the areas are known, so the volumes can be converted to a product of area and length, giving a length flow rate. The concept of length per unit time (m/s) is a velocity, so we arrive at what Bernoulli tells us, that the velocity increases when the area is smaller. Figure 2 illustrates the main aspects of internal flow for a venturi tube.
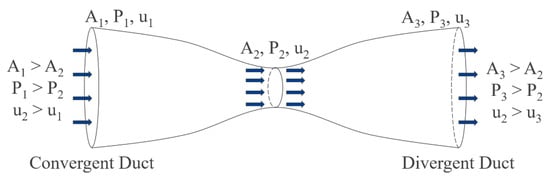
Figure 2.
Internal flow through a venturi tube, giving a reduction in pressure and an increase in velocity of the flow through the converging section and an increase in pressure and a reduction in velocity through the divergent section.
2.1.3. Coanda
The Coanda effect is the entrainment of stationary fluid into a jet of the same fluid moving within it. This results in a lower pressure around the jet, as the ambient fluid has experienced an increase in dynamic pressure and hence will have a lower static pressure. If this is near a constriction, such as a surface, there will be a pressure gradient across the jet towards the surface due to the lower pressure between the jet and the surface. That is, between the jet and the surface, the air is continuously entrained into the flow, rarefying that layer of air; this results in a flow from the ambient pressure inside the jet towards the lower pressure at the surface. Figure 3 shows an extreme example of a jet mixing with the air around it from the exhaust of an engine. Importantly, for an airfoil, there is no jet of air, and, hence, there is no entrainment, so the force noted for attaching the fluid to a surface is simply not present around an airfoil. That is, Coanda is not applicable to lift.
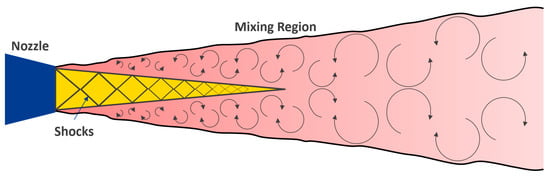
Figure 3.
The mixing of ambient air into a jet of fluid is an extreme example of entrainment.
2.1.4. Magnus
The Magnus effect is the additional force on a spinning ball [12], resulting in a curved or bent trajectory. This was originally studied by Robins [13] investigating the trajectories of spinning artillery shells. While this is an interesting feature of aerodynamics and has been studied for numerous sports, it is not applicable to lift generated by an airfoil.
2.2. Aerodynamics
While many great names in physics applied themselves to understanding the problem of aerodynamic forces [7], modern aerodynamics really begins with Prandtl [3]. Prior to Prandtl, viscosity was not included in aerodynamics, although there were attempts to capture its effects. The missing feature of viscosity, as first introduced by Navier and Stokes, was incorporated by Prandtl into the boundary layer, a critical element today, and a revolutionary idea that greatly simplified the governing equations. The boundary layer (literally a thin layer of air touching the wing’s surface in this context) is the only part of the fluid where viscosity needs to be considered (illustrated in Figure 4); outside the boundary layer, analytic solutions like those derived by D’Alembert and Euler can be used if the influence of the boundary layer is included. That is, if circulation and the Kutta condition are incorporated, these simple theories or models can calculate lift but not drag [14]. This leads to the modern aerodynamicist’s definition of how wings work—“a wing induces circulation in the air flow”—illustrated in Figure 5. As just described, the underlying physical mechanism for this circulation is the viscosity in the boundary layer; noting that flow without viscosity returns to the solutions of D’Alembert with no lift or drag, referred to as D’Alembert’s paradox [15].
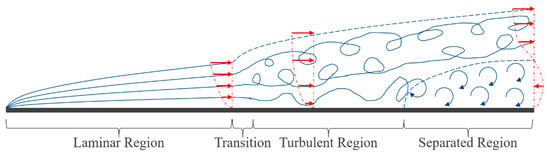
Figure 4.
The important features of a boundary layer: the flow starts laminar, then transitions to turbulent, and may separate. In the laminar and turbulent regions, the average velocity (red arrows) is positive (pointing right), while in the separated region, it is negative (pointing left). Importantly, at the surface, the flow velocity is zero (the speed of the surface), called the no-slip condition, and at the top of the boundary layer, the flow velocity is effectively equal to the freestream velocity.
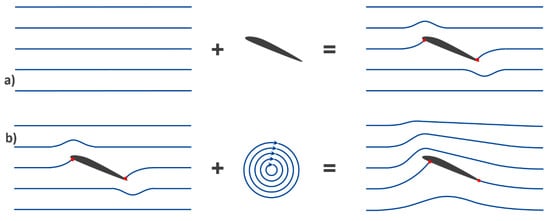
Figure 5.
(a) A uniform potential flow plus an airfoil gives a symmetric flow field that is non-lifting; (b) if just the right amount of circulation is added to the flow, it looks correct and hence is lifting.
While the modern aerodynamicist’s definition of lift is mathematically pleasing, it introduces a question that appears multiple times in the education literature. Does the induced circulation result in a “downwash” that is responsible for the lift force, or does it create a pressure difference that is responsible for the lift force? In other words, which paradigm of lift is correct, Newton’s 3rd Law (the air goes down so the wing goes up) or pressure difference (pressure above the wing is lower relative to the pressure below the wing)? The literature makes Bernoulli synonymous with a statement of pressure difference, even though it is not necessary. Similarly, some authors talk about Newton’s 3rd Law (action/reaction), and others talk about Newton’s 2nd Law (force equals the change in momentum), which, in this review, will be collectively referred to as Newton’s 3rd Law.
The ‘correct’ statement for aerodynamicists should be that “a wing induces circulation in the air flow due to viscosity resulting in a lower air pressure above the wing relative to below”. There are two points to discuss: the use of the word ‘correct’ and Bernoulli. As noted in Section 2.1.2, Bernoulli’s equation for energy along a streamline of a fluid can be derived from Euler’s equations of fluid motion [11], where the fluid is steady, incompressible, and inviscid, that is, not changing with time, having constant density, and having no viscosity, respectively. Outside the boundary layer, we assume the fluid is incompressible and inviscid; hence, Euler can be used to derive a potential flow solution if and only if circulation is added. The result of this is that Bernoulli is perfectly applicable outside the boundary layer. Furthermore, the boundary layer is said to be so thin that the pressure outside the boundary layer is equal to the pressure at the surface of the wing.
Bernoulli is wrongfully vilified because the cause-and-effect element needed to apply his equation is typically omitted, and, hence, he is left alone, simply noting a relationship between static pressure and flow speed. We know there is a difference in pressure, and Bernoulli tells us that a change in pressure corresponds to a change in flow speed. This leads the typical aviator to ask, where did the change in flow speed come from? Also, if there is a change in speed, does that come from a change in pressure? Then, did that change in pressure come from a change in speed? This gives the classic debate about the chicken or the egg. At this point, you are either preparing to debate or, maybe importantly, you remember the paragraph started with the word ‘correct’. Bernoulli can only be used because viscosity induces circulation. Circulation means the average speed above an airfoil relative to below is faster. Therefore, using Bernoulli, the average pressure above an airfoil relative to below is lower. Circulation is literally a rotation or vorticity in the fluid around an airfoil (shown in Figure 5b). The Kutta condition is intimately linked to this; Kutta noted that the amount of circulation needed is such that the rear stagnation point in D’Alembert’s solution (Figure 5a) is moved exactly to the sharp trailing edge of an airfoil, where it is observed in experiments. The stagnation points are illustrated as red dots in Figure 5, corresponding to the ends of streamlines, which terminate at the airfoil, such that all dynamic pressure is converted into static pressure.
At this point, you might think ‘eureka’, or you might be thinking about that other paradigm and that word ‘correct’ from before. There are two things: the ‘correct’, and then the other paradigm. Typically, aeronautical/aerospace engineering students will first learn about lift in a class that includes a wind tunnel experiment, ideally in their first year. In these experiments, they literally measure pressure. The standard off-the-shelf educational wind tunnel will provide you with the tunnel, a pressure-tapped airfoil, and a multi-manometer to measure pressures (shown in Figure 6). This pressure-tapped airfoil has tiny holes across the top and bottom surfaces, these each connect to one of the u-tube manometers, and the static pressure at a dozen points above and below can be recorded; the experiment usually involves varying the flow speed and the angle of attack. To be clear, most aerodynamicists have performed an experiment to calculate lift from pressure differences. To go one step further, in the same class, it is likely that the students have also looked up a coefficient of lift for NACA airfoils (the National Advisory Committee on Aeronautics, the precursor to NASA). Those data were measured in a wind tunnel as pressure differences [16]. The entire introduction to practical aerodynamics focuses on pressure first. Then, when armed with some college mathematics, in a second course on aerodynamics, students will use potential flow with circulation to calculate the coefficient of lift; some interpret this as a fundamental calculation of lift, an analytic solution, when, in fact, it is just a mathematical trick. In that same class, Prandtl and the boundary layer will also be covered, but the conceptual physics appears to be missed given that there is little appreciation for the physical mechanisms behind circulation.

Figure 6.
An educational wind tunnel showing an airfoil in the test section, with pipes taking the pressure distribution from around the airfoil to the multi-manometer above. Reproduced with permission from GDJ Inc. (gdjinc.com).
The ability to calculate the correct answer appears to become the defining feature of knowledge. All of that pressure difference knowledge and observations are replaced with a neat mathematical trick. Critically, the amount of circulation added is also an experimental observation, but this point is not stressed. Furthermore, the interrelationship between circulation and pressure should be apparent to the reader from above (see the “correct” aerodynamicist’s explanation). However, since pressure was not used in the circulation integral, it appears to have been displaced by the second paradigm of Newton’s 3rd Law. That is, the incorrect statement from aerodynamicists becomes “a wing induces circulation in the air flow which results in a downwash in the air behind the wing, and via Newton’s 3rd Law there is an upwards force on the wing”. Interestingly, at no point do these students calculate the downward momentum of the air; however, this is still the resultant interpretation. They are now calculating the integral of circulation, to determine the coefficient of lift, and the intimate relationship this has to the coefficient of the pressure integral they learnt first is lost; the link between them is Bernoulli. Furthermore, all of this is using 2D flow, in which there is technically no downwash. Downwash refers to the flow behind a wing that is accelerated down, which results due to wing tip effects. As such, this cannot happen in 2D flow, although there is a downward turning of the flow, where the flow from the trailing edge will flow down and back from the trailing edge, returning to horizontal as shown in Figure 5.
You may think that Newton’s Laws of Motion are fundamental, so that paradigm is superior. This is another misconception. In the education literature on lift, many authors refer to Newton’s Laws of Motion like fluid mechanists and aerodynamicists have missed the most fundamental physical principle. This is absurd. The Navier–Stokes equations are literally Newton’s Laws of Motion applied correctly to a fluid, including viscosity. They underpin many areas of study in fluids, including aerodynamics. The modern Airbus A350 and Boeing 787 were designed using Navier–Stokes. Force equals mass times acceleration, action/reaction, and inertia are all captured in Navier–Stokes. So, is saying it is ‘just’ Newton’s 3rd Law ‘correct’? The short answer is “no”, in the literal semantic sense. The long answer is “it is complicated”. If we return to the statement about NACA airfoil measurements in a wind tunnel, a piece of information was omitted; the pressure there, unlike in modern teaching labs, is not measured around the airfoil, but rather, it was measured along the top and bottom surfaces of the wind tunnel [16]. Thinking of Newton’s Laws, this should be perfectly reasonable; if there is a force on the airfoil that is directed upwards, there must be a restoring force equal and opposite since it is not accelerating. This is a pressure distribution on the surface of the tunnel, the thing measured by NACA. So internally, the force is balanced in the fluid. In fluid mechanics terms, if we create a control volume (the volume of fluid we want to analyze, like a free body diagram for a fluid), we note a pressure force at the airfoil that is balanced by the pressure force at the walls. This scenario and control volume are illustrated in the upper part of Figure 7. This is true of real aircraft and was presented by Prandtl [3] over a hundred years ago. The earth ultimately provides the restoring force that supports flying aircraft, though modern texts incorrectly dispute this [17]. That said, we can define a different control volume. Instead of looking at the entire test section, we can define the thinnest slice of the fluid, which is across the airfoil (the bottom of Figure 7). Here, we have upwards-turned flow into the control volume and downwards-turned flow out of the control volume, giving a difference in momentum. However, the top and bottom surfaces of the control volume still have a pressure component. So, there is clearly a momentum transfer across the airfoil; however, it can never equate to all of the lift force, and, hence, a statement purely on momentum transfer is not possible.
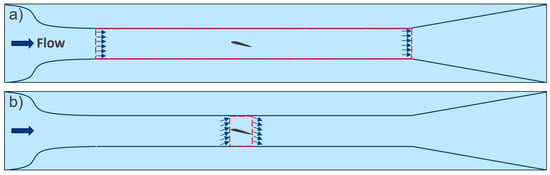
Figure 7.
Control volumes (dashed red boxes) around an airfoil in a wind tunnel. (a) A long control volume will result in the force being described as a pressure on the top and bottom surfaces, with horizontal flow in and out having negligible vertical momentum. (b) A truncated control volume will have vertical momentum up in, and down out, but some pressure on the top and bottom surfaces. Note this is not downwash, as the flow returns to horizontal.
Hopefully it is clear that a few statements about lift can be made. To repeat, it is possible to say, “a wing induces circulation in the air flow due to viscosity, resulting in a lower air pressure above the wing relative to below”. Given that pressure is the fundamental force, it is also possible to say, “due to viscosity, a wing has an asymmetric pressure distribution around it, with lower air pressure above the wing relative to below”. Those statements need no reference to momentum, nor do they need a reference to Bernoulli. Writing a statement that includes momentum needs a conditional statement. Referring directly to Prandtl [3], we have (p. 177):
the resulting impulse is directed downward (the upward velocity in front of the wing is changed into a downward one behind the wing), this means that the reaction of the fluid against the wing is a lift of the wing upward. The amount of the impulse furnishes (…) only half the lift. The other half comes from the pressure differences on the control surfaces.
Hence, we can conclude that for a circular control volume, half of the lift can be captured as momentum transfer, and a pressure term is needed to capture the other half of the lift force. This is very neat, as it highlights the symmetry between the pressure difference and momentum flux. However, a qualitative description should ideally be limited to pressure.
3. Preliminaries
Many of the aspects in the literature are discussed multiple times. This comes about because the number of references utilized on average is very limited. Looking at the number of cross-references between the 140 articles reviewed, the average is (1.3 ± 0.5) per article, with a median of 0! That is, more than half of these articles cite no other article on lift education. As such, many points, even misconceptions, are repeated multiple times. To facilitate a simpler review, these concepts will be covered here and referred to when needed in the review.
3.1. Activities and Demonstrations
3.1.1. Flight Mechanics
Practical activities are great to use in a classroom. The wind tunnel is a perfect example. Figure 6 shows an open loop wind tunnel with an enclosed test section. This is similar to what the Wrights used in their early experimentation [14]. Larger wind tunnels tend to be closed loops like those used by NACA to characterize airfoils [16]. More common to see in a classroom for a demonstration is an open test section wind tunnel, which can simply be a desk fan.
Another tool used by the Wrights was the model glider. This too is used frequently as an educational tool for lift education. More generally, model aircraft can also be used. These can be unpowered gliders or simple rubber-band-powered toys. Prior to remote control, a control line was commonly used. This can be thought of as a hybrid between a powered aircraft and a kite that is able to be flown around in a circle (the radius of which is governed by the length of the control lines). The control lines control the pitch of the aircraft, enabling it to perform loops while flying around in a horizontal circle. In a demonstration, a rigid control line, a rod, would be utilized. A kite is also an aerodyne; that is, moving air is responsible for the aerodynamic reaction force, unlike an aerostat, where the aerodynamic reaction force is buoyancy. However, there are no examples in the literature where a kite is used to demonstrate lift, likely because there are misconceptions about the associated forces; that is, some may assume it is like the drag force of a parachute. Consider the parafoil, which many call a parachute when it is actually an inflatable wing.
There are other similar “toys” like a model glider. There is the frisbee, which interestingly adds gyroscopic stability and precession. Similarly, there is the boomerang, which has more complex aerodynamics than a frisbee but combines similar aspects. The most common tool is the paper airplane. This can be a dart or a glider or even the ring wing. In addition to paper, thin expanded polymers (foams) can also be used to make simple aircraft, such as the humble polystyrene foam cup. Simple designs can be like paper airplanes, while more complicated designs are like the gliders discussed previously, which are typically made from balsa wood.
3.1.2. General Aerodynamics
In addition to the demonstrations and activities that are clearly about flight mechanics, there are others that are better categorized as just aerodynamics. The term ‘aerodynamics’ is used here to denote a force from the movement of air. While ‘lift’ is clearly a force from the movement of air, the examples in this subsection represent cases that are not directly relevant to flight mechanics.
The first example is the venturi tube as described in Section 2.1.2. In these demonstrations, the changes in static pressure can be observed with simple u-tube manometers; noting that the venturi effect is commonly used in devices such as airbrushes, a simple version of this can be made from a pair of straws with one blowing over the other. Given that this is external flow and not pure internal flow, it is more akin to the half venturi. This is a literal construct; in a 2D view, if you remove the top half of the venturi, you are left with a half venturi (Figure 8b). While some criticize the use of a half venturi because it is no longer internal flow, and, hence, the exact same mechanics is not at work, this is incorrect. To be clear, you obtain a much more significant effect with internal flow in a venturi, and the exact area ratio can be used to determine the change in pressure expected via the wind tunnel equations (relating area ratio to pressure and velocity changes, derived from Bernoulli’s equation). The issue with the half venturi is that the area ratio is not only dependent on the size of the “hump” used but also on the properties of the flow such as speed. This is because the jet of air can react to the obstruction and partially move out of the way to flow around it. However, the air still has inertia, so it cannot effortlessly move around an obstacle, and it will still experience a constriction at the top of the “hump”, resulting in the lowest static pressure and the highest dynamic pressure. It should be noted that this is a property of inviscid flow; hence, Coanda does not need to be invoked to explain any aspect of flow constriction producing pressure changes.
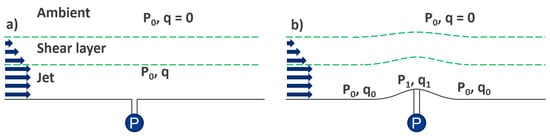
Figure 8.
(a) A jet against a flat surface with an orifice, where the static pressure (P) in the jet is equal to the static pressure in the ambient air and the dynamic pressure varies through the shear layer from maximum (q) in the jet to zero in the ambient air. (b) The same jet with a surface obstruction, which now has a reduced static pressure at the orifice with a corresponding increase in dynamic pressure. Compared to Figure 2, this case will have a smaller pressure reduction because the other “wall” is ambient air here. The dashed lines show the different regions of flow, the fast moving jet of air, the static ambient air, and the boundary (shear) layer between them, where the arrows indicate the flow speed.
The paper tent is a good example of a venturi effect, although it does require some input from Coanda to explain. Again, a paper tent is a literal construct; it is a small tent made from paper. Students are invited to blow underneath this and observe that it is crushed. The issue is that when we blow air out, it has the same static pressure, and technically, it is slightly lower, but this does equalize once outside. The pushing from the diaphragm and the constriction we form with our lips produces an excess in dynamic pressure. That is, the flow we produce is not directly creating a low pressure; however, the Coanda effect, the entrainment of air into the jet, does create a low pressure around the jet. The Coanda effect means that through viscous mixing, the air around a jet is pulled along with it. The result is a reduction in static pressure for the surrounding air due to the increase in dynamic pressure (according to Bernoulli). So, if we blow under a paper tent, the jet produces a lower pressure caused by the entrainment that reduces the pressure under the tent, which is then collapsed by the atmospheric pressure on the outside (see Figure 9).
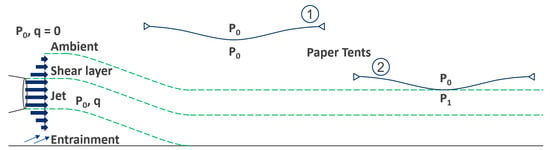
Figure 9.
A jet from a nozzle close to a surface will entrain surrounding air, lowing the pressure around it, and that jet will experience a force towards the surface (the Coanda effect). The jet then flows under two paper tents. As (1) is so far above, it experiences ambient pressure above and below; however, (2) is low enough such that on the underside there is reduced pressure, since the tent is flexible, the force will accelerate the surface down. Once closer to the jet, it will restrict the flow exactly like a venturi, further reducing the static pressure underneath.
Another example involves blowing across a curved strip of paper, illustrated in Figure 10a. There are many aspects to the levitating paper strip. Bernoulli and Coanda are required to explain the movement of the paper and the resultant motion. The same combination of effects as with the paper tents is present. However, now as the jet follows the curved surface, the result is a momentum change vertically, which produces a greater reaction force lifting the paper. Interestingly, once the paper is lifted (no longer curved down), this component disappears, and only a pressure difference will be present to explain the lift. An older example is blowing through a cotton spool to levitate a sheet of card, held central with a pin or thumb tack. This is illustrated in Figure 10b.
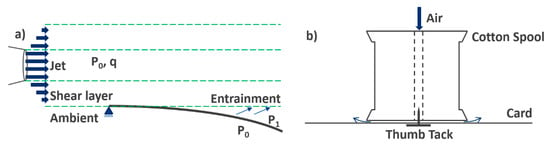
Figure 10.
(a) The levitating paper strip, with entrainment (Coanda), resulting in a pressure difference across the paper. (b) The cotton spool and card trick uses moving air to generate the reaction force.
A more direct demonstration of the Coanda effect can be seen by blowing between two round objects. An early example used two apples hanging on a string next to each other. The modern version of this uses two balloons. Given the need for lightweight curved objects, empty soda cans have become a common tool. These can also be hung on a string or can be placed on soda straws as rollers. While there are Bernoulli effects occurring, the movement of air around the curved surfaces producing a change in momentum is a key feature of these. This is because the change in pressure associated with entrainment will be less direct than the application of dynamic pressure from the jets of air.
There are also several demonstrations that utilize ping pong balls. The first uses a funnel to support a ping pong ball. This is identical to the case of the cotton spool and card, except now the curved ball provides a mechanism for the Coanda effect to provide flow around the ball, giving an additional force. There are many ways to levitate a ball in a stream of air, from a small ping pong ball and a straw to a large beachball and a leaf blower. Again, Bernoulli and Coanda effects are working together, and if the ball is spinning, this also adds a Magnus effect. The other simple demonstration is the trick of moving a ping pong ball from one cup to another without touching it. This is achieved by blowing firmly across the top of the cup.
3.1.3. Not Aerodynamics
The teapot effect is often offered as a demonstration of Coanda. This is simply incorrect. The requirement for entrainment is that there will be shear mixing of the fluids at the boundary. With very different densities, this is going to be very difficult. As such, when tea is poured from a spout, the fluid runs around the lip and down the pot because of surface tension effects [18]. Once the tea is pouring in a smooth continuous way, the inertia of the fluid means that all of it will continue to flow in the correct direction. That is, the teapot effect is observed when you start pouring. Another way to demonstrate this effect is by using a curved spoon and a stream of water, typically from a faucet. Again, this is not Coanda; it is surface tension that causes the fluid to follow the curved surface. Finally, demonstrations can involve the outside of a glass, which is also curved. It should be noted that in these cases, because of the surface tension, the water does flow down and around the object. As such, it is accelerated, and, hence, a force is produced. This force, however, is not at all related to an aerodynamic reaction force. It would be analogous to using jets of water directed down and back over the top surface of a wing; this will result in a downward motion, producing a reaction force upwards on the aircraft, but this is of no practical relevance to a real aircraft.
3.2. Erroneous Points
3.2.1. Inverted Flight
Many authors claim that Bernoulli-based explanations cannot explain inverted flight. However, Bernoulli explanations are not at fault; it is the misconception that the underpinning aspect of Bernoulli is the path length difference. This implies that an airfoil that is more curved on top cannot fly upside down. In general, this is incorrect. Almost any incorrect theory of flight will still predict inverted flight. This is because an inverted aircraft has a relative negative angle of attack to generate lift, which is illustrated in Figure 11. An argument that inverted flight cannot be explained needs two misconceptions. The first is the path length difference coupled with an equal transit time to give the difference in velocity, and the second misconception is that the flow splits precisely at the forwardmost point of an airfoil. This second misconception would radically change the flow in Figure 11b, always producing a lower pressure on the more curved side. So, to conclude inverted flight is not possible requires multiple misconceptions to be combined.

Figure 11.
Incorrect flat-bottom flow around an airfoil that is (a) right side up, and (b) upside down. Any incorrect theory of lift should still predict inverted flight due to the required large negative angle of attack (α).
3.2.2. Thrust and Lift
Lift from thrust is a point of significant confusion in aerodynamics [19]. The principle is that a rotor wing, like that found on a helicopter, is similar in cross-section to a conventional fixed wing. As such, the aerodynamics involved are also similar. This is incorrect and is a gross simplification. In general, lift from rotor wings and thrust from propellers is a pure momentum transfer phenomenon. The basic principle of how momentum change produces thrust from a propeller and lift for a rotor is illustrated in Figure 12. Like any other turbomachine (a pump or compressor), the propeller or rotor increases the speed of the flow through it, resulting in a change in momentum (p), which is a force.

Figure 12.
Thrust (F) from a propeller, which is also lift for a rotor wing, is given as the momentum change across the disc due to the increase in velocity (u to v).
4. The Literature Review
The first article appears to be Webster [20], who presents the lift force as a pressure difference. Two options are given as the source of the pressure difference; the preference is a streamline curvature and the resultant “centrifugal effect”. The other is Bernoulli, which Webster [21] uses exclusively, where he notes “the resultant force [is] due to pressure differences”. Critically, Webster [21] states that “if air had no viscosity, and then the wing would have no lift”; clearly, knowledge of D’Alembert’s paradox was behind early literature. Interestingly, Webster [20] states that “the difference between empiricism and science is the existence of ‘whys’ in science”, although Webster does not address the question of ‘why’ there is an asymmetric streamline curvature unlike the symmetric streamlines predicted by D’Alembert’s paradox. Rather, he goes on to say, “In the physics of flight…we must formulate our laws in such a way that they can be used quickly and accurately…”. In this early pair of papers, we have the correct underpinning knowledge coupled with a dislike of complexity. The early images presented by Webster are very good, noting that they were used in the “1941 edition of the Civil pilot training manual” [21].
Richardson [22] noted that he needed demonstrations for lectures on aeronautics. While these are more generally fluid mechanics, he does present the first open test section wind tunnel. Richardson also utilizes a control line model aircraft with control surfaces to demonstrate maneuvers and control, with its own propulsion from a propeller. The controllable aircraft and wind tunnel were also combined to demonstrate the movement of the aircraft. In terms of theory, Richardson presented Lanchester [2], which is an early circulation approach. This is shown using a Magnus effect demonstration with a rotating cylinder in front of the fan. An important demonstration presented by Richardson is Hele-Shaw flow, a type of creeping flow [23]. Critically, Hele-Shaw flow is potential flow, and if this was an early way to visualize and show fluid flows, it is possible that this is the origin of misconceptions.
Otis [24] presents an introduction to mathematics education for aeronautics. In his introduction, he notes that there have been previous articles; as was common at the time, these deal with general education, especially with the need for aviators in the war effort. As such, Otis is the first technical mathematical education article. Bernoulli is effectively presented as a case study, given that an entire outline is presented for all mathematics and science in aeronautics. Unlike the realistic flow illustrated by Webster before, we see the first example of ‘flat bottom flow’ (like Figure 11). While Bernoulli is well presented, the causal link comes from the path length difference and a statement of equal transit time. The only reference is to Otis’s own book, given as the source for the images [25]. This early book likely represents a significant source of misinformation.
Practical education aspects, such as demonstrations and laboratories, occur very early in the education literature. This is not a surprise, given that there was a long tradition of experimentalism in fluid mechanics due to the difficulties in developing theories that provided predictive power, etc. Blanchard [26] discusses a number of aviation-relevant experiments, including radio and instrumentation. Of more relevance is the venturi tube with u-tube manometer measurements. This is followed very quickly with another open wind tunnel using a fan [27]. Bates [28] presents a slightly improved design, which gave better results. Later, Katz [29] presented an airfoil device similar to these, intended to show the difference between lift on a flat plate and a curved airfoil; the associated theory is that of Bernoulli, where the shape of the airfoil is responsible for the observed differences. Overstreet [30] also presented an open wind tunnel as their student project and once again utilized Bernoulli in terms of pressure difference to explain lift.
The October 1954 edition of the National Science Teachers Association’s (NSTA) Elementary School Science Bulletin was entitled “Ideas for Aviation Science” [31]. The content starts with the general concept of pressure. This immediately becomes problematic, as they claim that air from a fan has reduced static pressure, which is incorrect. The fan adds kinetic energy to the fluid, above the static pressure, giving it a higher total pressure. This information may represent a fundamental source of this misinformation, which is likely well entrenched. Also presented is the demonstration of blowing between two apples and the cotton spool card levitation trick, both as explained as pure Bernoulli demonstrations; however, the Coanda effects need to be considered. Finally, they also present the same flat-bottom flow visualization used in Otis. The underlying principle discussed is Bernoulli, with the shape described as being responsible for faster flow above relative to below and hence a lower pressure above relative to below.
The next work is by Wild [32]. It is apparent that Wild was an engineer as opposed to Webster, who was a physicist. Wild, as most engineers do, states that in air, viscosity is negligible but critically notes Prandtl’s boundary layer, which contains the viscous effects. This is a common point from engineers: “(1) we can ignore viscosity, (2) all viscous effects are in the boundary layer”. At a basic level, this is true—viscosity is negligible outside the boundary layer—but without it, there is no boundary layer; that is, if there is a boundary layer, then viscosity cannot be ignored. Wild starts as most aerodynamic approaches do, with potential flow around a cylinder, and importantly notes that Bernoulli can be applied to relate the pressure and velocity, a correct statement when viscous effects are negligible. Following this, the Kutta condition is presented, with the sharp leading edge of an airfoil being the mechanism as to ‘why’ there is circulation. This is a common point of confusion by engineers, the notion that D’Alembert’s paradox is resolved by the Kutta condition and the need for a sharp trailing edge, when it is, in fact, resolved by including viscosity.
Heck [33] presents similar manometer flow experiments to Blanchard, giving the first straw-to-straw venturi activity. Heck also presents a “hump” as an analog to a wing, in a half venturi tube to emulate how a wing produces lift, with a reduction in pressure over the top surface; while related, this is too much of a simplification. The underlying knowledge is Bernoulli, where the shape of the airfoil is what is needed to produce the difference in pressure resulting in lift. Similar examples are provided by Fiorello [34], who presents a “flying machine” for education purposes. The knowledge here mirrors almost everything in the NSTA’s 1954 bulletin. That is, Bernoulli coupled with the shape results in the lift force. Interestingly, there is correspondence from De Waard [35], but the criticism is only about which of Newton’s laws is applicable to thrust.
Smith [36] rightly states that Bernoulli’s “theorem was never postulated to deal with dynamic lift but is only an expression for the law of conservation of energy inside an isentropic stream-tube of fluid”. That is, any statement to the effect that “lift is explained by Bernoulli alone” is incorrect. As mentioned before, outside the boundary layer, in inviscid flow, Bernoulli correctly relates the static pressure and velocity along a streamline; as such, if you know one, you can determine the other. In fact, this is what is taught to aero students in that second course on aerodynamics; they use potential flow and circulation to calculate the velocity vector field, and then they literally use Bernoulli to calculate the corresponding static pressure at every point in the field [37]. Smith notes issues in science education in the USA; he is critical of the general dependence on Bernoulli, which we have noted is in almost every proceeding article to date. Smith also notes equal transit time as being standard in textbooks in the USA; he goes on to say, “We can quote no physical law that tells us this”, although equal transit time is a result of D’Alembert’s paradox [8]. Smith correctly attributes the lifting force to a pressure difference; however, he goes on to be the first to use an incomplete Newton’s 3rd Law argument. Crucially, if you compare the images in Wild [32] and Webster [21] to those of Smith, you can understand why he made a poor inductive leap to this conclusion (see Figure 13); Smith’s illustrations of air flow around an airfoil are fundamentally wrong and are repeated numerous times in future articles. Interestingly, Smith notes a critical and insurmountable issue with Newton’s 3rd Law explanation, saying, “We cannot easily set up an experiment or a calculation of dynamic lift to prove this principle”. Rather, Smith relies on the analog of a helicopter (a rotor wing) or a propeller, which work by momentum transfer as noted in Section 3.2.2. He further softens his position by saying, “although the wing is much simpler than the propeller, we cannot easily set up an experiment (or a calculation) to illustrate or prove the momentum principle…”. What makes this odd is that Smith was a NASA engineer, who should have been aware of the circulation method to correct potential flow and estimate lift at small angles of attack. Smith published similar work the following year [38,39].
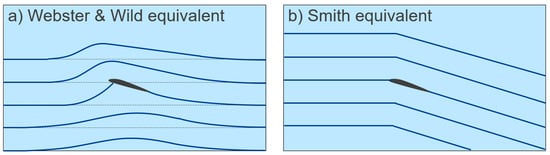
Figure 13.
A comparison between correct streamlines (a) and “intuitive” streamlines (b).
Fletcher [40] cites previous work, with a classical text [41], and a modern classic [42]. Fletcher does not give any specifics. He states that his physics curriculum includes a discussion of Bernoulli and the force and momentum discussion for propellers to produce thrust; the how and why of wings are not discussed in the article. Fletcher follows this with an extended version [43]. Fletcher also derives a sin law analogous to Newton’s sine-squared law (discussed in the Summary section below), which is controversial (and results from the incorrect flow in Figure 13b). Fletcher correctly uses the important coefficients of lift and drag, as necessitated when referring to a text like Kermode [42]. However, he uses an incomplete Newton’s 3rd Law statement to explain their origin.
While Barnes and Potter [44] discuss the aerodynamics in sporting applications, they present the first account that captures the key aspects of Prandtl. The only issue in their work is a lack of Navier–Stokes; however, this is trivial since they clearly use viscosity confined to the boundary layer as the source of the flow asymmetry resulting in lift.
The great debate around the use of Bernoulli starts with Bedford and Lindsay [45], though not directly about lift. May [46] presents a simple activity based on toy gliders, and Bernoulli based on the shape of the wing is given as the mechanism for lift. Consuegra [47] presents a similar activity but using paper airplanes, although no theory is presented for flight mechanics. Another preliminary paper is Martin [48], which has follow-up correspondence [49,50]. Martin presents a paradox in Bernoulli, which is often overlooked. When most consider a venturi tube, the flow speed is shown higher at the narrow section. This is acceleration, which needs an associated force that is not covered by Bernoulli. However, to force the air faster into the narrow section, there is an increase in pressure on the wall during the constriction. Most only plot the pressure and velocity along the middle of a venturi and ignore what happens at the surface; both are included in Figure 14. Barnes [51] critically misinterprets Bernoulli, noting that it dictates that if fluid flows past a surface, then the pressure will just be lower. While this is true if the Coanda effect is included, there is nothing inherent in Bernoulli that suggests this. Barnes presents many of the fundamental educational activities such as blowing across curved paper, the cotton spool, etc. The underlying principle in terms of lift is Bernoulli and the shape of the airfoil. Brusca [52] appears to cause the biggest impact on the Bernoulli debate, which is not surprising because he incorrectly uses Bernoulli to explain the Magnus effect for a rotating ball and a Flettner rotor; he also uses an exclusively Bernoulli explanation for a stream of air lifting a piece of paper and levitating a ball. There is a letter and response from Murphy and Brusca [53], although this does not add much. There is another letter and response from McCaughan and Brusca [54]. Kesling [55] presents similar activities, also noting the misconception that “faster air has lower pressure”. These articles, especially the correspondence, highlight that these demonstrations, such as the levitating ball, should be avoided when discussing lift. While they involve aerodynamics, moving air creating forces, they do not directly relate to wings.
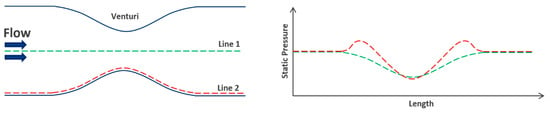
Figure 14.
A venturi tube and the plot of pressure along the centerline (Line 1, green) and along the wall (Line 2, red).
Wegener [56] presents similar material to Wild [32] and Barnes and Potter [44]. He discusses the boundary layer containing the viscous effects. Of note is the insight he gives to potential flow solutions, from which we may infer how aviators have incorrectly applied Bernoulli. Wegener notes that the solution to Laplace’s equation gives the velocity potential and the stream function. Knowing the velocity field, the application of Bernoulli gives the resultant pressure, although this is for inviscid flows that do not produce lift. Still, it highlights that many want a heuristic shortcut to remove the complex and incomplete mathematics of potential flow such that if they had a velocity difference (circulation), it could then be used to give the pressure via Bernoulli, which is the source of lift. Another key feature of Wegener is that it is the first 3D flow visualization presented in the educational literature. While Wild [32] mentions wingtip vortices and downwash, Wegener gives a thorough description, which importantly does not include statements about this being the source of a momentum transfer and hence a Newton’s 3rd Law explanation for lift, which is a growing common misconception. Figure 15 illustrates the issue, which shows that for 2D flow (bound vortex only), there is no acceleration to the flow such that it has a sustained velocity; this only occurs in 3D flow (coupled bound and tip vortices). This is discussed further by Wild [57].
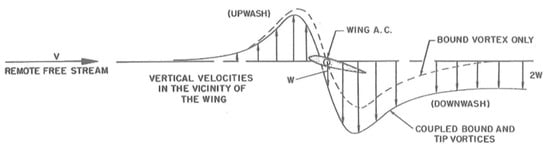
Figure 15.
Wing vortex system, illustrating the vertical velocities (W) in the vicinity of the wing and the rear flow [58]. This work is in the public domain.
Flynn [59] and a correspondence by Monce [60] do not discuss the principle of lift, only other aspects of flight mechanics. The mistake of Flynn as pointed out by Monce is that the angle of attack of an aircraft does not equal its climb angle. In general, this is another common confusion students have: “if the nose of an aircraft is pointing up, it must be flying up”. As correctly illustrated by Monce, before an aircraft touches down, it has its highest angle of attack, and it is landing, not climbing.
While Weltner [61] correctly attributes lift to a pressure difference, he incorrectly asserts that Bernoulli is the underlying principle. He goes on to use an inverted-flight argument to disprove equal transit time. He includes another incorrect argument against equal transit time; this relates to the fact that at some angles of attack for some airfoils, the pressure may be above ambient across the lower surface. While this will mean the flow velocity underneath will always be below the freestream velocity, it does not directly preclude equal transit time. Weltner then references Smith and goes on to utilize a Newton’s 3rd Law explanation. The mechanics of propellers and rotors are used as the basis for this. Looking at the images presented by Weltner, you can see the logical approach taken and the reason for this erroneous conclusion (see Figure 13b). A jet of air close to an airfoil is used to blow it as if it were a sail tacking across the wind, and Weltner equates this to a literal jet on the boat such that it produces the same force components. This is not freestream, and, hence, it does not produce the required upwash. It is effectively the first visual representation of what will become the modern Coanda explanation. This is compounded with a sin law argument. Weltner highlights another important point of confusion, where the flow at the trailing edge is equated to the flow in the rear far field, which is not the case. One further point, as with Webster, is that the streamline curvature is also presented. The final twist to Weltner is that he references Prandtl as evidence to support a Newton’s 3rd Law statement, which was provided at the end of Section 2. Clearly, Prandtl is not implying that a simple statement of Newton’s 3rd Law alone is applicable, as Weltner claims.
Weltner [61] is also the start of the second great debate on Bernoulli in the literature. Auerbach’s [62] correspondence to Weltner immediately and correctly defeats the inverted flight argument, although this has not prevented it from being used by others. While Auerbach defends Bernoulli hard, it is not clear if he is insisting that Bernoulli alone is responsible for lift, which would be incorrect. Importantly, he does give the context of an elliptic partial differential equation, and the issue with ascribing cause and effect in such a context. Auerbach concludes with a statement that deflection (Newton’s 3rd Law), as presented by Weltner, is “important” and appears to represent a misunderstanding of circulation. This is the first case of ‘circulation plus downwash gives lift’. Weltner [63] responds with a statement that ‘streamline curvature plus Bernoulli explains lift’. While not correspondence, Huebner and Jagannathan [64] immediately follow Weltner, who is cited. They also cite Smith’s Newton’s 3rd Law explanation and incorrectly state that Bernoulli is technically not applicable because it “violate[s] the conditions assumed in deriving [it]”. Indirectly, Badeer and Synolakis [65] add to the discussion, noting that Bernoulli is often incorrectly applied, supported by both Smith and Weltner. Weltner [66] is a clear continuation of his previous work [61]; in 1987, he proposed experiments to validate what he was saying, and in 1990, there are photos of real experiments. Importantly, none of the conclusions in his earlier work were wrong in their context; they were just not applicable to freestream flow around an airfoil. Hence, it is no surprise that these experiments affirm Weltner’s position; they just do not demonstrate how a wing works. To give an example, in air ducts around corners, vanes are commonly used to reduce losses, the concept that a vane will more efficiently turn air through 90 degrees is true, and at the corner, there is also a reaction force as the flow accelerates (changes direction); however, none of that is directly related to how a wing produces lift. This is the same as sticking a vane on top of a frictionless cart and blowing a jet of air at it; it produces motion, but that is not how a wing works. Weltner again cites Prandtl as a source for lift being explained by Newton’s 3rd Law, which is not the case. Unnecessarily, Weltner [67] continues with a second article in the same publication, repeating the other aspects of his 1987 work not covered in the previous pages. In correspondence to Weltner, Freier [68] repeats Wild (1966) that circulation is the correct explanation. Interestingly, the circulation argument by Freier is used to explain both a pressure difference (Bernoulli explanation) and a downward momentum in the flow (Newton’s 3rd Law explanation). Freier also appears to be the first to state that you cannot apply Bernoulli across streamlines and hence that Bernoulli cannot be used to compare the upper and lower streamlines. In fact, you can if the total pressure in the two streamlines started at the same value and you apply conservation of energy, which is true outside the boundary layer; you can simply track each streamline independently. In his response to Freier, Weltner [69] clearly articulates the key criticism of just using circulation; that is, circulation is an effect, not a cause (the underlying cause is viscosity).
Bauman and Schwaneberg [70] link the first debate (Brusca and others) and this second debate (Weltner and others) about the relevance of Bernoulli. There are essentially no new points added. The fact that Bernoulli is derived from Newton and hence applicable is well stressed. Bernoulli is invoked again as the only reason for a curved piece of paper to lift when blown across (and to explain the curvature of a spinning ball); that is, there is no reference to Coanda or Magnus, which are needed. They do correctly defeat the inverted argument, noting that the angle of attack is typically omitted (see Figure 11). They assume that helicopters are simply wings “moving”; Smith (1972) previously noted the difficulty in this reasoning. On the topic of circulation, they say, “The mathematical fiction has apparently led to the common statement that one cannot explain lift in terms of irrotational flow”, which is not fiction; it is literally D’Alembert’s paradox. Oddly, they conclude their section on lift by stating that downwash from wingtip vortices adds to lift, when these reduce lift [14]. Weltner and Ingelman-Sundberg [71] follow up on Bauman and Schwaneberg [70], repeating much of Weltner’s prior points, although the new and revolutionary notion of Coanda is utilized following Raskin [72]. Similarly, at the same time, Weltner and Ingelman-Sundberg [73] presented further similar work. It should be noted that there are more modern versions of these 1999 articles online, and they first appear in the literature cited by Eastwell [74].
Fields [75] gives a wonderfully soft introduction. Importantly, while demonstrations of the lifting paper are used, no names are referred to, and, hence, no confusion is presented; this is probably the ideal solution—to present the concept that moving air can move objects, with no exclusive statements about pressure or momentum, and no names. As such, there can be no confusion. The approach to middle school aerodynamics should be a simple clear empirical science endeavor. Pols, et al. [76] also present aeronautics for middle schoolers; however, a radically different approach is taken. Interestingly, these mechanical engineers use an equal-transit-time-related explanation (path length difference). They also utilize levitating paper and ping pong ball demonstrations explained by Bernoulli with no Coanda. Importantly, they do present the first classroom wind tunnel with an enclosed test section. Holmes [77] also presents the blowing across a straw demonstration used by Pols, Rogers and Miaoulis [76], and first used by Heck [33]. Telfer [78] presents some middle school mathematics based on flight, using both Bernoulli and the shape of a wing to explain lift, along with a statement of Newton’s 3rd Law. Macalalag, et al. [79] used paper butterflies to talk about lift, and while this is admirable, the aerodynamics of very small flapping wing animals is radically different from the fan blowing against paper analogous to flying a kite. Hoover [80] presents flight with Bernoulli, using many of the previous aerodynamics activities as presented by the NSTA in the 1950s, which are likely very common demonstrations nowadays. The issue with Hoover in contrast to Fields is that the use of a label means you need to be correct, or you are presenting misinformation. The original hanging apple demonstration was replaced by a pair of empty soda cans standing on a bed of drinking straw rollers by Hewitt [81]. Hoover’s version of this has the soda cans laying on their side, which potentially eliminates the Newton’s 3rd Law aspect of the Coanda argument; he then goes on to blow between two hanging balloons, which reintroduces the problem. In general, the demonstrations presented are great examples of fluid mechanics and aerodynamics; however, they are not relevant to flight mechanics.
Sprigings and Koehler [82] present a sports science introduction to dynamic lift, although a better one was presented previously by Barnes and Potter [44]. Given that Koehler is a physicist, much of the material above regarding Bernoulli verses Newton is covered. However, from “simple assumptions”, they derive Newton’s sine-squared law, which Newton himself knew was wrong. This is hand-waved away by claiming the small angle approximation and then simply presenting the correct lift equation. The curvature of a spinning ball is used as evidence to support the conclusions, noting that one of the simplifying assumptions was that the speed of the flow around the body does not change, which is needed for the Magnus effect to give an additional force on a spinning ball [12].
Gerhab and Eastlake [83] do not directly contribute to the how or why of lift; however, their presentation of projects around boundary layer control is a good description of boundary layers and their importance. This is beneficial to the lift education literature and is cited more than once by future authors.
Raskin [72] is a pivotal paper and not for a good reason. This marks the first presentation of Coanda. While Coanda was described in Section 2.1.3, in the literature, Coanda becomes the deus ex machina for lift education. That is, it explains the unexplainable, as the concept is used well beyond the actual definition of the effect to encompass the continuum hypothesis and all viscous effects. It even gives the streamline curvature providing a direct Newton’s 3rd Law explanation for lift. Raskin combines this idea with Smith before him, and the legitimacy given by many intervening authors, giving the modern Coanda paradigm. Importantly, around an airfoil, there is no jet of fluid entraining the surrounding fluid. In fact, a goal in aerodynamics is to achieve laminar flow over an airfoil, which would preclude entrainment, and the flow initially starts laminar, where there can be no entrainment. As such, Coanda is not involved in aerodynamic lift.
Tamarkin and Bourne [84] use paper airplanes for very young students. This is a great endeavor, although the oversimplified statement that the force of air under a wing pushes it upwards is an issue (ski effect). Baird, et al. [85] present another paper airplane approach, using the equal transit time theory to explain lift. Greene [86] also presents many of the same aerodynamics activities by blowing across paper, etc., and using paper airplanes. Here, Bernoulli is not used, but only an explanation based on pressure difference. Chiles [87] demonstrates a similar approach to Fields, also utilizing paper airplanes for year six students. It is clear that Chiles has a larger syllabus, but no details are provided to conclude if names like Bernoulli or Newton are used. Oliver and Ng [88] present a slightly different approach to the paper airplanes, using a rubber-band-powered toy aircraft contest for primary and secondary students. Waltham [89], building on from previous work [90], presented an advanced way to utilize a model glider, like those proposed for primary and secondary education prior. The experimental approach is ideal as intended, and the only issue is the explanation and details of lift. The simple explanation is a statement of Newton’s 3rd Law, where wings “deflect air downwards”. Schneidermeyer [91] also presents a simple aerodynamic activity, this time with flying discs; the underlying theory presented is Bernoulli, with the explanation based on the shape of the disc. Sterling [92] also appears to be addressing education at lower levels. In this, she simply uses a pressure difference explanation for how, and no names appear to be used to “label” the effects. McGrath [93] presents the use of paper airplanes, along with some demonstrations around pressure, a key feature of lift, although the curved shape of the wing is used as the explanation for lift. Bun [94] also uses a rubber-band-powered model aircraft, similar to Oliver and Ng. Mason, et al. [95] utilize polystyrene foam to make model gliders, and the underlying science of lift is provided by NASA based on a path length difference and Bernoulli. Bautista [96] utilized paper airplanes to talk about lift but with no theory. Katchmark, et al. [97] present the use of paper airplanes while not using Bernoulli; lift is explained as a pressure difference. In general, there is a very large body of literature on paper airplanes. These have many educational applications, far from just the mechanics of flight. Most tend to focus on science and mathematics, but there are many others. Likely, only a fraction of those that use paper airplanes as a tool to teach about lift have been captured. However, the sample here appears homogenous in approach, and the topics discussed tend to focus on early simple theories, coupled with fallacious reasoning.
Beaty [98] represents the modern view of all Bernoulli arguments. That is, it is inherently wrong because it is associated with a curved upper surface, longer path lengths, or equal transit time. This is simply not true and is the default argument used by those who want to dismiss the pressure difference as the source of lift. This is clear from Beaty’s conclusion, which is that Newton’s 3rd Law is more intuitive and thus should be used at elementary levels. Again, if Bernoulli is used on its own, it has no hope of explaining lift, and all of these incorrect crutches have been used in education contexts; however, looking at the fact that there is a pressure difference and that it is used to determine the coefficient of lift, you are supposed to be compelled via the scientific method to find a reason for that.
Lissaman [99], like Barnes and Potter [44] and Wegener [56] before him, is another tour de force. Sadly, Lissaman has only a single citation recently from McLean [18]. Lissaman simply and elegantly explains what we know because of Prandtl and his contemporaries. It is a shame this engineering article made no impact on the science education community because Lissaman was a clear authority, a statement easy to make in hindsight, though the reason for this is clear in the heavy use of calculus. The previous derivation and quote from Prandtl [3] demonstrated that for a circular control volume, the momentum and pressure terms each contribute half the lift. Lissaman shows the same result for a square control volume around an airfoil and concludes that for the case of Figure 7a (long horizontal control volume), the pressure term will dominate, and if an equivalent long vertical slice can be produced, the momentum term will dominate. Importantly, pressure and momentum do not exist without each other. Lissaman combines circulation, Bernoulli, and Newton.
Waltham [100], like Fletcher [40], derives another sin law equation. As with Fletcher and Sprigings and Koehler [82], the incorrect application of Newton’s 3rd Law is at play here, along with another version of Figure 13b illustrating the “intuitive” air flow.
Anderson and Eberhardt [101] incorrectly state that Bernoulli requires equal transit. It is possible to have a Bernoulli argument and not require equal transit [32]. Similarly, they link this “popular explanation” (Bernoulli) to wing shape, which, again, in the proceeding literature is not always the case. Anderson and Eberhardt go on to state that because of the link to wing shape, Bernoulli cannot explain lift at different angles of attack, a statement made on the premise that changing the angle of attack somehow does not constitute a change in geometry. The underlying misconception here is that the flow splits at the leading edge, which is not true. Critically, they present what is called the “physical description”, which they state has “no design or simulation capabilities”, which, for a physical law, is very problematic. Further, they criticize the Bernoulli-based explanation with the inverted flight argument, which was covered in Section 3.2.1. and dismissed previously in the literature. While presenting weak points, they also clearly articulate the correct issue with Bernoulli, noting that it is applicable, but it is not self-consistent enough to give the velocity changes to enable the correct pressure calculation. Anderson and Eberhardt [101] also present an elegant statement of Newton’s 1st Law, which has been absent in the literature until now; this links Newton to streamline curvature nicely. While they correctly use viscosity, they conflate this with Coanda. To make matters worse, to show the Coanda effect, they use a spoon with water and not air, which is actually a demonstration of surface tension [18]. They present the “wing as a scoop”, which looks very similar to the sin and sine-squared law images incorrectly presented above (Figure 13b). One of the key points to take away from Anderson and Eberhardt [101] is their criticism of lift from airfoils in 2D, claiming that it is not a real-world effect. Consider the question, does an airfoil work on the passing air? If we use potential flow, the answer to this is no. This is an issue if the Kutta condition and circulation are included as quasi-viscous effects such that the result is lift and no drag. In both cases, the compression and expansion (either symmetric for the pure potential flow or asymmetric for the circulating flow) are isentropic. However, if viscosity is included as the actual mechanism for asymmetry and hence lift production, then there cannot be adiabatic and reversible processes, as viscosity gives a loss of energy due to friction. The criticism and even dismissal of airfoil lift is compounded by the conflation of lift with downwash and wingtip vortices (see Figure 16); it is well known that these vortices constitute a reduction in lift, and the energy needed to produce them is a source of drag [14,102]. Their final point is around the ground effect and how the observed increase in lift comes about due to a reduction in upwash; however, this is actually because of a reduction in downwash, which reduces the effective angle of attack and induced drag [103]. Kunzig [104] presents the work of Anderson & Eberhardt in Discover magazine, repeating their key points and noting they are easier for a third grader. While their first article was in Sport Aviation, the work of Anderson and Eberhardt [105] is similar, just as a preprint on the Fermilab server, submitted to the American Journal of Physics but never published. In this second work, the authors have softened the extreme links between Bernoulli and fallacious arguments. They attempt to validate their preferred Newtonian explanation by claiming that it predates Bernoulli in education texts; as noted above, this is not the case. Webster was using Bernoulli in 1920 and was responsible for the official training syllabus during the exact time period mentioned by Anderson & Eberhardt. The study by Anderson and Eberhardt [106] appears to be unpublished work that directs readers to their book and ultimately repeats the previous points. The preprint article by Ceil [107] presents the information from Anderson & Eberhardt. Similarly, the lift for biological science from Ingle, et al. [108] also repeats the ideas of Anderson & Eberhardt.

Figure 16.
The wingtip vortex of an aircraft visualized through rising red smoke (NASA Langley Research Center).
Auerbach [109] highlights the relationship between the need to use the pressure difference and momentum flux together. Like Figure 7, different-shaped control volumes are presented. The point of clarity is that one can consider the atmosphere that contains an aircraft flying, where an infinite horizontal distance is possible (the curved geometry of the earth facilitates this) and, hence, a pure pressure lift is possible. However, since the wing is finite, using a bounding vertical rectangle, which cannot be infinitely high (there is the earth surface and the top of the atmosphere), it means that a pure momentum flux case cannot be constructed.
Hoffren [110] adds more to the discussion. As with other aeroengineers, there are good points that mirror the central discipline. He highlights the vortex-based explanation used to justify circulation, with names such as Helmholz, Thomson, and Kelvin [7]. Importantly, Hoffren answers the question about why there are those that think the upper and lower surfaces have exact fractional contributions, which is not the case with a PDE solution. This is based on a “faulty interpretation” of Eiffel and the 2/3-1/3 rule. While Eiffel had a rule, it is incorrectly extrapolated to mean that 2/3 of the lift is due to suction on the top surface and 1/3 is due to higher pressure on the bottom surface, which is not the case. Interestingly, Hoffren does not agree that viscosity is the underlying mechanism, although he gives seven references in support of viscosity, and one against, and then states “…there is no rigorous proof for the claim [against viscosity], and that the discussion is mostly of academic interest…”. Hoffren is also perplexed by the singular perturbation problem (the boundary layer represented mathematically), stating that “This kind of behavior in any physical phenomena is extremely rare, if known at all”. The general description presented by Hoffren is very good, and this is the first instance where an image correctly illustrates the collinear nature of the streamlines in the far field (see Figure 13a), supported by an explanation. However, Hoffren goes through the effort of establishing the correct flow field only to fall back on a Newton’s 3rd Law statement, based on the downward turning of the streamline after the airfoil.
Eastlake [111] makes a plea that is worth repeating, if you focus on one aspect, the pressure difference or momentum flux, you should not preclude the other because there will be issues. As previously mentioned, this is more problematic when precluding pressure because a control volume can be constructed that facilitates a purely pressure explanation, but the same is not true for momentum (see Figure 7). Furthermore, Eastlake gives “Newton” as an explanation, which should actually be Navier–Stokes, the correct application of Newton’s Laws of Motion for fluids. Eastlake correctly states that the confusion with inverted flight arguments is due to the lack of stagnation points showing where the flow divides and hence where the “upper” and “lower” surfaces are aerodynamically rather than geometrically (see Figure 17). Unfortunately, Eastlake does state that it would be possible to measure the vertical velocity of the flow and determine the lift from it. Since a control volume cannot be constructed that purely uses momentum, this is not actually possible.

Figure 17.
(a) the geometrically defined upper (red) and lower surface (green) between the cord lines, and (b) the aerodynamically defined upper (red) and lower surface (green) between the stagnating streamlines.
There are also educational articles that utilize rotor wing demonstrations. The first of these uses a simple party favor style toy with a balloon used as a reservoir of pressurized air to start a set of three rotor blades spinning via a jet effect (momentum transfer), which, in turn, lifts the toy with another momentum transfer effect [112]. A related article by Yin-Soo [113] and another Edge [114] goes into more detail about rotor wing downwash generating lift, as well as a link to Bernoulli. Liebl [115] utilizes a more complex RC rotor wing to demonstrate and quantify the lift from a rotor wing. There is correspondence from Strong [116] and Carr [117], with a reply to Carr [118]. It appears that there are confounding variables in the experiment initially presented, which cannot be confirmed due to a lack of an experimental diagram from Liebl. Amir [119] utilized a simple toy rotor wing to investigate work. In contrast, Monteiro, et al. [120] used a DJI Phantom drone to demonstrate the flight physics of quadcopters, which is a rotor wing. However, as noted in Section 3.2.2, lift from rotor wings and thrust from propellers is a pure momentum transfer phenomenon, which, when invoked to explain wings, causes problems, as first seen by Smith (1972).
Babinsky [121] presents the streamline curvature as an explanation for how wings work. Surprisingly, he describes this as a “correct explanation for lift” [122], like it did not previously exist in the literature. It was noted in 1920 that Webster spoke of streamline curvature, and many of Weltner’s articles have also presented streamline curvature. As Babinsky states in his companion lecture, the relationship between streamline curvature and pressure is a known fact. Several years later, Hermans [123], Silva and Soares [124], and then Bastianello [125] present Babinsky’s explanation after discussing some misconceptions and fallacies. An important aspect of Babinsky’s explanation is that the asymmetry in the curvature is not explained. Hence, while Babinsky does provide an answer to the question of how wings work, it does not explain why. That is, the potential flow solution of D’Alembert is also curved, just symmetrically, and, hence, there is no net force. As previously stated, there is an intimate relationship between pressure gradients and streamline curvature, but there needs to be a reason why curvature is asymmetric. Babinsky also incorrectly uses Coanda as the label for the underlying mechanism.
Colwell [126] does not add much with his review of three books. There is a clear dislike of pressure and a preference for Newton’s 3rd Law.
Zetie [127] correctly criticizes the flat-bottom flow illustration around an airfoil and simplifies it to Newton. However, he appears unaware that in 2D flow, there is no constant force downward on the air, that the flow does return to horizontal after, just not immediately after, and that it is parallel, and collinear, to the flow ahead.
Hewitt [128] is an important addition to the literature, given that he is the author of a widely used physics text, Conceptual Physics, which has become a general approach to teaching physics. With the application of the conceptual physics approach, Hewitt can correctly criticize issues with a pure Newton’s 3rd Law approach. His discussion of his own failure to reconcile a molecular explanation is key. The insightful statement here is the concept of a layer of dust on a rotating fan blade clearly illustrating that the hail of bullets (molecules) are not bouncing off the surface. The reason Hewitt could not get his particle model to work, and why there are a few particle physicists (some of the previous authors) perplexed, is that they have not considered the effect of viscosity between the particles, which is the key. The dust is in the boundary layer, and the freestream effectively interacts with the boundary layer and not the surface; that is, the molecules of the freestream bounce off the boundary layer. The issue is the size of the imaginary “billiard-balls”, how many of them there are, and how many collisions they experience as they move around an airfoil.
There are a few examples in the education literature that make use of simulations, although these do not directly contribute to a fundamental understanding of lift. Fazio, et al. [129] is the first example reported using an aircraft flight simulator. Lane [130] presents some nice simple dynamics of flight using simulations. This is arguably an underutilized tool in the basic physics education around lift [131]. Critically, it is typically specialized software that is not easily accessible and usable by educators who are not aviators. As such, it is more likely to be seen in an engineering context [132,133].
Ison [134] is another middle ground supporting both Bernoulli and Newton. The lack of viscosity and Navier–Stokes means there is no underlying ‘why’, but the books referred to and content are very reflective of an aviation perspective.
Eastwell [74] is very similar to Raskin, which is cited. The same issues are apparent, and many of the effects attributed to Coanda are just viscosity, which interestingly is the title of the paper (Bernoulli? Perhaps, but What about Viscosity?). However, not all viscus effects can be ascribed to Coanda as the content implies, although this appears to be a growing misconception.
Zembal-Saul, et al. [135] present a simple blow-through wind tunnel, a great way to demonstrate Bernoulli. The curriculum they present is full of many demonstrations that require Coanda and Bernoulli, as indicated by Yost [136] in his letter, which was highly critical of the original paper. The criticism is based on the use of Bernoulli alone, while interestingly, Yost insists that Coanda and Newton’s 3rd Law are all that is required to explain lift. Unfortunately, the response from Cole and Zembal-Saul [137] is very dismissive and does not really cause any skepticism or serious reflection; simply a reference that supports the Bernoulli approach is presented. This is a common theme in the debates that have occurred in the pages of journals. In principle, every criticism of every paper is worth serious contemplation, and most just reflexively respond with “here is some literature that supports my world view”. While the original XKCD cartoon about lift incorrectly uses the inverted flight argument (see Figure 18), the underlying message is correct, and falsification and skepticism are cornerstones of the scientific method.
Figure 18.
The original XKCD comic about lift education (Munroe, R (ND) https://xkcd.com/803/), (accessed on 18 May 2023).
Linton presents a series of papers on all manner of aerodynamic phenomena for the education audience [138,139,140]. Surprisingly, Linton cites Babinsky (2003) as the one responsible for exposing the misconceptions and fallacies around lift; it is clear from this review that countless authors have addressed this. Linton presents all-new aerodynamics [138]; there is no sin or sine-squared law, but there are still invalid assumptions starting with Newton’s laws. By using traditional aerodynamics [14], real power curves can be calculated and compared to Linton’s results, proving that his approach is incorrect. In fact, just looking at the values presented in Linton’s third figure, there is an obvious problem [92]. The takeoff-induced power for the B747-400 can be correctly calculated as 21.3 MW (assuming a standard atmosphere and knowing the wing area, takeoff, speed, and takeoff weight, with a fundamental text such as Hurt [58]). In contrast, Linton has calculated the induced power at more than 50 MW, more than twice the actual value. Similarly, knowing the lift-to-drag ratio, the cruise power can be determined using the same information; this is equal to 57 MW, and Linton has this at 90 MW, another significant margin of error. The following papers [137,138] are not at all representative of flapping wing aerodynamics [141]; although they do provide qualifying statements in the conclusion.
The third Bernoulli debate starts with Kamela [142] and is much softer given that the author has read at least some of the prior debates and adjusted explanations to suit the growing body of knowledge. The letter from Eastwell [143] highlights potential viscous effects. The reply by Kamela [144] is very nice because it employs instrumentalism in that it uses the simple theory to estimate a value and uses a more detailed theory to predict a similar value. It should be noted that Bernoulli and the selected potential flow employed by Kamela are effectively the same theory, which is Newton’s Laws of Motion applied to inviscid fluids, so it is not surprising that they give the same result. The topic of discussion is how air blown across an orifice, which is flush to a flat surface, does not result in a reduction in pressure; instead, the orifice needs to be raised up to produce a reduction in pressure, as illustrated in Figure 8. It should be noted that if entrainment were at work here as claimed by Eastwell, then the fluid in Figure 8a would be drawn up, as the entrained air from inside the port would now be at a lower pressure. This is not observed, and, hence, entrainment (Coanda) is not needed to explain Figure 8b.
The third Bernoulli debate continues with McCarthy [145], which is controversial, based on the quote, “Because of [Bernoulli’s] contribution… modern flight is possible”. While some fundamental aspects of fluid dynamics were observed and quantified by Bernoulli, flight is not possible because of those observations. This is the fundamental issue with using names on effects, principles, laws, equations, etc. Admittedly, the historical context of science is essential to science education, but given that McCarthy stresses the significance of language in the science context, the language in the history and education context must also be considered. McCarthy presents the equal transit time theory and Bernoulli to explain lift, with Bernoulli being the centerpiece of the article. The brief letter from Kerr [146], noting equal transit time is incorrect, does not really add to the debate. The letter from Eastwell [147] is more critical, pointing out potential issues with using Bernoulli to explain any of the four air-blowing activities presented by McCarthy. Eastwell simply states that by removing mention of Bernoulli and replacing it with entrainment (Coanda), the article can be saved. Given that the original article is not about aerodynamics but science education and history, with specific context to Bernoulli, one wonders if Eastwell understood the intent of the paper. The actual resolution to the problem is to correctly contextualize Bernoulli as the originator of these thoughts about moving fluids and pressure. A correct description of the paper tent is provided in Section 3.1.2 above. Falsification requires Eastwell’s proposed pure Coanda explanation with Newton’s 3rd Law to explain all the cases; instead, he empirically justifies one (that uses curved surfaces) and then rationalizes to all four, noting that a paper tent does not involve a curved surface. Sadly, the response by McCarthy [148] is worse than the criticism. As demonstrated in Section 3.1.2, with sufficient knowledge, it is possible to contextualize Bernoulli along with Coanda to fix the entire content of the original paper; however, McCarthy simply uses uncertainty and confusion on the topic as a defense to pick and choose the preferred science that fits the narrative. To quote McCarthy “We, as science teachers, are left to decide…the explanation of lift that we wish our students to derive.” This is dangerous language that mirrors the attitudes and behaviors of climate change deniers, flat-earthers, and anti-vaxxers [149].
McCabe [150] is interesting. The introduction starts well, putting Navier–Stokes front and center. The important limitation that Navier–Stokes describes the flow of a continuum, which, as a mathematical object, effectively embodies Zeno’s paradox (a continuum is infinitely divisible), is noted. It is known that air is made of discrete elements. However, at the scale of incompressible aerodynamics for aircraft, the predictive power of Navier–Stokes means it is the tool of choice for aircraft design. There are molecular models, such as lattice Boltzmann, and these are applied to hypersonic aerodynamics for spacecraft re-entry, etc. [151]. Following this, McCabe proves that Bernoulli alone cannot explain lift, with a similar statement made for circulation alone. However, it is confusing if he is for or against Coanda; initially against Coanda, he states that “there is no genuine force of attraction between the wing surface and the boundary layer airflow”. In contrast, the second half of the article focuses heavily on Coanda in Formula 1 car aerodynamics.
López-Arias, et al. [152] is the first in a series of papers by the group. In this, they are not concerned with aerodynamics and present “Coanda” in terms of the teapot effect. The apparatus they show facilitates a great quantitative investigation. However, as noted in Section 3.1.3, the teapot effect demonstrates surface tension, and the two justifying citations used from the Journal of Fluid Mechanics are about fluid jets in the same fluid (air in air and water in water) and not as is presented here, water in air. The author’s following papers appear to inductively leap from the conclusion that the teapot effect is Coanda to a conclusion that Coanda explains lift [153,154]. This is supported by a reference to Anderson & Eberhardt. The authors state that viscosity is needed to accelerate the air; this is simply not true, the pressure gradient is the mechanism by which the flow is accelerated, and the viscosity provides an asymmetric acceleration above the airfoil relative to below. They go on to say that the viscous interactions that are important are those at the airfoils’ surface, and this is also not true. The induced upwash, which is greater in viscous fluids relative to inviscid ones, is occurring prior to the airfoil and so is clearly a fluid–fluid effect. Similarly, the Kutta condition, which is the other key viscous effect, is the fluid interacting with itself to create the starting vortex, resulting in the movement of the rear stagnation point. The authors then present similar experiments that have been in the literature since the 1980s and the first great debate about Bernoulli. Importantly the authors state “airplanes do not fly in air jets but are fully embedded by the flow”; however, this does not prevent them from claiming that their version of Weltner’s demonstration (using jets of air) is still an equivalent comparison to how a wing works. The self-citation is a clear indication that the authors do not see a difference between a water stream in air (their previous work) and the work they previously cited, which used jets of the same fluid (air jets in air or water jets in water), which fluid mechanists do! The viscometry experiment presented by the authors, which is in none of the preceding lift education literature, is a great addition. The lack of a Nobel Prize for Prandtl and the boundary layer cannot be stressed enough, and this experiment is a clear visual demonstration of this. The authors present the same experiments again in a following publication [155]. In this article, they describe an aircraft as an “iron tube”, which is not a suitable word to use when describing an aircraft; metal, yes, given that aluminum is the primary metal, but steel (alloys of iron) is only 10% of the mass for a Boeing 787 and mostly in the engine. The authors’ flowing paper is a good example of an experiment to quantify the Coanda effect [156]. In this, they now have a jet of air in air; hence, Coanda is applicable. The discussion of viscosity to explain the effect is also well presented. If there is a need to demonstrate and quantify Coanda, this approach is ideal. The final paper of the groups is interesting because it clearly, and correctly, states that Coanda is not applicable to how a wing works and is only applicable in terms of boundary layer flow control devices [157].
Spathopoulos [158] repeats many of the mistakes that others have before. The approach is an emphatic statement that Newton’s 3rd Law is all that is needed to explain lift, and then they state, ‘here is the traditional equation to quantify lift’, noting the presented equation cannot be derived directly from Newton. In fact, the coefficient of lift (CL), which is the central feature of the equation as presented, was initially measured in a wind tunnel from pressure measurements and not measurements of airmass deflection.
A better approach to a wind tunnel with an open test section is presented by Heavers and Soleymanloo [159]. This could be further improved with modern approaches to STEM. Šlégrová and Šlégr [160] achieve similar things to the author before them who placed airfoils on stands on digital scales. However, they do so with a load cell attached to an Arduino, which is a great addition to a fundamental wind tunnel experiment, where the angle of attack could be controlled by the Arduino and the force on a load cell could be measured in response. Similarly, pitot tubes for drones can be connected to Arduinos, which would further add to a contemporary wind tunnel with automation and instrumentation. Liang and Wei [161] produce a small wind-tunnel-like device. This is great with respect to the use of u-tube manometers to show pressure changes around the airfoil. However, there is a major flaw. The flow visualization is achieved with a “flexible” string. Since this is manually divided ahead of the airfoil, it does not allow for sufficient upwash at high angles of attack and, therefore, does not correctly illustrate the flow streamlines.
Brown and Friedrichsen [162] present a more education-focused study. However, the underlying assumption for the experiments they use to tackle confusion is aerodynamics. As seen before in the literature, and debated previously, there are issues with using a pure Bernoulli explanation for aerodynamic demonstrations that involve blowing air. Coanda clearly needs to be considered. The confusion is exemplified in the proposed “molecule talk” the authors advocate. The simulation of internal flow within a venturi tube is used to show that random collisions between molecules are reduced when the streaming velocity is increased and the static pressure is decreased. This is true; the definition of pressure in the kinetic theory of gases is that it is related to random collisions. However, when there is a jet of air, the static pressure in the jet will equalize with the ambient air because the jet will expand to have the same static pressure, although it will have greater dynamic pressure because it has a velocity relative to the ambient air. As such, the random collisions inside the jet are the same as the random collisions in the ambient air. The thing missing in the “molecule talk” is the viscosity. The result of this is that the kinetic energy of the jet is transferred to the neighboring ambient air, entraining it into the flow and thereby reducing the pressure of the ambient air. It is not the jet that has less pressure; the jet pulls some ambient air along with it, thereby reducing the pressure around it. That explains the tent experiment and the flow attachment in the soda can experiment. Faulkner and Ytreberg [163] also use a simulation of molecules to demonstrate pressures and velocity changes in a venturi.
Robertson [164] presents a very strange introduction where Newton is not appliable because of forces that result in losses, a claim without a reference. On the topic of lift, Robertson takes an all-in approach with Bernoulli, Coanda, and streamline curvature combined. As with similar papers before, Robertson does not add anything to the literature, with the list of conclusions being the key features of Anderson & Eberhardt, although Robertson states that the ultimate reaction force for an aircraft is pressure at the earth’s surface, unlike Anderson & Eberhardt.
Jones [165] provides another increment on the path of Coanda, not Bernoulli. While discussing how an air stream can levitate a cupcake, Jones unnecessarily adds an “impact” force, which is presumably a Newtonian ski effect. Recall Hewitt’s observation of dust on a simple fan; “impact” with the surface is not something associated with fluid flow. Lipscombe and Mungan [166] is another contemporary Coanda and not Bernoulli paper, this time for blowing across pieces of paper as has been well established in the literature.
Deshpande and Sivapragasam [167] and their companion paper [168] achieve a similar outcome to the works of previous aerodynamicists before them, in the best way, with Navier–Stokes front and center. The authors do present an amusing paradox to the streamline curvature argument that is worth reading.
Singh, et al. [169] present a formalization of the stream tube pinching model of lift, or what is referred to as the area difference model. Ultimately, the theory is developed due to a complete misunderstanding of how viscosity is involved in the creation of a starting vortex and how an airfoil, any airfoil, capable of creating lift at any angle of attack, will have a flow asymmetry, which is the missing element they seek.
Koumaras and Primerakis [170] simply repeat the previous work by Kamala; however, they offer a Coanda explanation, as was discussed in the correspondence of Kamala’s work at the time. They have a deus ex machina approach to Coanda, where it captures viscous effects and the continuum hypothesis; that is, there are no voids in a fluid. Consider water around a dolphin; if one of its fins were to become stalled, the flow “separates”, and it does not become a vacuum; there is not immediately an air pocket underwater. Stall or separation means there is a recirculation region where on average, relative to the free stream velocity, the stalled/separated flow is traveling backwards (see Figure 4). Importantly, it must be noted that there is always fluid in that region; this is the nature of a continuum—it is smooth and continuous at the smallest scale. This is an issue for air, where we intuitively and incorrectly link lower pressures to lower densities, such that if there is a lower pressure in a region, we think of fewer molecules. Hence, the choice of a dolphin in water, given the notion of a vacuum or air pocket in deep water, is absurd. So, the Coanda effect does not describe this feature of fluid flow. Furthermore, the effect observed again by Koumaras & Primerakis can be explained by Bernoulli if applied correctly (see Figure 19). The neglected aspect of Bernoulli is that if a blower is used as the source of air, the air in that blower is the same air that is in the room. That is, it has the same static pressure, likely 101,325 Pa. This air is given kinetic energy, raising the total pressure of the fluid in the stream but not changing the static pressure. A stable jet in an ambient fluid will have the same static pressure; otherwise, it would also be subject to pressure gradient forces. So, the air that is blown across the flat orifice has static pressure P and dynamic pressure q, illustrated in Figure 19. The test end feels this static pressure P, which, as just mentioned, is the same P at the reference end of the manometer. If that jet is then constricted as in a venturi effect, it will now have a higher q and a lower P; this means the P at the test end is now less than the P at the reference end, giving the measure difference in pressure. The likely point of confusion comes from the fact that we feel the wind from a fan. This is pressure; it is just not static pressure. It is dynamic pressure due to the flow speed.
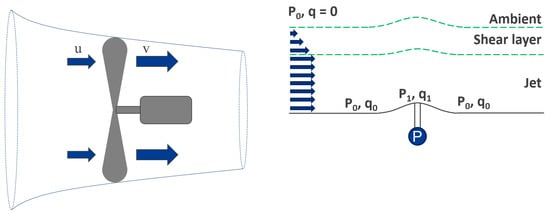
McLean continues the tradition of qualified aerodynamicists trying to produce a top-down explanation of lift [171,172]. His proceeding book is a masterpiece [18]. However, it is full to the brim with calculus, hence the reason for the two articles in The Physics Teacher. McLean and the previous work by Lissaman as cited provide solid footing for not using a pure momentum transfer statement. Ultimately, McLean falls back on a heavily asterisked Newton’s Laws of Motion statement, which, based on the above readings, will likely result in misuse by those in Newton’s trenches against those in the Bernoulli trenches.
Mahajan [173], as with many, incorrectly criticizes Bernoulli. Again, there is nothing in Bernoulli that relates longer path lengths, curved surfaces, or transit times to pressure, as referred to by Mahajan. Bernoulli is only a relationship between the total pressure (energy per unit volume), dynamic pressure (kinetic energy per unit volume), and static pressure. Bernoulli will correctly determine the pressure across an airfoil if an inviscid solution to the stream function of potential flow with circulation has been determined. This can then give the pressure coefficient along the top and bottom surfaces, which can be integrated to give the coefficient of lift. However, if you have neither pressure nor velocity, then Bernoulli can do nothing. These misconceptions are not unique to Mahajan; they have grown in the literature for decades, as camps for and against Bernoulli have grown and become entrenched. The poorly stated aspect of what Mahajan, and others against Bernoulli, point to is that pure Bernoulli explanations cannot describe the asymmetry in velocity around an airfoil. As such, those that do not understand fluids need to add additional elements to be able to support a Bernoulli statement. These additional elements are not part of Bernoulli; they are crutches used by those who do not understand enough about aerodynamics but who do know that aerodynamicists measure pressure differences to determine lift force.
Genz and Falconer [174] discuss an expert-validated Flight Physics Concept Inventory (FliP-CoIn). This was presented in the preceding years at various conferences [175,176,177]. It would be interesting to look at the inventory, the questions, and the solutions. As noted above, there are clear disagreements in the literature about flight concepts. The safest thing to do would be to avoid controversial aspects and focus on what is agreed upon. They found that “within one mind—naïve concepts can coexist with expert concepts”. Based on the presented body of knowledge from the literature and in the associated textbooks, this is not surprising. Several examples above have highlighted technical derivations, which are then undercut with an intuition that is a belief but not knowledge; however, that belief is forced into the ultimate definition presented. The main reason this is not surprising is that it is the same cognitive dissonance that exists with climate change deniers and many others [178].
Wild [8] discussed the origin of the equal transit time fallacy. This was accompanied by a discussion of potential flow, circulation, and Navier–Stokes to explain the flows associated with lift at those different levels. The fact that equal transit is a feature of pure potential flows is significant pedagogically, given the use of these methods in engineering is ubiquitous, albeit with the corrections noted in Section 2.2. However, the concept that potential flows produce equal transit times is not documented in the corresponding texts utilized in aerodynamics education. Follow-up work demonstrated a low-cost accurate wind tunnel, which was used to demonstrate that the curved shape of the airfoil was not important to lift generation [179]. The most recent work by Wild investigated illustrations in the educational literature of the flow around airfoils and wings [57]. It was found that more than half claiming to show flow around airfoils incorrectly illustrated flow around a wing. Of the cases, 28% did not include upwash, and 56% did not illustrate stagnation, resulting in significant confusion about the extent of flow asymmetry in lift production.
5. Summary
In general, all of the explanations of lift fall into the two broad categories noted in the background section: those based on Newton’s 3rd Law (action/reaction) and those based on pressure differences (Bernoulli). In each of these, there are many variations in the theme. To facilitate a complete understanding of the knowledge landscape, a summary is provided below.
5.1. Bernoulli
Pressure difference is immediately linked to Bernoulli. Without a causal explanation, Bernoulli is then linked to:
- Equal transit time;
- Path length difference;
- Curved airfoil or hump;
- Area difference or stream tube pinching;
- Venturi effect.
As previously mentioned, the concept of equal transit time comes from D’Alembert [8]. More interestingly, while many point to Babinsky for debunking equal transit time, equal transits are possible [180]. The actual transit time depends on the thickness of the airfoil and the angle of attack. The upper flow may transit in more, less, or equal time relative to the lower flow, although, in most practical cases, the upper flow is much faster. The transit time is also often incorrectly related to path lengths, usually relying on the geometry of the airfoil (a curve or hump). This is because the missing causal link for all Bernoulli explanations is the reason for the velocity difference; rather, it is inferred that velocity is simply given by the distance divided by time (path length and equal transit). The other common feature to exploit is that there is a constriction in the flow, which results in a reduction in the area available for the flow, pinching the stream tubes. Then, via conservation of mass for an incompressible flow, the fluid must go faster through a smaller area to have the same mass flow rate. While this is true, an acceleration requires a force, and stream tube pinching is not a force; it is an observation. The issue with Bernoulli-only explanations is the missing cause for the fluid velocity, which gives the pressure difference needed for the lift force.
5.2. Newton
There is several ways Newton’s 3rd Law can be utilized to rationalize a lifting force. These include:
- Ski effect, or steppingstone;
- Sine-squared law;
- Sine law;
- Downwash or downward turning;
- Magnus;
- Coanda.
These approaches literally originate with Newton, who notably tried and failed to explain the forces observed in fluids. Using conservation of momentum for elastic collisions, he derived his famous sine-squared law. Just sticking your hand outside a moving car, you can disprove a sine-squared relationship, since it only varies between 0 and 1. The relationship must be at least a sin law, which gives 0 lift at 0 degrees and 90 degrees and maximal lift at 45 degrees, which is a sin2x relationship. However, lift has a linear relationship with the angle of attack [14], beyond the small angle approximation assumed by some in the education literature [82]. In fact, this linear relationship was forced up to 45 degrees for an RAF 19 airfoil with six slots by Handley Page [181]. These Newton approaches appear rooted in the mistaken intuition about flow as shown in Figure 13b. If the flow becomes parallel to the airfoil, this results in a sin relationship, and the requirement to reflect “billiard-balls” necessitates a sine-squared relationship (not illustrated).
Downwash is an exclusively 3D phenomenon and appears to be associated with a fundamental confusion about lift production [19]. Downward turning, however, is present in the flow around an airfoil, as is upward turning before. Without viscosity, the amount of upwash and downwash and the relative gradients result in no net momentum flux and, hence, no lift. However, with viscosity, the momentum flux can be used to understand lift. As noted in the background, while there is a momentum flux across an airfoil, it does not equate to all of the lift force generated.
While the idea that “the Magnus effect equals lift” is not in the literature, it is effectively implied when the approach is to “consider the forces on a spinning ball (or cylinder)”. The inductive leap is implicit. Admittedly, the streamlines are very similar, but the mechanism is clearly different, although both are fundamentally viscous effects.
Coanda has become the almost de facto explanation in modern education [17], given the long list of complaints against Bernoulli. Interestingly, if you read actual Coanda literature, there is no claim that this effect is responsible for conventional lift [182]. Modern proponents of Coanda appear to want to change its definition such that it describes the unintuitive things that fluids do, that is, Coanda as deus ex machina. However, an extra name is not needed here. Navier and Stokes’ addition of viscosity means they describe how real fluids flow. The Coanda effect does not need to be distorted into a term that means “all things fluid”. Around an airfoil, there is no jet and there is no entrainment; hence, there is no Coanda effect!
5.3. Both Newton and Bernoulli
There are other explanations, which technically do not constitute their own paradigm, and are used by both camps. These include:
- Streamline curvature;
- Circulation.
The streamline curvature, which has been derived in a number of the papers above, is more commonly associated with a pressure difference, seen with Webster [20]. However, the approach of Babinsky [121] uses the curvature as a mechanism for downward turning. For circulation, the same is true. Wild [32] used circulation coupled with Bernoulli to give the pressure of the lift force, while Weltner [61] used circulation as another downward-turning mechanism.
5.4. Navier–Stokes
Figure 20 below shows the full set of equations for Navier–Stokes in three dimensions from the NASA Glenn Research Center. This is shown to illustrate the complexity of the topic. However, we can express it in a highly simplified version, where all of the vector calculus is hidden:
here, ρ is the density, at is the acceleration in time, as is the acceleration in space (like circular motion), g is the acceleration due to gravity, ∇P is the pressure gradient force, and τμ is the viscous force. This is almost F = ma, except the mass is density, so it is per unit volume. That said, it is still the correct version of Newton’s 2nd Law to use for fluids. Importantly, the equation tells us accelerations in fluids are related to specific forces, gravitational, pressure, or viscous (in aerodynamics, we ignore gravity). This is a statement of equality and does not describe one-way causation. If we want a reduction in pressure over the airfoil, we need acceleration. However, if we want acceleration in the fluid, we need a pressure gradient. The saving grace comes from the obstacle, the airfoil itself; in the streamwise direction, the stagnation of the streamline is a deceleration (see Figure 17b). This then gives a pressure gradient that accelerates the flow around the airfoil. Without viscosity, we obtain D’Alembert’s paradox, a symmetric pressure field. With viscosity, there are additional forces and accelerations such that we end up with an asymmetry, giving less pressure above relative to below, along with an induced upward turning of the flow and a downward turning of the flow.
ρ(at + as) = ρg − ∇P + τμ,
The causal relationship for Navier–Stokes can be summarized as:
- A rigid solid body in a continuum flow produces a pressure gradient (P);(Flowing fluid must move around an obstacle due to changes in pressure);
- The P accelerates flow correspondingly (+a if P ↓, −a if P ↑);(The changes in pressure slow the flow in some places and accelerate it in others);
- The “lower flow” has a favorable P until ~rear stagnation point (TE);(The “lower flow” tends to be forced towards the airfoil all the way along the bottom with minimal changes in speed);
- The “upper flow” has favorable P until LE, then P unfavorable to TE;(The “upper flow” is accelerated rapidly around the leading edge and then slowly decelerates towards the trailing edge);
- The freestream pressure P∞ gives a P “towards” the airfoil between stagnation points, primarily for the upper surface;(For the upper surface, the lower pressure near the obstacle relative to the pressure far away accelerates the flow towards the surface);
- Viscosity is the attractive force between fluid elements;
- LE viscosity induces more flow upward, and TE viscosity results in vorticity;
- TE vorticity “fed” by P moves the rear stagnation point to TE (creating the starting vortex);
- The result is flow asymmetry: vup > vlo; hence, Pup < Plo and momentum flux (upward and downward turning);
In a steady state, all of the processes are happening at the same time, and isolating them is effectively impossible. The order represents what happens in a transient situation, where the flow will establish a quasi-inviscid field before the starting vortex is shed. This just has acceleration and pressure. Points 6 to 8 clearly occur after motion starts, and the asymmetry in 9 is the result. The Navier–Stokes equations indicate that Newton’s Laws of Motion, when accounting for viscosity, give the pressure difference around an airfoil that equates to the lift force experienced.

Figure 20.
Full Navier–Stokes for 3-dimensional unsteady flow, shown to illustrate how complex fluid mechanics and aerodynamics is. This work is in the public domain.
The concept of a favorable pressure gradient has not previously been discussed. Referring to the wind tunnel in Figure 6 and Figure 7, the inlet can be a short “sharp” curve, as the pressure gradient is “pushing” the fluid together; this is a favorable pressure gradient. In contrast, the outlet needs to be a shallow gradual expansion; otherwise, the flow separates or stalls. A favorable pressure gradient is one that keeps the fluid together, like a support or brace, while an unfavorable pressure gradient does not.
In the above description of Navier–Stokes, Coanda is incorrectly invoked by many to explain the fifth aspect. This aspect is just the result of the fact that for the upper surface flow, the lowest pressure occurs at the surface of the airfoil. As such, the pressure gradient is towards the surface. If the angle of attack is low, below 10 degrees, this will result in flow that is attached. If the angle of attack is high, above 15 degrees, this will result in separated or stalled flow. These are indicative numbers, and they depend on the curvature of the airfoil, the air speed, and other features as noted previously [181]. Importantly, most explanations of lift miss points six to eight, with many also combining these into the incorrect deus ex machina label of ‘Coanda’.
The subtle undertones of this section and the subsection headings are that of names. Narratives and storytelling are part of our traditions, even in science [183]. As such, the name of a protagonist is usually essential. Hence, if a name is needed to explain lift, the honor belongs to Navier and Stokes. Both Bernoulli and Newton, in terms of their specific contributions, are insufficient, and Coanda is not applicable. The only debate to be had is if you are a traditionalist (a fluid mechanist) and say Navier and Stokes, or maybe you are more modern (an aerodynamicist) and want to say Prandtl. Either would technically be acceptable.
6. Conclusions
Importantly, we have known since Prandtl [3] that both a pressure difference and a momentum flux can be described across an airfoil. Prandtl also established that the aircraft is ultimately supported by the over-pressure on the earth surface. We also know that a fluid only acts on an object via pressure and shear forces at its surface [102]. The need to claim one of pressure or momentum and not the other has been a dominant feature of the literature for the past 50 years, since Smith [36]. All attempts to produce a classical Newtonian explanation for lift ultimately fail because of the nature of fluid mechanics and the governing set of partial differential equations. That is, to claim lift is the result of air being deflected down ignores three-quarters of what is happening. This is exemplified by the fact that experimental aerodynamicists measure pressure differences in wind tunnels when characterizing lift. Similarly, the circulation used by more mathematical aerodynamicists is directly linked via Bernoulli to the same difference in pressure, which is ultimately the force acting at the surface of an airfoil. This simplification, however, is responsible for misconceptions that Bernoulli can explain lift, which is incorrect. The full set of governing equations is that of Navier–Stokes and requires viscosity to produce flows that match our real-world observations. Importantly, these equations are Newton’s Laws of Motion for real fluids; hence, in the end, a Newtonian description of lift is possible. Viscous effects were incorporated by Prandtl with his boundary layer theory, a crucial turning point in the development of aerodynamics.
For science educators, it should be obvious that until the concept of momentum is taught, there is no way to include momentum flux across an airfoil, especially the important subtleties regarding the choice of a control volume. Since air pressure is taught at lower levels, a pressure-based explanation is going to be preferred. While Bernoulli’s relationship gives the needed pressure to explain lift, there is nothing in Bernoulli that gives the required difference in velocity, and, hence, it should be avoided. Importantly, the use of Coanda also needs to be avoided, given that it is not applicable to aerodynamic lift. The features incorrectly attributed to Coanda include the continuum hypothesis, where there are no voids in the fluid. This can be better explained by a pressure gradient that prevents voids from forming, again using water flow and not air to avoid confusion. The other feature people incorrectly ascribe to Coanda is just viscosity, the stickiness of a fluid. So rather than using Bernoulli and a velocity difference to explain the difference in pressure, which will result in a follow-up question about why the velocities are different, one should use viscosity to explain the flow asymmetry. Because air sticks to itself a little, it does not flow symmetrically around a wing. We can draw how it does flow, and the result is less pressure on top relative to below. The nature of viscous flow is complicated and explained in Part 2 [19].
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
My study of lift education in 2022 included my 15-year-old son, Graham Derrick Wild. I helped him build a wind tunnel for his high school science project, and he used it to win first place (engineering) in the state science fair (SEAACT Science and Engineering Fair), something I never did. Sadly, he passed away on 14 December 2022, not long after that achievement, and before learning that he had become a published author [179], something he was looking forward to. I miss his collaboration and contribution.
Conflicts of Interest
The author declares no conflict of interest.
References
- Lilienthal, O. Birdflight as the Basis of Aviation; Isenthal, A., Translator; Markowski International: Hummelstown, PA, USA, 1889. [Google Scholar]
- Lanchester, F.W. Aerodynamics: Constituting the First Volume of a Complete Work on Aerial Flight; Archibald Constable & Company: London, UK, 1907. [Google Scholar]
- Prandtl, L. Applications of Modern Hydrodynamics to Aeronautics; US Government Printing Office: Washington, DC, USA, 1921.
- Von Kármán, T. Aerodynamics; McGraw-Hill: New York, NY, USA, 1954. [Google Scholar]
- Bloor, D. The Enigma of the Aerofoil: Rival Theories in Aerodynamics, 1909–1930; University of Chicago Press: Chicago, IL, USA, 2011. [Google Scholar]
- Goldstein, S. Fluid mechanics in the first half of this century. Annu. Rev. Fluid Mech. 1969, 1, 1–29. [Google Scholar] [CrossRef]
- Anderson, J.D. A History of Aerodynamics: And Its Impact on Flying Machines; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Wild, G. On the origins and relevance of the equal transit time fallacy to explain lift. arXiv 2021, arXiv:2110.00690. [Google Scholar]
- Sevryugin, V.A.; Skirda, V.D. Viscosity of molecular newtonian liquids. Colloid J. 2021, 83, 490–499. [Google Scholar] [CrossRef]
- Sutherland, W. Lii. The viscosity of gases and molecular force. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1893, 36, 507–531. [Google Scholar] [CrossRef]
- Van Lear, G.A. Pressure energy—A misconception. Am. J. Phys. 1934, 2, 99–100. [Google Scholar] [CrossRef]
- Seifert, J. A review of the magnus effect in aeronautics. Prog. Aerosp. Sci. 2012, 55, 17–45. [Google Scholar] [CrossRef]
- Robins, B. New Principles of Gunnery: Containing, the Determination of the Force of Gun-Powder, and An Investigation of the Difference in the Resisting Power of the Air to Swift and Slow Motions; Wingrave: London, UK, 1742. [Google Scholar]
- Anderson, J.D. Introduction to Flight; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Spalart, P.R. Extensions of d’alembert’s paradox for elongated bodies. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150106. [Google Scholar] [CrossRef]
- Von Doenhoff, A.E.; Abbott, F.T. The Langley Two-Dimensional Low-Turbulence Pressure Tunnel; NACA-TN-1283; National Advisory Committee for Aeronautics: Washington, DC, USA, 1947.
- Anderson, D.W.; Eberhardt, S. Understanding Flight, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2009. [Google Scholar]
- McLean, D. Understanding Aerodynamics: Arguing from the Real Physics; Wiley: West Sussex, UK, 2012. [Google Scholar]
- Wild, G. Misunderstanding flight part 2: Epistemology and the philosophy of science. Educ. Sci. 2023, 2023, 2539334. [Google Scholar]
- Webster, D.L. The physics of flight. J. Frankl. Inst. 1920, 189, 553–580. [Google Scholar] [CrossRef]
- Webster, D.L. What shall we say about airplanes? Am. J. Phys. 1947, 15, 228–237. [Google Scholar] [CrossRef]
- Richardson, E.G. Some lecture and laboratory experiments in aeronautics. Am. J. Phys. 1934, 2, 22–25. [Google Scholar] [CrossRef]
- Van Dyke, M. An Album of Fluid Motion; Parabolic Press: Kirkland, WA, USA, 1982. [Google Scholar]
- Otis, A.S. Mathematics and science in aeronautics. Math. Teach. 1942, 35, 102–111. [Google Scholar] [CrossRef]
- Pope, F.; Otis, A.S. Elements of Aeronautics; World Book Company: New York, NY, USA, 1941. [Google Scholar]
- Blanchard, H.R. High school aeronautics experiments. Sci. Teach. 1946, 13, 18–43. [Google Scholar]
- Blanchard, H.R. Lift and drag. Sci. Teach. 1946, 13, 68. [Google Scholar]
- Bates, C.W. Building a wind tunnel. Sci. Teach. 1951, 18, 207–209. [Google Scholar]
- Katz, M. Airfoil device. Sci. Child. 1972, 10, 29. [Google Scholar]
- Overstreet, M. Wing designs verified in a low-speed wind tunnel. Sci. Teach. 1975, 42, 6–7. [Google Scholar]
- Stollberg, R.; Munch, T. How does an airplane stay in the air? Elem. Sch. Sci. Bull. 1954. Available online: https://www.jstor.org/stable/43085602 (accessed on 18 May 2023).
- Wild, J.M. Airplane flight. Phys. Teach. 1966, 4, 295–307. [Google Scholar] [CrossRef]
- Heck, J. With bernoulli and torricelli. Sci. Teach. 1968, 35, 64–67. [Google Scholar]
- Fiorello, A. The flying machine. Sci. Child. 1970, 8, 18–20. [Google Scholar]
- De Waard, E.J. The second, not the third. Sci. Child. 1971, 8, 2. [Google Scholar]
- Smith, N.F. Bernoulli and newton in fluid mechanics. Phys. Teach. 1972, 10, 451–455. [Google Scholar] [CrossRef]
- von Mises, R. Mathematical problems in aviation. Am. Math. Mon. 1940, 47, 673–685. [Google Scholar] [CrossRef]
- Smith, N.F. Bernoulli, newton, and dynamic lift. Part i*. Sch. Sci. Math. 1973, 73, 181–186. [Google Scholar] [CrossRef]
- Smith, N.F. Bernoulli, newton, and dynamic lift. Part ii*. Sch. Sci. Math. 1973, 73, 327–335. [Google Scholar] [CrossRef]
- Fletcher, N.H. Mechanics of flight as part of an introductory physics course. Aust. Phys. 1973, 10, 179–181. [Google Scholar]
- Prandtl, L. Essentials of Fluid Dynamics; Blackie: Glasgow, UK, 1952. [Google Scholar]
- Kermode, A.C. Mechanics of Flight, 7th ed.; Pitman: Lanham, MD, USA, 1962. [Google Scholar]
- Fletcher, N.H. Mechanics of flight. Phys. Educ. 1975, 10, 385. [Google Scholar] [CrossRef]
- Barnes, F.; Potter, A. Swing and lift. Phys. Educ. 1974, 9, 87. [Google Scholar] [CrossRef]
- Bedford, D.; Lindsay, R. A misinterpretation of bernoulli’s theorem. Phys. Educ. 1977, 12, 311. [Google Scholar] [CrossRef]
- May, D. Gliding through a science lesson. Sci. Child. 1978, 15, 18–19. [Google Scholar]
- Consuegra, G.F. Paper airplanes. Sci. Child. 1980, 17, 16–17. [Google Scholar]
- Martin, D.H. Misunderstanding bernoulli. Phys. Teach. 1983, 21, 37. [Google Scholar] [CrossRef]
- Iona, M. Beyond bernoulli. Phys. Teach. 1983, 21, 282. [Google Scholar] [CrossRef]
- Martin, D.H. The author replies. Phys. Teach. 1983, 21, 282. [Google Scholar] [CrossRef]
- Barnes, G.B. Curve balls, airplane wings, and prairie dog holes. Sci. Child. 1984, 21, 13–15. [Google Scholar]
- Brusca, S. Buttressing bernoulli. Phys. Educ. 1986, 21, 14. [Google Scholar] [CrossRef]
- Murphy, A.B.; Brusca, S. Bernoulli effect. Phys. Educ. 1986, 21, 262. [Google Scholar] [CrossRef]
- McCaughan, J.B.T.; Brusca, S. Bernoulli bunkum. Phys. Educ. 1987, 22, 9. [Google Scholar] [CrossRef]
- Kesling, M.D. Up in the air with bernoulli. Sci. Child. 1987, 24, 26–27. [Google Scholar]
- Wegener, P.P. The science of flight. Am. Sci. 1986, 74, 268–278. [Google Scholar]
- Wild, G. Is that lift diagram correct? A visual study of flight education literature. Phys. Educ. 2023, 58, 035018. [Google Scholar] [CrossRef]
- Hurt, H.H. Aerodynamics for Naval Aviators; Aviation Supplies & Academics: Newcastle, WA, USA, 1965. [Google Scholar]
- Flynn, G.J. The physics of aircraft flight. Phys. Teach. 1987, 25, 368–369. [Google Scholar] [CrossRef]
- Monce, M. Further physics of aircraft flight. Phys. Teach. 1988, 26, 202. [Google Scholar] [CrossRef]
- Weltner, K. A comparison of explanations of the aerodynamic lifting force. Am. J. Phys. 1987, 55, 50–54. [Google Scholar] [CrossRef]
- Auerbach, D. On the problem of explaining lift. Am. J. Phys. 1988, 56, 853. [Google Scholar] [CrossRef]
- Weltner, K. Response to ‘‘on the problem of explaining lift’’. Am. J. Phys. 1988, 56, 853. [Google Scholar] [CrossRef]
- Huebner, J.S.; Jagannathan, S. Explaining airfoil lift in introductory physics. Am. J. Phys. 1988, 56, 855–856. [Google Scholar] [CrossRef]
- Badeer, H.S.; Synolakis, C.E. The bernoulli-poiseuille equation. Phys. Teach. 1989, 27, 598–601. [Google Scholar] [CrossRef]
- Weltner, K. Aerodynamic lifting force. Phys. Teach. 1990, 28, 78–82. [Google Scholar] [CrossRef]
- Weltner, K. Bernoulli’s law and aerodynamic lifting force. Phys. Teach. 1990, 28, 84–86. [Google Scholar] [CrossRef]
- Freier, G.D. Lift and flow. Phys. Teach. 1990, 28, 518. [Google Scholar] [CrossRef]
- Weltner, K. Author’s response. Phys. Teach. 1990, 28, 518–519. [Google Scholar] [CrossRef]
- Bauman, R.P.; Schwaneberg, R. Interpretation of bernoulli’s equation. Phys. Teach. 1994, 32, 478–488. [Google Scholar] [CrossRef]
- Weltner, K.; Ingelman-Sundberg, M. Misinterpretations of bernoulli’s law. Eur. J. Phys. 1999. Available online: https://www.researchgate.net/publication/303974495_Misinterpretations_of_Bernoulli’s_Law (accessed on 18 May 2023).
- Raskin, J. Foiled by the coanda effect. Quantum 1994, 5, 5–11. [Google Scholar]
- Weltner, K.; Ingelman-Sundberg, M. Physics of flight–reviewed. Eur. J. Phys. 1999. Available online: https://www.angelfire.com/dc/nova/flight/PHYSIC4.html (accessed on 18 May 2023).
- Eastwell, P. Bernoulli? Perhaps, but what about viscosity? Sci. Educ. Rev. 2007, 6, 1–13. [Google Scholar]
- Fields, S. Hang a left at that cumulus! (how to steer an airplane). Sci. Scope 1990, 13, 10–14. [Google Scholar]
- Pols, Y.D.; Rogers, C.B.; Miaoulis, I.N. Hands-on aeronautics for middle school students. J. Eng. Educ. 1994, 83, 243–247. [Google Scholar] [CrossRef]
- Holmes, B.W. My teacher is a blowhard. Phys. Teach. 1996, 34, 362. [Google Scholar] [CrossRef]
- Telfer, C. Counting on a good flight. Math. Teach. Middle Sch. 2002, 8, 118–121. [Google Scholar] [CrossRef]
- Macalalag, A.; Johnson, B.; Johnson, J. Engineering encounters: Stem-ify me: It’s elementary! Designing butterfly wings. Sci. Child. 2018, 55, 76–82. [Google Scholar] [CrossRef]
- Hoover, T. Flight and the bernoulli effect. Sci. Scope 2018, 42, 12–15. [Google Scholar] [CrossRef]
- Hewitt, P.G. Conceptual Physics: Practicing Physics; Addison-Wesley: Boston, MA, USA, 2002. [Google Scholar]
- Sprigings, E.J.; Koehler, J.A. The choice between bernoulli’s or newton’s model in predicting dynamic lift. Int. J. Sport Biomech. 1990, 6, 235–245. [Google Scholar] [CrossRef]
- Gerhab, G.; Eastlake, C. Boundary layer control on airfoils. Phys. Teach. 1991, 29, 150–151. [Google Scholar] [CrossRef]
- Tamarkin, C.; Bourne, B. Soaring with science. Sci. Child. 1995, 33, 20–23. [Google Scholar]
- Baird, K.A.; Hara, L.; Perryman-Dyer, K.; Buckabee, D.A. When science soars: Paper airplanes help demonstrate bernoulli principles in native American educational settings. Sci. Teach. 1997, 64, 30–33. [Google Scholar]
- Greene, S.N. Take off with scientific methodology. Sci. Child. 1998, 36, 38–71. [Google Scholar]
- Chiles, M.A. Fearless fliers. Sci. Scope 1999, 22, 22. [Google Scholar]
- Oliver, D.; Ng, T. Rubber-band-driven airplane contest. Phys. Teach. 1999, 37, 108–109. [Google Scholar] [CrossRef]
- Waltham, C. The flight of a balsa glider. Am. J. Phys. 1999, 67, 620–623. [Google Scholar] [CrossRef]
- Waltham, C. Scaling in model aircraft. Am. J. Phys. 1997, 65, 1082–1086. [Google Scholar] [CrossRef]
- Schneidermeyer, K. Constructing flying discs. Sci. Child. 1999, 36, 28–31. [Google Scholar]
- Sterling, D.R. Science and engineering. Sci. Scope 2000, 24, 24–28. [Google Scholar]
- McGrath, S. Let’s take flight. Phys. Educ. 2003, 38, 487. [Google Scholar] [CrossRef]
- Bun, T.H. High fliers with rubber power. Phys. Educ. 2003, 38, 484. [Google Scholar] [CrossRef]
- Mason, K.; Rodenberg, S.; Kravik, R.; Polk, J.; Freit, B.; Schauf, S.; Brewer, B. If you build it, will it fly? Sci. Scope 2014, 37, 16–20. [Google Scholar] [CrossRef]
- Bautista, J. Engineering encounters: The paper airplane challenge: Students learn about variables and trials while designing an investigation. Sci. Child. 2017, 55, 82–87. [Google Scholar] [CrossRef]
- Katchmark, L.; McCabe, E.; Matthews, K.; Koomen, M. In flight with paper airplanes an exploration with elementary engineering. Sci. Child. 2020, 57, 42–47. [Google Scholar]
- Beaty, W. Airfoil lifting force misconception widespread in k-6 textbooks. Sci. Hobbyist 1996. Available online: https://gatepathshala.com/pdf/download/airfoilliftingforcemisconception.pdf (accessed on 18 May 2023).
- Lissaman, P. The facts of lift. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 15–18 January 1996; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1996. [Google Scholar]
- Waltham, C. Flight without bernoulli. Phys. Teach. 1998, 36, 457–462. [Google Scholar] [CrossRef]
- Anderson, D.; Eberhardt, S. How airplanes fly: A physical description of lift. Sport Aviat. 1999, 1999, 85–95. [Google Scholar]
- Anderson, J.D. Fundamentals of Aerodynamics; McGraw-Hill Education: New York, NY, USA, 2016. [Google Scholar]
- Cui, E.; Zhang, X. Ground effect aerodynamics. In Encyclopedia of Aerospace Engineering; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Kunzig, R. Why we go up. Discover 2001, 22, 21–22. [Google Scholar]
- Anderson, D.; Eberhardt, S. The newtonian description of lift of a wing. Am. J. Phys. 2001. submitted. Available online: https://inspirehep.net/literature/555685 (accessed on 18 May 2023).
- Anderson, D.; Eberhardt, S. A Physical Description of Flight; Fermi National Accelerator Laboratory: Seattle, WA, USA, 2004. [Google Scholar]
- Ceil, C. The science behind how planes fly. SSRN 2012, 2012, 2060875. [Google Scholar] [CrossRef]
- Ingle, D.; Bruellman, R.; Espana, E.; Galloway, K.; Anderson, T.; Meredith, T.; Porter, M. Science behind the lesson: It’sa bird! It’sa plane! It’s biomechanics! Coursesource. CourseSource 2019, 6, 1–6. [Google Scholar] [CrossRef]
- Auerbach, D. Why aircraft fly. Eur. J. Phys. 2000, 21, 289. [Google Scholar] [CrossRef]
- Hoffren, J. Quest for an improved explanation of lift. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001; AIAA: Reston, VA, USA, 2001. [Google Scholar]
- Eastlake, C.N. An aerodynamicist’s view of lift, bernoulli, and newton. Phys. Teach. 2002, 40, 166–173. [Google Scholar] [CrossRef]
- Ng, Y.-K.; Mak, S.-Y.; Chung, C.-M. Demonstration of newton’s third law using a balloon helicopter. Phys. Teach. 2002, 40, 181–182. [Google Scholar] [CrossRef]
- Yin-Soo, T. Affordable flying saucer toy illustrates the physics of flight. Phys. Educ. 2006, 41, 374. [Google Scholar]
- Edge, R. Caught in the draft. Phys. Teach. 2007, 45, 338–339. [Google Scholar] [CrossRef]
- Liebl, M. Investigating flight with a toy helicopter. Phys. Teach. 2010, 48, 458–460. [Google Scholar] [CrossRef][Green Version]
- Strong, J.C. Downwash and lift force in helicopter flight. Phys. Teach. 2011, 49, 132. [Google Scholar] [CrossRef]
- Carr, J.J. Toy helicopters and room fans. Phys. Teach. 2011, 49, L2. [Google Scholar] [CrossRef]
- Liebl, M. Liebl’s response. Phys. Teach. 2011, 49, L2–L3. [Google Scholar] [CrossRef][Green Version]
- Amir, N. Visualising ‘work done’ with a simple flying wheel toy. Phys. Educ. 2018, 53, 043003. [Google Scholar] [CrossRef]
- Monteiro, M.; Stari, C.; Cabeza, C.; Martí, A.C. Simple physics behind the flight of a drone. Phys. Educ. 2022, 57, 025029. [Google Scholar] [CrossRef]
- Babinsky, H. How do wings work? Phys. Educ. 2003, 38, 497–503. [Google Scholar] [CrossRef]
- Babinsky, H. Correct explanation for lift takes off. Phys. Educ. 2016, 51, 030108. [Google Scholar] [CrossRef][Green Version]
- Hermans, L.J. Physics in daily life: Why planes fly. Europhys. News 2009, 40, 30. [Google Scholar] [CrossRef][Green Version]
- Silva, J.; Soares, A.A. Understanding wing lift. Phys. Educ. 2010, 45, 249–252. [Google Scholar] [CrossRef]
- Bastianello, F. Lift generation: Some misconceptions and truths about lift. Young Sci. J. 2013, 6, 12–16. [Google Scholar] [CrossRef]
- Colwell, B. Leave bernoulli out of this. Computer 2003, 36, 10–12. [Google Scholar] [CrossRef]
- Zetie, K. Teaching about wing lift. Phys. Educ. 2003, 38, 486–487. [Google Scholar] [CrossRef]
- Hewitt, P.G. Bernoulli’s principle. Sci. Teach. 2004, 71, 51–55. [Google Scholar]
- Fazio, C.; Sperandeo-Mineo, R.M.; Tarantino, G. The physics of the aircraft pilotage. In Teaching and Learning Physics in New Contexts; GIREP: Ostrava, Czech Republic, 2004; Volume 150, pp. 213–218. [Google Scholar]
- Lane, W.B. Simulation of the physics of flight. Phys. Teach. 2013, 51, 242–244. [Google Scholar] [CrossRef]
- Somerville, A.; Pollock, L.; Wild, G. Incorporating a flight simulator based laboratory for physics of motion. In Proceedings of the 24th Congress of the Australian Institute of Physics, Adelaide, Australia, 11–16 December 2022. [Google Scholar]
- Franklin, M.; Ryan, J.; Somerville, A.; Pollock, L.; Wild, G. Simulation of the stability and control characteristics of a box-wing aircraft. In AIAA AVIATION Forum; American Institute of Aeronautics and Astronautics: Chicago, IL, USA, 2022. [Google Scholar]
- Somerville, A.; Pollock, L.; Joiner, K.; Lynar, T.; Wild, G. Sustainable aircraft design in engineering education: Conceive, design, implement, and operate virtually. In Proceedings of the 19th International CDIO Conference, Trondheim, Norway, 26–29 June 2023. [Google Scholar]
- Ison, D. Bernoulli or newton: Who’s right about lift? Plane Pilot 2006, 2006. [Google Scholar]
- Zembal-Saul, C.; Huckans, J.H.; Walker, D.C.; Hershberger, K.; Kurz, N.A.; Reed, D.; Cole, M.W. Taking flight: Using a wind tunnel to teach aeronautic principles. Sci. Scope 2007, 30, 27–31. [Google Scholar]
- Yost, D. Roundtable: Taking flight. Sci. Scope 2007, 30, 8. [Google Scholar]
- Cole, M.W.; Zembal-Saul, C. Roundtable: Taking flight reply. Sci. Scope 2007, 30, 8. [Google Scholar]
- Linton, J.O. The physics of flight: I. Fixed and rotating wings. Phys. Educ. 2007, 42, 351. [Google Scholar] [CrossRef]
- Linton, J.O. The physics of flight: Ii. Flapping wings. Phys. Educ. 2007, 42, 358. [Google Scholar] [CrossRef]
- Linton, J.O. The physics of flight: Iii. Hovering. Phys. Educ. 2007, 42, 496. [Google Scholar] [CrossRef]
- Shyy, W.; Kang, C.-k.; Chirarattananon, P.; Ravi, S.; Liu, H. Aerodynamics, sensing and control of insect-scale flapping-wing flight. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20150712. [Google Scholar]
- Kamela, M. Thinking about bernoulli. Phys. Teach. 2007, 45, 379–381. [Google Scholar] [CrossRef]
- Eastwell, P. Thinking some more about bernoulli. Phys. Teach. 2008, 46, 134. [Google Scholar] [CrossRef]
- Kamela, M. Kamela’s response. Phys. Teach. 2008, 46, 134–135. [Google Scholar] [CrossRef]
- McCarthy, D. Bernoulli’s principle: Science as a human endeavor. Sci. Scope 2008, 32, 18–25. [Google Scholar]
- Kerr, M. Bernoulli blowback. Sci. Scope 2009, 32, 6. [Google Scholar]
- Eastwell, P. Bernoulli and entrainment. Sci. Scope 2009, 32, 6–7. [Google Scholar]
- McCarthy, D. Author’s response. Sci. Scope 2009, 32, 6–7. [Google Scholar]
- Cook, J. Understanding and countering climate science denial. J. Proc. R. Soc. New South Wales 2017, 150, 207–219. [Google Scholar] [CrossRef]
- McCabe, G. Explanation and discovery in aerodynamics. arXiv 2005, arXiv:0512224. [Google Scholar]
- Succi, S. Lattice boltzmann beyond navier-stokes: Where do we stand? Aip. Conf. Proc. 2016, 1786, 030001. [Google Scholar]
- López-Arias, T.; Gratton, L.M.; Bon, S.; Oss, S. “Back of the spoon” outlook of coanda effect. Phys. Teach. 2009, 47, 508–512. [Google Scholar] [CrossRef]
- Zendri, G.; Gratton, L.; Lopez-Arias, T.; Oss, S. Flying with the right principles at hand: An interactive lab to understand the physical origin of lift. In International Workshop on Multimedia in Physics Teaching and Learning; Societa Italiana di Fisica: Udine, Italy, 2009; Volume 14, pp. 89–94. Available online: https://www.fisica.uniud.it/URDF/mptl14/ftp/full_text/FLYING%20WITH%20THE%20RIGHT%20PRINCIPLES%20AT%20HAND.pdf (accessed on 18 May 2023).
- Zendri, G.; Gratton, L.; Lopez-Arias, T.; Oss, S. Flying with the right principles at hand: An interactive lab to understand the physical origin of lift. Il Nuovo Cim. C 2010, 33, 89–94. [Google Scholar] [CrossRef]
- Oss, S.; López-Arias, T.; Gratton, L.M. Physics of flight at school: The safe route. Aip. Conf. Proc. 2010, 1263, 37–39. [Google Scholar]
- López-Arias, T.; Gratton, L.M.; Zendri, G.; Oss, S. Forces acting on a ball in an air jet. Phys. Educ. 2011, 46, 146. [Google Scholar] [CrossRef]
- López-Arias, T.; Gratton, L.M.; Zendri, G.; Oss, S. Using jets of air to teach fluid dynamics. Phys. Educ. 2011, 46, 373. [Google Scholar] [CrossRef]
- Spathopoulos, V. Flight physics for beginners: Simple examples of applying newton’s laws. Phys. Teach. 2011, 49, 373–376. [Google Scholar] [CrossRef]
- Heavers, R.M.; Soleymanloo, A. Measuring lift with the wright airfoils. Phys. Teach. 2011, 49, 502–504. [Google Scholar] [CrossRef]
- Šlégrová, L.; Šlégr, J. Simple apparatus for demonstrating factors that influence lift and drag. Am. J. Phys. 2022, 90, 359–364. [Google Scholar] [CrossRef]
- Liang, Q.; Wei, Y. An inexpensive apparatus for classroom visualization of the lift on airplane wings. Phys. Teach. 2018, 56, 612–613. [Google Scholar] [CrossRef]
- Brown, P.L.; Friedrichsen, P.M. Teaching bernoulli’s principle through demonstrations. Sci. Act. 2011, 48, 65–70. [Google Scholar] [CrossRef]
- Faulkner, B.E.; Ytreberg, F.M. Understanding bernoulli’s principle through simulations. Am. J. Phys. 2011, 79, 214–216. [Google Scholar] [CrossRef]
- Robertson, D. What supports an aeroplane? Force, momentum, energy and power in flight. Phys. Educ. 2014, 49, 75–82. [Google Scholar] [CrossRef]
- Jones, E. How an air stream can support a cupcake. Phys. Teach. 2015, 53, 264–265. [Google Scholar] [CrossRef]
- Lipscombe, T.C.; Mungan, C.E. Levitating a strip of paper by blowing over it. Eur. J. Phys. 2016, 37, 065002. [Google Scholar] [CrossRef]
- Deshpande, M.D.; Sivapragasam, M. How do wings generate lift? Popular myths, what they mean and why they work. Resonance 2017, 22, 61–77. [Google Scholar] [CrossRef]
- Deshpande, M.D.; Sivapragasam, M. How do wings generate lift? Myths, approximate theories and why they all work. Resonance 2017, 22, 135–147. [Google Scholar] [CrossRef]
- Singh, N.; Raja, K.S.; Janardhan, P. Clearing certain misconception in the common explanations of the aerodynamic lift. arXiv 2018, arXiv:1810.11461. [Google Scholar]
- Koumaras, P.; Primerakis, G. Flawed applications of bernoulli’s principle. Phys. Teach. 2018, 56, 235–238. [Google Scholar] [CrossRef]
- McLean, D. Aerodynamic lift, part 1: The science. Phys. Teach. 2018, 56, 516–520. [Google Scholar] [CrossRef]
- McLean, D. Aerodynamic lift, part 2: A comprehensive physical explanation. Phys. Teach. 2018, 56, 521–524. [Google Scholar] [CrossRef]
- Mahajan, S. Energy cost of flight. Am. J. Phys. 2020, 88, 903–905. [Google Scholar] [CrossRef]
- Genz, F.; Falconer, K.A. Naïve concepts of aerodynamic lift–data lessons from different (learning) cultures. In Proceedings of the Physics Education Research Conference (PERC), Virtual, 4–5 August 2021; pp. 147–153. [Google Scholar]
- Genz, F.; Falconer, K.A.; Bresges, A. Flight physics concept inventory: Current challenges and design for the flip-coin. In Proceedings of the American Association of Physics Teachers Winter Meeting, Atlanta, GA, USA, 14–17 January 2017. [Google Scholar]
- Genz, F.; Falconer, K.A.; Bresges, A. Electronic flight physics concept inventory: Eflip-coin. In Proceedings of the American Association of Physics Teachers Winter Meeting, San Diego, CA, USA, 14–17 January 2018. [Google Scholar]
- Genz, F.; Falconer, K.A.; Möhring, L.; Bresges, A. Flight physics concept inventory a multi-cultural concept inventory for flight physics. In Proceedings of the American Association of Physics Teachers Summer Meeting, Provo, UT, USA, 31 July–5 August 2019. [Google Scholar]
- Grossman, W.M. Cognitive dissonance. Philos. Mag. 2015, 2015, 30–31. [Google Scholar] [CrossRef]
- Wild, G.D.; Wild, G. An experimental investigation on the generation of lift by a flat plate. J. Stud. Res. 2022, 11, 4. [Google Scholar] [CrossRef]
- Bai, C.; Wu, Z. Transit time difference and equal or non-equal transit time theory for airfoils with lift. Chin. J Aeronaut 2022, 35, 8–11. [Google Scholar] [CrossRef]
- Smith, A.M.O. High-lift aerodynamics. J. Aircr. 1975, 12, 501–530. [Google Scholar] [CrossRef]
- Lubert, C.P. On some recent applications of the coanda effect. Int. J. Acoust. Vib. 2011, 16, 144–153. [Google Scholar] [CrossRef]
- Allchin, D. How not to teach historical cases in science. J. Coll. Sci. Teach. 2000, 30, 33–37. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).