Bringing Together Mathematics and Philosophy with Logic and Poly-Universe
Abstract
1. Introduction
2. Materials and Methods
2.1. Corpus, Data Gathering, and Analysis
2.2. Pedagogical Approach
2.2.1. Poly-Universe Materials
2.2.2. Exercises Implemented
2.2.3. Implementation
3. Results
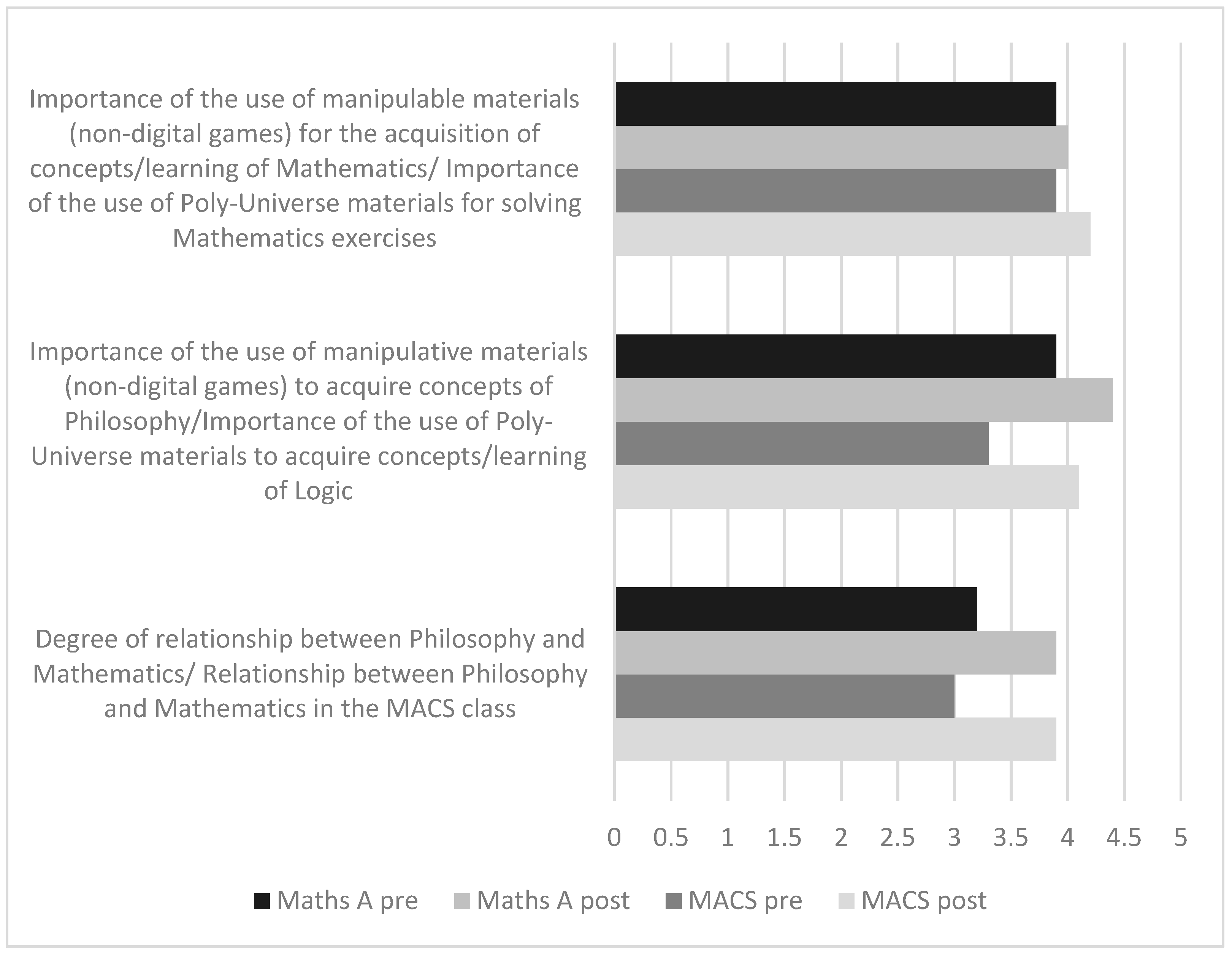
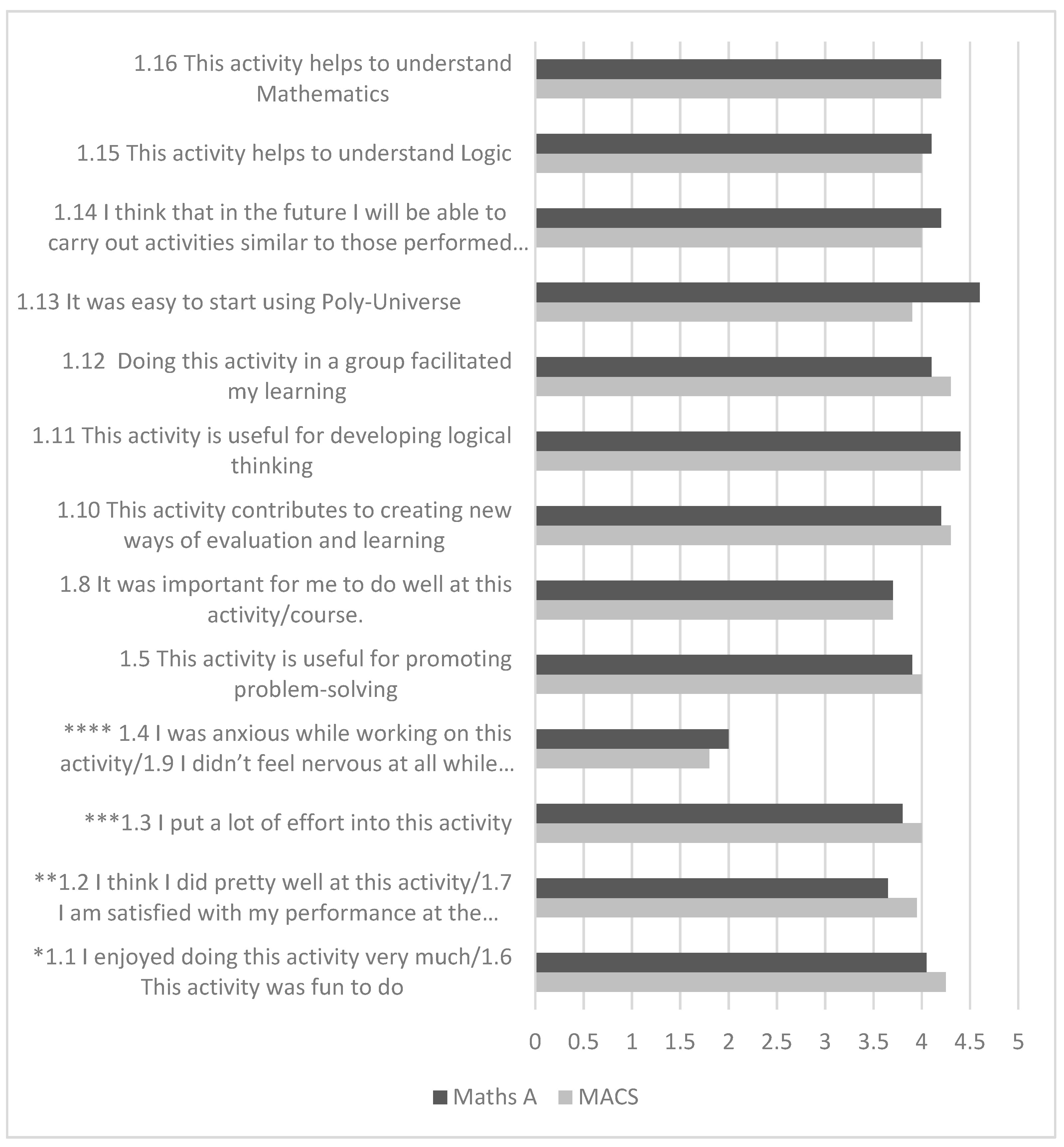
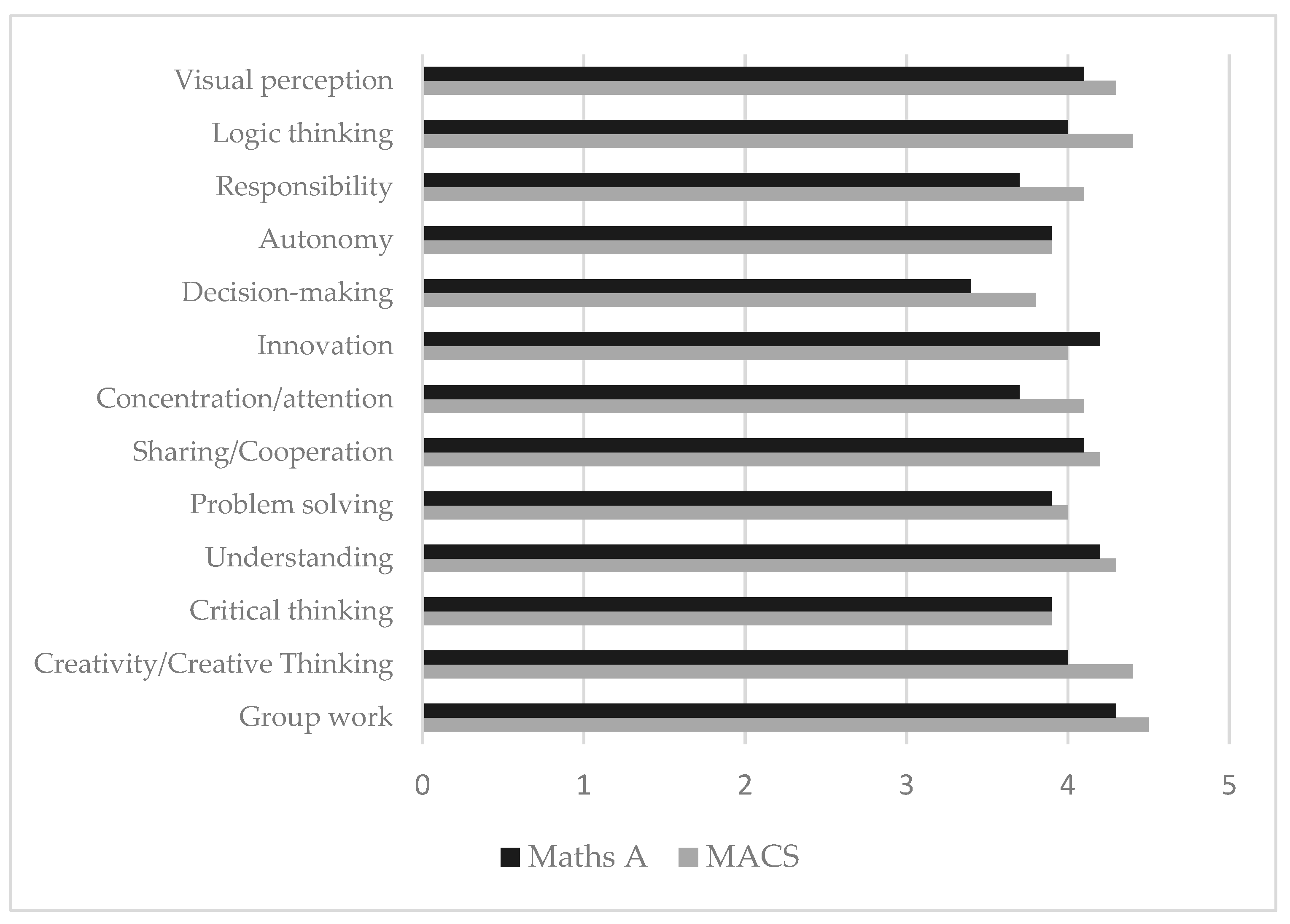
3.1. Students’ Perceptions of the Activity That Was Carried Out
3.2. Evaluation of Learning
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Doig, B.; Williams, J.; Swanson, D.; Borromeo Ferri, R.; Drake, P. Interdisciplinary Mathematics Education: The State of the Art and Beyond. In ICME-13 Monographs; Springer Nature: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Iversen, S.M. Modeling interdisciplinary activities involving mathematics and philosophy. Math. Enthus. 2006, 3, 85–98. [Google Scholar] [CrossRef]
- Hargreaves, A. Os Professores em Tempos de Mudança: O Trabalho e a Cultura dos Professores na Idade Pós-Moderna; Mc-Graw-Hill: Irvine, CA, USA, 1998. [Google Scholar]
- Morin, E. Os Sete Saberes Necessários à Educação do Future; Edições Piaget: Lisboa, Portugal, 2004. [Google Scholar]
- Gusdorf, G. Conhecimento Interdisciplinar. In Olga Pombo, Teresa Levy e Henrique Guimarães (org.), Antologia I, (9-40); Projecto Mathesis, Departamento de Educação da Faculdade de Ciências de Lisboa: Lisboa, Portugal, 1990. [Google Scholar]
- Perfil dos Alunos à Saída da Escolaridade Obrigatória, 2017. Disponível em. Available online: https://dge.mec.pt/sites/default/files/Curriculo/Projeto_Autonomia_e_Flexibilidade/perfil_dos_alunos.p (accessed on 12 December 2022).
- Decreto-Lei nº 55/2018 da Presidência do Conselho de Ministros, 2018. Diário da República: I Série, n°129. Available online: https://data.dre.pt/eli/dec-lei/55/2018/07/06/p/dre/pt/html (accessed on 11 December 2022).
- Despacho nº 6944-A/2018 do Gabinete do Secretário de Estado da Educação, 2018. Diário da República: IISérie, n° 138, 1° suplemento. Available online: https://dre.pt/dre/detalhe/despacho/6944-a-2018-115738779 (accessed on 11 December 2022).
- Moreira, S. Cooperar Para o Sucesso com Autonomia e Flexibilidade Curricular; Pactor: Lisboa, Portugal, 2019. [Google Scholar]
- Trindade, R. Autonomia, Flexibilidade e Gestão Curricular: Relatos de Práticas; Leya Educação: Lisboa, Portugal, 2018. [Google Scholar]
- Cohen, A.C.; Fradique, J. Guia da Autonomia e Flexibilidade Curricular; Raíz Editora: Lisboa, Portugal, 2019. [Google Scholar]
- Mansilla, V.B. Interdisciplinary work at the frontier: An empirical examination of expert interdisciplinary epistemologies. Issues Integr. Stud. 2006, 24, 1–31. Available online: http://hdl.handle.net/10323/4485 (accessed on 14 December 2022).
- Ashby, I.V.; Exter, M. Designing for Interdisciplinarity in Higher Education: Considerations for Instructional Designers. TechTrends 2018, 63, 202–208. [Google Scholar] [CrossRef]
- Klein, J. Typologies of interdisciplinarity. In The Oxford Handbook of Interdisciplinarity, 2nd ed.; Frodeman, R., Ed.; Oxford Press: Oxford, UK, 2017. [Google Scholar]
- Danesi, M. (Ed.) Interdisciplinary Perspectives on Math Cognition. Mathematics in Mind; Springer: Cham, Germany, 2019. [Google Scholar] [CrossRef]
- Otte, M.F.; de Barros, L.G.X. Philosophy, Mathematics and Education. Rev. História Educ. Matemática 2018, 4. Available online: https://histemat.com.br/index.php/HISTEMAT/article/view/204 (accessed on 10 January 2022).
- Friedman, K. The challenge of interdisciplinary research. In Proceedings of the 9th ACM Conference on Creativity & Cognition, Sydney, Australia, 17–20 June 2013. [Google Scholar] [CrossRef]
- Mancosu, P. The Adventure of Reason: Interplay Between Philosophy of Mathematics and Mathematical Logic, 1900–1940, 2nd ed.; Oxford University Press: Oxford, UK, 2014; ISBN 13 978-0198701514. [Google Scholar]
- Oliver, A. Review of Logic, Mathematics and Philosophy, by George Boolos. Br. J. Philos. Sci. 2000, 51, 857–873. Available online: http://www.jstor.org/stable/3541730 (accessed on 13 February 2023). [CrossRef]
- Aristidou, M. Is Mathematical Logic Really Necessary in Teaching Mathematical Proofs? Athens J. Educ. 2020, 7, 99–122. [Google Scholar] [CrossRef]
- Mesnil, Z. A Reference for Studying the Teaching of Logic. CERME 10; HAL Open Science: Dublin, Ireland, 2017. [Google Scholar]
- Saxon, J.S.; Stettner, E. (Eds.) Poly-Universe in School Education. Puse Methodology-Visual Experiences Based Mathematics Education. Available online: http://www.poly-universe.com/puse-methodology/ (accessed on 23 October 2019).
- Tegalsi, I. Motivation and Development—Using Poly-Universe Game in Teaching Mathematics and Other School Subjects. Athens J. Sci. 2022, 9, 177–192. [Google Scholar] [CrossRef]
- Schmidthaler, E.; Schalk, M.; Schmollmüller, M.; Sabitzer, B.; Andic, B.; Lavicza, Z. The Effects of Using Poly-Universe on Computational Thinking in Biology and Physical Education. In Proceedings of the 14th International Conference on Education Technology and Computers, Barcelona, Spain, 28–30 October 2022. [Google Scholar] [CrossRef]
- Hoffman, M. Discovering Information Visualization through Poly-Universe, Symmetry. Cult. Sci. 2020, 31, 15–22. [Google Scholar] [CrossRef]
- Despacho n.º 8476-A/2018, de 31 de agosto 2018. Diário da República n.º 168/2018, 2º Suplemento, Série II de 2018-08-3. Available online: https://dre.tretas.org/dre/3454131/despacho-8476-A-2018-de-31-de-agosto (accessed on 11 December 2022).
- Center for Self-Determination Theory. Self-Determination Theory. (n.d.). Available online: https://selfdeterminationtheory.org/intrinsic-motivation-inventory/ (accessed on 20 June 2022).
- Poly-Universe in Teacher Education. PUNTE. Available online: http://www.punte.eu/ (accessed on 22 June 2022).
- Poly-Universe in Teacher Education. Glossary. Available online: https://www.punte.eu/wp-content/uploads/PUSE_GLOSSARY.pdf (accessed on 22 June 2022).



| Questions | |||
|---|---|---|---|
| 1. Select the set of triangular pieces for which the proposition | P: The base field is green. | ||
| 1.1. For the set of fields obtained previously, indicate, justifying, the logical value of the following propositions. | Q: The smaller field is an equilateral triangle. | ||
| R: The largest field is yellow. | |||
| S: The middle field is red. | |||
| 1.2. Given the meanings of P, Q, R, and S, formalise the following propositions and state their logical value. | 1.2.1. The base field is green and the smaller field is an equilateral triangle. | ||
| 1.2.2. The base field is green and the larger field is yellow. | |||
| 1.2.3. The middle field is red and the base field is green. | |||
| 1.2.4. The largest field is yellow and the middle one is red. | |||
| 1.3. Calling A and B any two propositions, and taking into account the conclusions obtained in Question 1.2, complete the following table. | A | B | AB |
| V | V | ||
| V | F | ||
| F | V | ||
| F | F | ||
| Questions | |||
|---|---|---|---|
| 2. Select the set of circular pieces for which the proposition is true | P: The larger area is blue. | ||
| 2.1. Suppose that the areas (larger, intermediate, and smaller) in each of the pieces have diameters equal to 4, 2, and 1, respectively. For the set of pieces obtained previously, indicate, justifying, the logical value of the following propositions. | Q: The sum of the areas of the fields, major, intermediate, and minor is equal to . | ||
| R: The base area is circular. | |||
| S: The smaller area is yellow. | |||
| 2.2. Given the meaning of P, Q, R, and S, formalise the following propositions and state their logical value. | 2.2.1. The larger field is blue or the sum of the areas of the regions, larger, intermediate, and smaller, is equal to . | ||
| 2.2.2. The larger field is blue or the base region is circular. | |||
| 2.2.3. The smaller field is yellow or the base field is circular. | |||
| 2.3. Calling A and B any two propositions, and taking into account the conclusions obtained in Question 2.2, complete the following table. | A | B | AB |
| V | V | ||
| V | F | ||
| F | V | ||
| F | F | ||
| Questions | |||
|---|---|---|---|
| 3. Select the set of square tiles for which the proposition is true P: The base region is blue. Suppose that the fields (largest, middle, and smallest) on each of the pieces have sides equal to 4, 2, and 1, respectively. | |||
| 3.1. For the set of pieces obtained previously, indicate, justifying, the logical value of the following propositions. | Q: The piece has three similar fields. | ||
| R: The area of the larger region is twice the area of the intermediate region. | |||
| 3.2. Taking into account the meanings of P, Q, and R, formalise the following propositions and state their logical value. | 3.2.1. If the base region is blue, then the piece has three similar fields. | ||
| 3.2.2. If the base region is blue, then the area of the larger region is twice the area of the intermediate region. | |||
| 4. Now consider all the pieces (triangles, squares. and circles). | |||
| 4.1. State the logical value of the following propositions. | P: The larger field is blue. | ||
| Q: The smaller field is not blue. | |||
| R: The piece has 4 fields. | |||
| 4.2. Taking into account the meanings of P, Q, and R, formalise the following propositions and state their logical value. | 4.2.1. If the larger field is blue, then the smaller field is not blue. | ||
| 4.2.2. If the largest field is blue, the piece has 4 fields. | |||
| 5. Calling A and B any two propositions, and taking into account the conclusions obtained in Questions 3.2 and 4.2, complete the following table. | A | B | AB |
| V | V | ||
| V | F | ||
| F | V | ||
| F | F | ||
| Tasks | Determining the Logical Value of Propositions—Conjunction | True Table Construction | ||||
|---|---|---|---|---|---|---|
| 1.2.1 VV | 1.2.2 VF | 1.2.3 FV | 1.2.4 FF | 1.3 | ||
| MACS | Pre-test | 0.9 | 0.9 | 0.8 | 0.8 | 0.6 |
| Activity PUNTE | 1.0 | 1.0 | 1.0 | 1.0 | 1 | |
| Post-test | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| Mathematics A | Pre-test | 1.0 | 1.0 | 1.0 | 0.9 | 0.9 |
| Activity PUNTE | 1.0 | 1.0 | 1.0 | 0.9 | 0.9 | |
| Post-test | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| Tasks | Determining the Logical Value of Propositions—Disjunction | True Table Construction | ||||
|---|---|---|---|---|---|---|
| 1.2.1 V | 1.2.2 F | 1.2.3 V | 1.2.4 F | 1.3 | ||
| MACS | Pre-test | 0.8 | 0.5 | 0.3 | 0.6 | 0.2 |
| Activity PUNTE | 1.0 | 1.0 | 0.67 | 1.0 | 1.0 | |
| Post-test | 0.8 | 0.7 | 0.7 | 0.7 | 0.6 | |
| Mathematics A | Pre-test | 0.8 | 0.3 | 0.2 | 0.8 | 0.6 |
| Activity PUNTE | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | |
| Post-test | 0.9 | 0.8 | 1.0 | 1.0 | 0.9 | |
| Tasks | Determining the Logical Value of Propositions—Implication | True Table Construction | ||||
|---|---|---|---|---|---|---|
| 1.2.1 V | 1.2.2 F | 1.2.3 V | 1.2.4 F | 1.3 | ||
| MACS | Pre-test | 0.4 | 0.8 | 0.8 | 0.3 | 0.3 |
| Activity PUNTE | 1.0 | 1.0 | 0.67 | 0.0 | 0.33 | |
| Post-test | 0.6 | 0.8 | 0.5 | 0.3 | 0.7 | |
| Mathematics A | Pre-test | 1.0 | 0.9 | 0.3 | 0.3 | 0.6 |
| Activity PUNTE | 1.0 | 1.0 | 0.7 | 0.7 | 0.9 | |
| Post-test | 0.6 | 0.6 | 0.6 | 0.6 | 0.6 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mouro, A.P.; Brito, M.C.; Lopes, G.; Bidarra, M.d.G.; Vaz-Rebelo, P. Bringing Together Mathematics and Philosophy with Logic and Poly-Universe. Educ. Sci. 2023, 13, 356. https://doi.org/10.3390/educsci13040356
Mouro AP, Brito MC, Lopes G, Bidarra MdG, Vaz-Rebelo P. Bringing Together Mathematics and Philosophy with Logic and Poly-Universe. Education Sciences. 2023; 13(4):356. https://doi.org/10.3390/educsci13040356
Chicago/Turabian StyleMouro, Ana Paula, Margarida Cid Brito, Graça Lopes, Maria da Graça Bidarra, and Piedade Vaz-Rebelo. 2023. "Bringing Together Mathematics and Philosophy with Logic and Poly-Universe" Education Sciences 13, no. 4: 356. https://doi.org/10.3390/educsci13040356
APA StyleMouro, A. P., Brito, M. C., Lopes, G., Bidarra, M. d. G., & Vaz-Rebelo, P. (2023). Bringing Together Mathematics and Philosophy with Logic and Poly-Universe. Education Sciences, 13(4), 356. https://doi.org/10.3390/educsci13040356






