Design and Validation of a Test for the Types of Mathematical Problems Associated with Reading Comprehension

Abstract

Being able to understand a written text is an essential life skill, as is solving a problem, which configures a bidirectional relationship between both skills. With regard to reading comprehension, at least three specific levels are required to achieve a full understanding of a text: literal, inferential, and critical. For its part, mathematics has changed substantially in recent decades, prioritizing problem-solving as the central axis of the teaching process as it constitutes a resource for learning. This study connects both skills and aims to design and validate a mathematical problem-solving test contextualized to the quadratic function, to assess the level of reading comprehension of secondary school students. The study is nonexperimental, cross-sectional, and focused on psychometric aspects since it aims to validate a measurement instrument. It was applied on a pilot basis to three municipal secondary education courses in Chile. The content, construct, discrimination, and reliability validation tests carried out allowed us to demonstrate that the problem-solving test contextualized to the quadratic function is a reliable instrument to produce knowledge in educational research.

1. Introduction

Currently, reading comprehension is recognized as a fundamental skill for the integral development of students, since it is related to multiple personal and contextual factors for the performance of individuals, especially in the educational field [1]. However, in several studies around the world, researchers have found low levels of reading comprehension in students [2,3,4,5,6,7,8,9,10,11].

According to [12], regardless of its definition, reading is done to understand and this objective is divided into understanding explicit expressions in a text (literal comprehension) and configuring meaning from the implicit messages in a text, which is equivalent to making an inference [13,14,15].

On the other hand, the process of problem-solving in mathematics is defined as a complex process that requires multiple skills together. This process constitutes the understanding of the problem [16], the choice of the required information among the data, and converting this information into mathematical symbols to reach a solution through the required operations. According to [17], the process of reading comprehension of a mathematical problem is followed by solution planning and planning implementation steps.

Such is the importance of the relationship between reading comprehension and problem-solving that, in the international context, the Organization for Economic Cooperation and Development (OECD) for the Program for International Student Assessment PISA 2018 test, which measured 600,000 students from 80 countries, defined reading comprehension as a core assessment competency. The nature of reading, what is read, and how it is read, has changed substantially during the last decade, particularly due to the growing influence and development of information and communication technologies. Although reading is still done in a printed format, it is increasingly done in a digital format, which is not only textual but also auditory and visual. For such reason, the OECD has revised the conceptual framework for reading literacy to reflect these transformations [18].

As far as Chile’s reality is concerned, the latest PISA 2018 report as the main instrument of educational measurement of the countries belonging to the OECD indicates that students belonging to Chilean educational institutions present difficulties mainly in the areas of mathematics and language. It should be noted that the measurement is carried out with students who are 15 years old, which in Chile is equivalent to students who should be in the third year of secondary education [18].

Regarding language, the results conclude that only 32% of Chilean students surpass level 2 in reading comprehension. The 68% who are at levels 1 or 2 according to the OECD, at a minimum, can identify the main idea in a text of moderate length, find information based on explicit, though sometimes complex criteria, and can reflect on the purpose and form of texts when explicitly instructed to do so. About 3% of students in Chile obtained better results in reading, which means that they reached Level 5 or 6 in the PISA reading test. At these levels, students can comprehend long texts, deal with concepts that are abstract or counterintuitive, and make distinctions between fact and opinion based on implicit cues related to the content or source of the information. As in all the participating countries, in Chile, women show higher reading skills than men. This trend has been consistently maintained over time.

With respect to mathematical competence, the OECD explicitly relates it to a student’s ability to formulate, use and interpret mathematics in a variety of contexts [18]. The PISA 2018 report notes that about 48% of students in Chile achieved level 2 or higher in mathematics. At a minimum, these students can interpret and recognize, without direct instruction, how a (simple) situation can be represented mathematically (e.g., comparing the total distance between two alternative routes or converting prices in a different currency). The report concludes that, in Chile, 1% of students obtained a level of five or higher in mathematics. Systematically, females in Chile show lower mathematical competencies than males [18].

According to the current reform in Chile, in the Algebra unit, students begin the recognition of functions and their distinction with relationships in different contexts. In this unit, it is possible to identify topics related to the types of functions, particularly the quadratic function, whose teaching and learning are linked to the second year of secondary education according to the Ministry of Education in Chile (MINEDUC). It is explicitly stated that the student “…must show that he/she understands the quadratic function $f\left(x\right)=a{x}^2+bx+c(\mathrm{where}a,b\mathrm{and}c\mathrm{are}\mathrm{real}\mathrm{numbers},\mathrm{and}a\ne 0$), recognizing it in daily life situations and other subjects” [19] (p.16). Quadratic functions are used in many disciplines such as physics, economics, biology, and architecture. They are useful to describe movements with constant acceleration, projectile trajectory, profits, and costs of enterprises, and to obtain information without the need for experimentation [20]. In addition, quadratic functions are widely used in science, business, and engineering. However, there is an agreement in recent research, regarding the difficulty for students in learning the quadratic function [21,22], which has its origin not only in the cognitive domain but also in the affective domain.

In Chile, great difficulties have been evidenced in the understanding of the function, associated with its teaching and learning [23]. According to [24], students cannot solve problems when the mathematical object is a quadratic function. A study on quadratic functions by [25] concluded that teaching only focuses on conversion from an algebraic, tabular, and graphical representation, although students manage to solve tasks related to recognition. Several authors have proposed research on the teaching and learning of the quadratic function based on the use of representations, models, and technological environments [26,27,28,29,30,31,32,33], but there is no evidence of studies that relate reading comprehension with the mathematical object quadratic function.

We are certain that there is a bidirectional relationship between reading comprehension and mathematical problem-solving, that is, that reading comprehension can affect and become an integral part of problem-solving, and can in turn be affected by the content of the mathematical text or by the mathematical problem situation when reading the text. Based on reading comprehension theories and the literature review, the relationship under study is complex. The reading process can affect and act as an integral part of the problem-solving process, but little research has focused on this relationship. Unfortunately, in Chile, there are no validated instruments available to measure these types of variables, which would allow for the monitoring and diagnosis of their status and evolution.

The present research will place in perspective the existence of reading comprehension skills in the ability to problem-solve a specific mathematical object. In this context, the following objectives are formulated: The main objective of this study was to design and validate a mathematical problem-solving test contextualized to the quadratic function, to evaluate the reading comprehension level of high school students. The secondary objectives were to determine the degree of validity and reliability of the test for solving types of mathematical problems.

2. Theoretical Frameworks

Reading comprehension is a process in which diverse potentialities are put into play, since multiple factors influence the results at the moment of understanding a text, such as attention, effort and personal interest, and previous knowledge, among others. Reading comprehension can be defined by taking into account different approaches. Some of them consider the particular abilities of the readers [34,35], others emphasize the cognitive processes that are developed [36], and others are more comprehensive, considering several elements to define it [37,38].

Although there are several methodologies for the practice of reading comprehension, most of them are based on Barret’s taxonomy created in 1968. According to [39], a taxonomic evaluation conceives reading as a set of phases characterized by certain skills such as knowing the meaning of words, formulating inferences or anticipations, and understanding the author’s purpose, among others. The importance of Barret’s taxonomy, according to the research of [40], lies in the fact that it is based on a double dimension: cognitive and affective. Both allow for the development of critical and creative thinking.

2.1. Reading Comprehension

There are various definitions of reading comprehension. The OECD has defined it as “[…] the ability of students to understand, use, evaluate, reflect on, and engage with texts to achieve one’s goals, develop knowledge and potential, and participate in society [.]” [18] (p.29). This definition seeks to describe the greatest number of elements considered when understanding a text; that is when constructing the meaning of what is being read. Likewise, it includes purposes such as the use of texts to find some information or to reflect on the encounter established between the reader’s ideas and the ideas expressed in the text.

In the context of the research presented here, the definition of reading comprehension corresponds to that of the author [41] who states that reading comprehension means understanding and using the information obtained through the interaction between the reader and the author. Reading comprehension is a type of dialogue between an author and a reader in which written language becomes the medium.

For specific theories about the problem-solving process that includes reading the text of the problem as an important part, it is necessary to start by reading the text of the given problem to try to understand the problem [42,43,44,45]. Operationally, the reading comprehension construct consists of three hierarchical levels: literal, inferential, and critical. These levels, which must be developed to achieve full comprehension of a text, group together thought processes that are activated during the reader’s interaction with the text, in which he/she combines his/her previous experiences and ideas with those presented in the text, and builds new knowledge. The authors [46,47] and more recently [48], describe them in a similar way.

2.2. Reading Comprehension Levels

2.2.1. Literal Comprehension Level

This level of comprehension represents the minimum level of participation on the part of the reader and corresponds to the comprehension of what is explicit in the text, recognizing the basic structure of the text. That is, the reader recognizes the key phrases and words in it, without going beyond it, and captures what the text says without a very active intervention of the reader’s cognitive and intellectual structure.

2.2.2. Inferential Comprehension Level

This level is characterized by going beyond the ideas and information presented in the text, seeking a broader explanation of it, and relating ideas and personal experience, thereby formulating hypotheses and new opinions. This level goes beyond literal comprehension as it requires a degree of abstraction, encompassing logical deductions, and conjectures that can be made from certain data that can be extracted from the text. The main goal of this level is the elaboration of conclusions, favoring the relationship with other fields of knowledge and the integration of new knowledge into a whole.

2.2.3. Critical Comprehension Level

This level is considered ideal since critical reading implies that the reader makes a value judgment on the text read, and expresses his opinion by accepting or rejecting it, but with arguments; comparing the ideas of the text with his own experience or with external criteria. On the other hand, critical reading has an evaluative character in which the formation of the reader, his criteria, and knowledge of what he read, intervenes. Such judgments take into account qualities of accuracy, acceptability, and probability.

2.3. Mathematical Problem-Solving

The ability to solve mathematical problems is an important component of mathematical knowledge. Although students encounter many difficulties in problem-solving [49,50,51], there is evidence to suggest that the effective use of reading comprehension may be an important factor associated with successful outcomes.

The author [52], in research, carried out with students from third to eighth grade in which the reading comprehension and changes in mathematical achievement components such as problem-solving and data interpretation, mathematical concepts, and estimation were examined, reports that early reading comprehension is a positive and significant predictor of change for these math components. According to [53], in a description of the problem-solving behaviors of sixth and seventh-grade students, the use of the context, the registration of the information given in a problem, and the possibility of giving explanations and justifications were indicated as being associated with better performance tests in reading and mathematics.

Problem-solving is recognized in international educational measurements as well as in many national curricula [54]. Thus, the mathematical framework of PISA 2021 defines the theoretical foundations of mathematics assessment as being based on the fundamental concept of mathematical competence, relating mathematical reasoning, and three processes of the problem-solving cycle. The framework describes how mathematical content knowledge is organized into categories of content and categories of real-world contexts in which students will face mathematical challenges [55].

In formal education, in mathematics subjects, students will face problems. These problems can come from mathematics itself or real life [56], involving facts and contexts that can be modeled in mathematics. The current challenge is to have students develop mathematical competencies that are considered essential in the curriculum during the school years, integrating the knowledge and skills that provoke a positive attitude toward understanding a problem, and the ability to implement effective problem-solving processes [57].

Clearly, problem-solving is an important aspect of the curriculum, and even more important if the problems are contextualized. For this reason, the classification of types of problems by the authors [58,59,60] was chosen, who have been working in different areas of mathematics and consider both the nature of the problem and the context of the application.

Mathematical Problems

The typology considered is shown in Figure 1.

Nature of the problem: According to their nature, they are classified as routine and nonroutine.

• Problems will be routine if the student knows a previously established routine for their resolution.
• Problems will be nonroutine if the student does not know an answer or a previously established procedure.

Problem context: Depending on the context, they are classified as real, realistic, fantasist, or purely mathematical.

• Real Context Problem: A problem is a real context problem if it actually occurs in reality and engages the learner’s actions in reality.
• Realistic Context Problem: A problem will be realistic if it is likely to actually occur. It is a simulation of reality or a part of it.
• Fantasist Context Problem: A problem will be fantasist if it is the fruit of the imagination and has no basis in reality.
• Purely Mathematical Context Problem: A problem will be purely mathematical if it refers exclusively to mathematical objects: numbers, arithmetic relations and operations, and geometric figures, among others.

3. Methodology for Validation of the Mathematics Test

3.1. Procedure and Participants

The present study is nonexperimental, cross-sectional, and focused on psychometric aspects since its objective is to validate a measurement instrument [61]. For its implementation, a nonprobabilistic selection of municipal educational establishments was made. Once the educational establishments had been selected, the test was administered to students in mathematics courses at the third level of secondary school.

Before the application of the test, the nature of the study was informed, it was pointed out that there were no right or wrong answers and it was explained how to answer, emphasizing that the test was anonymous and that express consent was required to participate. The application was self-administered individually through the internet.

The criteria for the selection of the sample were the following: (a) attending the third year of secondary education and (b) voluntarily participating in the study. In this way, the sample was made up of 72 students belonging to three mathematics courses taught in a region in southern Chile. This group was made up of 35 men and 37 women, with an average age of 17 years.

3.2. Evaluation Test

In order to measure reading comprehension in the resolution of quadratic function application problems, a math test was designed and elaborated, whose construction stages included conceptually defining the types of problems and the levels of reading comprehension, operationalizing the conceptual definitions through indicators expressed in the problems elaborated, with questions that required a response from the student.

The mathematics test was structured based on the types of problems classified according to their nature as routine and nonroutine, and according to their context as real, realistic, fantasist, and purely mathematical [58], and in the three levels of reading comprehension defined as literal, inferential, and critical [48].

This instrument consists of five quadratic function application problems (realistic, purely mathematical, fantasist, and nonroutine). The response options to each type of problem contextualized to this mathematical object were in turn written with ten questions, nine of which were answered with four multiple-choice response options and the tenth with an open response.

The first four questions of each of the five problems correspond to the first literal level of reading comprehension, in that the student has the possibility of identifying the unknown of the problem, the data of the problem, the conditions for solving the problem, and determining the operations for its resolution.

Questions five, six, and seven of each of the five problems correspond to the second inferential level of reading comprehension, through the correct determination by the student, the order of operations of the problem, the establishment of the number of data involved in the problem, and the determination of the solution and verification of the problem.

Questions eight, nine, and ten of each of the five problems highlight the third critical level of reading comprehension through the establishment of a conclusion and a value judgment about the problem. Specifically, only question ten concludes with an open answer in which the student can establish a relationship between the mathematical problem posed and previous knowledge, and evaluate the statements of the problem by contrasting them with his own knowledge.

The analysis contemplates four phases that corresponded to the validation of the instrument: the analysis of the content validity of the test; the item discrimination analysis; the construct validity analysis of the test; and the determination of the reliability of the test.

Problem number four of the test of a nonroutine nature is presented below.

A passenger in a drifting lifeboat fires a first emergency flare into the air. The height (in meters) of the flare above the water is given by the function f(t) = −16t (t − 8), where t is the time (in seconds) since the flare was fired.   The passenger fires a second flare whose trajectory is represented on the graph. Find the function and determine the height of the flare that reaches the highest.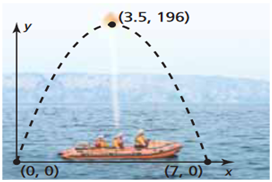

Instructions: For each question, mark the alternative that in your opinion is correct.

1. 

What is the unknown of the problem?

(a)

The final parabolic trajectory of both flares.

(b)

The formula that represents the dwell time of the flare.

(c)

The height of the flare that remains the longest in the air.

(d)

The function and the highest height of the flare in a given time.

2. 

What data do you have to solve the problem?

(a)

The given function and the three points of a parabolic trajectory.

(b)

The time and the points of intersection of the parabolic trajectory.

(c)

The concavity of the functions, both with t ˂ 0.

(d)

The function and the vertex associated with the trigger over time.

3. 

What is the condition to solve the problem?

(a)

Establish and compare the coordinates of the intersection with the Y-axis.

(b)

Establish and compare the coordinates of the intersection with the X-axis.

(c)

Establish the function that passes through three points and compare the vertices.

(d)

Establish the discriminant of the function whose vertex is given.

4. 

What operations must be performed to solve the problem?

(a)

Calculate the residence times in the air of both flares.

(b)

Calculate the values of the discriminant of each function associated with the flares.

(c)

Set the missing function and compare the vertices of the two throws.

(d)

Calculate the “y” coordinates of the vertex of the parabolas.

5. 

What is the answer to the problem?

(a)

The formula is f(t) = −16t² + 112t and the greatest height reached by a flare is 256 m.

(b)

The formula is f(t) = −16t² + 128t and the greatest height reached by a flare is 196 m.

(c)

The formula is f(t) = −16t² − 128t and the greatest height reached by a flare is 118 m.

(d)

The formula is f(t) = −16t² − 112t and the greatest height reached by a flare is 112 m.

6. 

How do you check that your answer is correct?

(a)

By establishing the concavity of the parabola.

(b)

By evaluating the x-value of the vertex in the function.

(c)

By graphing the points of intersection with the x-axis.

(d)

By graphing the vertex of each function.

7. 

What can you say about the number of data to solve the problem?

(a)

Too much data.

(b)

Missing Data.

(c)

Exact data.

(d)

The amount of data does not matter.

8. 

What can you conclude about the given problem?

(a)

It is required to establish the points of intersection of the quadratic equation.

(b)

It corresponds to a problem of analysis of the maxima of a function.

(c)

The statement does not allow setting the height of the second flare.

(d)

Corresponds to a problem of analysis of the zeros of a function.

9. 

In your opinion, on what does it depend that problems that are not practiced routinely can be solved?

(a)

Of the practice that they allow to address their resolution.

(b)

From the approach of easy-to-understand unknowns.

(c)

From the statement of the mathematical function associated with the problem.

(d)

Prior knowledge.

10. 

What is your opinion regarding the type of problem raised and the data provided for its resolution? _______________________________________________________

3.3. Pilot Application

An application of the mathematics test was carried out on a pilot sample of high school students to identify and correct the terms that are difficult to understand for the students to whom the instrument is oriented, for the analysis of its psychometric properties and validity of the construct.

The modifications proposed by the specialists, together with that of the students of the pilot study, allowed the elaboration of the final version of the test which will be applied in a future stage to a definitive sample.

4. Results

4.1. Instrument Validation Process

4.1.1. Content Validity

The content validity of the mathematics test was assessed by the judgment of eight subject matter experts [62]. The collaboration of professionals with experience in mathematics, in the reading comprehension construct, and the evaluation of measurement instruments was requested through an Expert Evaluation Questionnaire, which contained the definitions of the aspects to be evaluated. The problem was accepted as valid when the degree of agreement between them was greater than or equal to 85% congruence [63].

The experts gave their opinions and/or suggestions on modifications to the instrument. The proposed changes were modifications in the wording of some of the questions and the elimination of others, validating the content of the test, and obtaining version two with 5 problems and 50 questions.

The validation in terms of relevance, representativeness, and clarity guaranteed for the mathematics test the types of problems according to nature and context, and the three levels of reading comprehension.

4.1.2. Validity of Discrimination

The psychometric properties of the math test problems are generally good. No problem has more than 1.9% of nonresponses.

In relation to the averages obtained, most of the problems have an intermediate value and, together with this, the standard deviations are high enough to affirm that most of the questions discriminate between the different subjects. On the other hand, after analyzing the kurtosis and asymmetry, the vast majority of the problems have a mesokurtic and symmetric distribution (the coefficients are between −0.5 and 0.5), accounting for moderate asymmetries or kurtosis, showing that the answers to the types of problems are not distributed concentrated.

As can be seen in

Table 1. Psychometric properties of the problems.

N° of Problem	Type of Problem	% Nonresponse	Mean	Standard Deviation	Asymmetry	Kurtosis
1	Realistic	0.4	3.3	1.06	−0.25	−0.37
2	Nonroutine	1.9	2	1.03	−0.72	−0.19
3	Fantasist	0.8	3.7	1.15	−0.63	−0.36
4	Purely Mathematical	0.3	3	1.01	−0.16	−0.4
5	Nonroutine	0.6	1.6	0.93	−1.76	2.76

, the first four problems were shown to be highly desirable for the subjects, concentrating their responses on the highest values. Problem 5 (mean = 1.6; kurtosis = 2.76) was shown to be highly undesirable.

4.1.3. Construct Validity

For construct validity based on the underlying theoretical model of reading comprehension in mathematical problem-solving, the factors conceived as latent variables and their respective observed variables were designed using the estimation program AMOS version 19.0 [64].

For the estimation of the parameters, the maximum likelihood method was used. In all cases, to evaluate the goodness of fit of the corresponding model, the chi-square test $\left(X^2\right)$ was calculated, which indicates the probability that the divergence between the sample variance–covariance matrix and that generated from the hypothetical model is due to chance. Because $X^2$ is very sensitive to sample size variations [65], additional measures of model goodness-of-fit were employed [66].

Once a model has been estimated, it is necessary to evaluate its quality. For this purpose, we used the goodness-of-fit statistic. It should be noted that there are three types of goodness-of-fit statistics: absolute goodness-of-fit statistics (assess the residuals), relative goodness-of-fit statistics (compare the fit with respect to another model with a worse fit), and parsimonious goodness-of-fit statistics (assess the fit with respect to the number of parameters used). None of them provides all of the information needed to assess the model, and usually, a set of them is used and reported simultaneously [67].

Table 2. Goodness-of-fit statistics and reference criteria used in the research.

Goodness-of-Fit Statistics	Abbreviation	Criteria
Absolute fit
Chi-squared	$X^2$	p > 0.05
Chi-square ratio/degrees of freedom	$X^2/g.l.$	<3
Comparative fit
Comparative goodness-of-fit index	CFI	≥0.90
Tucker–Lewis index	TLI	≥0.90
Others
Goodness-of-fit index	GFI	≥0.90
Corrected goodness-of-fit index	AGFI	≥0.95
Square root of the mean of standardized residuals	RMR	close to zero
Root Mean Square Residual Approximation	RMSEA	<0.08

shows those used in the present study.

4.1.4. Reliability Estimation

Reliability was analyzed through Cronbach’s alpha. Acceptable alpha values were those greater than or equal to 0.7 [61]. As part of the Confirmatory Factor Analysis, the adequacy of the correlation matrix was verified to ensure its possible factorization using the Kaiser–Meyer–Olkin (KMO) test and Bartlett’s sphericity test, using SPSS version 20.0. The reliability of the math test presented an ordinal alpha of 0.79, which shows adequate internal consistency.

5. Conclusions

The main objective of this study was to design, validate, and apply a contextualized problem types test to the quadratic function, and to assess the level of reading comprehension of secondary school students belonging to educational establishments in southern Chile. The secondary objectives were to determine the validity and reliability of the test. For this, the test was applied to a pilot sample of three high school courses, to identify and correct the students’ understanding of the proposed problems, and to analyze the psychometric properties of the test as a whole.

The modifications and comments proposed by the expert judges and the students of the pilot study allowed the elaboration of the final version of the test, which will be applied in a future stage to a definitive sample.

From the evaluation of the psychometric attributes of the mathematics test, it is possible to affirm that there is evidence of its content and construct validity, of the good discrimination capacity of its items, and the good reliability of the final version of the test.

Consequently, it is possible to affirm that the final version of the test, composed of five problems and fifty questions associated with them, constitutes a reliable and valid instrument to evaluate reading comprehension in the teaching of the mathematical quadratic function of Chilean high school students. The psychometric attributes of the test guarantee the use of purely mathematical, realistic, fantasy, and nonroutine types of problems, to discover the different levels of reading comprehension such as literal, inferential, and critical.

Therefore, this instrument can be used to measure the reading comprehension of high school students, with respect to the mathematical learning that can be generated by solving problems contextualized to the quadratic function.

It should be noted that this work offers opportunities and research lines that are in the process of being built. Among the opportunities, the validity of this type of instrument for the production of robust and pertinent statistical information that contributes to the knowledge of the relationship between problem-solving and reading comprehension is highlighted.

The data collected through this math test becomes a substantial basis for knowing, discussing, and reflecting on the impact of this evaluative instrument on teaching and student learning, and on the quadratic function mathematical object, whose learning is considered of high difficulty by high school students at different levels.