Contextualized Mathematical Problems: Perspective of Teachers about Problem Posing

Abstract

This research describes the perspective of secondary school teachers on the selection, elaboration, and implementation of contextualized mathematical problems in secondary education in Costa Rica. An exploratory and descriptive quantitative study is carried out, applying a questionnaire to 67 in-service secondary school mathematics teachers. The dimensions of the sources used by teachers, the difficulties encountered and the learners’ background considered for problem selection and elaboration are analyzed. In addition, the contexts present in the problems that teachers propose are classified. The results indicate that teachers use textbooks for the selection of mathematical problems. In addition, they give a favorable opinion regarding the use of realistic contexts in the creation of new problems. However, several of the proposed problems present fictitious or mathematical contexts. The highest percentage of the participants points out the need for training for the elaboration of contextualized mathematical problems.

1. Introduction

Several investigations in Mathematics Education have acknowledged the need for and importance of considering the sociocultural context within the process of teaching mathematics [1]. Indeed, it would be necessary to “encourage students to link the mathematics they learn at school with the world in which they live” (p. 6, own translation) [2]. In particular, Rosa and Orey [3] highlight that, through curricular pedagogical actions, mathematics should foster the connection between the mathematical practices present in the community and the mathematics taught in educational centers. This is achieved through the creation of culturally relevant mathematical activities.

From the Ethnomathematics Program perspective, mathematics is considered a cultural construction. Therefore, it is advocated that its teaching be characterized by the implementation of activities based upon the particularities and needs of the environment [4]. This research program allows us “to understand mathematical knowledge/doing throughout the history of humanity, contextualized in different interest groups, communities, people and nations” (p. 17, own translation [5]).

Likewise, a contextualized school practice favors student learning and motivation. In this line, it has been observed that the process of creating contextualized mathematical activities close to the educational center reality contributes to the motivation of both the student and the teacher involved, while favoring the learning of the contents developed [6].

Costa Rica, the country where this research is developed, has incorporated into its mathematics curriculum the use of problems with active contextualization to develop mathematical knowledge. In fact, since the implementation of the new curriculum, documented in the Mathematics Study Programs of the Ministry of Public Education (MEP) [7], problem solving has been promoted, enhancing, as a result, modeling. The methodological changes proposed in this curriculum have required teachers to search for and invent contextualized mathematical problems to implement them in the classroom.

Within this panorama, the need to strengthen the competence called “problem posing” arises, which consists precisely in the ability to search, detect, discover and create events that allow mathematical problematization of environmental situations [8]. In this same line, Cai et al. [9] state that “If we recognize problem posing as an important intellectual activity in school mathematics, then we must determine if teachers and students are capable of posing important and worthwhile mathematical problems” (p. 6).

Although it is true that mathematics teachers have received training on various aspects of the current Mathematics Study Programs [10], it becomes imperative to know their perspectives on their roles in the selection and creation of contextualized problems within the teaching-learning context, especially in periods of educational reform. As expressed by Flores [11], it is difficult to apply a reform satisfactorily if teachers, as the main practical agents, do not feel it necessary, do not assume it as their own, and do not contribute the necessary efforts to carry it out. In this regard, Gil and Rico [12] point out the need to know the perceptions and beliefs of teachers as diagnostic elements that allow designing training and training plans with greater success possibilities. This idea is shared by Handal and Herrington [13], who indicate that knowing teachers’ perceptions of innovative curricular reforms is essential for planning and executing training processes. Like a domino effect, the beliefs of teachers and the methodology they develop in their classes can have a direct impact on the attitudes that students have towards mathematics [14].

MEP, in turn, promotes for teachers to use modeling as an excellent resource to contextualize mathematics in the formal education system. Modeling makes it possible to translate a problem situation into mathematical language [15] and constitutes a proposal for pedagogical action [16], which allows connecting the mathematical practices of cultural groups through ethnomodeling. In the words of Kaiser and Sriraman [15], there are various modeling perspectives, among which realistic or applied modeling (where solving real-world problems is promoted) and contextual modeling (linked to the subject’s environment) stand out. Both options (modeling and ethnomodeling) constitute a cognitive challenge for teachers [17], who may present difficulties in searching for and developing problems of this nature. This is especially due to the disconnection that some have with nearby reality and the little or no training they have received in this regard [18,19]. Indeed, to ensure the success of problem-posing tasks in the classroom, it is necessary to strengthen initial and ongoing teacher training programs through work spaces that allow future teachers and practicing professionals to pose problems [8].

In this scenario, teachers must not only know mathematical content, but also be researchers of the environment where they work, to create mathematical problems that make more sense for students. Hence, we formulate the research question: what is the opinion of secondary school teachers in relation to the selection and creation of contextualized problems in their mathematics lessons?

Then, the objective of this work is to describe the perspective of secondary school teachers in Costa Rica on the selection and elaboration of contextualized mathematical problems.

2. Mathematical Contextualization and Problem Posing

Various researchers have built their own definitions of what is meant by a school math problem. For the purposes of this study, the construct presented by MEP [7] in the Mathematics Study Programs has been adopted: “a problem is an approach or a task that seeks to generate interrogation and student action using mathematical concepts or methods” (p. 29, own translation) so that students “solve problems that they have not encountered before.” (p. 29, own translation [7]). In this document, it is clarified that the problem must allow the student to think about mathematical ideas without these having been previously explained. It also encourages that the mathematical concepts and procedures be linked to the context of said problem. This approach agrees with the position of various researchers who propose that mathematical problems are situations that require a high cognitive demand for the solver, this is because there is no algorithmic guide procedure that leads directly to the solution [20,21,22].

Starting from the premise that mathematics is implicit in one’s daily life, impregnated by the context, it is desirable that the curricula and class activities contemplate the cultural values of mathematics [1,5].

Solving problems from the sociocultural context plays a very important role in learning mathematics, because the student can appreciate mathematics from a closer and more useful perspective. Problem solving must be considered as an integral part of mathematical learning, and when possible, that the contexts of these problems refer to familiar experiences, environments and applications for the students [23,24]. When the contexts are familiar and close to the student, these constitute starting points for their mathematical practice and promote cognitive strategies through the use of common sense; thus, allowing the student to move towards levels of greater formalization. Indeed, “rich contexts act as domains of reality disclosed to the learner to be mathematised” (p. 74, [25]).

The Mathematics Study Programs of MEP [7] propose, precisely, the use of contextualized problems that strengthens the active role of the student, in such a way that it commits them to their learning through the design of mathematical models. In this way, active contextualization is proposed as a disciplinary axis of the curriculum. A problem presents an active contextualization if, for its resolution, the context provided is effectively necessary. In contrast, if a mathematical task can be context-free, then the contextualization is artificial [26]. Therefore, an active contextualization seeks to stimulate student action and to use mathematical models. Hence, it awakens interest and participation in order to build higher cognitive abilities [7], while allowing “intellectual involvement of the student through situations that will allow them to develop their mathematical skills and abilities” (p. 74, own translation [10]).

It is important to clarify in this regard that, for a problem to have an active contextualization, it is not necessary for a scenario to exactly resemble reality, in which case we would be facing a significant contextualization [26], a concept that will be discussed later in this document.

In the following paragraphs, we will review different aspects related to the selection and creation of problems, this review being the origin of the dimensions of analysis that will be presented in the methodology.

2.1. Sources for the Selection and Elaboration of Contextualized Problems

Incorporating problem solving and mathematical contextualization in didactic planning is one of the greatest challenges that teachers face in their daily work, especially when having to create or search for contextualized problems that adapt to the needs of their students [27].

The teacher must exhaustively search on the internet and review other sources, to choose, invent and adapt mathematical problems that promote learning in their students through contextualized situations. Being the selection of problems one of the crucial tasks of the teacher, other factors to consider are the characteristics of the students, their cognitive level, needs, motivations, previous mathematical knowledge, mathematical skills to be developed and the sociocultural context [17]. In this sense, students and the community are also important sources of information for teachers [28].

In the case of Costa Rica, teachers are free to use the textbook that best suits their needs or they can create their own material. In most educational centers there is access to the Internet, and you can search for information to implement mathematics problems in your mathematics lessons. In addition, teachers have Mathematics Study Programs (both in physical and digital versions), which include specific indications that consist of concrete examples of problems and activities to guide their work in the classroom.

2.2. Contexts of Mathematical Problems

In this study, the problems are classified according to the contexts they present; therefore, it is necessary to clarify this concept. For this purpose, our work is based on the construct of Ramos and Font [29], who indicate that a context can be seen both as a purely mathematical entity, for example, the context of invertible matrices, or as the real or realistic situation where some particular mathematical content it is used, in which case it is known as context with ecological use. In this way, these authors separate problems with a mathematical context from problems that simulate real life situations. The latter are called contextualized problems, real world problems, or situated problems.

In the same vein, there are authors who categorize problems according to their contexts as: real, when the situation actually occurs in reality; or fictitious, if they are the result of the imagination and purely mathematical [30]. Other researchers group them into non-applied, referring to those with a mathematical context; fictitious, whose conditions and data are fictitiously created by the author of the problem; and authentic or real, where the conditions and data are taken from real or perceived situations of the daily life of the students themselves [31]. Based on these definitions, for the purposes of this research, realistic contexts are considered as those that represent a situation that occurs in real life and fictitious contexts as the ones that pose a situation that would not arise or would not be of interest to resolve in real life. It should be noted that fictitious contexts can be associated with artificial contextualization, as defined in the Costa Rican curriculum [7], which are mathematical problems whose context serves only as a diversion but it is not relevant to solving the problem.

Within the realistic contexts, the indigenous context is considered. This refers to a context that includes typical situations of any native group of the country, given that these contexts usually present distinctive characteristics with respect to other non-indigenous rural contexts and taking into account the presence of various native populations in Costa Rica [32]. Historical contexts are also considered in this study, always within realistic contexts, in response to MEP [7], which indicates the use of history as one of the disciplinary axes of the mathematics curriculum.

3. Materials and Methods

This research is exploratory, descriptive and correlational in nature, developing a quantitative data analysis [33]. The perspective of teachers regarding the use of different contexts to choose and elaborate mathematical problems was explored through the application of a questionnaire. The sources and resources used by teachers for the creation and selection of contextualized problems and the difficulties to implement them in the classroom were also investigated.

Likewise, the possible significant opinion differences obtained in the applied questionnaire were analyzed, dividing the sample by groups determined by age, work experience, hours devoted to class planning, gender, origin and academic degree. Finally, the contexts present in the problems that the teachers proposed were classified.

Design Phase

In order to inquire the perspective of teachers when selecting and creating contextualized problems for the teaching of mathematics in Costa Rica, a questionnaire (Questionnaire available at https://drive.google.com/drive/folders/143AcAbfLg7lk5TLASDmunShgEidvsFok?usp=sharing (accessed on 1 December 2022)) was designed. Here, the results of 42 Likert-type Scale questions are reported (which anticipated a single response in terms of degree of agreement on a given statement), as well as an open-ended question that asked to provide a contextualized mathematical problem recently proposed to students (results about other items have been published elsewhere [34,35]). The Likert scale used had five options, 1: strongly disagree, 2: disagree, 3: undecided, 4: agree, 5: strongly agree.

The questions were built around 5 dimensions related to the creation or selection of contextualized mathematical problems by the teacher. These dimensions are used as reference for the data analysis presented below:

• Contexts of the problems raised by the teacher in class (15 items).
• Inclusion of historical context in mathematical problems (3 items).
• Sources used by the teacher when posing problems in mathematics lessons (5 items).
• Consideration of the near reality of the student to create or select problems by the teacher (9 items).
• Difficulties presented by the teacher in the creation or selection of mathematical problems (10 items).

It is important to clarify that dimension 1 is analyzed both in the Likert Scale questions and in the open-ended enquiries of the questionnaire.

Following the guidelines of Escobar-Pérez and Cuervo-Martínez [36], the instrument was validated by nine expert judges from different countries: Spain, Colombia and Costa Rica. The validators examined whether the items belonging to the same dimension were sufficient to obtain its measurement. In addition, for each item, the evaluators rated the clarity (whether the wording was easily understood), coherence (the item responds to the dimension to be measured) and relevance (the item is essential or important, that is, it should be included). Taking into account 1 as non-compliance with the criterion and 4 as the highest level of compliance, the sufficiency of all dimensions was greater than 3.5. In addition, in the various items an average between 3.44 and 4.00 was obtained in clarity, coherence and relevance. Likewise, the comments were addressed, and the suggestions of the judges were incorporated in order to improve the instrument.

To determine the sample, a virtual sampling was carried out [37]. The instrument was shared with teachers through social networks and contacts obtained by the National Mathematics Advisory through the Google Forms tool. Sixty-seven (67) in-service instructors, who teach at the secondary level (educational level ranging from seventh to eleventh grades, with student populations between the ages of 13 and 17) from all provinces of the country (rural and urban areas) participated. The characteristics of the participants, in terms of gender, work experience, professional degree and working area, are summarized in

Table 1. Participant characteristics.

	Gender		Experience		Academic Degrees		Work Area
	Male	Female	Less than 10 Years	More than 10 Years	High School Degree	College Degree or Master	Rural	Urban
Percentage	40	60	43	57	36	64	51	49
Absolutes	27	40	29	38	24	43	34	33

Source: Own elaboration.

.

In relation to the number of hours that the participants dedicate to planning, 32 declare that they dedicate 3 or more hours per week to the selection or elaboration of problems (48%), while 35 invest two or less hours in this task (52%). It is important to explain that since all the items were mandatory, the 67 participant-teachers answered all the inquiries in the questionnaire.

For the analysis of the questions with the Likert Scale, a methodology based on quantitative techniques was applied using the Statistical Package for the Social Sciences (SPSS) software. In order to determine if there were significant differences between the opinions of the participants and the different variables (age, experience, workplace, …) non-parametric Mann–Whitney U tests were performed, due to the small size of the sample. In addition, Wilcoxon sign tests were performed, again due to the sample size, to establish whether there were significant differences in the opinions of the participants in regard to the creation and selection of mathematical problems according to each of the types of contexts. On the other hand, to classify the contexts present in the problems proposed by the teachers, a content analysis was carried out [38] following the categories obtained in the bibliographic analysis: real, fictitious, mathematical, historical and indigenous. According to the definitions that are considered in this research, the real, fictional and mathematical contexts are mutually exclusive. Historical and indigenous contexts are particular cases of realistic contexts.

4. Results and Discussion

The main results that emerged from the analysis of the data collected from the questionnaire are presented and organized according to the dimensions detailed in the methodology and contrasted with the theoretical framework to discuss the findings.

4.1. Contexts Used in Mathematical Problems

This section will analyze the data corresponding to the teaching perspective about problem posing according to their context: mathematical, fictional, real, historical, indigenous, and applied in other sciences. Here, dimensions 1 and 2 described previously merge. These concepts are familiar to the participant teachers, since they are used in the Mathematics Study Programs [7].

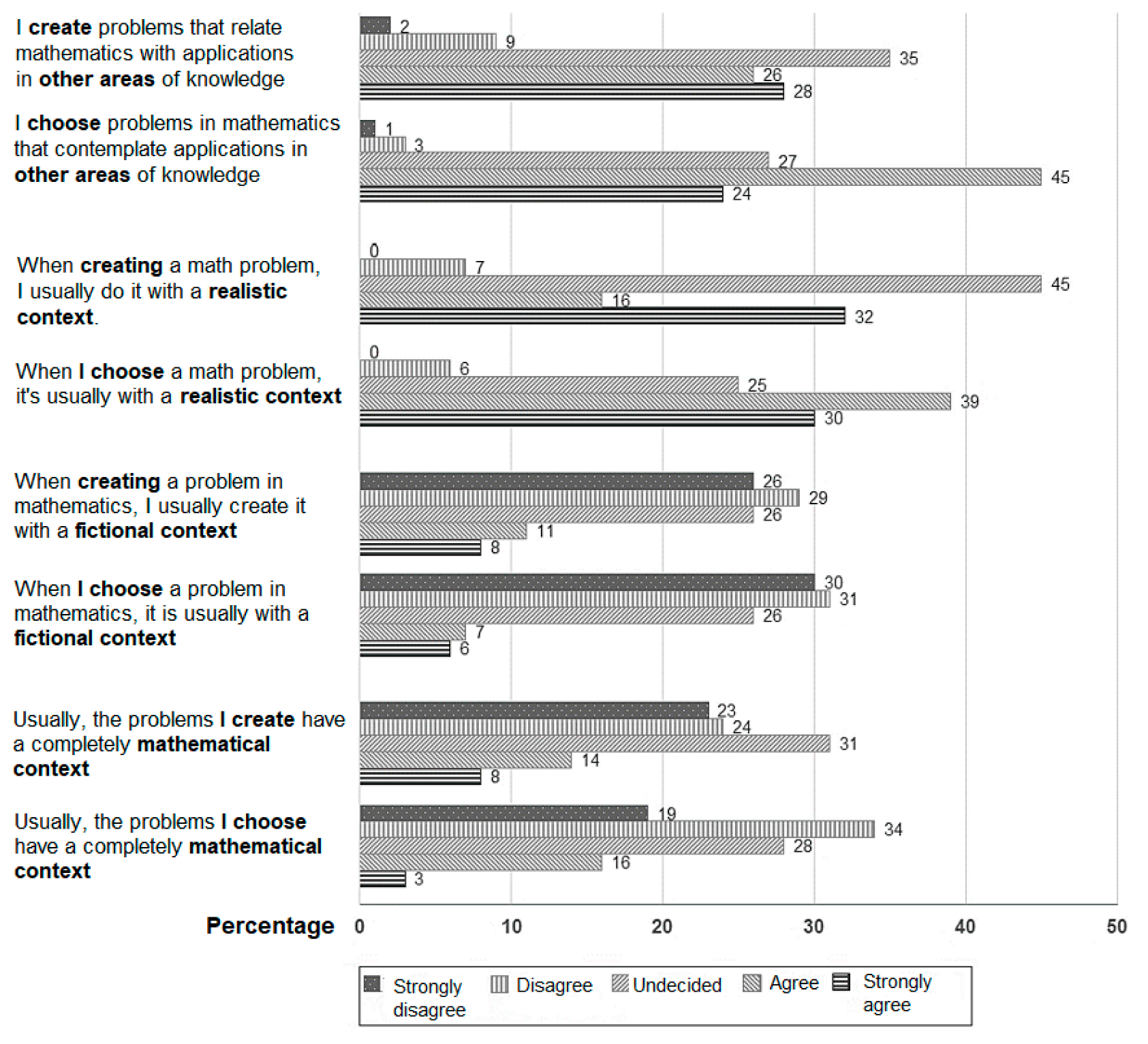
Figure 1 allows us to visualize that a higher percentage of favorable opinions are given towards the selection and creation of problems with realistic contexts, in comparison with the approach of problems with fictitious or mathematical contexts, which is in line with what MEP [7] proposes in the Costa Rican mathematics curriculum.

Indeed, more than half of the teachers stated a degree of disagreement regarding the selection of problems with mathematical contexts. These answers are interesting if we consider that 59.5% of the examples proposed by MEP [7] as a guide in the main indications of the Mathematics Study Programs pose a purely mathematical context [26].

Of the four types of problems that were consulted, those related to realistic contexts were those that reached the highest mean of favorable opinions (3.78 regarding the selection, 3.80 regarding the creation) while the problems with fictitious contexts obtained the lower average (2.37 in the selection and 2.69 in the creation) (

Table 2. Statistical measures on the opinions of teachers regarding the type of problem they create in mathematics.

Type of Problem		Selection			Creation
	Mean	Standard Deviation	Mode	Mean	Standard Deviation	Mode
Completely mathematical	2.65	1.06	2	2.83	1.16	3
With fictional context	2.37	1.08	2	2.69	1.17	3
With realistic context	3.78	0.83	4	3.80	0.95	3
With applications	3.70	0.83	4	3.67	1.02	3

Source: Own elaboration.

).

On the other hand, Wilcoxon sign tests were carried out to determine if there are significant differences in the opinions of teachers between creating and selecting mathematical problems according to each of the types of context. No significant differences were found in this regard. Indeed, respectively, the values found were in the fictitious contexts Z = −1.785, p = 0.074, in the case of mathematical contexts Z = −0.383, p = 0.702, in the problems that contemplate applications in other areas of knowledge Z = −0.023, p = 0.981 and in realistic contexts Z = −0.242, p = 0.80.

However, using the Mann–Whitney U test, significant differences were ruled out between the opinions of teachers on the selection and creation of the various types of problems and the variables of age, experience, academic degree and time spent planning. Nevertheless, the value that relates the teacher’s workplace and their opinions on the selection of problems with fictitious contexts indicates that there are significant differences depending on whether they work in a rural or urban area (y Z = −3.05; p = 0.02). Indeed, the mean is lower in the group of teachers from urban areas (1.82) in contrast to the mean (2.74) of teachers from rural areas. That is, the opinions of teachers in urban areas are more unfavorable with respect to using fictitious contexts than those in rural areas.

Despite the fact that MEP [7] promotes the use of history in mathematics classes, the highest percentage of teachers surveyed do not take a position regarding proposing historical problems in their mathematics classes (see Figure 2). In addition, when asked about proposing mathematical problems with indigenous contexts, the highest percentage of participants indicated that they disagreed or totally disagreed. Contrary to these opinions, D’Ambrosio [5] advocates, from the Ethnomathematics Program perspective, to consider mathematics coming from the worldview, ideologies, intellectual achievements and historical values of various civilizations including the indigenous cultures.

4.2. Sources Used for the Selection and Creation of Contextualized Mathematical Problems

We have already underlined that within the competences of mathematics teachers in the didactic planning of the class, there is the selection and/or elaboration of mathematical problems [39,40,41]. In the Costa Rican context, it is also expected that the teacher promotes the resolution of problems with active contextualization, as it is one of the disciplinary axes of the curriculum. In this sense, teachers were asked how much they agreed with using the different resources available for the selection and creation of contextualized mathematical problems. These results respond to dimension 3 of this study. 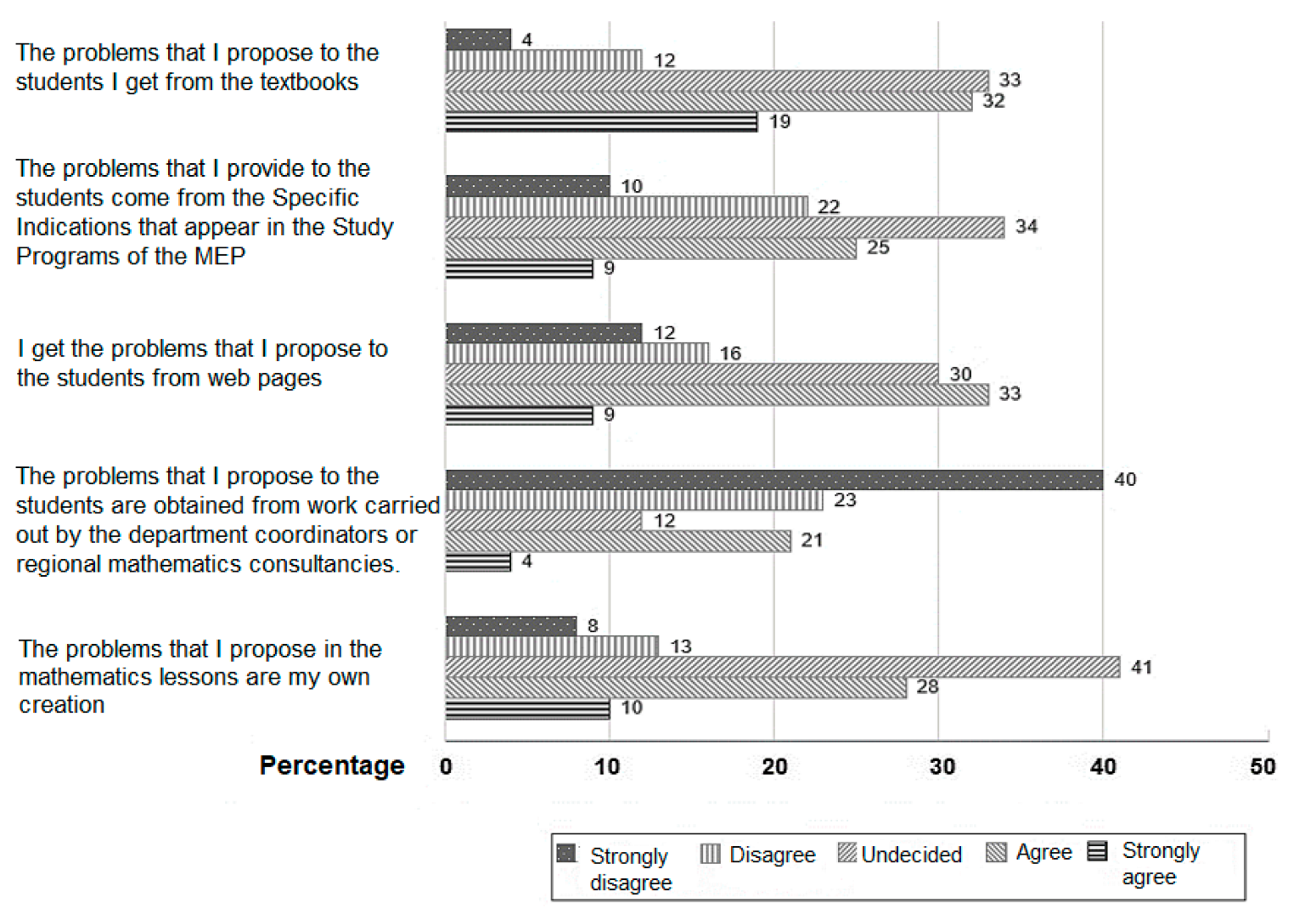The information collected is summarized in Figure 3.

In the case of the use of textbooks, the participants in this study generally gave a favorable opinion of their use. This agrees with the results of a research carried out almost two decades ago by Murillo [42] in Costa Rica, who showed that the teachers involved were in favor of the use of textbooks for the teaching of mathematics. These similarities occur even when the study programs and the methodology in the periods in which the two researches are located are different. A similar situation was documented in the research carried out in Chile by Pino-Fan et al. [43], where the preference of teachers for using textbooks to select or adapt the problems they use in their classes is highlighted.

On the other hand, as evidenced in Figure 3, the participants do not show a noticeable tendency when giving their opinion on the use of specific indications of the Mathematics Study Programs given by MEP [7]. In addition, using problems developed in work teams, such as coordination or regional advisory services, is not a common practice for these Costa Rican teachers. In summary, of the five resources consulted, the use of textbooks reached the highest mean of favorable opinions (3.34), while using problems obtained by department coordinators or consultancies obtained the lowest mean (2.27), as can be seen in

Table 3. Statistical measures on the opinions of teachers regarding the use of resources for the creation of contextualized mathematical problems.

Resources	Mean	Standard Deviation	Mode
Textbooks	3.49	1.07	3
Websites	3.10	1.15	4
Specific indications of the MEP	3.01	1.12	3
Department coordination or consultancies	2.27	1.30	1
Own creation	3.21	1.05	3

Source: Own elaboration.

.

Regarding the use of self-created problems, Malaspina et al. [44] express that mathematics teachers must develop skills to create their own problems to work with their students and not limit themselves to using the problems found in books or online. However, the majority of teachers seem not to take a position on the matter.

When performing Mann–Whitney U tests, no significant differences were documented in opinions regarding reference sources such as textbooks, study programs, and coordination between groups determined by sex, academic degree, dedication to planning, or area of origin.

On the other hand, when consulting about the use of web pages for problem posing, there is a significant difference when comparing teachers from urban areas with those who live in rural areas. In fact, when performing the Mann–Whitney U test, the values Z = −2.09, p = 0.035 are obtained. The mean of the opinions of teachers who come from rural areas is 2.85, while in participants from urban areas the mean is 3.35. We can infer that more limited access to Internet networks in rural areas may influence these results.

4.3. Close Reality of the Student in the Elaboration of Mathematical Problems

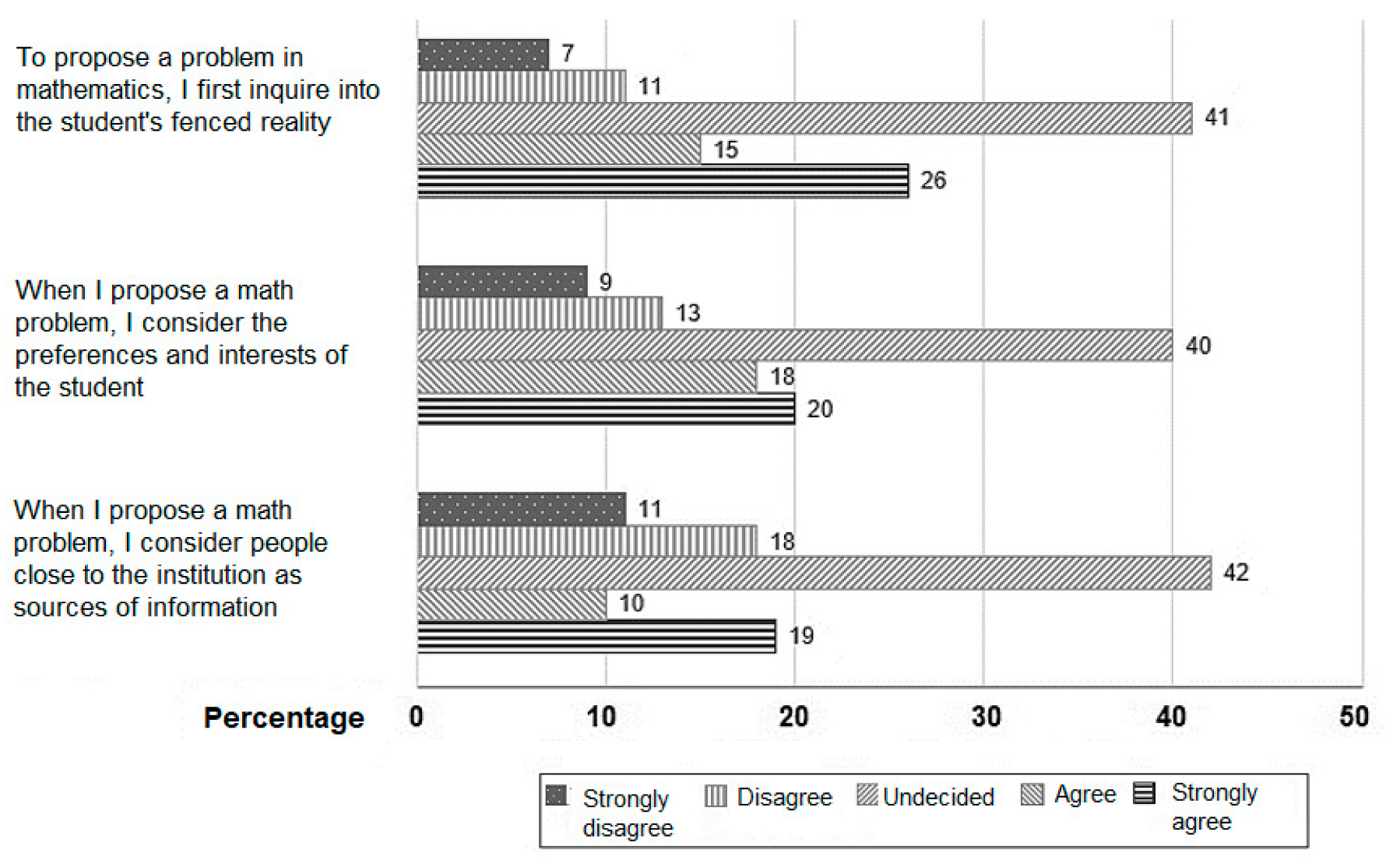
Teachers were asked, in three questions (corresponding to dimension 4), their opinion regarding considering the reality of the student, the educational center and the community near to the educational center, as sources of information to propose mathematical problems in the classroom.

As shown in Figure 4 and

Table 4. Statistical measures on the opinion of teachers regarding considering the reality of the student and their environment to propose problems in mathematics.

Resources	Mean	Standard Deviation	Mode
To propose a problem in mathematics, I first inquire into the student’s fenced reality	3.37	1.17	3
When I propose a math problem, I consider the preferences and interests of the student	3.14	1.15	3
When I propose a math problem, I consider people close to the institution as sources of information	3.05	1.23	3

Source: Own elaboration.

, the highest percentage of teachers was undecided in each of the statements made in terms of considering the reality of the students, their educational center and people close to the institution. In this regard, more favorable answers were desirable. As explained by Osana and Pelczer [28], for problem posing the interactions of teachers with students are essential, so that the learners’ prior knowledge and interests are considered in the problem statement.

On this issue, and in contrast to the majority of answers obtained by the participants, Gerdes [45], in a study on various mathematical experiences of African students, explains the importance of teachers being aware that mathematics is a sociocultural process and that students have a mathematical potential learned from their environment. For this reason, it is essential that the teacher knows the reality of the students, of the social groups that are close to the educational institutions and of the cultural practices that are important for the educational community. These realities, according to this author, should be taken into account when planning mathematics lessons. When performing Mann–Whitney U tests, no significant differences in opinions about considering the reality of students between groups determined by sex, academic degree, dedication to planning, or workplace were established.

4.4. Difficulties in Implementing Contextualized Mathematical Problems

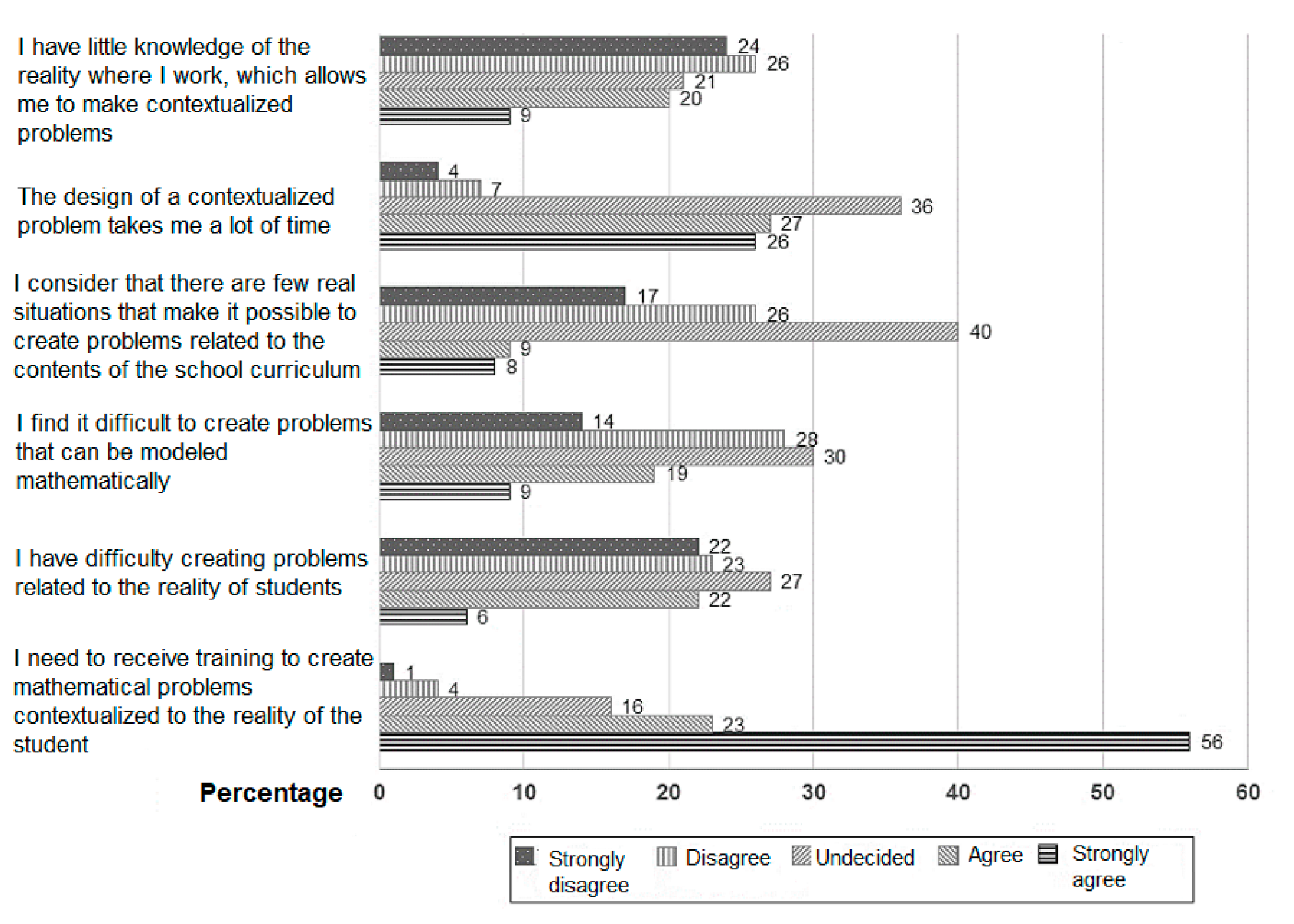
Applying the resolution of contextualized mathematical problems as the disciplinary axis of the curriculum requires the teacher to possess skills to select and create learning situations that are appropriate to the educational level and reality of the students [27]. In this regard, Espinoza [46] explains that this is not an easy task for the teacher since it requires an exhaustive search and analysis of information that allows him to develop a problem. Therefore, in the questionnaire, teachers were asked, through 5 items, if they considered it difficult to design contextualized mathematical problems. In general, teachers disagree that they have difficulties creating contextualized mathematical problems. These results respond to dimension 5 of the questionnaire. Figure 5 and

Table 5. Statistical measures on the opinion regarding the difficulties in designing contextualized mathematical problems.

Affirmation	Mean	Standard Deviation	Mode
I have little knowledge of the reality where I work, which allows me to make contextualized problems	2.58	1.21	2
The design of a contextualized problem takes me a lot of time	3.65	1.04	3
I consider that there are few real situations that make it possible to create problems related to the contents of the school curriculum	2.65	1.02	3
I find it difficult to create problems that can be modeled mathematically	2.79	1.05	3
I have difficulty creating problems related to the reality of students	2.71	1.19	3
I need to receive training to create mathematical problems contextualized to the reality of the student	4.13	1.03	5

Source: Own elaboration.

summarize the data obtained.

It should be noted that half of the participants indicate a degree of disagreement with respect to having little knowledge of the reality of their educational community to create problems. Furthermore, almost half of the teachers are undecided when asked if there are few real situations that make it possible to create mathematical problems. In relation to the difficulty of modeling situations to elaborate problems, opinions are divided.

The participants generally believe that there are no considerable difficulties for problem posing. In contrast, there are studies that indicate that mathematics teachers tend to present difficulties in creating problems that students recognize as relevant to their daily lives, as well as in developing problems that are adapted to the specific educational level and to the curricular contents to be developed [23].

The difficulty in which the teachers agree the most is related to the time they invest in creating these problems. This agrees with other studies, such as the one by Pino-Fan et al. [43], where teachers also indicated that the greatest difficulty in creating mathematical problems is precisely the time they would need.

In addition, and despite the encouraging data provided by the questionnaire, 79% of those interviewed affirm that there is a need to receive training to create problems that are contextualized to the student’s reality. This agrees with the research by Singer and Voica [8], who indicate that, despite the fact that there is a natural predisposition of mathematics teachers to problem posing, teacher training in this pedagogical tool is necessary.

According to the Mann–Whitney tests, there are no significant opinion differences of teachers in regard to the difficulties experienced when developing contextualized mathematical problems between groups determined by age, experience, area where they work, academic level and time dedicated to planning.

4.5. Contexts of the Mathematical Problems Provided by Teachers

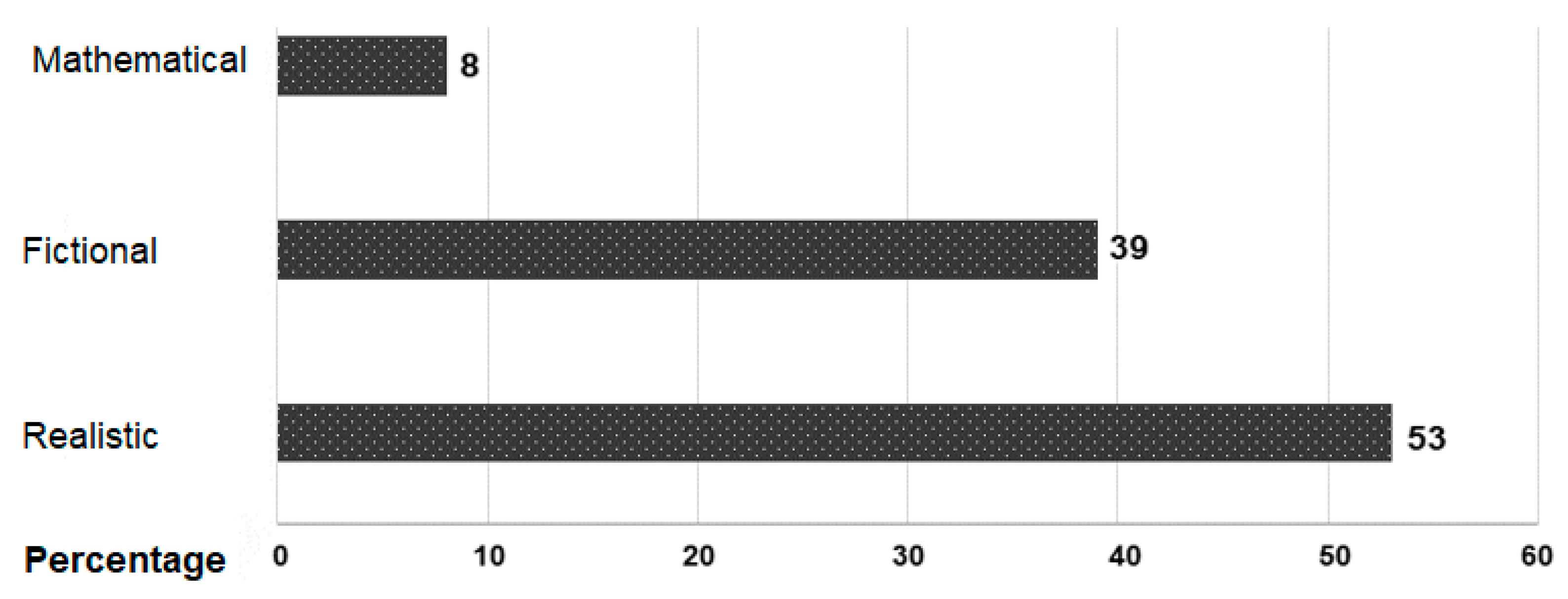
Through an open question (dimension 1 of the study), each teacher had to provide a problem that they had recently worked on with their students. Of the 67 participants, only 38 (57% of the total) presented the requested problem.

In contrast to the opinions presented in Figure 1, 39% of the participants who did respond to the item (equivalent to 15 teachers) provided problems with fictitious contexts (see Figure 6). These findings coincide with those reported by Cai et al. [9], where 30% of the teachers who participated in their study posed unrealistic problems.

A problem with this type of context is the following:

If the screen in Britany’s house is 32 inches and the width is 18 inches, what is the length of her screen?

In this example, the context is fictitious; it presents a situation that is unlikely for the learner to encounter. Among the 20 problems with realistic contexts (53% of those provided) there is an evident lack of variety of situations proposed. In fact, almost half of the problems (9) are related to purchasing items to develop the topic of operations with integers and rational numbers. Five of those problems refer to situations of calculation of areas, measurement of land, or calculations for masonry work. Three situations are based on personal activities (walks, hikes, Internet access), which aim to solve problems in the areas of analytical geometry and integers. Moreover, one problem was contextualized to the COVID-19 situation to develop the theme of exponential functions. There is a problem that refers to national statistics and another one that describes the creation of a recipe, both of these problems are posed to develop the knowledge of rational numbers. Likewise, it is observed that no participant used historical contexts, despite the importance given to this axis in the national curriculum of Costa Rica, and only two problems present an indigenous context, both related to the conical house of the Bribri people, symbol of their cosmology. An example of a problem with realistic context is the following:

Luis goes to the grocery store and buys: 2 kg of sugar that costs CRC 825 per kg, a little bag of rice for CRC 5800, 1 kg of coffee at CRC 3750, 1 kg of onion at CRC 500 per kilo, 30 eggs at CRC 100 each; (a) how much money did you spend? (b) if you have CRC 7500, do you have any money left?

In accordance with the opinions summarized in Figure 1, where teachers indicated that they disagreed with the mathematical contexts, only three participants (8% of the proposed problems) poised problems with this type of context (Figure 6).

5. Conclusions

In general, teachers are undecided regarding their opinions related to considering the reality of students and their environment when developing math problems. A similar situation is evident in their opinions about the use of various sources and the difficulties they face in the elaboration of contextualized mathematical problems.

Despite the fact that a large number of the teachers indicate that they disagree with the use of fictitious contexts, several of the problems proposed by the teachers themselves are precisely related to this type of context. On the other hand, the favorable opinions regarding the use of realistic contexts agree with the context that presents half of the proposed problems. Likewise, there is coherence between the unfavorable opinions related to the use of mathematical contexts and the number of problems posed that present this context. It is important to highlight that despite the fact that most of the participants indicated that they had no difficulties in developing contextualized problems, over two fifths of the teachers did not provide a problem, leaving the question unanswered.

In most of the questions, the opinion of the teachers interviewed do not present any significant correlation to their academic preparation, hours of planning, age, experience or gender. Nevertheless, a significant difference can be seen when correlating the answers regarding the use of the Internet to create a problem with the work area of the respondents. It was determined that the agreement of people from rural areas was significantly lower than that of urban areas; this may be the result of less access to Internet service in rural areas. Possibly, although this study could not delve into this issue, the lesser access to information through digital media may be a reason why teachers in rural areas agreed more with the use of fictitious contexts than their counterparts in urban areas.

A third of those surveyed stated being in favor of using the problems proposed by MEP [7] in the specific indications, but none of the problems evidenced came from said indications.

Although creating problems and selecting them from other sources are different teaching practices, this research did not show significant differences between the opinions of the participants, in any of the items consulted, regarding the elaboration and selection of contextualized mathematical problems.

For Espinoza [46], preparing problems in mathematics implies a higher level of demand on teachers. However, in general, the teachers surveyed disagreed with the idea of having difficulty preparing contextualized mathematical problems. Even so, almost half of the participants developed problems with mathematical or fictitious contexts, moving away from what MEP [7] proposes.

Teachers indicate that they need training to elaborate contextualized mathematical problems. Therefore, it is recommended to address this concern through courses that delve into this issue, promoting the use of realistic contexts and significant contextualization, which constitutes the starting point for the next step of our project.

Finally, few teachers admitted to working together with colleagues and advisors to write contextualized problems. Therefore, it is recommended that educational authorities encourage cooperative work in different areas of the country, to enrich the teaching work. Actually, this finding has motivated the creation and implementation of a training course focused on the elaboration of problems, which encourages collaborative work and reflection on the teaching task [47].

Within the limitations of this study and as a consequence of communication difficulties due to the COVID-19 pandemic, it was not possible to delve into the specific reasons why many teachers were undecided in some of the questions posed.

On the other hand, this research provides a validated instrument to study the perspective of teachers regarding the contextualization of mathematical problems, which can be applied in future studies with different samples.