Introduction to Computational Mathematics Using the Historical Solutions of the “Hundred Fowls” Problem
Abstract
1. Introduction
1.1. On Problem Solving
1.2. On the “Hundred Fowls” Problem
Problem 1
“A partridge is worth 5 coins; a dove 3 coins; and three sparrows 1 coin. With 100 coins we buy 100 of them. How many partridges, pigeons and sparrows do we have?”(China, fifth century, cited in Shen et al. [10], 1999, p. 416)
Problem 2
“A merchant said: I want to buy 100 pigs for 100 denarii; however, he would pay 10 denarii for a male, 5 for a female, and one for two piglets. Say, whoever knows, how many males, how many females and how many piglets should there be so that none are left over or missing?”(Alcuin [11], 1863, 804, p. 1145)
Problem 3
“A certain paterfamilias had 20 servants. He ordered that 20 modios of corn be distributed to them in the following way: that the men receive three modios, the women two, and the children half a modius. Say, who can, how many men, how many women and how many children should there be?”(Alcuin [11], 1863, 804, p. 1154)
Problem 4
“A certain bishop ordered 12 loaves to be distributed among the clergy. He thus provided for each priest to receive two loaves; a half deacon and a reader a quarter. Acting in this way the number of clerics and loaves is the same. Say, who wants, how many priests, deacons and readers should there be?”(Alcuin [11], 1863, 804, p. 1155)
Problem 5
A man buys 30 birds that are partridges, pigeons and sparrows, for 30 pence. He buys a partridge for 3 pence, a dove for 2 pence, and 2 sparrows for 1 denarius, that is, 1 sparrow for 1/2 denarius. He asks himself how many birds he buys from each kind.(Fibonacci [12], 1202, p. 257)
1.3. On Computational Tasks Based on Programming as Problem Solving Tasks
- Analyzing the problem situation and planning its solution;
- Choosing and applying a resolution strategy;
- Checking and verifying the complete program and the solution.
2. Aims
- Aim 1
- To design a programming teaching trajectory using the historic solutions of the “Hundred Fowls” problem
- Aim 2
- To discuss the implementation of the designed pathway with first-year students taking a degree in chemistry
3. Material and Methods
3.1. The Design of the Teaching Trajectory
3.2. The Exploratory Teaching Experiment
4. The Programming Teaching Trajectory Using the “Hundred Fowls” Problem
4.1. The Data of the Problem: Input and Output Variables
| Algorithm 1: Introduction of input variables |
a = input(’Input the price of the partridges\n’); |
b = input(’Input the price of the sparrows\n’); |
d = input(’Input the price of the pigeons\n’); |
p = input(’Input the total number of animals that you want to buy\n’); |
| Algorithm 2: Paint variables on the screen | |
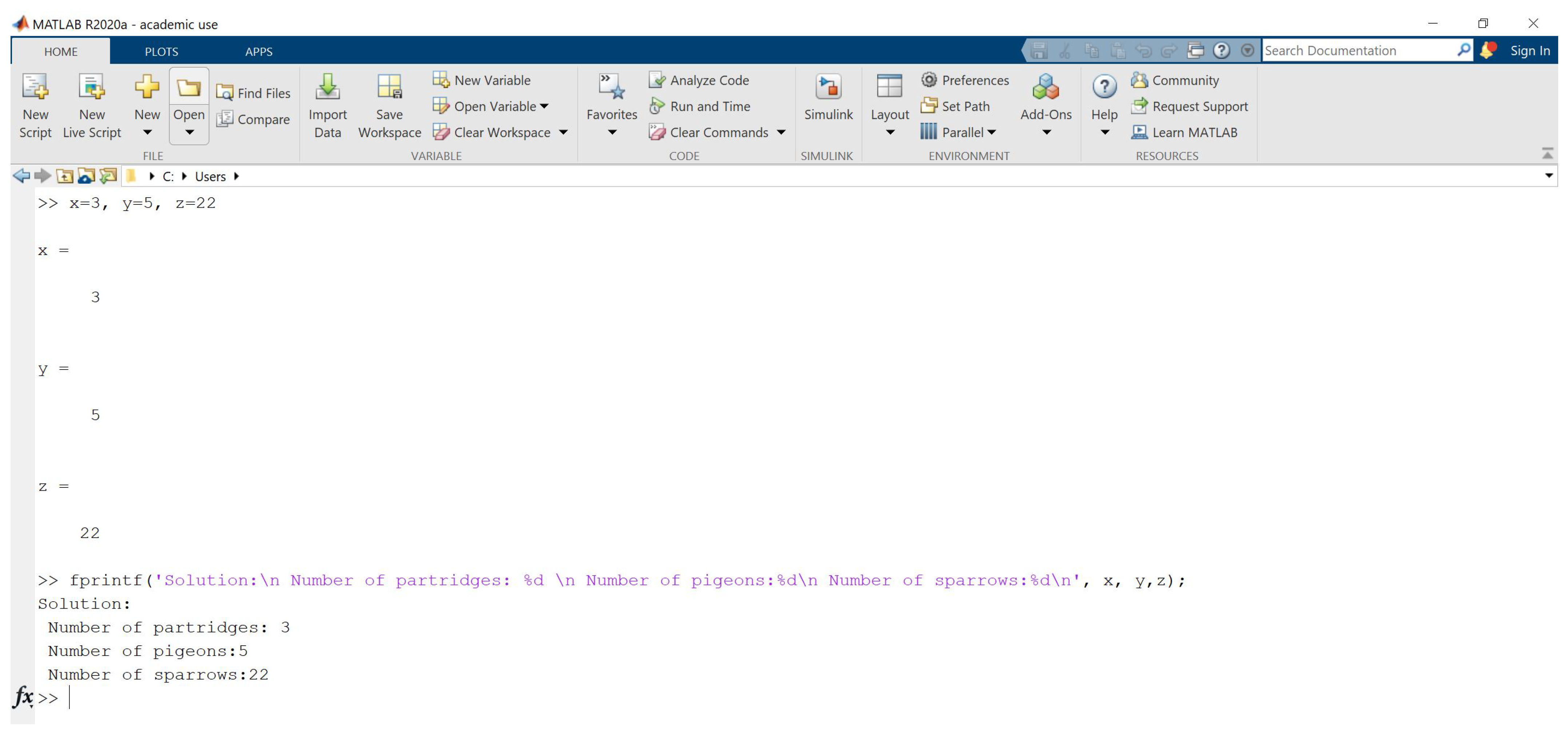
x = | 3; y = 5; z = 22; |
fprintf ([’Solution: \n Number of partridges: %d\n’… | |
’Number of pigeons: %d\n’… | |
’Number of sparrows: %d\n’], … | |
x, y, z); | |
4.2. Programming Qiujian’s Solution with Trial and Error: The if and for Statements
| Algorithm 3: Program to calculate the sum of the first 10 numbers | |
S = 0; | %Initialize the variable S to 0. |
for i = 1:10 | %(i from 1 to 10) |
S = S + i; | %(It assigns to S, the value S+i). |
end | |
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| S | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 |
| Algorithm 4: Program to calculate the factorial of a number entered by the user | |
n = input(’Insert a number \n’); | |
f = 1; | %Initialize the result, f = 1. |
for i = 1:n | %(i from 1 to 10) |
f = f ∗ i; | |
end | |
f | |
| Algorithm 5: Function of the if command | |
k = 1; | %Initialize k = 1. |
p = 1; | %Initialize p = 1. |
if p == 1 | %It means: if p is equal to 1 |
k = 2; | %then 2 is inserted in the variable k |
end | |
k | |
| Algorithm 6: Function of the if command | |
k = 1; | %Initialize k = 1. |
p = 2; | %Initialize p = 1. |
if p == 1 | %It means: if p is equal to 1 |
k = 2; | %then 2 is inserted in the variable k |
end | |
k | |
| Algorithm 7: Program hundredfowls0 to solve the HF problem |
a = input(’Input the price of the partridges\n’); |
b = input(’Input the price of the sparrows\n’); |
d = input(’Input the price of the pigeons\n’); |
p = input(’Input the total number of animals that you want to buy\n’); |
%x from 1 to p/a |
for x = 1:p/a |
%y from 1 to p/b |
for y = 1:p/b |
%We force that z satisfies the second equation. |
z = p − (x + y); |
%We check the first equation |
if (a ∗ x + b ∗ y + d ∗ z == p) |
%We show the solutions |
fprintf ([’Solution: \n Number of partridges: %d\n’,… |
’Number of pigeons: %d\n Number of sparrows:%d\n’],… |
x, y, z) |
end |
end |
end |
4.3. Programming the Fibonacci Solution: The mod Function
Divide the 30 pence by the 30 birds; the quotient will be 1 denarius. Say, therefore, I have with 1/2, money with 2 and money with 3, and I want to have money with 1. It is clear that, as in similar problems, the procedure is by the method of alloys, since we have an integer bird’s. Therefore, since the cheapest kind of birds is equal in number to the most expensive kind, say, I have money with 1/2, and money with 2, and money with 3, and wish to have money with 1; that is, I have money with 1, and money with 4, and money with 6, and I want to have money with 2; make the first alloy with the sparrows and partridges and you will get 5 birds for 5 denarii, or 4 sparrows and 1 partridge, and make a second alloy with the sparrows and doves, and you will have 3 birds for 3 de-narii, or 2 sparrows and 1 dove; then in order to have 30 birds in the alloy, put the first alloy three times which will be 12 sparrows and 3 partridges, and there will be 15 birds left to alloy, for which put the second alloy five times, and you will have 10 sparrows and 5 pigeons, and thus, of the previously mentioned 30 birds, there will be 22 sparrows and 5 pigeons and 3 partridges, as shown in the problem.(Gómez, 2016 citing Fibonacci, 1202, p. 256)
| Algorithm 8: Program to solve the HF problem using the Fibonacci solution |
a = input(’Input the price of the partridges\n’); |
b = input(’Input the price of the sparrows\n’); |
d = input(’Input the price of the pigeons\n’); |
p = input(’Input the total number of animals that you want to buy\n’); |
c = 1/d; |
A = (c∗a-1)/(c-1); |
B = (c∗b-1)/(c-1); |
k = p/B; |
for yb = 1:k %We start with yb from 1 to p/B |
r = mod(p-B∗yb,A); |
if r == 0 |
x = (p-B∗yb)/A; |
y = yb; |
z = p-(x + y); %We calculate z, using the second equation. |
fprintf ([’Solution: \n Number of partridges: %d\n’… |
’Number of pigeons:%d\n Number of sparrows: %d\n’],… |
x, y, z); |
end |
end |
4.4. Programming the Ventallol Solution
A man wants to make a treat and gave his buyer 36 salaries to buy three kinds of fowls, that is, blackbirds, 3 for a salary, chickens, at 2 salaries a piece and capons, at 3 wages the piece; and he wants, that among all there are 36, and that they cost him 36 salaries. I ask, how many will he buy of each lot? He buys the 36 of those that are worth less, that is, shit, and you will find that they cost 12 salaries. Take them out of 36, there are 24 left. See first what a shit is worth and you will find that it is worth 1/3 of salary. Now see how much more a chicken is worth than a piece of shit and you’ll find 1 2/3, put them aside. Then he looks at how much more a capon is worth than a piece of shit, and you will find 2 salaries and 2/3. Now make thirds of everything, that is, of 1 2/3 and they will be 5/3, and likewise of 2 2/3 and they will be 8/3, then you will make 24 thirds of salaries, and they will be 72/3. Now of these 72 make such two parts that one can be divided by 5 and the other by 8 and that there is nothing left in the partition. You will find this like this: remove 5 from 72 as many times, until there is a number that can be divided by 8 exactly, and you will find that it will be 32; and the other will be 40. Divide 32 by 8 and 4 will come; then divide 40 by 5, and 8 will come. And so you see that there will be 4 capons and 8 hens, which are 12, up to 36 there are 24, and there will be so many pieces of shit. And so you will do of all the similar ones.(Gómez, 2016 citing a Ventallol, 1521/1621, pp. 472–473)
| Algorithm 9: Program to solve HF problem using Ventallol’s solution |
a = input(’Input the price of the partridges\n’); |
b = input(’Input the price of the sparrows\n’); |
d = input(’Input the price of the pigeons\n’); |
p = input(’Input the total number of animals that you want to buy\n’); |
c = 1/d; |
A = (c∗a-1); |
B = (c∗b-1); |
k = (c-1)∗p/(c∗b-1); |
for yb = 1:k |
r = mod((c-1)∗p-B∗yb,(c∗a-1)); |
if r == 0 |
x = ((c-1)∗p-B∗yb)/(c∗a-1); |
y = yb; |
z = p-(x+y); |
fprintf ([’Solution: \n Number of partridges: %d\n’… |
’Number of pigeons:%d\n Number of sparrows: %d\n’],… |
x, y, z); |
end |
end |
4.5. Diophantine Equations and Their Solutions
“God granted him to be a boy for a sixth of his life, and adding to this a twelfth part, He covered his cheeks with hair; He enlightened her with the light of marriage after a seventh part, and five years after their marriage he gave her a son. But alas! Unhappy child born late; after reaching half the measure of his father’s life, cold fate took him away. After consoling his sorrows with the science of numbers for four more years, he ended his life.”(Boyer, 1986, p. 235 citing Cohen & Drabkin, 1948, p. 27)
“On the other hand, it is impossible to separate a cube into two cubes, or a biquadrate into two biquadrates, or generally any power except a square into two powers with the same exponent. I have discovered a truly marvelous proof of this, which however the margin is not large enough to contain”.(Cohen & Drabkin, 1948 p. 30)
4.5.1. On the Diophantine Equation
4.5.2. Euclid’s Algorithm as a Solution of the Diophantine Equation
Given two unequal numbers and successively subtracting the smaller one from the larger one, if the remaining one never measures the previous one until one unit remains, the initial numbers will be relatively prime numbers.(Proposition 1. The Elements, Book VII, Euclid; cited in [26])
4.5.3. Programming a Solution for Diophantine Equations: Functions, Use of Vectors, the while Statement and the abs and ceil Commands
| Algorithm 10: Insert the vector as a Matlab variable |
v(1) = 7; v(2) = −8; v(3) = 5; |
| Algorithm 11: Program to add the first 10 numbers using the command while |
k = 0; S = 0; %Initialize the variables. |
while (k< = 10) |
S = S + k; |
k = k + 1; |
end |
S |
| Algorithm 12: Extended Euclidean algorithm |
function [x,y,m]=algeuclext(A,B) |
r(1)=A; %Initialize the vector r |
r(2)=B; |
s(1)=1; %Initialize the vector s |
t(1)=0; |
s(2)=0; |
t(2)=1; |
i=2; |
while (r(i)~=0) |
q(i)=floor(r(i-1)/r(i)); |
r(i+1)=mod(r(i-1),r(i)); |
s(i+1)=s(i-1)-q(i)∗s(i); |
t(i+1)=t(i-1)-q(i)∗t(i); |
i=i+1; |
end |
m=r(i-1); %solution. |
x=s(i-1); |
y=t(i-1); |
| Algorithm 13: Algorithm to solve the HF problem from the diophantine equations |
a=input(’Input the price of the partridges\n’); |
b=input(’Input the price of the sparrows\n’); |
d=input(’Input the price of the pigeons\n’); |
p=input(’Input the total number of animals that you want to buy\n’); |
c=1/d; |
A=a∗c-1; |
B=b∗c-1; |
[x0,y0,k]=algeuclext(A,B); %We use the function showed in Alg. 12 |
S1=ceil(-(y0∗(c-1)∗p/k)∗k/A); |
S2=(x0∗(c-1)∗p/k)∗k/B; |
for t=S1:S2 |
x=(x0∗(c-1)∗p/k)-t∗B/k; |
y=(y0∗(c-1)∗p/k)+t∗A/k; |
z=p-(x+y); |
fprintf ([’Solution: \n Number of partridges: %d\n’… |
’Number of pigeons: %d\n’… |
’Number of sparrows: %d\n’… |
x, y, z); |
end |
5. Discussion on the Exploratory Teaching Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kieran, C. Research on the teaching and learning of algebra. In Handbook of Research on the Psychology of Mathematics Education: Past, Present, and Future; Gutiérrez, Á., Boero, P., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2006; pp. 11–49. [Google Scholar]
- Kieran, C. Algebra Teaching and Learning. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 27–32. [Google Scholar]
- Schoenfeld, A.H. Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 1992; pp. 334–370. [Google Scholar]
- Sutherland, R.; Rojano, T.; Bell, A.; Lins, R. (Eds.) Perspectives on School Algebra; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Stanic, G.; Kilpatrick, J. Historical perspectives on problem solving in the mathematics curriculum. In The Teaching and Assessing of Mathematical Problem Solving; Charles, R., Silver, E., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 1988; pp. 1–22. [Google Scholar]
- National Council of Teachers of Mathematics. Principles and Standards for School Mathematics; NCTM: Reston, VA, USA, 2000. [Google Scholar]
- Puig, L. Elementos de Resolución de Problemas; Comares: Granada, Spain, 1996. [Google Scholar]
- Gómez, B. Problemas descriptivos y pensamiento numérico: El caso de las cien aves de corral. PNA 2016, 10, 218–241. [Google Scholar] [CrossRef]
- Martín, P. El problema de las cien aves: De Alcuino a Fibonacci. SUMA Revista Sobre Enseñanza y Aprendizaje de las Matemáticas 2017, 86, 19–27. [Google Scholar]
- Shen, K.; Crossley, J.N.; Lun, A. The Nine Chapters on the Mathematical Art: Companion and Commentary; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Alcuin. Propositiones ad acuendos juvenes. In Patrologiae Cursus Completus: Patrologiae Latinae; Migne, J.P., Ed.; Petit-Montrouge: Paris, France, 1863; pp. 1143–1160. [Google Scholar]
- Fibonacci. Liber Abaci. In A Translation into Modern English of Leonardo Pisano’s Book of Calculation (Original, 1202); Sigler, L., Ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Hoyles, C.; Lagrange, J.B. (Eds.) Mathematics Education and Technology-Rethinking the Terrain: The 17th ICMI Study; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Papert, S. Mindstorms: Children, Computers and Powerful Ideas; Basic Books: New York, NY, USA, 1980. [Google Scholar]
- Clements, D.H. Logo and cognition: A theoretical foundation. Comput. Hum. Behav. 1986, 2, 95–110. [Google Scholar] [CrossRef]
- Noss, R. How do children do mathematics with LOGO? J. Comput. Assist. Learn. 1987, 3, 2–12. [Google Scholar] [CrossRef]
- Blume, G.W.; Schoen, H.L. Mathematical Problem-Solving Performance of Eighth-Grade Programmers and Nonprogrammers. J. Res. Math. Educ. 1988, 19, 142–156. [Google Scholar] [CrossRef]
- Dorling, M.; White, D. Scratch: A Way to Logo and Python. In Proceedings of the 46th ACM Technical Symposium on Computer Science Education, Kansas City, MO, USA, 4–7 March 2015; pp. 191–196. [Google Scholar] [CrossRef]
- Sáez, J.M.; Cózar, R. Pensamiento computacional y programación visual por bloques en el aula de Primaria. Educar 2017, 53, 129–146. [Google Scholar] [CrossRef]
- Beatty, R.; Geiger, V. Technology, Communication, and Collaboration: Re-thinking Communities of Inquiry, Learning and Practice. In Mathematics Education and Technology-Rethinking the Terrain: The 17th ICMI Study; Hoyles, C., Lagrange, J.B., Eds.; Springer: New York, NY, USA, 2010; pp. 251–284. [Google Scholar] [CrossRef]
- Chao, P.Y. Exploring students’ computational practice, design and performance of problem-solving through a visual programming environment. Comput. Educ. 2016, 95, 202–215. [Google Scholar] [CrossRef]
- Mannila, L.; Dagiene, V.; Demo, B.; Grgurina, N.; Mirolo, C.; Rolandsson, L.; Settle, A. Computational Thinking in K-9 Education. In Proceedings of the ITiCSE-WGR ’14: Working Group Reports of the 2014 on Innovation & Technology in Computer Science Education Conference, Uppsala, Sweden, 23–25 June 2014; ACM: New York, NY, USA, 2014; pp. 1–29. [Google Scholar] [CrossRef]
- Burton, D.M. Elementary Number Theory, 6th ed.; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Bashmakova, I.G. Diophantus and Diophantine Equations; Nauka: Moscow, Russia, 1997. [Google Scholar]
- Boyer, C.B. A History of Mathematics; Wiley: Hoboken, NJ, USA, 1968. [Google Scholar]
- Puertas, M.L. Elementos (Libros V-IX); Gredos: Madrid, Spain, 1994. [Google Scholar]
- Ulum, H. The effects of online education on academic success: A meta-analysis study. Educ. Inf. Technol. 2022, 27, 429–450. [Google Scholar] [CrossRef] [PubMed]
- Guo, L. How should reflection be supported in higher education?—A meta-analysis of reflection interventions. Reflective Pract. 2022, 23, 118–146. [Google Scholar] [CrossRef]
- Alomyan, H.; Au, W. Exploration of instructional strategies and individual difference within the context of web-based learning. Int. Educ. J. 2004, 4, 86–91. [Google Scholar]
- Zhang, P.; Bhattacharyya, S. Students’ Views of a Learning Management System: A Longitudinal Qualitative Study. Commun. Assoc. Inf. Syst. 2008, 23, 20. [Google Scholar] [CrossRef]
- Uden, L.; Sulaiman, F.; Lamun, R.F. Factors Influencing Students’ Attitudes and Readiness towards Active Online Learning in Physics. Educ. Sci. 2022, 12, 746. [Google Scholar] [CrossRef]
- Poynton, T.A. Computer literacy across the lifespan: A review with implications for educators. Comput. Hum. Behav. 2005, 21, 861–872. [Google Scholar] [CrossRef]
- Christiansen, H. Teaching computer languages and elementary theory for mixed audiences at university level. Comput. Sci. Educ. 2004, 14, 205–234. [Google Scholar] [CrossRef]
- Hartnett, M. The Importance of Motivation in Online Learning. In Motivation in Online Education; Hartnett, M., Ed.; Springer Singapore: Singapore, 2016; pp. 5–32. [Google Scholar] [CrossRef]
- Kim, K.J.; Frick, T.W. Changes in Student Motivation During Online Learning. J. Educ. Comput. Res. 2011, 44, 1–23. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Moreno, M.Á.; Yáñez, D.F.; Diago, P.D. Introduction to Computational Mathematics Using the Historical Solutions of the “Hundred Fowls” Problem. Educ. Sci. 2023, 13, 18. https://doi.org/10.3390/educsci13010018
García-Moreno MÁ, Yáñez DF, Diago PD. Introduction to Computational Mathematics Using the Historical Solutions of the “Hundred Fowls” Problem. Education Sciences. 2023; 13(1):18. https://doi.org/10.3390/educsci13010018
Chicago/Turabian StyleGarcía-Moreno, Miguel Á., Dionisio F. Yáñez, and Pascual D. Diago. 2023. "Introduction to Computational Mathematics Using the Historical Solutions of the “Hundred Fowls” Problem" Education Sciences 13, no. 1: 18. https://doi.org/10.3390/educsci13010018
APA StyleGarcía-Moreno, M. Á., Yáñez, D. F., & Diago, P. D. (2023). Introduction to Computational Mathematics Using the Historical Solutions of the “Hundred Fowls” Problem. Education Sciences, 13(1), 18. https://doi.org/10.3390/educsci13010018







