Approach to the Formulation of the Variable Change Theorem
Abstract
:1. Introduction
2. Theoretical–Methodological Foundations of the Research
- There will be an initial situation and a final situation.
- The route from one situation to another one must be unknown or cannot be accessed immediately.
- There must be a student who wants to solve it and has the necessary elements to seek relationships that allow him to transform the situation.
- Action 1. Approach to the problem.
- Action 2. Deepening the problem.
- Action 3. Selection of a work path.
- Action 4. Application of the selected route.
- Action 5. Assessment.
3. Didactic Strategy to Favor the Assimilation of Theorems
4. Application of the Didactic Strategy to Favor the Assimilation of the Variable Change Theorem
4.1. Experimental Population
4.2. Activity Design and Application Dynamics
Analysis and Discussions
- (a)
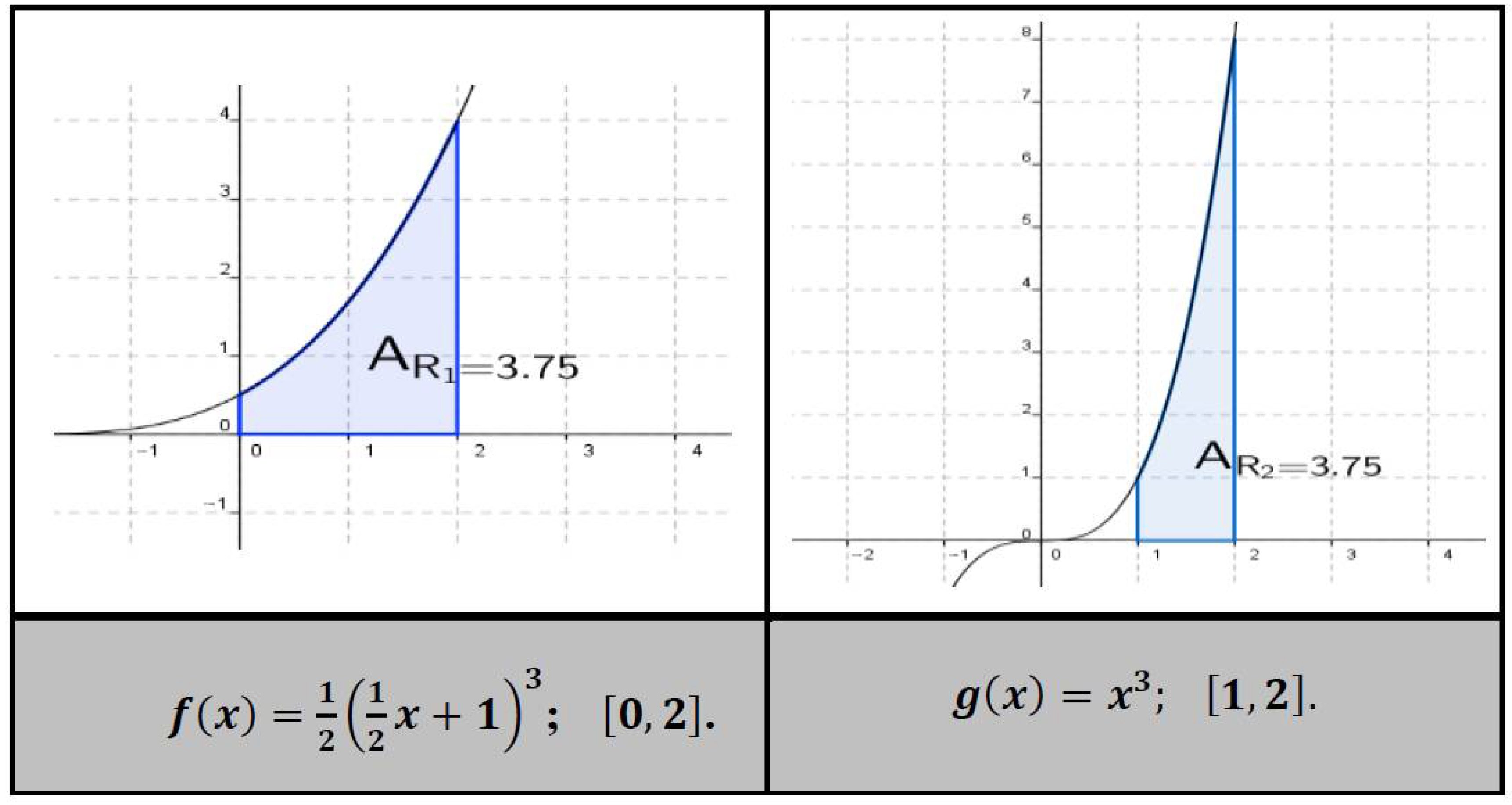
- Determine the value of a to verify that the area of the region under the curve f (x) = ax, above the horizontal axis, and between the lines x = 0 and x = 4, is 16 square units.
- (b)
- Can we construct another region bounded superiorly by the curve of f (x) = ax, inferiorly by the horizontal axis, and laterally by the lines x = x1, x = x2, whose area is 16 square units? Argue your answer and determine, if possible, the values of a, x1, and x2.
- (c)
- What relationships exist between the previously constructed regions, based on their shape and area, respectively? Discuss your answers.
- (a)
- How can you justify that, in fact, the areas of the regions are equal?
- (b)
- What are the implications of making a variable change?
- (c)
- What effects does the application of the Variable Change Theorem have on the resolution of the integral ?
- Student B: choose a suitable substitution for a variable in such a way that its derivative is related to the original function, and thus, it remains in simpler terms.
- Student F: to change a variable is to take a function to a simpler one. For this, we modify the evaluation interval that depends on the new variable that has been chosen.
- Student N: it helps us to make our work easier, but it is not always necessary to do so.
- Student P: transform the function in a certain interval into another function defined in another interval, of which it is easy to calculate the area delimited by the same function.
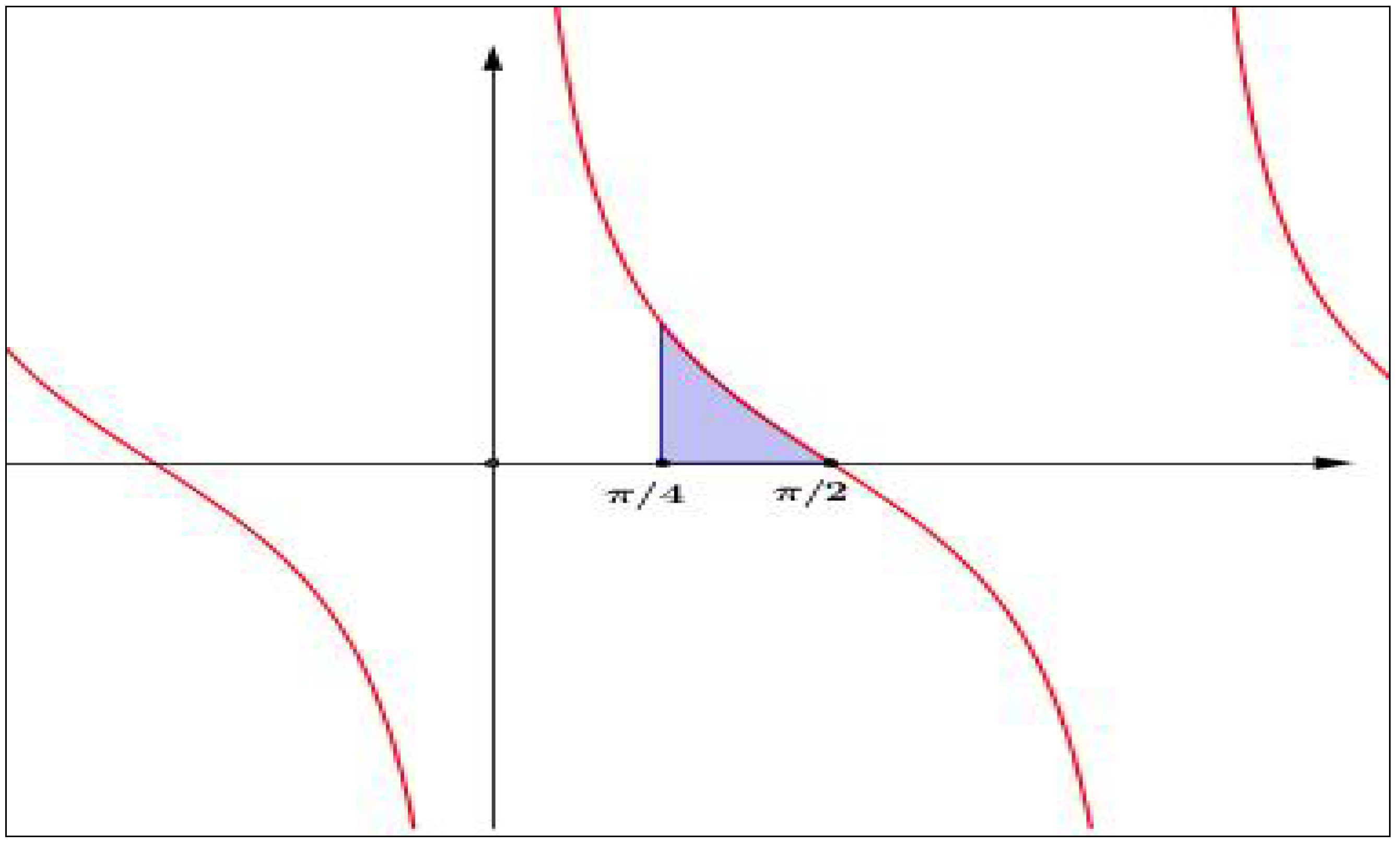
- (a)
- Make a graphical representation of the region and calculate its area without using integral calculus.
- (b)
- To calculate the area of the region above, the following integral is proposed. Applying the change of variable, u = x + 1, with du = dx, it follows that . Discuss the obtained results.
- Student L: I do not see any errors.
- Student H: The figure shown is not a trapezoid.
- Student E: in order to solve the integral , we make , , evaluate → u 1 and → , then
- (a)
- Which is the relationship between and ?
- (b)
- While solving a definite integral using the change of variable theorem, what variations can you consider to occur in the main function for the given interval?
- Student B: The integral remains in terms of a function of easy integration; in addition, such change of variable must be adequate.
- Student C: The change of variable is used to put an integral in its simplest way to calculate, now when the change of variable is completed in a definite integral, the intervals of the function change.
- Student F: The change of variable is a method that allows us to solve integrals, this is completed in order to transform an integral to another simpler one, what the change of variable does is change a function for another simpler one; this implies that the evaluation intervals change with respect to the new variable.
- Student M: What makes the integral less complex by making it easier to integrate, since it changes the integration intervals and is less complex.
- Student Q: The change of variable modifies a function and its intervals of integration in such a way that it produces another function defined in a different interval, but that when integrating it turns out to have the same area as the function on which the change of variable was applied.
- Student H: If we make in , then we obtain that the new limits of integration are . It transforms a region with positive area into a point.
- Student K: If we transform the integral , to an undefined one, and solve it by using the change of universal variable, the integral gives us = , but if we derive it, then it does not fulfill the function over the entire interval [0,2π].
- Student B: given a function f(x), and the variable change theorem allows to find F(x), such that: , then through a change of variable , the change of variable is based on a suitable substitution in such a way that the integral is simpler.
- Student E: , where , when using the change of variable also changes the interval.
- Student F: theorem. If f(x) is continuous, then the integral .
- Student J: let f(x) be an integrable function on the interval [a, b] and continuous. When solving for change of variable, we obtain: , the function and the limits of integration change, and we evaluate the function in the upper and lower limits obtained when changing the variable.
- Student Q: if a function f(x) is continuous on the interval [a, b], let u = φ (x) be differentiable function composed of f(u), then .
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aldana, E.; González, M.T. Comprensión del concepto de integral definida, el caso de un alumno Universitario. In Proceedings of the XIII Simposio de la Sociedad Española de Investigación Matemática (SEIEM), Santander, Spain, 10–12 September 2009. [Google Scholar]
- Ricardo, A.; Moya, D. Propuesta metodológica al tratamiento de teoremas y sus demostraciones. EduSol 2007, 7, 1–8. [Google Scholar]
- Olave, M. Un Estudio Sobre las Estrategias de los Estudiantes de Bachillerato al Enfrentarse al Cálculo del Área Bajo Una Curva. Ph.D. Thesis, Instituto Politécnico Nacional, Mexico City, México, 2005. [Google Scholar]
- Ponce, J.C.; Rivera, A. A discussion on the substitution method for trigonometric rational functions. Math. Comput. Educ. 2011, 45, 44–51. [Google Scholar]
- Llorens, J.; Santonja, F. Una Interpretación de las Dificultades en el Aprendizaje del Concepto de Integral. Divulg. Matemáticas 1997, 5, 61–76. [Google Scholar]
- Mejía, O. Percepción de las Nociones de Conservación, Comparación y Cuantificación del Área por Estudiantes Universitarios. Un estudio Socioepistemológico a Través de sus Argumentos. Master’s Thesis, (Maestría en Ciencias Área: Matemática Educativa)-Facultad de Matemáticas, Universidad Autónoma de Guerrero, Guerrero, México, 2009. [Google Scholar]
- Cabañas, M.G.; Cantoral, R. Un Estudio Sobre la Reproducibilidad de Situaciones Didácticas: El Papel de la Noción de Conservación del Área en la Explicación Escolar del Concepto de Integral. IX Simposio Sociedad Española de Investigación en Educación Matemática. 2006. Available online: https://www.seiem.es/docs/comunicaciones/GruposIX/gidam/cabanascantoral.pdf (accessed on 15 July 2021).
- Díaz, Y.; Cruz, M.; Velázquez, Y.; Molina, S. Estrategias didácticas para desarrollar el proceso de enseñanza-aprendizaje de los contenidos de las Derivadas de funciones reales de una variable real y aplicaciones. Épsilon 2019, 103, 7–23. [Google Scholar]
- Morales, A. Estrategia metodológica de carácter heurístico para el estudio de las relaciones de medidas geométricas. Rev. De La Soc. Argent. De Educ. Matemática 2012, 14, 20–31. [Google Scholar]
- Paschos, T.; Faumak, V. The reflective abstraction in the construction of the concept of the definite integral. A case study. In Proceedings of the 30th Conference of Internacional Group for the Psychology of Mathematics Education, Prague, Czech Republic, 16–21 July 2006; Novotna, J., Moraova, H., Kretke, M., Stehlikova, N., Eds.; pp. 337–344. [Google Scholar]
- Schoenfeld, A.H. Objetivos y métodos de la investigación en educación matemática. La Gac. 2001, 47, 185–205. [Google Scholar]
- Ferreiro, R. Estrategias Didácticas del Aprendizaje Cooperativo. Una Nueva Forma de Enseñar y Aprender: El Constructivismo Social; Trillas: Mexico City, México, 2003. [Google Scholar]
- Ferreiro, R. Cómo Ser Mejor Maestro. In El Método ELI; Trillas: Mexico City, México, 2012. [Google Scholar]
- García, H.J.; Ortiz, A.M.; Martínez, J.; Tintorer, O. La teoría de la actividad de formación por etapas de las acciones mentales en la resolución de problemas. Rev. Científica Int. Inter Sci. Place 2009, 2, 9. [Google Scholar]
- Ausubel, D.P. Adquisición y retención del conocimiento. In Una Perpsectiva Cognitiva; Editorial Paidós Ibérica: Barcelona, Spain, 2002. [Google Scholar]
- Ballester, S. ET AL. Metodología de la Enseñanza de la Matemática Tomo I y II. La Habana; Editorial Pueblo y Educación: La Havana, Cuba, 1992. [Google Scholar]
- Gagné, R. The Conditions of Learning; Holt, Rinehart and Winston: New York, NY, USA, 1970. [Google Scholar]
- Galperin, Y. Introducción a Las Psicología; Pueblo y Educación: La Habana, Cuba, 1985. [Google Scholar]
- Leóntiev, A.N. The Genesis of Activity. J. Russ. East Eur. Psychol. 2005, 43, 4. [Google Scholar] [CrossRef]
- Piaget, J. La Equilibración de las Estructuras Cognitivas; Problema Central del Desarrollo: Madrid, Spain, 1975. [Google Scholar]
- Rogers, C. El proceso de convertirse en persona. In Mi Técnica Terapéutica; Departamento de Psicología y Psiquiatría, Universidad de Winsconsin: Madison, WI, USA, 1992. [Google Scholar]
- Cruz, M. La Enseñanza de la Matemática a Través de la Resolución de Problemas; Educación Cubana: La Habana, Cuba, 2006. [Google Scholar]
- Martínez, J.E.; Infante, R.; Brito, M. Los procesos didácticos para el tratamiento de teoremas matemáticos en el nivel medio superior. Univ. Y Soc. 2017, 9, 145–153. [Google Scholar]
- Pérez, Y.; Ramírez, R. Estrategias de enseñanza de la resolución de problemas matemáticos. Fundamentos teóricos y metodológicos. Rev. De Investig. 2011, 3, 35. [Google Scholar]
- Cedeño, F.O.; Caballero, H.H.; Alcívar, S.; Macías, M. Resolución de problemas estrategia didáctica de Poggioli para mejorar el aprendizaje de la matemática en la educación superior. Rev. Atlante Cuad. Educ. Desarro. Available online: https://www.eumed.net/rev/atlante/2018/11/resolucion-problemas-poggioli.html (accessed on 15 July 2021).
- Murcia, S.M.; Valdivieso, M.A. Aspectos a considerar en la resolución de un problema. In Proceedings of the II Encuentro Internacional de Matemáticas, Estadística y Educación Matemática, Tunja, Colombia, 14–16 August 2013. [Google Scholar]
- Silva, M.; Rodríguez, A.; Santillán, O. Estrategias de Resolución de Problemas Matemáticos Empleados por Estudiantes de Sexto Grado de Primaria. X Congreso Nacional de Matemática Educativa. 2019. Available online: http://www.comie.org.mx/congreso/memoriaelectronica/v10/pdf/area_tematica_05/ponencias/1729-F.pdf (accessed on 15 July 2021).
- Sigarreta, J.M.; Laborde, J.M. Estrategia para la resolución de problemas como recurso para la interacción sociocultural. Rev. PREMISA 2004, 20, 15–29. [Google Scholar]
- Rubinstein, J. El Desarrollo de la Psicología Principios y Métodos; Consejo Nacional de la Universidad: Habana, Cuba, 1964. [Google Scholar]
- Cala, A.; Buendía, A.M.; Herrera, L.J. Métodos y Estrategias Para la Resolución de Problemas Matemáticos: Una Revisión Desde las Investigaciones de la Última Década; Proyecto de Investigación: Medellín, Colombia, 2017. [Google Scholar]
- Campistrous, L.; Rizo, C. Estrategias de resolución de problemas en la escuela Cuba. Rev. Latinoam. De Investig. En Matemática Educ. 1999, 2, 31–45. [Google Scholar]
- Campos, M. The job of the heuristic procedures in the resolution of geometric exercises. Boletín REDIPE 2019, 8, 185–193. [Google Scholar]
- Polya, G. Cómo Plantear y Resolver Problemas; Trillas: México City, México, 1999. [Google Scholar]
- Santos-Trigo, M.; Moreno-Armella, L.; Camacho-Machín, M. Problem solving and the use of digital technologies within the mathematical working space framework. ZDM Math. Educ. 2016, 48, 827–842. [Google Scholar] [CrossRef]
- Schoenfeld, A. Mathematical Problem Solving; Academic Press: Orlando, FL, USA, 1985. [Google Scholar]
- Valle, M.C.; Curotto, M.M. La resolución de problemas como estrategia de enseñanza y aprendizaje. Rev. Electrónica De Enseñanza De Las Cienc. 2008, 7, 2. [Google Scholar]

| Theorems | Actions |
|---|---|
| Search for the theorem | -Search for assumptions -State a thesis -Formulate a theorem |
| Search for the proof | -Find an idea of the proof -Come up with a demonstration plan -Develop or complete the proof |
| Strategy for Solving Problems | Stages of the Assimilation Process | Operations |
|---|---|---|
| Approach to the problem | Comprehension | -Read the problem. -Are all the terms involved in formulating the problem familiar to you? -State the problem in your own words, specify what is given and what is sought, identify the knowledge that is related to what is given and what is sought. -Is it an intra-mathematical or extra-mathematical problem? -What field of knowledge can you associate the problem with? -Does it require the use of mathematical knowledge? -Have you seen any other one formulated in a similar way? -Is it a problem related to your sociocultural environment? |
| Deepening the problem | Identification | -Determine the necessary knowledge to face the problem. -Have you seen any other one formulated in a similar way? -Establish analogies, experiment with other data, and propose regularities. -Have all possible cases been checked? -Underline the expressions that you consider to have the greatest semantic value in the problem. -Look for synonyms and antonyms of the terms that you consider fundamental. -Establishes the unknown(s), that is, what is being sought. -Determine the data that are given directly in the formulation of the problem. -Between what values should it be found? -In a second moment you can think of developing a scheme, diagram, table, etc. -Is there enough, or is there too much data? -Are there contradictory elements? |
| Selecting a work path | Fixation | -Transform the problem into another equivalent one. -How can the data be related to the unknown(s)? -What inferences can be made from the data found? -Evaluate counterexamples. -Correctly use mathematical terminology and symbols. -Choose an appropriate language or a suitable notation. -Define what knowledge is related to the elements of the problem. -Justify ideas, judgments, and arguments. -Select the properties or definitions that may be useful to you. -Assume the problem is solved. -In which field of knowledge does the proposed problem move: arithmetic, algebraic, or geometric? -Define which knowledge system is related to the elements of the problem. -Which one of them is related to the premise or thesis of the problem? -Could a possible answer be given? |
| Application of the selected route | Application | -Establish relationships in correspondence with the forms of work. -Use cognitive and metacognitive strategies. -Execute an action plan and consciously apply the procedures. -Make equivalent transformations in the premise and/or the thesis. -Analyze the possible ways of solution. -Consider particular and general cases. -Integrate the possible results so that they can be used in different contexts. -Can you apply that same work technique to another situation? -Can the method used to solve other problems be generalized? -Make assumptions based on possible solutions. |
| Assessment. Consider and take a critical stance on the system of actions and operations carried out | Valoration | -What conjectures can you make? -Analyze the steps and actions taken; analyze errors and their possible causes; specify how to avoid errors. -Explain the reasoning process carried out and give details about it. -Think upon the procedures and methods used. -Choose an appropriate language or a suitable notation. -Are all the solutions found for the problem? -Explain with your words how you arrived at the solution. -Does the answer given make sense in relation to your experience? -Does the proposed solution really answer the problem in question? -What have you contributed from the social and/or mathematical point of view with the work on the problem? |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carballo, A.M.; Locia Espinoza, E.; Sigarreta Almira, J.M.; Yero, I.G. Approach to the Formulation of the Variable Change Theorem. Educ. Sci. 2021, 11, 357. https://doi.org/10.3390/educsci11070357
Carballo AM, Locia Espinoza E, Sigarreta Almira JM, Yero IG. Approach to the Formulation of the Variable Change Theorem. Education Sciences. 2021; 11(7):357. https://doi.org/10.3390/educsci11070357
Chicago/Turabian StyleCarballo, Armando Morales, Edgardo Locia Espinoza, José M. Sigarreta Almira, and Ismael G. Yero. 2021. "Approach to the Formulation of the Variable Change Theorem" Education Sciences 11, no. 7: 357. https://doi.org/10.3390/educsci11070357
APA StyleCarballo, A. M., Locia Espinoza, E., Sigarreta Almira, J. M., & Yero, I. G. (2021). Approach to the Formulation of the Variable Change Theorem. Education Sciences, 11(7), 357. https://doi.org/10.3390/educsci11070357







