Identifying the Characteristics of Non-Digital Mathematical Games Most Valued by Educators
Abstract
1. Introduction
1.1. Students Are Engaged
1.2. Skill and Luck
1.3. Mathematics Is Central
1.4. Flexibility for Learning and Teaching
1.5. Home-School Connections
1.6. Games into Investigations
1.7. The Current Study
- What are the characteristics of games that educators identify as important for supporting mathematics learning?
- What are the characteristics of games that influence the likelihood of an educator using the game in a classroom with students/children if given the opportunity?
2. Materials and Methods
2.1. Participants
2.2. Procedure
2.3. Measures
2.3.1. Measuring the Characteristics of Educationally Rich Mathematical Games (CERMaGs)
2.3.2. Perceived Game Value
2.3.3. Intentions to Use the Game
2.4. Data Analysis
3. Results
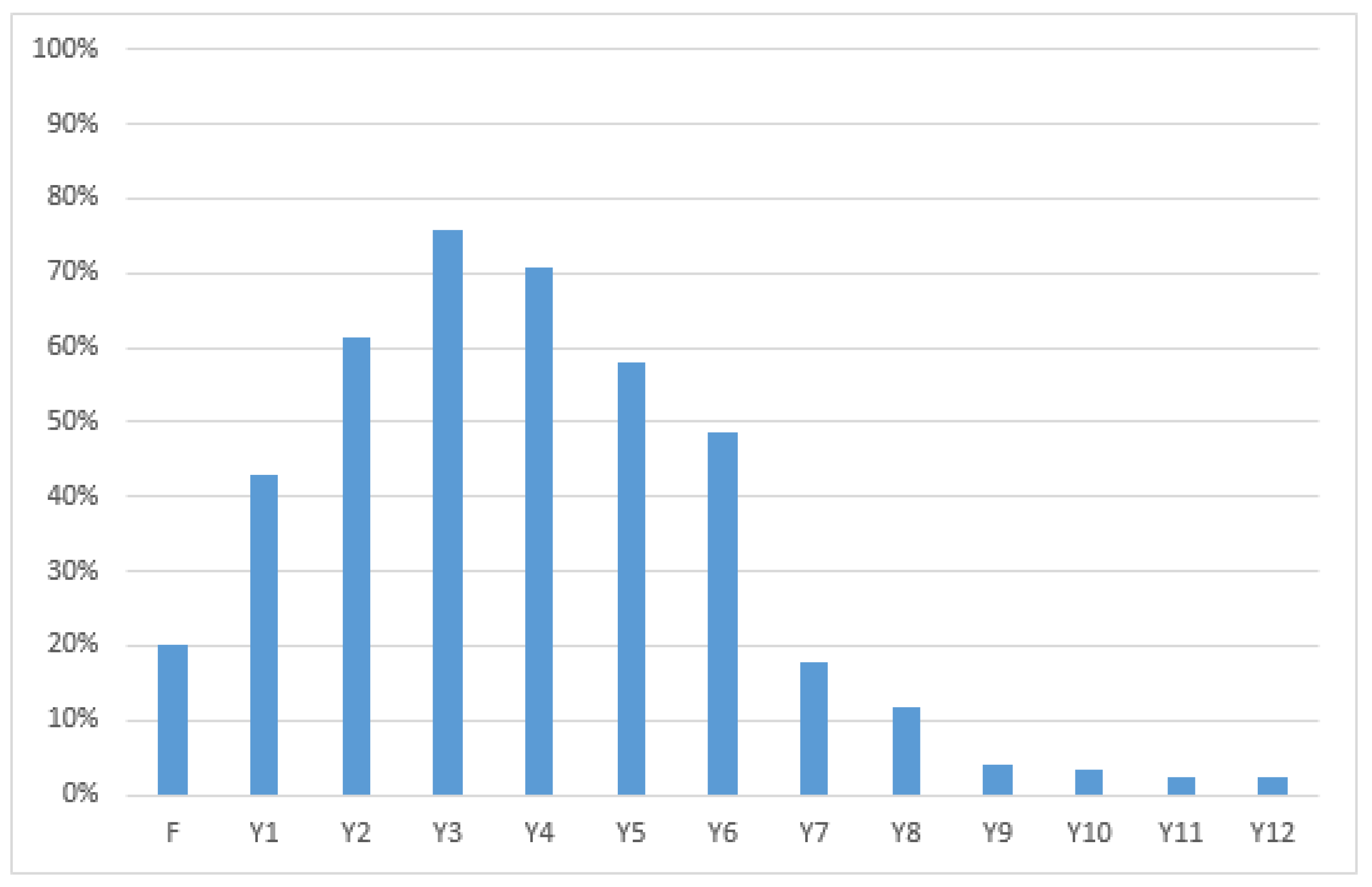
3.1. Descriptive Statistics
3.2. Describing the Characteristics of the Educationally Rich Mathematical Games (CERMaGs) Measure
3.3. Characteristics of Games That Educators Identify as Important for Supporting Mathematics Learning
3.4. Characteristics of Games That Influence the Likelihood of an Educator Using the Game
4. Discussion and Conclusions
4.1. Value of Educationally Rich Mathematical Games across Multiple Year Levels
4.2. Understanding How Games Support Mathematical Discussion
4.3. Games Are ‘More Than Fun’
4.4. Supporting Home-School Connections
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- British Museum Top 10 Historical Board Games. Available online: https://www.britishmuseum.org/blog/top-10-historical-board-games (accessed on 16 December 2022).
- Green, J. The Best Selling Board Games in America. Available online: https://247wallst.com/special-report/2022/09/04/the-best-selling-board-games-in-america/ (accessed on 16 December 2022).
- Fang, Y.M.; Chen, K.M.; Huang, Y.J. Emotional reactions of different interface formats: Comparing digital and traditional board games. Adv. Mech. Eng. 2016, 8, 1687814016641902. [Google Scholar] [CrossRef]
- Russo, J.; Bragg, L.; Russo, T. How primary teachers use games to support their teaching of mathematics. Int. Elec. J. Elem. Educ. 2021, 13, 407–419. [Google Scholar] [CrossRef]
- Bofferding, L.; Kastberg, S.; Hoffman, A. Family mathematics nights: An opportunity to improve preservice teachers’ understanding of parents’ roles and expectations. Sch. Sci. Math. 2016, 116, 17–28. [Google Scholar] [CrossRef]
- Downton, A.; Cheeseman, J.; Roche, A. Goals and Challenges of School Mathematics Leaders. Math. Teach. Educ. Dev. 2022, 24, 96–115. [Google Scholar]
- Guo, L.; Wang, J. Relationships between teacher autonomy, collaboration, and critical thinking focused instruction: A cross-national study. Int. J. Educ. Res. 2021, 106, 101730. [Google Scholar] [CrossRef]
- Sullivan, P.; Clarke, D.J.; Clarke, D.M.; Farrell, L.; Gerrard, J. Processes and priorities in planning mathematics teaching. Math. Educ. Res. J. 2013, 25, 457–480. [Google Scholar] [CrossRef]
- Russo, J.; Russo, T.; Bragg, L.A. Five principles of educationally rich mathematical games. Aust. Prim. Math. Classr. 2018, 23, 30–34. [Google Scholar]
- Russo, J.; Russo, T. Transforming mathematical games into investigations. Aust. Prim. Math. Classr. 2020, 25, 14–19. [Google Scholar]
- Cevikbas, M.; Kaiser, G. Student engagement in a flipped secondary mathematics classroom. Int. J. Sci. Math. Educ. 2022, 20, 1455–1480. [Google Scholar] [CrossRef]
- Collie, R.J.; Martin, A.J.; Bobis, J.; Way, J.; Anderson, J. How students switch on and switch off in mathematics: Exploring patterns and predictors of (dis)engagement across middle school and high school. Educ. Psychol. 2019, 39, 489–509. [Google Scholar] [CrossRef]
- Wouters, P.; van Nimwegen, C.; van Oostendorp, H.; van der Spek, E.D. A meta-analysis of the cognitive and motivational effects of serious games. J. Educ. Psychol. 2013, 105, 249–265. [Google Scholar] [CrossRef]
- Zyda, M. From visual simulation to virtual reality to games. Computer 2005, 38, 25–32. [Google Scholar] [CrossRef]
- Csikszentmihalyi, M.; Csikzentmihaly, M. Flow: The Psychology of Optimal Experience; Harper & Row: New York, NY, USA, 1990. [Google Scholar]
- Silva, R.; Rodrigues, R.; Leal, C. Play it again: How game-based learning improves flow in Accounting and Marketing education. Account. Educ. 2019, 28, 484–507. [Google Scholar] [CrossRef]
- Elias, G.S.; Garfield, R.; Gutschera, K.R. Characteristics of Games; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Skilling, K.; Bobis, J.; Martin, A.J. The “ins and outs” of student engagement in mathematics: Shifts in engagement factors among high and low achievers. Math. Educ. Res. J. 2021, 33, 469–493. [Google Scholar] [CrossRef]
- Tze, V.; Daniels, L.M.; Klassen, R.M. Evaluating the relationship between boredom and academic outcomes: A meta-analysis. Educ. Psychol. Rev. 2016, 28, 119–144. [Google Scholar] [CrossRef]
- Cardano, G. The Book on Games of Chance: The 16th-Century Treatise on Probability; Courier Dover Publications: Mineola, NY, USA, 2015. [Google Scholar]
- Pandit, R.A.; Waghmare, S.A.; Bhagat, P.M. History of Probability Theory. J. Soc. Sci. Hum. 2022, 4, 140–142. [Google Scholar]
- Bewersdorff, J. Luck, Logic, and White Lies: The Mathematics of Games; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Nurnberger-Haag, J.; Wernet, J.L.; Benjamin, J.I. Gameplay in perspective: Applications of a conceptual framework to analyze features of mathematics classroom games in consideration of students’ experiences. Int. J. Educ. Math. Sci. Technol. 2023, 11, 267–303. [Google Scholar] [CrossRef]
- Gough, J. Dice and board games. Aust. Prim. Math. Classr. 2001, 6, 14–17. [Google Scholar]
- Bay-Williams, J.M. Enriching addition and subtraction fact mastery through games. Teach. Child. Math. 2014, 21, 238–247. [Google Scholar] [CrossRef]
- Bouck, E.C.; Long, H.M. Does making tens add up: Exploring game play to support math fluency. Prev. Sch. Fail. 2022, 66, 256–266. [Google Scholar] [CrossRef]
- Buchheister, K.E.; Jackson, C.; Taylor, C.E. Math games: A universal design approach to math reasoning. Aust. Prim. Math. Classr. 2017, 22, 7–12. [Google Scholar]
- Jackson, C.; Taylor, C.E.; Buchheister, K. Bingo! Select games for mathematical thinking. Math. Teach. Mid. Sch. 2013, 18, 424–429. [Google Scholar] [CrossRef][Green Version]
- Bay-Williams, J.; Kling, G. Math Fact Fluency: 60+ Games and Assessment Tools to Support Learning and Retention; ASCD: Reston, VA, USA, 2019. [Google Scholar]
- National Center on Intensive Intervention. Principles for Designing Intervention in Mathematics; Office of Special Education, U.S. Department of Education: Washington, DC, USA, 2016. [Google Scholar]
- Hopkins, S.; O’Donovan, R. Developing Assessments for Students with Intellectual Disability to Support Differentiation. Math. Teach. Educ. Dev. 2021, 23, 132–147. [Google Scholar]
- Trinter, C.P.; Brighton, C.M.; Moon, T.R. Designing differentiated mathematics games: Discarding the one-size-fits-all approach to educational game play. Gift. Child Today 2015, 38, 88–94. [Google Scholar] [CrossRef]
- Shen, C.C.; Tsai, C.H.; Tseng, T.A. The Influence of Flow Experience and Serious Leisure on Attachment in Board Game. Leis. Sci. 2022, 1–25. [Google Scholar] [CrossRef]
- Cai, J. Investigating parental roles in students’ learning of mathematics from a cross-national perspective. Math. Educ. Res. J. 2003, 15, 87–106. [Google Scholar] [CrossRef]
- Daucourt, M.C.; Napoli, A.R.; Quinn, J.M.; Wood, S.G.; Hart, S.A. The home math environment and math achievement: A meta-analysis. Psychol. Bull. 2021, 147, 565. [Google Scholar] [CrossRef]
- Berkowitz, T.; Schaeffer, M.W.; Maloney, E.A.; Peterson, L.; Gregor, C.; Levine, S.C.; Beilock, S.L. Math at home adds up to achievement in school. Science 2015, 350, 196–198. [Google Scholar] [CrossRef]
- Scalise, N.R.; DePascale, M.; Tavassolie, N.; McCown, C.; Ramani, G.B. Deal Me in: Playing Cards in the Home to Learn Math. Educ. Sci. 2022, 12, 190. [Google Scholar] [CrossRef]
- Ramani, G.B.; Scalise, N.R. It’s more than just fun and games: Play-based mathematics activities for Head Start families. Early Child. Res. Q. 2020, 50, 78–89. [Google Scholar] [CrossRef]
- Bragg, L.A.; Herbert, S.; Brown, J.P. Successful home-school collaboration: Let’s talk about maths at home. Aust. Prim. Math. Classr. 2020, 25, 18–22. [Google Scholar]
- Keen, B. Using Misconceptions to Improve Engagement and Preventative Effects within Gambling Education; The University of Sydney: Sydney, Australia, 2019; Available online: https://hdl.handle.net/2123/21190 (accessed on 18 July 2022).
- Swan, P.; Marshall, L. Probability Chance Experiments Upper Primary (Years 5—6); A–Z Type: Perth, Australia, 2021. [Google Scholar]
- Keen, B.; Blaszczynski, A.; Anjoul, F. Systematic review of empirically evaluated school-based gambling education programs. J. Gambl. Stud. 2017, 33, 301–325. [Google Scholar] [CrossRef] [PubMed]
- Byrne, M. Using games to engage students in inquiry. PRIMUS 2017, 27, 271–280. [Google Scholar] [CrossRef]
- Setiyadi, D.; Zaenuri, Z.; Mulyono, M. The Problem Based Learning Model with Etnomatematics Nuance by Using Traditional Games to Improve Problem Solving Ability. J. Prim. Educ. 2018, 7, 176–186. [Google Scholar]
- Cohen, J. Statistical power analysis. Curr. Dir. Psychol. Sci. 1992, 1, 98–101. [Google Scholar] [CrossRef]
- Ellis, P.D. The Essential Guide to Effect Sizes: Statistical Power, Meta-Analysis, and the Interpretation of Research Results; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Gilrein, E.; Wolfe, J. Bridging Silos. Learn. Prof. 2016, 37, 12–16. [Google Scholar]
- Heshmati, S.; Kersting, N.; Sutton, T. Opportunities and challenges of implementing instructional games in mathematics classrooms: Examining the quality of teacher-student interactions during the cover-up and un-cover games. Int. J. Sci. Math. Educ. 2018, 16, 777–796. [Google Scholar] [CrossRef]
- De Bondt, M.; Willenberg, I.A.; Bus, A.G. Do book giveaway programs promote the home literacy environment and children’s literacy-related behavior and skills? Rev. Educ. Res. 2020, 90, 349–375. [Google Scholar] [CrossRef]
| Principle | Items |
|---|---|
| Students are engaged | 1a The game will engage students |
| 1b Students will enjoy playing the game | |
| 1c Students playing the game will likely get off task ^ | |
| Skill and luck | 2a The game gives all students a chance to win |
| 2b The game represents a good balance between skill and luck | |
| 2c The game allows more skilful players to dominate ^ | |
| Mathematics is central | 3a Important mathematical ideas are central to gameplay |
| 3b The game encourages mathematical discussion between students during gameplay | |
| 3c Mathematics seems ‘tacked-on’ to the game ^ | |
| Flexibility for learning and teaching | 4a The game is suitable for learners of different ability levels |
| 4b The game can be easily modified to cater to a variety of different learners | |
| 4c The game offers a good level of challenge for students | |
| 4d Many students who struggle with mathematics would find this game too challenging ^ | |
| 4e High performing students would find the game too easy ^ | |
| Home-school connections | 5a The game requires minimal special materials and set-up |
| 5b The game offers a good opportunity for building connections between home and school | |
| 5c The game is hard to explain and describe to a non-teacher ^ | |
| Games into investigations | 6a The game could lead to a rich mathematical investigation |
| 6b The game could be used to launch a mathematical inquiry | |
| 6c I think the game is more suited to a ‘warm-up’ or ‘quick game’ than a deep exploration of mathematical ideas ^ |
| Setting | Frequency |
|---|---|
| Observing students playing the game in a classroom | 49 (40%) |
| Playing the game in a workshop, tutorial, or other professional learning context | 37 (30%) |
| Watching an online video clip, such as YouTube, Vimeo, etc. | 28 (23%) |
| Other | 8 (7%) |
| Mean (Out of 10) | SD | Median | |
|---|---|---|---|
| Perceived game value (all educators) | 8.95 | 1.21 | 9 |
| Perceived game value (used game already) | 8.97 | 1.09 | 9 |
| Perceived game value (not yet used game) | 8.93 | 1.34 | 9 |
| Intentions to use the game (all educators) | 9.57 | 1.04 | 10 |
| Intentions to use (used the game already) | 9.73 | 0.93 | 10 |
| Intentions to use (not yet used the game) | 9.42 | 1.12 | 10 |
| Principle | Items | Game Value (ρ) | Intentions to Use (ρ) |
|---|---|---|---|
| Students are engaged | 1a The game will engage students | 0.36 * | 0.30 * |
| 1b Students will enjoy playing the game | 0.34 * | 0.34 * | |
| 1c Students playing the game will likely get off task ^ | −0.15 | −0.15 | |
| Skill and luck | 2a The game gives all students a chance to win | 0.19 * | 0.28 * |
| 2b The game represents a good balance between skill and luck | 0.10 | 0.04 | |
| 2c The game allows more skilful players to dominate ^ | −0.01 | −0.17 | |
| Mathematics is central | 3a Important mathematical ideas are central to gameplay | 0.21 * | 0.15 |
| 3b The game encourages mathematical discussion between students during gameplay | 0.28 * | 0.30 * | |
| 3c Mathematics seems ‘tacked-on’ to the game ^ | −0.19 * | −0.15 | |
| Flexibility for learning and teaching | 4a The game is suitable for learners of different ability levels | 0.19 * | 0.24 * |
| 4b The game can be easily modified to cater to a variety of different learners | 0.39 * | 0.28 * | |
| 4c The game offers a good level of challenge for students | 0.39 * | 0.17 | |
| 4d Many students who struggle with mathematics would find this game too challenging ^ | −0.10 | −0.18 * | |
| 4e High performing students would find the game too easy ^ | −0.22 * | −0.14 | |
| Home-school connections | 5a The game requires minimal special materials and set-up | 0.18 * | 0.13 |
| 5b The game offers a good opportunity for building connections between home and school | 0.17 | 0.13 | |
| 5c The game is hard to explain and describe to a non-teacher ^ | −0.02 | −0.14 | |
| Games into investigations | 6a The game could lead to a rich mathematical investigation | 0.36 * | 0.30 * |
| 6b The game could be used to launch a mathematical inquiry | 0.30 * | 0.15 | |
| 6c I think the game is more suited to a ‘warm-up’ or ‘quick game’ than a deep exploration of mathematical ideas ^ | −0.11 | 0.08 |
| Characteristic | Exemplary Quotation |
|---|---|
| Principle 4c: The game offers a good level of challenge for students | “The kids will be able to be challenged and (we) will be able to extend and enable students.” |
| Principle 4b: The game can be easily modified to cater to a variety of different learners | “So many ways to adapt the game to suit learners.” |
| Principle 6a: The game could lead to a rich mathematical investigation | “I think there are a lot of strong underlying mathematics ideas that can be explored in this game. It is also adaptable and allows for deeper investigation.” |
| Principle 1a: The game will engage students | “The level of engagement with this game is astounding. I work with very reluctant students and it was this game that ‘won’ them over!” |
| Principle 1b: Students will enjoy playing the game | “Students showed a high level of enjoyment (playing the game)” |
| Principle 6b: The game could be used to launch a mathematical inquiry | “The game could also be used as a springboard for inquiry into other areas of maths, such as capacity and volume, given the right questions and materials.” |
| Characteristic | Exemplary Quotation |
|---|---|
| Principle 1b: Students will enjoy playing the game | “I have used it many times! My students love it!” |
| Principle 3b: The game encourages mathematical discussion between students during gameplay | “It would allow for rich discussion amongst students and I liked how playing against the teacher allows students to collaborate and share ideas” |
| Principle 6a: The game could lead to a rich mathematical investigation | “It would provide (an) engaging activity when working on multiplication as well as opportunities for investigation.” |
| Principle 1a: The game will engage students | “There is maximum engagement for student and opportunities for students to explain their thinking and strategies” |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Russo, J.; Bragg, L.; Russo, T.; Minas, M. Identifying the Characteristics of Non-Digital Mathematical Games Most Valued by Educators. Educ. Sci. 2023, 13, 30. https://doi.org/10.3390/educsci13010030
Russo J, Bragg L, Russo T, Minas M. Identifying the Characteristics of Non-Digital Mathematical Games Most Valued by Educators. Education Sciences. 2023; 13(1):30. https://doi.org/10.3390/educsci13010030
Chicago/Turabian StyleRusso, James, Leicha Bragg, Toby Russo, and Michael Minas. 2023. "Identifying the Characteristics of Non-Digital Mathematical Games Most Valued by Educators" Education Sciences 13, no. 1: 30. https://doi.org/10.3390/educsci13010030
APA StyleRusso, J., Bragg, L., Russo, T., & Minas, M. (2023). Identifying the Characteristics of Non-Digital Mathematical Games Most Valued by Educators. Education Sciences, 13(1), 30. https://doi.org/10.3390/educsci13010030








