Abstract
A poorly elaborated learner’s understanding of models has been reported to be one of the major sources for learning difficulties in the quantum domain. To be able to provide physics education in schools with evidence as to how this problem can be tackled, a deeper theoretical understanding of the structure of learners’ mental models in quantum physics seems essential. In this respect, previous research has proposed two dimensions in learners’ mental models in the atomic hull context, labelled Fidelity of Gestalt and Functional Fidelity. In this article, we investigate whether this proposed two-factorial structure can be transferred to quantum concepts beyond the atomic hull context. To approach this, we surveyed the structure of students’ mental models in the context of photons’ properties and behavior. We conducted a questionnaire study: 170 secondary school students completed a survey instrument adapted from the literature. Using exploratory factor analysis, the two factors Fidelity of Gestalt and Functional Fidelity to describe the students’ mental models could be replicated for the photon context. We provide a selection of results from physics education literature to reveal that our two-factor framework to describe the students’ mental models seems to be a promising endeavor in the landscape of science education research in general.
1. Introduction
Learning quantum physics is hard because quantum physics is counterintuitive. A relinquishment of classical physics models is regarded as the key towards learners’ conceptual understanding of quantum physics [1]. However, after learning classical physics concepts throughout introductory physics courses, a transition to quantum thinking is challenging for many students [2,3]. As a result, “the overlapping/mix-up of the conceptual frameworks of classical physics (CP) and QM” ([4], p. 257) may be observed: students are numerously stuck to their (naive-) realist views [5] or classic-mechanistic mental models [6], although quantum physics formalism does not enable space-time description of quantum phenomena. Possible origins for student difficulties in the quantum physics context have been summarized in Ref. [7]: for example, the authors point out that students—amongst others—blend mathematical formalism and physical reality, or that they have problems in understanding “the limitations of language to explain and express QP phenomena, concepts, and objects” ([7], p. 4).
Kalkanis et al. [4] regard learners’ lack of model understanding as one of the sources of students difficulties in general and of students’ classical-mechanistic mental models in particular when it comes to quantum concepts. Since quantum physics is “a prime example for the need for model descriptions” ([8], p. 2), learners are confronted with diverse abstract models in introductory courses on quantum mechanics. According to Ubben and Heusler [9], these models are often misunderstood by learners “as upscaled or downscaled exact representations of the ’real thing”’ (p. 1350). Hence, classical-mechanistic mental models on quantum concepts mirror the students’ difficulties in model-reality differentiation in general [10] and in quantum physics in particular [11].
Similar problems arise in the context of atomic physics: In their study on learners’ mental models of the atomic hull. Ubben and Heusler [9] collected data from 3108 participants using a questionnaire consisting of fifteen four-point Likert scale items (strongly agree to strongly disagree) adapted from the literature. From the participants’ ratings, the authors uncovered the underlying psychometric structure of mental models of the atomic hull using exploratory factor analysis: they found that the participants’ mental models of the atomic hull could be characterized by two dimensions, namely the Fidelity of Gestalt and Functional Fidelity, respectively.
The dimension Fidelity of Gestalt…
- …describes that one can understand their mental models “as exact visual representations of phenomena or exact depictions of how things look” ([9], p. 1356), and
- …“how much the mental models‘ gestalt is perceived as accurate” ([9], p. 1360).
On the other hand, the dimension Functional Fidelity…
- …describes that one can understand their mental models as “appropriate descriptions of how phenomena work” ([9], p. 1356) and
- …“how much the mental models’ underlying abstract functionality […] is perceived as accurate” ([9], p. 1360).
By combining these two empirically extracted factors, Ubben and Heusler [9] derived four archetypes of mental modelling in the context of the atomic hull: depending on the manifestation of Fidelity of Gestalt (FG) and Functional Fidelity (FF) in the learners’ mental models of the atomic shell, these archetypes were designated as non-developed type (low FG, low FF), architectural type (high FG, low FF), dual type (high FG, high FF) and functional type (low FG, high FF). Several starting points for further research arise from these findings:
- Further research is needed to explore the structure of students’ mental models in quantum physics beyond the context of the atomic hull.
- Empirical studies are needed to check the validity of the above-mentioned framework presented by Ubben and Heusler ([9], p. 1360) in quantum physics education and beyond. In this respect, confirmatory statistical methods are required.
- Finally, it would have to be clarified as to how and to what extent this framework describing the structure of mental models via the two dimensions Fidelity of Gestalt and Fidelity of Function could inform physics instruction or physics teacher education.
This paper will focus on the first aspect in more detail. Therefore, we have chosen to explore the structure of students’ mental models in a context close to but not restricted to the atomic hull. As we have outlined, the transfer of ideas from classical physics over to quantum physics often causes conceptual difficulties for learners: “These conceptual barriers become particularly apparent when investigating learners’ conceptions about the properties and behavior of quantum objects such as electrons or photons” ([8], p. 2). For example, various studies report on students’ mental models of electrons or photons as small (spherical) particles [12] that move along defined trajectories [13]. Therefore, this paper focuses on students’ mental models of quantum objects, more precisely on students’ mental models of single photons’ properties and behavior. Further arguments from a rather theoretical point of view support this specific topic choice:
- On the one hand, quantum effects whose explanation requires a photon model, have no classical analogues. Hence, no classical framework is valid for the description of such effects.
- In contrast to further quantum concepts without classical analogy (e.g., quantum entanglement), the photon concept is still an integral element of international secondary school curricula [14]. Hence, the context of photons (on the level typically presented in secondary schools seems a suitable one for our study: since the participating secondary school students have been introduced to photons in their regular classes on quantum physics prior to our study, they may already have built their own mental models of the topic under investigation.
- In fact, this specific topic choice goes along with some limitations for our study which we reflect on in Section 7 of this article.
A comprehensive overview of different mental models of light quanta and their historical development within the history of physics is provided in Ref. [15].
To sum up, in this research article we ask whether the two-factorial structure of mental models identified in the context of the atomic shell ([9], p. 1360) can also be found in mental models of photons’ properties and behavior (cf. Section 3 on our research question). Consequently, we report on a study exploring the structure of learners’ mental models on this topic (cf. Section 4 on the methods). In the next Section 2, we provide an overview of the term mental model against the backdrop of a large body of research. In particular, we include educational psychology and neurology perspectives.
2. Theoretical Background on Mental Models
When talking about cognition, the idea of mental models is often used to describe certain small domains of knowledge. The term mental model is traced back to Johnson-Laird [16] or Gentner and Stevens [17], although the idea behind it was already brought up by Craik [18]. One of the problems arising from the use of a mental model as a construct is its definition, which often is not entirely consistent in different parts of literature. Additionally, several areas of science have their own names for the same or a similar idea. Therefore, it is necessary to propose a definition of what a mental model is in the context of this paper. Such a definition should entail the general common properties of mental models and similar ideas and will be distilled by looking at educational psychology and neurology. Therefore, in a first step, we will show that there is an overlap in theoretical approaches to concepts and mental models of cognition. For example, the primary proposition of Craik [18] was that there is a “‘small-scale model’ of external reality” (p. 61) that people carry around in their minds. Though he did not use the term mental model, his ideas are seen as the groundwork for later uses of the term (cf. [19]).
In the context of this paper, we propose the following working definition of the term mental model emphasizing two main components: A mental model is an individual modal pattern—a certain gestalt—codifying some functionality.
This definition entails three aspects, which are found in the literature of different research disciplines, as we will outline in the following:
- some structural component (gestalt),
- some functional, abstract component it represents or codes (functionality),
- subjectivity of the mental model and being based on past experiences (individual).
The first component of a mental model, the gestalt, is in many cases closely linked with a pattern of visual modality (e.g., [20]). In fact, even Craik himself described it as being “symbolic” ([18], p. 57). However, this does not mean that the gestalt only has to be visual. Consider, for example, the prominent Cognitive Theory of Multimedia Learning ([21], see also [22,23]), which proposes coding via sensory patterns of visual and auditory modality. In this sense, gestalts of mental models will be assumed to exist in all modalities. They can also be interpreted as one gestalt when the different modalities are coherent—when they are different modal representations of the same thing, like the smell and shape of a piece of pie. This is possible because our above-mentioned working definition is only about a ‘modal pattern’ and not about ‘a pattern of exactly one modality’.
The second component, the functionality, is the set of functions that is coded in the mental model, making it the abstract component. The term functionality was chosen as it helps make this part of the mental model more value-independent. When dealing with gestalts—or in a more everyday sense with objects or situations—there are many possible functions that the gestalts signify. The idea of objects being seen through the lens of (a) what is possible to do with them or (b) what they can possibly do was first proposed by Gibson [24,25,26]. Therefore, one can not only attribute a single function to a gestalt. One can not even attribute a purely ‘good’ or ‘productive’ set of functions or a purely ‘bad’ or ‘destructive’ set of functions to one gestalt. What functions a gestalt codes depends on the context—on the situation the mental model is held in. An apple in front of you might codify something like ‘tool for reaching satiation’ when you are hungry, in another situation it might codify something like ‘disgusting thing to avoid’ when you are already stuffed. This idea has—amongst others—been further developed and elaborated by Panksepp [27] on a neurological level and by Peterson [28] on a psychological level amongst others. In summary, the term functionality was chosen for the set of (potential) functions a gestalt codes to…
- …circumvent having to ascribe a certain value to a gestalt and thus,
- …make the definition of a mental model more value-independent.
The third component of a mental model is its individual aspect. By this, several things are meant: The most obvious aspect is that the mental models we have in our heads are different from person to person. The reason for this can be given by using the constructivist perspective towards learning processes: we learn from experiences and individual properties like interest or personality make all learning individual [29]. Furthermore, a mental model can change over time, get more elaborated, more abstract or change in the functions it codes (cf. [19,30]).
In the following two subsections, we will more thoroughly elaborate the parallels between the working definition proposed in this article to the descriptors of mental models that are widely used in the literature. We will consider two areas for this purpose: a perspective from educational psychology—which often shows a more theoretical approach—and one being from neurology—which includes some more empirically based support.
2.1. Educational Psychology Perspective
The first perspective we will take when examining the idea of mental models in psychology and educational sciences is the perspective of educational psychology, as it is at the intersection of the former two. One of the first ideas similar to that of a mental model in the sense of this paper is Piaget’s idea of representations [31]. He suggested that a representation is something that goes “beyond the present, extending the field of adaptation” and that it “evokes what lies outside the immediate perceptual and active field” ([31], p. 273). In this sense, he ascribes a wider scope to the representation than simply being something that directly represents some sensory input pattern and some more abstract feature. Some efforts have been made to distinguish a representation of present objects and more abstract ones by using the term “perceptual representation” for the former and “conceptual representation” or “mental representation” for the latter [30]—and to some extent this difference is sensible. In the present analysis, however, this distinction will not be made. Thus, we will only look at Piaget’s broad definition of a representation and the two aspects it entails: namely a “signifier” and a “signified” ([31], p. 273). The signifier is seen as a visual component of a representation, something symbolic to aid recall, whereas the signified is the underlying meaning of the representation. These ideas are not only mappable to Craik’s discussions and to the working definition of a mental model presented in this paper, but they are also used in more recent literature (cf. [32]). In addition, even the individual aspect of representations has been emphasized [33], giving all three aspects of mental models an analogous idea in the context of representations.
The term mental model itself has found a wide use in literature and is often used with an emphasis on the modelling aspect of the mind. Horst [19], as probably one of the most recent examples, uses the label as the building block of his theory of Cognitive Pluralism. His idea of a mental model has two components: it is proposed to be an imagination of a structure observed on the one hand and something that can be transformed in the mind by applying actions to it, for example making it move or twist in the mind on the other [19], p. 121. This dynamic part of the mental model is characterized as being seen through an individual perspective. He draws on the ideas of Gibson [26] to evaluate the possible actions—the functionality of the model. In this sense, his idea is quite similar to the one presented in this paper, as the three core aspects of gestalt, functionality and individuality are present in his description as well.
In the context of learning in school, and in particular in science education research, there has been a lot of research into students’ conceptions. Unfortunately, many of these are not sufficiently elaborated and do not work well enough to get a grasp of functions and relations underlying a phenomenon. However, the term mental model has been used in this context as well (cf. [1,34]). In many cases the problem is not that learners have difficulties in developing a mental model, but rather that their conceptions do not work aptly enough or are interpreted insufficiently. Ref. [20] provides a very useful overview of the development of research and theories of conceptions held by students, starting from Piaget’s first ideas leading to a modern perspective. Their use of the term mental model differs from the one we are describing, as it only encompasses images as gestalts and not symbolic codes such as e.g., ‘+’ or ‘-’. Their version of image-schemata is more in accordance with it and entails a visual gestalt component as well as a component of dynamic or action (functionality, see e.g., for cases of this labelling Refs. [1,35]).
After making some arguments for the definition of a mental model in this paper being in accordance with a larger body of literature in educational psychology, the following subsection will show some more neurological findings.
2.2. Neurological Perspective
From a neurological point of view, similar components of mental models to those used in this paper can be found: The most striking parallel probably arises from split-brain research. The summary of the neurological literature given here is not only meant to show that our working definition is in line with neurological findings, but may also support the empirical findings later on. During research in the 70s, two main modes of partly hemispheric-dependent grouping were discovered [36]. These two were appearance and function as criteria to associate and group entities. Depending on the hemisphere, it was found that an association via appearance or function to a given visual cue was preferred. More recent research has further elaborated these findings, e.g., by concluding that the right hemisphere is more specialized for (visual) perception of causality and the left one more specialized on abstract inference of causality, though only both hemispheres working together can synthesise a ‘complete’ understanding of causality (for a review cf. [37]; for a case study cf. [38]). Though these findings seem to describe a rather general picture of hemispheric processes, the parallels to the fundamental blocks of mental models are not easily dismissed.
To illustrate some of the parallels between mental models as discussed previously and neurological findings for hemispheric specialisations, we will use the neurologically rather well-researched field of causality. Firstly, we want to draw attention to the work of Gopnik et al. [39], who proposed a theory of causal learning via causal maps. These causal maps are regarded as part of a causal learning system, which they propose makes “fundamental assumptions about how patterns of correlation and intervention are related to causal relations” [39], (p. 6). In their theoretical view, again, there are the two aspects that have shown up as well in other theories on mental models or similar constructs: (a) A sensory pattern which is related to some abstract relation or function, and (b) an observational aspect that is relevant during the generation of new causal representations [39]. In the closing remarks of their work [39], the authors even emphasize two aspects of science which roughly map to gestalt and functionality, respectively: one being natural history, which they describe as “discovering consistent patterns in visual experience and relating those patterns to the structure of objects in the world” and the other being natural philosophy, which they describe as seeking to “explain the world in mathematical terms” ([39], p. 30) and focusing more on a computational, functional part of cognition. From a purely terminological point, it is not clear if representations are to be seen in a Piagetian way in this context, but their two main components described by Gopnik et al. [39] point in that direction.
In the case of causation, there are several neurological findings that can be related to the theoretical ones by [39] and share many parallels to them: In particular, the study conducted by [38] sheds some more light on the neurological underpinnings of understanding causality with respect to hemispheric specialisations. One of the most common ways of conducting studies on this topic is the use of interactions between moving stimuli, such as collisions between balls in what is called the launching effect (e.g., [40]). This effect has been used in research on perceptual causality (e.g., [38,41]), where causality is studied in the context of visual structures, such as spatial and temporal object interactions. It was found that the right hemisphere with its tendency to be more specialized in ‘appearance’ is also the main actor in perceiving perceptual causality [38]. On the other hand, the left hemisphere is more based on conceptual knowledge and logical rules and functions, making it the more dominantly activated hemisphere in case of abstract causal events such as flicking a switch and a light bulb lighting up. These more abstract and functional causal phenomena that require a more functional understanding have shown to be attributable to mainly the left-hemisphere of the brain with its frequent specialisation on ‘function’ [38]. These studies do not only lend weight to the theory presented in Ref. [39], but also give hints for the two factors forming ‘causal understanding’ as being related to the two common specializations of the hemispheres. In patients with intact corpi collosa, these two systems are working closely together, merging the two. Of course, the given exemplary case of causal understanding is only roughly considered and the neurological mechanisms underpinning these findings are extremely complex. Nonetheless, when seen as situational mechanisms, they show quite an overlap to what we have outlined as a mental model previously.
3. Research Question
Following the results on the structure of mental models of the atomic hull presented by [9] and the literature discussed in Section 2, the question arises as to whether the two-factorial structure of mental models comprising the dimensions Fidelity of Gestalt and Fidelity of Function in student thinking can be transferred to concepts of quantum physics beyond the atomic hull context. To approach the clarification of this question, we have chosen to investigate the structure of students’ mental models in the context of photons’ properties and behavior in this research as we have argued in Section 1.
Consequently, we pose the following research question: Does the two-factorial structure of learners’ mental models of the atomic hull with the factors Fidelity of Gestalt and Fidelity of Function also show up in learners’ mental models of photons’ properties and behavior?
We expect a two-factor structure of the mental models on photons’ properties and behavior, assuming that the two factors can again be interpreted as Fidelity of Gestalt and Fidelity of Function. We justify this with two arguments:
- As has been shown in Section 2, findings from educational psychology and neurology suggest these two primary dimensions in students’ mental models.
- The topics of the atomic shell and photons are different at first glance, but close in terms of content, e.g., when we think about electrons in the atomic shell that are quantum objects in the same way that photons are.
However, we are open to any other uncovered structure in our study: after all, the previously extracted factors of mental models in the atomic hull context, namely Fidelity of Gestalt and Functional Fidelity, could possibly split into further subdimensions in a different context. For this reason, we use an exploratory approach to address this research question. This is important to not undergo confirmation bias by using confirmatory methods in an too early research stage.
4. Methods
4.1. Study Design and Sample
We conducted a questionnaire study to investigate secondary school students’ mental models of the photons’ properties and behavior. No intervention was included in our study.
The sample comprises (87 females, 83 males, 0 diverse) German secondary school students (grades 11 and 12, 16–18 years of age) with an average grade in physics of (). Note, that in Germany, 1 is the best and 6 is the worst grade. Prior to our study, all students participated in an introductory course on quantum physics during their regular physics lessons as is mandatory in the German curriculum. All students participated on a voluntary basis, according to ethical standards. Informed consent was obtained from all participants.
4.2. Instrument
To assess learners’ mental models of photons’ properties and behavior on large-scale, we used ten five-point Likert scale items (1 = disagree, 2 = rather disagree, 3 = undecided, 4 = rather agree, 5 = agree) from the literature (cf. Table 1). Our items have previously been used in empirical studies on learning quantum physics (cf. [8,42]). The original versions of our items originate from Ref. [43] and were adapted by Müller and Wiesner [44] in the course of the evaluation of the Munich teaching concept on quantum mechanics at the secondary school level [45].

Table 1.
English version of the items of our questionnaire taken from [8] and adapted from [44].
In terms of content, the items address the behavior of individual photons at the beam splitter cube and in the interferometer. We justify our item selection with an argument that has already been used by [46]: this experimental context chosen for our items includes “the fundamental concepts of quantum mechanics such as the wave-particle duality of a single photon, single-photon interference, and the probabilistic nature of quantum measurement” (p. 1). It is noteworthy, that the items we use are specifically intended to challenge mechanistic or deterministic ways of thinking [44]. Hence, these items seem suited to uncover students’ mental models (and their structure) of the topic under investigation.
4.3. Data Analysis
We use relative frequencies to indicate how subjects rated each item. As a measure of the correlation between the participants’ ratings on the different items, we use Spearman’s correlation coefficient as intended for ordinally scaled data. In line with [47], correlations are referred to as weak, as medium, and as strong.
In order to clarify our research, i.e., to uncover the structure of learners’ mental models of photons’ properties and behavior, we perform an exploratory factor analysis (EFA). Appropriateness of the dataset for EFA is examined via both the Kaiser-Mayer-Olkin criterion, and Bartlett’s test of sphericity. Factors resulting from EFA with eigenvalues larger than 1.0 are retained [48]. Varimax rotation is used to determine the rotation matrix [49]. We report factor loadings for all items, the eigenvalues of the factors retained and the amount of the total variance in all items that the respective factors account for. Finally, we provide an interpretation of the retained factors in terms of content. As we have justified in Section 3, we expect to retain two factors that can be interpreted as Fidelity of Gestalt and Fidelity of Function in line with the previous study by [9].
5. Results
5.1. Descriptives and Item Correlations
Spearman’s correlation coefficients between the students’ ratings for all eight items are shown in Table 2. Furthermore, we provide the distributions of the students’ ratings for all items in Table 3.

Table 2.
Spearman’s correlation coefficients between all the students’ ratings on the ten items (1–10) of the questionnaire. All correlations are suppressed. Weak correlations () are in normal font, intermediate correlations () are highlighted in italics and all strong correlations () are highlighted in bold italics.

Table 3.
Proportion of students’ (dis-)agreements (+, rating: 4 = rather agree, 5 = agree), disagreements (−, rating: 2 = rather disagree, 1 = disagree), and undecided votes (∘, rating: 3 = undecided) in all items (cf. Table 1) in %. Deviations from in the row totals are due to rounding. Furthermore, mean ratings with standard deviations are given for all items.
5.2. Exploratory Factor Analysis Results
The dataset was appropriate for EFA as can be justified via the Kaiser-Mayer-Olkin criterion (KMO ) and Bartlett’s test of sphericity (). Two factors with eigenvalues >1.0 were retained (cf. Figure 1).
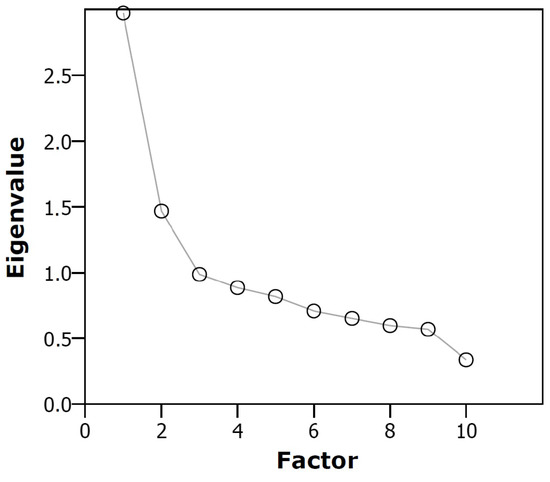
Figure 1.
Scree plot corresponding to our exploratory factor analysis. Two factors have eigenvalues greater than 1. Hence, according to the Kaiser citerion [48], two factors are retained.
These two factors accounted for of the total variance in all items. Figure 2 provides a graphical overview of the factor analysis results including (absolute values of) factor loadings. In Table 4, besides factor loadings, the eigenvalues and explained variance per factor are shown.
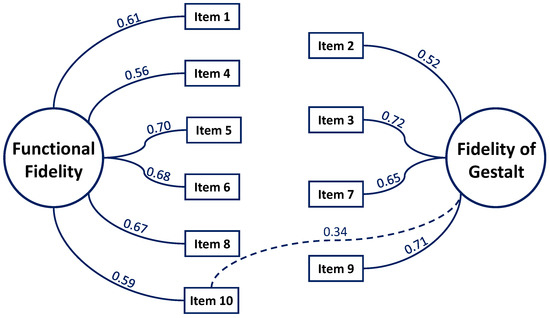
Figure 2.
Illustration of the exploratory factor analysis results including (absolute values of) factor loadings. Factor loadings below 0.3 are suppressed. Secondary loadings are represented by dashed lines. Below an interpretation of both factors in terms of content is given.

Table 4.
Factor loadings for our two-factor EFA solution. Retained factor loadings are in boldface for each item. Furthermore, eigenvalues for each factor and the percentage of variance that the factors account for are given.
5.3. Interpretation of Exploratory Factor Analysis Results
In terms of content, the two-factorial structure of learners’ mental models of photons’ properties and behavior is in line with the one presented previously by [9] in the atomic hull context: Factor 1 comprises the items 1, 4, 5, 6, 8 and 10 all of which refer to mental models’ Functional Fidelity. We justify that as follows:
- Item 1: In an interferometer the photon behaves like a particle and like a wave. It is none of them.This item can be associated with Functional Fidelity because of the key expression “behaves like” which necessarily refers to a functional aspect. Additionally, using a wave and a particle as possible options simultaneously is known to be low in Fidelity of Gestalt in some cases (cf. [50]), thus possibly shifting the attention to the functions.
- Item 4: I cannot make statements about the behavior of single photons inside the interferometer. I can only make statements about the statistical behavior of many identically prepared photons.This item can be associated with Functional Fidelity because of the key expression “behavior of single photons” which necessarily refers to a functional aspect. In addition to this, statistical behavior is addressed, which is functional as well.
- Item 5: The current position of a photon between source and detector is indeterminate in principle.This item can also be associated with Functional Fidelity because its emphasis does not lay on the single position but on how to determine the position, which is an interactive action between some entity and the photon, making this statement functional.
- Item 6: The current position of a photon between source and detector is not indeterminate in principle, but unknown to the experimenter.This item can be associated with Functional Fidelity because its emphasis does not lay on the single position but on how to determine the position, which is an interactive action between some entity and the photon, making this statement functional.
- Item 8: In quantum physics it is possible that a quantum object does not possess classically well-defined properties, such as position.This item can be associated with Functional Fidelity because of the key expression “does not possess classically well-defined properties” which necessarily refers to a functional aspect. Though many properties are functional, some of gestalt may be associated as well (like e.g., “shape”), which is consistent with the finding that this item loads onto the factor Fidelity of Gestalt as well (secondary loading , cf. Figure 2).
- Item 10: With sufficient knowledge of the initial conditions, it would be possible in classical physics to predict the outcome of a dice roll.This item can be associated with Functional Fidelity because the given statement fits to an abstract understanding of randomness in classical physics.
Factor 2 comprises the items 2, 3, 7 and 9, all of which refer to mental models’ Fidelity of Gestalt. We justify that as follows:
- Item 2: When the photon inside the interferometer moves towards the detector it takes a specific path, even if I cannot determine this path.This item can be associated with Fidelity of Gestalt because of the key expression “specific path” which necessarily refers to a gestalt aspect: one may think of a well-defined trajectory the photon follows. This seems to be counterintuitive, but paths have been found to mainly be associated with lines by students before [51], p. 191, making this finding indeed consistent with previous research.
- Item 3: The photon follows a specific path, regardless of whether I observe this path or not.This item can be associated with Fidelity of Gestalt because of the key expression “specific path” which necessarily refers to a gestalt aspect: one may think of a well-defined trajectory the photon follows. For the same reason as item 2, the categorization as addressing Fidelity of Gestalt is consistent.
- Item 7: No one can tell with certainty if a photon is transmitted or reflected at a beam splitter cube.Though at first glance, this item seems to be of functional nature by looking at the words “transmitted” and “reflected”, the main aspect appears to be the simultaneity of the actions, both of which can be imagined by different paths at once in one mental model. It is thereby the opposite of item 1, as not two gestalts are addressed that lead the focus on functions but two functions which bring the focus on the gestalt.
- Item 9: With sufficient knowledge of the initial conditions, it would be possible to predict if a single photon is transmitted or reflected at the beam splitter.This item can be associated with Fidelity of Gestalt because the prediction of a single photon’s behavior at the beam splitter cube is likely to go along with an imagination of a well-defined trajectory the photon follows (cf. the above argumentation for item 2).
6. Discussion
6.1. Functional Fidelity and Fidelity of Gestalt as Dimensions to Describe Students’ Mental Models of Photons
From the data we gathered, a two-factor model for describing students’ mental models in quantum physics—esp. with regards to the context of photons—appears to be a suitable one.
We describe the main factor that has been revealed in our study as Functional Fidelity. A focus on the interpretation of mental models’ functional component could be found in the items loading onto this factor, in accordance to what has previously been stated by [9] for a different physics context. For example, in item 1 (“In an interferometer the photon behaves like a particle and like a wave. It is none of them”.), the focus on the behavior and the functions of a photon are pronounced: Students thinking functionally are likely to agree with this statement. Hence, to sum up, high agreements with such items that load on factor 1, for instance the above mentioned item 1, reflect the extent of Functional Fidelity in students’ mental models.
Similarly, for example item 2 (“When the photon inside the interferometer moves towards the detector, it takes a specific path, even if I cannot determine this path”.), includes a more gestalt-focused statement. The emphasis in this item is on a path, which is often visualized and understood as a line by students and, thus, is mainly seen as gestalt-like (cf. [51]). This item—amongst others—proved to be a good indicator for the second factor, which we coined Fidelity of Gestalt in accordance with [9].
In summary, the two factors seem to fit with the theoretical expectations (cf. Section 2). Additionally, considering the neurological literature as given in Section 2, we suggest that the structure of Fidelity of Gestalt and Functional Fidelity is linked to the hemispheric specializations, making them so to speak “hardwired” cognitive mechanisms. The fit with theoretical expectations is underlined even more when comparing items (and their assignments to factors) used in the study presented in this article to those from…
- …Ubben and Heusler’s work [9], and
- …the original version of the items presented by Müller and Wiesner [44].
An exemplary comparison between these items is provided in Table 5: It is quickly apparent that our items loading highest onto our factors, also (in their adapted form) load highly on the two different factors found in Ref. [9]. It is to be emphasized that items more focused on addressing the two factors content-wise would lend this interpretation even more weight and such items should be created and used in further studies of this topic (cf. Section 7 on limitations of this study).

Table 5.
Exemplary high loading items for each of the two factors from the present study’s questionnaire in comparison to the corresponding items from (a) the previously published study in the atomic hull context [9], and (b) the items’ original formulations [44].
It is noteworthy, that these two cognitive dimensions of Fidelity of Gestalt and Functional Fidelity enable a more comprehensive analysis of student thinking than a collection of students’ conceptions would. That is, our two-factor framework seems promising for the categorization of students’ conceptions of photons from a rather overarching perspective: it seems to be a sensible approach to describe students’ mental models in the photon context (and probably beyond, as future research will have to show) via the extent of Fidelity of Gestalt (FG) and Functional Fidelity (FF) in student thinking. This leads to four archetypes of students’ understanding of (mental) models that have already been proposed for the atomic hull context (for a description of these archetypes, cf. Section 1):
- Non-developed type: low degree of FG and FF.Example: Students of this type have no knowledge about the term photon and, thus, their imagination is non-developed.
- Architectural type: high degree of FG, low degree of FF.Example: Students of this type describe a photon as a localised “billiard ball which carries energy and momentum” [52] or imagine a photon to be a small spherical particle that follows a wavelike trajectory [53].
- Dual type: high degree of FG, high degree of FF.Example: Students of this type describe photons as energy quanta of light in a very abstract way. However, whenever it comes to describing concrete experiments, these students fall back to a particle notion in a naïve sense (cf. [54]).
- Functional type: low degree of FG, high degree of FF.Example: Students of this type describe photons as energy quanta of light in a very abstract way (cf. [54]).
In the next subsection, we show that our two-factor structure is suitable to describe students’ mental models in science (education) beyond the contexts of the atomic hull [9] or photons (this paper).
6.2. Describing the Structure of Students’ Mental Models via the Dimensions Fidelity of Gestalt and Functional Fidelity
Though the findings appear to hold true for the context of quantum physics in both the mental models of the atomic hull as well as the mental models of photons, a more general question arises: Do learners’ mental models of physics concepts in general show characteristics of Fidelity of Gestalt and Functional Fidelity? For the purposes of this paper, only a trend will be given and this question will be further addressed in future research. However, when looking through literature of physics education, statements from learners that are in line with these two factors can readily be found. One prominent example are mental models of fields and field lines. Students tended to firstly show descriptive, image-focused statements about electric or magnetic fields (cf. ([55], p. 4) and ([56], p. 718)), before starting to ascribe more functional aspects to these gestalts (cf. ([57], p. 560) and ([58], p. 445)). However, although in this area a purely functional understanding is desired, this is mostly not achieved (cf. ([57], p. 564) and ([58], p. 458)).
Similarly, when considering light, initial focus in learning about the ray-model is gestalt-oriented (cf. [34,59]), before the functional implications of the model are discovered (cf. [60,61]). Again, the desired functionally-focused understanding is rarely achieved (cf. [61,62]).
These two areas illustrate that examining mental models through the lens of Fidelity of Gestalt and Functional Fidelity seems of value when it comes to describing understanding and learning progressions about physics concepts. Further research is needed in that direction.
7. Limitations
The study presented in this paper has some limitations that need to be tackled in follow-up projects:
- In this project, we have adopted a questionnaire to elicit students’ mental models [44] of photons’ properties and behaviour, which is accepted in the quantum physics education research community and which has previously been used in several empirical studies on learning quantum physics (e.g., [8,9,45]). However, this instrument is not specifically based on our theoretical framework on mental models in quantum physics. This means that it was not developed with the objective of operationalising the two factors of Fidelity of Gestalt and Functional Fidelity of mental models by means of test items. Consequently, by developing a survey instrument to investigate students’ mental models in the quantum physics context that addresses the two dimensions of Fidelity of Gestalt and Functional Fidelity in specifically developed test items, we expect an even clearer manifestation of the two factors in student thinking. The development of such an instrument is part of future research.
- In this study, we investigated the extent to which the description of mental models from a rather theoretical perspective by means of Fidelity of Gestalt and Functional Fidelity in student thinking is possible in quantum physics beyond the atomic hull context [9]. In order to investigate this transferability, we have decided to survey the structure of learners’ mental models on a central topic that covers the characteristic features of quantum physics in a first step: photons’ properties and behavior. Certainly, this selection limits the generalizability of our empirical findings; in particular, from our findings, we cannot conclude that learners’ mental models of all quantum concepts can be described by these two dimensions. It is possible that for certain quantum concepts, further sub-dimensions of Gestalt or Functional Fidelity could be found in the learners’ thinking. This needs to be addressed in follow-up studies.
- We note, that in teaching quantum physics at the secondary school level it is widespread practice to transfer properties to photons that were previously studied in the context of electrons (cf. [14,53]). However, an isomorphic mapping between electrons and photons is not valid from a subject-specific point of view, and the problem of using an analogy between photons and electrons has already been highlighted in Ref. [63], p. 650: for example, a photon position operator does not exist and, hence, no position eigenstates either [64]. Instead, photons are assigned a meaning as elementary field mode excitations in quantum electrodynamics [65]. Therefore, the question arises whether our results regarding the structure of students’ thinking about photons are not actually consistent with the findings of [9] presented earlier for the atomic hull context, because electrons and photons are usually introduced in secondary school lessons in analogy to each other without regarding them as different concepts from a subject-specific point of view. In order to tackle this limitation, we can come back to neurological findings presented in Section 2 of this article that suggest that the cognitive dimensions (Fidelity of Gestalt and Functional Fidelity) in learners’ mental models of photons empirically uncovered in this article, indeed, appear to be deeply rooted in human thinking. Nonetheless, we acknowledge a need for further research in this context: for example, analyzing the mental models of learners who were introduced to quantum field theory might add value to the field.
- Furthermore, it is noteworthy, that we limited our study to secondary school students. Therefore, generalising our findings to learners from other educational backgrounds is not straightforward. However, the earlier work of [9] suggests that one might find a congruent structure of mental models in individuals from different backgrounds, differing only in the expressions of Fidelity of Gestalt and Functional Fidelity in student thinking.
8. Conclusions and Outlook
In this paper, we managed to replicate the two factors Functional Fidelity and Fidelity of Gestalt to describe the structure of students’ mental models of photons. These factors had previously been found by Ubben and Heusler [9] in the atomic hull context. The description of mental models by these two factors seems to prove fruitful, as they have been found for related topics of quantum physics. Hence, the characterization of students’ mental models via the degree of Functional Fidelity (FF) and Fidelity of Gestalt (FG) seems a promising approach towards a theory of learning quantum physics. However, even with the results of this study, teachers will be able to more effectively understand learning difficulties in the quantum domain: Whether they stem from missing gestalts, from highly held gestalts or from missing functionalities. We hope that our findings will provide teachers with more effective means to facilitate development of adequate and useful mental models in learners. For each archetypical mental model, there are specific possible actions that could help this development. The non-developed type could profit from creative tasks such as visualizing to improve the FG dimension (which of course should be reflected upon critically later). The architectural model type could benefit from dynamic representations or interactive models to get to know more functions of the model and how it behaves to increase the FF dimension. The dual type could benefit from other visualizations that have different gestalts but similar functionalities, so that abstractions are possibly made easier. Lastly, a functional type could be made to be reevaluated by showing contexts that the mental model is not sufficiently applicable anymore, leading back to an enhancement of the mental model and thus making it a more powerful tool.
Additionally, our framework is promising in applications beyond learning quantum physics, as pointed out in the discussion (cf. Section 6). Further research is needed to investigate the transferability of our two-factor framework to the description of students’ mental models of further physics topics. Several points will have to be addressed in the future to further develop research on our empirical findings and theoretical framework of Fidelity of Gestalt and Functional Fidelity. One important aspect will be to use instruments including items more tailored towards addressing only one of the two factors. This means focusing on either just the visual associations or the functional associations in learners regarding specific mental models. As a first step, we suggest using qualitative evaluations to get an idea of what gestalts and functionalities learners hold regarding specific topics in science. From these evaluations, test instruments will then be constructed to evaluate which type of mental model the learners have to make evidence-based suggestions as to how help students’ development of towards a functional understanding of models in (quantum) physics. In more general, as has been shown in Section 6, it is not improbable that our theoretical descriptions may even be of great use to better understand science learning in general on a cognitive level.
Author Contributions
Conceptualization, M.S.U. and P.B.; methodology, M.S.U. and P.B.; formal analysis, M.S.U. and P.B.; investigation, M.S.U. and P.B.; writing—original draft preparation, M.S.U. and P.B.; writing—review and editing, M.S.U. and P.B.; visualization, M.S.U. and P.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Informed consent was obtained from the participant involved in the study.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study to publish this paper.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We acknowledge support from the Open Access Publication Fund of the University of Muenster. One of us (P.B.) was funded by the Emerging Talents Initiative (University of Erlangen, Germany).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ke, J.-L.; Monk, M.; Duschl, R. Learning Introductory Quantum Physics: Sensori-motor experiences and mental models. Int. J. Sci. Educ. 2005, 27, 1571–1594. [Google Scholar] [CrossRef]
- Abhang, R.Y. Making introductory quantum physics understandable and interesting. Res. J. Sci. Educ. 2005, 10, 63–73. [Google Scholar] [CrossRef]
- Singh, C.; Marshman, E. A Review of student difficulties in upper-Level quantum mechanics. Phys. Rev. ST Phys. Educ. Res. 2015, 11, 020117. [Google Scholar] [CrossRef]
- Kalkanis, G.; Hadzidaki, P.; Stavrou, D. An instructional model for a radical conceptual change towards quantum mechanics concepts. Sci. Educ. 2003, 87, 257. [Google Scholar] [CrossRef]
- Henriksen, E.K.; Angell, C.; Vistnes, A.I.; Bungum, B. What ist Light? Students’ Reflections on the Wave-Particle Duality of Light and the Nature of Physics. Sci. Educ. 2018, 27, 81–111. [Google Scholar] [CrossRef]
- Taber, K.S. Learning Quanta: Barriers to stimulating transitions in student understanding of orbital ideas. Sci. Educ. 2005, 89, 94–116. [Google Scholar] [CrossRef]
- Bouchée, T.; de Putter-Smits, L.; Thurlings, M.; Pepin, B. Towards a better understanding of conceptual difficulties in introductory quantum physics courses. Stud. Sci. Educ. 2021, 2021, 1–20. [Google Scholar] [CrossRef]
- Bitzenbauer, P. Effect of an introductory quantum physics course using experiments with heralded photons on preuniversity students’ conceptions about quantum physics. Phys. Rev. Phys. Educ. Res. 2021, 17, 020103. [Google Scholar] [CrossRef]
- Ubben, M.; Heusler, S. Gestalt and Functionality as Independent Dimensions of Mental Models in Science. Res. Sci. Educ. 2021, 51, 1349–1363. [Google Scholar] [CrossRef]
- Treagust, D.; Chittleborough, G.; Mamiala, T. Students’ understanding of the role of scientific models in learning science. Int. J. Sci. Educ. 2002, 24, 357–368. [Google Scholar] [CrossRef]
- Stefani, C.; Tsaparlis, G. Students’ levels of explanations, models, and misconceptions in basic quantum chemistry: A phenomenographic study. J. Res. Sci. Teach. 2009, 46, 520. [Google Scholar] [CrossRef]
- Mashhadi, A.; Woolnough, B. Insights into students’ understanding of quantum physics: Visualizing quantum entities. Eur. J. Phys. 1999, 2, 511. [Google Scholar] [CrossRef]
- Sayer, R.; Maries, A.; Singh, C. A quantum interactive learning tutorial on the double-slit experiment to improve student understanding of quantum mechanics. Phys. Rev. Phys. Educ. Res. 2017, 13, 010123. [Google Scholar] [CrossRef]
- Stadermann, H.K.E.; van den Berg, E.; Goedhart, M.J. Analysis of secondary school quantum physics curricula of 15 different countries: Different perspectives on a challenging topic. Phys. Rev. Phys. Educ. Res. 2019, 15, 010130. [Google Scholar] [CrossRef]
- Hentschel, K. Photons; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Johnson-Laird, P.N. Mental Models: Towards a Cognitive Science of Language, Inferences, and Consciousness; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Gentner, D.; Stevens, A.L. Mental Models; Erlbaum: Hillsdale, NJ, USA, 1983. [Google Scholar]
- Craik, K. The Nature of Exploration; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Horst, S. Cognitive Pluralism; The MIT Press: Cambridge, UK, 2016. [Google Scholar]
- Amin, T.G.; Smith, C.; Wiser, M. Student Conceptions and Conceptual Change: Three Overlapping Phases of Research. In Handbook of Research in Science Education; Lederman, N., Abell, S., Eds.; Chapter 4; Routledge: New York, NY, USA, 2014; Volume II. [Google Scholar]
- Mayer, R.E. Multimedia Learning; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Halpern, A.R.; Zatorre, R.J. When that tune runs through your head: A PET investigation of auditory imagery for familiar melodies. Cerebral Cortex 1999, 9, 697–704. [Google Scholar] [CrossRef]
- Paivio, A. Imagery and Verbal Processes; Holt, Rinehart and Winston: New York, NY, USA, 1971. [Google Scholar]
- Gibson, J.J. The Senses Considered as Perceptual Systems; Houghton Mifflin: Boston, MA, USA, 1966. [Google Scholar]
- Gibson, J.J. The theory of affordances. In Perceiving, Acting, and Knowing: Toward an Ecological Psychology; Shaw, R., Bransford, J., Eds.; Erlbaum: Hillsdale, NJ, USA, 1977. [Google Scholar]
- Gibson, J.J. An Ecological Approach to Visual Perception; Lawrence Erlbaum: New York, NY, USA, 1979. [Google Scholar]
- Panksepp, J. Affective Neuroscience; Oxford: New York, NY, USA, 1998. [Google Scholar]
- Peterson, J.B. Maps of Meaning: The Architecture of Belief; Routledge: New York, NY, USA, 1999. [Google Scholar]
- Dagar, V.; Yadav, A. Constructivism: A Paradigm for Teaching and Learning. Arts Soc. Sci. J. 2016, 7, 2–4. [Google Scholar]
- Carey, S. The Origin of Concepts; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Piaget, J. Play, Dreams and Imitation in Childhood; Routledge: New York, NY, USA, 1951. [Google Scholar]
- Fixione, M.; Lieto, A. Representing Non Classical Concepts in Formal Ontologies: Prototypes and Exemplars. In New Challenges in Distributed Information Filtering and Retrieval; Lai, C., Semeraro, G., Vargiu, E., Eds.; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Burge, T. Five theses on de re states and attitudes. In The Philosophy of David Kaplan; Almog, J., Leonardi, P., Eds.; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Hubber, P. Year 12 students’ mental models of the nature of light. Res. Sci. Educ. 2006, 36, 419–439. [Google Scholar] [CrossRef]
- Sherin, B. Common sense clarified: The role of intuitive knowledge in physics problem solving. Res. Sci. Teach. 2006, 43, 535–555. [Google Scholar] [CrossRef]
- Levy, J.; Trevarthen, C. Metacontrol of Hemispheric Function in Human Split-Brain Patients. J. Exp. Psychol. Human Percept. Perform. 1976, 2, 299–312. [Google Scholar] [CrossRef]
- Gazzaniga, M.S. Forty-five years of split-brain research and still going strong. Nat. Rev. Neurosci. 2005, 6, 653–659. [Google Scholar] [CrossRef]
- Roser, M.E.; Fugelsang, J.A.; Dunbar, K.N.; Corballis, P.M.; Gazzaniga, M.S. Dissociating processes supporting causal perception and causal inference in the brain. Neuropsychology 2005, 19, 591–602. [Google Scholar] [CrossRef] [PubMed]
- Gopnik, A.; Glymour, C.; Sobel, D.M.; Schulz, L.E.; Kushnir, T.; Danks, D. A Theory of Causal Learning in Children: Causal Maps and Bayes Nets. Psychol. Rev. 2004, 111, 3–32. [Google Scholar] [CrossRef] [PubMed]
- Scholl, B.J.; Tremoulet, P. Perceptual Causality and Animacy. Trends Cognit. Sci. 2000, 4, 299–309. [Google Scholar] [CrossRef]
- Scholl, B.J.; Nakayama, K. Causal Capture: Contextual Effects on the Perception of Collision Events. Psychol. Sci. 2002, 13, 493–498. [Google Scholar] [CrossRef]
- Ireson, G.A. multivariate analysis of undergraduate physics students’ conceptions of quantum phenomena. Eur. J. Phys. 1999, 20, 193. [Google Scholar] [CrossRef]
- Mashhadi, A.; Woolnough, B. Cognitive mapping of advanced level physics students’ conceptions of quantum physics. In Proceedings of the Conference on Educational Research (Australian Association for Research in Education), Singapore, 25–29 November 1996; Available online: https://files.eric.ed.gov/fulltext/ED414195.pdf (accessed on 20 January 2022).
- Müller, R.; Wiesner, H. Teaching quantum mechanics on an introductory level. Am. J. Phys. 2002, 70, 200. [Google Scholar] [CrossRef]
- Müller, R. Quantenphysik in der Schule; Logos: Berlin, Germany, 2003. [Google Scholar]
- Marshman, E.; Singh, C. Investigating and improving student understanding of quantum mechanics in the context of single photon interference. Phys. Rev. Phys. Educ. Res. 2017, 13, 010117. [Google Scholar] [CrossRef]
- Hemphill, J.F. Interpreting the Magnitudes of Correlation Coefficients. Am. Psych. 2003, 58, 78–79. [Google Scholar] [CrossRef]
- Kaiser, H. The application of electronic computers to factor analysis. Educ. Psychol. Meas. 1960, 20, 141. [Google Scholar] [CrossRef]
- Brown, J.D. Choosing the right type of rotation in PCA and EFA. Shiken JALT Test. Eval. SIG Newsl. 2009, 13, 20. [Google Scholar]
- Bormann, M. Das Schülervorverständnis zu Elektronen. In Vorträge der DPG; Kuhn, W., Ed.; DPG: Gießen, Germany, 1986. [Google Scholar]
- Kawalkar, A.; Vijapurkar, J.D. What Do Cells Really Look Like? Children’s Resistance to Accepting a 3-D Model. Proc. EpiSTEME 2009, 3, 187–193. [Google Scholar]
- Ayene, M.; Kriek, J.; Damtie, B. Wave-particle duality and uncertainty principle: Phenomenographic categories of description of tertiary physics students’ depictions. Phys. Rev. ST Phys. Educ. Res. 2011, 7, 020113. [Google Scholar] [CrossRef]
- Krijtenburg-Lewerissa, K.; Pol, H.J.; Brinkman, A.; van Joolingen, W.R. Insights into teaching quantum mechanics in secondary and lower undergraduate education. Phys. Rev. Phys. Educ. Res. 2017, 13, 010109. [Google Scholar] [CrossRef]
- Bitzenbauer, P.; Meyn, J.-P. Towards types of students’ conceptions about photons: Results of an interview study. In Physics Teacher Education—What Matters? Bonello, C., Marks, J.B., Galea, A., Eds.; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Fedele, B.; Michelini, M.; Stefanel, A. 5–10 year old pupils explore magnetic phenomena in Cognitive Laboratory (CLOE). In Cresils; Pint, R., Couso, D., Eds.; University of Udine: Udine, Italy, 2005. [Google Scholar]
- Greca, I.M.; Moreira, M.A. The kinds of mental representations - models, propositions and images—Used by college physics students regarding the concept of field. Int. J. Sci. Educ. 1997, 19, 711–724. [Google Scholar] [CrossRef]
- Saglam, M.; Millar, R. Upper High School Students’ Understanding of Electromagnetism. Int. J. Sci. Educ. 2006, 28, 543–566. [Google Scholar] [CrossRef]
- Guisasol, J.; Almud, J.M.; Zubimed, J.L. Difficulties in Learning the Introductory Magnetic Field Theory in the First Years of University. Sci. Educ. 2004, 88, 443–464. [Google Scholar] [CrossRef]
- Galili, I.; Hazan, A. Learners’ knowledge in optics: Interpretation, structure and analysis. Int. J. Sci. Educ. 2000, 22, 57–88. [Google Scholar] [CrossRef]
- Djanette, B.; Fouad, C. Determination of university students’ misconceptions about light using concept maps. Procedia—Soc. Behav. Sci. 2014, 152, 582–589. [Google Scholar] [CrossRef][Green Version]
- Goldberg, F.M.; McDermott, L.C. Student difficulties in understanding image formation by a plane mirror. Phys. Teach. 1986, 24, 472–480. [Google Scholar] [CrossRef]
- Heywood, D.S. Primary trainee teachers’ learning and teaching about light: Some pedagogic implications for initial teacher training. Int. J. Sci. Teach. 2005, 27, 1447–1475. [Google Scholar] [CrossRef]
- Strnad, J. Photons in introductory quantum physics. Am. J. Phys. 1986, 54, 650. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Bialynicka-Birula, Z. Why photons cannot be sharply localized. Phys. Rev. A 2009, 79, 032112. [Google Scholar] [CrossRef]
- Hobson, A. There are no particles, there are only fields. Am. J. Phys. 2013, 81, 211. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).