Next Article in Journal
The Impact of Language and Location on the Curriculum Preferences of Online Entrepreneurship Students: An Application of Google Analytics
Next Article in Special Issue
Self-Assessment in the Development of Mathematical Problem-Solving Skills
Previous Article in Journal
Using Integrative Career Construction Counselling to Promote Autobiographicity and Transform Tension into Intention and Action
Previous Article in Special Issue
Teaching Mathematics to Non-Mathematics Majors through Problem Solving and New Technologies
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 12
Issue 2
10.3390/educsci12020079
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Analysis of Differences in the Levels of TPACK: Unpacking Performance Indicators in the TPACK Levels Rubric

by
Irina Lyublinskaya
1,* and
Aleksandra Kaplon-Schilis
2
1
Department of Mathematics, Science, and Technology, Teachers College, Columbia University, New York, NY 10027, USA
2
Upper School, Durham Academy, Durham, NC 27705, USA
*
Author to whom correspondence should be addressed.
Educ. Sci. 2022, 12(2), 79; https://doi.org/10.3390/educsci12020079
Submission received: 28 September 2021 / Revised: 23 December 2021 / Accepted: 20 January 2022 / Published: 24 January 2022
(This article belongs to the Special Issue Using Technology in Teaching Mathematics)
Browse Figures
Versions Notes

Abstract

:
Since the development of the technological pedagogical content knowledge (TPACK) framework, researchers have been developing a variety of instruments to measure the TPACK of pre-service and in-service teachers. The task of developing an efficient, reliable, and valid instrument is difficult. Even validated instruments require guidance for consistent use that preserves the instrument fidelity. The purpose of this study is to provide guidance for using the TPACK Levels Rubric, a validated instrument that was developed on the basis of the model for the progressive levels of TPACK. The authors systematically examined the criteria of the rubric in order to understand the differences in the levels of TPACK for each rubric component, and developed lesson exemplars to create guidelines for educators using this tool in assessing the TPACK levels of teachers. The iterative instrument analysis also led to the revision of the original rubric to establish the horizontal and vertical alignments and the consistency of the rubric, for each level across four components, and for each component across five levels. The construct validity of the revised rubric was confirmed on the basis of a exploratory factor analysis of 175 mathematics lesson plans and videos of taught lessons developed by graduate special education pre-service and in-service elementary school teachers.

1. Introduction

Over the past decade, teachers have been expected to integrate digital technologies into their teaching practices [1]. The need for teaching with technology, especially in virtual learning environments, became even more critical in 2020, when the whole world switched to online teaching because of the COVID-19 pandemic. However, many teachers struggle with using technology in their classrooms, whether in physical or virtual environments [2]. According to the 2018 Teaching and Learning International Survey (TALIS), on average, fewer than half of all teachers felt well enough prepared to use technology in their classrooms [3]. Studies show that many pre-service graduates feel unprepared to use technology effectively in their classrooms on the first day of teaching [4]. The teacher education programs need to prepare pre-service teachers (PSTs) to relearn, rethink, and reframe learning and teaching by taking advantage of the communication, collaboration, and inquiry technologies for 21st century instruction.
About two decades ago, discussions about teacher preparation for technology integration led to the development of the technological pedagogical content knowledge (TPACK) framework, first proposed for mathematics education [5], and then extended to different subjects and contexts by the authors of [6]. This framework added technology-related knowledge domains to Shulman’s [7] framework for pedagogical content knowledge (PCK), which resulted in seven domains of teacher knowledge: The technological knowledge (TK) of technology tools; The content knowledge (CK) of the subject matter; The pedagogical knowledge (PK) in using effective instructional methodologies; The technological content knowledge (TCK) in using technology to support subject matter development; The pedagogical content knowledge (PCK) in scaffolded content-specific instruction; The technological pedagogical knowledge (TPK) in utilizing technology to support effective pedagogy; and TPACK, which is knowledge that relies on the interaction of content, pedagogy, and technology (Figure 1).
As is shown in Figure 1, the framework and the central knowledge domain are both called TPACK. This presents different perspectives on the “teacher knowledge” defined by the framework. Niess [8] suggests that this duality might be described using two terms: integrated and interdisciplinary. An interdisciplinary vision of TPACK considers the individual domains of knowledge (TK, CK, PK, TCK, TPK, PCK, and TPACK) to be independent knowledge domains in the model. The central TPACK domain is then considered as an integrated knowledge, a distinct form of knowledge where the inputs have been integrated in such a way that none are individually discernible [8]. The integrated TPACK is the focus of this study.
In the last decade, the TPACK framework quickly became a widely referenced conceptual framework within teacher education, particularly since teacher education programs began redesigning their curriculums to provide a systematic and meaningful way of preparing teachers for technology integration [9,10,11]. Studies show that pre-service teachers could benefit greatly from TPACK-framework-based courses [12,13,14]; however, there is no consensus on the most effective approach to TPACK development [15].
Frameworks need to be tested in the real world, and the only method for this is the development of research instruments that are both “consistent with the theory and measure what they set out to measure” [16] (p. 17). Since the development of the TPACK framework, researchers have been designing a variety of instruments to measure the TPACK of teachers. The task of developing an efficient, reliable, and valid instrument is difficult, especially when assessing “how teacher’s knowledge influences actual teaching practices” [17] (p. 288). This study uses the TPACK Levels Rubric, an instrument developed by Lyublinskaya and Tournaki [18], that is based on Niess’ [19] model for the growth of teachers in their pedagogical content knowledge (PCK) towards TPACK, through five progressive levels. This instrument has been used in various studies to assess teacher growth for technology integration in mathematics and science classrooms [20,21]. However, an analysis of these studies indicates that the use of the rubric is inconsistent and often does not preserve the instrument fidelity. Therefore, the purpose of this study is to unpack the rubric in order to provide guidance for using this tool in assessing the TPACK of teachers for teaching mathematics.

2. Assessing TPACK

The constructs in the TPACK framework need to be precisely defined, and reliable instruments for assessing TPACK need to be created for various contexts [22]. Numerous studies focus on assessing the various domains in the TPACK framework. According to Mouza and Karchmer-Klein [23], the TPACK assessment of pre-service and in-service teachers has been conducted using interviews, classroom observations, self-reported surveys, open-ended questionnaires, and performance-assessment instruments. On the basis of the type of data in these studies, the TPACK measurement instruments can be categorized into “self-assessment” and “external assessment”.
The reviews of the qualitative and quantitative TPACK measures [24,25] show that most of the earlier works on measuring TPACK rely on self-assessment surveys, in which various knowledge domains are rated individually [26,27,28]. Although self-assessment instruments are easy to use and cost effective, and they enable reaching a large number of participants, their precision in measuring the true TPACK of teachers is constrained by the ability of the survey-takers to assess their own knowledge [17]. These surveys usually evaluate teacher confidence, rather than their knowledge in practice, which are different constructs [29,30]. For an accurate assessment of the TPACK, “teachers need to demonstrate what they can actually do with technology in their subject for enhancing teaching and learning” [31] (p. 119).
The external assessment of TPACK is based on observed behavior, e.g., classroom instructions, microteaching [14], teaching artifacts, including lesson plans, student handouts, and teaching portfolios [32,33], and knowledge tests [34], and it could have higher objectivity compared to self-reports. Most recent studies focus on distinguishing the different constructs in the TPACK framework and most recognize the interdisciplinary nature of TPACK. To the contrary, Lyublinskaya and Tournaki [18] developed and validated the TPACK Levels Rubric to assess the progressive development of the TPACK of teachers as an integrated construct based on lesson plans and classroom observations. The scoring of teaching artifacts using a research instrument requires a full understanding of the instrument in order to use it with fidelity. Therefore, guidelines are needed for any research instrument so that it may be used as intended. Building on and extending an earlier study [18], this paper presents an analysis of the TPACK Levels Rubric, which was conducted to examine the differences between these levels in order to provide such guidance. This study addresses the following research question: What are the distinct features of the specific levels of the TPACK of teachers in the context of teaching mathematics?

3. Conceptual Framework

The analysis and revision of the TPACK Levels Rubric was based on the conceptual framework that aligns the model for the progressive development of the teachers’ knowledge, from PCK to TPACK [19], with the frameworks for the cognitive demand of tasks [35,36] and inquiry-based learning [37] in order to assess the knowledge growth of teachers for teaching mathematics or science with technology.

3.1. Progressive Levels of TPACK

Niess et al. [19] reframed Rogers’ [38] five-stage sequential model of the innovation–decision process to develop qualitative schema for the five progressive levels of TPACK. In this schema, teachers progress through the five levels of TPACK: Level-1 (Recognizing), where teachers are able to use the technology and recognize the alignment of the technology with the mathematics content, yet they do not integrate the technology in the teaching and learning of mathematics; Level-2 (Accepting), where teachers form a positive or negative attitude toward teaching and learning with an appropriate technology; Level-3 (Adapting), where teachers make decisions to adopt or reject technology for teaching and learning; Level-4 (Exploring), where teachers integrate an appropriate technology for the teaching and learning of mathematics; Level-5 (Advancing), where teachers evaluate the results of integrating an appropriate technology for the teaching and learning mathematics (Figure 2).
For each level, four components of TPACK were identified by adapting Grossman’s components of PCK [40] to represent the integration of technology into teaching, as follows: (1) An overarching conception about the purposes for incorporating technology into the teaching of mathematics; (2) Knowledge of the students’ understanding of, thinking about, and learning of mathematics with technology; (3) Knowledge of the curriculum and the curricular materials that integrate technology into the learning and teaching of mathematics; (4) Knowledge of instructional strategies and representations for teaching and learning mathematics with technologies [5] (p. 511).

3.2. Cognitive Demand of Tasks Framework

Research shows that, in mathematics education, the level of the “cognitive demand of enacted instructional tasks” [36] (p. 661) is associated with student gains in high-level thinking and reasoning. Students learn best when their teachers maintain a high level of cognitive demand throughout lessons. Stein and Smith [35] used a task analysis guide to classify instructional tasks into high- and low-cognitive-demand levels. Cognitive Demand Level-1 represents memorization tasks, for which a student is asked to reproduce previously seen material. These tasks have no connection to the concepts or meaning that underlie the facts, rules, formulae, or definitions being learned or reproduced. At Cognitive Demand Level-2, the tasks are algorithmic, and they explicitly tell the students what to do. These tasks still do not have any connection to the concepts or meanings that underlie the procedures being used, and they do not require explanations. Memorization and procedures without connections are low-cognitive-demand tasks. At Cognitive Demand Level-3, the tasks focus on the uses of the procedures for the purpose of developing deeper levels of understanding of the concepts and ideas. These tasks require some degree of cognitive effort and cannot be followed mindlessly. At Cognitive Demand Level-4, students are doing mathematics, and the tasks require complex and nonalgorithmic thinking that require the students to explore and understand the nature of the mathematical concepts, processes, and relationships, which requires considerable cognitive effort. These two levels represent high-cognitive-demand tasks.

3.3. Inquiry-Based Learning Framework

Inquiry-based learning (IBL) can be viewed as a set of learning and assessment strategies where student learning is grounded in inquiry that is driven by questions and problems relevant to the learning objectives. At the heart of IBL are inquiry teaching and learning processes, where learning activities and assessments are purposefully designed to cultivate knowledge building and higher-order thinking through the exploration of authentic and meaningful questions and problems [37]. Research shows that the appropriate selection of technology may support inquiry instruction and facilitate the transition to student-centered instruction [41].
This study used a model of inquiry continuum that defines the levels of inquiry according to how much guidance and information the teacher provides to the students. Four levels of inquiry are identified: (1) Confirmation inquiry; (2) Structured inquiry; (3) Guided inquiry; and (4) Open inquiry [42]. In a confirmation inquiry, the teacher provides students with the prescribed procedure to confirm the results that the students already know. In a structured inquiry, students investigate teacher-presented questions through a prescribed procedure. Guided inquiry involves students investigating teacher-provided questions using their own procedures. In an open inquiry, students select or design their own procedures to investigate their own topic-related questions.

3.4. Development of Conceptual Framework

An analysis of these frameworks suggests an alignment between the level of a teacher’s knowledge about integrating technology into teaching and learning, the tasks that a teacher provides to students with technology, and the levels of inquiry of these tasks (Table 1).
According to Niess [8], at the Recognizing level of TPACK, teachers believe that mathematics is a subject learned through the memorization of rules, algorithms, and procedures, without the use of technologies, which corresponds to the lowest level of cognitive demand tasks: memorization. Instructional strategies for teaching mathematics at this level of TPACK are based on teacher-directed lectures, followed by individual student practice and repetition to solidify the ideas, which represents the lack of inquiry. At the Accepting level of TPACK, the instructional style is primarily teacher-directed, with technology used mostly as a demonstration tool. The teacher expects the students to follow prescribed procedures when using the technology, and the technology tasks focus mostly on computation [8]. These descriptions align with the “procedures without connections and confirmation” inquiry. At the Adapting level of TPACK, teachers view technology as a tool to support the student exploration of a topic through structured activities, which aligns with the “structured inquiry” level. The technology also supports students in making connections, for example, between different representations of mathematical objects. This aligns with the “procedures with connections” level of the cognitive demand tasks framework. At the Exploring level of TPACK, teachers begin to transform their knowledge by including student-centered instructional practices with technology that guides the students toward the intended content ideas, which aligns with the “guided inquiry”. At the same time, teachers start including discovery-type and application-type technology-based tasks for the students, which suggests that the students are “doing mathematics” at this level. Finally, at the Advancing level of TPACK, teachers willingly explore and extend the curriculum, and technology is used as a problem-solving tool for students. The teachers encourage student exploration and experimentation with technology. Thus, the students have the opportunity to “do mathematics” through an “open inquiry”.
The alignment between these three frameworks forms the conceptual framework for this study, which guided the revision process of the TPACK Levels Rubric.

3.5. TPACK Levels Rubric

The original TPACK Levels Rubric is organized as a matrix, with four rows representing the components of TPACK, and five columns representing the levels of TPACK [18]. Two performance indicators, one for teacher actions, and one for student actions, or digital materials, have been developed for each level of each component, consistent with the model for the progressive development of TPACK and the frameworks for the cognitive demand of tasks and inquiry-based learning. The scores for each component at each level can range from 0 to 5, where the component score can be an integer (both performance indicators are met) or a half-integer (one out of two performance indicators are met). The score is assigned for each component independently, and the overall TPACK score is calculated as an average of the four component scores. The score is then used to determine the TPACK level of the teacher. The rubric has been validated for use with lesson plans and videos of teaching for the population of elementary and high school mathematics teachers. (Revised rubric can be found in Supplementary Materials).

4. Research Methodology

The study followed the systematic iterative content analysis to unpack the performance indicators of the TPACK Levels Rubric in order to understand the differences between the levels of TPACK for teaching mathematics. A scoring rubric represents a set of scoring guidelines that describe the characteristics of the different levels of performance. Unpacking the rubric means identifying “the unique elements of information and skill” [43] (p. 12). The scoring guidelines serve a dual purpose: to judge a performance, and to provide numerical scores for the statistical analysis of the assessed work [44]. The guidelines for the rubric design followed in this study stress the importance of the clarity of the descriptors used in the rubric, the need for consistent wording to describe the performance indicators across the performance levels, and the need for the clear differentiation through a description of the performance levels [45,46].
The rubric performance indicators were examined and revised as necessary in order to maintain consistency across different components of the same level, while highlighting the distinctions between the different levels. The revised rubric was tested on 175 mathematics lesson plans and videos of taught lessons developed by the elementary school teachers enrolled in a special education graduate program at a New York City public university (see Supplementary Materials for the complete dataset). The data were collected over eight consecutive semesters. The internal consistency of the rubric was tested using Cronbach’s α. The values of the α ranged from 0.951 to 0.968 for four components of the rubric, with an overall value of 0.985, which indicated the high internal consistency of the rubric.
An analysis of the correlations between the four observed components of TPACK completed in SPSS 28 indicates strong positive correlations between all four items, with the Pearson’s r ranging from 0.884 to 0.922 (p < 0.001), suggesting a one-factor model. An exploratory factor analysis (EFA) with four items was completed in SPSS 28 using the principal component analysis (PCA) extraction method with varimax rotation. Bartlett’s test of sphericity was significant (χ2 = 1026.14, df = 6, p < 0.001), confirming that the R-matrix is not an identity matrix. The determinant of the correlation matrix was 0.003 > 0.000001, supporting the assumption that the R-matrix was not singular. The Kaiser–Meyer–Olkin (KMO = 0.880) measure verified the sampling adequacy, and the KMO values for the individual items ranged between 0.849 and 0.919, well above the acceptable limit of 0.5, while the nondiagonal values of the anti-image matrix were relatively small [47]. Both the scree plot (Figure 3) and Kaiser’s criterion suggested a one-factor solution, with an eigenvalue of 3.725, explaining the 93.14% of variance, with item loadings ranging from 0.953 to 0.973.
In order to confirm the results of the EFA, a parallel analysis (PA), with 1000 randomly generated datasets, was completed using SPSS, and the mean eigenvalues from the random correlation matrices were compared to the eigenvalues from the correlation matrix of the actual dataset (Table 2). On the basis of the criteria of PA, only factors with eigenvalues greater than the PA random eigenvalues should be retained [48]. Thus, the PA confirmed the one-factor model for the TPACK Levels Rubric.
Thus, the TPACK Levels Rubric defines the integrated TPACK domain through four observable variables, the components of TPACK, which is consistent with the theoretical framework.

5. Unpacking TPACK Levels Rubric

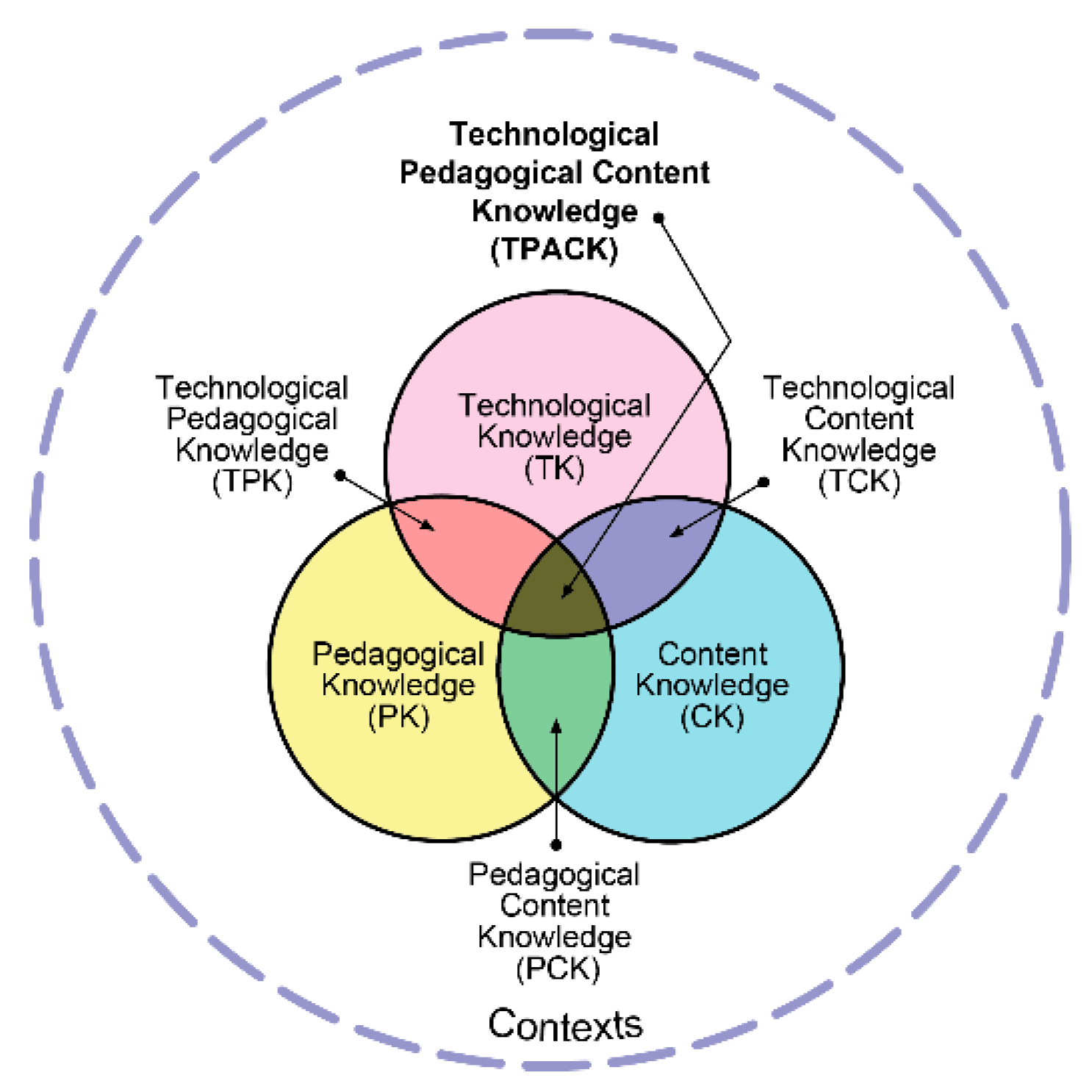
In this section, the progressions of the teacher-related and student-related indicators across different levels of TPACK are examined, and the indicators are unpacked for each TPACK component. In the process of unpacking, the language of the rubric was revised to achieve a better alignment between the three theoretical frameworks in order to maintain consistency across the different components for each level (vertical alignment), and distinction across the different levels for each component (horizontal progression), and to maintain the distinction between the two performance indicators within each component of each level. The meaning of each indicator is then illustrated by the examples from the lesson plan exemplars.

5.1. Lesson Plan Exemplars

The lesson plan exemplars for each level of TPACK were developed from the elements of the lessons created by the elementary school teachers for a second-grade topic on the addition and subtraction of numbers within 1000, using place values and the properties of the operations. The following common technology was available in their classrooms: a SMART Board with SMART Notebook software, the teacher’s computer with access to the Internet and an LCD projector, and student laptops with Microsoft Office and access to the Internet.

5.1.1. Recognizing Level of TPACK

The teacher reviews the place values by projecting the images of base-ten blocks onto the SMART Board. The teacher asks the students to identify three-digit numbers for the projected images of the base-ten block combinations but does not ask for any explanations. The teacher uses a SMART Board for writing notes to introduce the rules of addition and subtraction in a whole-class setting. As part of the assessment, the teacher provides students with a calculator to check their answers while the students are solving the addition and subtraction problems. The teacher explains to the students how to use the calculator in order to check the addition and subtraction within 1000. The students use an online quiz to practice addition and subtraction within 1000, without using place values and/or the properties of the operations. The online quiz scores the student responses, without explanations.

5.1.2. Accepting Level of TPACK

The teacher uses a premade SMART Notebook presentation to review the place values and to introduce the rules for addition and subtraction. The teacher projects a BrainPOP Jr. video [49] about addition and subtraction and plays it without pauses in a whole-class setting. Multiple-choice questions at the end of the BrainPOP Jr. video are answered by the whole class, without discussion or explanations. The teacher then models solving addition and subtraction problems by writing problems on the SMART Board while the students follow in their notebooks. Afterwards, the students use a multimedia tutorial developed by the teacher in a 1:1 setting. The multimedia tutorial is an interactive PowerPoint presentation that provides a review of addition and subtraction strategies based on place values. The multimedia tutorial has easy-to-navigate action buttons supporting a nonlinear structure, and it includes opportunities for students to self-assess their understanding using a multiple-choice quiz with built-in immediate feedback. However, it does not provide students with a place for active exploration. The students solve the addition and subtraction problems included in the multimedia tutorial in the same way that was modeled by the teacher earlier, and as was shown in the tutorial examples. The students have the option of using virtual base-ten blocks as needed to support their practice of addition and subtraction.

5.1.3. Adapting Level of TPACK

The teacher starts the lesson with a review of the place values using an interactive matching activity presented on the SMART Board. Then, in a 1:1 setting, students use the multimedia tutorial with various visual resources to learn about algorithms for addition and subtraction using the place values and the properties of the operations. The teacher develops an interactive multimedia tutorial similar to the previous example. However, at this level, it is used for the students’ independent learning of the strategies for the addition and subtraction of numbers within 1000. Therefore, a multimedia tutorial provides content that is new to students, as well as opportunities for students to self-assess their understanding through solving the addition and subtraction problems provided in the tutorial. At the end of the lesson, the teacher presents a summary of the rules for addition and subtraction using a SMART Notebook presentation with interactive activities for the students in a whole-class setting. The interactive activities in the SMART Notebook use an infinite cloner feature and a checker tool for the students to model addition and subtraction within 1000, using pictures of base-ten blocks.

5.1.4. Exploring Level of TPACK

The teacher designs an activity with virtual base-ten block manipulatives (e.g., [50]) so that students can develop their own strategies for the addition and subtraction of numbers using place values. The teacher sets up small collaborative groups for the students and provides them with a handout that includes instructions for the use of manipulatives and questions that guide the student exploration. During small group work, the teacher walks around and questions the students to assess their understanding. At the end of the activity, the students use virtual base-ten blocks to present their strategies and to explain why they work. They also use virtual base-ten blocks to question each other about these strategies. At the end of the lesson, the teacher summarizes the student strategies on a SMART Notebook in a whole-class setting.

5.1.5. Advancing Level of TPACK

The teacher provides students with access to several different technological tools, e.g., virtual base-ten blocks manipulatives, PhET online simulation [51], and a basic four-function calculator, in order to experiment and develop multiple strategies for the addition and subtraction of whole numbers within 1000, using place values and the properties of the operations. Students select one or more tools of their choice to develop, test, and evaluate their own multiple strategies for addition and subtraction using place values. Using the selected technology tools, the students reason whether the different strategies for addition and subtraction lead to correct answers and justify their choices of strategies. As a summary, the teacher facilitates a student analysis of the multiple strategies for addition and subtraction that they developed. The teacher challenges the students to apply their strategies to addition and subtraction within 10,000.

5.2. Unpacking Teacher-Related Indicators

The wording of the teacher-related indicator was revised to explicitly include the word, “teacher”, in order to emphasize that this indicator addresses how the teacher uses technology in the lesson. Then, for each component of the rubric, the progressions of the performance indicators across the TPACK levels were examined, explained, and illustrated using lesson plan exemplars.

5.2.1. Overarching Conception

Progression of teacher-related performance indicators for the overarching conception component of TPACK is provided in Table 3.
At the Recognizing level, the teacher uses instructional technology for motivation only, rather than for subject matter development. This means that the addition of technology does not change the way new material is presented to the students, or the way in which students learn the new material. In the lesson exemplar, the teacher uses the SMART Board to record notes. The interactive features of this tool that can support the student learning of addition and subtraction are not utilized.
At the Accepting level, the teacher uses technology for subject matter development as part of direct instruction. In the lesson exemplar, the teacher uses a premade SMART Notebook presentation and a BrainPOP Jr. video to introduce the rules for addition and subtraction, a new topic for students.
At the Adapting level, the teacher adapts the instructional technology to previously taught lessons in order to enhance student learning and to support subject matter development. In the lesson exemplar, the teacher uses the interactive features of the SMART Notebook, such as a matching activity, an infinite cloner, and a checker tool, to engage students in the review of the place values at the beginning of the lesson, and in the summary of the addition and subtraction rules at the end of the lesson.
At the Exploring level, the teacher is no longer the primary user of technology when it comes to the subject matter development. The teacher develops technology-based tasks for the student use of technology to construct their own knowledge. In the lesson exemplar, the teacher designs an activity with virtual base-ten blocks for students to develop their own strategies for the addition and subtraction of numbers within 1000 using place values.
At the Advancing level, the teacher develops tasks with instructional technology that focus on the development of a deeper conceptual understanding of the topic. Deep conceptual understanding is the process of the “creation of a robust framework representing the numerous and interwoven relationships between … ideas, patterns, and procedures. This framework can be used to coherently integrate new knowledge and solve unfamiliar problems.” [52]. In the lesson exemplar, the teacher provides the students with a choice of technological tools to develop multiple strategies for addition and subtraction on the basis of the place value, the properties of the operations, and the procedures for adding and subtracting numbers as they relate to one another.

5.2.2. Knowledge of Student Understanding

Progression of teacher-related performance indicators for the knowledge of student understanding component of TPACK is provided in Table 4.
At the Recognizing level, the teacher’s use of technology does not support the students’ thinking. In the lesson exemplar, the SMART Board is used by the teacher only as a projection screen and a note-writing device. The teacher shows the images of the base-ten block combinations for students to identify corresponding numbers but does not ask students to explain their answers.
At the Accepting level, the teacher uses instructional technology to present the students with the new material and then expects the students to use the technology to repeat the same tasks, in exactly the same way as demonstrated, without any explorations. In the lesson exemplar, the teacher models the solving of addition and subtraction problems on the SMART Board. Later in the lesson, the students independently solve similar problems, included in the multimedia tutorial, using the exact approach modeled by the teacher earlier.
At the Adapting level, the teacher develops technology-based tasks for students to promote their thinking. According to Ritchhart and Perkins [53], in order to promote student thinking, student learning tasks must include making observations, building explanations and interpretations, reasoning with evidence, making connections, considering different viewpoints and perspectives, and forming conclusions. In the lesson exemplar, the teacher prepares a multimedia tutorial using PowerPoint, which becomes a guided learning tool for the students, filled with various visual resources (e.g., images, videos, diagrams), and examples of using virtual base-ten blocks to solve problems. The tutorial includes questions designed to promote student thinking about addition and subtraction based on place values and the properties of the operations.
At the Exploring level, the teacher experiments with different ways of integrating technology as learning tools to support student thinking about mathematical concepts and the development of a conceptual understanding of a topic. According to the National Council of Teachers of Mathematics [54], “conceptual understanding” is defined as the comprehension of mathematical concepts, operations, and relations, and it enables students to apply, and to possibly adapt, acquired mathematical ideas to new problems or situations. In the lesson exemplar, the teacher designs technology-based tasks for small groups of students in order to support student discourse and collaboration, while providing opportunities for all of the students to develop their own strategies for the addition and subtraction of numbers.
At the Advancing level, the teacher makes changes to the curriculum to take advantage of the technology affordances in order to promote higher-level thinking and to provide students with opportunities to develop a deeper conceptual understanding. At this level, the teacher shifts the instruction so that it becomes fully student-centered. The teacher integrates technology in a variety of ways, from building mathematical concepts and ideas, to facilitating the independent thinking of students. In the lesson exemplar, the teacher provides students with a selection of technology tools to encourage the students’ exploration and experimentation with technology in order to develop, test, and evaluate various strategies for the addition and subtraction of numbers within 1000.

5.2.3. Knowledge of the Curriculum

Progression of teacher-related performance indicators for the knowledge of the curriculum component of TPACK is provided in Table 5.
At the Recognizing level, the teacher does not have a sufficient understanding of the instructional technology in order to align the features of the technology tools with the curriculum topics. As shown in the lesson exemplar, the teacher does not understand the affordances of a SMART Board to effectively support the teaching of the topic of addition and subtraction.
At the Accepting level, the teacher has some understanding of how to use instructional technology but has difficulty identifying topics in the curriculum that could be effectively supported by technology. As shown in the lesson exemplar, the teacher provides the students with access to virtual base-ten blocks to support their practice in solving addition and subtraction problems. However, because this virtual manipulative is optional and the students are not required to provide explanations, they could easily avoid using place values in the problem solving.
At the Adapting level, the teacher selects an instructional technology to replace the nontechnology tasks with technology-based tasks, and the use of technology in these tasks is only partially effective for a specific curriculum topic. In the lesson exemplar, the teacher provides the students with the multimedia tutorial that explains the topic of the lesson; however, the tutorial is a technology-based analogy of a printed textbook. Students can read a section of the textbook, review solved examples, go back and forth between slides as needed, and practice problems that provide the answers.
At the Exploring level, the teacher actively integrates technology into the teaching and learning of the important topics in the curriculum. The teacher examines different ways for teaching with technology, and designs technology-based activities to align with the taught curriculum. In the lesson exemplar, the teacher develops an activity for the students with an alternative way of learning about addition and subtraction, using virtual base-ten blocks.
At the Advancing level, the teacher selects technology that supports the teaching and learning of the essential curriculum topics in an innovative and constructive way. At this level, the teacher challenges the traditional curriculum by making decisions about the inclusion (or not) of curriculum topics on the basis of the technology affordances and a careful analysis of the knowledge and skills necessary for the development of the student understanding of the essential topics. In the lesson exemplar, the teacher selects several technology tools and allows the students to develop their own strategies for the addition and subtraction of numbers, which is very different from the traditional approach of teaching students how to add/subtract first, and then providing them with practice. The teacher challenges the students to apply their strategies to numbers within 10,000 that go beyond the capabilities of these two tools, and that is also not part of the second-grade curriculum. The students can use their strategies for addition and subtraction with larger numbers without technology, and they can then use a basic calculator to test their strategies.

5.2.4. Instructional Strategies

Progression of teacher-related performance indicators for the instructional strategies component of TPACK is provided in Table 6.
At the Recognizing level, the teacher focuses on how to use instructional technology, rather than on the “why” of using it. In the lesson exemplar, the teacher uses several instructional strategies to teach the students addition and subtraction within 1000. For example, student practice happens at the end of the lesson, when students are given a worksheet with problems and a calculator to check their answers. Here, the students are using technology, but the teacher only focuses on providing them with instructions on how to use a calculator, rather than on thinking about how a calculator can help the students explore the properties of addition and subtraction.
At the Accepting level, the instruction with technology is predominantly teacher-led. The use of instructional technology by the students does not involve independent explorations. In the lesson exemplar, the teacher projects a BrainPOP Jr. video [49], which explains the strategies for addition and subtraction in a whole-class setting. The teacher does not pause the video to assess the student understanding, explain any misconceptions, or offer the students a chance to ask questions.
The main difference between the Adapting level and the Accepting level is the teacher’s shift towards including structured inquiry explorations with technology for the students. In the lesson exemplar, the students learn new material using a multimedia tutorial. The multimedia tutorial supports the student learning of the new material at their own pace; however, the teacher controls the progression and the content of this activity.
At the Exploring level, the teacher uses multiple instructional strategies with technology to support the student learning of mathematics, which include both deductive (teacher-directed) and inductive (student-centered) approaches. The emphasis on the student-centered learning of new material is the most important distinction in the instructional strategies of teachers, compared to the Adapting level. In the lesson exemplar, the teacher develops a guided inquiry activity with virtual base-ten blocks to support the students’ thinking about addition and subtraction in terms of the place value.
At the Advancing level, the teacher uses multiple inductive instructional strategies with instructional technology to support the students’ experimentation as they explore mathematical ideas. In the lesson exemplar, the students are engaged in an open inquiry while experimenting with various technology tools in small collaborative groups. The students develop and test their strategies for addition and subtraction, which engages metacognition. The technology tools provide the students with immediate feedback. The summary of the lesson is conducted as a whole-class discussion, with the students using the technology tools to demonstrate and justify their strategies. During this discussion, the students are engaged in the analysis and evaluation of each other’s strategies, thereby engaging in peer feedback.

5.3. Unpacking Student-Related Indicators

Similar to the changes in the teacher-related indicators, the wording of the student-related performance indicators was revised to make explicit reference to the student activities with technology, the digital materials used by the students, and the technology-based tasks assigned to the students.

5.3.1. Overarching Conception

Progression of student-related performance indicators for the overarching conception component of TPACK is provided in Table 7.
At the Recognizing level, the students use technology for drills and practice only, with a focus on the repetition of the skill, without making connections to the previously learned material. These types of activities do not include inquiry tasks. In the lesson exemplar, the students were provided with two different activities with technology. In the first one, they practiced addition and subtraction and used a calculator to check their answers. This is an example of technology being used for routine tasks that do not allow students to construct their own knowledge. In the second task, the students were assessed using an online quiz; however, this technology-based activity did not provide the students with an opportunity to make connections to the topics of place values or the use of the properties of the operations, as the only feedback they received was a score.
At the Accepting level, the digital materials created or selected by the teacher for the students still do not support the students in making connections to previously learned material, but they do provide confirmation inquiry tasks. Technology-based practice is more meaningful and goes beyond drills. In the lesson exemplar, the teacher-developed multimedia tutorial does not provide the students with active explorations; the students solve the addition and subtraction problems following the rules introduced by the teacher. However, the activity does provide students with the practice that helps them to confirm these rules.
At the Adapting level, the technology-based tasks engage the students in a structured inquiry and support them in making connections to previously learned topics. In the lesson example, the multimedia tutorial actively engages the students in learning new topics through a nonlinear structure, and action buttons to access bookmarked pages with important information, examples, and the self-assessment quiz with immediate feedback. However, the students only have access to material that is selected by the teacher and only follow procedures prescribed by the teacher. The teacher concludes the lesson with interactive activities for the students to model addition and subtraction, using pictures of the base-ten blocks on the SMART Notebook, thereby supporting the students in making connections between the strategies for addition, subtraction, and place values.
At the Exploring level, the student tasks with technology represent a guided inquiry, e.g., the students are doing mathematics with technology, and they are guided in their use, and the development of connections to prior topics while constructing new knowledge. In the lesson exemplar, students are provided with a handout that includes instructions for the use of virtual manipulatives, as well as questions that guide the students in linking the place value and the properties of the operations to addition and subtraction as they are developing their own strategies for these operations.
At the Advancing level, the student technology-based tasks represent an “open inquiry”, with “high cognitive demand”. According to Tekkumru-Kisa, Stein, and Schunn [35], high-cognitive-demand tasks require students to think abstractly, analyze information, draw conclusions, and make connections to mathematical meanings and understandings. In an open inquiry, students are provided with resources and learning objectives, and it is their choice as to how to proceed and as to what questions to ask themselves in order to accomplish their tasks and justify their choices. In the lesson exemplar, students are provided with a selection of technological tools and the task to develop strategies for addition and subtraction within 1000. The teacher expects the students to consider the place value, the properties of the operations, and the procedures for adding and subtracting numbers as they relate to one another, and to the symbols and language, leading to an abstract (deeper conceptual) understanding of the topic. The students then have to test their strategies and analyze the efficiency and effectiveness of these strategies. This process also leads to the development of strategic knowledge.

5.3.2. Knowledge of Student Understanding

Progression of teacher-related performance indicators for the knowledge of student understanding component of TPACK is provided in Table 8.
At the Recognizing level, the digital materials only provide space for student practice and drills, mostly without meaningful feedback. In the lesson exemplar, the students use an online quiz to practice addition and subtraction within 1000, without using place values and/or the properties of the operations; thus, the digital materials do not provide the students with the opportunity to apply new knowledge in their practice.
At the Accepting level, the digital materials for students are structured similar to the traditional textbook presentation of material in a “teacher-led/student-followed” format, without active explorations. In the lesson exemplar, the multimedia tutorial is designed by the teacher and follows the structure of the textbook, first presenting the rules of addition and subtraction and examples of the solved problems, followed by the practice problems at the end of the tutorial.
At the Adapting level, the digital materials for students provide space for the student-structured exploration of mathematics. As a result, the students are mostly engaged in procedures for the purpose of developing an understanding of mathematical concepts and ideas. In the lesson exemplar, the students use a multimedia tutorial to build their own understanding of strategies for the addition and subtraction of numbers using place values and the properties of the operations. The students have opportunities to work at their own paces, to go back and forth between different slides that provide explanations, to study examples of solved problems, and to practice problems. However, their explorations are limited by the teacher’s choice of content and approach to the topic.
At the Exploring level, the students deliberately take meaningful actions on mathematical objects using instructional technology. The digital materials designed by the teacher place students in a learning environment where they can take mathematical actions on these objects and then reflect on what they do. However, the digital materials do not support students in understanding the meaningful subject-specific consequences of these actions, and, therefore, the explicit guidance of teachers is required. In the lesson exemplar, the students use virtual base-ten blocks to develop strategies for addition and subtraction by composing and decomposing hundreds and tens. In the dynamic technological environment, they can observe the various consequences of these actions. However, the teacher needs to help the students develop strategies for addition and subtraction on the basis of these observations.
At the Advancing level, the digital materials provide the students with an environment to easily and intuitively take mathematical actions on mathematical objects. It is the attention to the action–consequence reflection and sense-making structures that distinguish these technology-based activities at the Advancing level. For example, by using PhET simulation, students can compose and decompose numbers and immediately see the results of the addition represented using place values, which could help them develop various strategies for addition. The simulation then offers a game where they can test their strategies and can receive immediate feedback, which could lead to the evaluation and revision of their strategies. Such technology tools provide opportunities for students to change and manipulate mathematical models, and, in return, the students can immediately see the meaningful consequences of their actions, which supports a deeper understanding of the topic.

5.3.3. Knowledge of Curriculum

Progression of teacher-related performance indicators for the knowledge of curriculum component of TPACK is provided in Table 9.
At the Recognizing level, the technology-based tasks do not support students in making connections between curriculum topics. In the lesson exemplar, the teacher provides students with calculators to check their answers while solving addition and subtraction problems. The use of a calculator does not support students in making connections between the operations of addition, subtraction, and place values.
At the Accepting level, the teacher is aware that the technology tasks should support the students in making connections between the topics in the curriculum. However, a limited understanding of both the curriculum and the affordances of technology does not lead to such tasks. In the lesson exemplar, a multimedia tutorial provides a review that explains how to use place values in addition and subtraction problems, but the structure of the practice problems and the superficial role of the virtual base-ten blocks do not support the students in making these connections.
At the Adapting level, the students’ tasks with technology are fully aligned with the curriculum. However, these tasks support only a basic understanding of the topic, through procedures with connections that require some degree of cognitive effort. In the lesson exemplar, the teacher uses a SMART Notebook presentation to summarize the strategies for addition and subtraction using place values and the properties of the operations in a whole-class setting. The students are not given opportunities to present their own understanding of the topic on the basis of their work with the multimedia tutorial. The interactive activity, which uses an infinite cloner and a checker tool, only provides students with space to practice solving the problems by applying the strategies provided by the teacher, rather than a focus on a deeper understanding of these strategies and their connections with the place values and the properties of the operations.
The curriculum-based tasks with technology at the Exploring level foster the student understanding of the topic through independent explorations, and they support the students in making connections between the curriculum topics that expand their ideas beyond the topics they have just learned. In the lesson exemplar, the students use virtual manipulatives to develop the strategies for addition and subtraction within 1000. As they explore, they might also observe the consequences of the repeated addition of 10 s or 100 s to arrive at a conceptual understanding of the multiplication of one-digit numbers by 10 or 100.
At the Advancing level, the students’ tasks with technology focus on deepening the understanding of mathematical concepts, and on making connections between topics, inside and outside of the curriculum. In the lesson exemplar, providing the students with several different technology tools supports the task of developing multiple strategies for addition and subtraction, which is necessary for a deeper conceptual understanding of the topic. Virtual base-ten block manipulatives and PhET simulation provide a dynamic environment that helps students activate their prior knowledge of place values in order to develop an understanding of addition and subtraction.

5.3.4. Instructional Strategies

Progression of teacher-related performance indicators for the instructional strategies component of TPACK is provided in Table 10.
At the Recognizing level, the digital materials support drill and practice only. In the lesson exemplar, an online quiz serves the purpose of a basic assessment tool, which provides no meaningful feedback to the students.
At the Accepting level, the teacher selects the digital materials for the students as a tool for the delivery of information and for practice. In the lesson exemplar, both the BrainPOP Jr. video and the multimedia tutorial are used for the delivery of information and for practice (e.g., multiple-choice questions at the end of the video, and problems at the end of the tutorial).
At the Adapting level, a structured inquiry with technology does not promote student reflection. In the lesson exemplar, the students are using the multimedia tutorial to learn about strategies for addition and subtraction. Then, they take a multiple-choice quiz, developed for the purpose of the self-assessment of their understanding of the new material. However, at this age, students will most likely continue to guess their answers until they obtain the correct answer, without any reflection on their learning.
At the Exploring level, the digital materials for students are built around mathematical objects and support student reflection and the posing of questions. In the lesson exemplar, the mathematical objects are numbers represented with virtual base-ten blocks. The students manipulate these objects to develop their own strategies for addition and subtraction. After the students develop their strategies, they are asked to provide explanations of their strategies using the virtual base-ten blocks. This happens in small groups, when students are posing questions to each other about their developed strategies.
At the Advancing level, the teacher selects digital materials that have features that support sense making and reasoning, including explanation and justification. In the lesson exemplar, these specific features of digital materials are dynamic and linked representations, interactive capabilities, and immediate feedback.

6. Discussion

There is a gap between the theoretical definition and the practical measurements that calls for further reflection on TPACK as a framework. The diverse definitions and interpretations of TPACK that have emerged in the literature in recent years contribute to this gap. The majority of TPACK studies focus on the interdisciplinary nature of TPACK, and on distinguishing its different domains. This study focuses on assessing an integrated TPACK domain [6] and its development through progressive levels [19], specifically for teaching mathematics. The development of an assessment instrument for a complex theoretical construct helps to close the gap between theory and practice.
This study attempts to reconceptualize the levels of performance for an integrated TPACK construct by unpacking the performance indicators of the TPACK Levels Rubric [18]. This process required multiple iterations and revisions in order to achieve the clarity of the descriptors used in the rubric and the clear differentiation between the TPACK levels.

7. Conclusions

In the process of unpacking and revising the performance indicators of the original TPACK Levels Rubric, this study elaborated the roles of the frameworks for the cognitive demand of tasks and inquiry-based learning in the model for the progressive levels of TPACK, and it highlights the differences in the TPACK levels for teaching mathematics. As a result of the rubric analysis, the performance indicators were revised to maintain both consistency across the different components for each level (vertical alignment), and the distinction across different levels for each component (horizontal progression). The language of the rubric was also revised to maintain the distinction between the two performance indicators within each component of each level. The significance of this study is in the revision and validation of an instrument that could help in bridging the theoretical definition of the integrated TPACK domain with the practical demands in the field of teacher education. The lesson plan exemplars developed as part of the study illustrate the distinctions between the TPACK levels, providing further guidance for educational researchers and practitioners. Further studies are needed to test the validity of the rubric, with different populations of teachers in different contexts.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/educsci12020079/s1. Table S1: TPACK Levels Rubric 2.0-mathematics. Table S2: VideoMathBlind.

Author Contributions

Conceptualization, I.L. and A.K.-S.; data curation, I.L.; formal analysis, I.L. and A.K.-S.; investigation, I.L. and A.K.-S.; methodology, I.L.; project administration, I.L.; supervision, I.L.; validation, I.L.; writing—original draft, I.L. and A.K.-S.; writing—review and editing, I.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of the City University of New York (protocol #344755, 6 August 2012).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data presented in this study are available in Supplementary Materials.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Darling-Hammond, L.; Oakes, J. Preparing Teachers for Deeper Learning; Harvard Education Press: Cambridge, MA, USA, 2019. [Google Scholar]
  2. Hyndman, B. Ten reasons why teachers can struggle to use technology in the classroom. Sci. Educ. News 2018, 67, 41–42. [Google Scholar]
  3. OECD. TALIS 2018 Results (Volume II): Teachers and School Leaders as Lifelong Learners; TALIS, OECD Publishing: Paris, France, 2020. [Google Scholar] [CrossRef]
  4. Ottenbreit-Leftwich, A.T.; Brush, T.A.; Strycker, J.; Gronseth, S.; Roman, T.; Abaci, S.; Shin, S.; Plucker, J. Preparation versus practice: How do teacher education programs and practicing teachers align in their use of technology to support teaching and learning? Comput. Educ. 2012, 59, 399–411. [Google Scholar] [CrossRef]
  5. Niess, M.L. Preparing teachers to teach science and mathematics with technology: Developing a technology pedagogical content knowledge. Teach. Teach. Educ. 2005, 21, 509–523. [Google Scholar] [CrossRef]
  6. Mishra, P.; Koehler, M. Technological pedagogical content knowledge: A framework for teacher knowledge. Teach. Coll. Rec. 2006, 108, 1017–1054. [Google Scholar] [CrossRef]
  7. Shulman, L.S. Those who understand: Knowledge growth in teaching. Educ. Res. 1986, 15, 4–14. [Google Scholar] [CrossRef]
  8. Niess, M.L. Central component descriptors for levels of technological pedagogical content knowledge. J. Educ. Comput. Res. 2013, 48, 173–198. [Google Scholar] [CrossRef]
  9. Lyublinskaya, I. Evolution of a course for special education teachers on integrating technology into math and science. In Handbook of Research on Teacher Education in the Digital Age; Niess, M.L., Gillow-Wiles, H., Eds.; IGI Global: Hershey, PA, USA, 2015; pp. 532–559. [Google Scholar]
  10. Voogt, J.; McKenney, S. TPACK in teacher education: Are we preparing teachers to use technology for early literacy? Technol. Pedagog. Educ. 2017, 26, 69–83. [Google Scholar] [CrossRef]
  11. Niess, M.L.; Gillow-Wiles, H. Online instructional strategies for enhancing teachers’ TPACK: Experiences, discourse, and critical reflection. In Research Anthology on Developing Effective Online Learning Courses; Information Resources Management Association, Ed.; IGI Global: Hershey, PA, USA, 2021; pp. 326–348. [Google Scholar]
  12. Lyublinskaya, I.; Tournaki, N. A study of special education teachers’ TPACK development in mathematics and science through assessment of lesson plans. J. Technol. Teach. Educ. 2014, 22, 449–470. [Google Scholar]
  13. Purwaningshi, E.; Nurhadi, D.; Masjkur, K. TPACK development of prospective physics teachers to ease the achievement of learning objectives: A case study at the State University of Malang, Indonesia. J. Phys. Conf. Ser. 2019, 1185, 012042. [Google Scholar] [CrossRef]
  14. Oner, D. A virtual internship for developing technological pedagogical content knowledge. Australas. J. Educ. Technol. 2020, 36, 27–42. [Google Scholar] [CrossRef]
  15. Hall, J.A.; Lei, J.; Wang, Q. The first principles of instruction: An examination of their impact on preservice teachers’ TPACK. Educ. Technol. Res. Dev. 2020, 68, 3115–3142. [Google Scholar] [CrossRef]
  16. Koehler, M.J.; Shin, T.S.; Mishra, P. How do we measure TPACK? Let me count the ways. In Educational Technology, Teacher Knowledge, and Classroom Impact: A Research Handbook on Frameworks and Approaches; Ronau, R., Rakes, C., Niess, M., Eds.; IGI Global: Hershey, PA, USA, 2012; pp. 16–31. [Google Scholar]
  17. Abbitt, J.T. Measuring technological pedagogical content knowledge in preservice teacher education: A review of current methods and instruments. J. Res. Technol. Educ. 2011, 43, 281–300. [Google Scholar] [CrossRef]
  18. Lyublinskaya, I.; Tournaki, E. The effects of teacher content authoring on TPACK and on student achievement in algebra: Research on instruction with the TI-Nspire handheld. In Educational Technology, Teacher knowledge, and Classroom Impact: A Research Handbook on Frameworks and Approaches; Ronau, R., Rakes, C., Niess, M., Eds.; IGI Global: Hershey, PA, USA, 2012; pp. 295–322. [Google Scholar]
  19. Niess, M.L.; Sadri, P.; Lee, K. Dynamic spreadsheets as learning technology tools: Developing teachers’ technology pedagogical content knowledge (TPCK). In Proceedings of the American Education Research Association Annual Conference, Chicago, IL, USA, 9–13 April 2007. [Google Scholar]
  20. Balgalmis, E.; Cakiroglu, E.; Shafer, K. An investigation of a pre-service elementary mathematics teacher’s TPACK within the context of teaching practices. In Proceedings of the Society for Information Technology & Teacher Education International Conference, Jacksonville, FL, USA, 17 March 2014; Searson, M., Ocho, M., Eds.; AACE: Chesapeake, VA, USA, 2014; pp. 2210–2217. [Google Scholar]
  21. Handal, B.; Campbell, C.; Cavanagh, M.; Petosz, P. Characterising the perceived value of mathematics educational apps in preservice teachers. Math. Educ. Res. J. 2016, 26, 199–221. [Google Scholar] [CrossRef] [Green Version]
  22. Shinas, V.H.; Yilmaz-Ozden, S.; Mouza, C.; Karchmer-Klein, R.; Glutting, J.J. Examining domains of technological pedagogical content knowledge using factor analysis. J. Res. Technol. Educ. 2013, 45, 339–360. [Google Scholar] [CrossRef]
  23. Mouza, C.; Karchmer-Klein, R. Promoting and assessing pre-service teachers’ technological pedagogical content knowledge (TPACK) in the context of case development. J. Educ. Comput. Res. 2013, 48, 127–152. [Google Scholar] [CrossRef]
  24. Archambault, L. Exploring the use of qualitative methods to examine TPACK. In Handbook of Technological Pedagogical Content Knowledge for Educators, 2nd ed.; Herring, M.C., Koehler, M.J., Mishra, P., Eds.; Routledge: New York, NY, USA, 2016; pp. 65–86. [Google Scholar]
  25. Chai, C.S.; Koh, J.H.L.; Tsai, C.C. A review of the quantitative measures of technological pedagogical content knowledge (TPACK). In Handbook of Technological Pedagogical Content Knowledge for Educators, 2nd ed.; Herring, M.C., Koehler, M.J., Mishra, P., Eds.; Routledge: New York, NY, USA, 2016; pp. 87–106. [Google Scholar]
  26. Karatas, I.; Tunc, M.P.; Yilmaz, N.; Karaci, G. An investigation of Technological Pedagogical Content Knowledge, self-confidence, and perception of pre-service middle school mathematics teachers towards instructional technologies. Educ. Technol. Soc. 2017, 20, 122–132. [Google Scholar]
  27. Saubern, R.; Urbach, D.; Koehler, M.; Phillips, M. Describing increasing proficiency in teachers’ knowledge of the effective use of digital technology. Comput. Educ. 2020, 47, 103784. [Google Scholar] [CrossRef]
  28. Schmidt, D.A.; Baran, E.; Thompson, A.D.; Mishra, P.; Koehler, M.J.; Shin, T.S. Technological Pedagogical Content Knowledge (TPACK): The development and validation of an assessment instrument for preservice teachers. J. Res. Technol. Educ. 2009, 42, 123–149. [Google Scholar] [CrossRef]
  29. Lyublinskaya, I.; Tournaki, N. Examining the relationship between self and external assessment of TPACK of pre-service special education teachers. In Proceedings of the Society for Information Technology & Teacher Education International Conference, Las Vegas, NV, USA, 2 March 2015; Rutledge, D., Slykhuis, D., Eds.; AACE: Chesapeake, VA, USA, 2015; pp. 2977–2983. [Google Scholar]
  30. Tomayko, M. Pre-service teachers self-assessing TPACK using a visual quantitative mode. In Proceedings of the Society for Information Technology & Teacher Education International Conference, Washington, DC, USA, 26 March 2018; Langran, E., Borup, J., Eds.; AACE: Chesapeake, VA, USA, 2018; pp. 2123–2127. [Google Scholar]
  31. Voogt, J.; Fisser, P.; Roblin, N.P.; Tondeur, J.; van Braak, J. Technological Pedagogical Content Knowledge–a review of the literature. J. Comput. Assist. Learn. 2013, 29, 109–121. [Google Scholar] [CrossRef] [Green Version]
  32. Akyuz, D. Measuring technological pedagogical content knowledge (TPACK) through performance assessment. Comput. Educ. 2018, 125, 212–225. [Google Scholar] [CrossRef]
  33. Harris, J.; Grandgenett, N.; Hofer, M. Testing a TPACK-based technology integration assessment rubric. In Proceedings of the Society for Information Technology & Teacher Education International Conference, San Diego, CA, USA, 29 March 2010; Gibson, D., Dodge, B., Eds.; AACE: Chesapeake, VA, USA, 2010; pp. 3833–3840. [Google Scholar]
  34. Lachner, A.; Fabian, A.; Franke, U.; Preiß, J.; Jacob, L.; Führer, C.; Küchler, U.; Paravicini, W.; Randler, C.; Thomas, P. Fostering pre-service teachers’ technological pedagogical content knowledge (TPACK): A quasi-experimental field study. Comput. Educ. 2021, 174, 104304. [Google Scholar] [CrossRef]
  35. Stein, M.K.; Smith, M.S. Mathematical tasks as a framework for reflection: From research to practice. Math. Teach. Middle Sch. 1998, 3, 268–275. [Google Scholar] [CrossRef]
  36. Tekkumru-Kisa, M.; Stein, M.K.; Schunn, C. A framework for analyzing cognitive demand and content-practices integration: Task analysis guide in science. J. Res. Sci. Teach. 2015, 52, 659–685. [Google Scholar] [CrossRef]
  37. Levy, P.; Little, S.; McKinney, P.; Nibbs, A.; Wood, J. The Sheffield Companion to Inquiry-Based Learning; Centre for Inquiry-Based Learning in the Arts and Social Sciences, The University of Sheffield: Sheffield, UK, 2010. [Google Scholar]
  38. Rogers, E.M. Diffusion of Innovations; The Free Press of Simon and Schuster Inc.: New York, NY, USA, 1995. [Google Scholar]
  39. Niess, M.L.; Ronau, R.N.; Driskell, S.O.; Kosheleva, O.; Pugalee, D.; Weinhold, M.W. Inquiry into Mathematics Teacher Education; Association of Mathematics Teacher Educators: Houghton, MI, USA, 2009. [Google Scholar]
  40. Grossman, P.L. The Making of a Teacher: Teacher Knowledge and Teacher Education; Teachers College Press: New York, NY, USA, 1990. [Google Scholar]
  41. Maeng, J.L.; Mulvey, B.K.; Smetana, L.K.; Bell, R.L. Preservice teachers’ TPACK: Using technology to support inquiry instruction. J. Sci. Educ. Technol. 2013, 22, 838–857. [Google Scholar] [CrossRef]
  42. Bell, R.L.; Smetana, L.; Binns, I. Simplifying inquiry instruction. Sci. Teach. 2005, 72, 30–33. [Google Scholar]
  43. Marzano, R.J. Formative Assessment & Standards-Based Grading; Solution Tree Press: Bloomington, IN, USA, 2008. [Google Scholar]
  44. Clements, D.H.; Sarama, J.; DiBiase, A.M. (Eds.) Engaging Young Children in Mathematics: Standards for Early Childhood Mathematics Education; Routledge: New York, NY, USA, 2003. [Google Scholar]
  45. Moskal, B.M. Recommendations for developing classroom performance assessments and scoring rubrics. Pract. Assess. Res. Eval. 2003, 8, 14. [Google Scholar] [CrossRef]
  46. Tierney, R.; Simon, M. What’s still wrong with rubrics: Focusing on the consistency of performance criteria across scale levels. Pract. Assess. Res. Eval. 2004, 9, 2. [Google Scholar] [CrossRef]
  47. Field, A. Discovering Statistics Using SPSS, 5th ed.; Sage Publications: Thousand Oaks, CA, USA, 2018. [Google Scholar]
  48. Hayton, J.C.; Allen, D.G.; Scarpello, V. Factor retention decisions in Exploratory Factor Analysis: A tutorial on parallel analysis. Organ. Res. Methods 2004, 7, 191–205. [Google Scholar] [CrossRef]
  49. BrainPOP Jr. Available online: https://jr.brainpop.com/ (accessed on 27 September 2021).
  50. Didax Virtual Manipulatives. Available online: https://www.didax.com/math/virtual-manipulatives.html (accessed on 27 September 2021).
  51. PhET Interactive Simulations. Available online: https://phet.colorado.edu/en/simulation/make-a-ten (accessed on 27 September 2021).
  52. Sbar, E. Schemas Are Key to Deep Conceptual Understanding: A Blog from MIND Research Institute. Available online: https://blog.mindresearch.org/blog/schemas-deep-conceptual-understanding (accessed on 27 September 2021).
  53. Ritchhart, R.; Perkins, D.N. Learning to think: The challenges of teaching thinking. In The Cambridge Handbook of Thinking and Reasoning; Holyoak, K.J., Morrison, R.G., Eds.; Cambridge University Press: Cambridge, UK, USA, 2005; pp. 775–802. [Google Scholar]
  54. National Council of Teachers of Mathematics. Principles and Standards for School Mathematics; NCTM: Reston, VA, USA, 2000. [Google Scholar]
Education 12 00079 g001 550
Figure 1. Technological pedagogical content knowledge (TPACK) framework. Reproduced with the permission of the publisher, © 2022 by tpack.org.
Figure 1. Technological pedagogical content knowledge (TPACK) framework. Reproduced with the permission of the publisher, © 2022 by tpack.org.
Education 12 00079 g001
Education 12 00079 g002 550
Figure 2. Model for progressive development of teachers’ knowledge, from PCK to TPACK. Reproduced with permission from Niess et al. [39] (Copyright permission received from the author).
Figure 2. Model for progressive development of teachers’ knowledge, from PCK to TPACK. Reproduced with permission from Niess et al. [39] (Copyright permission received from the author).
Education 12 00079 g002
Education 12 00079 g003 550
Figure 3. EFA scree plot suggesting one-factor solution.
Figure 3. EFA scree plot suggesting one-factor solution.
Education 12 00079 g003
Table
Table 1. Conceptual framework for the study.
Table 1. Conceptual framework for the study.
TPACK LevelCognitive Demand of Tasks
with Technology		Inquiry-Based Level of Tasks with Technology
RecognizingMemorizationNo inquiry
AcceptingProcedures without connectionsConfirmation inquiry
AdaptingProcedures with connectionsStructured inquiry
ExploringDoing mathematicsGuided inquiry
AdvancingDoing mathematicsOpen inquiry
Table
Table 2. Comparison of eigenvalues in PCA and PA.
Table 2. Comparison of eigenvalues in PCA and PA.
FactorEigenvalues
PCAPA
13.7251.172
20.1251.046
30.0860.948
40.0640.835
Table
Table 3. Teacher-related performance indicators for the overarching conception component of TPACK.
Table 3. Teacher-related performance indicators for the overarching conception component of TPACK.
TPACK LevelTeacher-Related Performance Indicator
RecognizingTeacher uses instructional technology for motivation only, rather than subject matter development. New ideas are presented by the teacher mostly without technology.
AcceptingTeacher uses instructional technology for subject matter development. However, a larger part of technology use is for teacher demonstrations, which include presentations of new knowledge.
AdaptingTeacher uses instructional technology as a way to enhance student learning. This use of technology supports subject matter development.
ExploringTeacher plans for instructional technology to be used mostly by students who explore and experiment with technology for subject matter development.
AdvancingTeacher develops instructional technology tasks for students that provide them with a deeper conceptual understanding of the subject matter.
Table
Table 4. Teacher-related performance indicators for the knowledge of student understanding component of TPACK.
Table 4. Teacher-related performance indicators for the knowledge of student understanding component of TPACK.
TPACK LevelTeacher-Related Performance Indicator
RecognizingTeacher uses instructional technology in a way that does not support student thinking and learning of new content.
AcceptingTeacher uses instructional technology in a teacher-led/student-followed format, without focusing on the students’ thinking.
AdaptingTeacher structures students’ use of instructional technology to promote the students’ thinking about mathematics.
ExploringTeacher facilitates students’ use of instructional technology to develop thinking leading to a conceptual understanding of mathematics.
AdvancingTeacher facilitates students’ use of instructional technology to develop higher-order thinking, leading to a deep understanding of mathematics.
Table
Table 5. Teacher-related performance indicators for the knowledge of the curriculum component of TPACK.
Table 5. Teacher-related performance indicators for the knowledge of the curriculum component of TPACK.
TPACK LevelTeacher-Related Performance Indicator
RecognizingTeacher selects instructional technology that is not aligned with curriculum topics.
AcceptingTeacher selects instructional technology that is partially aligned with one or more curriculum topics. Technology use is not effective for the curriculum topics.
AdaptingTeacher selects instructional technology that is aligned with curriculum topics, but only replaces nontechnology-based tasks with technology-based tasks. Technology use is partially effective for the curriculum topics.
ExploringTeacher selects instructional technology that is aligned with curriculum topics, and provides an alternative way of topic exploration. Technology use is effective for the curriculum topics.
AdvancingTeacher selects instructional technology that is aligned with curriculum topics, but also challenges the traditional curriculum by engaging students to learn about different topics with technology. Technology use is highly effective for the curriculum topics.
Table
Table 6. Teacher-related performance indicators for the instructional strategies component of TPACK.
Table 6. Teacher-related performance indicators for the instructional strategies component of TPACK.
TPACK LevelTeacher-Related Performance Indicator
RecognizingTeacher focuses on how to use instructional technology, rather than on mathematical ideas.
AcceptingTeacher structures lessons without student explorations, with instructional technology. The instruction is teacher-led.
AdaptingTeacher uses a deductive approach to teaching, with instructional technology, to maintain control of the progression of the exploration activities.
ExploringTeacher uses deductive and inductive instructional strategies that support the students’ thinking about mathematics.
AdvancingTeacher mostly uses multiple inductive instructional strategies that support the students’ experimentation with mathematical ideas with instructional technology.
Table
Table 7. Student-related performance indicators for the overarching conception component of TPACK.
Table 7. Student-related performance indicators for the overarching conception component of TPACK.
TPACK LevelStudent-Related Performance Indicator
RecognizingTechnology-based activities do not include inquiry tasks. Technology procedures do not provide space for students to use or make connections.
AcceptingTechnology-based activities include confirmation inquiry tasks. Technology procedures do not provide space for students to use or make connections.
AdaptingTechnology-based activities include structured inquiry tasks towards intended ideas. Technology procedures concentrate on mathematical tasks that use or make connections.
ExploringTechnology-based activities include guided inquiry tasks of high cognitive demand. Technology procedures concentrate on doing mathematics while using or making connections.
AdvancingTechnology-based activities include open inquiry tasks of high cognitive demand. Technology procedures concentrate on tasks that use or develop deep mathematical knowledge representing connections and strategic knowledge.
Table
Table 8. Student-related performance indicators for the knowledge of student understanding component of TPACK.
Table 8. Student-related performance indicators for the knowledge of student understanding component of TPACK.
TPACK LevelStudent-Related Performance Indicator
RecognizingDigital materials only provide space for student practice and drills.
AcceptingDigital materials for students mirror the structure of the traditional textbook presentation of mathematics.
AdaptingDigital materials provide an environment for students to engage in active explorations of mathematics with teacher guidance.
ExploringDigital materials provide an environment for students to deliberately take mathematically meaningful actions on mathematical objects, but the teacher still guides students to recognize the meaningful consequences of those actions.
AdvancingDigital materials provide an environment for students to deliberately take mathematically meaningful actions on mathematical objects, and to immediately see the meaningful consequences of those actions.
Table
Table 9. Student-related performance indicators for the knowledge of curriculum component of TPACK.
Table 9. Student-related performance indicators for the knowledge of curriculum component of TPACK.
TPACK LevelStudent-Related Performance Indicator
RecognizingStudents’ tasks with technology do not support making connections between topics in the curriculum.
AcceptingStudents’ tasks with technology do not support making connections between topics in the curriculum.
AdaptingStudents are given curriculum-based tasks with technology to develop a basic understanding of curriculum topics with teacher guidance.
ExploringStudents are given curriculum-based tasks with technology and are asked to expand mathematical ideas on the basis of technology explorations.
AdvancingStudents’ tasks with technology focus on deepening their understanding of mathematical concepts, and the making of connections between topics, inside and outside of the curriculum.
Table
Table 10. Student-related performance indicators for the instructional strategies component of TPACK.
Table 10. Student-related performance indicators for the instructional strategies component of TPACK.
TPACK LevelStudent-Related Performance Indicator
RecognizingDigital materials are built around drill and practice only.
AcceptingDigital materials are built around delivery of information as well as drill and practice.
AdaptingDigital materials are built around mathematical objects but do not promote student reflection.
ExploringDigital materials are built around mathematical objects and explicitly promote student reflection, especially the posing of questions for sense making.
AdvancingDigital materials are built around mathematical objects and explicitly promote student reflection—especially the posing of questions for sense making and reasoning, including explanation and justification.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Lyublinskaya, I.; Kaplon-Schilis, A. Analysis of Differences in the Levels of TPACK: Unpacking Performance Indicators in the TPACK Levels Rubric. Educ. Sci. 2022, 12, 79. https://doi.org/10.3390/educsci12020079

AMA Style

Lyublinskaya I, Kaplon-Schilis A. Analysis of Differences in the Levels of TPACK: Unpacking Performance Indicators in the TPACK Levels Rubric. Education Sciences. 2022; 12(2):79. https://doi.org/10.3390/educsci12020079

Chicago/Turabian Style

Lyublinskaya, Irina, and Aleksandra Kaplon-Schilis. 2022. "Analysis of Differences in the Levels of TPACK: Unpacking Performance Indicators in the TPACK Levels Rubric" Education Sciences 12, no. 2: 79. https://doi.org/10.3390/educsci12020079

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop