Abstract
Self-assessment, in the education framework, is a methodology that motivates students to play an active role in reviewing their performance. It is defined as “the evaluation or judgment of ‘the worth’ of one’s performance and the identification of one’s strengths and weaknesses with a view to improving one’s learning outcomes”. The goal of this research is to study the relationship between self-assessment and the development and improvement of problem-solving skills in Mathematics. In particular, the investigation focuses on how accurate the students’ self-evaluations are when compared to external ones, and if (and how) the accuracy in self-assessment changed among the various processes involved in the problem-solving activity. Participants are grade 11 students (in all 182 participants) in school year 2020/2021 who were asked to solve 8 real-world mathematical problems using an Advanced Computing Environment (ACE). Each problem was assessed by a tutor and self-assessed by students themselves, according to a shared rubric with five indicators: Comprehension of the problematic situation, identification of the solving strategy, development of the solving process, argumentation of the chosen strategy, and appropriate and effective use of the ACE. Through a quantitative analysis, students’ self-assessment and tutors’ assessment were compared; data were cross-checked with students’ answers to a questionnaire. The results show a general correlation between tutor assessment and self-assessment, with a tendency of students to underestimate their performance. Moreover, students were more precise in self-assessing in the indicators: Development of the solving process and use of the ACE, while they had major difficulties in self-assessment for the indicators: Comprehension of the problematic situation and argumentation.
1. Introduction
As defined by Klenowski in 1995 [], self-assessment is “The evaluation or judgment of ‘the worth’ of one’s performance and the identification of one’s strengths and weaknesses with a view to improving one’s learning outcomes”. It is a valuable approach to support learning since students are involved in playing an active role in reviewing their performances [,]. By doing so, they look back to how much they have achieved, and they can set higher goals to improve their abilities [,]. It is therefore an efficient way for effective and permanent learning []. Some studies have highlighted how self-assessment can be effective for promoting problem-solving competences in Mathematics [,,,,]. In fact, problem-solving deeply requires meta-cognitive skills [,], and reflection on one’s work has been pointed out as one of the promotional approaches to teach problem solving [,]. Metacognition and reflection are at the core of self-assessment processes [].
This research arises from the desire for studying the relationship between self-assessment and the development of problem-solving skills in Mathematics, and for finding out if there is a relationship between the improvement of problem-solving skills and the self-assessment accuracy. The special focus of this research is investigating which processes of problem solving pose more difficulties to students in self-assessing their work. In the literature, there are many studies which suggest using self-assessment as a strategy to improve problem-solving skills. However, the relation between the two seems to be under-investigated. Moreover, the students’ accuracy and difficulties in self-assessment in the different processes involved in problem solving are not much explored. This study is an explorative study which attempts to find some preliminary results through quantitative analyses, compared, when needed, with qualitative data.
The study has been carried out within the Digital Math Training (DMT) project [] funded by the Fondazione CRT within the Diderot Project and organized by the University of Turin (Italy). The first edition of this project took place during the academic year 2014/2015, while the eighth edition is ongoing in 2021/2022. Every year, the DMT project engages about 3000 upper secondary school students of Piemonte and Valle d’Aosta (Italy). The aim of the project is developing mathematical and computer science competences through the resolution of real-world mathematical problems using an Advanced Computing Environment (ACE) []. The core of the project is the “online training”, where selected students are challenged with non-standard problems in a Digital Learning Environment (DLE). The DLE is designed to host several activities, including collaborative assessment and self-assessment activities, aimed at improving the participants’ problem-solving skills through technologies. Students are asked to submit the solution to 8 problems during the online training, and for each problem they receive an external assessment by trained tutors. Moreover, they have the chance to self-assess their solution before knowing the tutors’ evaluation. Assessment and self-assessment are performed through a shared rubric which includes five indicators, corresponding to the problem-solving processes: Comprehension of the problematic situation, identification of the solving strategy, development of the solving process, argumentation of the chosen strategy, and appropriate and effective use of the ACE. At the end of the online training, the data about the tutors’ assessment and the students’ self-assessment of the 8 problems were collected, with the aim of comparing them and investigating a possible relationship. The aim is understanding how accurate are the students’ self-evaluations when compared to the tutors’ ones, and if (and how) the accuracy in self-assessment changed among the various indicators. Thus, the research questions that guided this study are the following:
- RQ1: Is there a relation between external (tutors’) assessment and students’ self-assessment?
- RQ2: In which problem-solving phase did students show more difficulties in self-assessing their work?
This paper is structured as follows. In Section 2 (Theoretical framework), the main issues of this study, which are self-assessment, doing, and assessing problem solving with the technologies, are discussed. In Section 3 (Materials and methods), the development of self-assessment within the DMT project is presented and the quantitative methods of analysis are outlined. Section 4 (Results) displays the results obtained through the analyses, in Section 5 (Discussion), the results are discussed in light of the theoretical framework, and in Section 6 (Conclusions), perspectives for research and education are drawn.
2. Theoretical Framework
2.1. Self-Assessment
During the last two decades, there has been a growing body of interest about self-assessment in the educational environment, especially because of evidence that it enhances student acquisition of some academic and social skills [,,,,,]. In addition, several studies revealed that self-assessment is a sine qua non for effective learning [,,]. It is a valuable approach to support learning, when used with educational value []. Self-assessment is mainly referenced as a particular kind of formative assessment [,,]; Black and Wiliam [], in their well-known theory of formative assessment, include self-assessment in the fifth key strategy of formative assessment, which refers to giving students an active role and supporting their self-control of their learning processes. Besides self-assessment, there are a number of other forms of assessment which can contribute to activate a student-centered paradigm in learning. These forms of assessment can be enacted through a variety of activities such as: Master classes, problem solving, gamification activities, or lab sessions []. Varying the range of activities within a course can help collect and return meaningful information about learning achievements, so that grades can acquire a deeper sense [].
Self-assessment involves students themselves as agent of the evaluation process; thus, self-assessment is opposed, or complementary, to the “external” assessment, where the assessment action is performed by a teacher or a tutor, an objective agent, and to peer assessment, where the agents are peers [,].
Self-assessment is particularly relevant to the development of students’ capacity to learn how to learn and to learn autonomously []. In this sense, self-assessment is related to self-regulated learning []. According to Zimmerman, self-regulated learning is “self-generated thoughts, feelings, and actions that are planned and cyclically adapted to the attainment of personal goals” []. Self-assessment involves monitoring and reflection on one’s work, which are metacognitive processes typical of self-regulated learning []. In particular, self-assessment is rooted on three main processes that self-regulating students use to observe and monitor their behavior [,]. Firstly, students produce self-observations, deliberately focusing on specific aspects of their performance which are related to their subjective standards of success. Secondly, students make self-judgments in order to determine how well their general and specific goals were met. Thirdly, they make self-reactions: students study the rate of goal achievement which shows how satisfied they are by the result of their job. By doing so, students’ attention focuses on particular aspects of their performance, and they redefine their standards and fix all previous ones. Self-assessment contributes to self-efficacy and to students’ comprehension, whose main goal is learning and not only performing well [,].
These metacognitive processes are also useful in problem-solving, especially in non-routine problems where the solving strategy is not evident and students need to choose a method, change strategy when it does not work, monitor the solving process, check and interpret the results [,,,]. In Schoenfeld’s framework [], “control” (which refers to the metacognitive processes mentioned above) is one category of necessary behaviors to successfully solve problems. Self-assessment has been using as an alternative form of assessment to improve problem-solving competences of students in Singapore []. Other studies point out that self-assessment skills are positively influenced by performance in mathematical problem solving []. Thus, self-assessment and problem solving seem to be strictly and mutually connected.
Certainly, self-assessment is a complex process. Bloom’s revised taxonomy places evaluation at one of the top positions of the hierarchy of cognitive processes []. Despite the validity of self-assessment being debated, Ross [], through an analysis of the literature, points out that students’ self-evaluations can be reliable especially at secondary school level (age 11–17) and when they have been trained on it, while they seem to be less reliable with young children. In the literature, there are tips concerning how to use self-assessment efficiently and in a beneficial way. From the literature, we collected a set of key points to prepare students to use self-assessment in order to develop self-regulation.
First, the criteria used to assess the students’ work should be defined and shared. It is very important to use an intelligible language for students and to address competences that are familiar to them [,,].
The next step should be teaching students how to apply the criteria, such as, for example, showing them the application model, which increases the credibility of the assessment and student understanding of the rubric. Showing examples of good performance should be helpful to illustrate required standards and in which way they can be satisfied. It is also important for the students to be able to compare their performances with a good one, so that they can understand how to improve their solutions [,].
In addition, giving students feedback on their performances should help them understand the level achieved according to the required standard. Feedback should be focused not only on strengths and weaknesses, but also on offering corrective advice, which leads students to higher order learning goals. In the research literature there are studies about this issue which compare self-assessment with and without feedback: Outcomes suggest that self-regulation with feedback helps students recognize mistakes and correct them because it directs them to a higher level of awareness and comprehension of failures [,].
In conclusion, students need assistance in using self-assessment data in order to improve their performance []. Students’ sophistication in processing data improves with aging []. However, they should be directed towards the self-assessment importance, which supports growth and establishes goals for better learning and skills [,].
Moreover, it has been proved that self-assessment not only increases academic achievement, but also contributes to helping students in recognizing the necessary skills to everyday and working life, thanks to the approach which focuses on identifying standards and goals and on establishing the actions to be carried out in order to reach them [].
2.2. Doing and Assessing Problem Solving with Technologies
The term “problem solving” in Mathematics Education refers to “mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development” []. Problem solving is one of the objectives of Mathematics learning and a key component of mathematical competence []. Mathematical problems should be central in mathematics teaching, to develop understanding and foster students’ learning [,,]. Problems acquire meaningfulness when they are connected to the student’s daily experience [,]. A real-life situation familiar to students can be used as a context to connect school Mathematics and personal experiences []. According to Samo, Bana, and Kartasasmita [], contextual teaching and learning involves connecting school activities with the external world of which students have experience in their everyday life, and this should help transfer knowledge acquired at school in the real situations they can face in working, social, and personal settings. In this way, problem solving can favor interest and motivation towards Mathematics, generating realistic considerations and developing modeling skills []. Moreover, through problem-solving activities, students can develop ways of thinking, persistence, curiosity, and confidence in unfamiliar situations that will turn out to be useful for their life []. To master problem solving, students should be exposed to various types of problems regularly over a prolonged period. The use of non-routine problems and open problems can help students develop creativity, flexibility, and adaptivity in the strategy choice [,].
In [], Pólya lists four principles that should be followed when solving a mathematical problem: Understanding a problem, devising a plan, carrying out the plan and looking back on the work done. These four phases are still shared by most researchers as fundamental during the problem-solving process [,,,,,]. They entail the ability of interpreting mathematically a real-word situation, choosing a solving strategy, developing the solving process, even changing strategy if needed, and reflecting on one’s work and results [].
The use of technologies deeply affects the whole problem-solving practice. On the one side, the nature of problems that can be proposed can change, since tasks can, for example, entail computations hard to perform by hand, dynamic explorations, algorithmic solutions to approximate results, and many other aspects depending on the technology used []. On the other side, the solving process itself can be enhanced by the capabilities of the technology in use and the forms of representations that it allows []. Since mathematical thinking and modelling deeply rely on the forms of representation used to express the mathematical objects [,,], the use of digital technologies can influence the way students approach problems, the strategy choices, and even the results obtained [,,].
The most used technologies for problem solving in education are: Electronic spreadsheets, graphic calculators such as Graphing Calculator 4.0 [], online computational engines such as Wolfram Alpha [], dynamic geometry systems such as Geogebra or Cabri Geometry [], Computer Algebra Systems [], Advanced Computing Environments such as Maple or Mathematica [], but also Digital Learning Environments (DLE) [] or Automatic Assessment Systems [,]. These, and many other, technologies can foster conjecturing, justifying, and generalizing by enabling fast, accurate computations, data collection and analysis, and exploration of different registers of representation []. The increasing availability and enhanced capabilities of electronic devices open new possibilities for communicating and analyzing mathematical thinking []. Freed from the burden of calculation, students can focus their attention on understanding the solving process and the results, exploring, conjecturing, searching, and argumentation. Moreover, a DLE can foster social interactions in problem solving through discussions in a community of practice; the construction of shared meaning and knowledge are encouraged []. In a DLE, automatic assessment systems can enhance problem-solving skills through interactive feedbacks and reflection on one’s mistakes []. Very recently, there are growing experiences of innovative technologies such as artificial intelligence [], gamification [], augmented or virtual reality [,], automated questions generation [], virtual laboratory and simulations [,], enhancing DLEs for problem solving.
The assessment of problem solving is not a trivial issue. According to the current literature, one of the best ways to evaluate students’ performance in problem solving is using rubrics, since they are constituted by a set of standard criteria and a limited scale of quality levels through which a performance can be measured [,]. Rubrics can be described as tables composed of a set of indicators, which refer to the assessment criteria, and levels of performance (usually in a number between 3 and 5). The level of performance for each indicator is described through descriptors, which guide the evaluator in establishing the proper level []. The choice of appropriate indicators and the formulation of clear descriptors is fundamental to make rubrics usable and sharable tools for assessment. The indicators should refer to the various traits of the problem-solving process and competence. The rubrics’ power derives from the fact that the same rubric, if appropriately designed, can be used for different problems on different topics, making their assessment comparable. Moreover, it is also a simple tool to communicate students the assessment criteria, making explicit the indicators on which their work is assessed and the rules to assign scores. They are also powerful as a feedback tool, because the descriptors of the various levels explain students how their performance was under the different points of views expressed through the indicators [,,].
In DLEs, there are tools to assess students’ problem-solving skills through rubrics, which automatize the assignment of levels, the computation of the scores and the communication of the feedback to the students.
3. Materials and Methods
3.1. Self-Assessment within the Digital Math Training Project
DMT’s activities focus on using digital tools as an ACE and a DLE to solve real-life mathematical problems []. An ACE is a computer platform which allows users to carry out numerical and symbolic computations, to produce graphs in 2D or in 3D, to insert interactive components which automatize computations and display graphs by using charts, formulas, sliders, text areas, and results of various kinds. It is also possible to compute procedures by using a basic programming language and write comments on the worksheet itself []. Some solving examples are showed in Figure 1 and Figure 2. For the DMT project, we chose Maple ACE since, compared with other ACEs, it has more functions for didactics and, in Italy, it is largely employed in didactic projects in secondary schools and universities [,].
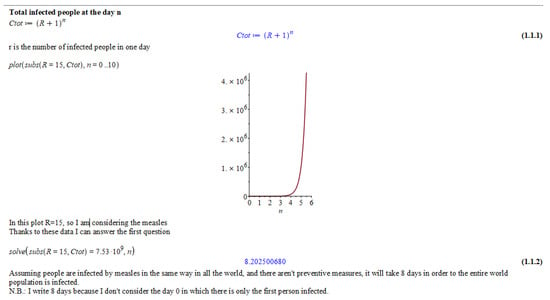
Figure 1.
Example of a student’s solution to a problem of the online training within the DMT project.
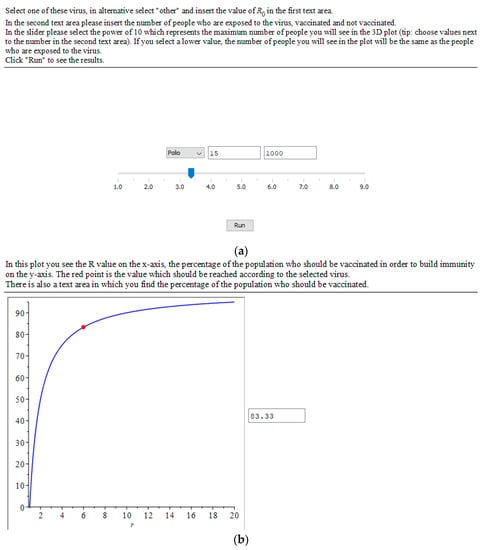
Figure 2.
(a,b) show an example of interactive components that a student realized in order to solve a problem proposed by the online training within the DMT project.
In the DMT project, each class joins an initial meeting during which two tutors present the project and introduce mathematical problem solving using the Maple ACE to the students. In each class which joins the initial meeting, five of the most motivated students are selected and enrolled in a Moodle platform. In the DLE, there are three courses dedicated to the three school grades (10, 11, and 12); students can access the course corresponding to their grade.
Every 10 days, from December to March, a new real-life mathematical problem is published, and students are asked to solve it by using their mathematical skills which they should have learned in class. The problems proposed by the online training are 8. Within 10 days, students are asked to upload the files with their solutions on the DLE. The solutions will be analyzed and assessed by tutors using the DLE. Meanwhile, synchronous and asynchronous tools for tutoring and discussion are activated within the DLE:
- A weekly synchronous online tutoring in web-conference, conducted by a tutor and focused on how to use the ACE to solve the problems;
- A discussion forum monitored by tutors in which students can interrelate with the other participants and discuss their solving strategies;
- A questionnaire which guides students to the self-assessment of the submitted problems according to the parameters chosen for grading the problems [].
Moreover, students earn scores when they complete the online activities such as by submitting solution to problems, by posting pertinent questions in the forum, by answering to a question in the forum, by joining tutoring activities and by filling the self-assessment questionnaire []. These scores are called “Digital Math Coins” (DMC) and are taken into account in the evaluation of a leaderboard, which allows students with top scores to move towards an advanced training which lasts one month and leads students to join the final race. At the end of the activities, the top-ranking students will be rewarded. We point out that the project’s activities are not mandatory for students, and that they are extra-curricular, so that each student could choose the amount of time to dedicate to the project and which activities to engage with.
The mathematical problems are always contextualized in real life and have a growing difficulty according to the confidence in solving problems using the ACE developed by students during the online training. All of them are aligned with the National Guidelines set forth by the Italian Ministry of Education. They are non-routine problems open to multiple approaches and conceived to be solved through an ACE. At the beginning of the online training, participants are told that problems can allow for multiple solutions and that original ones are appreciated. Each problem usually has 3 or 4 tasks: The first ones guide students to exploring and mathematical modeling the purposed situation; meanwhile, the last one requires a generalization of the problematic situation by using plots or interactive components. In Appendix A, the text of the first and the last problem of the online training for grade 11 students are reported, in order to understand the growing level of difficulty. Moreover, a brief description of the other 6 problems included in the online training for 11th grade is provided.
The problems’ solutions worked out by the students are assessed by tutors and self-assessed by students according to the same rubric designed to evaluate the competences in problem-solving while using an ACE. The rubric is an adaptation of the one proposed by the Italian Ministry of Education to assess the national written exam in Mathematics at the end of Scientific Lyceum, developed by experts in pedagogy and assessment. The rubric has 5 indicators, each of which can be graded with a level from 1 to 4. The first four indicators have been drawn from Polya’s model and refer to the four phases of problem solving; they are the same included in the ministerial rubric. The project’s adaptation mainly involves the fifth indicator, and entails the use of the ACE, which we chose to separate from the other indicators to have, and to return to students, precise information about how the ACE was used to solve the problem. Since the objective of the project is developing problem solving with technologies, it has been considered appropriate to evaluate the improvements also in the use of the ACE in relation to the problem to solve. The five indicators are the following:
- Comprehension: Analyze the problematic situation, represent, and interpret the data and then turn them into mathematical language;
- Identification of a solving strategy: Employ solving strategies by modeling the problem and by using the most suitable strategy;
- Development of the solving process: Solve the problematic situation consistently, completely, and correctly by applying mathematical rules and by performing the necessary calculations;
- Argumentation: Explain and comment on the chosen strategy, the key steps of the building process and the consistency of the results;
- Use of an ACE: Use the ACE commands appropriately and effectively in order to solve the problem.
The whole rubric is shown in Appendix B. Before beginning using it as an evaluation instrument in the DMT project in 2014, it underwent a validation process: 4 senior researchers in Mathematics Education applied it to assess samples of students’ solutions of problems and their evaluations were compared, showing reliable results. It has been shared with students through the DLE in order to allow them to self-assess their solutions consciously and consistently. It has been implemented in the Moodle “Assignment” activity so that tutors can use it directly on the DLE when grading the participants’ work.
Students use the same rubric to self-assess their work. In this case, it has been implemented though a questionnaire; students have to answer 5 questions, listed below, one for each indicator of the rubric, by choosing a level from 1 to 4. The questionnaire modality has been chosen to facilitate participants in using the rubric. The students’ answers indicate the self-assessed level for each indicator. They are told to make reference to the shared rubric table to choose the most suitable level. Moreover, an additional question asked for their difficulties in solving the problem. The questions are the following:
- To what level do you think you understood—and showed that you understood—the problematic situation?
- To what level do you think you identified and described the solution strategy?
- To what level do you think you developed the chosen solving process?
- To what level did you discuss your steps clearly and in detail?
- To what level do you think you effectively used Maple?
- Did you find some difficulties in solving this problem?
The questionnaires were implemented online through a “Questionnaire” activity. Students were asked to fill in the questionnaire after submitting their solution but before knowing the tutors’ assessment. The questionnaire visibility depends on time criteria so that students cannot fill it in after seeing their results. To encourage students to fill in the self-assessment form, they were rewarded with 3 DMCs for each questionnaire.
Before publishing the first problem, at the beginning of the online training, students can find a section called “Get ready for the training!” in which there is a sample problem. The participants can download the file and try to solve the task, then they can self-assess their work by filling in the self-assessment questionnaire. In this section, they can also find a solution proposed by tutors. By doing so, they will not earn DMC, because these activities are conceived to let students practice with the evaluation criteria and understand what a good performance is.
In addition, to allow the students to engage with the required standards, some solutions are published after each problem, when the time for submission has expired: One proposed by tutors and the others selected among the best files created by participants. In this way, the students could engage with several solving approaches.
All the problems submitted by participants are assessed through the rubric. The tutors assigned, for each indicator, a level between 1 and 4, and a score as indicated in the rubric. The total score for a problem ranged from 1 to 100 DMC. In order to ensure reliability of scores, for the first problems, each solution was assessed by two tutors and they were asked to discuss their grades and reach a common decision if they were different. The average difference between the two tutor’s grades was computed; the assessment process shifted to a single tutor for problem when the average differences were below 3% of the total score (it happened at the second problem). The assessment is released with additional personalized feedback elaborated by the tutor who evaluated the solution. This feedback explains the level obtained in each indicator, but it also includes observations about both mistakes and original strategies and tips on how to improve the solution. The students can therefore have feedback about their mistakes and obtain constructive and personalized tips which can be employed in the following problems.
At the end of the training, a questionnaire is submitted to all participants concerning several aspects of the project, including the students’ experiences in problem solving, assessment, and self-assessment. It is mainly composed of 5-points Likert scale items and open questions.
The activities of the online training are conceived to help students develop self-assessment skills, according to the framework based on the literature and presented above. In particular:
- To establish and share the evaluation criteria, an assessment rubric has been created and shared through the DLE;
- To show how to apply the established criteria and clarify what a good performance is, the section “Get ready for the training!” has been designed; moreover, proposed solutions to the problems are published after the submission deadline. To increment the range of solving approaches, besides the tutors’ resolution, also some of the most original participants’ submissions are selected;
- To provide feedback to students, the tutors’ assessment is provided though the rubric, which has explicit descriptors; moreover, detailed and personalized comments and tips are released by tutors together with the evaluation;
- To encourage self-assessment, participants receive an explanation about the importance of filling the self-assessment questionnaire. Moreover, they are rewarded with 3 DMC for each questionnaire filled.
3.2. Participants
Since this is an exploratory study, to answer the research questions, we reduced the sample to the 182 11th grade participants (16 years old) to the online training program in the academic year 2020/2021. In this way, we could refer the results to particular problems (problems are different from grade to grade). The 11th grade was selected because, with respect to the other grades, students were more active both with the forum discussions and with the problems’ submission. In fact, we registered a higher number of submissions and forum discussions in the 11th grade course than the in the other grades. We believe that 10th grade students were less active because they were in a smaller number than the other grades. Moreover, 12th grade students had probably a heavier workload due to the fact that they were towards the end of their school path, and it prevented them from dedicating much effort in the DMT project. Participants are selected students from the classes which joined the initial meeting; they enrolled to the online training on voluntary basis. Thus, they are mainly medium-high achievers, with a strong background in Mathematics.
The tutors who assessed the students’ resolutions were third-year Bachelor’s or Master’s students in Mathematics. In all, ten tutors participated to the study; they were aged between 21 and 26. Before starting the project, they joined a 10-h training course on problem solving with an ACE and assessment of problem-solving competence using rubrics. Four out of the ten tutors had previous experience as tutors in the DMT project.
3.3. Research Method
At the end of the training, we collected the data about the tutors’ assessment and the students’ self-assessment for each problem. For the tutors’ assessment, we considered the level assigned to each indicator (from 1 to 4) and for the self-assessment we considered the level indicated by students to each indicator (from 1 to 4), so that data are comparable. We did not consider the total score out of 100 earned by students in the problems. For each problem, the sample was reduced to the only students who submitted the problem and filled in the self-assessment questionnaire, taking into account that the project’s activities were not mandatory. We checked the reliability of tutors’ assessment and self-assessment grades for the eight problems by computing the Cronbach Alphas. For each problem, we created a table with the level assigned by tutors and that self-assigned for each student and for each of the 5 indicators. We then carried out preliminary analyses.
Firstly, for each student, we calculated the differences between the level assigned by tutors and the self-assigned one. The differences were calculated both in absolute value, to see how far the 2 evaluations were in absolute terms, and by subtracting the self-assessment from the tutor’s assessment, to investigate if students tended to overestimate or underestimate their performance.
For each student, we computed the general level for each problem, computing the mean of the tutors’ grades in the 5 indicators, and the average value of the self-assessment levels in the 5 indicators. Then, for each problem, we calculated the average values for all the students of the levels assigned by tutors indicator by indicator, and then, the means of the general levels and those of the differences.
In conclusion, for each problem, we plotted the obtained data to compare the average level and the average difference in absolute value for each indicator with the general average level and difference in absolute value. By doing so, we were able to analyze the general trend of the development of the problem-solving skills and of the use of self-assessment, but also study the trend of each indicator.
After these steps, we carried out an advanced analysis. In particular, we employed correlation tests with the aim of checking whether a relationship between assessment and self-assessment exists. We then calculated the Pearson correlation coefficient, which expresses the intensity of a linear relation between the two variables considered. The Pearson coefficient has been calculated between the average level assigned by tutors and that self-assessed by students, firstly, for the general level and then, for each indicator for each of the 8 problems.
Moreover, we selected some of the final questionnaire’s questions because of their utility in the interest of this research. These selected questions were about the difficulties that students founded by solving the problems and by trying to satisfy the standard required by the 5 indicators which is contained in the assessment rubric:
“In solving the problems, how much did the following aspects hinder you? Comprehension of the problematic situation; Identification of a solving strategy; Completion of the solving process; Argumentation; Generalization by using interactive components; Use of Maple.”
For each item, they could select a value on a Likert scale from 1 to 5, in which 1 is “No difficulties” and 5 is “Lot of difficulties”.
We then collected the answers with the aim of understanding if a relationship between the reported difficulty and the accuracy of the self-assessment exists. By doing so, we employed the Analysis of Variance (ANOVA). We selected and grouped students in accordance with their answers. For each group, we calculated the mean on the 8 problems of the absolute difference of the indicator which is linked to the question in the questionnaire. In this way, we realized the ANOVA table with the respective statistics.
All the analyses were conducted by using the software Excel and the statistical software SPSS (Statistical Package for Social Science).
4. Results
The Cronbach Alphas computed for the tutors’ assessment and the self-assessment of each problem were satisfactory (for the tutors’ assessment they were, respectively, for problems 1 to 8: 0.88, 0.86, 0.95, 0.95, 0.96, 0.92, 0.99, 0.93; for the students’ self-assessment, they were, respectively, for problem 1 to 8: 0.69, 0.74, 0.91, 0.92, 0.91, 0.89, 0.95, 0.90). Thus, the assessment data considered are reliable.
The preliminary analyses revealed that students basically underestimated their performances in all the indicators and in all the problems: The means of the non-absolute differences between the tutors’ grades and self-assessment values are positive, as shown in Table 1.

Table 1.
This table contains the means of the non-absolute difference between the tutors’ assessment and the self-assessment for each indicator for the 8 problems.
This is quite a surprising result, since other studies, such as [,,], report the students’ tendency to overestimate themselves in self-assessment. Table 2 also shows the number of students who, for each problem, both submitted their solution receiving the tutors’ assessment and submitted the self-assessment questionnaire. These are the numbers of students on which we could compute the following statistics as well. One can notice that the numbers decrease after the first half of the training: This is probably due to the increasing in the problems’ difficulty and to the fact that the projects’ activities were not mandatory and extra-curricular, so that participants could have difficulties in carrying them out after the other school duties.

Table 2.
This table contains the Pearson coefficients and p-values which are calculated comparing the tutors’ grades and the students’ self-assessment (average values over the 5 indicators).
By analyzing the general average level reached by the students, according to the Pearson coefficient it turns out that tutor’s assessment and self-assessment are significantly correlated. In particular, the correlation starts to become stronger from the third problem: After that, the Pearson coefficients are all values greater than 0.5, and the maximum is achieved by the seventh problem (0.735, p-value < 0.001), as shown in Table 2. This can indicate that the first two problems served as a training to self-assessment.
We will now analyze the obtained results for each indicator.
4.1. Comprehension of the Problematic Situation
In all the 8 problems, the tutor’s grades in the indicator “Comprehension of the problematic situation” are, on average, greater than the general average of the tutors’ grades in the 5 indicators for those problems, as shown in Figure 3a. Here and in the following graphs, the bar “Comprehension” stands for the average value of the tutors’ grades in this indicator for each of the 8 problems, while the bar “General” refers to the general level obtained by students for those problems, computed with the mean of the tutors’ grades in the 5 indicators. This means that, for students, it was one of the easiest steps of the problem-solving process.
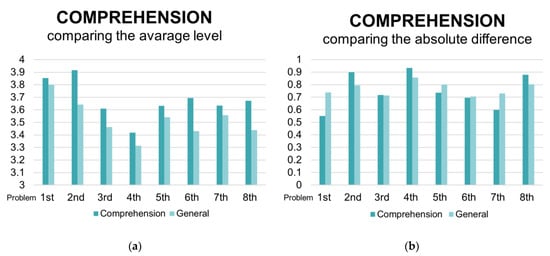
Figure 3.
(a) Trend of the average level of the indicator “Comprehension of the problematic situation” by comparing that with the general trend, computed over the 5 indicators.; (b) trend of the average absolute difference between tutors’ and students’ assessment in the indicator “Comprehension of the problematic situation” by comparing that with the general trend of the absolute difference, computed over the 5 indicators.
The trend of the average absolute difference between tutors’ assessment and self-assessment for this indicator is similar to that of the average one (computed over the 5 indicators), as shown in Figure 3b. In particular, it is lower than the general one, despite of the 2nd, the 4th, and the 8th problem. It seems that, except for these problems, self-assessment in this indicator is closer to tutors’ assessment than other indicators. This appears also in the Pearson coefficients calculated when correlating the average level assigned by tutor and that self-assigned for this indicator, as presented in Table 3. The Pearson coefficients for the 2nd, the 4th, and the 8th problems are respectively: 0.074 (p-value 0.422), 0.379 (p-value < 0.001), 0.228 (p-value 0.086). It turns out that the 2nd and the 8th problems don’t show a significative correlation between assessment and self-assessment for the indicator “Comprehension of the problematic situation”. To understand the reason, a qualitative analysis on the data offered by the DLE was conducted.

Table 3.
This table contains the Pearson coefficients and p-values calculated between the average level assigned by tutors and the self-assigned ones for the indicator “Comprehension of the problematic situation”.
In the 2nd problem, students found several interpretations of the text and discussed them in the forum, without reaching a common solution. From their discussion in the forum, it is possible to perceive their confusion, probably because they are used to traditional textbooks problems which have only one possible solving approach and correct solution. By checking the question of self-assessment questionnaire involving the difficulties faced in solving the problem, 38% of the students explicitly mentioned difficulties in the interpretation of the text. In the following lines, some of the answers are listed:
“I found it difficult to select only one strategy because the text could be interpreted differently”;“The text wasn’t so clear”;“I found it more difficult to understand the text than to use Maple. That is why I tried to underline the points in the text from which the different interpretations originated and then I employed my strategy. Furthermore, I found the forum useful because other participants had my doubts and reading the answers to their posts helped me.”
The issue of this problem presented a situation which could be interpretated in two different ways. Tutors considered both of them valid, but students, after checking the forum, probably thought that just one of the two was the correct one. This uncertainty reflected in their self-assessment grades, which were different from the tutors’ evaluations.
Meanwhile, the 8th problem was very complex. The trouble in understanding how to model the proposed mathematical situation could account for the lack of understanding. In particular, on the discussion forum, students started five discussions about the first task and one about the general interpretation of the problem.
Then the final questionnaire answers to the question “How much did the comprehension of the problematic situation hinder your problem-solving abilities?” was considered. The students’ answers to this question reflect their difficulties in carrying out this process (1 means that they had low difficulties in comprehending the situation and 5 that they had many difficulties). An ANOVA test was carried out, considering these answers as independent variable and the mean of the absolute difference between the tutors’ and self-assessment grades in this indicator over the 8 problems as dependent variable. The goal is understanding if higher difficulties in this process lead to higher discrepancies between external assessment and self-assessment.
Table 4 show the means of the absolute differences between tutors’ and self-assessment grades for each selected answer.

Table 4.
This table contains the mean of the absolute difference between the tutors’ and self-assessment grades in this indicator over the 8 problems, computed for each value of Likert scale selected by students to the question “How much did the comprehension of the problematic situation hinder your problem-solving abilities?”.
From these results, it seems that the discrepancy between assessment and self-assessment for the 8 problems in the comprehension of the problematic situation increases by increasing the students’ declared difficulty in this process. However, this relation is not statistically significant (p-value 0.448).
In conclusion, it seems that students found it relatively easy to understand the problematic situation and to self-assess in this indicator, except for the problems in which the problematic situation was very complex or allowed different interpretations.
4.2. Identification of a Solving Strategy
The trend of the indicator Identification of a solving strategy is close to that of the general level for all the 8 problems for both the average level (tutors’ evaluations) and the average absolute difference between tutors’ and students’ assessment, as shown in Figure 4a,b. So, it seems that self-assessing in this indicator was of medium difficulty.
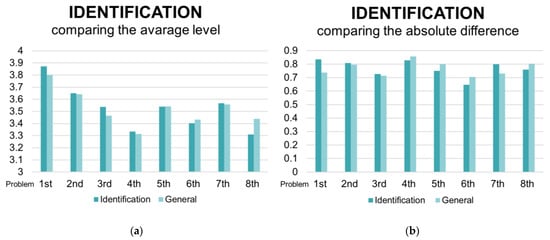
Figure 4.
Graph which represents the trend of the indicator “Identification of a solving strategy” by comparing that with the general trend, computed over the 5 indicators. (a) The trend of the average level; (b) The trend of the average absolute difference between tutors’ and students’ assessment.
According to the analyses on the Pearson coefficient, it turns out that the correlation between assessment and self-assessment in this process is particularly strong from the 3rd problem, as shown from data in Table 5. The 2nd problem has the minimum value (0.200, p-value 0.029), which probably reflects the students’ difficulties in the interpretation of the text explained previously. Again, it seems that the first two problems acted as a gym for self-assessment.

Table 5.
This table contains the Pearson coefficients and p-values calculated between the average level assigned by tutors and that self-assigned for the indicator “Identification of a solving strategy”.
By exploring the final questionnaire answers about the question “How much did the identification of a strategy hinder your problem-solving abilities?”, it turns out that the discrepancy between external assessment and self-assessment for the 8 problems in this indicator increases by increasing the selected answer, as shown in Table 6. This relation is statistically significant (p-value 0.016). This means that, the easier it was for students to identify a solving strategy, the more accurate was their self-assessment of their work under this perspective.

Table 6.
This table contains the mean of the absolute difference between the tutors’ and self-assessment grades in this indicator over the 8 problems, computed for each value of Likert scale selected by students to the question “How much did the identification of a strategy hinder your problem-solving abilities?”.
4.3. Development of the Solving Process
The average level (assigned by tutors) of the indicator “Development of the solving process” has values between 3.3 and 3.6 out of 4 starting from the 2nd problem, as shown in Figure 5a. Therefore, after the first problems, which were simpler than the following, students were more challenged by the development of the solving process, and they set their level. The 1st and the 7th problems show the highest average levels. The 7th problem has also the highest correlation coefficient between self-assessment and assessment (0.740, p-value < 0.001), as shown in Table 7. The high level in this indicator in the first problem can be related to its simplicity with respect to the following one: It was rather similar to other textbook problems that students could have experience of. The results in the 7th problem could indicate how, after more than two months of online training, students could have gained confidence with problem solving and self-assessment. Results decrease in the last problem which, as pointed out before, was particularly complex to understand and this could have undermined the students’ performance and self-assessment in all the indicators. The absolute differences between tutors’ and students’ assessments in this indicator are lower than the average values (computed over the 5 indicators), as shown in Figure 5b. This means that students found self-assessment in this indicator relatively easy.

Figure 5.
Graph which represents the trend of the indicator “Development of the solving process” by comparing that with the general trend, computed over the 5 indicators. (a) The trend of the average level; (b) The trend of the average absolute difference between tutors’ and students’ assessment.

Table 7.
This table contains the Pearson coefficients and p-values which are calculated between the average level assigned by tutor and that self-assigned for the indicator “Development of the solving process”.
By considering the final questionnaire answers to the question “How much did the development of the solving process hinder your problem-solving abilities?”, no significant relation can be found between an increasing declared difficulty in this process and the average absolute difference between assessment and self-assessment.
4.4. Argumentation
The average level in the indicator “Argumentation” is generally lower than the general level for the problems, as shown in Figure 6a. In the first problem, the gap is particularly evident: We can argue that students are generally not used to commenting all the steps and results in their daily school activities, so they were penalized in this indicator. The average absolute difference between tutors’ and students’ evaluations in this indicator is lower in the first three problems and it grows on the next ones, as shown in Figure 6b. Interestingly, in this indicator the students self-assessed more accurately in the first problems which are mathematically easier and more similar to the traditional problems usually encountered in class, while the difference increases when facing more complex and non-standard ones.
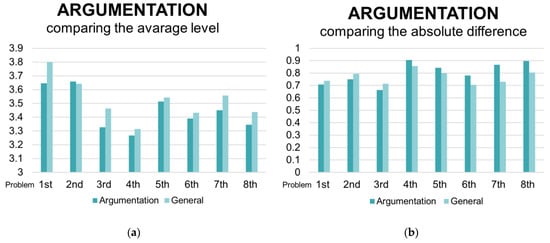
Figure 6.
Graph which represents the trend of the indicator “Argumentation” by comparing that with the general trend, computed over the 5 indicators. (a) The trend of the average level; (b) The trend of the average absolute difference between tutors’ and students’ assessment.
“Argumentation” is the indicator with the lowest correlation coefficients in the 8 problems, which are given in Table 8: The minimum value is in the 2nd problem, and it is 0.182 (p-value 0.046); the maximum is in the 7th problem, and it is 0.576 (p-value < 0.001). These results could again reflect the difficulties in understanding the problematic situation for the second problem and the familiarity with self-assessment developed toward the end of the online training. It seems that self-assessing the argumentation process is not so easy for students, especially in problems where they had difficulties in interpreting the text.

Table 8.
This table contains the Pearson coefficients and p-values calculated between the average level assigned by tutors and that self-assigned for the indicator “Argumentation”.
By exploring the final questionnaire answers about the question “How much did the argumentation hinder your problem-solving abilities?”, it turns out that there is a relation between the increasing answer and the discrepancy between external and self-assessment, as shown in Table 9. This relation is statistically significant (p-value 0.010).

Table 9.
This table contains the mean of the absolute difference between the tutors’ and self-assessment grades in this indicator over the 8 problems, computed for each value of Likert scale selected by students in their answers to the question “How much did the argumentation hinder your problem-solving abilities?”.
4.5. Use of the ACE
For the indicator “Use of the ACE”, the trend of the average level assigned by tutors decreases during the first four problems and then increases, as shown in Figure 7a. For the first four problems, the decrease can be explained with an increasing of required standards. In particular, the first two problems were generally more basic, and the programming of interactive components was not required: the ACE was employed mainly for computations and graphs. The first four problems were conceived to help students get acquainted with the use of the ACE which was unknown for most of them before taking part in DMT project. In particular, 50% of the students, in the self-assessment questionnaire, pointed out their difficulties in programming the interactive components in the generalization of the 4th problem. For example, some of them commented as follows by filling the self-assessment questionnaire:
“I found it difficult to solve the third task. I had problems in programming the interactive components”;“I found it difficult to develop the interactive components by plotting the moving average”;“I found it difficult to understand some tasks and so I did the best I could, even though I’m not so sure I satisfied the requests”.
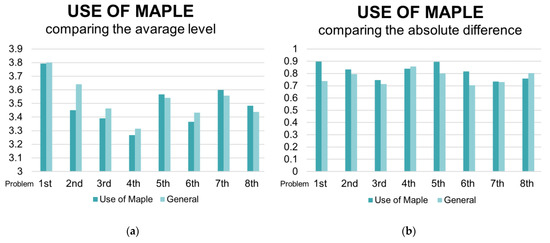
Figure 7.
Graph which represents the trend of the indicator “Use of the ACE” by comparing that with the general trend, computed over the 5 indicators. (a) The trend of the average level; (b) The trend of the average absolute difference between tutors’ and students’ assessment.
On the other hand, the last problems required an advanced use of the ACE, but this was accompanied by an increasing of the students’ skills, who developed mastery in the use of the ACE by solving problems and by joining the tutoring activities during the project, so an increase in their level in this indicator can be appreciated.
The average absolute difference of the indicator “Use of the ACE” decreases onto the last problem, as shown in Figure 7b. Thus, achieving competence in the use of the ACE helped students improve self-assessment in this indicator.
“Use of the ACE” is the indicator with the highest Pearson coefficients, shown in Table 10: the minimum is 0.322 (p-value < 0.001) in the 2nd problem, the maximum is 0.637 (p-value < 0.001) in the 7th one, reproposing the same trend seen in the previous indicators.

Table 10.
This table contains the Pearson coefficients and p-values calculated between the average level assigned by tutors and that self-assigned for the indicator “Use of the ACE”.
By checking the final questionnaire answers about the question “How much did the use of the ACE hinder your problem-solving abilities?”, it turns out that there is no relation between the increasing declared difficulty in this process and the average absolute difference between assessment and self-assessment.
5. Discussion
This research has been carried out within the DMT project and based on the following research questions: (RQ1) Is there a relation between external (tutors’) assessment and students’ self-assessment? (RQ2) In which problem-solving phase did students show more difficulties in self-assessing their work?
The study has been conducted by cross-checking tutors’ assessment and students’ self-assessment to problem solving activities using an ACE. The assessments are given through a rubric with 5 indicators, referred to the Polya’s framework of problem solving, adding the use of technologies. They are the following: comprehension of the problematic situation, identification of the solving strategy, development of the solving process, argumentation of the chosen strategy, and appropriate and effective use of the ACE. The analyses have been conducted both globally and indicator-by-indicator, in order to draw information about how the trend in the students’ self-assessment change among the indicators. Students were trained to self-assessment through a set of activities implemented in a DLE, following literature-based tips and suggestions.
The analyses carried out allow us to positively answer the (RQ1): In fact, there is a positive correlation between students’ self-assessment and tutors’ assessments. The correlation coefficients calculated get stronger beginning with the 3rd problem. This shows that the students self-assessed more and more properly and accurately as the online training proceeded. This shows that the digital activities proposed within the online training were effective to train participants to self-assess their work. The first two problems were conceived as a gym to practice with problem solving with an ACE and with the assessment process within the project, as well as with the self-assessment process. By receiving feedback and self-judging their work, they become more and more confident with the assessment criteria, improved their problem-solving competence and consequently improved their self-assessment skills. This result is in line with other studies which show that, when for upper-secondary students who received training in self-assessment, and are generally medium-high achievers, the accuracy in self-assessment is high [,]. On the other hand, the tendency to underestimate one’s performance that emerged in this study does not find confirmation in the literature, where other studies, such as [,,], report the opposite tendency. This could be due to the high difficulty of the problems, which could have led students not to overreach themselves by saying that they solved the problems fully correctly. Moreover, through the forum discussions among participants, students were exposed to different solving strategies and interpretations of the problems: they could have raised doubts about their own resolutions, and this could have been reflected in their self-assessment.
Moving on to the second research question, we can affirm that the indicators with the lower correlation coefficients between external assessment and self-assessment are “Comprehension of the problematic situation” and “Argumentation”, which refer to the “comprehension” and “reflection” phases in Polya’s framework. So, it turns out that if students found it difficult to understand the task, then they found it trickier to comment and illustrate clearly and completely the steps they did, so that they were in trouble by self-assessing appropriately. This again is in line with the literature, where studies show that performance positively influences self-assessment []. If for the comprehension indicator results show that generally students found it easy to accomplish and self-assess this step, except for particular problems, the argumentation seems to be a weak point in all the problems, both for performance and self-assessment. These results are a mirror of the usual teaching practices. On one side, it is still not common to find examples of complex problems, open to multiple solutions, on Mathematics textbooks and teaching materials [,], so students were confused when facing a problem which could admit several interpretations, and generally had problems in interpreting the text of complex problems and translating it into mathematical models. On the other side, often classroom instruction does not pose enough attention to argumentation processes which go beyond a series of calculations, or does not offer students an active role in explaining processes and results []. Some strategies to improve the argumentation capacities of students can be the production of examples as a starting point to build proofs [], or the use of dynamic explorations to gain a direct experience of the mathematical objects under study and to support conjecturing [].
The indicators which show the highest correlation coefficients are “Development of the solving process and Use of the ACE”. By exploring the final questionnaire, it turns out that, respectively, 92 and 91 students (out of a total of 120 filled questionnaire) answered the questions about the difficulty for these two indicators by setting out a value between 1 and 3 in the Likert scale (in which 1 = “Any difficulties” and 3 = ”Few difficulties”). This reveals that most of the participants found it simple to develop the solving process and use the ACE, so that they self-assessed more accurately in these indicators.
The results obtained in this study repeatedly highlighted that the students’ ability to self-assess in the various indicators was stabilized after the first problems and grew towards the end of the online training. The first problems served as a training to acquire familiarity with self-assessment. On one side, this can be due to the low exposure of students to self-assessment, and in general to different forms of assessment than the classic external evaluation in the daily teaching practices []. On the other hand, it seems that the design of the activities in the online training according to the suggestions found in the literature (defining and sharing assessment criteria, teaching students how to apply the criteria, giving feedback and encouraging self-assessment) [,,,,] was effective to train students to self-assess their performance.
It is interesting to note that at the end of the project performances in the indicator “Argumentation” (according to the tutors’ judgments) are the lowest ones, meanwhile “Use of the ACE” is the second indicator with the highest levels. It shows that the indicators in which students self-assess more accurately, i.e., those having the strongest correlation coefficients, are also those in which there are the higher scores at the end of the project. Again, it shows the correlation between performance and accuracy in self-assessment [].
6. Conclusions
Summarizing the results obtained in this study, a strong correlation between external assessment and self-assessment of problem-solving activities was found, analyzing results achieved by 11th grade students. Moreover, the highest discrepancies between self-assessment and external assessment were found in the understanding and argumentation processes of problem-solving activities, while in developing the solving strategy and using the technologies, students were more accurate in self-assessment.
This study has several limitations, first of all, the limited numbers of participants involved and their medium-high level of performance in Mathematics. These limitations hinder the generalization of the results. However, it was an explorative study and the restricted sample allowed to relate the obtained statistics to particular problem tasks and search for confirmations in open answers and forum discussions. Since there are no other studies which investigate self-assessment in the various processes of problem solving, the results obtained here might be useful to other researchers in this field. It would be interesting to expand the research involving also grade 10 and 12 and seeing if results are confirmed also when considering different problems. Moreover, this study mainly focuses on the comparison between students’ and tutors’ assessment. Future research could explore this theme by investigating how students self-assess their work. It would be interesting to enquire if students conduct retrospective assessments, i.e., if they rely on how they approach the solving process and their efforts [], or alternatively, if they found it more helpful to engage with their peers or with the proposed activities []. Moreover, the frequency of self-assessment could be added as a variable to this study, in order to investigate if it may influence the quality of the performance and the accuracy of self-assessment itself.
The online training of the DMT project involves only selected students from several schools in extracurricular activities, while, for the development of problem solving and self-assessment skills of all the students, it is necessary to share these good practices with the teachers, so they can be part of everyday teaching practices. To this purpose, all the project’s problems are sent to the teachers of all the classes participating to the project, so that they can use them with their whole classes for their lessons. Teachers usually find it a precious support to propose different problems from those they can commonly find on textbooks. Moreover, the project includes a teacher training course, in which teachers are shown how to use the problems in their didactic activities and how to use the ACE to solve the problems. It would be interesting to include also assessment and self-assessment issues in the training course, so that teachers can learn how to use alternative ways of assessment to improve problem-solving skills in their classes.
Author Contributions
Conceptualization, A.B., G.B. and M.M.; methodology, A.B., G.B. and M.M.; formal analysis, A.B., G.B. and M.M.; investigation A.B., G.B. and M.M.; data curation, A.B., G.B. and M.M.; writing—original draft preparation, A.B., G.B. and M.M.; writing—review and editing, A.B., G.B. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funds from the Fondazione CRT through the “Diderot Project”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy reasons.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Here the text of the first and last problem of the online training for 11th grade students are reported. Moreover, a brief description of the other problems included in the online training for 11th grade students is provided.
- Problem 1—Gasoline
Marco’s car’s consumption is 5.4 L of gasoline per 100 km on average.
- How many km can he travel with a liter of gasoline?
Marco stops for gas and the gasoline price is EUR 1.348 per liter. He traveled 610 km from the last full tank of gas.
- 2.
- How much will the full tank of gas cost this once?
After refueling, Marco goes to some relatives who live far from him. The distance Marco has to travel is 1043 km.
He stops for gas twice.
The first time he spends EUR 18 and the gasoline price is EUR 1.291 per liter.
The second time he spends EUR 37 and the gasoline price is EUR 1.412 per liter.
He arrives with three quarters of a tank.
- 3.
- How many liters does Marco’s tank contain, if the gasoline consumption remained the same throughout the journey?
- 4.
- Assuming that the refueling stops were 305th km and at 940th km, plot the value pointed by the tank indicator of Marco’s car in terms of the crossed km.
- Problem 8—Antibiotic therapy
Returning from a trip, Marco doesn’t feel well. He decides to consult his doctor who recommends a more thorough examination. These tests reveal the presence of 2 harmful bacteria: There are 100 units of bacteria of type A, and 50 units of bacteria of type B. A study established that both type of bacteria, which were considered independently, increase 5% per day. The study also showed how they are in competition which each other, i.e., one decreases proportionally to the concentration of the other, in addition to the natural increase previously explained: they both decrease by 0.1% of the mathematical product of the quantity per day. Fortunately, there is an antibiotic which reduces both bacterial growths by 10 units per day.
- If the therapy starts the first day after the medical prescription and is done properly, how many days would it take to remove both bacteria from the organism? Discuss it by using graphical representations.
- Supposing that Marco begins to feel better when only one of the two bacteria has disappeared, and he decides to stop the treatment. What happens to type A bacteria in the 3 following weeks? Does it grow more or less than it would grow if the therapy hadn’t started? Discuss it by using graphical representations.
- Create a system of interactive components which estimates how many days it would take to remove one of the 2 types of bacteria by inserting the initial concentration, the natural increment of the 2 types of bacteria, the competitive decrease (assuming they are the same), the antibiotic sensitivity (in term of the absolute decrease of concentrations). Be careful: It isn’t required to display how many days it would take to remove both bacteria.
- The other problems
Problem 2 deals with bank interests and financial education. In particular, the problem investigates what happens when the frequency of applying compound interest increases to infinity. Students have to draw a formula for the compound interest, introduce a variable for the frequency of applying interest, and understand what happens when the variable goes to infinity.
Problem 3 deals with the optimization of the measures of boxes for deliveries. Students are asked to find the optimal measures for the box sizes of a given volume giving some logistic constraints. The problem asks also for a generalization of the resolution: students have to create an interactive worksheet which, giving as input the constraints, automatically computes the optimal sizes for the box.
Problem 4 concerns the computation of the simple moving average of infected cases during an epidemic. The problem supposes that the number of daily infected cases varies according to a particular function and, after introducing the concept of moving average, asks students to compute it in particular situations. A request of generalization of the resolution completes the task.
Problem 5 is focused on the propagation of seismic waves during an earthquake. Given the position of some seismographs and the times in which they firstly registered longitudinal and transversal waves, the problem asks to find the position of the hypocenter and to represent the event graphically.
Problem 6 concerns the computation of the herd immunity thanks to vaccines. In particular, it asks to study the difference of growth of infected cases in a group with and without vaccinated people, and to compute how many people should be vaccinated to obtain the herd immunity. The problem asks to apply the solution to several illnesses with different rates of infection.
Problem 7 shows data about the Italian gross domestic product and asks students to verify which of four linear models provided better describes the trend, using the definition of the least squares regression lines introduced in the problem. As a generalization, the problem asks to create an interactive worksheet which returns the expected gross domestic product on the base of the chosen model.
Appendix B
In Table A1, the whole rubric used to assess and self-assess students’ solutions is reported.

Table A1.
The rubric developed to assess problem solving competence in the DMT project.
Table A1.
The rubric developed to assess problem solving competence in the DMT project.
| Indicators | Level (Score) | Description |
|---|---|---|
| Comprehension Analyze the problematic situation, represent and interpretate the data and then turn them in mathematical language | L1 (0–3) | You don’t understand the tasks, or you do incorrectly or partially, so that you fail to recognize key points and information, or you recognize some of them, but you interpret them incorrectly. You incorrectly link information, and you use mathematical codes insufficiently and/or with big mistakes. |
| L2 (4–8) | You analyze and you understand the tasks only partially, so that you select just some key points and essential information or, if you identify all of them, you make mistakes by interpreting some of them, by linking topics and/or by using mathematical codes. | |
| L3 (9–13) | You properly analyze the problematic situation by identifying and correctly interpreting the key points, the information and the links between them by recognizing and skipping distractors. You properly use the mathematical codes by employing plots and symbols, but there are some inaccuracies and/or mistakes. | |
| L4 (14–18) | You analyze and interpret the key points, the essential information and the links between them completely and in a relevant way. You are able to skip distractors and use mathematical codes by employing plots and symbols with mastery and accuracy. Even if there are some inaccuracies, these don’t influence the complex comprehension of the problematic situation. | |
| Identification of solving strategy Employ solving strategies by modeling the problem and by using the most suitable strategy | L1 (0–4) | You don’t identify operating strategies, or you identify them improperly. You aren’t able to identify relevant standard model. There isn’t any creative effort to find the solving process. You don’t establish the appropriate formal instruments. |
| L2 (5–10) | You identify operating strategies that are not very effective and sometimes you employ them not very consistently. You use known models with some difficulties. You show little creativity in setting the operating steps. You establish the appropriate formal instruments with difficulties and by doing some mistakes. | |
| L3 (11-16) | You identify operating strategies, even if they aren’t the most appropriate and efficient. You show your knowledge about standard processes and models which you learned in class, but sometimes you don’t employ them correctly. You use some original strategies. You employ the appropriate formal instruments, even though with some uncertainties. | |
| L4 (17–21) | You employ logical links clearly and with mastery. You efficiently identify the correct operating strategies. You employ known models in the best way, and you also propose some new ones. You show creativity and authenticity in employing operating steps. You carefully and accurately identify the appropriate formal instruments. | |
| Development of the solving process Solve the problematic situation consistently, completely and correctly by applying mathematical rules and by performing the necessary calculations | L1 (0–4) | You don’t implement the chosen strategies, or you implement them incorrectly. You don’t develop the solving process, or you employ it incompletely and/or incorrectly. You aren’t able to use procedures and/or theorems or you employ them incorrectly and/or with several mistakes in calculating. The solution isn’t consistent with the problem’s context. |
| L2 (5–10) | You employ the chosen strategies partially and not always properly. You develop the solving process incompletely. You aren’t always able to use procedures and/or theorems or you employ them partially correctly and/or with several mistakes in calculating. The solution is partially consistent with the problem’s context. | |
| L3 (11–16) | You employ the chosen strategy even though with some inaccuracy. You develop the solving process almost completely. You are able to use procedures and/or theorems or rules and you employ them correctly and properly. You make a few mistakes in calculating. The solution is generally consistent with the problem’s context. | |
| L4 (17–21) | You correctly employ the chosen strategy by using models and/or charts and/or symbols. You develop the solving process analytically, completely, clearly and correctly. You employ procedures and/or theorems or rules correctly and properly, with ability and originality. The solution is consistent with the problem’s context. | |
| Argumentation Explain and comment on the chosen strategy, the key steps of the building process and the consistency of the results | L1 (0–3) | You don’t argue or you argue the solving strategy/process and the test phase wrongly by using mathematical language that is improper or very inaccurate. |
| L2 (4–7) | You argue the solving strategy/process or the test phase in a fragmentary way and/or not always consistently. You use broadly suitable, but not always rigorous mathematical language. | |
| L3 (8–11) | You argue the solving process and the test phase correctly but incompletely. You explain the answer, but not the solving strategies employed (or vice versa). You use a pertinent mathematical language, although with some uncertainty. | |
| L4 (12–15) | You argue both the employed strategies and the obtained results consistently, accurately, exhaustively and in depth. You show an excellent command of the scientific language. | |
| Use of an ACE (Maple) Use the ACE commands appropriately and effectively which is the software Maple, in order to solve the problem | L1 (0–5) | You use Maple as a plain white sheet on which you transpose calculus and arguments which are somewhere else employed. You don’t use Maple’s capabilities in order to plot, to perform mathematical operations and to solve the problem. |
| L2 (6–12) | You partially use Maple’s commands in order to perform some non-basic calculus by making decisions about commands and instruments which aren’t always the most pertinent. You only use basic functions and show that you aren’t able to employ advanced features. | |
| L3 (13–19) | You appropriately use basic Maple’s commands and show that you are able to employ advanced features, even with some indecision, several attempts or by making some mistakes, or in a non-effective way in order to represent the data, the solutions and to solve the problem. | |
| L4 (20–25) | You display mastery in the use of Maple, you make correct and efficient decisions about commands and instruments which you employ. You are able to employ them gracefully and with originality by using Maple’s capabilities in order to solve the problem. |
References
- Klenowski, V. Student Self-evaluation Processes in Student-centred Teaching and Learning Contexts of Australia and England. Assess. Educ. Princ. Policy Pract. 1995, 2, 145–163. [Google Scholar] [CrossRef]
- Black, P.; Wiliam, D. Assessment and Classroom Learning. Assess. Educ. Princ. Policy Pract. 1998, 5, 7–74. [Google Scholar] [CrossRef]
- Ross, J.A. The Reliability, Validity, and Utility of Self-Assessment. Pract. Assess. Res. Eval. 2006, 11, 10. [Google Scholar] [CrossRef]
- Brookhart, S.M.; Andolina, M.; Zuza, M.; Furman, R. Minute Math: An Action Research Study of Student Self-Assessment. Educ. Stud. Math. 2004, 57, 213–227. [Google Scholar] [CrossRef]
- Nicol, D.J.; Macfarlane-Dick, D. Formative Assessment and Self-regulated Learning: A Model and Seven Principles of Good Feedback Practice. Stud. High. Educ. 2006, 31, 199–218. [Google Scholar] [CrossRef]
- Andrade, H.; Valtcheva, A. Promoting Learning and Achievement Through Self-Assessment. Theory Pract. 2009, 48, 12–19. [Google Scholar] [CrossRef]
- Tachie, S.A. Meta-Cognitive Skills and Strategies Application: How This Helps Learners in Mathematics Problem-Solving. EURASIA J. Math. Sci. Technol. Educ. 2019, 15, em1702. [Google Scholar] [CrossRef]
- Yoong, D.W.K. Helping Your Students to Become Metacognitive in Mathematics: A Decade Later. Math. Newsl. 2002, 12, 1–7. [Google Scholar]
- Schoenfeld, A. Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In Handbook of Research on Mathematics Teaching and Learning; Macmillian: New York, NY, USA, 1992; pp. 334–370. [Google Scholar]
- Kilpatrick, J. A retrospective account of the past 25 years of research on teaching mathematical problem solving. In Teaching and Learning Mathematical Problem Solving: Multiple Research Perspectives; Silver, E.A., Ed.; Lawrence Erlbaum: Hillsdale, NJ, USA, 1985; pp. 1–15. [Google Scholar]
- Liljedahl, P.; Santos-Trigo, M.; Malaspina, U.; Bruder, R. Problem Solving in Mathematics Education; ICME-13 Topical Surveys; Springer: New York, NY, USA, 2016; ISBN 978-3-319-40729-6. [Google Scholar]
- Barana, A.; Marchisio, M. From digital mate training experience to alternating school work activities. Mondo Digit. 2016, 15, 63–82. [Google Scholar]
- Barana, A.; Brancaccio, A.; Conte, A.; Fissore, C.; Floris, F.; Marchisio, M.; Pardini, C. The Role of an Advanced Computing Environment in Teaching and Learning Mathematics through Problem Posing and Solving. In Proceedings of the 15th International Scientific Conference eLearning and Software for Education, Bucharest, Romania, 11–12 April 2019; Volume 2, pp. 11–18. [Google Scholar]
- Ninness, H.A.C.; Ninness, S.K.; Sherman, S.; Schotta, C. Augmenting Computer-Interactive Self-Assessment with and Without Feedback. Psychol. Rec. 1998, 48, 601–616. [Google Scholar] [CrossRef][Green Version]
- McDonald, B.; Boud, D. The Impact of Self-Assessment on Achievement: The Effects of Self-Assessment Training on Performance in External Examinations. Assess. Educ. Princ. Policy Pract. 2003, 10, 209–220. [Google Scholar] [CrossRef]
- Black, P.; Wiliam, D. ‘In Praise of Educational Research’: Formative Assessment. Br. Educ. Res. J. 2003, 29, 623–637. [Google Scholar] [CrossRef]
- Black, P.; Wiliam, D. Developing the Theory of Formative Assessment. Educ. Assess. Eval. Account. 2009, 21, 5–31. [Google Scholar] [CrossRef]
- Sánchez-Ruiz, L.-M.; Moll-López, S.; Moraño-Fernández, J.-A.; Roselló, M.-D. Dynamical Continuous Discrete Assessment of Competencies Achievement: An Approach to Continuous Assessment. Mathematics 2021, 9, 2082. [Google Scholar] [CrossRef]
- Castoldi, M. Le rubriche valutative. L’Educatore 2006, 5, 6–10. [Google Scholar]
- Yan, Z. Self-Assessment in the Process of Self-Regulated Learning and Its Relationship with Academic Achievement. Assess. Eval. High. Educ. 2020, 45, 224–238. [Google Scholar] [CrossRef]
- Zimmerman, B.J. Attaining Self-Regulation: A Social Cognitive Perspective. In Handbook of Self-Regulation; Boekaerts, M., Pintrich, P.R., Zeidner, M., Eds.; Elsevier: San Diego, CA, USA, 2000; pp. 13–39. [Google Scholar]
- Ross, J.A.; Hogaboam-Gray, A.; Rolheiser, C. Student Self-Evaluation in Grade 5-6 Mathematics Effects on Problem- Solving Achievement. Educ. Assess. 2002, 8, 43–58. [Google Scholar] [CrossRef]
- English, L.D.; Sriraman, B. Problem Solving for the 21st Century. In Theories of Mathematics Education; Springer: Berlin/Heidelberg, Germany, 2010; pp. 263–290. [Google Scholar]
- Schoenfeld, A. Mathematical Problem Solving; Academic Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Fan, L.; Zhu, Y. From Convergence to Divergence: The Development of Mathematical Problem Solving in Research, Curriculum, and Classroom Practice in Singapore. ZDM 2007, 39, 491–501. [Google Scholar] [CrossRef]
- Chen, P.P. Relationship between Students’ Self-Assessment of Their Capabilities and Their Teachers’ Judgments of Students’ Capabilities in Mathematics Problem-Solving. Psychol. Rep. 2006, 98, 765–778. [Google Scholar] [CrossRef]
- Krathwohl, D.R. A Revision of Bloom’s Taxonomy: An Overview. Theory Pract. 2002, 41, 212–218. [Google Scholar] [CrossRef]
- Semana, S.; Santos, L. Self-Regulation Capacity of Middle School Students in Mathematics. ZDM 2018, 50, 743–755. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics. Executive Summary Principles and Standards for School Mathematics; National Council of Teachers of Mathema: Reston, VA, USA, 2000. [Google Scholar]
- Council of the European Union. European Parliament and Council Council Recommendation of 22 May 2018 on Key Competences for Lifelong Learning. Off. J. Eur. Union 2018, C 189/1, 1–13.
- Pólya, G. How to Solve It; Princeton University: Princeton, NJ, USA, 1945. [Google Scholar]
- D’Amore, B.; Pinilla, M.I.F. Che problema i problemi! L’insegnamento Della Mat. E Delle Sci. Integr. 2006, 6, 645–664. [Google Scholar]
- Samo, D.D.; Darhim, D.; Kartasasmita, B. Culture-Based Contextual Learning to Increase Problem-Solving Ability of First Year University Student. J. Math. Educ. 2017, 9, 81–94. [Google Scholar] [CrossRef]
- Bonotto, C.; Baroni, M. Using maths in a daily context: Experiences in Italian compulsory education. In Planting Mathematics, Publication of the Comenius Network Developing Quality in Mathematics Education II—DQME II; Henn, H.W., Meier, S., Eds.; TU Dortmund: Dortmund, Germany, 2006; pp. 19–47. [Google Scholar]
- Acevedo Nistal, A.; Dooren, W.; Clarebout, G.; Elen, J.; Verschaffel, L. Conceptualising, Investigating and Stimulating Representational Flexibility in Mathematical Problem Solving and Learning: A Critical Review. ZDM 2009, 41, 627–636. [Google Scholar] [CrossRef]
- Silver, E.A. Fostering Creativity through Instruction Rich in Mathematical Problem Solving and Problem Posing. ZDM 1997, 29, 75–80. [Google Scholar] [CrossRef]
- Olivares, D.; Lupiáñez, J.L.; Segovia, I. Roles and Characteristics of Problem Solving in the Mathematics Curriculum: A Review. Int. J. Math. Educ. Sci. Technol. 2021, 52, 1079–1096. [Google Scholar] [CrossRef]
- Toh, T.L.; Chan, C.M.E.; Tay, E.G.; Leong, Y.H.; Quek, K.S.; Toh, P.C.; Ho, W.K.; Dindyal, J.; Ho, F.H.; Dong, F. Problem Solving in the Singapore School Mathematics Curriculum. In Mathematics Education in Singapore; Toh, T.L., Kaur, B., Tay, E.G., Eds.; Mathematics Education—An Asian Perspective; Springer: Singapore, 2019; pp. 141–164. ISBN 9789811335723. [Google Scholar]
- Yap, R.A.S.; Leong, Y.H. Using Video Clubs to Learn for Mathematical Problem-Solving Instruction in the Philippines: The Case of Teaching Extensions. In Cases of Mathematics Professional Development in East Asian Countries; Ng, S.F., Ed.; Springer: Singapore, 2015; pp. 83–106. ISBN 978-981-287-404-7. [Google Scholar]
- Leong, Y.H.; Tay, E.G.; Toh, T.L.; Quek, K.S.; Dindyal, J. Reviving Pólya’s “Look Back” in a Singapore School. J. Math. Behav. 2011, 30, 181–193. [Google Scholar] [CrossRef]
- Carreira, S.; Jones, K.; Amado, N.; Jacinto, H.; Nobre, S. Youngsters Solving Mathematical Problems with Technology; Mathematics Education in the Digital Era; Springer: Cham, Switzerland, 2016; Volume 5, ISBN 978-3-319-24908-7. [Google Scholar]
- Lesh, R.; Lehrer, R. Models and Modeling Perspectives on the Development of Students and Teachers. Math. Think. Learn. 2003, 5, 109–129. [Google Scholar] [CrossRef]
- Santos-Trigo, M.; Moreno-Armella, L.; Camacho-Machín, M. Problem Solving and the Use of Digital Technologies within the Mathematical Working Space Framework. ZDM 2016, 48, 827–842. [Google Scholar] [CrossRef]
- Artigue, M. Instrumentation Issues and the Integration of Computer Technologies into Secondary Mathematics Teaching. In Proceedings of the Annual Meeting of the GDM, Potsdam, Germany; 2000; pp. 7–17. Available online: http://webdoc.sub.gwdg.de/ebook/e/gdm/2000/artigue_2000.pdf (accessed on 19 January 2022).
- Kuzniak, A.; Parzysz, B.; Vivier, L. Trajectory of a Problem: A Study in Teacher Training. Math. Enthus. 2013, 10, 407–440. [Google Scholar] [CrossRef]
- Moreno-Armella, L.; Santos-Trigo, M. The use of digital technologies in mathematical practices: Reconciling traditional and emerging approaches. In Handbook of International Research in Mathematics Education; English, L.D., Kirshner, D., Eds.; Taylor & Francis: New York, NY, USA, 2016; pp. 595–616. [Google Scholar]
- Avitzur, R. Graphing Calculator (Version 4.0); Pacific Tech.: Berkeley, CA, USA, 2011. [Google Scholar]
- Dimiceli, V.A.; Lang, A.S.I.D.; Locke, L.A. Teaching Calculus with Wolfram|Alpha. Int. J. Math. Educ. Sci. Technol. 2010, 41, 1061–1071. [Google Scholar] [CrossRef]
- Hohenwarter, M.; Hohenwarter, J.; Kreis, Y.; Lavicza, Z. Teaching and Learning Calculus with Free Dynamic Mathematics Software GeoGebra. In Proceedings of the 11th International Congress on Mathematics Education, Monterrey, Mexico, 6–13 July 2008; pp. 1–10. [Google Scholar]
- Artigue, M. Learning Mathematics in a CAS Environment: The Genesis of a Reflection about Instrumentation and the Dialectics between Technical and Conceptual Work. Int. J. Comput. Math. Learn. 2002, 7, 245–274. [Google Scholar] [CrossRef]
- Barana, A.; Marchisio, M. Analyzing Interactions in Automatic Formative Assessment Activities for Mathematics in Digital Learning Environments. In Proceedings of the 13th International Conference on Computer Supported Education, SCITEPRESS, Online, 23–25 April 2021; Volume 1, pp. 497–504. [Google Scholar]
- Barana, A.; Marchisio, M.; Sacchet, M. Interactive Feedback for Learning Mathematics in a Digital Learning Environment. Educ. Sci. 2021, 11, 279. [Google Scholar] [CrossRef]
- Beevers, C.E.; Paterson, J.S. Automatic Assessment of Problem Solving Skills in Mathematics. Act. Learn. High. Educ. 2003, 4, 127–144. [Google Scholar] [CrossRef]
- Goos, M.; Galbraith, P.; Renshaw, P.; Geiger, V. Perspectives on Technology Mediated Learning in Secondary School Mathematics Classrooms. J. Math. Behav. 2003, 22, 73–89. [Google Scholar] [CrossRef]
- Barana, A.; Fissore, C.; Marchisio, M.; Roman, F. Enhancement of Mathematical Problem Solving by Discussing and Collaborating Asynchronously. In Proceedings of the Edulearn20 Conference, Online, 6–7 July 2020; pp. 2827–2836. [Google Scholar]
- Tan, D.Y.; Cheah, C.W. Developing a Gamified AI-Enabled Online Learning Application to Improve Students’ Perception of University Physics. Comput. Educ. Artif. Intell. 2021, 2, 100032. [Google Scholar] [CrossRef]
- Kang, K.; Kushnarev, S.; Wei Pin, W.; Ortiz, O.; Chen Shihang, J. Impact of Virtual Reality on the Visualization of Partial Derivatives in a Multivariable Calculus Class. IEEE Access 2020, 8, 58940–58947. [Google Scholar] [CrossRef]
- Buentello-Montoya, D.A.; Lomelí-Plascencia, M.G.; Medina-Herrera, L.M. The Role of Reality Enhancing Technologies in Teaching and Learning of Mathematics. Comput. Electr. Eng. 2021, 94, 107287. [Google Scholar] [CrossRef]
- Kushnarev, S.; Kang, K.; Goyal, S. Assessing the Efficacy of Personalized Online Homework in a First-Year Engineering Multivariate Calculus Course. In Proceedings of the 2020 IEEE International Conference on Teaching, Assessment, and Learning for Engineering (TALE), Takamatsu, Japan, 8–11 December 2020; pp. 770–773. [Google Scholar]
- Cheong, K.H.; Koh, J.M. Integrated Virtual Laboratory in Engineering Mathematics Education: Fourier Theory. IEEE Access 2018, 6, 58231–58243. [Google Scholar] [CrossRef]
- Cheong, K.H.; Koh, J.M.; Yeo, D.J.; Tan, Z.X.; Boo, B.O.E.; Lee, G.Y. Paradoxical Simulations to Enhance Education in Mathematics. IEEE Access 2019, 7, 17941–17950. [Google Scholar] [CrossRef]
- Comoglio, M. Le Nuove Prospettive Della Valutazione Scolasica. L’Educatore 2008, 11, 29–34. [Google Scholar]
- Leong, Y.H.; Janjaruporn, R. Teaching of Problem Solving in School Mathematics Classrooms. In The Proceedings of the 12th International Congress on Mathematical Education; Cho, S.J., Ed.; Springer: Cham, Switzerland, 2015; pp. 645–648. ISBN 978-3-319-10685-4. [Google Scholar]
- Comoglio, M. La Valutazione Autentica. Orientamenti Pedagog. 2002, 49, 93–112. [Google Scholar]
- Maple. Available online: https://www.maplesoft.com/products/Maple/ (accessed on 7 August 2019).
- Pajares, F.; Miller, M.D. Mathematics Self-Efficacy and Mathematics Performances: The Need for Specificity of Assessment. J. Couns. Psychol. 1995, 42, 190–198. [Google Scholar] [CrossRef]
- Ewers, C.A.; Wood, N.L. Sex and Ability Differences in Children’s Math Self-Efficacy and Prediction Accuracy. Learn. Individ. Differ. 1993, 5, 259–267. [Google Scholar] [CrossRef]
- Sriraman, B.; Umland, K. Argumentation in Mathematics Education. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Dordrecht, Germany, 2014; pp. 46–48. ISBN 978-94-007-4977-1. [Google Scholar]
- Cusi, A.; Olsher, S. Design of Classroom Discussions and the Role of the Expert in Fostering an Effective and Aware Use of Examples as a Means of Argumentation. Int. J. Sci. Math. Educ. 2021. [Google Scholar] [CrossRef]
- Boero, P. Argumentation and Mathematical Proof: A Complex, Productive, Unavoidable Relationship in Mathematics and Mathematics Education. Int. Newsl. Teach. Learn. Math. Proof 1999, 7, 8. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).