Math Instrument Development for Examining the Relationship between Spatial and Mathematical Problem-Solving Skills
Abstract
1. Introduction
- Individuals inherently represent numbers spatially, (i.e., the number line), meaning that people with higher levels of spatial reasoning skills are more adept at mathematical processing
- Spatial and numerical processing rely on a shared region in the brain, particularly the intraparietal sulcus
- Spatial visualization plays an important role in a person’s ability to think about and to model complex and novel problems they have not encountered previously
- Spatial visualization is a proxy for other cognitively demanding skills, such as working memory or general intelligence, meaning that individuals with high levels of spatial skills are generally more likely to have higher numerical skills through these other mechanisms
1.1. Spatial/Mathematics Studies in the Middle Grades
1.2. Categories of Mathematics Problems
- Number and Operations
- (1)
- Understand numbers, ways of representing numbers, relationships among numbers, and number systems
- (2)
- Understand meanings of operations and how they relate to one another
- (3)
- Compute fluently and make reasonable estimates
- Algebra
- (1)
- Understand patterns, relations, and functions
- (2)
- Represent and analyze mathematical situations and structures using algebraic symbols
- (3)
- Use mathematical models to represent and understand quantitative relationships
- (4)
- Analyze change in various contexts
- Geometry
- (1)
- Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships
- (2)
- Specify locations and describe spatial relationships using coordinate geometry and other representational systems
- (3)
- Apply transformations and use symmetry to analyze mathematical situations
- (4)
- Use visualization, spatial reasoning, and geometric modeling to solve problems
- Measurement
- (1)
- Understand measurable attributes of objects and the units, systems, and processes of measurement
- (2)
- Apply appropriate techniques, tools, and formulas to determine measurements
- Data Analysis and Probability
- (1)
- Formulate questions that can be addressed with data and collect, organize, and display relevant data to answer them
- (2)
- Select and use appropriate statistical methods to analyze data
- (3)
- Develop and evaluate inferences and predictions that are based on data
- (4)
- Understand and apply basic concepts of probability
2. Research Questions
- What are the characteristics of math problems that correlate with spatial skills?
- Are correlations impacted by math problems’ characteristics, such as inclusion of a figure, formatting the questions as fixed choice or open-ended responses, etc.?
- What are the lessons learned for educators and researchers to consider during the development and selection process of items for a math instrument for use in spatial skills research?
3. Methods
3.1. Setting
3.2. Participants
3.3. Instruments
3.3.1. Spatial Instruments
3.3.2. Math Instruments
- The problems were grade-level appropriate for the age of the students at the time they were being tested
- The problems represented a range of difficulties with an average % correct on the instrument overall targeted at 50%
- A total testing time of around 15–20 min, since teachers were hesitant to give up too much class time for testing
- The problems were likely to exhibit a correlation with spatial skills (according to the insights of the researchers and results reported in the literature).
3.3.3. Verbal Instruments
4. Results
4.1. Correlations of the Math Instruments with Spatial and Verbal Ability
4.2. Item Analyses of Math Instruments
4.3. Unanticipated Difficulties
4.4. Analysis by NCTM Content Strand
4.5. Construct Validity and Reliablity Evidence of Math Instruments
4.6. Figure versus No Figure Included in the Problem Statement
4.7. Open-Ended or Fixed-Choice Response When Answering the Problem
4.8. Term Location Matters
- The cost to rent a boat is $10. There is also a charge of $2 for each person. Which expression represents the total cost to rent a boat for p persons?
- A.
- 10 + 2p
- B.
- 10 − 2p
- C.
- 2 + 10p
- D.
- 2 − 10p
- Joan needs $60 for a class trip. She has $32. She can earn $4 an hour mowing lawns. If the equation shows this relationship, how many hours must Joan work to have the money she needs?4h + 32 = 60
- A.
- 7 h
- B.
- 17 h
- C.
- 23 h
- D.
- 28 h
5. Discussion
5.1. Lessons Learned
5.2. Limitations of the Study
6. Conclusions
- linguistic, needed to transcribe statements that assign values to parameters or describe relations between parameters,
- semantic, needed to comprehend the context of the problem and
- schematic, needed to develop or select the correct mathematical schema for the problem.
- procedural, needed to implement the correct mathematical procedures to solve the mathematical representation of the problem and
- strategic, needed to adopt the correct strategy and order of operations in the solution
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Wave 1 Final Mathematics Instrument
- The cost to rent a boat is $10. There is also a charge of $2 for each person. Which expression represents the total cost to rent a boat for p persons?
- A.
- 10 + 2p
- B.
- 10 − 2p
- C.
- 2 + 10p
- D.
- 2 − 10p
Answer: ________ - Joan needs $60 for a class trip. She has $32. She can earn $4 an hour mowing lawns. If the equation shows this relationship, how many hours must Joan work to have the money she needs?4h + 32 = 60
- A.
- 7 h
- B.
- 17 h
- C.
- 23 h
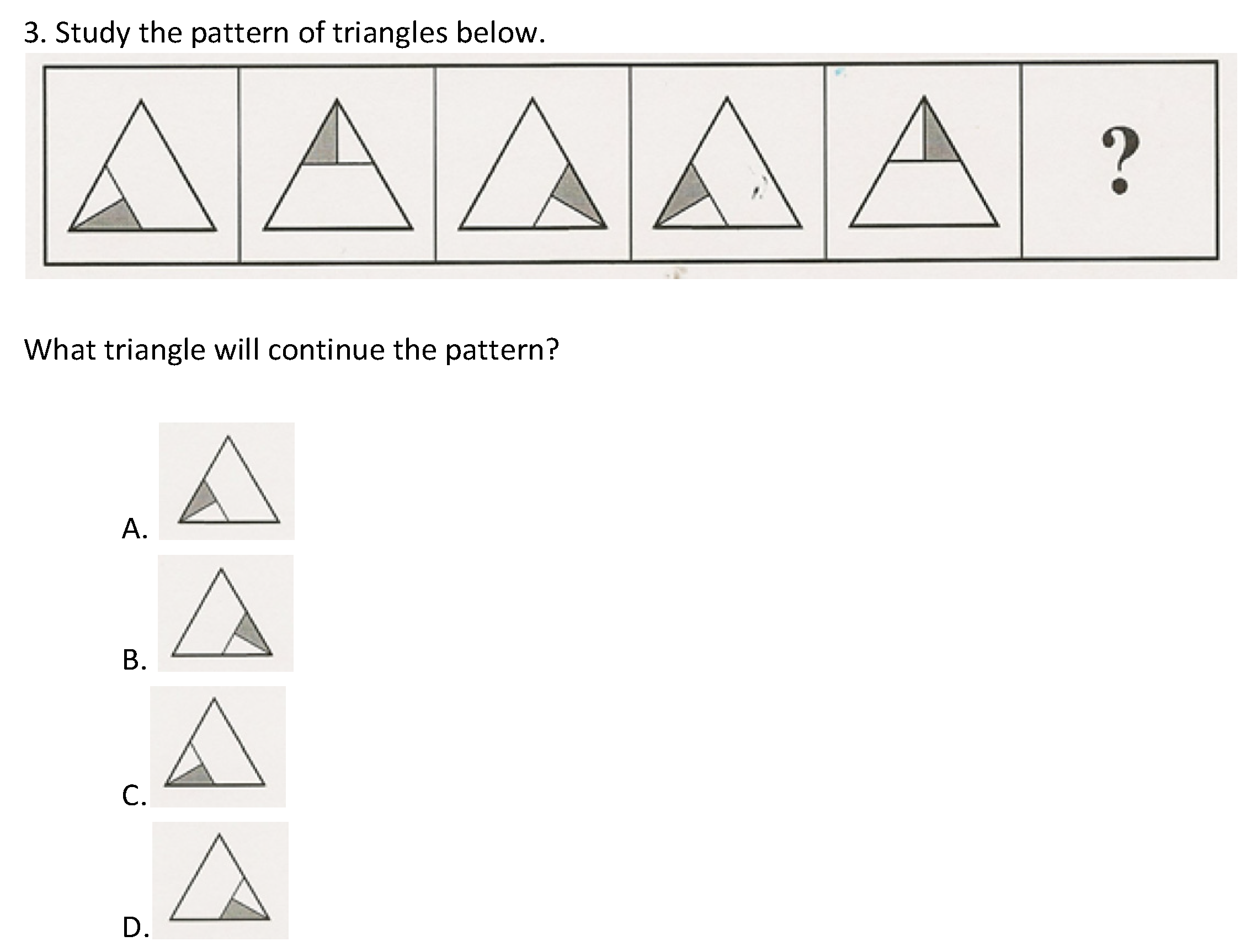
- Study the pattern of triangles below.What triangle will continue the pattern?
- A.
- B.
- C.
- D.
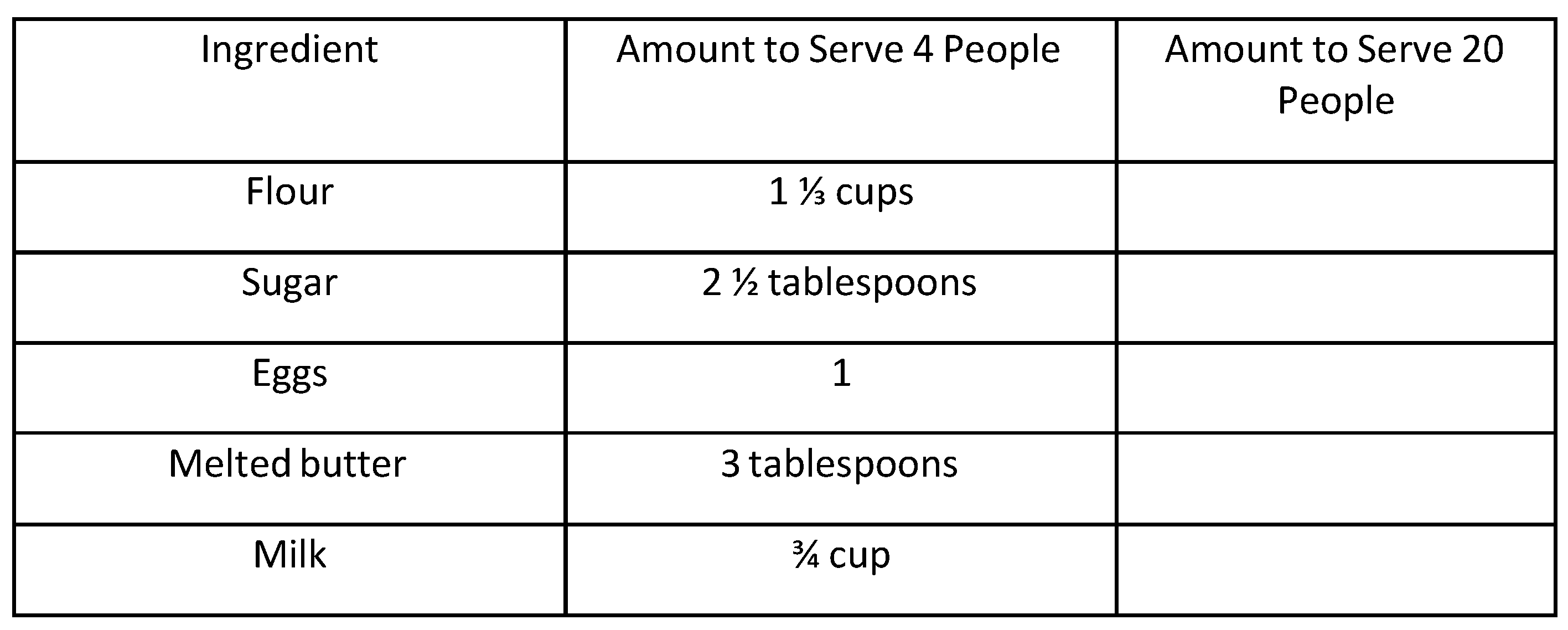
Answer: ________ - Bill will make pancakes for 20 members of his Boy Scout troop He will use the pancake recipe that serves 4 people, shown in the table below. Complete the table to show the amount of each ingredient Bill will use to make pancakes to serve 20 people.
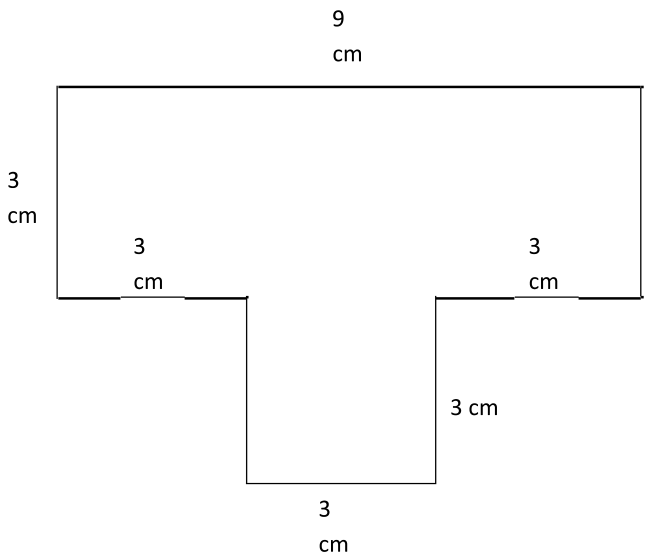
Ingredient Amount to Serve 4 People Amount to Serve 20 People Flour 1 ⅓ cups Sugar 2 ½ tablespoons Eggs 1 Melted butter 3 tablespoons Milk ¾ cup - Edgar drew the shape on his Spirit Day poster.What is the area of this shape? ________
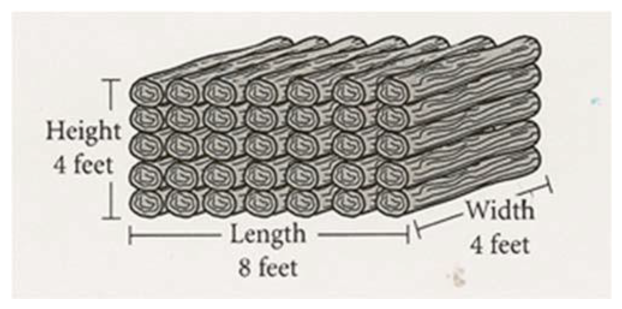
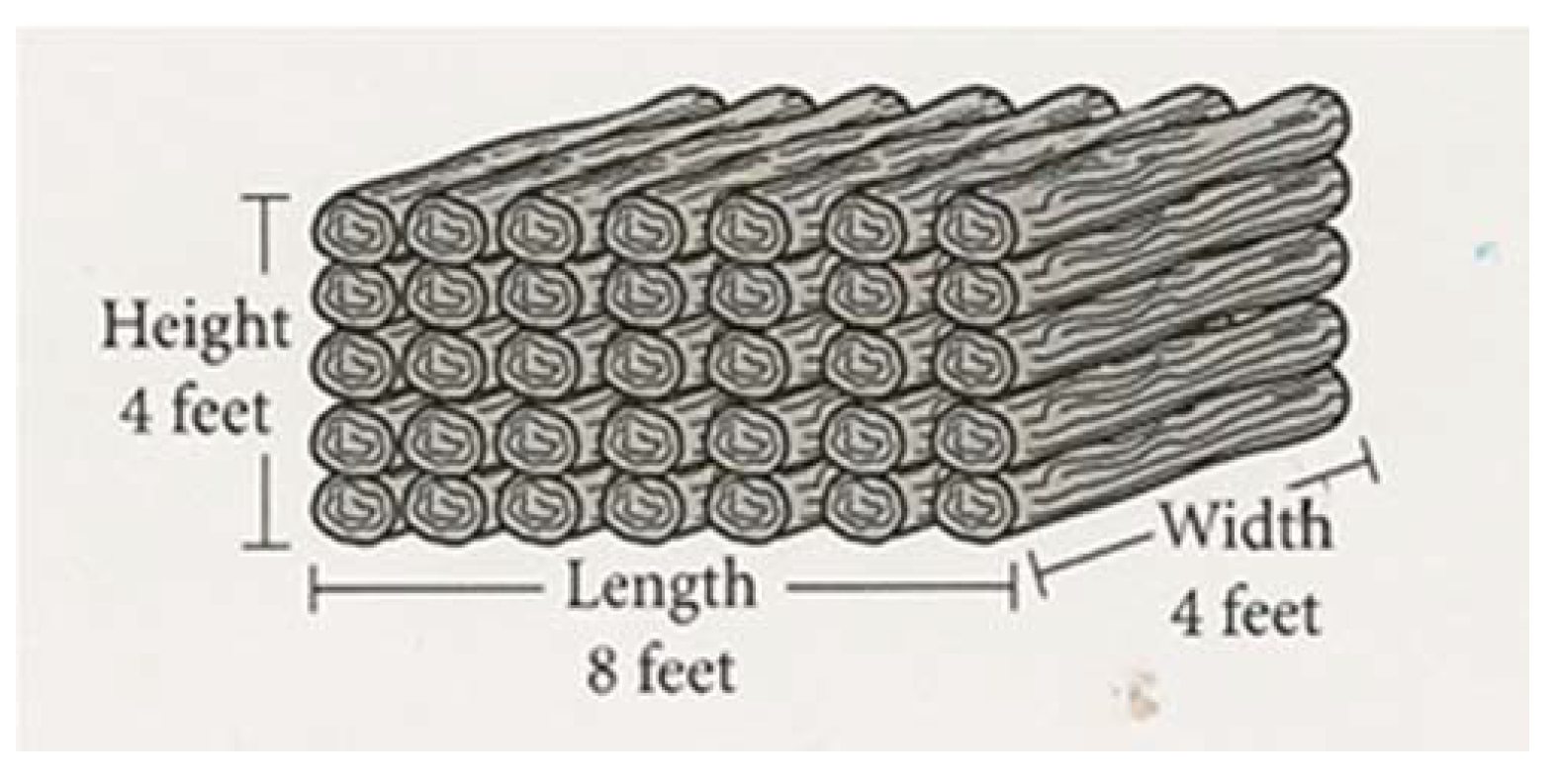
- Carl has a stack of wood with the measurements shown below. He will cover the top and all 4 sides of the stack with a plastic sheet.
- Wave 2 Final Mathematics Instrument
- 1.
- Jeff wants to wrap ribbon around a package, as shown below. He also needs 10 more inches of ribbon to tie a bow.How much ribbon does he need to wrap the package and to tie the bow?
- A.
- 34 inches
- B.
- 48 inches
- C.
- 50 inches
- D.
- 58 inches
Answer: ________ - 2.
- Joan needs $60 for a class trip. She has $32. She can earn $4 an hour mowing lawns. If the equation shows this relationship, how many hours must Joan work to have the money she needs?4h + 32 = 60
- A.
- 7 h
- B.
- 17 h
- C.
- 23 h
- D.
- 28 h
Answer: ________ - 3.
- The cost to rent a boat is $10. There is also a charge of $2 for each person. Which expression represents the total cost to rent a boat for p persons?
- A.
- 10 + 2p
- B.
- 10 − 2p
- C.
- 2 + 10p
- D.
- 2 − 10p
Answer: ________ - 4.
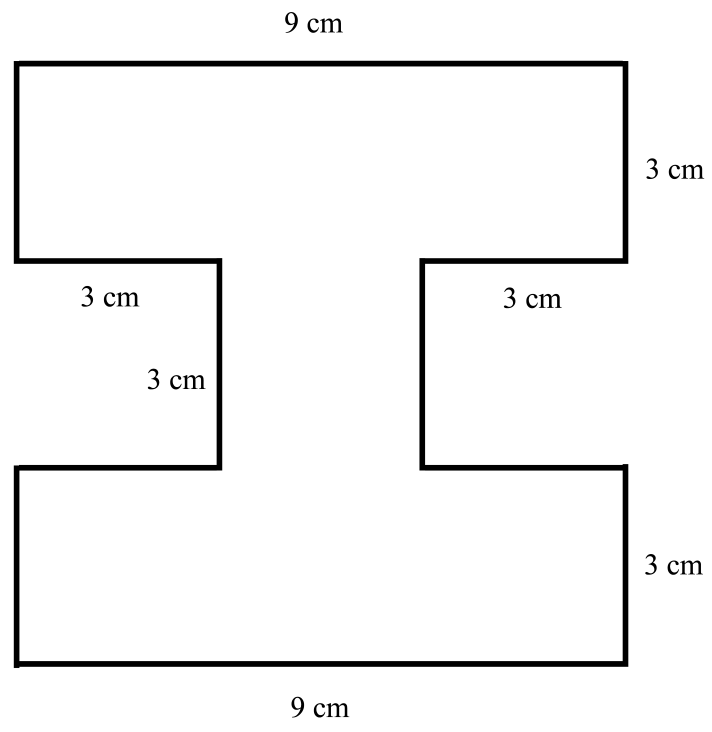
- Edgar drew the shape on his Spirit Day poster.What is the area of this shape?
- A.
- 21 cm2
- B.
- 54 cm2
- C.
- 63 cm2
- D.
- 81 cm2
- 5.
- Carl has a stack of wood with the measurements shown below. He will cover the top and all 4 sides of the stack with a plastic sheet.
- 6.
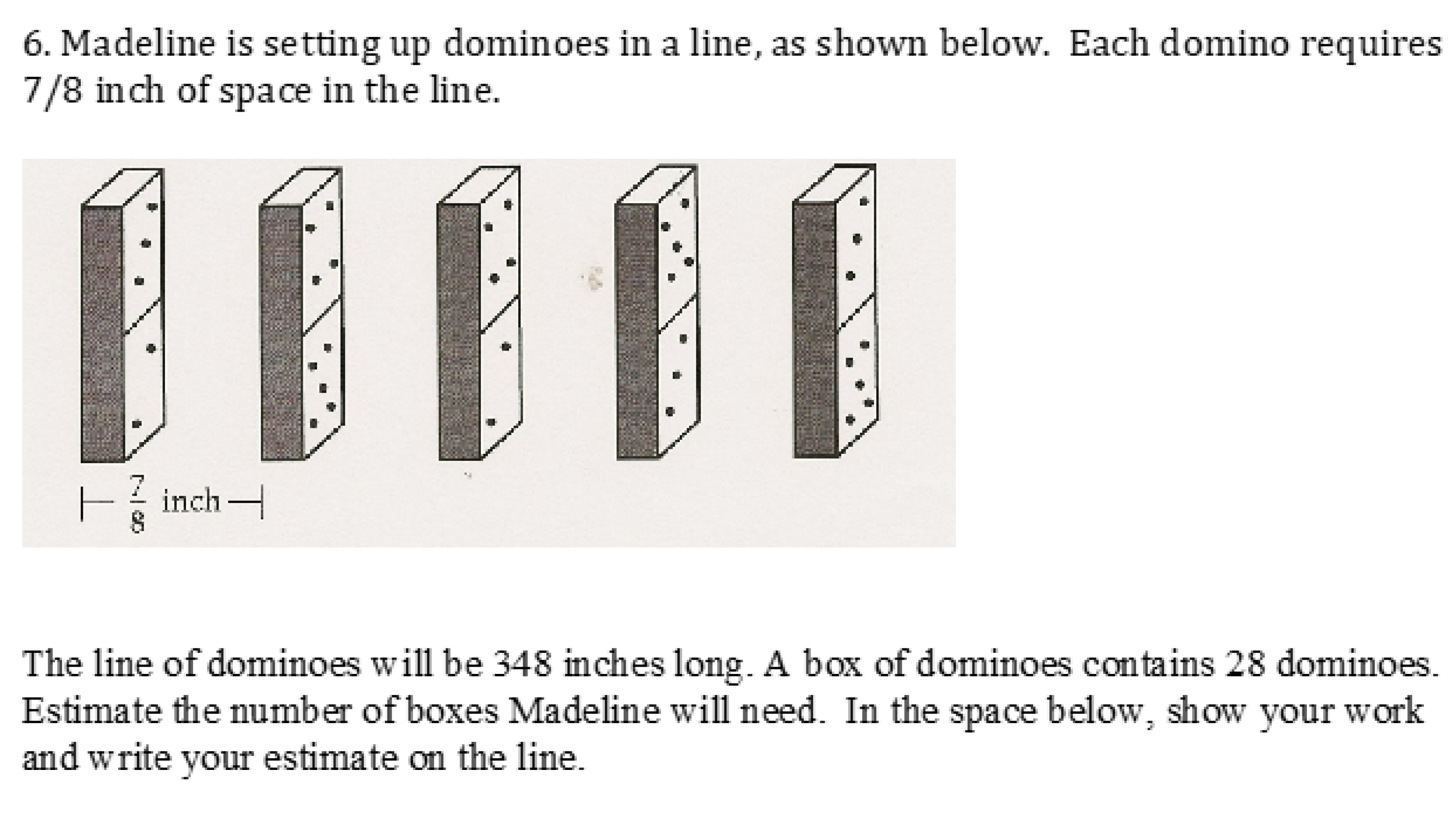
- Madeline is setting up dominoes in a line, as shown below. Each domino requires 7/8 inch of space in the line.
- 7.
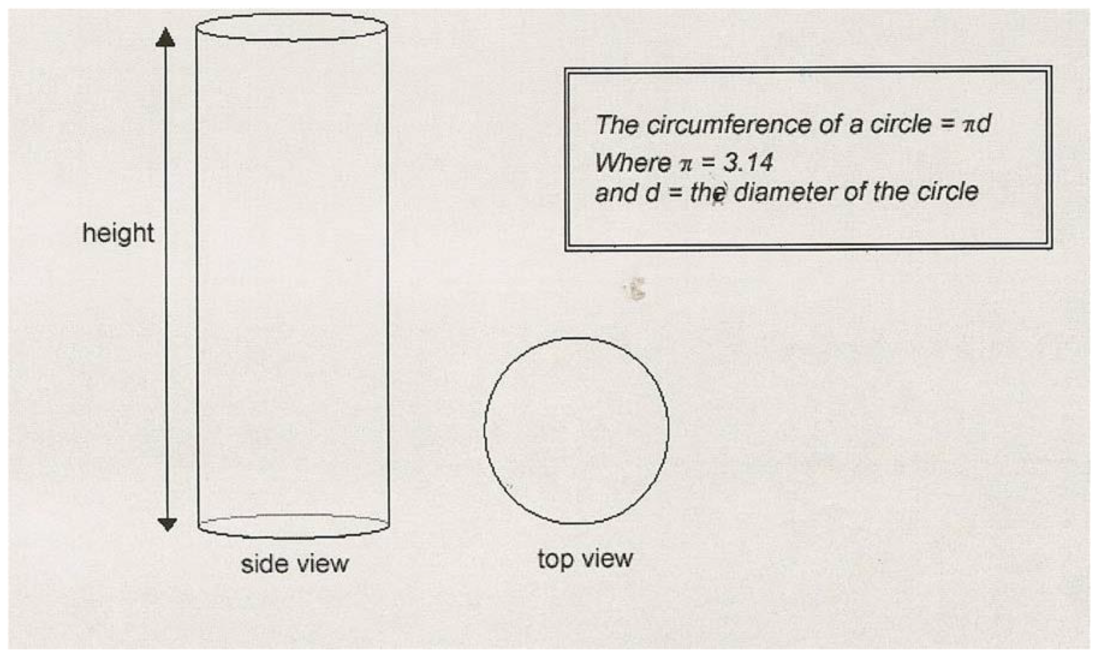
- Which is bigger? This problem gives you the chance to take measurements from a scale drawing and calculate the circumference of a circle from the diameter.Below is a diagram showing a side view and a top view of a glass vase.Both views of the glass vase are drawn accurately and are ½ of the real size.
- Wave 3 Final Mathematics Instrument
- 1.
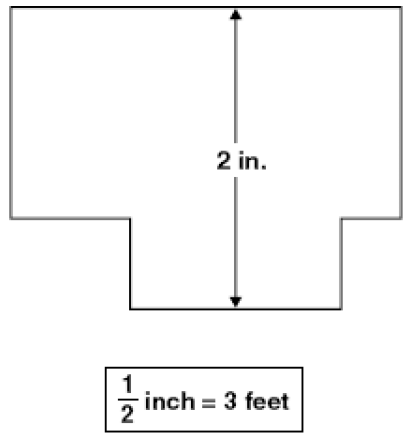
- Mr. Craig made a scale drawing of his office.The width of the scale drawing of the office is 2 inches. What is the actual width, in feet, of Mr. Craig’s office?
- A.
- 3 ft
- B.
- 6 ft
- C.
- 9 ft
- D.
- 12 ft
- 2.
- Maria bought wood, paper, and string to make one kite. The list shows the amount and the unit cost of each item she bought.
- 12 square feet of paper at $1 per square foot
- 4 feet of wood at $3 per foot
- 14 yards of string at $2 per yard
- 3.
- Jordan’s dog weighs p pounds. Emmett’s dog weights 25% more than Jordan’s dog. Which expressions represent the weight, in pounds, of Emmett’s dog? Select each correct answer.
- A.
- 0.25p
- B.
- 1.25p
- C.
- p + 0.25
- D.
- p + 1.25
- E.
- p + 0.25p
- 4.
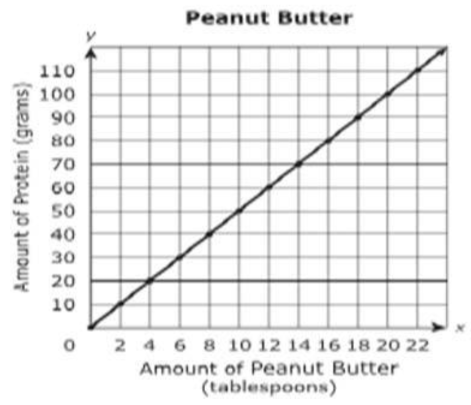
- The graph shows the amount of protein contained in certain brand of peanut butter.Which statement describes the meaning of the point (6, 30) on the graph?
- A.
- There are 6 g of protein per tablespoon of peanut butter
- B.
- There are 30 g of protein per tablespoon of peanut butter
- C.
- There are 6 g of protein in 30 tablespoons of peanut butter
- D.
- There are 30 g of protein in 6 tablespoons of peanut butter
- 5.
- Which situation can be represented by the equation 1 ¼ x 6 = 7 ½?
- It took Calvin 1 ¼ hours to run 6 miles. He ran 7 ½ miles per hour
- Sara read for 1 ¼ hours every day for 6 days. She read for a total of 7 ½ hours
- Matthew addressed 1 ¼ envelopes in 6 min. He addressed 7 ½ envelopes per minute.
- It took Beth 1 ¼ minutes to paint 6 feet of a board. She painted a total of 7 ½ feet of the board.
- 6.
- The amount Troy charges to mow a lawn is proportional to the time it takes him to mow the lawn. Troy charges $30 to mow a lawn that took him 1.5 h to mow.Which equation models the amount of dollars, d, Troy charges when it takes him h hours to mow a lawn?
- A.
- d = 20h
- B.
- h = 20d
- C.
- d = 45h
- D.
- h = 45d
- 7.
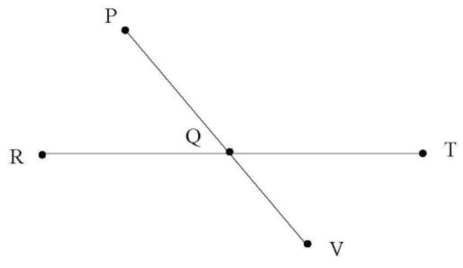
- Angle PQR and angle TQV are vertical angles. The measure of the two angles have a sum of 100 degrees. Write and solve an equation to find x, the measure of angle TQV is ________ degrees.Put your equation and solution below.
- Wave 4 Final Mathematics Instrument
- 1.
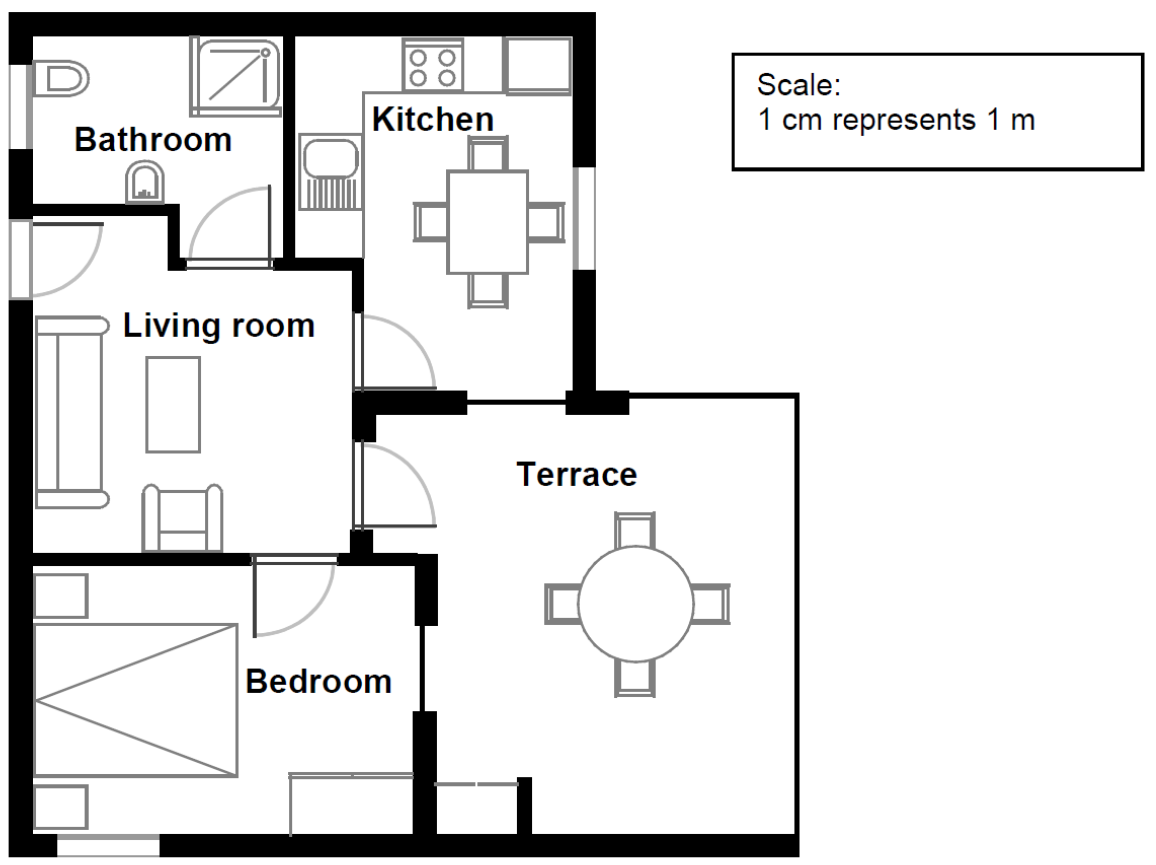
- This is the plan of the apartment that George’s parents want to purchase from a real estate agency.
- 2.
- Here, you see a photograph of a farmhouse with a roof in the shape of a pyramid. Below is a student’s mathematical model of the farmhouse roof with measurements added.The attic floor, ABCD in the model, is a square. The beams that support the roof are the edges of a block (rectangular prism) EFGHKLMN. E is the middle of AT, F is the middle of BT, G is the middle of CT and H is the middle of DT. All the edges of the pyramid in the model have length 12 m.Part A: Calculate the area of the attic floor ABCD.The area of the attic floor ABCD = ________ m²Part B: Calculate the length of EF, one of the horizontal edges of the block.The length of EF = ________ m.
- 3.
- On the right, there is a picture of two dice.Dice are special number cubes for which the following rule applies:

| Shape | Obeys the Rule that the Sum of Opposite Faces is 7? |
| | | Yes/No |
| || | Yes/No |
| ||| | Yes/No |
- 4.
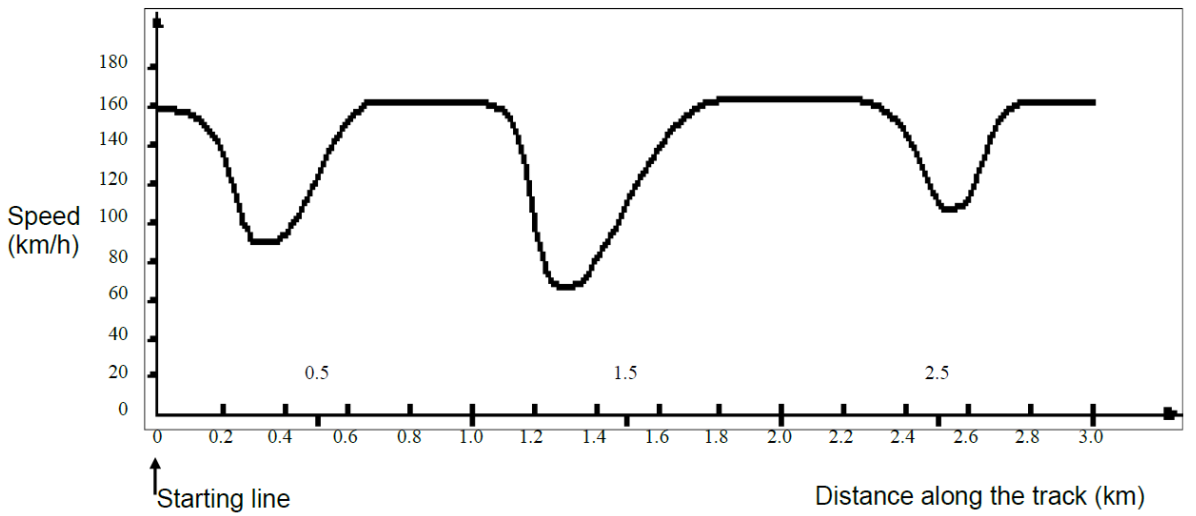
- SPEED OF RACING CARThis graph shows how the speed of a racing car varies along a flat 3 km track during its second lap.Part A: What is the approximate distance from the starting line to the beginning of the longest straight section of the track?
- A.
- 0.5 km
- B.
- 1.5 km
- C.
- 2.3 km
- D.
- 2.6 km
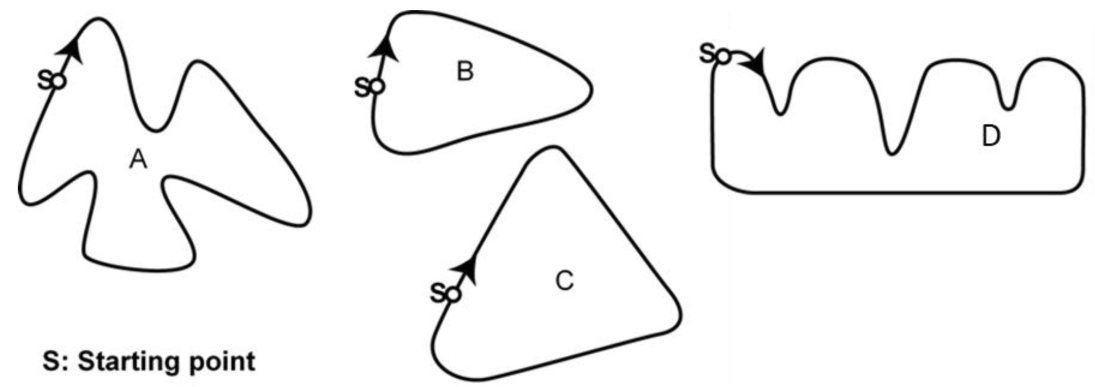
Part B: Here are pictures of five tracks: Along which one of these tracks was the car driven to produce the speed graph shown above? Circle the correct answer. - 5.
- People living in an apartment building decide to buy the building. They will put their money together in such a way that each will pay an amount that is proportional to the size of their apartment.
| Statement | Correct/Incorrect |
| A person living in the largest apartment will pay more money for each square meter of his apartment than the person living in the smallest apartment. | Correct/Incorrect |
| If we know the areas of two apartments and the price of one of them, we can calculate the price of the second. | Correct/Incorrect |
| If we know the price of the building and how much each owner will pay, then the total area of all apartments can be calculated. | Correct/Incorrect |
| If the total price of the building were reduced by 10%, each of the owners would pay 10% less. | Correct/Incorrect |
- 6.
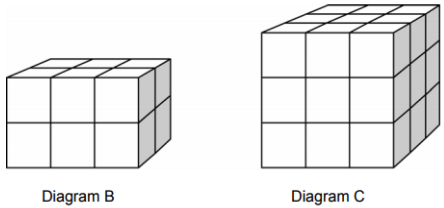
- Susan likes to build blocks from small cubes like the one shown in the following diagram:


References
- National Science Board. Preparing the Next Generation of Stem Innovators: Identifying and Developing our Nation’s Human Capital; National Science Foundation: Alexandria, VA, USA, 2010.
- Wai, J.; Lubinski, D.; Benbow, C.P. Spatial ability for STEM domains: Aligning over 50 years of cumulative psychological knowledge solidifies its importance. J. Educ. Psychol. 2009, 101, 817–835. [Google Scholar] [CrossRef]
- Shea, D.L.; Lubinski, D.; Benbow, C.P. Importance of assessing spatial ability in intellectually talented young adolescents: A 20-year longitudinal study. J. Educ. Psychol. 2001, 93, 604. [Google Scholar] [CrossRef]
- Smith, I.M. Spatial Ability: Its Educational and Social Significance; University of London Press Ltd.: London, UK, 1964. [Google Scholar]
- Kell, H.J.; Lubinski, D.; Benbow, C.P.; Steiger, J.H. Creativity and technical innovation: Spatial ability’s unique role. Psychol. Sci. 2013, 24, 1831–1836. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.; Burnett, G. Spatial ability and learning to program. Hum. Technol. Interdiscip. J. Hum. ICT Environ. 2008, 4. [Google Scholar] [CrossRef]
- Mix, K.S.; Cheng, Y.-L. Chapter 6—The Relation Between Space and Math: Developmental and Educational Implications. In Advances in Child Development and Behavior; Benson, J.B., Ed.; JAI Academic Press: San Diego, CA, USA, 2012; Volume 42, pp. 197–243. [Google Scholar] [CrossRef]
- Hawes, Z.; Ansari, D. What explains the relationship between spatial and mathematical skills? A review of evidence from brain and behavior . Psychon. Bull. Rev. 2020, 27, 465–482. [Google Scholar] [CrossRef] [PubMed]
- van Garderen, D. Spatial Visualization, Visual Imagery, and Mathematical Problem Solving of Students with Varying Abilities. J. Learn. Disabil. 2006, 39, 496–506. [Google Scholar] [CrossRef] [PubMed]
- Casey, M.B.; Nuttall, R.L.; Pezaris, E. Spatial-Mechanical Reasoning Skills versus Mathematics Self-Confidence as Mediators of Gender Differences on Mathematics Subtests Using Cross-National Gender-Based Items. J. Res. Math. Educ. 2001, 32, 28. [Google Scholar] [CrossRef]
- Verdine, B.N.; Golinkoff, R.M.; Hirsh-Pasek, K.; Newcombe, N.S.; Filipowicz, A.T.; Chang, A. Deconstructing Building Blocks: Preschoolers’ Spatial Assembly Performance Relates to Early Mathematical Skills. Child Dev. 2013, 85, 1062–1076. [Google Scholar] [CrossRef] [PubMed]
- Hegarty, M.; Kozhevnikov, M. Types of visual–spatial representations and mathematical problem solving. J. Educ. Psychol. 1999, 91, 684–689. [Google Scholar] [CrossRef]
- Duffy, G.; Sorby, S.; Bowe, B. Spatial ability is a key cognitive factor in the representation of word problems in mathematics among engineering students. J. Eng. Educ. 2020, 109, 424–442. [Google Scholar] [CrossRef]
- Judd, N.; Klingberg, T. Training spatial cognition enhances mathematical learning in a randomized study of 17,000 children. Nat. Hum. Behav. 2021, 5, 1548–1554. [Google Scholar] [CrossRef] [PubMed]
- Bulunuz, N.; Jarrett, O.S. The Effects of Hands-on Learning Stations on Building American Elementary Teachers’ Understanding about Earth and Space Science Concepts. Eurasia J. Math. Sci. Technol. Educ. 2010, 6, 85–99. [Google Scholar] [CrossRef]
- Harmer, A.J.; Columba, L. Engaging Middle School Students in Nanoscale Science, Nanotechnology, and Electron Microscopy. J. Nano Educ. 2010, 2, 91–101. [Google Scholar] [CrossRef]
- Lanzilotti, R.; Montinaro, F.; Ardito, C. Influence of Students’ Motivation on Their Experience with E-Learning Systems: An Experimental Study. In Proceedings of the International Conference on Universal Access in Human-Computer Interaction, San Diego, CA, USA, 2 July 2009; pp. 63–72. [Google Scholar] [CrossRef]
- Tai, R.H.; Liu, C.Q.; Maltese, A.V.; Fan, X. Planning Early for Careers in Science. Science 2006, 312, 1143–1144. [Google Scholar] [CrossRef] [PubMed]
- Microsoft. Why Europe’s Girls Aren’t Studying STEM. 2017. Available online: https://news.microsoft.com/uploads/2017/03/ms_stem_whitepaper.pdf (accessed on 6 October 2018).
- Bowe, B.; Harding, R.; Hedderman, T.; Sorby, S. A National Spatial Skills Research & Development Project. In Proceedings of the 36th International Pupils’ Attitudes towards Technology Conference, Westmeath, Ireland, 18–21 June 2018; p. 333. [Google Scholar]
- Xie, F.; Zhang, L.; Chen, X.; Xin, Z. Is Spatial Ability Related to Mathematical Ability: A Meta-analysis. Educ. Psychol. Rev. 2019, 32, 113–155. [Google Scholar] [CrossRef]
- Uttal, D.H.; Meadow, N.G.; Tipton, E.; Hand, L.L.; Alden, A.R.; Warren, C.; Newcombe, N.S. The malleability of spatial skills: A meta-analysis of training studies. Psychol. Bull. 2013, 139, 352–402. [Google Scholar] [CrossRef] [PubMed]
- NCTM. Principles and Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 2000; Volume 1. [Google Scholar]
- Guay, R.B. Purdue Spatial Visualization Test; Purdue Research Foundation: West Lafayette, IN, USA, 1976. [Google Scholar]
- Bennett, G.K.; Seashore, H.G.; Wesman, A.G. Differential Aptitude Tests: Forms S and T: Psychological Corporation; The Psychological Corporation: New York, NY, USA, 1973. [Google Scholar]
- Muthén, L.K.; Muthén, B.O. Mplus User’s Guide, 8th ed.; Muthén & Muthén: Los Angeles, CA, USA, 2017. [Google Scholar]
- Brown, T.A. Confirmatory Factor Analysis for Applied Research, 2nd ed.; Guilford Press: New York, NY, USA, 2015. [Google Scholar]
- George, D.; Mallery, P. SPSS for Windows Step by Step: A Simple Guide and Reference, 11.0 Update, 4th ed.; Allyn & Bacon: Boston, MA, USA, 2003. [Google Scholar]
- Gliem, J.A.; Gliem, R.R. Calculating, interpreting, and reporting Cronbach’s alpha reliability coefficient for Likert-type scales. In Proceedings of the 2003 Midwest Research-to-Practice Conference in Adult, Continuing and Community Education, Columbus, OH, USA, 8–10 October 2003. [Google Scholar]
- Cheng, Y.-L.; Mix, K.S. Spatial Training Improves Children’s Mathematics Ability. J. Cogn. Dev. 2013, 15, 2–11. [Google Scholar] [CrossRef]
- Mayer, R.E. Thinking, Problem Solving, Cognition; W.H. Freeman: New York, NY, USA, 1992. [Google Scholar]


| Cohort | 2015–16 | 2016–17 | 2017–18 | 2018–19 | 2019–20 |
|---|---|---|---|---|---|
| Baseline (1) | 7th Grade | 8th Grade | 9th Grade | ||
| Cohort 2 | 7th Grade | 8th Grade | 9th Grade | ||
| Cohort 3 | 7th Grade | 8th Grade | 9th Grade | ||
| Cohort 4 | 7th Grade | 8th Grade | |||
| Cohort 5 | 7th Grade |
| Wave 1 | Wave 2 | Wave 3 | Wave 4 | |
|---|---|---|---|---|
| Sample Size | 3217 | 3823 | 2417 | 1031 |
| Wave | Grade | DAT:SR | PSVT:R | DAT:SR + PSVT:R | Correlation | |||
|---|---|---|---|---|---|---|---|---|
| n | Cronbach’s α | n | Cronbach’s α | n | Cronbach’s α | R | ||
| 1 | 7 | 1691 | 0.550 | 1775 | 0.579 | 1579 | 0.690 | 0.405 * |
| 2 | 7 | 2505 | 0.619 | 2608 | 0.645 | 2388 | 0.743 | 0.452 * |
| 3 | 8 | 2274 | 0.667 | 2315 | 0.675 | 2180 | 0.778 | 0.482 * |
| 4 | 9 | 1469 | 0.712 | 1482 | 0.688 | 1427 | 0.806 | 0.610 * |
| Draft Instrument (Cohort 1) | Final Instrument (Cohorts 2–5) | |||||
|---|---|---|---|---|---|---|
| n | Average Score (% correct) | Correlation with Spatial Test | n | Average Score (% correct) | Correlation with Spatial Test | |
| Wave 1 | 1164 | 13.6 | 0.277 * | 2053 | 49.7 | 0.443 * |
| Wave 2 | 1901 | 37.3 | 0.370 * | 1918 | 47.9 | 0.482 * |
| Wave 3 | 1420 | 53.6 | 0.518 * | 997 | 58.0 | 0.541 * |
| Wave 4 | 693 | 45.7 | 0.485 * | 338 | 44.4 | 0.623 * |
| Problem | Figure Y/N | Fixed Choice (FC) or Open Ended (OE) | NCTM Category | Item Difficulty | Item Discrimination | Correlation with Spatial |
|---|---|---|---|---|---|---|
| Cost of Boat Rental | N | FC | Algebra | 0.910 | 0.359 | 0.138 * |
| Earning Money for a Class Trip | N | FC | Algebra | 0.670 | 0.606 | 0.265 * |
| 2-D Rotation of Triangle-Pattern Recognition | Y | FC | Algebra | 0.440 | 0.456 | 0.085 * |
| Quantity of Ingredients for Pancakes | N | OE | Number | 0.411 | 0.688 | 0.424 * |
| T-shaped Spirit Day Poster | Y | OE | Measure | 0.190 | 0.580 | 0.393 * |
| Cover for Stack of Logs | Y | OE | Measure | 0.430 | 0.533 | 0.174 * |
| Problem | Figure Y/N | Fixed Choice (FC) or Open Ended (OE) | NCTM Category | Item Difficulty | Item Discrimination | Correlation with Spatial |
|---|---|---|---|---|---|---|
| Ribbon to Wrap Package | Y | FC | Measure & Geometry | 0.200 | 0.481 | 0.270 * |
| Earning Money for a Class Trip | N | FC | Algebra | 0.770 | 0.562 | 0.282 * |
| Cost of Boat Rental | N | FC | Algebra | 0.870 | 0.489 | 0.218 * |
| I-shaped Spirit Day Poster | Y | FC | Measure | 0.430 | 0.578 | 0.323 * |
| Cover for Stack of Logs | Y | OE | Measure | 0.430 | 0.512 | 0.181 * |
| Falling Dominoes | Y | OE | Number | 0.470 | 0.509 | 0.165 * |
| Height and Circumference of Vase | Y | OE | Measure | 0.252 | 0.559 | 0.372 * |
| Problem | Figure Y/N | Fixed Choice (FC) or Open Ended (OE) | NCTM Category | Item Difficulty | Item Discrimination | Correlation with Spatial |
|---|---|---|---|---|---|---|
| Scale Drawing of Office | Y | FC | Measure & Number | 0.770 | 0.549 | 0.303 * |
| Wood, String, and Paper to make one Kite (Part A) | N | OE | Number | 0.80 | 0.521 | 0.272 * |
| Wood, String, and Paper to make four Kites (Part B) | N | OE | Number | 0.543 | 0.601 | 0.312 * |
| Comparing Weights of Dogs | N | FC | Algebra | 0.250 | 0.437 | 0.268 * |
| Interpreting Graph of Protein in Peanut Butter | Y | FC | Analysis & Probability | 0.800 | 0.621 | 0.345 * |
| Interpreting Algebraic Equation | N | FC | Algebra | 0.640 | 0.589 | 0.297 * |
| Charging for Lawn Mowing | N | FC | Algebra | 0.480 | 0.514 | 0.247 * |
| Vertical Angles PQR and TQV | Y | OE | Geometry | 0.380 | 0.611 | 0.399 * |
| Problem | Figure Y/N | Fixed Choice (FC) or Open Ended (OE) | NCTM Category | Item Difficulty | Item Discrimination | Correlation with Spatial |
|---|---|---|---|---|---|---|
| Dimensions on Apartment | Y | OE | Measure | 0.400 | 0.475 | 0.255 * |
| Pyramid-shaped Roof Part A | Y | OE | Measure | 0.380 | 0.608 | 0.417 * |
| Pyramid-shaped Roof Part B | Y | OE | Measure | 0.580 | 0.393 | 0.285 * |
| Dice Pattern I | Y | FC-2 | Geometry | 0.710 | 0.498 | 0.295 * |
| Dice Pattern II | Y | FC | Geometry | 0.760 | 0.490 | 0.331 * |
| Dice Pattern III | Y | FC | Geometry | 0.770 | 0.411 | 0.259 * |
| Interpreting Speed of Car Graph | Y | FC | Analysis & Probability | 0.640 | 0.421 | 0.333 * |
| Identifying the Shape of Race Track | Y | FC | Analysis & Probability | 0.260 | 0.442 | 0.384 * |
| Cost of Apartment I | N | FC | Number | 0.340 | 0.424 | 0.280 * |
| Cost of Apartment II | N | FC | Number | 0.690 | 0.454 | 0.263 * |
| Cost of Apartment III | N | FC | Number | 0.410 | 0.246 | 0.049 (N.S.) |
| Cost of Apartment IV | N | FC | Number | 0.500 | 0.193 | 0.000 (N.S.) |
| Open-ended Cost of Apartment Calculation | N | OE | Number | 0.160 | 0.581 | 0.429 * |
| Number of Small Cubes for 3 × 3 × 3 Cube with Missing Center | Y | OE | Measure & Geometry | 0.190 | 0.514 | 0.403 * |
| Number of Small Cubes for 6 × 5 × 4 Cube with Missing Center | Y | OE | Measure & Geometry | 0.080 | 0.460 | 0.341 * |
| Algebra | Number | Measurement | Analysis and Probability | Geometry | |
|---|---|---|---|---|---|
| No. of problems * | 8 | 10 | 12 | 3 | 7 |
| Mean Item difficulty | 0.63 | 0.48 | 0.36 | 0.57 | 0.64 |
| Mean Correlation with Spatial test | 0.22 | 0.25 | 0.31 | 0.35 | 0.34 |
| Wave 1 | Wave 2 | Wave 3 | Wave 4 | |||||
|---|---|---|---|---|---|---|---|---|
| EFA | CFA | EFA | CFA | EFA | CFA | EFA | CFA | |
| n | 1383 | 1383 | 1263 | 1263 | 795 | 794 | 377 | 376 |
| No. of Items | 6 | 4 | 7 | 6 | 8 | 8 | 15 | 13 |
| a Q1 | 0.457 * | 0.400 * | 0.496 * | 0.519 * | 0.625 * | 0.655 * | 0.483 * | 0.499 * |
| Q2 | 0.653 * | 0.658 * | 0.666 * | 0.648 * | 0.412 * | 0.408 * | 0.710 * | 0.723 * |
| Q3 | 0.178 * | 0.696 * | 0.691 * | 0.535 * | 0.541 * | 0.398 * | 0.393 * | |
| Q4 | 0.742 * | 0.754 * | 0.500 * | 0.495 * | 0.429 * | 0.403 * | 0.703 * | 0.730 * |
| Q5 | 0.800 * | 0.765 * | 0.377 * | 0.786 * | 0.762 * | 0.775 * | 0.790 * | |
| Q6 | 0.316 * | 0.409 * | 0.410 * | 0.581 * | 0.590 * | 0.550 * | 0.530 * | |
| Q7 | 0.568 * | 0.580 * | 0.475 * | 0.432 * | 0.379 * | 0.355 * | ||
| Q8 | 0.563 * | 0.585 * | 0.494 * | 0.506 * | ||||
| Q9 | 0.430 * | 0.445 * | ||||||
| Q10 | 0.446 * | 0.334 * | ||||||
| Q11 | 0.007 | |||||||
| Q12 | −0.063 | |||||||
| Q13 | 0.737 * | 0.944 * | ||||||
| Q14 | 0.691 * | 0.640 * | ||||||
| Q15 | 0.792 * | 0.755 * | ||||||
| Fit Index | ||||||||
| Chi-square | 2.467 | 33.084 | 61.075 | 142.498 | ||||
| df | 2 | 9 | 20 | 65 | ||||
| p | 0.291 | 0.0001 | <0.001 | <0.001 | ||||
| RMSEA | 0.013 | 0.046 | 0.051 | 0.056 | ||||
| 90% CI | 0.000, 0.057 | 0.030, 0.063 | 0.040, 0.066 | 0.044, 0.069 | ||||
| CFI | 0.999 | 0.957 | 0.925 | 0.924 | ||||
| TLI | 0.996 | 0.928 | 0.895 | 0.909 | ||||
| SRMR | 0.021 | 0.049 | 0.056 | 0.090 | ||||
| Cronbach’s α | 0.572 | 0.537 | 0.681 | 0.727 | ||||
| Item Characteristics | No Figure | Figure | Independent t-Test | Effect Size | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | M | SD | n | M | SD | t | df | p | Hedges’ g | |
| Item Difficulty | 15 | 0.56 | 0.23 | 21 | 0.45 | 0.22 | 1.47 | 34 | 0.151 | 0.486 |
| Item Discrimination | 15 | 0.48 | 0.14 | 21 | 0.51 | 0.07 | –0.66 | 18.8 | 0.517 | –0.493 |
| Correlation with Spatial | 15 | 0.25 | 0.12 | 21 | 0.30 | 0.09 | –1.49 | 34 | 0.145 | –0.243 |
| Item Characteristics | Open-Ended | Fixed-Choice | Independent t-Test | Effect Size | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | M | SD | n | M | SD | t | df | p | Hedges’ g | |
| Item Difficulty | 16 | 0.38 | 0.18 | 20 | 0.59 | 0.22 | −3.18 | 34 | 0.003 | −1.042 |
| Item Discrimination | 16 | 0.55 | 0.07 | 20 | 0.46 | 0.11 | 2.65 | 34 | 0.012 | 0.869 |
| Correlation with Spatial | 16 | 0.32 | 0.09 | 20 | 0.25 | 0.10 | 2.33 | 34 | 0.026 | 0.765 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sorby, S.A.; Duffy, G.; Yoon, S.Y. Math Instrument Development for Examining the Relationship between Spatial and Mathematical Problem-Solving Skills. Educ. Sci. 2022, 12, 828. https://doi.org/10.3390/educsci12110828
Sorby SA, Duffy G, Yoon SY. Math Instrument Development for Examining the Relationship between Spatial and Mathematical Problem-Solving Skills. Education Sciences. 2022; 12(11):828. https://doi.org/10.3390/educsci12110828
Chicago/Turabian StyleSorby, Sheryl Ann, Gavin Duffy, and So Yoon Yoon. 2022. "Math Instrument Development for Examining the Relationship between Spatial and Mathematical Problem-Solving Skills" Education Sciences 12, no. 11: 828. https://doi.org/10.3390/educsci12110828
APA StyleSorby, S. A., Duffy, G., & Yoon, S. Y. (2022). Math Instrument Development for Examining the Relationship between Spatial and Mathematical Problem-Solving Skills. Education Sciences, 12(11), 828. https://doi.org/10.3390/educsci12110828