Abstract
Nowadays, science, technology, engineering, and mathematics (STEM) play a critical role in a nation’s global competitiveness and prosperity. Thus, there is a need to educate students in these subjects to meet the current and future demands of personal life and society. While applications, especially in science, engineering, and technology, are directly obvious, mathematics underpins the other STEM disciplines. It is recognized that mathematics is the foundation for all other STEM disciplines; the role of mathematics in classrooms is not clear yet. Therefore, the question arises: What is the current role of mathematics in secondary STEM classrooms? To answer this question, we conducted a systematic literature review based on three publication databases (Web of Science, ERIC, and EBSCO Teacher Referral Center). This literature review paper is intended to contribute to the current state of the role of mathematics in STEM education in secondary classrooms. Through the search, starting with 1910 documents, only 14 eligible documents were found. In these, mathematics is often seen as a minor matter and a means to an end in the eyes of science educators. From this, we conclude that the role of mathematics in the STEM classroom should be further strengthened. Overall, the paper highlights a major research gap, and proposes possible initial solutions to close it.
1. Introduction
Science, technology, engineering, and mathematics—STEM for short—has been the focus of government policy development and education research for more than a decade [1]. The ability to adaptively, critically, and creatively use science, technology, engineering, and mathematics skills when confronted with real-world problems is central to productive participation in personal and civic life as well as in the workplace [2,3,4]. This joint integrated consideration is sensible and necessary against the background of a critical and reflective participation, which is characterized by rapid technological, industrial, and social change. It is important to be aware of the basics needed to comprehensively serve this integrated perspective.
Since the aim of education “[…] means to adjust him [the student] to those elements of his environment that are of concern in modern life, and to develop, organize, and train his power so that he may make efficient and proper use of them[.]” [5] (p. 39), the calls to increase STEM education effort led to research of STEM integration in schools. From an educational theory perspective, leveraging synergies across disciplines is particularly important because it can help students develop a better understanding of disciplinary concepts and facilitate the transfer of knowledge from one disciplinary context to another [6].
However, over the last decade, educational research has discussed STEM primarily from the perspective of science, while mathematics generally has played a superficial role in classroom activities [7]. At this point, it becomes obvious that more attention should be paid to mathematics, the last-but-not-least letter in the term STEM. On the one hand, this is because mathematics works as a means of communication or language of all disciplines mentioned in the term. On the other hand, the applications from science, technology, and engineering are usually based on (more or less complex) mathematical models. Identifying and sharing the essential mathematical characteristics enables users to interpret existing results and, if necessary, apply them to contexts that differ from those in which they were originally developed.
There have been various discussions and approaches to how mathematics should be integrated into STEM and what role mathematics should play. In doing so, this work on the role of mathematics focused on highlighting exemplary approaches for integrating mathematics into STEM education (e.g., [1,5,6]).
In this systematic literature review, we identified a research gap. This was discerned by analyzing the current state of research on the current role of mathematics in STEM education in secondary school classrooms. The results of the review are presented in this paper.
This analysis aims to contribute a first step in highlighting the role of mathematics in STEM classrooms and points to how mathematics can be profitably integrated into the classroom and inspire further research.
2. Theoretical Frameworks as the Basis for the Research Questions and Analysis
2.1. STEM Activities at School Model of Teacher Collaborations or Subject Collaborations
While there is a broad consensus that the interplay of different disciplines in STEM is necessary and useful against the background of a critical and reflective participation [1,2,3,8], in many countries, there is no subject called STEM that combines science, technology, engineering, and mathematics in one subject (e.g., Australia, Germany, …). For example, in the southern German state Bavaria, there is a subject that combines technology and natural sciences in years 5 to 7. The subject aims to form a basis of scientific, technical/engineering education, and computer science by combining these subjects in one [9].
However, even though the subject combines those disciplines, the subject itself is taught with separated focusses on biology, propaedeutic chemistry, computer science, and physics. The subject is taught in grade five to seven usually by biology, physics, or geography teachers without a central role of mathematics.
There are different ways to characterize the integration of subjects in STEM education: first, as the degree of integration; and second, as the structure of integration [9]. In our analysis, we refer to Hobbs et al. [10] who expanded on Duggers’ categorized collaborations [11] and curricular models of how STEM is practiced in schools. They differentiate five distinct approaches to implementing STEM in schools, as shown in Figure 1. The authors emphasize that this is not meant to be limiting [10].

Figure 1.
Approaches for implementing STEM according to Hobbs [9] (p. 144).
At the top of Figure 1, the integrated approach is shown in symbolic form. This is one of four ways to incorporate STEM into the classroom, combining all STEM disciplines equally in a real-world problem. This approach is one way to incorporate STEM into the classroom, combining all STEM disciplines and is the highest level of integration of the disciplines [10]. This could correspond to a realization of a subject called STEM.
Alternatively, the subjects can be taught completely separately, as shown on the bottom. In this case, each discipline is taught as an independent subject [10]. This is, for example, the case in the current German curriculum in secondary school after the eighth grade. Beginning from this grade, the disciplines are taught separately by different subject teachers.
Between the extremes of teaching the subject completely integrated or separated, there are (at least) three approaches to integrate STEM education without integrating all subjects to the same extent.
The first of those is called “emphasis on one or two subjects in a teaching sequence” [10] (p. 144). In this approach, the focus is on one or two disciplines, with a minor consideration of the other disciplines. The disciplines in focus are marked with capital letters [10]. Figure 1 illustrates a possible symbolic presentation in which science and mathematics are emphasized. An example for this is a lesson in which students manipulate graphs (M) to explore evolutionary selection (S—biology), as presented in one of the included documents presented.
The second of those approaches is the integration of other disciplines in a superordinate subject, while in regular teaching, the other disciplines continue to be considered separately. One iconic representation is shown in the middle of Figure 1: the main subject is written on the top. In this approach, a problem is identified in the superordinate discipline, for example engineering, to solve the problem. The other disciplines are integrated, but there are little or no links between the other subjects [10].
The last approach added by Hobbs et al. [10] is a division of a superordinate real-world problem into the different subjects. Individual collaboration with other subjects demands teacher engagement.
2.2. The Role of Mathematics in STEM
In recent years, STEM education has emerged as a meta-discipline that aims to take an integrated approach and, thus, has a holistic view of STEM education [12]. If one takes the term STEM in its entirety seriously, it must not lead to a disadvantage in one discipline. Nevertheless, in educational research in recent years, the perspective of science is frequently in the center, while mathematics remains in the background [7].
Often, mathematics plays a service role in the learning experiences associated with science, as an auxiliary discipline (e.g., [4,13,14]). Hereby, students apply existing knowledge and use simple procedural applications, such as calculations to solve the mathematical problems. This is problematic, on one hand, because this is exactly what computers can do nowadays [15]. On the other hand, it shows that this is problematic for the development of students’ mathematical knowledge and skills [8,13].
This lack of focus in STEM from the perspective of mathematics education was taken as an opportunity to address this topic from this perspective as well. In recent years, there has been various research works on how mathematics could and should be included as well as what added value mathematics can contribute (e.g., [1,15,16,17,18]).
An important part of STEM education is the relation to reality: understanding the world and social contexts is only possible if basic mathematical competencies have been acquired to work descriptively as well as normatively with mathematical methods. Mathematics, for example, plays an important role for understanding and making assumptions [1]. In the next section, we will look at mathematical activities and skills in STEM.
2.3. Describing and Characterising the Application of Mathematics
In considering the role of mathematics in STEM education, we should be particularly clear about what constitutes mathematical education. In this article, we will not take the approach of mathematical specific topics but look at mathematical skills and activities, although these cannot be considered completely separately. In the Encyclopedia of Mathematics Education, Kilpatrick [19] defines mathematical competence as “a structural plan for organizing the cognitive skills and abilities used in learning and doing mathematics” (p. 85). In the hand search for mathematical skills, we could identify a large overlap in the activity domain of skills and competencies (e.g., [8,15]). In the PISA Framework 2018 [20], they use “the mathematical processes and the fundamental mathematical capabilities (in previous frameworks the ‘competencies’)” (p. 74) to describe organizing the domain of mathematics.
In our analysis, we use the described mathematical activities in the mathematical competencies to characterize mathematical activities in the included papers. We justify this with the fact that mathematical skills and abilities are part of the definition of competences and that we cannot analyze competencies with this approach.
In this way, we can use the framework for competencies as an analytical means to describe and characterize the actual pursued or unpursued attainment of mathematical activities in a particular segment of the learning system, as Niss and Højgaard [21] themselves describe in their article for the competencies.
We do so to compare and contrast the state of affairs in different segments of the educational system, including issues of transition from one element to another. Niss and Højgaard [21] assign the competencies to two different categories, which we will use for the evaluation:
- “Handling the language, constructs and tools of mathematics” (p. 17).
- “Posing and answering questions in and by means of mathematics” (p. 15).
The first category includes representation, symbols and formalism, communication, as well as aids and tools. This category focuses on mathematics as a language and tool.
The second category implies mathematical thinking, problem handling, modelling, and reasoning.
To integrate mathematics fully into STEM education, mathematics must not be perceived and used solely as an operational discipline. Instead, “posing and answering questions in and by means of mathematics” [21] (p. 15) has to be included as well. We have chosen this approach to categorize the role of mathematics in the described activities of the sequences in the included data.
3. Research Questions
There have been several approaches and suggestions to strengthen the role of mathematics (e.g., [1,18,22]). In our study, we aim to systematically analyze the current role mathematics plays in STEM classrooms. The main purpose of our study is to answer the two following research questions (RQ1 and RQ2):
- RQ1:
- What is the distribution of studies on STEM activities in secondary classrooms, and how can they be characterized by authors’ country of origin, time of occurrence, type of work (theoretical or empirical; conference papers or journal articles), use of research methods, and grade level?
- RQ2:
- What is the current role of mathematics in secondary STEM classrooms?
We attempt to answer the overall question about the current role of in STEM classrooms through answering the following sub-questions:
- Under which model of teacher collaboration or subject collaboration are STEM activities currently framed in STEM classrooms?
- In what kind of (certain) educational settings is STEM practiced?
- How is mathematics applied in STEM classrooms?
- What role do the authors assign to mathematics in their STEM activities?
To answer the two research questions RQ1 and RQ2 and the four related sub-questions, we systematically reviewed the literature on STEM education and mathematics over the past 5 years.
4. Methodology of the Systematic Literature Review
In this section, we describe the methods we used for this literature review and present the results afterwards. We give a description of our research strategies and manuscript selection procedure. To do so, we have identified inclusion (4) and exclusion (5) criteria based on [23,24], which is an appropriate methodology, as shown, for example, by Cevikbas et al. [25].
4.1. Search Strategies and Manuscript Selection Procedure
Given the amount of research literature on this topic, we aim to provide an up-to-date summary of the state-of-the-art research on the current role of mathematics in STEM education by systematically reviewing primary research on STEM activities in schools.
The current review followed the preferred reporting items for systematic reviews and meta-analysis (PRISMA) guidelines [23], and its extension PRISMA-S PRISMA statement for reporting literature searches in systematic reviews [24]. The final literature search was conducted on 31 May 2022, in the following databases: (1) Web of Science (WoS) Core Collection; (2) ERIC; (3) Teacher Reference Center. To identify studies for this systematic review, we used the search terms shown transparently in the following table. STEM * AND (math * or mathematics *) AND (school or classroom) Peer Reviewed; Date Published: 1 January 2018–31 December 2022 AND apply equivalent subjects.
In our conducted search, we considered articles published in English only and related to STEM tasks or STEM teaching scenarios at the secondary level. Our search included studies at all levels of STEM instruction related to mathematics, conducted in the last 5 years, as the search was intended to explore the current research. To specify the manuscripts eligible for review, we formulated inclusion and exclusion criteria and created, additionally, a scale classification of relevance. Because we wanted to identify the role of mathematics in the secondary STEM classroom, we excluded studies that targeted elementary school students and university or college students. For this reason, we also excluded studies that did not address activities in the regular, compulsory classroom, such as electives or extracurricular activities for, e.g., summer camps.
The selection of contributions was carried out in three main steps: (1) identification, (2) screening, and (3) inclusion [23]. The search terms from Table 1 were used in the identification phase and a literature search of the three databases listed yielded 2766 entries. After limiting the search to secondary school, the number of articles was reduced to 1910. Excel served as the software to manage the references and remove duplicate entries. After removing 91 duplicate entries, 1819 entries were screened. We then manually screened the titles, abstracts, and keywords of the remaining 1819 reports based on our ICs and ECs and found 80 potentially relevant studies. In addition, we found 3 potentially eligible datasets by content referencing the included data. Of these, two were excluded based on the inclusion and exclusion criteria after screening of abstract and title. One article was included in the full-text screening.

Table 1.
Information sources.
We examined the full-text versions of these 81 studies at the end of the screening phase based on our eligibility criteria listed in Table 2. Subsequently, we included 14 studies in the systematic review. The entire manuscript selection process is illustrated in Figure 2.

Table 2.
Eligibility criteria.
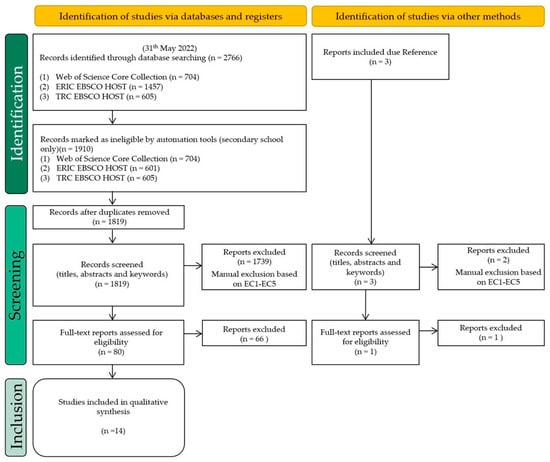
Figure 2.
Flow diagram of the manuscript selection process.
Our search may have excluded some studies of interest, such as those not published in English or in journals or books not listed in the included databases. We did not include studies from German-speaking journals/countries that were listed only with the German translation of STEM (MINT). Furthermore, we excluded studies that were conducted outside of school. We excluded these activities because the aim of our study was to take a literature-based view of the role of mathematics in the secondary classroom, rather than in STEM education in general. These would potentially bias data collection, as extracurricular activities are sometimes targeted at students with higher math achievement or higher math/science interest. Nevertheless, our sample and results may be biased in these aspects, as new approaches may more easily fall outside of curricular boundaries in this setting due to freer design options. This may be considered a limitation of our study. There was no hand search performed except for the 3 documents listed that the authors of the source documents explicitly referenced in terms of content related to the STEM unit in the classroom.
4.2. Data Analysis
After screening, fourteen papers were included for systematic review. These papers are listed in the Supplementary Materials (Refs. [26,27,28,29,30,31,32,33,34,35,36,37,38,39] are cited in the Supplementary Materials). For the analysis, we developed a coding scheme and categorized them according to the research questions and sub-questions:
- Study characteristics and research methodologies which were asked in research question 1.
- Educational settings and approach.
- Mathematical application.
Table S4 in the Supplementary Materials illustrates our coding with regarding to the educational settings. We analyzed the studies that pertained to our research interests systematized by the three main categories. To answer the first research question, we categorized the general characteristics of the examined studies using subcategories (e.g., publication year, document type, authors’ countries, research methods, sample size, and class levels). In the second category, we analyzed the educational settings and approaches in which the student activities were or are supposed to be implemented. In the last category, we used several subcategories (e.g., mathematical application, role of mathematics, and author’s view of the use of mathematics).
The main parts of the coding manual can be found in the Supplementary Materials in Tables S1–S3.
5. Results of the Systematic Literature Review
Our results are presented in three parts: First, the results concerning the first research question (RQ1). This includes the characteristics and research methods of the studies considered. Second, we present the results on the educational setting and teacher collaboration or subject collaboration. Third, we report the results regarding the type of application of mathematics as well as the assigned role of mathematics.
5.1. Results concerning Study Characteristics and Research Methodologies (RQ 1)
5.1.1. Types of Documents
The 14 papers included in our study consisted of 13 journal articles and 1 non-journal article, that were published in 12 different journals.
Considering that different underlying disciplines can lead to a different view of the role of mathematics, we analyzed the journals by underlying disciplines according to their titles, aims, and scopes. We classified the results in journals with one discipline. The distribution of journals among disciplines is shown in Figure 3a; only those disciplines are listed in the figure to which at least one contribution was assigned. We classified the results into different categories: on the one hand, journals that primarily address one discipline (these have been listed separately); on the other hand, we have listed journals that combine two disciplines and summarized these as mixed journals. Journals that address at least three disciplines have been grouped together as STEM journals. Other journals are those that are not directly related to a discipline.
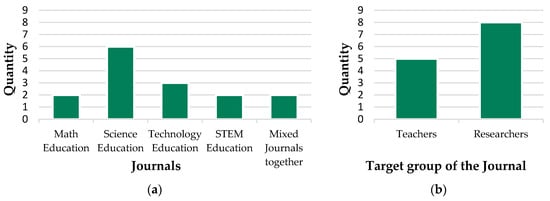
Figure 3.
(a) Topics that the Journals are primarily assigned to (b) Target group of the Journal.
The included papers consisted of only two journals (15%) that could be assigned primarily to math education. Most of the journals were in the natural science discipline (n = 6, 46%). The remaining journals were assigned to technology education (n = 3, 23%), STEM education (n = 2, 15%), and mixed journals (n = 2, 15%). Of the articles considered, none were included in a journal purely related to technology education.
We further analyzed the dispersion of journals in terms of target group. We did this because the purpose of the study can impact on the focus, and we wanted to identify trends in the target groups. We classified the results into two main categories—teachers and researchers. The journal “the mathematics teacher” is an example for the target group teacher, whereas the journal “Eurasia Journal of Mathematics, Science, and Technology Education” primarily addresses researchers. In our analysis, we were able to assign five (38%) journals primarily to teachers, and eight journals (62%) to researchers. This is shown in Figure 3b.
5.1.2. Publication Years and Countries of Authors
When looking at the publication years, it is noticeable that they are not continuous. There is even a downward trend in Figure 4, although this interpretation should be treated with caution due to the low number of documents. It is noticeable that no document was included that was published in 2022, although the data were included up to the middle of the year (31 May 2022).
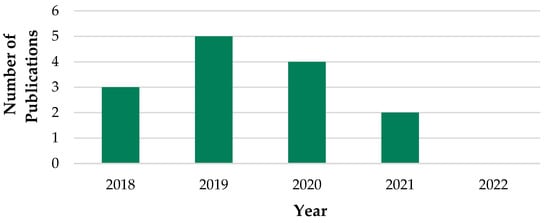
Figure 4.
Years of Publications.
The results regarding geographic distribution show the contributions of researchers from different countries to research on STEM activities in the classroom. Predominantly, the first authors were from the same country. There was one document where the authors were from three different countries. We included them in the table with the factor of one third. We considered the origin of authors because of the different educational systems and to identify a research focus.
Table 3 shows the distribution of authors by country and continent. Almost 50% of authors were from Asia, followed by North America, Europe, and South America. There were no manuscripts with authors from Australia included.

Table 3.
Country of authors.
5.1.3. Research Designs
57% (n = 8) of the documents did not provide information about the research design. The other journals mainly used mixed or multiple methods (n = 3, 21%) in their research methodology, followed by design-based research/research design (n = 2, 14%) and one case study. This is shown in the following Figure 5. This illustrates clearly the number of contributions that did not provide research design information.
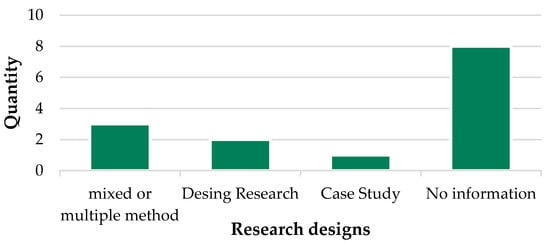
Figure 5.
Distribution of the research designs.
5.1.4. Sample Sizes and Grade Level
The secondary grades were almost all represented except for 6th and 12th grade, with middle school being particularly prominent. This is shown in the following Figure 6. In the case of authors’ statements about several grades, we included them individually in the survey so that, in total, we arrive at a higher number than the number of documents considered. One unit grade was assigned to each of the grades: 5, 7, 10, and 11. Two units referred to a ninth grade and three to an eighth grade, which was, thus, the most frequently present. No explicit unit was indicated for grade 6. Furthermore, there were two documents that gave no indication regarding grade level. The small number in fifth and sixth grades is due, in part, to the fact that we excluded elementary schools in our analysis. It should be noted that in various school systems, elementary school continues up to and including the sixth grade.
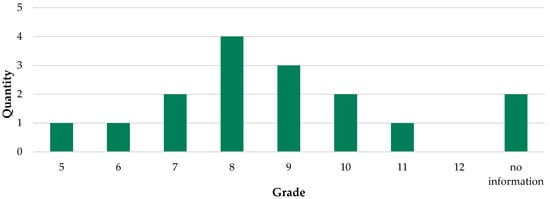
Figure 6.
Distribution of the grades.
The sample sizes were widely spread; there was a sample group with sixteen students at a private school and group sizes of over 400 for data collection. Table 4 lists the distribution of sample sizes; if no exact sample number was given but the reference size was one class, we adopted this value exactly, since class sizes vary widely and this could distort the results, especially for the size 30 classes. Furthermore, there were two documents that did not specify a sample size.

Table 4.
Sample size.
As shown in the table, the group sizes are distributed very similarly in the small intervals until the leap to the larger sample sizes. If we combine the group sizes below 100 and above 100, there are 10 (71%) sample sizes below 100 and 2 (14%) above. This also fits with our search since we explicitly searched for a classroom situation.
5.2. Results concerning Educational Settings and Approaches
In the analysis of the approaches according to the Hobbs scheme, more than half of the STEM units were in such a way that one or two subjects were emphasized (n = 7, 57%). In five documents, the approach was primarily intended as integrated STEM units (n = 5, 36%). There was no unit that integrated one subject into the other three that were taught separately. In addition, there was an article on each of the other two approaches. The distribution of applied approaches is shown in Figure 7a.
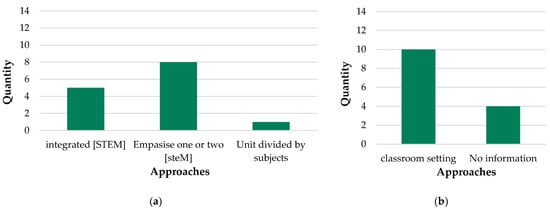
Figure 7.
(a) Approaches (b) Setting of the implementation.
The setting of the implementation was arranged so that the units of the articles that provided information about the implementation were included in the regular classes.
In terms of content, the STEM units were mainly project-based in their design. This is possibly due to the reference to reality, although a problem-oriented approach would also be possible here, for example.
5.3. Results concerning the Mathematical Application
In the evaluation, we analyzed the way mathematics was applied and how the application of mathematics could be applied by slightly modifying the supplementary materials or tasks. In doing so, we used Niss and Højgaard’s head categories as skills and activities as described in Section 2.3.
The qualitative content analysis was conducted based on Mayring [40]. The description of competencies according to Niss and Højgaard was used as a coding frame [21]. For this purpose, the authors’ descriptions of the competencies were coded as activities. In addition, the activity was assigned to the top category that had the greater focus. The classification was carried out using the content descriptions of the authors of the investigated publications.
The three distinctions, concerning mathematical activities (1) and mathematical activities from the authors’ point of view (2), as well as the possibilities for small changes (3), were based on three different perspectives:
For (1), the entire sequence described by the authors was considered, including those that were assigned to engineering, for example. For (2), only those activities were considered that were assigned to or with mathematics. For (3), questions and material were considered where given models or deferred activities, such as a validation, were coded with the modeling activity.
The results are shown in the Figure 8a below. In six (43%) of the incorporated documents, the focus of the application of mathematics was on handling the language, constructs, and tools of mathematics. In contrast, the focus of eight (57%) manuscripts was on posing and answering questions in and by means of mathematics.
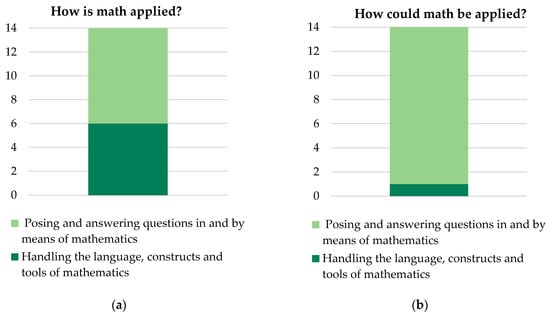
Figure 8.
(a) Application of mathematics; (b) Possible applications for mathematics.
In addition, we analyzed the content and evaluated the extent to which slight changes in the material and the task could generate further possibilities for the application of mathematics. The results of the opportunities in the application of mathematics after a small adjustment of material and tasks are presented in Figure 8b. It is obvious that by this change, mathematics can be applied with focus on the category “posing and answering questions in and by means of mathematics” [21] (p. 15). Here, of course, the skills and abilities of the previous are still involved.
Considering previous research on the role of M in STEM and applied mathematics, e.g., in the workplace, we divided the role of mathematics into two categories: is mathematics used here as an auxiliary science or as mathematics itself? The assignment of the auxiliary science was made when students only applied existing knowledge and used simple procedural applications such as calculations to solve the mathematical problem. Here, mathematics serves primarily as a tool and is hardly ever questioned or applied algorithmically (e.g., [4,13,14]). In 36% (n = 5) of the documents considered, mathematics was used as an auxiliary science; in 64% (n = 8) of the cases, it was not.
We have contrasted this with the view of authors of the investigated publications shown in Figure 9b. In distinguishing the necessity of mathematics and the necessity of mathematics from perspective, we proceeded analogously to the previous categories. In this perspective, mathematics is more often seen as an auxiliary discipline than used. For example, one author of the investigated publications attributed only the ability to calculate the resistance and the application of Ohm’s law to mathematic literacy in the whole unit shown in column three in Table 5 [39]. The purpose of the article was to develop a sequence for eighth grade and measure the effect on STEM literacy. Therefore, the authors divided the developed STEM literacy in the disciplines. Some disciplines are repeatedly presented because the developed STEM literacies are listed in chronological order.
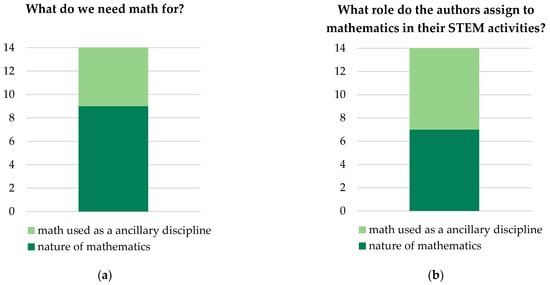
Figure 9.
(a) Necessity of mathematics; (b) Necessity of mathematics from the authors point of view.

Table 5.
Example of reducing mathematics as an auxiliary discipline. “Content summary of STEM learning worksheets”—column “Developed STEM Literacy” [20] (p. 81).
According to the authors, the outcome of the intervention showed no improvement in STEM literacy overall or across disciplines. An exception is the discipline of mathematics. As a result of this intervention, the mathematical literacy decreased clearly according to the test results. The author of the included paper reported that the n-gain score, i.e., the difference between pre- and post-test score of the students was −0.87 [39] (p. 92). This is a typical example for interventions that failed to improve mathematics achievement. According to Honey, Pearson, and Schweingruber [8], mathematics only as an auxiliary discipline can lead to problems in the development of students’ knowledge and skills in mathematics.
6. Discussion
This review study systematically investigated the current role of mathematics in STEM classrooms through analyzing 14 included papers. In the following section, we conclude with an implication about the role of mathematics from the results of the previous sections to answer the second research question. We then discuss the results and interpret them in the context of previous research and point to possible future research directions.
6.1. Conclusion on the Role of Mathematics
We now attempt to use the results of the subordinate questions to answer the second research question. First, we considered the question of access to STEM implementation. Here, it became clear that STEM is implemented primarily with the emphasis on one or two subjects, as shown in Figure 7a. This corresponds to a medium level of integration, as the subjects are not integrated equally.
In the division of the journal according to the subject focus, journals of the natural science disciplines were particularly strongly represented, which may have a different view of mathematics due to their subject background. This possibly leads to the fact that mathematics as a fully fledged subject is underrepresented.
The evaluation highlights the fact that mathematics is seen primarily as an auxiliary discipline, as shown in Figure 9b. This is consistent with previous research (e.g., [7]). Mathematics is often assigned as a purely utilitarian activity and the second part of the categories of competencies is almost overlooked. Thus, the mathematical concepts and procedures remain hidden underneath [14].
Considering mathematics in STEM with a real-world problem, one would expect modeling activities to be at the center, given Niss and Højgaard’s description of the categories [21]. Here, the translation from the real situation to the mathematical world has an important meaning. However, this was not assigned to mathematics but to other disciplines in the description of the authors of the included publications. Here, it is particularly noticeable that modeling activities were often completely attributed to the engineering discipline. With this view of mathematics, it is reasonable that mathematics might be seen as less important by teachers, students, and society [4].
Thus, the goal of integrated STEM education with equivalent disciplines has not been achieved because only small subsets of mathematics are seen. At the same time, the analysis shows what possibilities could arise for mathematics education if the units were slightly transformed.
To sum up, our study reveals that the role of mathematics has a low relevance especially from the authors’ perspective, although the activities are not attributed to mathematics. Thus, the perception of mathematics as an auxiliary discipline can be passed on to the students accordingly in this way and it may even be, as in the study by Yasin et al. [39], that mathematical literacy deteriorates in the intervention in the test result.
6.2. Connection to Related Work
Our results provide an initial indication of the current state of the role of mathematics in the STEM classroom. The assigned reduced relevance of mathematics in the included articles is consistent with the results of previous studies [1,7,17].
Our results, concerning parts of our first research question, revealed that less than half of the reviewed manuscripts provided information about their study design. This is consistent with the result of the systematic review of STEM education research of Kayan-Fadlelmula [2]. Methodological issues, for example the lack of comparative and longitudinal approaches, are also reflected in this overview. In particular, the lack of information on class size or grade level and methodology makes it difficult to reproduce the data.
The application of mathematics, especially in the eyes of science educators, is viewed as a minor matter and a means to an end. Concerning the theoretical frameworks, mathematical activities are mainly assigned to operative work, e.g., calculation of area and volume, whereas the category “Posing and answering questions in and by means of mathematics” [21] (p. 15) is not assigned to mathematics but primarily to the engineers. As criticized in previous research (e.g., [15]), not much is left to the students to decide what mathematical information is necessary to solve the problem. Niss and Højgaard emphasize in their work the importance of referring to the real situation in mathematical modeling, since in some cases mathematical ideas or expressions are stated or the modelling activity is assigned to the other disciplines, so that mathematics in the sense of modeling takes hardly place. This is particularly evident in the comparison of the described application areas of mathematics and the potential application areas of mathematics in Figure 8.
If mathematics is primarily perceived in a limited way as an operational activity, the consequence of viewing mathematics as an auxiliary science is also understandable and can be seen in our results, as shown in Figure 9. A possible implication of this finding is that changing perceptions, e.g., through awareness and education about the domain of mathematics activities, could be a possibility to strengthen the role of mathematics.
7. Implication and Limitations
The results of our systematic literature review are limited by several constraints. A first considerable limitation results from the data basis. Since we did not carry out a hand search, the databases are limiting, as only documents that were listed in the databases under our search terms were included. In our inclusion and exclusion criteria, we excluded articles from books and journals that were not included in Web of Science, ERIC, or Teacher Reference Center, which could have provided interesting contributions. In addition, papers that were excluded included many potentially interesting papers, especially those from the Spanish/Portuguese or German-speaking countries.
Furthermore, the limitation for mathematical classroom units with respect to evidence-based reporting in mainstream schools sometimes led to the low number of included documents and may have biased the results about the role of mathematics in STEM classrooms because we did not conduct any on-site research in schools.
Manual screening excluded more articles than it included, because they were related to extracurricular activities, so the fact that there was no implementation as a project may be surprising. Nevertheless, it is to be appreciated that STEM is to be integrated into regular teaching and the inhibitions may be greater to conduct this as a larger project. On a positive note, the amount of extracurricular engagement and educational opportunities shown in the STEM field are enabled, although these can only ever address a small portion and thus do not reflect the role of mathematics in the classroom. However, STEM should not be promoted primarily in the voluntary out-of-school sector but must be integrated into classrooms for holistic development. To advance STEM education, more evidence-based frameworks for regular classes are needed. However, in the analysis, we found many sequences that were only carried out outside of schools, e.g., in summer camps.
Another limitation is that we only included documents that related to secondary education. Therefore, our research primarily allows us to make conclusions about the secondary level. Additionally, there is no clear international distinction between elementary and lower secondary education, with elementary education covering year 1 to 4 or 1 to 6, which must be considered.
Clearly, the small number of documents must also be considered, since only these were used for the evaluation and the number possibly reduces the significance. Nevertheless, this small number is also an important result of our research, as it reveals a research gap in this area.
8. Conclusions
In this study concerning the role of mathematics in STEM classrooms, we were able to identify tentative first indications of M in STEM to consistently integrate M in STEM. As a conclusion of the systematic literature review, two main points can be elaborated. First, despite the large amount of data at the beginning of the analysis, we were only able to include less than one percent—14 documents that provide evidence-based and situational evidence of the role of mathematics in the STEM classroom. Second, in the eyes of science educators, mathematics is viewed as a minor matter and a means to an end. Here, mainly operative work is attributed to mathematics, e.g., calculation of area and volume, and the problem-solving part is assigned to the other disciplines.
To advance STEM education, more evidence-based frameworks for regular classes are needed. However, in the analysis, we found many sequences that were only carried out outside of school, e.g., in summer camps.
As a result, consistent with previous findings (e.g., [18]), we see a need to promote and fund research projects and develop educational programs and curricula that focus on STEM integration with equal consideration of the disciplines, especially mathematics.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/educsci12090629/s1, List of reviewed studies; Table S1: Coding scheme for study characteristics and research methodologies of the studies reviewed; Table S2: Coding scheme for educational settings and approaches; Table S3: Coding scheme for the application of mathematics; Table S4: Sample coding.
Author Contributions
Conceptualization, methodology, J.J. and H.-S.S.; formal analysis, J.J.; data curation, J.J.; writing—original draft preparation, J.J. and H.-S.S.; writing—review and editing, J.J. and H.-S.S.; supervision, H.-S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article or Supplementary Materials. The data presented in this study are available in the Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maass, K.; Geiger, V.; Ariza, M.R.; Goos, M. The Role of Mathematics in interdisciplinary STEM education. ZDM Math. Educ. 2019, 51, 869–884. [Google Scholar] [CrossRef]
- Kayan-Fadlelmula, F.; Sellami, A.; Abdelkader, N.; Umer, S. A systematic review of STEM education research in the GCC countries: Trends, gaps and barriers. Int. J. STEM Educ. 2022, 9, 2. [Google Scholar] [CrossRef]
- Ortiz-Revilla, J.; Adúriz-Bravo, A.; Greca, I.M. A Framework for Epistemological Discussion on Integrated STEM Education. Sci. Educ. 2020, 29, 857–880. [Google Scholar] [CrossRef]
- Maass, K.; Engeln, K. Professional development on connections to the world of work in mathematics and science education. ZDM Math. Educ. 2019, 51, 967–978. [Google Scholar] [CrossRef]
- Ruediger, W.C. The Principles of Education; Houghton, Mifflin: Oxford, UK, 1910. [Google Scholar]
- Bell, D. The reality of STEM education, design and technology teachers’ perceptions: A phenomenographic study. Int. J. Technol. Des. Educ. 2016, 26, 61–79. [Google Scholar] [CrossRef]
- English, L.D. STEM education K-12: Perspectives on integration. Int. J. STEM Educ. 2016, 3, 3. [Google Scholar] [CrossRef]
- Honey, M.; Pearson, G.; Schweingruber, H. (Eds.) STEM Integration in K-12 Education: Status, Prospects, and an Agenda for Research; The National Academies Press: Washington, DC, USA, 2014. [Google Scholar]
- Moore, T.J.; Johnson, C.C.; Glancy, W.A. A Synthesis of Conceptual Frameworks and Definitions. In Handbook of Research on STEM Education; Johnson, C.C., Mohr-Schroeder, M.J., Moore, T.J., English, L.D., Eds.; Routledge: London, UK, 2020; pp. 3–16. ISBN 9780429021381. [Google Scholar]
- Hobbs, L.; Clark, J.C.; Plant, B. Successful Students—STEM Program: Teacher Learning Through a Multifaceted Vision for STEM Education. In STEM Education in the Junior Secondary; Jorgensen, R., Larkin, K., Eds.; Springer: Singapore, 2018; pp. 133–168. ISBN 978-981-10-5447-1. [Google Scholar]
- Dugger, W.E. Evolution of STEM in the United States (Paper). In Proceedings of the 6th International Conference on Technology Education Research, Gold Coast, QLD, Australia, 8–11 December 2010. [Google Scholar]
- Kennedy, T.; Odell, M. Engaging Students In STEM Education. Sci. Educ. Int. 2014, 2014, 246–258. [Google Scholar]
- Williams, J.; Wake, G. Black boxes in workplace mathematics. Educ. Stud. Math. 2007, 64, 317–343. [Google Scholar] [CrossRef]
- Straesser, R. Didactics of mathematics: More than mathematics and school! ZDM Math. Educ. 2007, 39, 165–171. [Google Scholar] [CrossRef]
- Gravemeijer, K.; Stephan, M.; Julie, C.; Lin, F.-L.; Ohtani, M. What Mathematics Education May Prepare Students for the Society of the Future? Int. J. Sci. Math. Educ. 2017, 15, 105–123. [Google Scholar] [CrossRef]
- Marco-Bujosa, L. Prospective Secondary Math Teachers Encountering STEM in a Methods Course: When Math is More Than “Just Math”. IJTE 2021, 4, 247–286. [Google Scholar] [CrossRef]
- Fitzallen, N. STEM Education: What Does Mathematics Have to Offer? In Mathematics Education in the Margins, Proceedings of the 38th Annual Conference of the Mathematics Education Research Group of Australasia, Sunshine Coast, QLD, Australia, 28 June–2 July 2015; Marshman, M., Geiger, V., Bennison, A., Eds.; Mathematics Education Research Group of Australasia: Sydney, Australia, 2015; pp. 237–244. [Google Scholar]
- Stohlmann, M. A vision for future work to focus on the “M” in integrated STEM. Sch. Sci. Math. 2018, 118, 310–319. [Google Scholar] [CrossRef]
- Kilpatrick, J. Competency Frameworks in Mathematics Education. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 85–87. ISBN 978-94-007-4977-1. [Google Scholar]
- PISA 2018 Mathematics Framework. PISA 2018 Assessment and Analytical Framework; OECD: Paris, France, 2019; pp. 73–95. ISBN 9789264940314. [Google Scholar]
- Niss, M.; Højgaard, T. Mathematical competencies revisited. Educ. Stud. Math. 2019, 102, 9–28. [Google Scholar] [CrossRef]
- Stohlmann, M. Three modes of STEM integration for middle school mathematics teachers. Sch. Sci. Math. 2019, 119, 287–296. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef] [PubMed]
- Rethlefsen, M.L.; Kirtley, S.; Waffenschmidt, S.; Ayala, A.P.; Moher, D.; Page, M.J.; Koffel, J.B. PRISMA-S: An extension to the PRISMA Statement for Reporting Literature Searches in Systematic Reviews. Syst. Rev. 2021, 10, 39. [Google Scholar] [CrossRef]
- Cevikbas, M.; Kaiser, G.; Schukajlow, S. A systematic literature review of the current discussion on mathematical modelling competencies: State-of-the-art developments in conceptualizing, measuring, and fostering. Educ. Stud. Math. 2022, 109, 205–236. [Google Scholar] [CrossRef]
- Bautista, N.; Diekman, A.; Fuesting, M. Why Not STEM? Communal experiences motivate students to pursue STEM careers. Sci. Teach. 2018, 86, 46–52. Available online: https://www.jstor.org/stable/26611966 (accessed on 16 August 2022).
- Chuasontia, I.; Sirirat, T. Designing an instructional module to teach light diffraction by a grating to secondary students applying a STEM-integrated approach. Phys. Educ. 2021, 56, 45011. [Google Scholar] [CrossRef]
- Daman Huri, N.H.; Karpudewan, M. Evaluating the effectiveness of Integrated STEM-lab activities in improving secondary school students’ understanding of electrolysis. Chem. Educ. Res. Pract. 2019, 20, 495–508. [Google Scholar] [CrossRef]
- Dasgupta, C.; Magana, A.J.; Vieira, C. Investigating the affordances of a CAD enabled learning environment for promoting integrated STEM learning. Comput. Educ. 2019, 129, 122–142. [Google Scholar] [CrossRef]
- Sönmez, D.; Özgün-Koca, S.A. Integrated Biology & Mathematics Activity to Investigate Photosynthesis & Linear Relationships. Am. Biol. Teach. 2020, 82, 488–493. [Google Scholar] [CrossRef]
- Goovaerts, L.; de Cock, M.; Struyven, K.; Dehaene, W. Developing a Module to Teach Thermodynamics in an Integrated Way to 16 Year Old Pupils. Eur. J. STEM Educ. 2019, 4. [Google Scholar] [CrossRef]
- Hacıoğlu, Y.; Dönmez Usta, N. Digital game design-based STEM activity: Biodiversity example. Sci. Act. 2020, 57, 1–15. [Google Scholar] [CrossRef]
- Khozali, N.B.; Karpudewan, M. An Interdisciplinary Facebook Incorporated STEM Education Strategy in Teaching and Learning of Dynamic Ecosystems. Eurasia J. Math. Sci. Technol. Educ. 2020, 16, em1902. [Google Scholar] [CrossRef]
- Lawrimore, C.; Surber, E. Graph It Out! Create Graphing Manipulatives to Explore Evolutionary Selection: A Lesson for High School Biology Students. Proc. Interdiscip. STEM Teach. Learn. Conf. 2018, 2. [Google Scholar] [CrossRef][Green Version]
- Ng, O.-L.; Chan, T. Learning as Making: Using 3D computer-aided design to enhance the learning of shape and space in STEM-integrated ways. Br. J. Educ. Technol. 2019, 50, 294–308. [Google Scholar] [CrossRef]
- Pérez, A.; Braaten, B.; MacConnell, R. Closing the Circuit on Function Concepts. Math. Teach. 2019, 112, 366–373. [Google Scholar] [CrossRef]
- Wan, A.; Ivy, J. It’s a Wrap: A New Dimension for Sinusoids. Math. Teach. 2021, 114, 473–476. [Google Scholar] [CrossRef]
- Wang, L.; Chiang, F.-K. Integrating novel engineering strategies into STEM education: APP design and an assessment of engineering-related attitudes. Br. J. Educ. Technol. 2020, 51, 1938–1959. [Google Scholar] [CrossRef]
- Yasin, A.I.; Prima, E.C.; Sholihin, H. Learning Electricity using Arduino-Android based Game to Improve STEM Literacy. J. Sci. Learn. 2018, 1, 77. [Google Scholar] [CrossRef]
- Mayring, P. Qualitative Content Analysis. Forum Qualitative Sozialforschung/Forum: Qualitative Social Research. Qual. Methods Var. Discip. I Psychol. 2000, 1. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).